劉瑤

(陜西師范大學數(shù)學與信息科學學院,陜西 西安 710119)

1 引言

考慮定義在L2[0,a]上的四組Sturm-Liouville問題:D-D問題

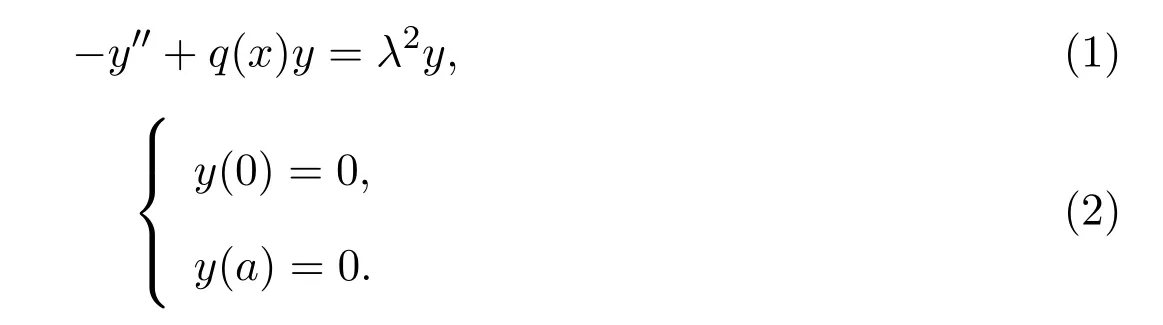
R-D問題

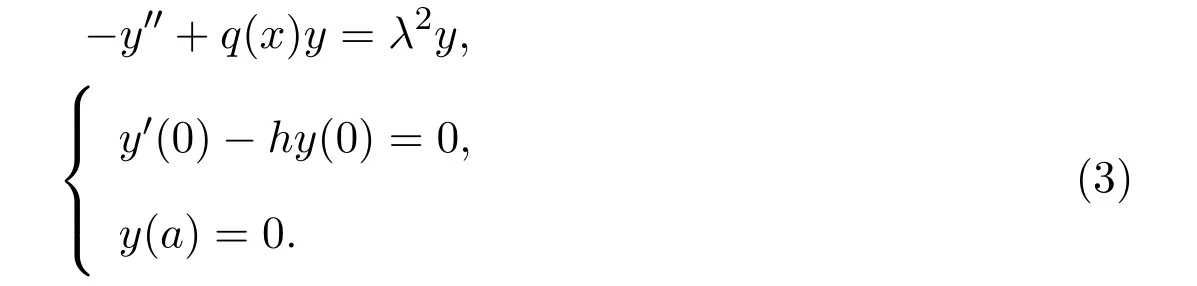
D-R問題

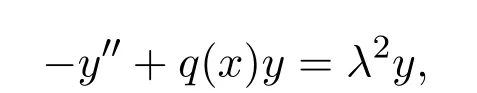
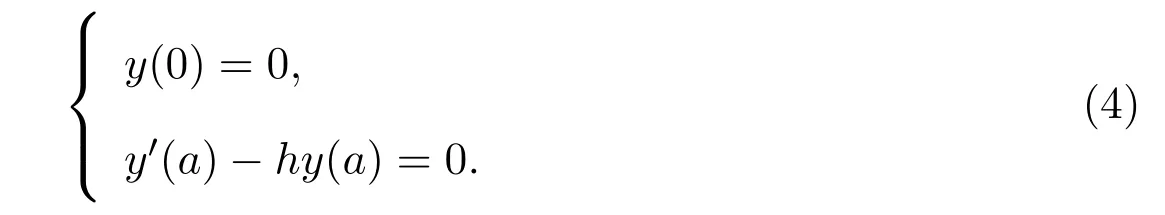
R-R問題

其譜分別記作

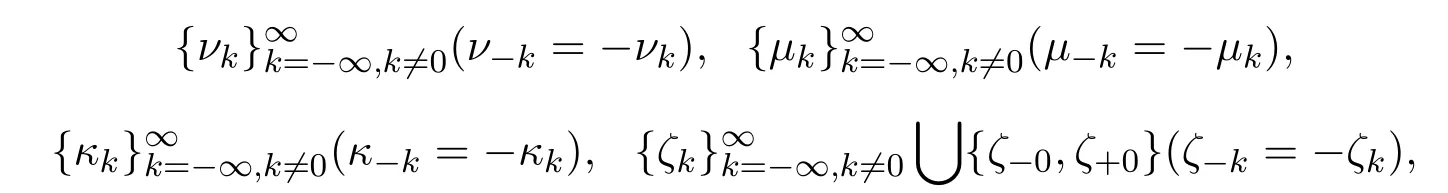
其中q(x)∈L2[0,a]為實值函數(shù),h∈R為一固定的常數(shù),由文獻[1-2]可知它的譜是簡單的無界的.

Sturm-Liouville算子的逆問題,特別是關于勢函數(shù)q(x)的唯一確定性問題,長期以來受到數(shù)學和物理學界的關注,并產(chǎn)生了許多的研究成果.Brog[3]于1946年首先提出并證明了通過兩組特征值可得到Sturm-Liouville微分算子勢函數(shù)q(x)的唯一確定性.Levitan[3]和Marchenko[3]分別證明了一組特征值及其對應的規(guī)范常數(shù)同樣能唯一確定勢函數(shù)q(x).如果邊界條件中的常數(shù)是給定的,那么重構(gòu)勢函數(shù)就不需要完整的兩組特征值,這一問題有時稱為”缺少特征值問題”,即通過部分特征值唯一確定未知區(qū)間的勢函數(shù)(見文獻[4-5]).

文獻[2]證明了四組譜定理,即對于給定的兩組數(shù)列,在一定條件下可劃分為四組數(shù)列,使其分別成為D-D,D-N,N-D,N-N四個Sturm-Liouvile問題的部分特征值,最后通過四組譜的部分特征值唯一確定了整區(qū)間上的勢函數(shù)q(x).同樣的方法也在文獻[6-7]中用于解決相關的反問題.

本文的目的在于,將Neumann邊界條件推廣到Robin邊界條件,上述結(jié)論依然成立.換言之,將給定的兩組數(shù)列在一定條件下劃分成三組數(shù)列,使其分別成為D-D,R-D,R-R三個Sturm-Liouville問題的部分特征值,并通過三組譜的部分特征值唯一確定區(qū)間[0,a]上的的勢函數(shù)q(x),再由Gelfand-Levitan方程給出區(qū)間[0,a]上勢函數(shù)q(x)的重構(gòu)公式.

2 預備知識

首先給出四組Sturm-Liouville問題的特征函數(shù)和特征值的漸近式,為本文結(jié)論的證明提供必要的準備.

定義φi(x,λ)(i=1,2)為(1)的解,分別滿足下列初始條件

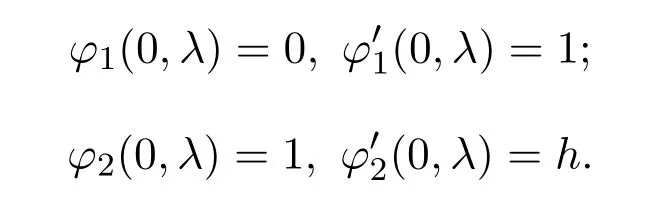
根據(jù)文獻[8-11]可得

利用分部積分法則有

對上述兩式求導

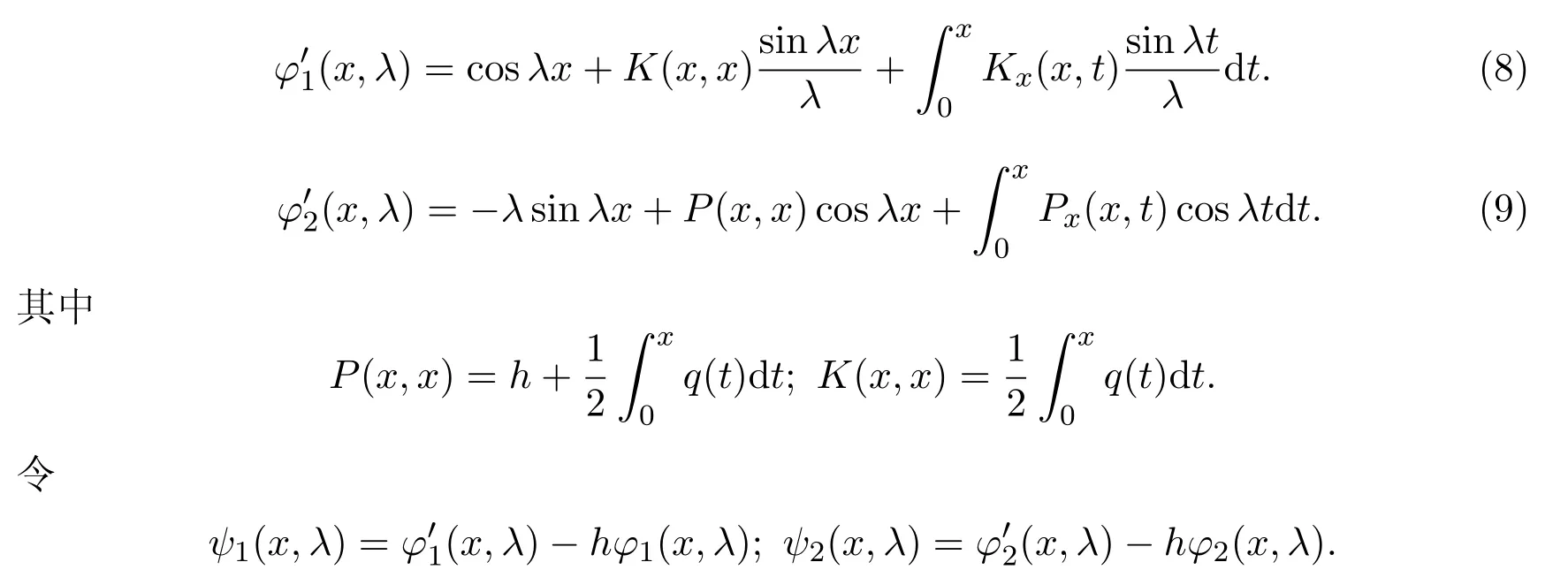
由 (6)式-(9)式可得

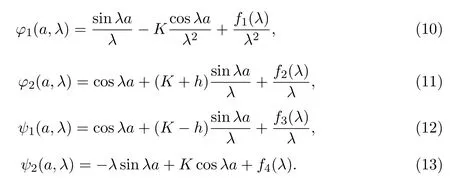
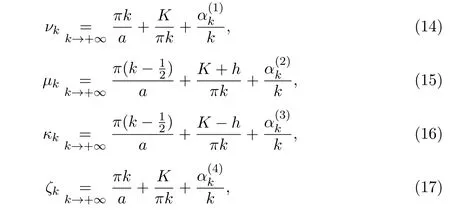
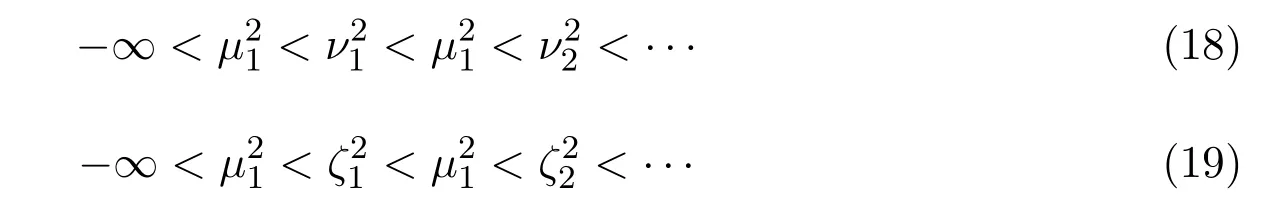
令ω(λ)=φ1(x,λ)ψ2(x,λ)?ψ1(x,λ)φ2(x,λ),由文獻 [12-13]可知ω(λ) 與x無關,且恒等于?1.

定義 2.1[14]若函數(shù)f(x)滿足以下三個條件

(i)指數(shù)階為a的整函數(shù);

(ii)函數(shù)的所有零點是單重的;

(iii)若存在正數(shù)L,M以及p>0,則

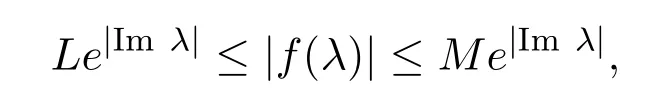
其中|Imλ|≥p,則稱f(x)為sine型函數(shù).

3 主要結(jié)論及其證明

本節(jié)給出主要結(jié)論,即通過將給定的兩組數(shù)列劃分為三組數(shù)列,使其分別為D-D,R-D,R-R三個Sturm-Liouville問題的部分特征值,由三組部分特征值唯一確定區(qū)間上[0,a]的勢函數(shù)q(x),最后通過Gelfand-Levitan方程給出區(qū)間[0,a]上勢函數(shù)q(x)的重構(gòu)公式.

定理 3.1設三組數(shù)列滿足,且有如下的交替性

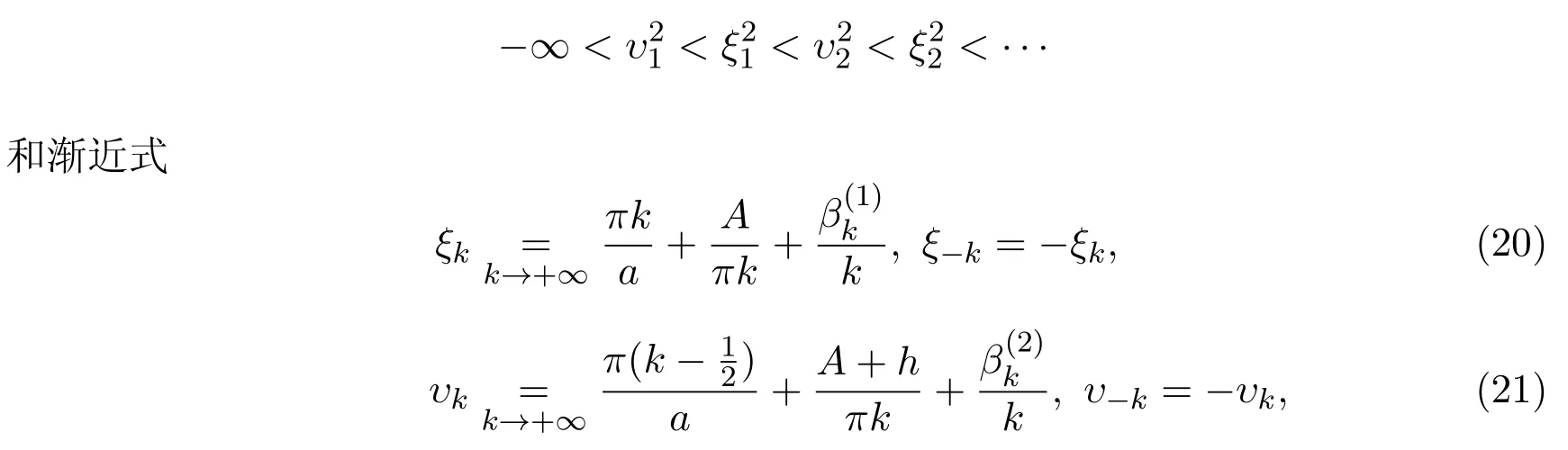
這里{rj}j∈A1?N,{sj}j∈A2?N為自然數(shù)數(shù)列,滿足,A是實常數(shù),則存在唯一勢函數(shù)q(x)∈L2[0,a],使得{νrj},{μk}和{ζsj}分別是問題 (1),(2),(1),(3)和 (1),(5)的特征值.

證明由 Borg兩組譜定理 (見文獻 [1])可知滿足交替性和漸近式,則存在唯一的勢函數(shù)(x)∈L2[0,a],使得分別是問題(1),問題(2)和問題(1),問題(3)的特征值,現(xiàn)在需要找到由(x)生成的問題(1),問題(4)和問題(1),問題(5)的特征值.

由文獻[10]可得

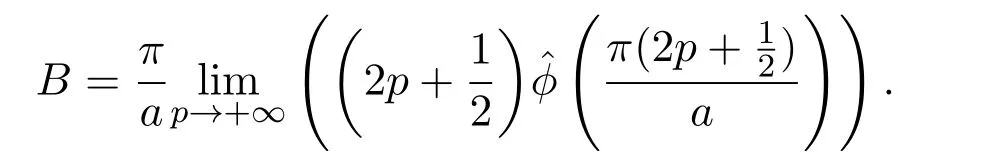
這里定義A=B?h.由構(gòu)造函數(shù)

由 sine型函數(shù)定義知λω(λ)是sine型函數(shù),由文獻 [10]則有

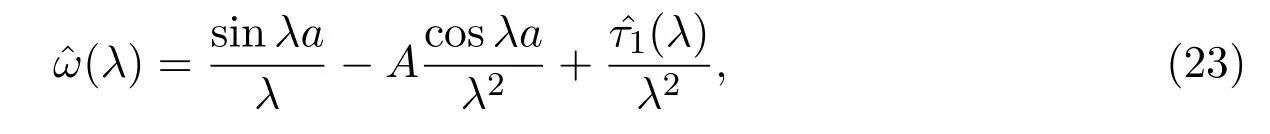
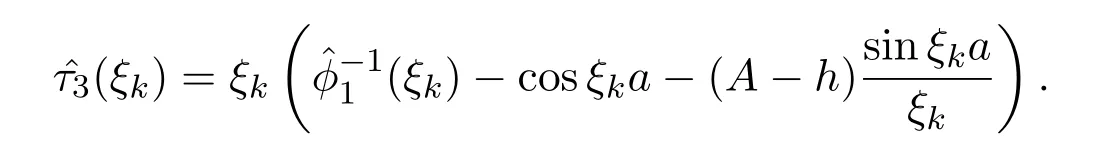
為節(jié)點處的函數(shù)值,結(jié)合(22)式有

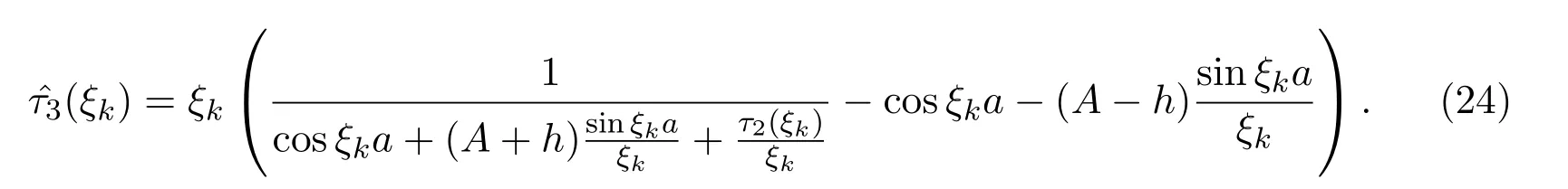
結(jié)合(20)式,利用三角函數(shù)的泰勒展式有

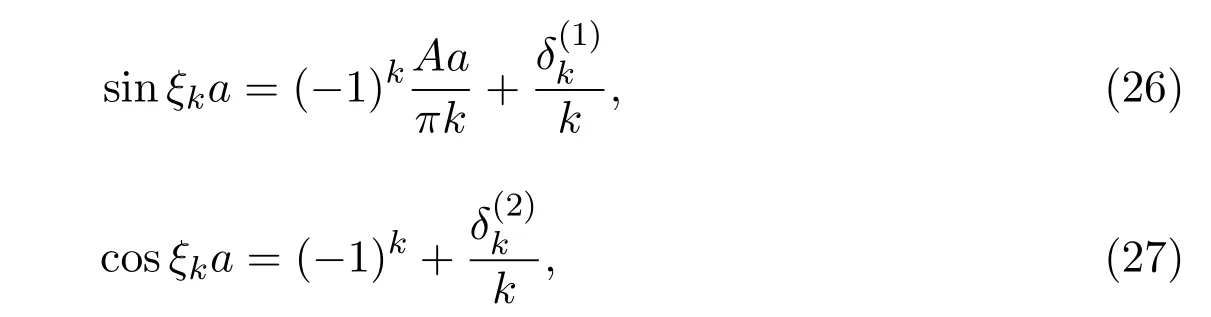
因此,由文獻[14]中的定理A(也可見文獻[15])可得上式的拉格朗日插值級數(shù)為

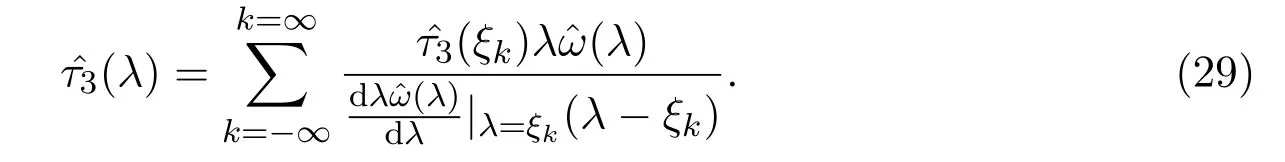
上式右邊的級數(shù)在復平面C的任一緊子集上一致收斂,按實數(shù)λ的L2(?∞,+∞)的范數(shù)收斂于一個屬于La的函數(shù).根據(jù)文獻[14]構(gòu)造的是下面插值問題的唯一解:給定插值節(jié)點和節(jié)點處的函數(shù)值,構(gòu)造函數(shù).令

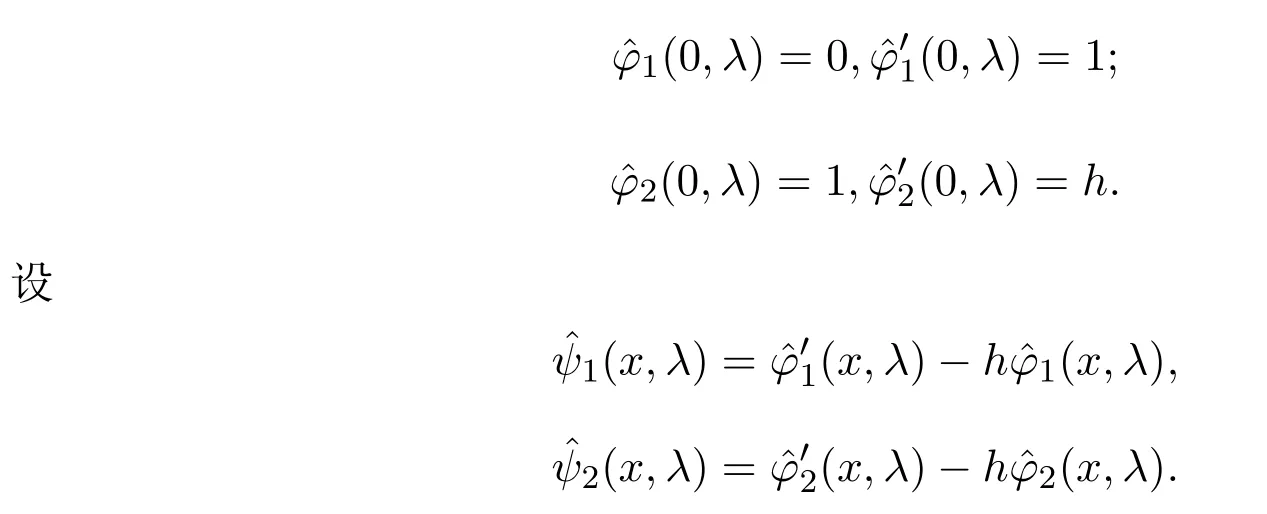
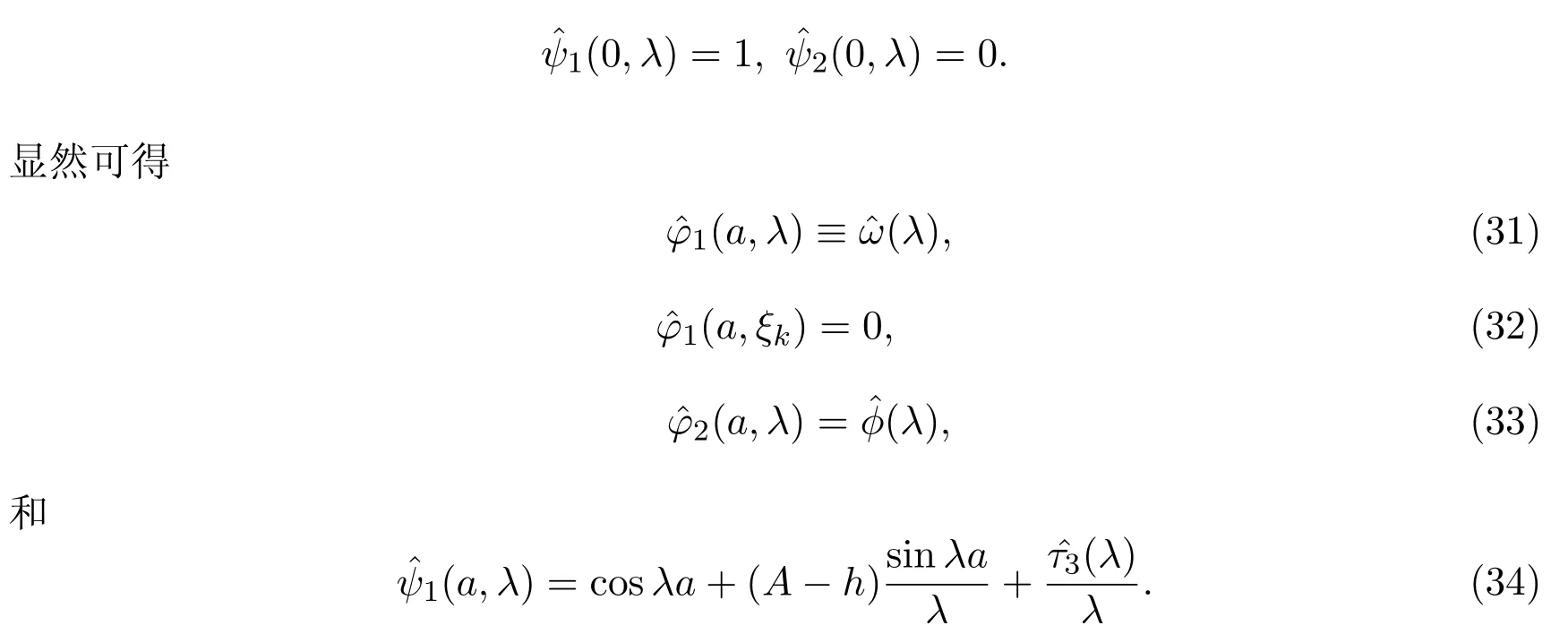
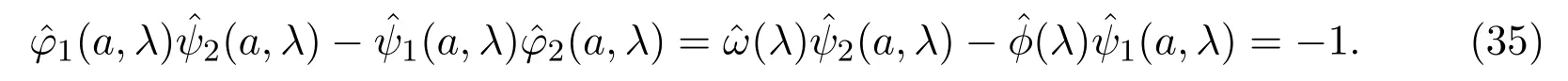
結(jié)合(32)式可得

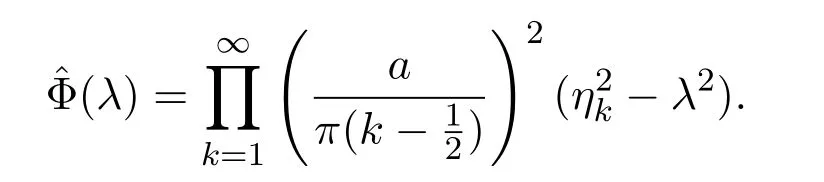
結(jié)合(16)式

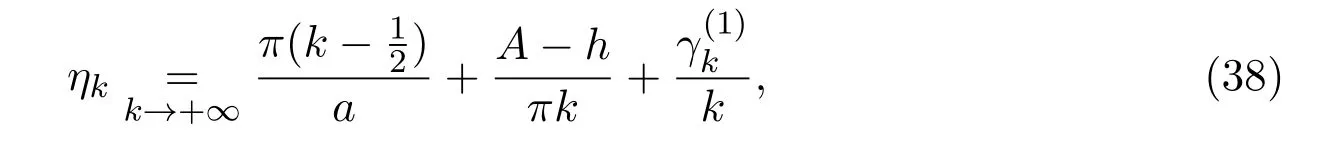
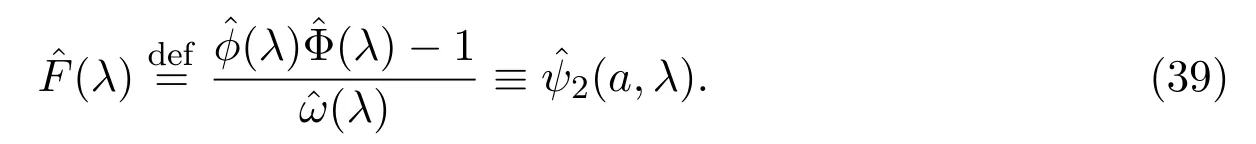
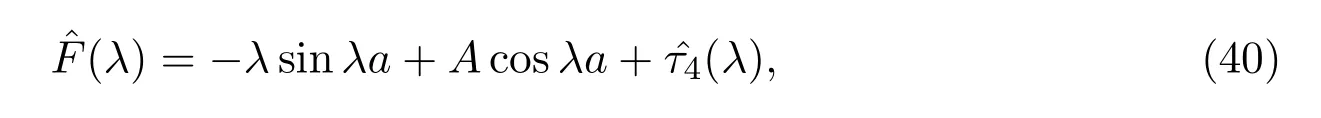
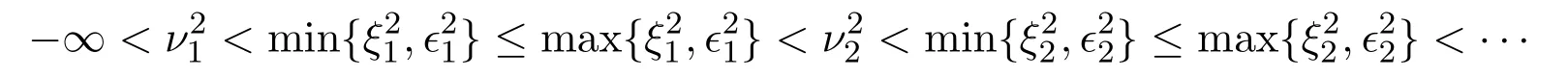
按照如下的形式劃分數(shù)列中的元素

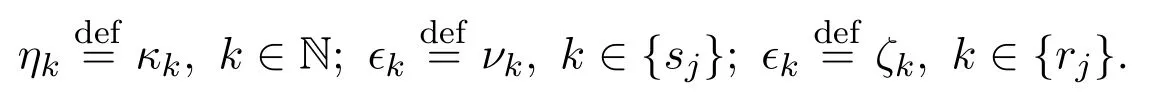
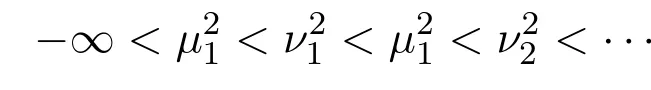
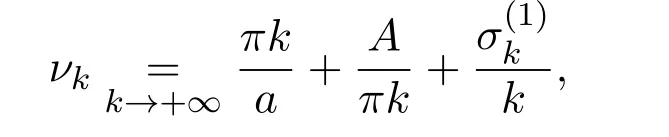
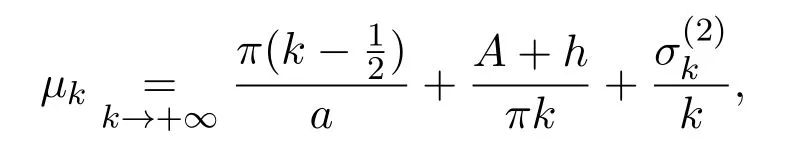
令

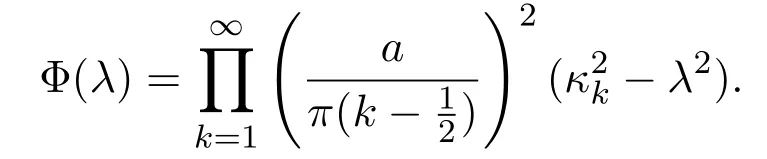
由文獻 [10]可知ω(λ),?(λ),Φ(λ)的表達式為

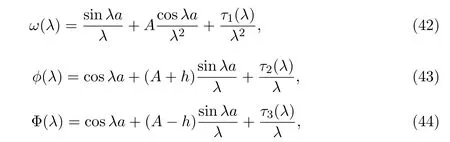
其中τi∈La,i=1,2,3.如果φi(x,λ),i=1,2是方程 (1)的解,那么φ1(a,λ)=ω(λ),φ2(a,λ)=?(λ),ψ1(a,λ)=Φ(λ),這表明φ1(a,νk)=0,k∈{rj},φ2(a,μk)=0,k∈N和ψ1(a,κk)=0,k∈N,接下來需要證明ψ2(a,ζk)=0,k∈{sj}.令

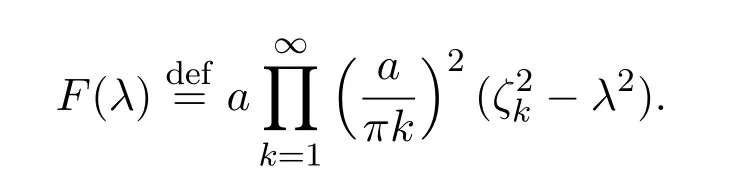
由文獻[10]可知表達式為

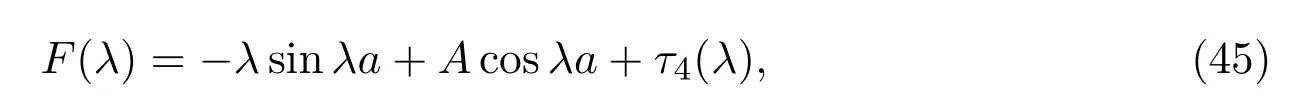
其中τ4∈La.從定義可得,這表明ω(λ)F(λ)的零點集和(λ)(λ)的零點集相同.由(23)式,(39)式,(42)式和(45)式則有

通過定義可知

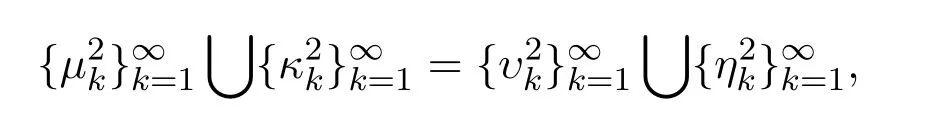
即?(λ)Φ(λ)的零點集和(λ)(λ)的零點集相同.結(jié)合(22)式,(30)式,(43)式和(44)式可得

將 (37)式和 (39)式代入(35)式,結(jié)合(46)式-(47)式得到

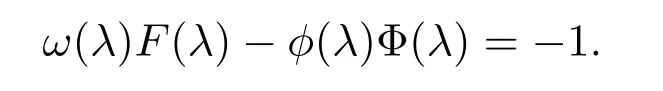
另一方面,由于

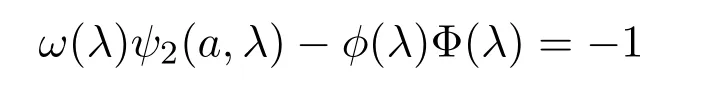
有唯一解,則有F(λ)≡ ψ2(a,λ),從而ψ2(a,ζk)=0,k∈{sj}.定理證畢.

下面給出勢函數(shù)q(x)的重構(gòu)方法(文獻[1]),概括如下:

(b)由αk=?(νk)?(νk),其中,計算可得αk.

(c)通過{αk,μk}k≥0構(gòu)造函數(shù)

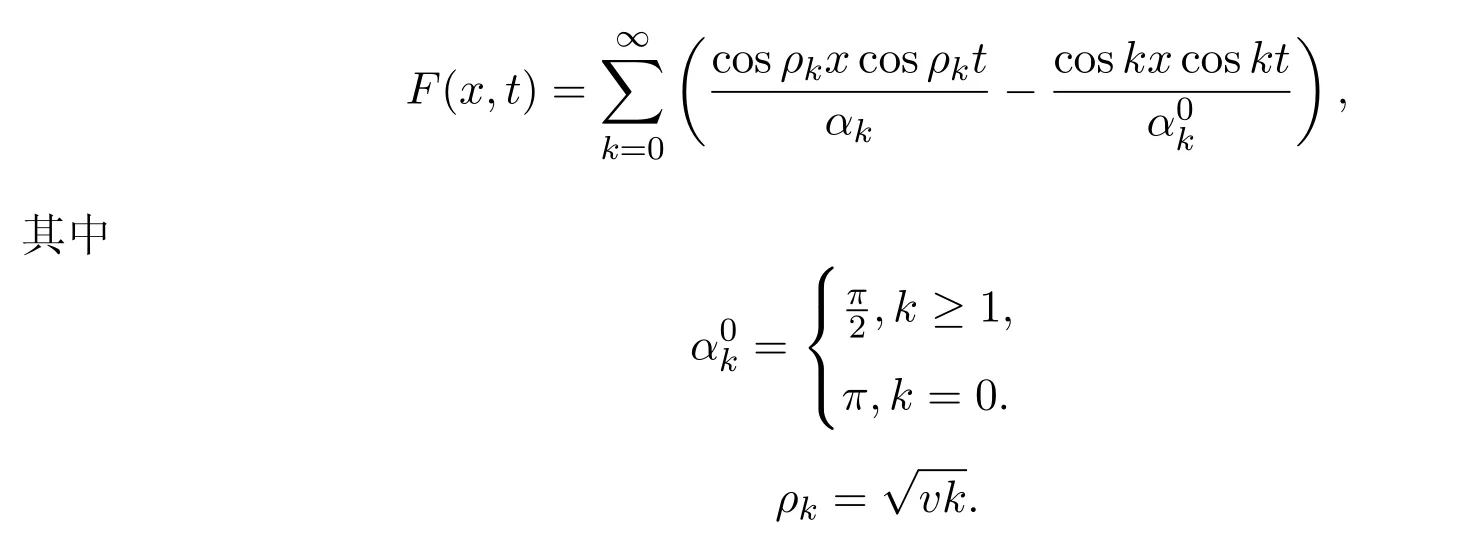
(d)解Gelfand-Levitan方程

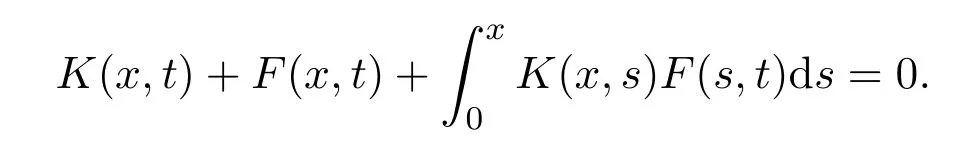
注意到上式是一個Fredholm積分型方程,因此有唯一解K(x,t),從而

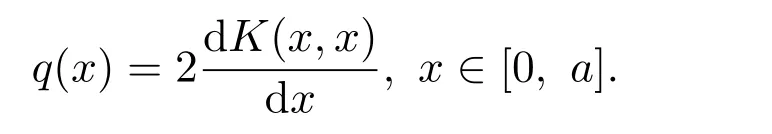
致謝:導師魏廣生教授對本文作了重要指導,提出了寶貴意見,作者在此表示衷心感謝.