Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
Payam Sadeghi Shabestari, Zahra Rostami, Viet-Thanh Pham,Fawaz E.Alsaadi, and Tasawar Hayat
1Biomedical Engineering Department,Amirkabir University of Technology,Tehran 15875-4413,Iran
2Nonlinear Systems and Applications,Faculty of Electrical and Electronics Engineering,Ton Duc Thang University,Ho Chi Minh City,Vietnam
3Department of Information Technology,Faculty of Computing and IT,King Abdulaziz University,Jeddah,Saudi Arabia
4Department of Mathematics,Quaid-I-Azam University 45320,Islamabad 44000,Pakistan
5NAAM Research Group,King Abdulaziz University,Jeddah,Saudi Arabia
Abstract Parkinson’s and Huntington’s diseases are two of the most common neurodegenerative disorders.Tremor,muscle stiffness,and slowness of movement are symptoms of Parkinson’s disease.The symptoms of Huntington’s disease are severe reduction in muscle control,emotional disturbance,and pathological disorders in brain cells.These diseases are caused by destruction of the cells that secrete a substance called dopamine.In this paper,a new discrete chaotic system is introduced,which can mimic the brain’s behavior for neurodegenerative diseases such as Parkinson,Huntington,and Hypokinesia.This system is described based on the similarity between the brain’s behavior in normal and abnormal conditions and the chaotic systems.Bifurcation analysis is carried out with respect to different parameters,providing full spectrum of the behavior for different parameter values.Our results can be used to mathematically study the mechanisms behind these diseases.
Key words: neurodegenerative diseases,Parkinson,Huntington,Hypokinesia,chaos,bifurcation
1 Introduction
Parkinson’s Disease (PD) is a neurodegenerative disease that often begins with trembling in one of the hands,sluggishness and muscle stiffness progressing throughout the body.It often occurs in old people,however some young individuals are also diagnosed with PD.[1?2]The neurodynamic dysfunction and destruction of the interactions between different parts of the nervous system,as well as communications within the neuromuscular system have been recognized in patients with Parkinson’s disease.[3?4]This disease occurs due to destruction of cells that secrete a neurotransmitter called dopamine,which is the active ingredient that regulates the movement.Increasing the ratio of acetylcholine to dopamine in the cerebral arteries leads to symptoms such as tremor,muscle stiffness,and slowness of movement.PD can be caused by the use of drugs such as phenothiazines (PTZ),brain damage,tumors,post-infectious encephalitis,infection with slow-growing viruses or possibly carbon monoxide poisoning.[5?6]Currently,laboratory tests,such as blood tests,are not available to diagnose PD.Diagnosis is usually based on physical examination accompanied by neurological examination and brain scans.
Huntington’s disease(HD),as another neurodegenerative disease,is a hereditary disease,which results in neurological degeneration and leads to motor neuron,cognitive and psychiatric disorders,and finally evolves to loss of autonomy and death.This disease occurs in adults aged between 35 and 50 years.The progression of the disease follows extremely different forms from one individual to another.The statistical studies evoke an average duration of about 20 years since the onset of motor symptoms to the most advanced stages,which involve severe motor and cognitive impairments.The clinical signs of this disease are of three types including motor,cognitive,and psychiatric.[7?8]As a neurological and psychiatric symptom,Hypokinesia is a lighter form of akinesia,that is to say“l(fā)ess moving”as opposed to“not moving”.Hypokinesia is one of the main symptoms of Parkinson’s syndrome and is a result of a disorder of the extrapyramidal system.In addition,it occurs in depression or schizophrenia.Hypokinesia also occurs as a side effect of neuroleptics.It is not to be confused with the bradykinesia in which not the frequency of movement but the speed is reduced.[9?10]
Generally,biological nervous system can present various modes of electrical activities that can produce particular patterns[11?13]to support specific functions and behaviors in both health and disease.[14?16]In order to detect these patterns,the analysis of the EEG signals has been considered frequently.[17]Some studies highlight differences in EEG signals for healthy persons and patients with neural diseases,such as the differences of synchronization in the EEG signals for these patient as compared to healthy subjects,[17?18]or lower alpha band connectivity and lower dominant frequency in these patients rather than healthy people,[19]etc.
In this manuscript,we introduce an analysis based on chaotic systems to model PD and HD.Chaos is a common feature that can occur in dynamical systems.There are several evidences indicating that many biological systems,especially human brain behaves in both chaotic and periodic manner.[20?24]Freemanet al.showed that the brain’s function always switches between different states.These alternations are because of abnormality or disorders.[25]Figure 1 displays the phase portrait of electroencephalogram(EEG)signals obtained from a rat in normal and abnormal situations,[26]supporting chaotic behavior of brain functions.Providing a useful tool for scrutinizing and better understanding of biological systems,chaotic models have been frequently used in research studies to analyze and model biological systems.[27?28]

Fig.1 (Color online)(a)Phase portrait of EEG signal taken from a rat in abnormal situation.(b)Phase portrait of EEG signal taken from a rat in normal situation.These figures are taken from Ref.[14].
From the dynamical view,external stimulus or alteration of intrinsic parameters can generate different responses and thus,different electrical patterns in the nervous system.On the other hand,chaotic systems are known to be capable of presenting multiple modes in oscillation.Therefore,chaotic models can be useful means to mimic the nervous system.In this study,a new chaotic map is proposed in order to mimic brain’s behavior in both normal and abnormal situations.The model is based on physiological interactions between thalamus,cortex,and basal ganglia.Results indicate that this model can be used to study the complex mechanisms behind neurodegenerative diseases.
2 Physiological Background
Basal ganglia comprises Striatum (caudate nucleus putamen),Globus pallidus,subthalamic nucleus,and substantia nigra.Globus pallidus is further divided into two distinct parts including the internal (or GPi) and the external (or GPe) segments.[29]Substantial nigra is also divided into two parts including SNc(substantia nigra compacta) and SNr (substantia nigra reticulate).All these components form the neural circuit of basal ganglia.[29?30]The input of Basal Ganglia is provided by cortex,providing the excitatory input for the striatum,which,in turn,acts as a gateway for basal ganglia.[31]Basal ganglia also provides input for the thalamus,which connects basal ganglia to the cortex.Scientists have found two major pathways from striatum to GPi/SNr.[29]These two pathways are known as direct and indirect pathways.In the indirect pathway,the neurons projecting from striatum inhibit the external segment of the Globus pallidus.The indirect pathway goes to striatum,GPe,STN and collectively GPi/SNr.Neurons from GPe inhibit STN,which has excitatory production to GPi/SNr that itself has tonic inhibition to thalamus.In sum the indirect pathway starts with striatum,which inhibits GPe,[29?31]and the net result of the inhibition and excitation processes are inhibition of the thalamus.[32?33]
Unlike the indirect pathway,the net result of the direct pathway is to reduce inhibition of thalamus.Eventually,the opposing effects of both pathways are regulated by SNc whose productions are the neurotransmitters called dopamine.[34]Thalamic neurons make excitatory projections on the cortex.Because SNC cells producing dopamine are progressively lost in PD patients,little dopamine is produced.Since dopamine increases the activity of direct pathway,the inhibition activity of direct pathway decreases in PD.However,the reverse occurs in HD,which means that the striatum inhibitory neurons in indirect pathways are damaged causing the lack of inhibition in neural circuit.[31,33]In summary,PD symptoms include loss of ability to keep and initiate movements,whereas HD is lack of inhibition against movements.[2,35]
3 Proposed Chaos-Based Model
In this section,a new mathematical model is proposed to mimic and predict the brain’s behavior in normal and abnormal situations associated with PD and HD.Our aim is to model neural circuit of cortex,basal ganglia,and thalamus.To this end,we used the model proposed by Baghdadiet al.[20]to model the Cortex.In this model,hyperbolic tangent function is used to mimic neurons activation function and Positive and negative signs model excitation and inhibition of neurons,respectively.According to physiological background discussed in previous section,we propose a neural network for Basal ganglia.This network comprises two direct and indirect paths in Basal ganglia.In the indirect path,G(x) indicates the Globus pallidus(GPe),which is modeled by hyperbolic tangent function.S1,S2,andS3are the synaptic weights that can be regulated by dopamine release.E(x) andI(x) are neurons activation functions which are modeled by hyperbolic tangent function.[20]ParametersS1,S2,andS3are all positive and the minus sign indicates inhibition function of the synapses.The input for Striatum comes from the Cortex and the output of SNr/GPi goes to thalamus.The overall model of the Brain (Cortex-Basal ganglia-Thalamus) can be seen in Fig.2.We assume that the input of Basal ganglia (or output of the Cortex) isx(n) and the output of Basal ganglia (or input of the Thalamus) isy(n).Therefore,the mathematical model is formulated as follows and its presented in Fig.3.
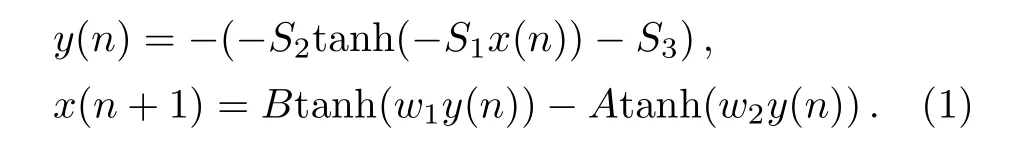

Fig.2 (Color online) The aggregate Brain model (Cortex-Basal ganglia-Thalamus) based on the proposed chaos-based model.

Fig.3 (Color online)Schematic of the proposed model.
4 Results and Discussion
In this section the dynamical properties of the model are scrutinized.The behavior of the proposed model is investigated for different values of parameters.There are a number of parameters in the proposed system whose values are essential to change its behavior.The bifurcation diagrams are plotted by changing one parameter while other parameters are fixed.The values of these parameters are same as Ref.[20] Computer simulations are performed by taking the parameters as follows:
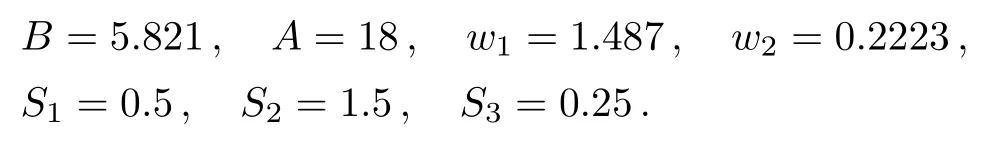
As mentioned in Sec.2,in PD the cells producing dopamine die off,and as a result,dopamine release reduces and the inhibition activity of direct pathway decreases.Considering the brain’s behavior and the proposed model,we anticipate that as parameterS3diminishes,the system switches from periodic behavior to chaotic behavior.In the previous studies[22,28]on biological systems,it is noted that the chaotic behavior is a signature of the existence of disorder in the system.The results represented in Fig.4 concur with these expectations while it can be seen that as parameterS3decreases the system exits from periodic region and enters into chaotic region.The period doubling route to chaos is observable in the system’s bifurcation diagram with respect to parameterS3.
In HD,the striatum inhibitory neurons in the indirect pathways are damaged leading to lack of the inhibitory activity of Basal ganglia’s indirect path.Considering the proposed model,HD occurs when parameterS1is sufficiently low,therefore we expect that if parameterS1decreases,the system should act chaotically.Accordingly,Fig.5 demonstrates that as the number of damaged neurons increases (i.e.parameterS1decreases) system starts to act in a chaotic manner.Although some small periodic windows exist in the wide chaotic region,finding the exact values of the parameters in which the system switches between chaotic behavior and periodic behavior is not the aim of this study.However,it can be noticed that even a small change in system’s parameters results in remarkable alteration of the system’s behavior.
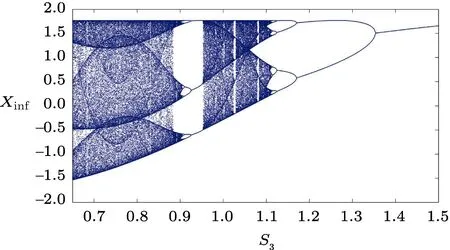
Fig.4 (Color online) Bifurcation diagram of the proposed model with respect to different values of parameter S3.

Fig.5 (Color online) Bifurcation diagram of the proposed model with respect to different values of parameter S1.
The thalamic neurons make excitatory projection on the cortex.It means that the more neurotransmitters release in the indirect pathway,which is responsible for the inhibition of the thalamus,the less thalamus excitation on the cortex is available.Thus,the motor movement,also known as Hypokinetic state,is reduced.[30?34]From modeling perspective,Hypokinetic occurs when the parameterS2is high enough.Therefore,as shown in Fig.6,it can be argued that as the absolute value of parameterS2increases,the system switches from periodic state(healthy) to chaotic state (Hypokinetic).For better displaying of different dynamic behaviors of System(1),twodimensional bifurcation diagrams of System(1)are shown in Fig.7.Regions denoting the periodic,chaotic and stable (fixed point) behaviors are shown in blue,green,and red,respectively.Figure 7 shows the distribution of fixed point and periodic region (normal condition) in two separated chaotic regions (abnormal condition).With help of Fig.7 inS1–S2andS1–S3parameter spaces,the relationships between different bifurcation processes can be constructed.
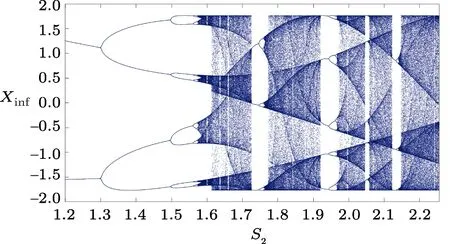
Fig.6 (Color online) Bifurcation diagram of the proposed model with respect to different values of parameter S2.
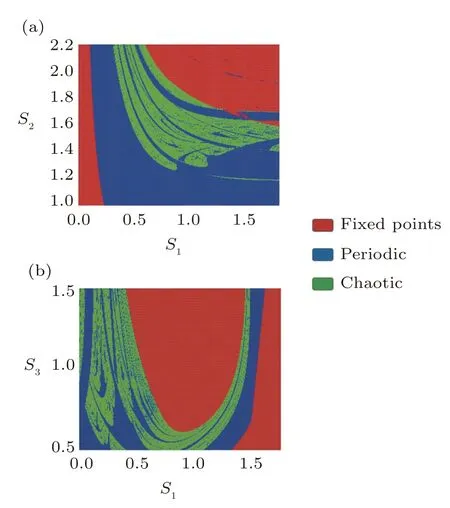
Fig.7 (Color online) Two-dimensional bifurcation diagram of system (1).For (a) the S1–S2 space with the fixed value of S3=0.25,and (b) the S1–S3 space with the fixed value of S2 =1.5.
5 Conclusion
In order to mimic the human brain behavior and better understanding of brain diseases,such as Parkinson,Huntington,and Hypokinesia,a new discrete mathematical model was proposed in this manuscript.This model is based on previous mathematical model of the Cortex and the interactions between the Cortex,Basal Ganglia,and Thalamus in the human brain.The dynamical properties of the model were investigated in different sets of parameters.We have also investigated the dynamics of the proposed system by one-dimensional and two-dimensional bifurcation diagrams by varying the control parameters.
We could explain three kinds of neurodegenerative diseases by changing the value of parameters in the proposed model.First,the occurrence of Huntington’s disease(HD)was explained.In HD,the striatum inhibitory neurons are damaged,so that the inhibitory activity of indirect path of Basal ganglia is reduced.This was in line with the reduction of parameterS1in model.Second,we showed how our model can explain Hypokinesia.The more neurotransmitters release in the indirect pathway of Basal ganglia,which is responsible for the inhibition of the thalamus,cause less thalamus excitation on the cortex called Hypokinesia state.In the model,this was in line with increase of the parameterS2.Finally,Parkinson’s Disease(PD)was explained through proposed model.In PD,dopamine release reduces and the inhibition activity of direct pathway in Basal ganglia decreases.From modeling perspective,it was in alignment with decrease of parameterS3.
We showed that by changing the values of parameters,system exhibits various behaviors.We also demonstrated that when system acts in chaotic manner it is sign of PD,HD or Hipokinesia.According to correspondence between the brain behavior and chaos theory,it was shown that the represented model is capable of simulating changes of brain’s behavior in some neurodegenerative diseases.
 Communications in Theoretical Physics2019年10期
Communications in Theoretical Physics2019年10期
- Communications in Theoretical Physics的其它文章
- Mapping Between Charge-Dyon and Position-Dependent Mass Systems?
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property?
- Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
- Gravitational Deflection of Massive Particles by a Schwarzschild Black Hole in Radiation Gauge?
