Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
U.S.Okorie,A.N.Ikot, G.J.Rampho, and R.Sever
1Department of Physics,AkwaIbom State University,IkotAkpaden,Uyo.Nigeria
2Department of Physics,University of Port Harcourt,Choba,Nigeria
3Department of Physics,University of South Africa,Florida Park 1710,South Africa
4Department of Physics,Middle East Technical University,06800,Ankara,Turkey
Abstract We discuss the thermodynamic properties of a modified Rosen-Morse potential using the q-deformed superstatistics approaches.We obtain the partition function with the help of the generalized Boltzmann factor from the modified Dirac delta distribution and uniform distribution.Other thermodynamic function is obtained for the superstatistics of the two distributions considered.We also discuss our results graphically and obtain the ordinary statistical quantities when the deformation parameter tends to zero.
Key words: superstatistics,partition function,thermodynamic function
1 Introduction
Studies of various interaction potential models became the focus of many researchers after Morse[1]proposed a three parameter empirical potential for diatomic molecules.This development significantly added value to quantum mechanics,with application in physics and chemistry especially in areas of molecular spectroscopy and dynamics.Since then,many researchers have remodeled this potential by developing different potentials with more parameters.The new models include Rosen-Morse potential,[2]Manning-Rosen potential,[3]and may others.[4?12]Modified and improved versions of the abovementioned potentials have been studied.[13?17]This has made practical applications possible in areas like calculation of thermodynamic properties,[18?21]determination of rotation-vibrational levels for diatomic molecules,[22?26]and many others.[27?30]
As an extension to thermodynamic studies,Beck and Cohen[31]initiated the concept of superstatistics where non-equilibrium systems with complex dynamics in stationary states were considered.Due to the large fluctuations observed and its statistical properties,they obtained different effective statistical mechanical descriptions.Superstatistics is defined as a superposition of two different statistics that describe non-equilibrium systems with a stationary state and parameter fluctuations.[32]In nonequilibrium statistical mechanics,βis not an inverse temperature,thus being seen as a random variable,but regarded as a constant parameter in the case of equilibrium statistical mechanics.[33]
Many investigates have been conducted on the concept of superstatistics both in the equilibrium and nonequilibrium statistical mechanics regime.[34?39]Most recently,Sobhaniet al.[40]studied the effects of cosmicstring framework on the thermodynamic properties of anharmonic oscillator,within the confinement of the ordinary statistics and theq-deformed superstatistics approaches.In another development,q-deformed superstatistics of the Schrodinger equation in the commutative and non-commutative spaces with magnetic field was studied by Sargolzaeiporet al.[41]In the relativistic regime of quantum mechanics,the superstatistics of the Klein-Gordon equation in deformed formalism for modified Dirac delta distribution was studied.[42]A deeper understanding of superstatistic of systems involving long range interactions is required,hence further investigations into thermodynamics of such systems are still necessary.The aim of this work is to extend the studies carried out by Dong and Cruz-Irison[43]on thermodynamic properties of a modified Rosen-Morse potential to the superstatistics regime.These results may be useful to studies of thermal fluctuations in atomic and molecular systems involving long range interactions.
2 Modified Rosen-Morse Potential
Different versions of Rosen-Morse potential have been proposed over the years to describe inter-atomic interactions in diatomic molecules.It begun in 1932 with Rosen and Morse[2]who proposed a potential model of the form
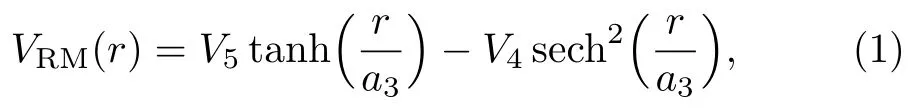
whereViare potential strength parameters anda3the potential range parameter.This potential is able to describe diatomic and poly-atomic molecules.In an effort to provide a more realistic potential energy model,Zhanget al.[14]modified the Rosen-Morse potential by considering effects of inner-shell radii of the two constituent atoms in diatomic molecules.The resulting modified Rosen-Morse potential is of the form
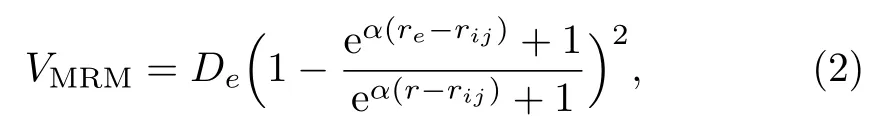
whereDeis the dissociation energy,rethe bond length andHererijis related to the inner-shell radii of the two atoms,Ka dimensionless constant andkethe equilibrium harmonic vibrational force constant.In Ref.[14] the authors established that the modified Rosen-Morse potential (2) is superior to the Morse and conventional Rosen-Morse potentials in fitting experimental data for diatomic molecules.
In another development,Sunet al.[44]studied the deformed modified Rosen-Morse potential function proposed by Egrifeset al.[45]
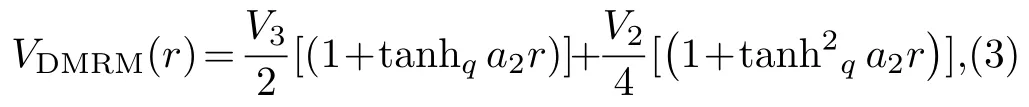
where tanhq xrepresents a deformed hyperbolic tangent function andqis the deformation parameter.From hereonViandajrepresent potential strength and range parameters,respectively,unless otherwise indicated.By applying the explicit parameters of equilibrium bond length and dissociation energy,Sunet al.[44]obtained an improved modified Rosen-Morse potential model of the form
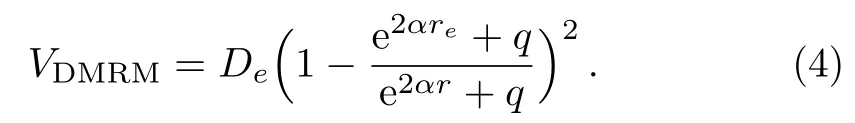
It was discovered that the improved expression for the deformed modified Rosen-Morse potential model is defined in terms of four independent parameters.The energy spectra of the modified Rosen-Morse potential have been obtained by different authors using various methods.[46?50]
Dong and Cruz-Irrison[43]studied a modified Rosen-Morse potential of the form[51]
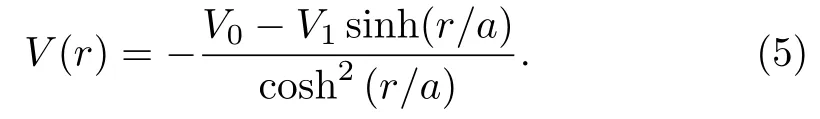
The authors applied the proper quantization rule to obtain the energy spectrum of the modified Rosen-Morse potential of Eq.(5) to be
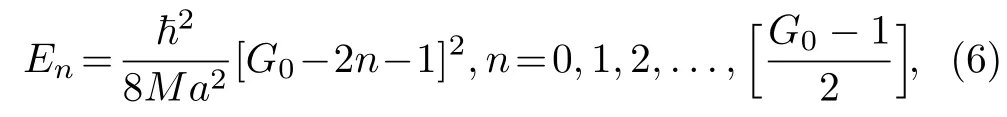
where [f] means the largest integer less thanf,and
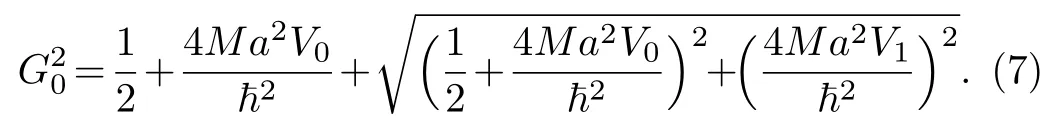
Thermodynamic properties of this potential (5) were also determined in ordinary statistics.We determine the thermodynamic quantities of this potential in superstatistics,in the next sections.
A number of superstatistics models,based on different generalizations of the Boltzmann factor,exit.[31]Beck and Cohen[31]also proved that all these models display a universal behaviour at low energies or low fluctuations.Hence,in this paper we focus only on the modified Dirac delta and the uniform distribution superstatistics,which are particular models of superstatistics.
3 Thermodynamic Functions for Modified Dirac Delta Distribution
In statistical mechanics,the Boltzmann factorBo(E)=exp(?β E),whereβ=1/(kBT) withkBas the Boltzmann constant andTtemperature,is an essential tool used to determine thermodynamic quantities such as the partition functionZ(β),free energyF(β),mean energyU(β),entropyS(β),and specific heat capacityC(β),for a given system.The thermodynamic quantities are obtained from the partition function as[52?53]
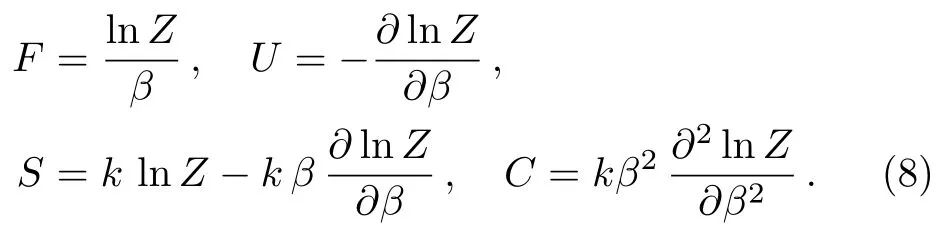
In superstatistics,the Boltzmann factor is averaged in the form

wheref(β′,β) is a probability density distribution of the random parameterβ′around the meanβ.In ordinary statistics,the probability density is defined by the Dirac delta function,f(β′,β)=δ(β′?β).[31]
Inq-deformed superstatistics,the probability density is modified to a more general form[41]

whereciare constants determined by requiringf(β′,β)to conform to certain physical conditions.[58]Such conditions lead to the values
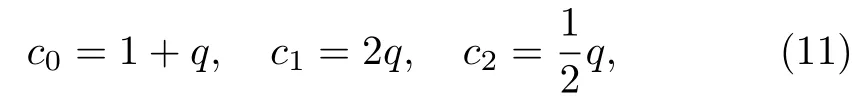
for the constants,whereqis a deformation parameter.The generalized Boltzmann factor for this distribution has the form
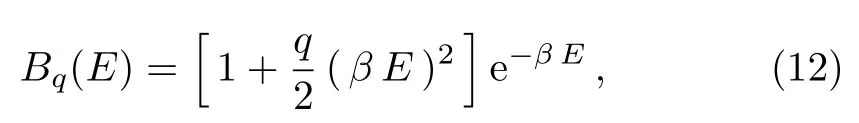
which reduces to the Boltzmann factor forq=0.Theq-deformed superstatistics reduce to ordinary statistical mechanics whenq →0.[54?56]
The partition functionZqinq-deformed superstatistics for the modified Rosen-Morse potential (5) is given by
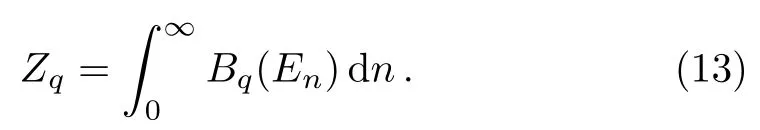
Using Eq.(11)withEnis given by Eq.(6),the integral evaluates to
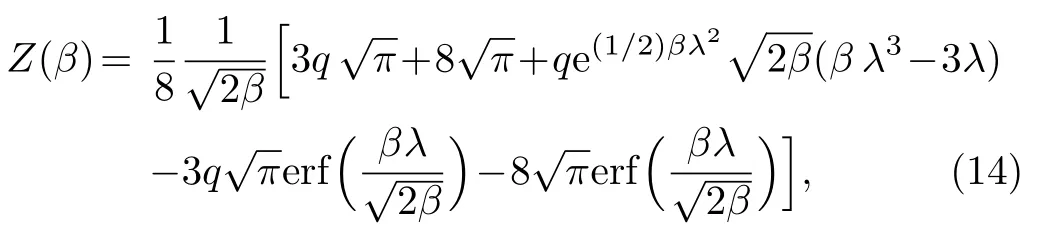
whereλ=(G0?1)/2 and we have adopted the natural units h=M=a=1.
4 Thermodynamic Functions for Uniform Distribution
A uniform distributionf(β) of a parameterβ >0 on an interval [a,a+b] is defined by[57]
andf(β)=0 elsewhere.This distribution has a meanβ0=a+b/2 and variance.The superstatistics of the uniform distribution is derived from the generalized Boltzmann factor[58]
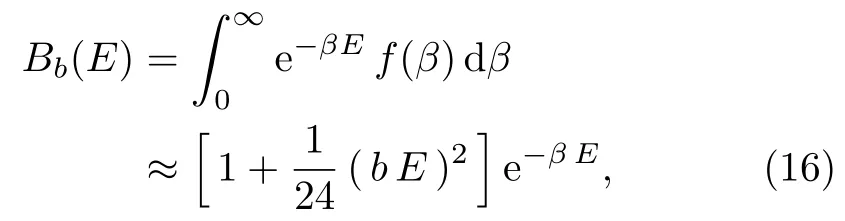
where the effective Boltzmann factor (16) follows from low energy reduction of the generalized Boltzmann factor.The superstatistics of the uniform distribution reduces to ordinary statistics whenb →0.
The partition functionZbin the uniform distribution superstatistics for the modified Rosen-Morse potential is given by
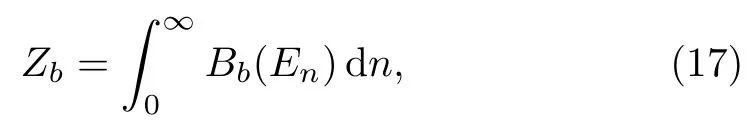
withEngiven by Eq.(6).Evaluating the integral leads to
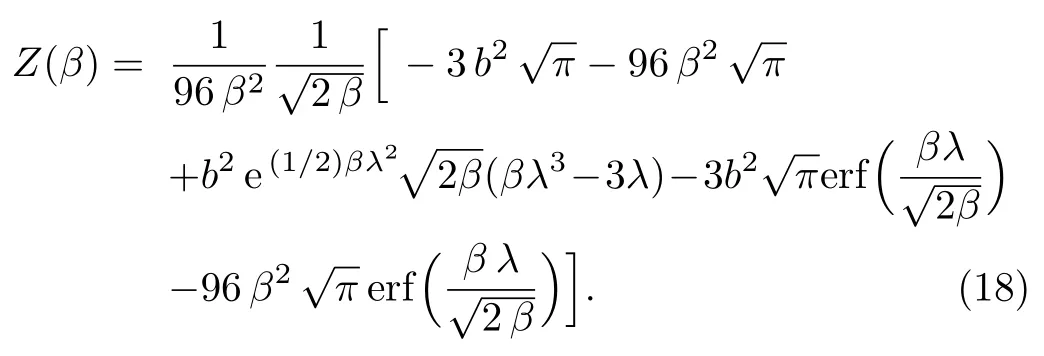
Thermodynamic functions of the modified Rosen-Morse potential using uniform distribution superstatistics can also be obtained using relations given in Eq.(12).
5 Results and Discussion
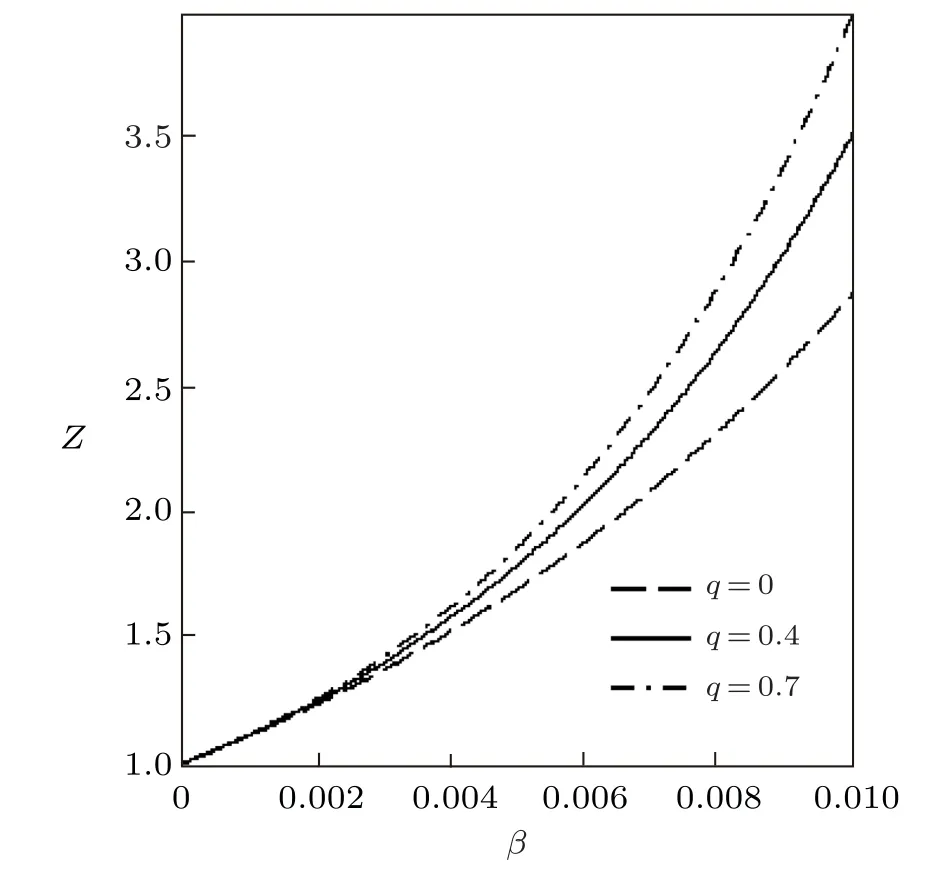
Fig.1 Partition function vs. β for different deformation paramters,with the modified Dirac delta distribution.
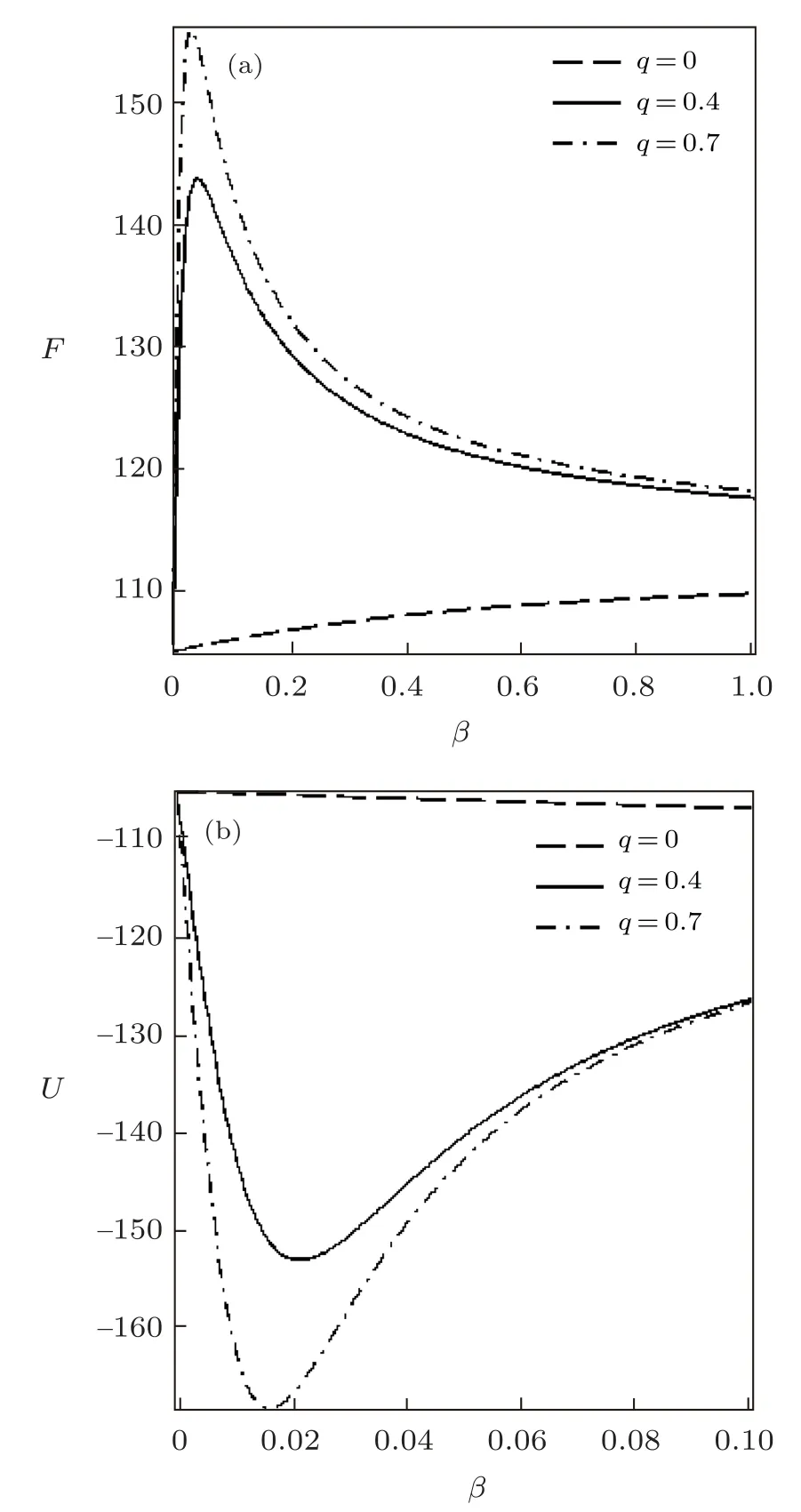
Fig.2 Free energy vs. β (a) and Mean energy vs. β (b),for different deformation paramters,with the modified Dirac delta distribution.

Fig.3 Entropy vs. β (a) and Specific heat capacity vs. β(b),for different deformation paramters,with the modified Dirac delta distribution.
The variation of the thermodynamic functions withβfor the modified Dirac delta distribution are shown in Figs.1?3.In these figures,we have consideredλ=15.The partition functionZis plotted in Fig.1 in terms ofβfor various deformation parameters.It is seen thatZincreases monotonically with increasingβandq.Figure 2 shows the free energy and mean energy variation withβfor different deformation parameters.In the absence ofq,the free energy increases slowly with increase in temperature parameter.Also,there is a sharp increase in the free energy asq >0,for increasingβ.As the temperature parameter continues to increase,the free energy drops and later increases slowly.The inverse behaviour of the free energy is observed for the mean energy.Figure 3 shows the behavior of the entropy and specific heat capacity asβvaries at different deformation parameters.Here,there is a slow decrease in entropy asβincreases whenq=0.Whenq >0,the entropySdeceases first and then increases sharply for increasingβ.A reverse behaviour is observed for specific heat capacity,whereCincreases and later decreases deeply for increasingβin the presence of the deformation parameters.In the absence of the deformation parameterq,Cincreases slowly with increasingβ.
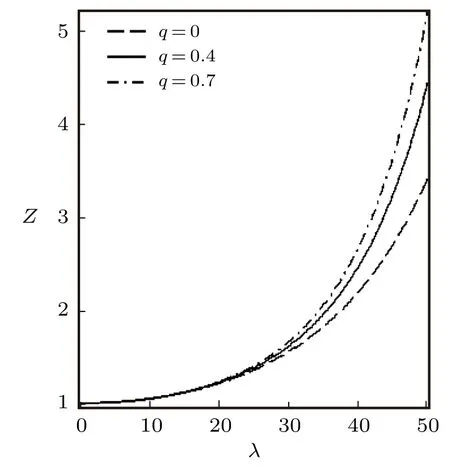
Fig.4 Partition function vs. λ for different deformation paramters,with the modified Dirac delta distribution.
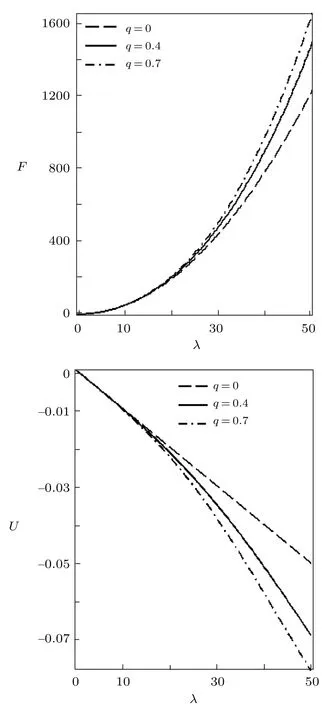
Fig.5 Free energy vs. λ (a) and Mean energy vs. λ (b),for different deformation paramters,with the modified Dirac delta distribution.
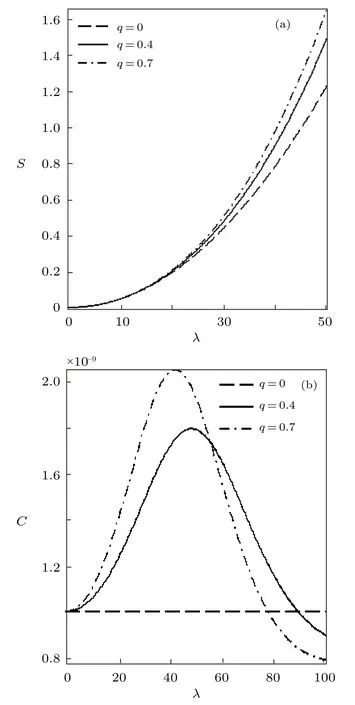
Fig.6 Entropy vs. λ (a) and Specific heat capacity vs. λ(b),for different deformation paramters,with the modified Dirac delta distribution.
We have also plotted the variation of different thermodynamic functions withλatβ=0.01 using the modified Dirac delta distribution,in the absence and presence of deformation parameters as shown in Figs.4?6.We see from these figure that all the thermodynamic functions follow an orderly trend asλincreases in the absence and presence of the deformation parameter,except for the specific heat capacity.In Fig.6,the specific heat capacity decreases very slightly for increasingλ,in the absence of the deformation parameter.But in the presence of the deformation parameter,Cincreases tangibly and later decreases for increasingλ.
Using the effective Boltzmann factor of the uniform distribution,the partition function variation withβfor different deformation parameterb,and other thermodynamic functions,are shown in Figs.7?9.The thermodynamic functions variation withλfor different deformation parameter with uniform distribution are shown in Figs.10?12.The variations of the thermodynamic functions display a similar trend as in the case of the modified Dirac delta distribution.This is expected because of the universal behaviour of superstatistics models at low energies.
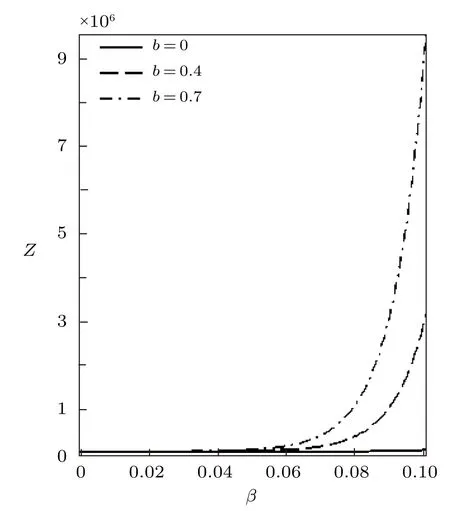
Fig.7 Partition function vs. β for different deformation paramters,with the uniform distribution.

Fig.8 Free energy vs. β (a) and Mean energy vs. β (b),for different deformation paramters,with the uniform distribution.

Fig.9 Entropy vs. β (a) and Specific heat capacity vs. β(b),for different deformation paramters,with the uniform distribution.
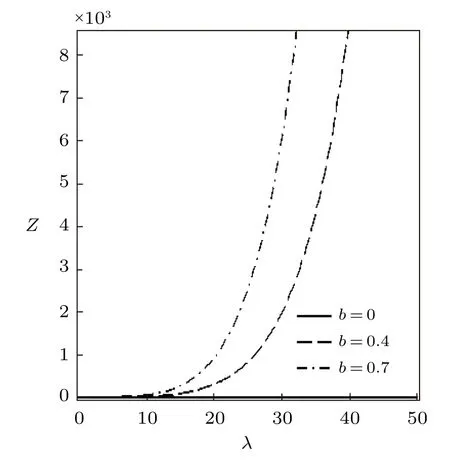
Fig.10 Partition function vs. λ for different deformation paramters,with the uniform distribution.

Fig.11 Free energy vs. λ (a) and Mean energy vs. λ(b),for different deformation paramters,with the uniform distribution.

Fig.12 Entropy vs. λ (a) and Specific heat capacity vs.λ (b),for different deformation paramters,with the uniform distribution.
6 Concluding Remarks
In this study,the energy spectra obtained for modified Rosen-Morse potential have been adopted to calculate the partition function,with the help of the generalized Boltzmann factor for both modified Dirac delta distribution and uniform distribution.Other thermodynamic functions such as free energyF,mean energyU,entropyS,and specific heat capacityChave been obtained using these superstatistics approaches.The variations of these thermodynamic functions withβandλin the absence and presence of the deformation parameters have been displayed graphically and discussed extensively.Specifically,interesting manifestations are obtained in the presence of the deformation parameter for uniform distribution.Also,our results agree with the ordinary statistics in the absence of the deformation parameter (q=b=0) using both superstatistical approaches.
 Communications in Theoretical Physics2019年10期
Communications in Theoretical Physics2019年10期
- Communications in Theoretical Physics的其它文章
- Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
- Gravitational Deflection of Massive Particles by a Schwarzschild Black Hole in Radiation Gauge?
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Background Dynamics of Pre-inflationary Scenario in Brans-Dicke Loop Quantum Cosmology?
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property?
