Cristhian Mendoza, Márcio Muniz de Farias

a Department of Civil Engineering, Universidad Nacional de Colombia Sede Manizales, Manizales, Colombia

b Department of Civil and Environmental Engineering, University of Brasília, Brasília, DF, Brazil

Abstract Structure is an evident determinant for macroscopic behaviors of soils. However, this is not taken into account in most constitutive models, as structure is a rather complex issue in models. For this, it is important to develop and implement simple models that can reflect this important aspect of soil behavior. This paper tried to model structured soils based on well-established concepts, such as critical state and sub-loading. Critical state is the core of the classic Cam Clay model. The sub-loading concept implies adoption of an inner (sub-loading) yield surface, according to specific hardening rules for some internal strain-like state variables.Nakai and co-workers proposed such internal variables for controlling density()and structure(),using a modified stress space,called tij.Herein,similar variables are used in the context of the better-known invariants(p and q)of the Cam Clay model.This change requires explicit adoption of a non-associated flow rule for the sub-loading surface.This is accomplished by modifying the dilatancy ratio of the Cam Clay model,as a function of the new internal variables.These modifications are described and implemented under three-dimensional (3D) conditions. The model is then applied to simulating laboratory tests under different stress paths and the results are compared to experiments reported for different types of structured soils. The good agreements show the capacity and potential of the proposed model.

2020 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Keywords:Elastoplasticity Cam clay with sub-loading Structured soil Tropical soil Non-associated flow rule

1. Introduction

Qualitative and quantitative understandings of loads and settlements in structured soils are important to determine the type and dimensions of geotechnical structures. Unfortunately, some models popularly used in geotechnical engineering practices do not include the characteristics of natural soils with structure (e.g.Graham and Houlsby, 1983; Wroth and Houlsby, 1985; Hayano et al., 2000; Cardoso, 2002; Díaz-Rodríguez, 2003; Caicedo et al.,2018). On the other hand, researches by Burland (1990), Leroueil and Vaughan (1990), Nova and Lagioia (1995), Cuccovillo and Coop (1999), Cotecchia and Chandler (2000), Liu and Carter(2006), Sorensen et al. (2007), and Caicedo et al. (2019) show the differences between reconstituted soils and natural soils,and these differences are attributed to particles arrangement and bonds created within the soil structure. In addition, the structured effect decreases when the stresses increase.

Some studies are reported on the soil-structure effects(e.g.Gens and Nova, 1993; Whittle, 1993; Wheeler, 1997; Kavvadas and Amorosi, 2000; Rouainia and Muir Wood, 2000; Liu and Carter,2002; Baudet and Stallebrass, 2004; , Masín, 2006; Fuentes et al.,2010; , Yan and Li, 2011; Nakai et al., 2011a; Pedroso, 2014; , Yang et al., 2014, 2015, 2016; Hashiguchi, 2016; Nguyen et al., 2017;Zhang et al., 2019). These studies included changes in the constitutive models using bonds degradation laws in the materials.These laws influence the model with changes in the yield-surface size,additional yield surfaces, additional void ratios by the bonds,additional strains, non-associated flow, and changes in the definition of stress invariants, changes in the hardening law (isotropic and anisotropic), transformed stress spaces, among others. However, these models require additional parameters and state variables in comparison with a model resembling unstructured soil.Therefore,some changes are complex to understand and difficult to implement in finite element modeling (FEM).

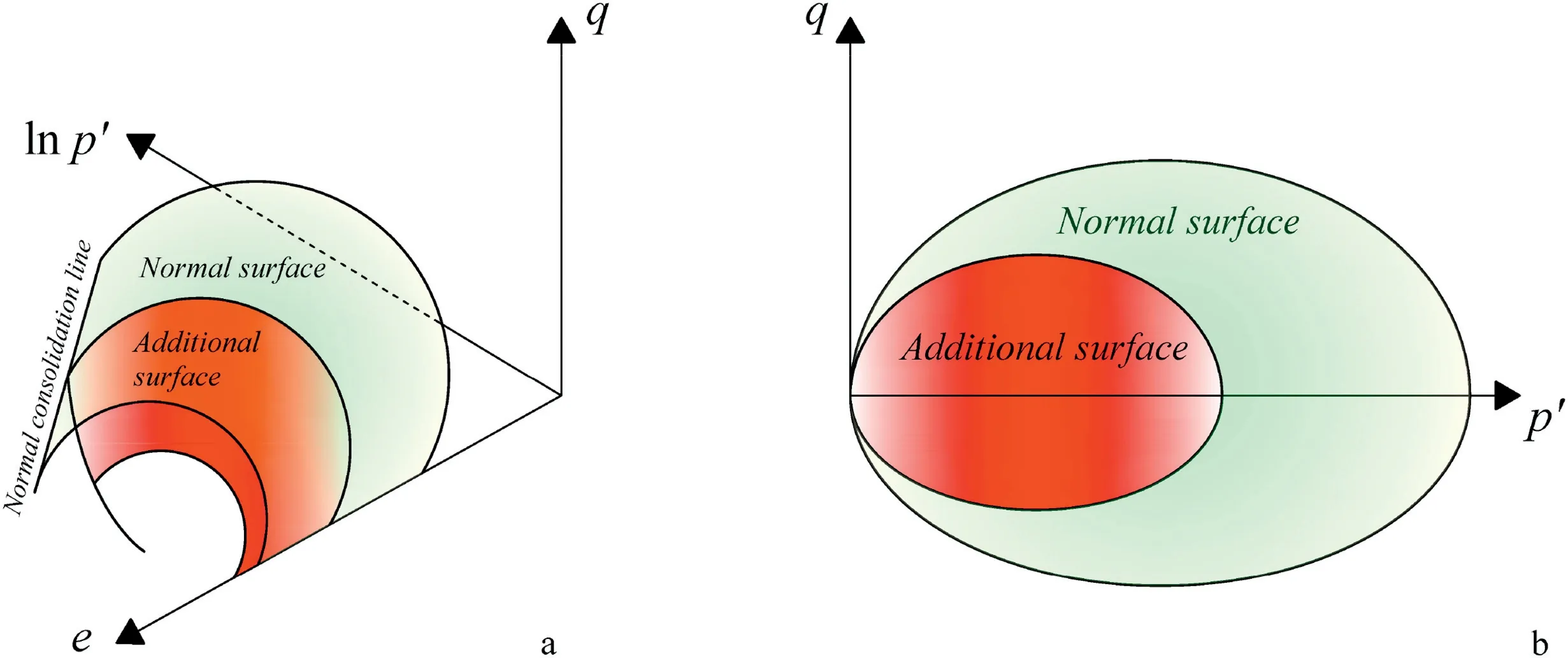
Fig.1. Yield surface for modified Cam Clay model and sub-load surface for the proposal.

In this paper,the soil of Brasilia(Brazil’s capital city)was used to obtain the parameters of a newly proposed model.The Brasilia soil is highly weathered residual and lateritic clay. Its mineralogical structure has a strong presence of aluminum and iron oxides.This is due to the lixiviation processes in the upper layers of tropical soils.As a consequence,the soil attains a cemented structure with sandsized grains, high porosity, high void ratio (ein the range of 1e2),and high permeability(103e104m/s).This material has a highly unstable structure,susceptible to change in volume(collapse)with changes in the stress states or water contents (Guimar?es, 2002;Camapum de Carvalho et al., 2006; Cord?o Neto et al., 2018).

For the above characteristics, a simple model was proposed,with ability to represent the main features of reconstituted and natural soils with respect to structure. The proposed formulation can be implemented in a finite element platform for use in threedimensional (3D) geotechnical problems.

2. Conceptual framework of the model

To understand the proposed model, some basic aspects of the behaviors of natural soils are initially stated and explained how they are modeled in the reference framework. One phenomenon observed for reconstituted and naturally structured soils in the model is the division of the compression curve into two states:over-consolidated (OC) and normally consolidated (NC). This is handled in conventional elastoplastic models by defining two different compressibility parameters and a single yield surface to separate the purely elastic and the elasticeplastic domains. This generates an unrealistic discontinuity in the stressestrain curve(Roscoe et al., 1963; Roscoe and Burland, 1968). Here, special attention is given to the “smooth” transition from an OC state to a NC state, which is modeled using the sub-loading concept (Mróz,1967; Hashiguchi,1980, 2016; Nakai et al., 2011b). This transition can be physically explained as the stage where the particles begin rearranging gradually, and strong rupture of the bonds between particles takes place. The second state of the curve (normal consolidated state) is that particle rearrangement is constant and the rupture of the bonds between particles is small(very few bonds remain in the structure of the soil in this second state).

Reconstituted and naturally cemented soils show stiffer behavior,which are typical OC clays at certain stress levels.OC clays are denser,showing lower void ratioein comparison with NC clay under the same stress levels.Naturally cement soils also exhibit OC behavior,despite being more porous or having higher values of void ratio,in many cases.The compressibility is,therefore,influenced by two state variables in the model: the state variable, which is a function of the realdensityof the soil, and the state variablewhich is a function of thestructureof the soil.This second variable()can be regarded as a fictitious increase of density to account for the gain in stiffness in structured (yet more porous) natural soils.These variables were originally and ingeniously proposed by Nakai et al. (2011a), in the context of a modified stress space, calledtij.These state variables evolve to control the size of an additional surface in the conventional stress space, defined in terms of the well-known invariants, the mean effective stressp, and the deviatoric stressq. For material with OC behavior, this additional surface, referred to as sub-loading surface, evolves towards the“normal”yield surface of the modified Cam Clay(MCC),as shown in Fig.1.This “normal”surface becomes dominant when the material achieves an NC behavior.

The influences of structure and density on the stressestrain curve of the soil are shown in Fig. 2. Fig. 2a shows the curve of deviatoric stress versus strain for an OC soil or structured soil(blue line).In this case,the two state variablesandcan work together or separately.For example,a reconstituted and OC soil may have a peak in the stressestrain curve but may not have cemented structure.In this case,only the state variableis working.The same behavior can be plotted in terms of volumetric compressibility in thee-lnpspace in Fig.2b.In both pictures,it is possible to observe unrealistic and abrupt discontinuity in the stressestrain behavior when a single yield surface is used, such as in conventional elastoplastic constitutive models. The advanced and simple subloading plasticity framework adopted provides a realistic and smooth transition for both cemented and non-cemented structured soils.

Another important phenomenon of soil behavior is the effect of interlocking between particles, which is reflected in soil dilatancy(Newson and Davies, 1996; Cotecchia and Chandler, 1997;Richardson, 1998; Li and Dafalias, 2000). These researches show that in soils with structure, normality relationship between yield surface and plastic potential surface is not met, i.e. the increment vector of the plastic strains is not perpendicular to the yield surface.Therefore, non-associated flow rule should be used to solve this problem.

Associated flow rule is a basic hypothesis for the “deduction”of the yield surface of the Cam Clay model. The classic elliptical shaped yield surface of the Cam Clay model is a consequence of this hypothesis applied to the dilatancy ratio of the increments of the deviatoric plastic strain to volumetric plastic strain (dεpd=dεpv),together with additional assumptions about the dissipation of plastic work.However,Nakai et al.(2011a)conclusively shows that hypothesis of a unique dilatancy curve does not hold soils under general stress paths in 3D conditions. They bypassed the need for an extra (plastic potential) surface by transforming the conventional stresses (ij) to another space (tij), by means of a mapping tensor(aij)defined from the normal vector to the so-called spatially mobilized plane (SMP). Their model development stems from imposing consistency and normality in this new modified stress space,denoted by its normal and deviatoric stress invariants(tNandts), instead ofpandq. The forced normality in the (tN,ts) space reflects non-normality when the stresses are mapped backed to the conventional (p,q) space.

Fig. 2. Schematic response of the model to shear and compression conditions.

Nakai et al. (2011a)’s proposition is innovative because the concept bypasses the need for an extra plastic potential surface.Additionally,Nakai et al.(2011a)’s results from triaxial tests showed that the deformation and strength of soils in 3D stress conditions cannot be described only bypandqinvariants. This is due to different behaviors of the soils under compressive and tensile stresses. Therefore, the constitutive models, which are formulated using these invariants, have some limits to describe properly the influence of the intermediate principal stress on the deformation and strength characteristics of soils.Nakai et al.(2011a)’s proposed the influence of the intermediate principal stress on the deformation and strength. However, most engineers and scholars fail to grasp the real meaning of such transformations. Therefore, we revisited the basic and well-establishedpandqstress invariants of the Cam Clay model and “deduced”a non-associated flow.The trick is to modify the original dilatancy ratio expression of the Cam Clay model to include the new state variables for density and structure(and), as further detailed in the next section.

3. Constitutive model

The model used herein is an enhancement of the sub-loading Cam Clay (SCC), proposed and implemented by Pedroso (2006).The SCC model is a modification of MCC, proposed by Roscoe and Burland (1968), which was developed for reconstituted soils. The SCC model is well described in Pedroso (2006), which basically included the density and structure variables (and) in the MCC model and also changed the shape of the yield surface in the(p,q)space to approach Matsuoka and Nakai (1974)’s failure criteria in the critical state, instead of the conventional Drucker-Prager cone.

The present paper proposes some changes in the SCC model,aimed towards improving the prediction capacity of the model.These changes include the implementation of a non-associated flow rule and the inclusion of the structure effect, in reference to the proposals made by Liu and Carter (2002) and Kyokawa(2010).These modifications were made without adding additional parameters to the model. The model was modified to reflect the differences in the behavior of reconstituted and natural soils. The importance of these changes is evident in various researches in terms of constitutive formulations that consider the effect of structure. Among the proposals are models by Gens and Nova(1993), Whittle (1993), Wheeler (1997), Kavvadas and Amorosi(2000), Rouainia and Muir Wood (2000), Liu and Carter (2002),Baudet and Stallebrass (2004), Masín (2006), Fuentes et al.(2010), Nakai et al. (2011a), Yan and Li (2011), Pedroso (2014),Hashiguchi (2016), Nguyen et al. (2017), among many others.However, some of these proposals are complex to understand and implement in FEM.This is a reason to develop a new model that is easy to implement and represent this soil type.

3.1. Modifications of the model

The first modification of the model is introduction of the state variablethat represents the soil overconsolidation.This variable is the difference between the current OC void ratio and the void ratio in the normal consolidation line (NCL)eNfor the same stress, as shown in Fig. 3b. Fig. 3a shows two surfaces in the stresses space:the normal surface of the MCC that memorizes the maximum stress applied to the soil with size(p1e)along thepaxis,and the second surface (sub-loading surface) with size (p1). The current state of stress always lies on the sub-loading surface, which has a smaller size than the MCC surface,but tends to this surface as the soil state approaches normal consolidation.The evolution of the sub-loading surface towards the normal surface of the MCC is visualized by the distancewhich is a measure of overconsolidation and is related to the density variable(Giraldo and Muniz, 2011;Mendoza et al., 2015). The distance d controls in the transition of the OC state to the NC state in a smoothed form,thus avoiding the discontinuity in the MCC model. This is achieved by means of an auxiliary functionGthat causesto evolve quadratically (Fig. 4a)and requires a material parameterc:

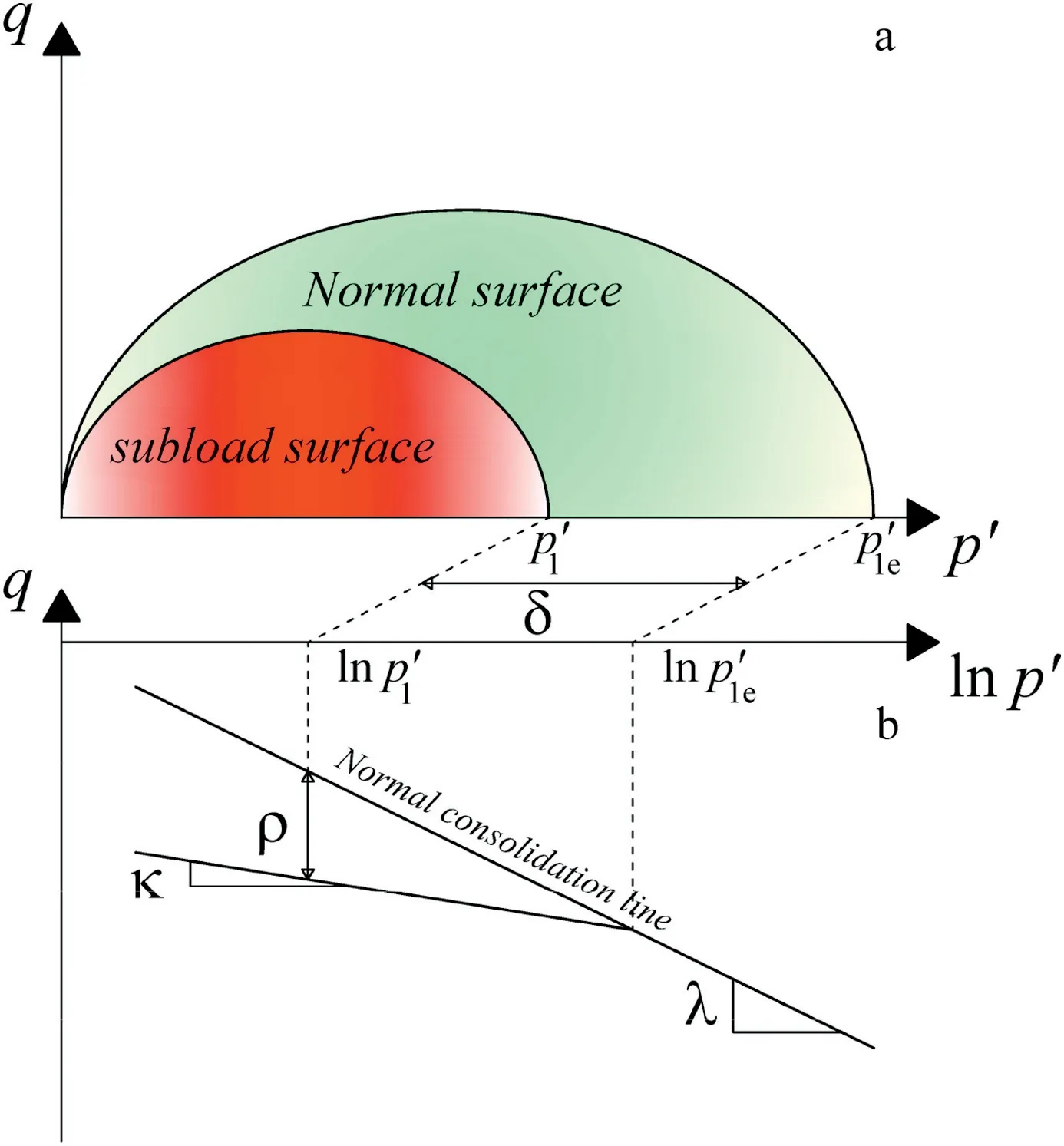
Fig.3. Sub-loading surface and measurement of the density(adapted from Farias et al.,2009).

The second modification of the model is inclusion of the effect of the soil structure by means of the state variable.This variable has a linear behavior (Fig. 4b) with respect to the functionQwhich requires another parameterb:

This second modification affects the state variablewith an“imaginary”density decrement that represents the structure of the soil. This allows the overconsolidation compression line to cross over the NCL and then fall back towards it, as depicted in Fig. 2b.Therefore,the stressestrain behavior of a structured soil cannot be described only by the effect of the density in Eq.(1),but also needs to take into account the effect of bonding(structure)in Eq.(2).The evolution ofcan be determined by combining the effects of functionsG() andQ() in the development of volumetric plastic strains. Nakai et al. (2011b) presented a comprehensive discussion on the evolution.

The third modification of the model is inclusion of a nonassociated flow rule with addition of the two previously defined state variables,iand.The first is due to the initial densityiand the second is a state variable by the structurethat evolves to almost disappear:

The addition of the state variablesandcreates a change in the shape of the plastic potential surface with respect to the shape of the yield surface,thus changing the direction of the plastic strain vectors. The last modification of the model accounts for different strengths of the soil under compression and extension paths.This is attained through the proposal by Sheng et al. (2000), who suggested a critical state stress ratioM(p/q) and made it vary as a function of Lode angle (). The equations for this modification are shown below:

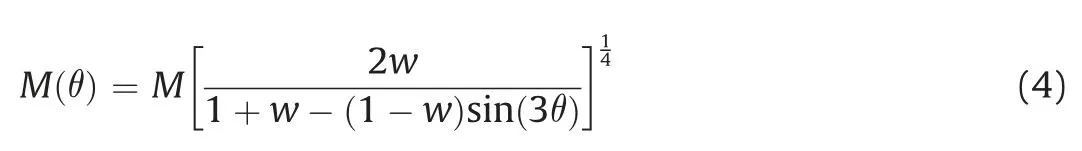
wherewis a constant that can be computed from the critical state friction angle obtained from a compression test(cr):

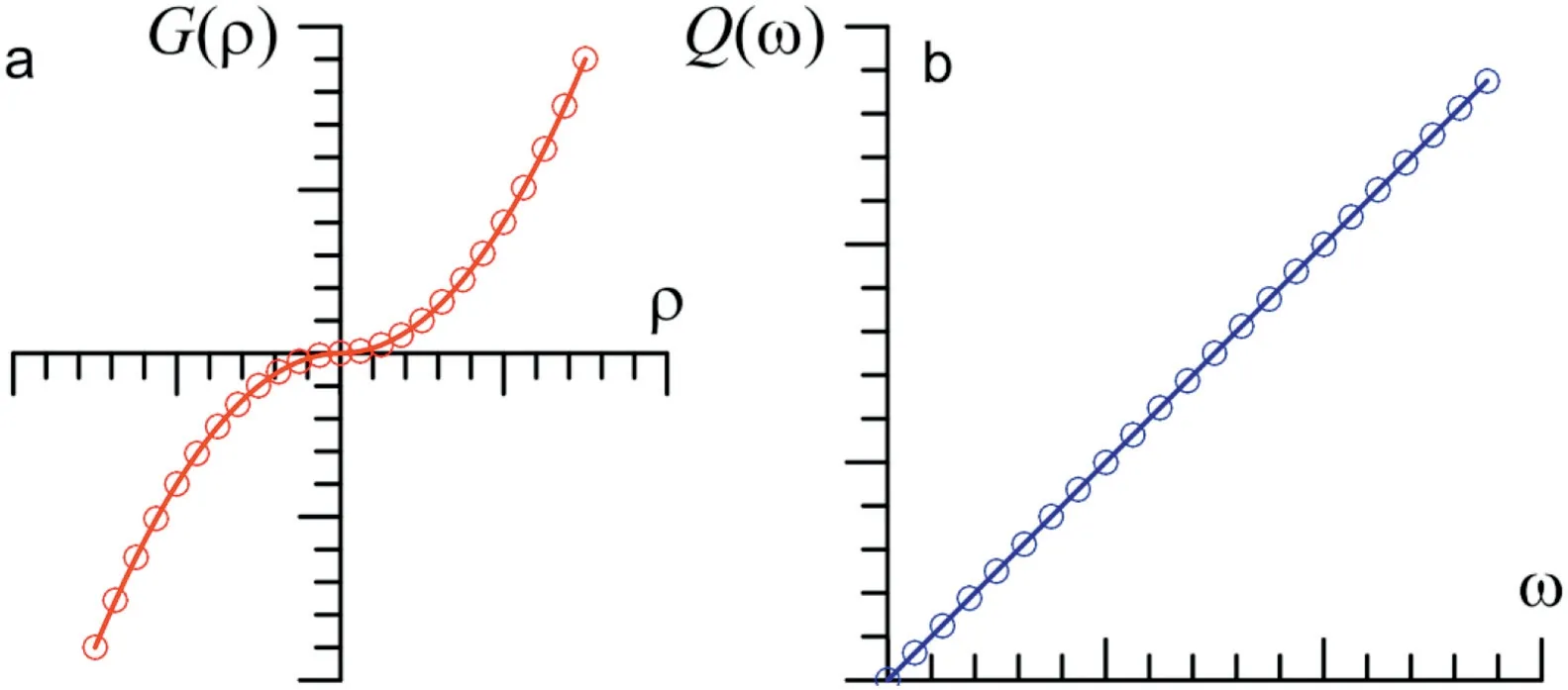
Fig. 4. Evolution of state variables and with the functions G() and Q().

and Lode angle varies with the stress state:

where x is the deviatoric stress tensor:

where 1 is a second-order unitary tensor.

From the above, the “sub-loading” yielding surface takes the following expression:

Eq.(8)also holds for the “normal”yield surface by replacingp1withp1e.

The yielding surface is one of the main characteristics of an elastoplastic model. This surface shows the point where the elastoplastic deformations begin in a stress path.The original surface of Cam Clay model was proposed by Roscoe et al. (1958) and subsequently modified by Roscoe and Burland (1968). Fig. 5a shows the surface shape proposed by Roscoe and Burland(1968),which plots as an ellipsoid in the principal stress space. However, this proposition does not take into account the difference of soil strength under compression and extension paths. For this, Sheng et al.(2000) related the stress ratioMto the Lode angle (Eq. (4)), as shown in Eq. (8). As shown above, this affects the yield surface equation in Eq. (8) and is illustrated in Fig. 5b. From this figure, it shows a lower resistance in extension paths compared to compression paths. The modified surface mimics the failure criterion proposed by Matsuoka and Nakai(1974)and has been used by other researches, such as Pedroso and Farias (2011) and Mendoza et al. (2014).

The size of the yield surface,given by the distance(p1)from the origin to the tip of the surface, evolves with the accumulation of volumetric plastic strains, similar to what happens in the conventional Cam Clay model. Therefore, the surfaces in Fig. 5 inflate or expand isotropically in all directions asp1increases.This evolution is controlled by the internal state variables,andand their hardening rules.

Besides yield surfaces and hardening rules, elastoplasticity also requires a different plastic potential function(gsf),in case of nonassociated flow rules. Here, this function is obtained from the dilatancy ratio of Eq. (3),which includes the effects of the internal variables (and), andgtakes the following expression:

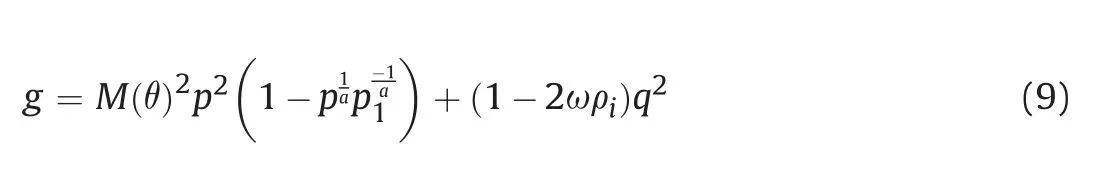
where

Observe that functiongcoincides with the yield surfacef,when density and structure are not taken into account,i.e.when0 and0,thena1 and normality is restored(gf).The shape of the plastic potential surface is shown in Fig.6 with the superposition of the yield surface, considering a non-associated flow rule.

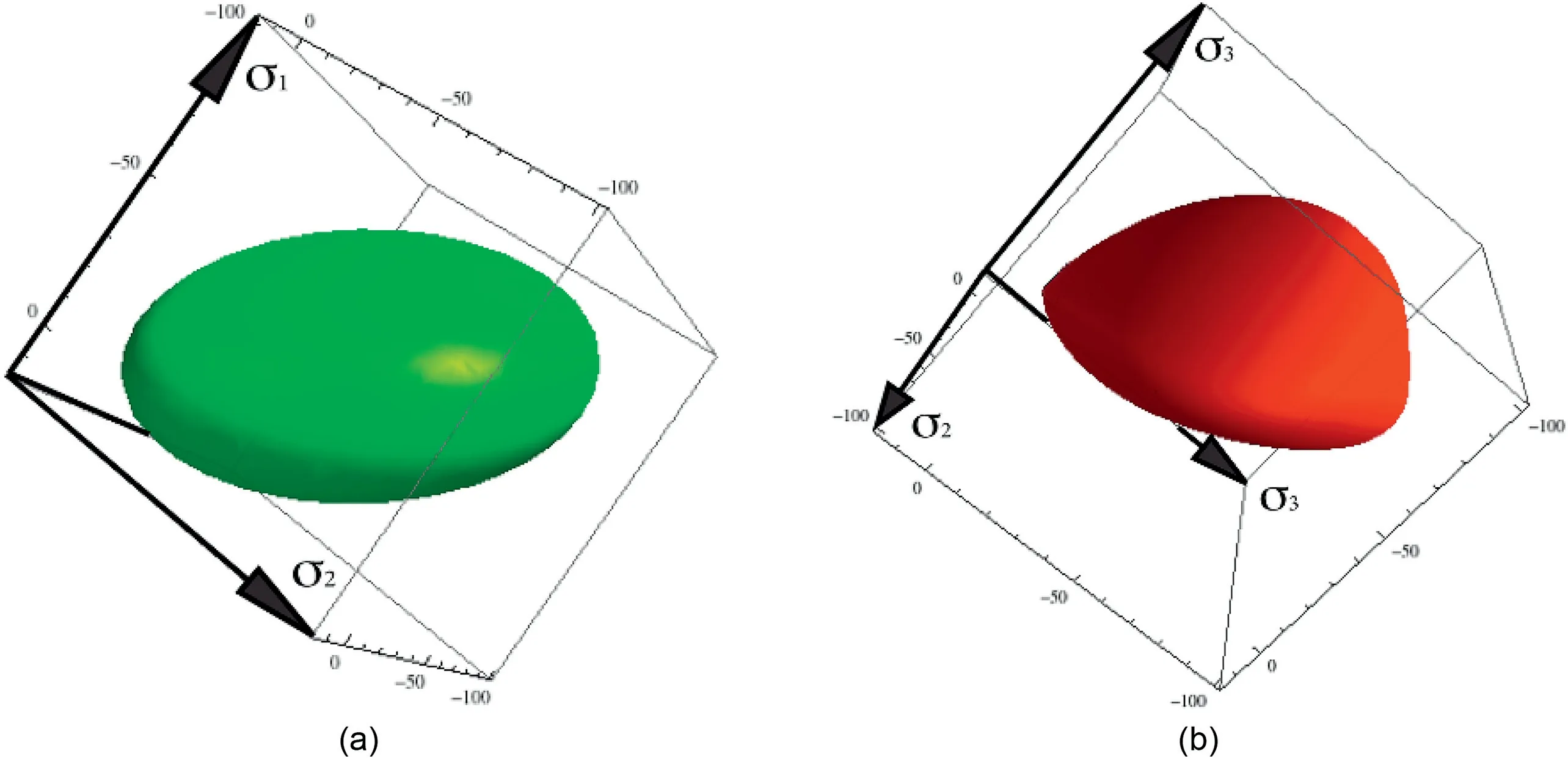
Fig. 5. Schematic illustration of yield surfaces (a) for the MCC model and (b) with the proposal by Sheng et al. (2000) (unit: kPa).

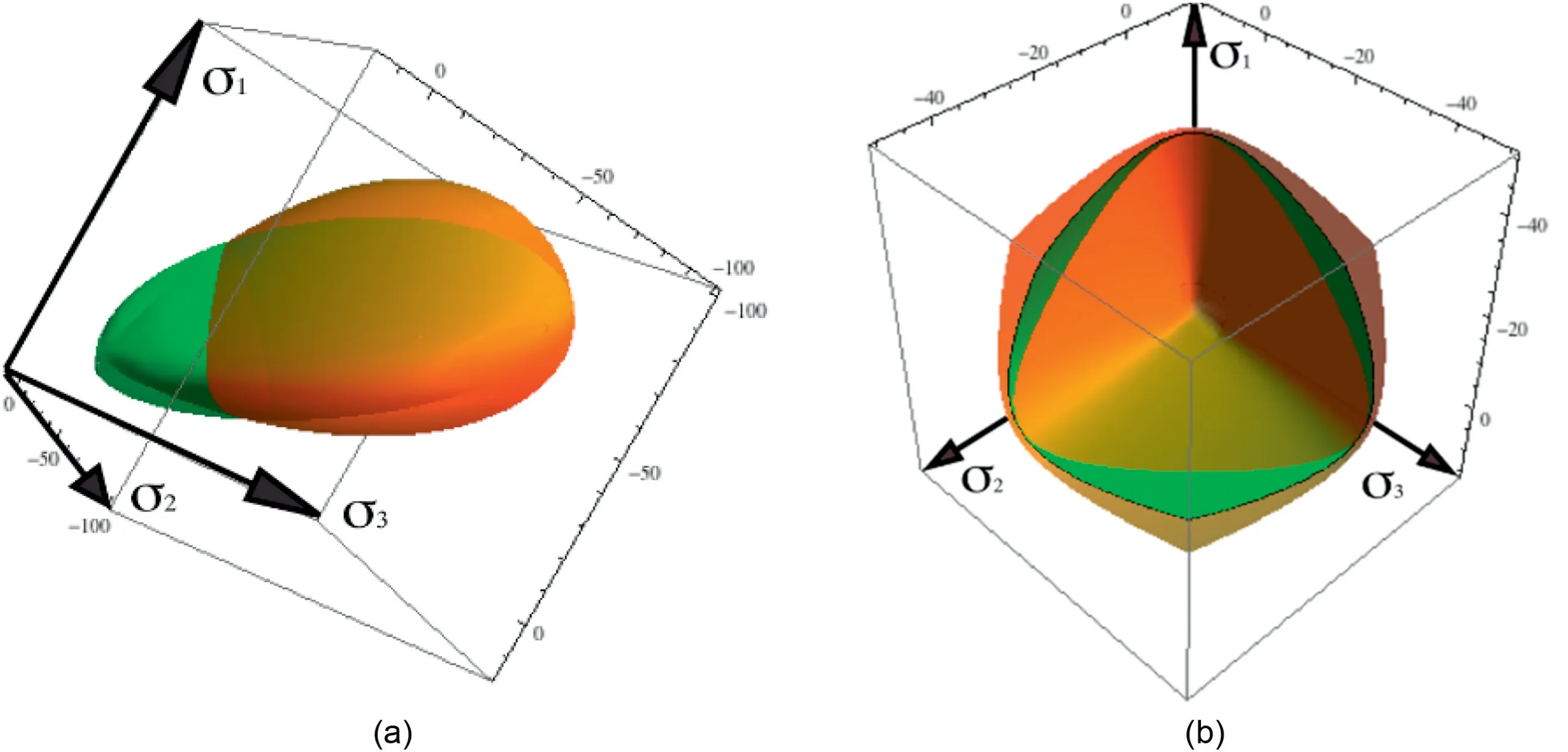
Fig. 6. Schematic illustration for (a) Overlapping of the plastic potential surface and yield surface of the MCC proposed by Sheng et al. (2000), and (b) A cut of the overlapping surfaces (unit: kPa).

3.2. 3D model formulation

As for any elastoplastic model,stress rates or increments can be related to strain rates or increments via a fourth order tensor of stiffness moduli:

The elastic part Ceis given by the following expression:

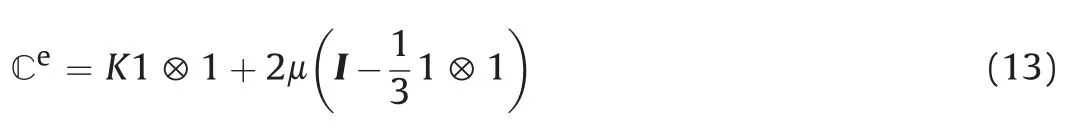
whereKand m are the elastic volumetric (bulk) and shear moduli,respectively.

The plastic part Cpis given by the following expression:

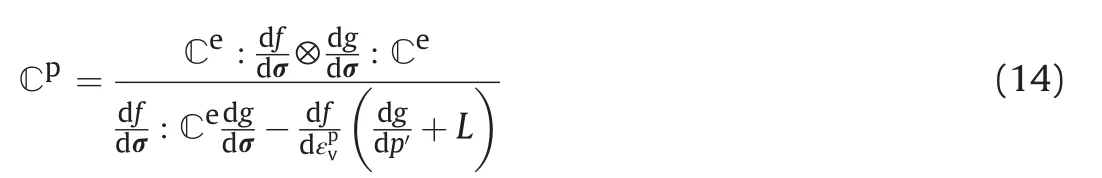
Eq. (14) is similar to that of conventional elastoplastic constitutive models,expect for the scalar term“L”in its denominator.This represents the combined effects of density and structure:

Density is accounted for via the scalar functionG() and structure by means ofQ(). Additionally, this equation is a function of the picnotropy and barotropy of the material.This is done indirectly with the mean effective stresspand the void ratioeo, and an alternative option was also shown in Eq. (15), in which the elastic modulus is obtained from the bulk modulus.This alternative option has different values of parameterscandb. Furthermore, Eq. (14)also includes the effects of the non-associated flow rule. This was attained by means of the derivatives with respect to the functiong,as shown in Appendix A.

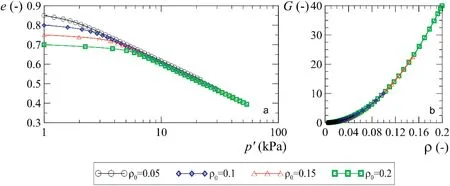
Fig. 7. Simulation of isotropic compression test with variation of the initial value of the state variable .

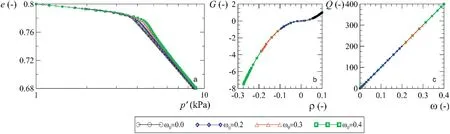
Fig. 8. Simulation of isotropic compression test with variation of the initial value of the state variable .

The hardening law is given in a semi-logarithmic space of the mean effective stress and the specific volume (v1te). This law relates the change of yield surface size(p1)with the increments of plastic strains, as shown in the following equation:

wherep1is the size of sub-loading surface at the beginning of the increment (Fig.1),is the virgin compression slope (of the NCL),and k is the unloading-reloading slope of material.The change rate of volumetric plastic strainis defined as the trace of the change rate of the plastic strainas in the normal Cam Clay model; andis an additional plastic volumetric strain, due to the subloading concept, and will be explained later. This allows for plastic strain accumulation during load reversal and reloading inside the normal (outer) yield surface and provides the model with the capability to address cyclic problems.

The increase of the plastic strain is a function of the nonassociated flow rule. This increment can be written as

wheregis the plastic potential function that is a function of the stresses (Eq. (9)) and _is the plastic multiplier, which is obtained from the consistency condition (df0):

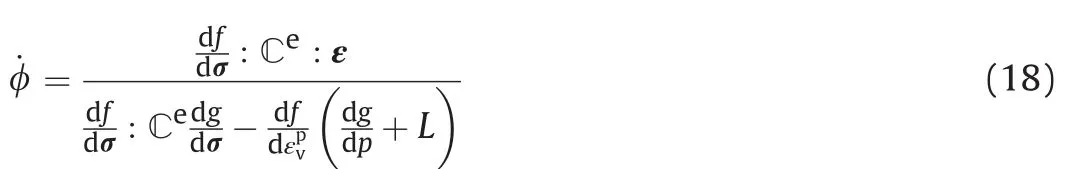
Eq.(16)was modified with respect to the MCC model,adding a part by the sub-loading plus the structure. This part is added_ in a rate of strainthat is the product of the plastic multiplierand the scalarL:

The derivatives with respect to the functionfand the tensor operations are shown in Appendix A.

4. Parametric analysis

The model requires seven material parameters.Five of them are those used in conventional Cam clay model (N,,k,,M). The two additional parameters introduced arecandb,which represent the density and the structure effects, respectively, and control the evolution of the state variablesand. These parameters can be obtained from a reconstituted or natural soil sample, through isotropic triaxial consolidation test, triaxial shear test, and unconfined compression test. From the consolidation, three parameters are obtained:N(void ratio at 0.01 times the atmospheric pressure),(the slope of the normal compression line) and k (the slope of swelling line). From a triaxial shear test, elastic modulus,E, and critical friction angle,cr,which is analogous to theMof the critical state of the Cam Clay, can be obtained. In addition, from the unconfined compression test, the Poisson’s ratiocan be obtained.The Young’s modulus can be obtained by elastic correlations.

A sensitivity analysis was performed for the new parameters and variables of the model,including the simulation of triaxial and compression tests.This was done to observe the influences of these parameters and variables on the different stress paths.

Table 1Parameters for the sensitivity analysis.

4.1. Isotropic compression simulations

An initial parametric analysis was made to verify the influence of the state variablesand. These state variables are not from the traditional MCC model, which is the reference model. This was done to understand the behavior of these variables, since they are addition of the sub-loading concept. Simulations of isotropic compression tests were performed by varying the initial density0, as illustrated in Fig. 7a. It was observed that a high0makes a longer transition to the normal consolidation condition.Fig. 7b shows the evolution of the state variable0when the parametercis constant. The influence of the structure in the model was obtained when the state variable0was varied from 0 to 0.4, leaving the constant value of the density00.1, as shown in Fig. 8a. The structure effect is obtained with a density decrement, as shown in Fig. 8b. This decrement causes the compression line to pass above the NCL and then fall back towards this line asymptotically. The parameters used in these simulations are shown in Table 1.

4.2. Simulations of triaxial tests

To observe the influences of density and structure when predicting soil behavior subjected to shear stresses, simulations of drained triaxial tests were performed.These tests were conducted following the same path used by Chowdhury(1994)with Fujimori Clay. This experimental procedure was carried out with a mean effective stress of 200 kPa,which was used to create a compression cycle until a deviatoric stress of 200 kPa was obtained, and decompression cycle until an extension deviatoric stress of 100 kPa was obtained.Then,a recompression process was carried out until it reached once more a state of compression of the material with a deviatoric stress of 300 kPa.

The first step in the methodology conducted in this study was the variation of the initial state variableofrom 0 to 0.9.The results obtained from this analysis are shown in Fig. 9. This figure shows the change of “area” in unloading and reloading or hysteresis loop with the change of variableo.This area is a measure of the cyclic plastic strain energy.At a grain scale,this energy is used to slide one particle past another and/or to break the bonds between them and should be released to the environment in the form of heat and mechanical waves(e.g.sound).It is seen that a higher initial value of variable, for instance representing a soil with higher initial particle bonding,implies in a stiffer initial response and a decrease of hysteresis energy (or more elastic behavior under cycling). It is also noted that the change in area of the loop does not affect the critical state because all stress paths lead to the same final stress state (Fig. 9a). However, this variable influences the behavior of deviatoric and volumetric strains(Fig.9b).Fig.9c and d shows the evolution of the two state variables.

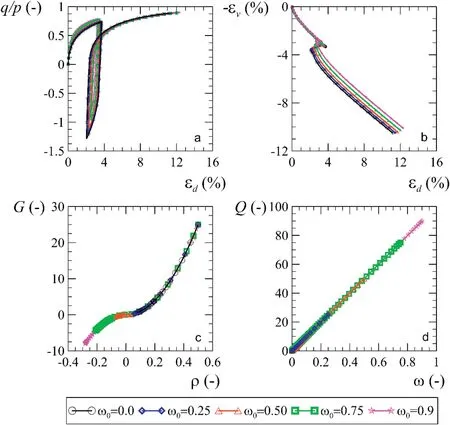
Fig. 9. Simulation of drained triaxial test of state variable with the initial value.

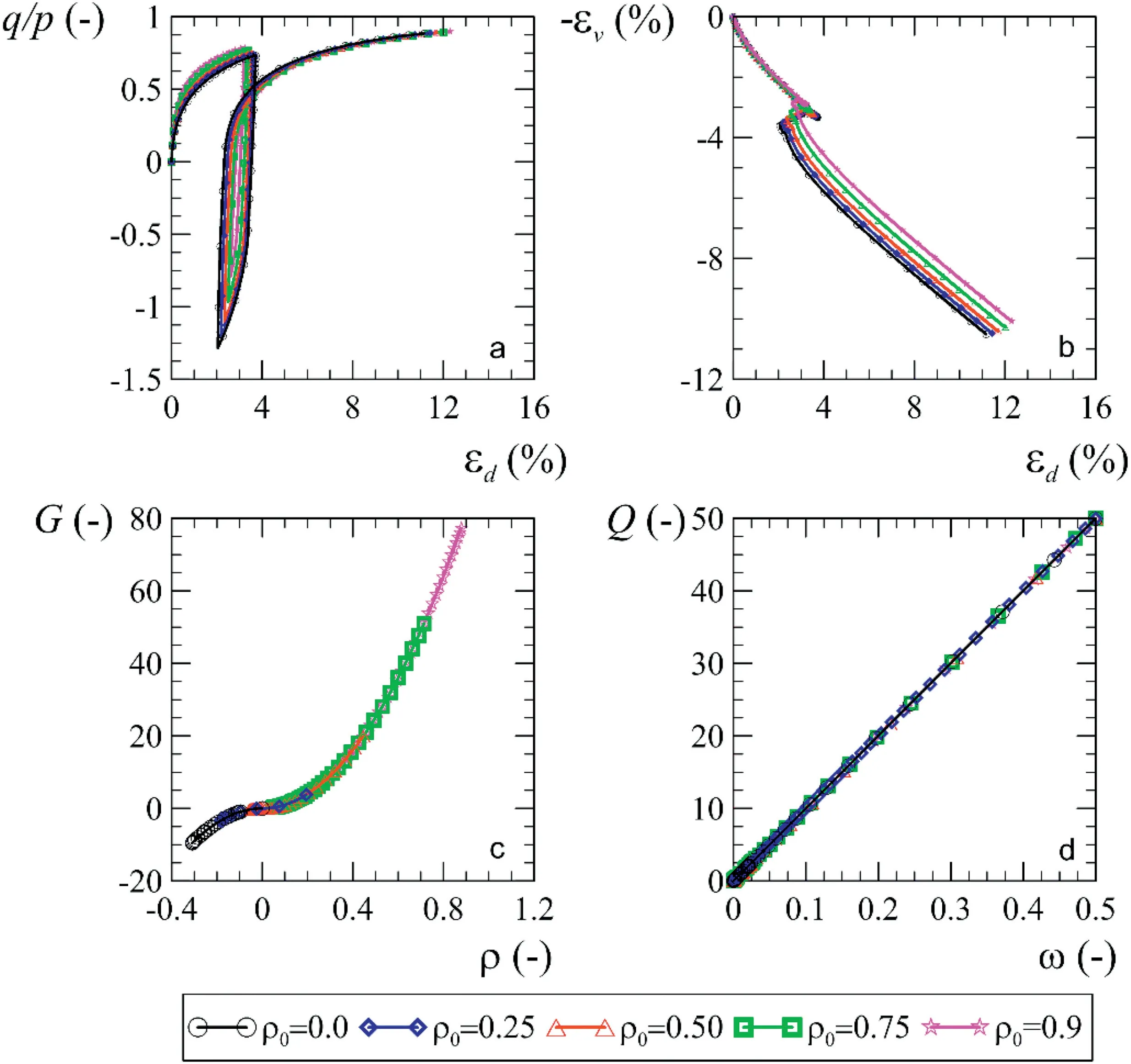
Fig.10. Simulation of drained triaxial test of state variable with the initial value.

In Fig. 10, the same parametric analysis was performed but varying the initial state variableofrom 0 to 0.9.From these results,the influence of this variable on hysteresis loop was also observed.The pattern is similar to that observed for variableo. Again, the change in size of the loop does not affect the critical state(Fig.10a).The influence on the ratio of the deviatoric strains and volumetric strains is shown in Fig.10b. In addition, the evolution of the state variables of the new model is presented in Fig.10c and d.

5. Evaluation of the model

The model’s capability to reproduce the mechanical behavior of real soils was evaluated through consolidation and drained triaxial tests performed on three different types of structured clays in the literature. The types of clays used were: Corinth Marl Clay from Anagnostopoulos et al. (1991), Bangkok Clay presented by Balasubramanian and Hwang (1980) and Rio de Janeiro Clay presented by Oliveira et al.(2011).Finally,some simulations were also performed for the Brasilia Clay.

5.1. Model validation with tests found in the literature

The validation of the proposed model was initially carried out with Corinth Marls Clay. This kind of clay is a soil deposit with calcium carbonate content of 70%e75%; the remaining fraction corresponds to clay minerals. This soil presents a structure with bonds between particles with calcium carbonate obtained during the sedimentation process or by the circulation of water rich in calcium after the consolidation by gravity(Anagnostopoulos et al.,1991). The parameters of the proposed model obtained for this material are shown in Table 2.

Fig.11 shows the comparison of two isotropic tests conducted by Anagnostopoulos et al. (1991) for a reconstituted and natural soil.The simulations were made in two steps. The first step was the simulation of the reconstituted soil by including only the effect of the internal variable (), because this type of soil does not have bonds but instead the influence of overconsolidation.Subsequently,the natural soil simulation was performed by increasing the state variable of the structure and keeping the variable of density. The model can predict the behaviors of the natural and reconstituted materials quite well. The destructured material has a preconsolidation stress around 200 kPa, whereas bonding increases the “apparent” pre-consolidation stress to around 5000 kPa. The transition of compressibility was well captured with the introduction of the structure effect by means of the internal bonding variable.

Table 2Parameters for Corinth Marls Clay.

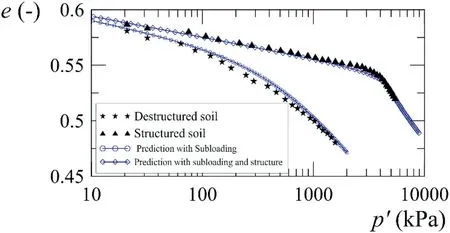
Fig.11. Simulation of isotropic compression test for Corinth Marls Clay(test data from Anagnostopoulos et al.,1991).

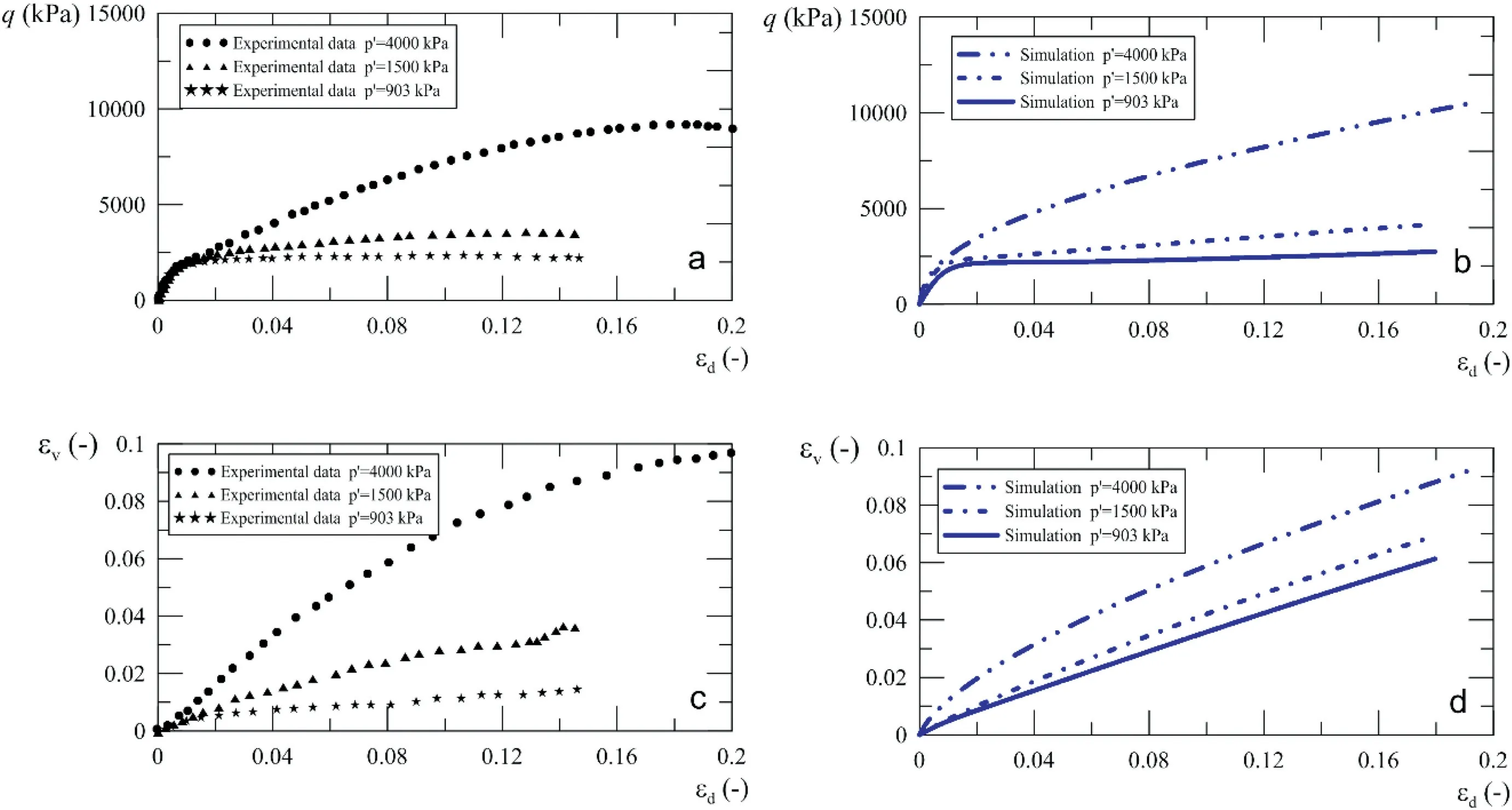
Fig.12. Simulation of drained triaxial behavior of Corinth Marls Clay (test data from Anagnostopoulos et al.,1991).

Moreover, the simulations of drained triaxial tests (at chamber pressures of 4000 kPa,1500 kPa and 903 kPa)were performed for the Corinth Marls Clay with the same above parameters. Fig. 12 shows the comparisons between laboratory results and model simulations. Again, the model could predict this soil’s behavior quite well under deviatoric stress paths. Both the results of deviatoric and volumetric strains are quantitatively and qualitatively reproduced with good accuracy.

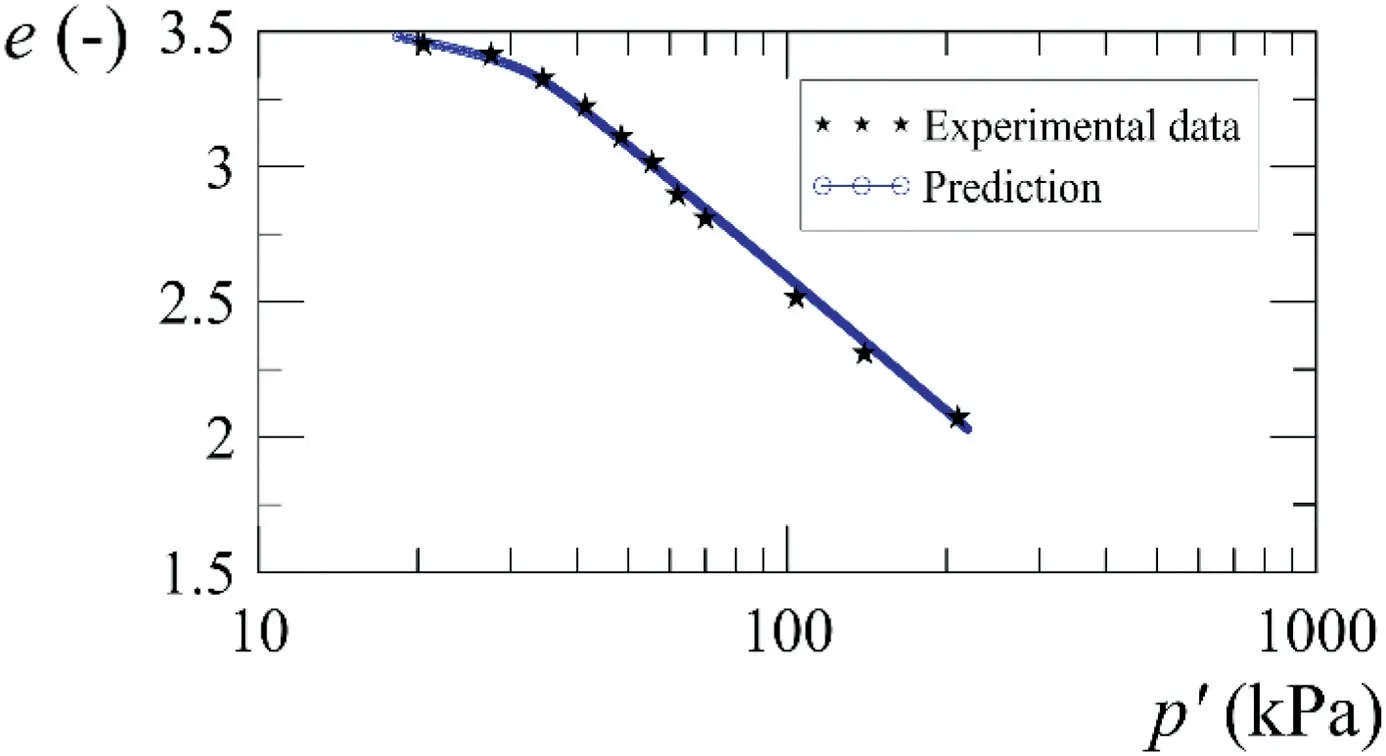
Fig.13. Simulation of isotropic consolidation test for Bangkok Clay (Balasubramanian and Hwang,1980).

Table 3Parameters of Bangkok Clay.

The proposed model was further validated by simulating more tests, but now using Bangkok Clay. This clay is a marine, sedimentary deposit,weathered by wetting and drying cycles,a process that caused the shallow clay to harden into a soft clay layer. The simulation was performed using one of the tests that Balasubramanian and Hwang (1980) described in their study of yielding with several stress paths. The test is shown in Fig. 13,where an isotropic consolidation was simulated. From this simulation, it is possible to observe the progressive stiffness change in the soil until it reaches the NCL. The parameters obtained for this simulation are shown in Table 3.

Simulations for a soil from Rio de Janeiro City (Oliveira et al.,2011) were also performed on reconstituted and natural samples,as shown in Fig.14. The parameters obtained from these simulations are shown in Table 4. This soil was selected due to its properties of structure, formation type and weathering process. These characteristics stem from a strong presence of the iron bonds in biotite minerals that bond quartz grains.Consequently,the change in compressibility is noticed clearly in the naturally structured soil,for which an apparent pre-consolidation stress is indicated around 1000 kPa. However, the simulations were made with the effect of density until reaching the NCL for the points of the destructured soil test. Then, after these points, the structure effect was to reach the curve of the natural soil.

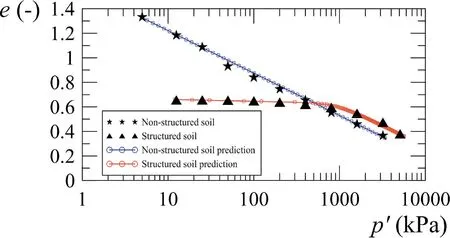
Fig.14. Simulations of oedometer consolidation test for Rio de Janeiro Clay (Oliveira et al., 2011).

Table 4Parameters of Rio de Janeiro Clay.

Fig.15. Scanning electron microscope images of Brasilia Clay:(a) Lateritic soil structure, and (b) Lump of cement particles (Guimar?es, 2002; Camapum de Carvalho et al., 2006).

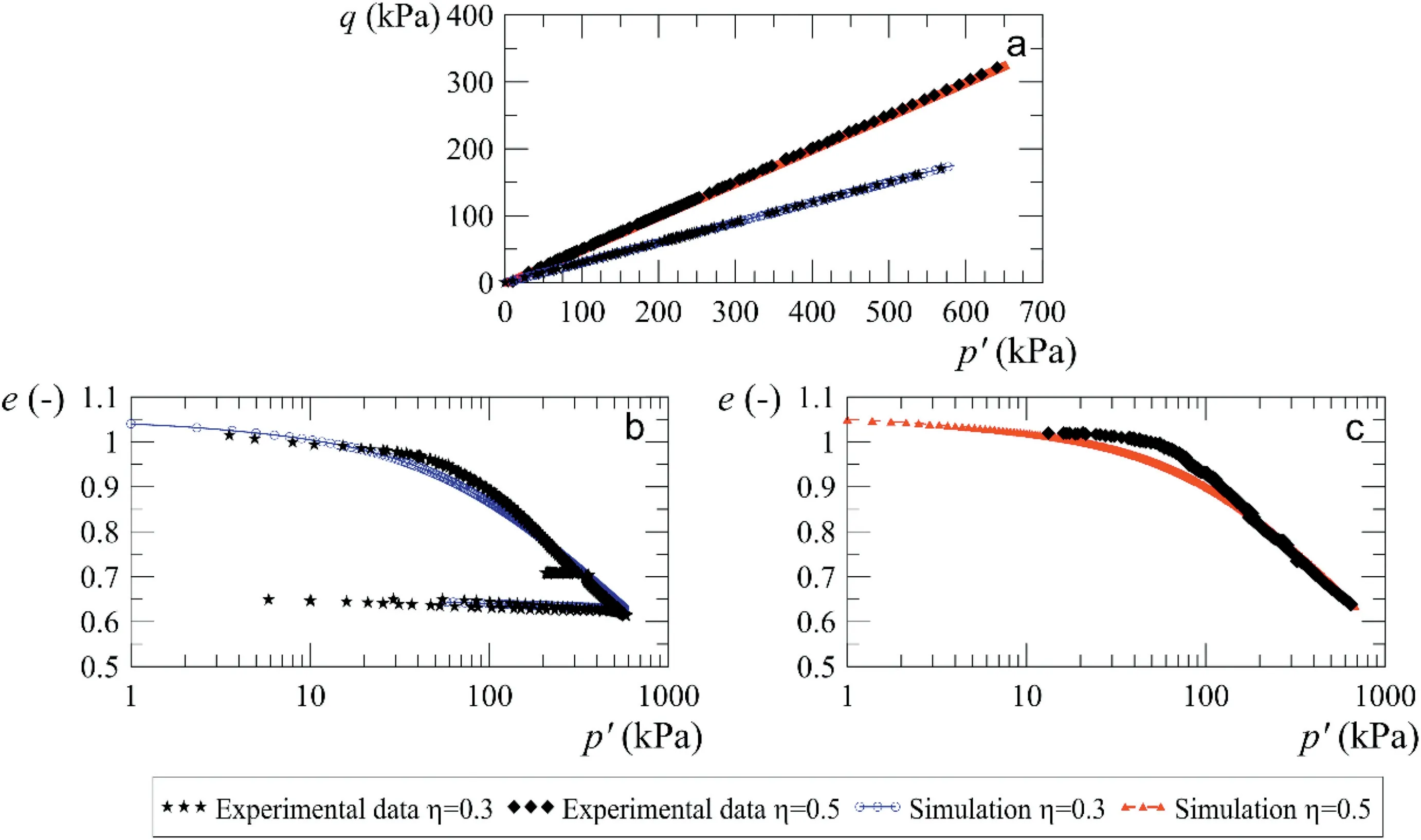
Fig.16. Simulation of triaxial compression with 0.3 and 0.5 for Brasilia Clay.

5.2. Validation of the model with Brasilia Clay

Five experimental tests were made in order to validate the proposed model for the Brasilia Clay. These tests were performed on a block sample obtained at a depth of 3 m is a site close to the University of Brasilia in the layer calledPorous Clay. This clay is a lateritic tropical soil, with bonds between particles forming lumps(Fig.15a).The bonds of these lumps generate a structure cemented with grains having the size of sand (Fig. 15b). This structure is created by a strong presence of iron and aluminum due to lixiviation processes in the upper layers.

Two consolidation tests were carried out with stress ratiosq/p0.3 and 0.5. In the first test, the consolidation was performed with a stress ratio of0.3 to mean effective stressp535 kPa and a constant rate of vertical strain of 0.02 mm/min.From this point on, the unloading began up top5 kPa and returned to a load with a stress ofp580 kPa.The second test was performed with a stress ratio of0.5. The test was performed with a rate of vertical strain of 0.01 mm/min,until a mean effective stress of 650 kPa.

Stress paths of the simulations and tests described above are shown in Fig.16a. Fig.16b shows the simulation of an anisotropic compression test0.3, in the plane of logarithm of the mean effective stress and void ratio.In addition,the simulation shows the model behavior in an unloading-reloading cycle. From this simulation,the parametersN,,k,candbwere obtained.Fig.16c shows the simulation with a stress ratio of0.5.In this simulation,the same parameters of the previous simulation were used. From the above simulations,it was observed that the parameters have a low variability.

Three conventional triaxial compression tests were performed in drained conditions at effective confining pressures of 110 kPa,200 kPa and 300 kPa, with a constant vertical strain rate of 0.03 mm/min. The tests were then simulated with the proposed model,as shown in Fig.17.From these simulations,two parameters of the proposed model (crandE) can be obtained. The value of Poisson’s ratio was obtained from the work of Janda et al. (2009).From these simulations, it is observed that the model is able to represent the mechanical behavior of the porous Brasilia Clay.Approximate values of model parameters were obtained,as shown in Table 5.It was also observed that the model is able to represent the effects of initial void ratio and confining pressure on this soil type. In addition, the non-associated flow rule generates an improvement in description of strains in the soil. On the other hand, the great variability of the new parameters in the structure and sub-loading concept was a function of the soil formation (i.e.sedimentary or residual),types of bonds of the material,geological history (e.g. wetting and drying cycles), weathering processes (i.e.physical or chemical), among other processes. All these variables influence the behavior of the structure in the smooth or rigid transition to an NC state.

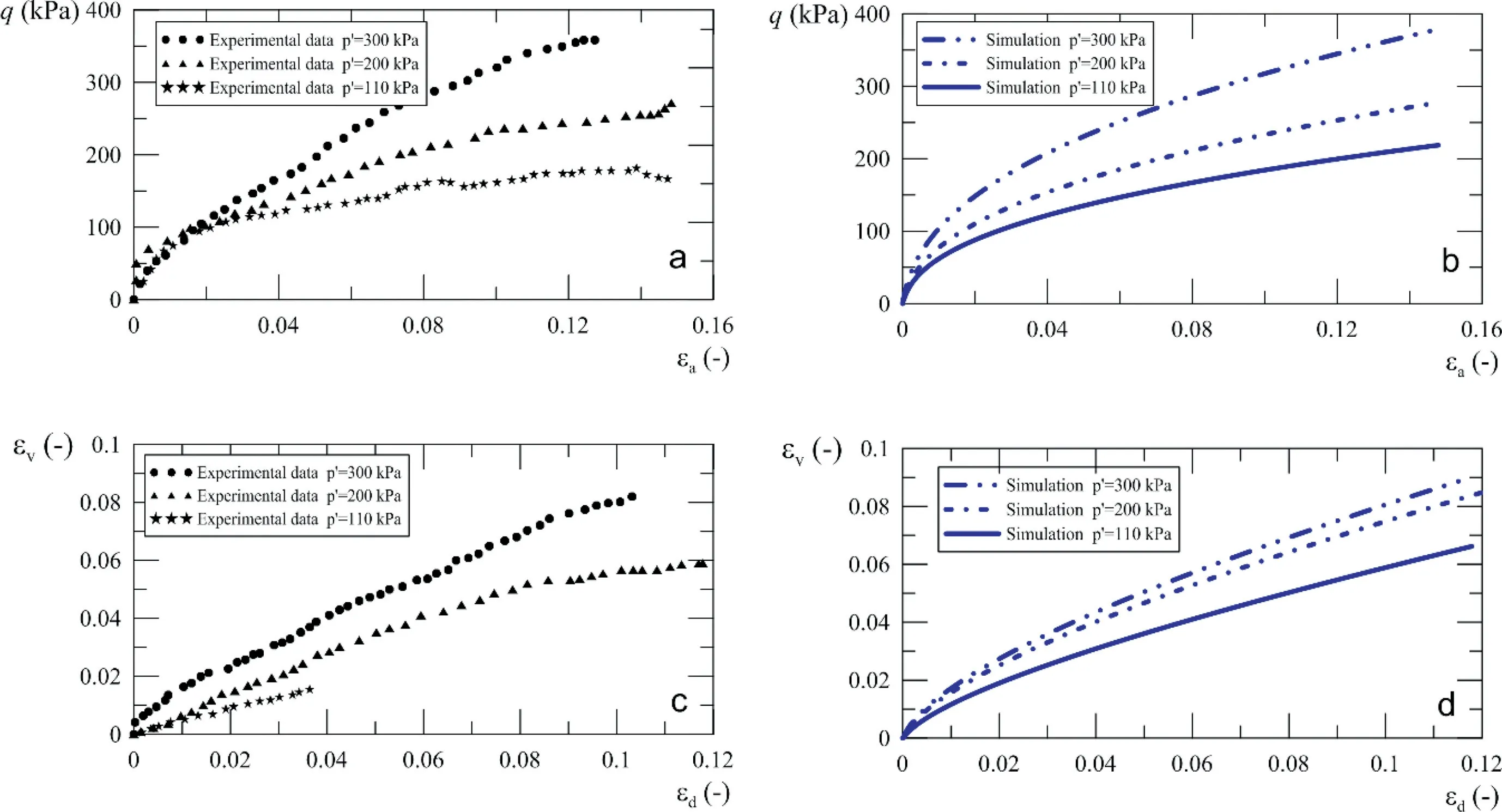
Fig.17. Simulations of triaxial tests in drained conditions.

Table 5Brasilia Clay parameters used in this study.

6. Conclusions

This paper demonstrated the validation and development of a theoretical framework for a new model to simulate the behavior of structured tropical soils.Simulations of the compression and shear trajectories tests were made by validating the model against experimental results in the literature for structured clays from different regions of the globe:Corinth Marl Clay(Greece),Bangkok Clay(Thailand)and Rio de Janeiro Clay(Brazil).In addition to these simulations, a plan for tests of shear and compression trajectories was made to validate the model in tropical clay with structure from Brasilia City. It shows that the model is able to simulate the soils with structure.

The constitutive model proposed in this context is a variation of the modified Cam Clay which has been widely used in the geotechnical field. This model used the well-known original five parameters of Cam Clay and included two additional parametersc(to represent the overconsolidation of the soil) andb(to represent the structure of the soil) into the functionsGandQ.The addition of the two parameters and state variables was done to better represent the influences of density and structure on soils. One of the main advantages of the model is that it can simulate accurately the behavior of natural soils with bonds, as well as reconstituted soils. Additionally, the two new parameters influence the flow rule of model that adopts non-associated flow rule. The new two parameters can be obtained from calibration of an isotropic compression test or oedometer test and triaxial drained test.

Declaration of Competing Interest

The authors wish to confirm that there are no known conflicts of interests associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The authors express their gratitude to Universidad Nacional de Colombia and Universidade de Brasília in Brazil for their technical and financial support of this study on constitutive models for residual soils.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2019.12.006.