Synchronization mechanism of clapping rhythms in mutual interacting individuals*
Shi-Lan Su(蘇世蘭), Jing-Hua Xiao(肖井華), Wei-Qing Liu(劉維清), and Ye Wu(吳曄)
1School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China
2School of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China
3Computational Communication Research Center,Beijing Normal University,Zhuhai 519087,China
4School of Journalism and Communication,Beijing Normal University,Beijing 100875,China
Keywords: synchronization mechanism,clapping rhythm,numerical simulation
1. Introduction
The spontaneously clapping synchronization process in a large concert hall is one of the typical synchronization phenomena. In the research of synchronization experiments, the complex clapping coupling system has been widely studied because of its simple setting and operation. Many physical methods have been used to study group clapping coupling dynamics, and a lot of rich results have been obtained.[1–10]N′eda et al.[1–5]show that the key to the clapping synchronization is the period-doubling of the clapping rhythms and model the globally coupled two-mode stochastic oscillators to explain the causes of the emergence and disappearance of group clapping synchronization. Xenides et al.[6]explain the emergence of spontaneous clapping synchronization based on the decision-based queuing process and point out that the audiences’clapping synchronization originated from the homoplasy of human behavior. Deyi Li et al.[7,8]construct a nonlinear emergence model based on the famous”crowd psychology”theory to analyze the conditions for the emergence of the clapping synchronization in concert halls and determine the law that the number and the distribution of informed subjects in the complex network affect the clapping synchronization.Mann et al.[9]find that clapping behavior is socially contagious, and the probability of being infected and beginning to clap is directly proportional to the number of audiences who have already started clapping. Michael Thomson et al.[10]find that the group’s clapping frequency in the synchronous state increases more quickly for the larger group size due to an asymmetric sensitivity in aural interactions. Previous studies on clapping synchronization are mostly from the viewpoint of rhythmic group applause, where the synchronization mechanism among a group is realized through the global output of the clapping system.[1–10]However, the interaction and the synchronization mechanism of the local individuals can reveal the synchronous processes more elaborately. Furthermore,the clapping rhythm interaction between two individuals can be taken as an example of the interpersonal coordination process.The research on the clapping interaction process can provide some new viewpoints for the interpersonal coordination.Here,we focus on the mode of interaction between two clapping individuals and aim to uncover the synchronization mechanism underlying clapping interaction by observing two individuals’synchronizing rhythms.
Our previous studies[11]show that the generation of clapping rhythm is predictive in the two individuals’clapping synchronization process. That is to say,the participant adjusts his(her)clapping period based on the upcoming rather than preceding clapping period of his(her)partner in the clapping synchronization process. Generally,anticipation can be classified as a strong one originated from lawful regularities embedded in the ordinary functioning mode of an organism and its environment, and a weak one originated from the internal model of the organism.[12]The typical examples of the strong anticipation are commonly observed in the physical system[13]and the biological system.[14]Moreover,strong anticipation can be revealed by the presence of long-range cross-correlations(LRCCs) between two time series.[15]The LRCC indicates that two series of the clapping period form a self-similar (fractal)structure. Here,self-similarity implies that trends in the clapping periods are likely to repeat on different timescales,i.e.the fluctuation pattern of one individual’s clapping period tends to be reproduced in a statistically similar manner at a later time-even in another individual’s clapping.[16]The LRCC exists widely in nonlinear coupling systems such as finance,[17]transportation,[18]climate,[19]human behavior.[20]In this paper, we study the synchronizing clapping rhythms related to the synchronization mechanism of individuals’ coordination processes. More specifically, we show that the synchronizing clapping period series of two individuals exhibit the LRCCs,which appears to be a general phenomenon because the LRCCs are found in all experimental results. Therefore, the interaction of the clapping rhythms can be seen as a stronganticipation process.
Strong anticipation has emerged as a new framework for studying prospective control. Stephen et al.[21]propose two approaches to achieve a strong anticipation process. The first approach assumes that the strong anticipation process is based on local interactions of two complex systems. Voss[22]presents an interesting example, which shows that during the synchronization process between the slave system and the master system,the time delay in the master system will cause the future synchronization state between the slave system and the master system. This local strong anticipation process is clearly pointed out by the coupled oscillator model. This concept assumes that anticipation is based on local time scales.The second approach assumes that the strong anticipation process is based on the global matching in statistical structures of fluctuation in long timescales of two complex systems.Stephen et al.[23]present initial evidence for the strong anticipation in an experiment which analyzes synchronization with a chaotic metronome. In the tapping task of synchronization with a chaotic metronome, the local prediction is difficultly conceivable, because of the intrinsically unpredictable nature of the external pacing signal. In fact,Stephen et al. point out that in this case, the tapping behavior shows the exhibited a mix of reaction, proaction (see Ref. [23]), and synchronization to the chaotic metronome signal. In this strong anticipation, organisms are not adapted to the state of the environment,but to their statistical structure. The origin of the strong anticipation process often appears elusive in many complex systems.[20]In this paper,we introduce two stochastic models for mutually interacting clapping individuals that generate the LRCCs and provide a physiologically motivated explanation for the occurrence of the clapping synchronization process.
Notably,the study on the rhythm of human movement has great practical significance. For example, the ability to synchronize with the beat may provide therapeutic applications for Parkinson’s disease.[24]The ability to synchronize with the beat of a metronome is deficient in all Huntington disease patients,deteriorated with the severity of disease.[25]This study provides a statistical framework for studying the internal synchronization mechanism of other complex systems.
The organizational structure of this paper is as follows.In Section 2, we introduce the experimental setup and procedure. We present the preliminary experimental results and discussion in Section 3. The theoretical model and the corresponding numerical simulation results are given in Section 4.Finally,we give the main conclusions.
2. Experimental setup and procedure
Twenty-four students from Beijing Normal University volunteered for the study with an average age of 24±3 years old. All participants have no known neurological injuries or musculoskeletal injuries in the upper limbs. The ethics committee of School of Science, Beijing University of Posts and Telecommunications approved the study. The clapping coupling system we constructed, which is the same as that in our previous study,[11]consists of participants, radio devices,and recording devices. Participants’ clapping dynamics are recorded with condenser microphones (frequency response:80–14000 Hz, sensitivity: -73±3 dB at 1000 Hz), which are light, cheap, and easily accessible to students. The microphones are all connected to different personal computers running Adobe Audition software,which is used to record the participants’clapping signals in files simultaneously.The temporal occurrences t1,t2,...,tnof the beats are extracted from the recorded signals. In order to measure the coupling state of two participants’ applause quantitatively, the average synchronous clapping errors(SEs)between the two clapping time series of participants A and B are calculated,

where n is the length of the time series,and SEs represents the degree of clapping synchronization of two participants where larger SEs correspond to weaker synchronization. The clapping period reads qi=ti-ti-1,i=1,2,...,n with t0=0,representing the participant’s clapping rhythm. The clapping period series is the non-stationary time series to be analyzed in this paper (Fig. 1(a)). The experiments are conducted as following respectively.
Experiment I: Bidirectional clapping interaction experiments A.24 participants are randomly arranged into 12 groups with two participants in each group. In each group, two participants sit back-to-back in a chair and begin to clap simultaneously without the influences of other groups. The applause of two participants in each group is recorded simultaneously with the microphone accessed to a computer. Each recording typically lasts 30–40 s and contains 70–110 beats.
Experiment II:Bidirectional clapping interaction experiments B.We record the swing sound of a metronome(period 0.5 s) into MP3 audio, which lasts for 40.5 s and contains a total of 81 beats. The process of Exp. II is similar to that of Exp. I; the difference is that two participants in each group are required to clap simultaneously under the influence of the playing back of the recorded beats of the MP3 audio from the metronome. The applause of two participants in each group is recorded simultaneously with the microphone accessed to a computer.
Experiment III: Unidirectional clapping interaction experiments A. 24 participants are randomly arranged into 12 groups with two participants in each group. In each group,the applause of one participant(marked as A)is recorded into MP3 audio, which lasts for 30–40 s and contains a total of 70–110 beats. The other participant(marked as B)is required to clap simultaneously with the recorded beats from participant A. The applause of participant B and the recorded beats of participant A are recorded simultaneously with the microphone accessed to a computer.
Experiment IV: Unidirectional clapping interaction experiments B. Each participant is required to clap simultaneously with the recorded beats of the metronome (period 0.5 s) of Exp. II. The applause of the participant and the metronome’s beats are recorded simultaneously with the microphone accessed to a computer.
In this paper, we compare the Exps. I and II to analyze the influence of extra regular signals on clapping synchronization process. The purpose of a comparison of unidirectional clapping interaction processes(Exps.III–IV)with the bidirectional clapping interaction processes (Exp. I), is to obtain a more comprehensive understanding of the clapping synchronization process.
3. Experimental results and discussion
For analysis of the cross-correlations between two clapping period series(Fig.1(a)),a modified version of detrended cross-correlation analysis (DCCA), which has been proved to be available in analyzing non-stationary signals in human behavior,[16]is introduced. In the method of the DCCA (see the supplementary materials for the detailed algorithm), the relations between the detrended covariance F2DCCA(s)and the window of size s determine the relation between two different time series. The LRCCs are present if F2DCCA(s)follows a power law F2DCCA(s)~s2λwith λ >0.5. In contrast,λ =0.5 indicates the absence of the LRCC.[16,20]Note that the limitation of the total length of the experimental data may affect the analysis results obtained from the method of the DCCA.[26]Because of the strong correlation between the two fractal analysis methods, the DCCA and detrended fluctuation analysis(DFA)(see the supplementary materials for the detailed algorithm),the interpretation of λ is similar to that of the DFA exponent α,and the errors of the DCCA exponent λ and the DFA exponent α are expected to be of a comparable size. Here,we estimate the error of the DCCA exponent λ by analyzing the error of the DFA exponent α in short time series. As shown in Fig.S1,the DFA results for the scaling exponent α =0.5 are expected to have a SD of ~±0.15 for data sets that are of the same size as ours,which is basically consistent with the calculation results of Ref.[26]. Therefore,we estimate that λ =0.5 is expected to have a SD of ~±0.15 for time series that are of the same size as ours.
We show a representative example of the findings from a recording of participants A and B clapping in synchrony(Exp. I) in Figs. 1(a) and 1(b). Evidence for the LRCCs between qAand qBis shown in Fig.1(b)with the DCCA exponent λ =1.46. The two participants are rhythmically bound together on a timescale up to the end, and the generation of the next beat of one participant depends on all previous clapping periods of both participants. The LRCCs are found in all performances(red circles in Fig.1(g)where all DCCA exponents are higher than 0.5±0.15(black lines)),even though the SEs between each pair of participants are different when two participants are synchronizing clapping rhythms(Exp.I).Thus,the interaction of clapping dynamics is a kind of stronganticipation process. In contrast, the LRCC is not significant in the Exp.II(blue rhombuses in Fig.1(g),a part of the DCCA exponents are lower than 0.5±0.15(black lines)). Moreover,the clapping periods of the two participants of each group in the Exp.II tend to be 0.5 s which is the metronome’s interbeat intervals (see Fig. S2, the clapping periods of all recordings in the Exp. II is 0.5±0.004 s). This result indicates that the introduced extra metronome’s beats strongly affect the two interacting participants in each group and the weaken interaction between themselves as shown the results in the Exp.II.
To sum up, we show that clapping interaction processes exhibit the LRCCs, but the LRCCs may be destroyed when the interaction processes are disturbed by the regular signals of the metronome. The conclusion indicates that the local interaction of two complex systems is a necessary prerequisite for the existence of the LRCC,i.e.,clapping synchronization process may result from the local interactions between two clapping individuals,which is consistent with the first approach to achieve the strong anticipation process proposed by Stephen et al.[21]
What are the correlations between clapping rhythms in unidirectional interaction processes (Exp. III)? Surprisingly,we also find the LRCCs in the unidirectional interaction processes(green star in Fig.1(g),all DCCA exponents are higher than 0.5±0.15 (black lines)). Obviously, the unidirectional clapping synchronization processes also can be seen as a strong-anticipation process.

Fig. 1. Two participants A and B synchronizing their clapping beats: comparison of experiments (a)–(b) with the model I (c)–(d) and model II(e)–(f). (a) The clapping periods of 80 beats of participant A (red curve) and B(blue curve) exhibit slowly varying trends. (b) Evidence of the LRCCs between qA and qB. The DCCA exponent is λ =1.46. (c)–(d) Model I for K1 =0.1, K2 =0.2, n=80, the initial clapping period qA1 =0.46,qB1 =0.45,the initial asynchrony SA1 =-0.037,wA(n)~N(0.0003,0.00582),wB(n)~N(-0.0002,0.00322)predicts λ =1.5,in excellent agreement with the experimental result. (e)–(f)Model II for a1=a2=0.2,n=80,the initial asynchrony SA1 =0,B1(n)~N(0.0054,0.01072),B2(n)~N(-0.0076,0.01072),b1=b2=1,q*A(n)and q*B(n)simulated by the ARFIMA procedure with d=0.4,W =0.8, δ1 =δ2 =0.04, εt,A(εt,B)~N(0,1) predicts λ =1.44, in excellent agreement with the experimental result. (g) The SEs vs. the DCCA exponent in the Exps.I–III and models I and II.Partial recordings of the Exp.II(blue rhombuses)are consistent with the absence of the LRCC,λ <0.5±0.15(black lines). Models I and II generate N=12 pairs of clapping period series with a length n=80,respectively. The predicted λ of model I(black stars)and model II(yellow asterisks)are excellent agreement with the results of Exp.I(red circles).
We use linear redundancy to measure the predictability of the period series of participant A’s clapping recording of each group in the Exp. III. Linear redundancy is a kind of information-theoretic statistics indexing the linear correlation across time, which is varying inversely with entropy.[23]For given observable y(t),calculate linear redundancy on a set of n lagged copies y(t+i),i=1,...,n. Over n time steps,linear redundancy equals

where ciiare the diagonal elements of the n×n covariance matrix and σiare the eigenvalues of the n×n covariance matrix. It should be noted that the given time series should be detrended before calculating the linear redundancy. We compare the linear redundancy of the period series of participant A’s clapping recording in the Exp. III with the linear redundancy of the series of the metronome’s interbeat intervals in the Exp. IV. The linear redundancy (0.38±0.18)for the period series of participant A’s clapping recording of each group is significantly lower than that for the series of the metronome’s interbeat intervals(1.03±0.68)(double sample t-test,P=0.0001). In other words,the period series of participant A’s clapping recording in the Exp.III exhibit extremely minimal predictability. In such a situation, local predictions seem to be difficult to work, because of the unpredictable internal nature of the time series of clapping recordings of participant A in each group. Therefore,we suggest that the clapping rhythms of two interacting individuals are cross-correlated in nature, which could be interpreted as that the clapping synchronization process may result from the global coordination in statistical structures of fluctuation in long timescales between two clapping individuals. This result is consistent with the second approach to achieve a strong anticipation process proposed by Stephen et al.[21]
By summarizing the analysis results in Fig. 1, we suggest that the clapping synchronization process may result from not only the local interaction between two clapping individuals, but also the global coordination in statistical structures of fluctuation in long timescales between two clapping individuals. This hypothesis requires additional investigations,as global coordination matching and local interactions are previously considered as mutually exclusive.[27]We will further explore this hypothesis in the theoretical model.
Since the method of the DCCA is not available to exhibit the natures of local interactions,the method of windowed detrended cross-correlation (WDCC) which has been widely used recently,[27,28]is introduced to explore the local crosscorrelation structure of two time series. For the two clapping period series qAand qBof length n (Fig. 1(a)), we calculate the cross-correlation function of the short window with length L from lag-10 to lag 10(see the supplementary materials for the detailed algorithm). In order to avoid detecting spurious cross-correlation due to the presence of drift in the window,the

data in each window is detrended before calculating the crosscorrelation. Noted that since the WDCC uses a very narrow window L (L=15 in this paper) and removes linear trends,it is difficult to find a significant correlation in the classical sense(i.e.,based on the Bravais-Pearson’s correlation test[29]).Therefore,we pay more attention to the average WDCC coefficients’symbols than their statistical significance.[29] We test the signs of averaged coefficients with two-tailed location ttests by comparing the obtained values to zero.We present the WDCC between qA and qB in Fig.2. Location t-tests show that the lag-zero cross-correlation is negative, and positive cross-correlations appear at lag -2 and lag-1 on the one hand,and at lag 1 and lag 2 on the other in the Exp.I.In the Exp.II,there are positive cross-correlations at lag-2,lag 1,and lag 2. In the Exp.III,the lag-zero crosscorrelation is negative, and the cross-correlations are positive at lag 1 and lag 2.In the Exp.IV,the lag-zero cross-correlation is negative, and the cross-correlations are positive at lag -2,lag -1, and lag 2. These results confirm that the clapping synchronization process seems to be emerged from period-toperiod influences.[20]We will study this conclusion in the theoretical model. Moreover, there is a positive lag-zero crosscorrelation in the Exp. II. The result indicates that clapping synchronization may occur within each period between the two participants in the Exp. II.[20] Note also that the WDCC function exhibits an asymmetry between the lag -1 and the lag 1 coefficients in the Exp.I,which reveals a leader/follower relationship between two participants.[29]
Fig.2. Average windowed detrended cross-correlation functions(from lag-10 to lag 10)between qA(n)and qB(n)(N =12)for the Exp.I in(a),Exp.II in(b),Exp.III in(c),and Exp.IV in(d). *: two-tailed location t-tests, p <0.01.
Another variable that may play an essential role during the interaction process is asynchrony, which is defined as the time delay between the occurrence of a given event in one individual and that of the corresponding event in the other.Many studies suggest that synchronization with regular metronome occurs based on discrete correction of asynchronies.[30]Asynchronies are calculated as the differences between the cumulated sums of the two clapping period series qA(n)and qB(n)generated in the synchronization process

We calculate the WDCC between SA(n) and qA(n), and the WDCC between SB(n)and qB(n).
The results of the WDCC between SA(n) and qA(n) are shown in Fig.3.We get similar results for the WDCC between SB(n)and qB(n). There are significant positive lag-zero crosscorrelation between SA(n) and qA(n) in the Exps. I–IV. The positive cross-correlations can reveal that the current clapping period in the clapping interaction process is based on the direct correction of the previous asynchrony.[30]In other words,the positive cross-correlations between SA(n)and qA(n)(and between SB(n) and qB(n)) may be the origin of the clapping synchronization process. We will study this problem in the theoretical model.
In the process of time series analysis, it is necessary to consider both the short-term and the long-term analysis,[31,32]since the results of the DFA may fail to determine the impure fractal process of biological series[33,34]due to the influences of noise and short-term related processes on the local scales.Because of the strong correlation between the two fractal analysis methods,the DCCA and the DFA(see the supplementary materials for details), it is necessary to explore the effects of the noise and short-term related processes on the local scales of clapping synchronization process by estimating the regression slopes in the short term (λs) (on the first five points of the DCCA diffusion plot)and the long term(λl)(the last five points of the DCCA diffusion plot).[20]
Figure 4(a) presents a representative example from recorded data of two participants clapping in synchrony(Exp. I) to show the effects of the noise and the short-term related processes on the local scales. The short-term exponent λs=2.23 is larger than the long-term exponent λl=1.53,which indicates FDCCA(s) decreases dramatically in the short term, denotes a quite low level of covariance in the short term, and shows that the local synchronization of the clapping rhythm of the two interacting participants is quite weak.This nature is widespread in the Exp.I.As shown in Fig.4(d),the short-term exponents of recordings in the Experiment I are significantly higher than the long-term exponents(most of the red circles in Fig. 4(d) are below the black line, double sample t-test,P=0.003). This result indicates that the interaction process of two participants clapping in synchrony (Exp. I) is weak synchronization in the local scope, consistent with the results of Ref.[20]on interpersonal coordination tasks. Similarly, the short-term exponents of recordings in the Exp. III are significantly higher than the long-term exponents(most of the green stars in Fig. 4(d) are below the black line, double sample t-test,P=0.019). In contrast,this nature is not significant in the Exp.II(part of the blue rhombuses are above the black line in Fig.4(d),double sample t-test,P=0.209). That is, the local synchronization of the clapping rhythm of each group in the Exp. II is relatively stable. We further analyze and find that the average coefficient of variation(CV)of interaction processes in Exp.II is lower than that in the Exps.I and III (see Fig. S2), which indicates that the variability of clapping periods becomes smaller when the interaction process of two participants is constrained by the regular signals of the metronome.Therefore,we conclude that the clapping rhythms in clapping synchronization processes(Exp.I)are closely related in the global scope,but weak synchronization in the local scope. In addition, the local synchronization of the clapping interaction process will be strengthened when the interaction process is affected by the regular signals of the metronome.

Fig.3. Average windowed detrended cross-correlation functions(from lag-10 to lag 10)between SA(n)and qA(n)(N =12)for the Exp.I in(a),Exp.II in(b),Exp.III in(c),and Exp.IV in(d). *: two-tailed location t-tests, p <0.01.

Fig. 4. Effect of the noise and short-term related processes on the local scales of the clapping synchronization process. (a) A representative example of the Exp.I.The λ short-term exponent is λs=2.23,the λ long-term exponent is λl=1.53. The long-term exponent is shorter than the short-term exponent. (b)Model I for n=80,K1 =0.1,K2 =0.2,the initial clapping period qA1 =0.45,qB1 =0.46,the initial asynchrony SA1 =0.05,wA(n)~N(0.0004,0.00932),wB(n)~N(-0.0007,0.00682)predicts that the λ short-term exponent is λs=2.02,and the λ longterm exponent is λl=1.74.The long-term exponent is shorter than the short-term exponent,in excellent agreement with the experimental result in(a). (c)Model II for a1=a2=0.2,n=80,the initial asynchrony SA1 =-0.14,B1(n)~N(0.0051,0.00462),B2(n)~N(-0.0043,0.00412),b1=b2=1,q*A(n)and q*B(n)simulated by the ARFIMA procedure with d=0.4,W =0.8,δ1=δ2=0.07,εt,A(εt,B)~N(0,1)predicts that the λ short-term exponent is λs=2.04,and the λ long-term exponent is λl=1.47.The long-term exponent is shorter than the short-term exponent,in excellent agreement with the experimental result in (a). (d) The long-term exponent λl vs. the short-term exponent λs in the Exps. I–III and models I–II.The analysis results of models I and II are based on 12 pairs of time series generated in Fig.1(g), respectively. Contrary to the results of the Exp.I,there is no significant difference between the long-term and short-term exponents reproduced by the model I(black stars). There is a significant difference between the long-term and short-term exponents reproduced by the model II(yellow asterisks),which is excellent agreement with the results of the Exp.I(red circles).
4. Theoretical model and the results of numerical simulations
4.1. Theoretical model
When exploring the dynamics of a group of audiences,each individual receives the average field of all audiences which can be taken as imposing stochastic and periodical driving on each individuals. That is, the synchronization mechanism among a group is realized through the global output of the clapping system.[1–8]Here, we mainly focus on the regimes of synchronous process of two interacting individuals where the direct interaction can’t be omitted. Our experimental results show that the clapping period series of two participants exhibit the LRCCs, which indicates that the interaction of clapping rhythm can be seen as a strong-anticipation process. However, the origin of synchronization and the LRCC often appears elusive.[20]We examined two distinct hypotheses to explain the synchronization mechanism of the observed clapping interacting process.
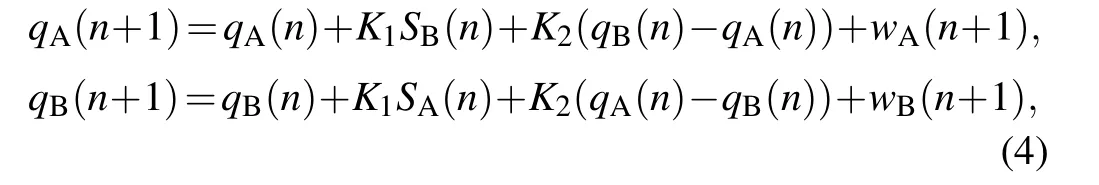
Hypothesis I We consider that the occurrence of the clapping synchronization process is based on local interactions of two complex systems. This hypothesis is consistent with the first approach to achieve a strong anticipation process proposed by Stephen et al.[21]We observe three experimental results to support the hypothesis. First, the local interaction of two complex systems is a necessary prerequisite for the existence of the LRCC(Fig.1). Second, the clapping synchronization process emerges from period-to-period influences (Fig. 2). Third, the clapping synchronization process’s current clapping period is based on the direct correction of the previous asynchrony(Fig.3). Considering the above three results we observed in our experiments, we propose that the current clapping period is based on asynchrony correction and period correction.[35]To test the hypothesis, we construct a mathematical model(model I)in Eq.(4)based on the method of Refs.[7,8,11]where qA(n) (qB(n)) is the clapping period of participant A(B) in the nthclapping, SA(n) (SB(n)) is asynchrony between participants A and B in the nthclapping (see Eq. (3)),and wA(n) (wB(n)) is a Gaussian-distributed noise term with mean value μA(μB)and standard deviation σA(σB)(the values of the mean and standard deviation refer to our previous research[11]). The coupling strength 0 <K1(K2)<1 describes the rate of compensation of an asynchrony (clapping period deviation) between individuals in the generation of the next beat. For K1=K2=0, there is no interaction between individuals. For K1(K2)≥1, individuals are overcompensating.As can be seen from Ref.[11],the clapping periods of all individuals obey Gaussian distribution,and the initial values of the periods of two individuals can be generated by Gaussian distribution. Asynchronies are the differences between the cumulated sums of the two clapping period series,thus involving all previous elements of the time series of clapping periods of both participants. Therefore, the two clapping period series qA(n)and qB(n)generated by the model I can exhibit the LRCCs.
Hypothesis II Considering the LRCCs we observed in unidirectional interaction with unpredictable signals(Exp.III)(Fig.1),we propose that the clapping synchronization process may result from not only the local interaction between two clapping individuals but also the more global coordination between two clapping individuals. This hypothesis is consistent with the conclusion of Ref. [29]. To test this hypothesis, a mathematical model(model II)is constructed in Eq.(5)based on the method of Ref.[29],

4.2. The results of numerical simulations
We generated 12 pairs of period series qA(n) and qB(n)by the model I. All the numerical simulations of the model I are done on these 12 pairs of time series.The two clapping period series qA(n) and qB(n) generated by the model I exhibit the LRCC,which is consistent with the analysis results of our experiments. As shown in Fig.1,a comparison of the model I(Figs.1(c)and 1(d))with our experiments(Figs.1(a)and 1(b))shows excellent agreement. The predicted DCCA exponents λ >0.5±0.15 by the model I (black stars in Fig. 1(g)) are consistent with those of the Exp. I (red circles in Fig. 1(g)).Model I can replicate the weak local synchronization. As shown in Fig.4(b),the short-term exponent λs=2.02 is larger than the long-term exponent λl= 1.74, which is consistent with the analysis results of our experiments(Fig.4(a)). However, the significant difference between the long-term exponent and the short-term exponent cannot be effectively replicated by the model I,which is not consistent with the Exp.I.As shown in Fig. 4(d), the difference between the long-term exponent and the short-term exponent in the model I is not significant (part of the black stars are above the black line in Fig. 4(d), double sample t-test, P=0.32). Furthermore, in the results of numerical simulations of the model I, there are not positive lag-1 and lag 1 cross-correlation between qA(n)and qB(n) (Fig. 5(a)), and there is not positive lag 0 crosscorrelation between qA(n)and SA(n)(Fig.5(b)),in contrast to the experimental observations(Figs.2(a)and 3(a)).
The numerical simulations of the model I show that the local interactions between two participants are not enough to completely reproduce the clapping synchronization process,which is consistent with the conclusion about the source of strong anticipation in Ref.[20]. In our opinion,the hypothesis I is not enough to explain the synchronization mechanism of the observed clapping interacting process.
Results are more convincing with the model II based on local interactions and global matching. We generated 12 pairs of period series qA(n)and qB(n)by the model II.All the numerical simulations of the model II are done on these 12 pairs of time series.The two clapping period series qA(n)and qB(n)generated by the model II exhibit the LRCC,which is consistent with the analysis results of our experiments. As shown in Figs.1(e),1(f),and yellow asterisks of Fig.1(g),the predicted DCCA exponents λ >0.5±0.15 by the model II are consistent with those of the Exp. I (Figs. 1(a), 1(b), and red circles of Fig.1(g)). Model II can effectively replicate the weak local synchronization. As shown in Fig.4(c), the short-term exponent λs=2.04 is larger than the long-term exponent λl=1.47,which is consistent with the analysis results of our experiments(Fig. 4(a)). The significant difference between the long-term exponent and the short-term exponent can be effectively replicated by the model II,which is consistent with the Exp.I(red circles in Fig.4(d)). As shown in Fig.4(d),the short-term exponents in the model II are significantly higher than the longterm exponents (most of the yellow asterisks in Fig. 4(d) are below the black line,double sample t-test,P=0.0008). There are positive lag-1 and lag 1 cross-correlations between qA(n)and qB(n)(Fig.5(c)),and positive lag 0 cross-correlation between qA(n)and SA(n)(Fig.5(d)),in accord with the experimental observations(Figs.2(a)and 3(a)).
The numerical simulations of the model II can completely reproduce the clapping synchronization process. Therefore,we believe that the hypothesis II is enough to explain the synchronization mechanism of the observed clapping interacting process. The conclusion prove theoretically that the generation of clapping synchronization process needs to consider both local interaction and global matching.
Obviously,the comparison of the models I and II with our experiments shows that the model II based on local interactions and global matching can effectively reveal the synchronization mechanism of clapping rhythms in mutual interacting individuals, and the model I can not. In previous studies,global matching and local interaction in the theoretical framework to explain the synchronization process are considered to be mutually exclusive.[27]However, our simulations suggest that beyond a clear discrete process of trial-to-trial correction of asynchronies and periods, a global matching between the two participants should be considered for a complete account of the experimental results. This conclusion may be the most crucial point in our present work.
It should be noted that since the study on the appearance and disappearance of clapping synchronization states is the main content of our previous study,[11]this part is not covered in the numerical simulations,which is different from previous studies on synchronization phenomena.[1–8,36,37]In fact, our model II can not only reveal the synchronization mechanism underlying clapping interaction(see Figs.1,4,and 5),but also reproduce the synchronization state of the clapping process.As shown in Fig. S7(c) of the supplementary materials, we can observe the synchronization states of the clapping interacting process, when 0.0004b21-0.0048b1+0.0546 <a1<-0.0004b21+0.0045b1+0.9463 and 0 ≤b1≤33(b1=b2and a1=a2in this paper). In addition,because this paper aims to uncover the synchronization mechanism underlying clapping interaction, the two models we proposed represent two synchronization mechanisms of interpersonal coordination.[23,29]Therefore, in the numerical simulations, we discuss which model can completely reproduce the statistical characteristics of the clapping rhythms, and does not involve the influence of each term in the model on the synchronization process.In the supplementary materials, we discuss the influence of each term in the model II on the synchronization process and find that the models without coupling terms(or without noise terms) can not completely reproduce the statistical characteristics of the clapping interaction(see Figs.S7,S8,S9,and S10 in the supplementary materials),and are not enough to explain the observed clapping interacting process.

Fig.5. Average windowed detrended cross-correlation functions(from lag-10 to lag 10)between qA(n)and qB(n)(N=12)for the model I in(a)and model II in(c). Average windowed detrended cross-correlation functions(from lag-10 to lag 10)between SA(n)and qA(n)(N=12)for the model I in(b)and model II in(d). *: two-tailed location t-tests, p <0.01.
5. Conclusion
The application of the synchronization in the practical system is important. However, the inner mechanism of the synchronous process is also an important question attracting many attentions. Here,we try to reveal the regimes of the synchronization process with a single clapping coupling system.First, the two individuals’ synchronizing clapping rhythms exhibit the LRCC; that is, the clapping synchronization process is a strong anticipation process. Strong anticipation has emerged as a new framework for studying prospective control. However, the origin of the strong anticipation process often appears elusive in many complex systems. Our results on the clapping synchronization process between two individuals provide new support for the theory of strong anticipation.Second,the clapping synchronization process may result from the local interaction between two clapping individuals by comparing the DCCA exponents and the WDCC coefficients between Exp. I and Exp. II. Third, considering the LRCCs we observed in unidirectional interaction with unpredictable signals (Exp. III), we propose that the clapping synchronization process may result from not only the local interaction between two clapping individuals but also the more global coordination between two clapping individuals. Forth, the rhythms in clapping synchronization processes are closely related in the global scope, but weak synchronization in the local scope by analyzing the effects of the noise and short-term related processes on the local scales.Finally,we introduce two stochastic models for mutually interacting clapping individuals that generate the LRCCs and prove theoretically that the generation of clapping synchronization process needs to consider both local interaction and global matching. Our model can also be applied to other complex systems of interaction, such as synchronization in finance, heartbeat, and traffic, where the origin of the LRCC and the resulting dynamics are often elusive.Furthermore,the clapping coupling system has the advantages of cheap materials and simple operation; it is very suitable for teaching demonstration and theoretical research of the synchronization phenomenon.
Some essential viewpoints in this paper are worthy of further study and discussion.For example,adding regular signals in the interaction process can weaken the interaction between individuals and strengthen the synchronization process’s stability. Then, whether adding regular signals to the complex system can control the system. Further, the WDCC function exhibits an asymmetry between the lag-1 and the lag 1 coefficients, which reveals a leader/follower relationship between two participants in each group. This result is helpful to identify the leader in the group clapping coupling system and determine the influences of network topology on the interaction characteristics. In addition, the stability of interacting processes with unpredictable signals is better than that with regular signals (see the analysis results of deviation series in the supplementary materials),which is fantastic and worthy of further study.
- Chinese Physics B的其它文章
- Two-dimensional finite element mesh generation algorithm for electromagnetic field calculation*
- Stable water droplets on composite structures formed by embedded water into fully hydroxylated β-cristobalite silica*
- Surface active agents stabilize nanodroplets and enhance haze formation*
- Theoretical study of the hyperfine interaction constants,Land′e g-factors,and electric quadrupole moments for the low-lying states of the 61Niq+(q=11,12,14,and 15)ions*
- Ultrafast photoionization of ions and molecules by orthogonally polarized intense laser pulses: Effects of the time delay*
- Probing time delay of strong-field resonant above-threshold ionization*

