Si-Qi Zhang(張思琪), Zhi-Jie Yang(楊志杰), Zhi-Xian Lei(雷志仙), Wei Feng(馮偉),Sheng-Peng Zhou(周勝鵬), Kai-Jun Yuan(元?jiǎng)P軍), Xue-Shen Liu(劉學(xué)深),and Jing Guo(郭靜)

Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

Keywords: photoelectron momentum distributions,photoelectron angular distributions,intense orthogonally polarized laser pulses,ultrafast photoionization model

1. Introduction

The strong-field physics is a hot topic in recent years,and interaction of laser with atoms or molecules can produce different physical phenomena,including high order harmonic generation (HHG),[1–3]strong-field ionization, and nonsequential double ionization (NSDI).[4]The electron processes of molecular reaction dynamics are investigated with the rapid advances of ultrashort and ultrafast intense laser technology[5–7]in the attosecond time regime(1 as=10-18s)and sub-nanometer dimensions.[8–10]The pump-probe technique is developed as a new tool in the femtosecond time regime.[11]Attosecond electron motion can be observed by monitoring photoelectron signal or photoelectron momentum distributions,for example,in the pump-probe technique,photoelectron momentum distributions are a function of the time delays between the pump pulses and the probe pulses.[12–15]In the past few years, a lot of researchers paid attention to photoelectron momentum and angular distributions of atoms and molecules which encode valuable and fruitful information about the electron dynamics.[16–18]It has been illustrated that the photoelectron momentum distributions(PMDs)of the He atom present vortex patterns,[19]which show the sensitivity of momentum distribution to the phases, time delays and the helicity of the laser pulses. Molecular photoionization of H+2presents electron vortices in PMDs in the circularly polarized laser fields,[18]such vortex patterns can only be observed for counter-rotating and co-rotating circularly polarized fields. In addition, Yuan et al.[20,21]demonstrated the molecular photoelectron-momentum distribution (MPMD) depends on the molecular orbital symmetry.

Orthogonally polarized laser pulses are new powerful tools for steering attosecond electron motion of atoms and molecules.[22,23]The electronic dynamics of molecules in orthogonally polarized attosecond ultraviolet laser pulses has been studied before.[21,24]It has been found that molecular photoelectron momentum and angular distributions of H+2molecules are sensitive to the relative phase of the laser pulses.However,the sensitivity of the ionic and molecular photoelectron momentum and angular distributions to the time delays in orthogonal polarized laser fields has not been studied. In this work, we present photoelectron momentum and angular distributions of ions and molecules by orthogonally polarized laser pulses with different time delays. The PMDs and photoelectron angular distributions (PADs) are dependent on the time delays,which are derived from the interference between coherent electron wave packets. The ultrafast photoionization model[25]and the evolution of the electron wavepackets are used to describe these results.

The paper is arranged as follows:In Section 2,we present the computational details for solving the two-dimensional(2D) time-dependent Schr¨odinger equation (TDSE) of He+ions, aligned H+2molecules and N2molecules. In Section 3, we present and discuss the results of PMDs and PADs with different time delays. Finally, we summarize our results in Section 4. Throughout this paper, atomic units (a.u.)e==me=1 are used unless stated otherwise.

2. Numerical Methods

The corresponding 2D TDSE for the He+ions, aligned H+2molecules,and N2molecules can be written as

where c=0.5 is the soft-core parameter,R is the internuclear distance (the equilibrium internuclear distance is R = Re=2.0 a.u.), and the ionization potential of the ground state is Ip=29.9 eV for H+2molecules.

The soft-core Coulomb potential of N2molecules has the form[26,30]

The initial wave function of ions and molecules are obtained by the imaginary evolution method. The initial electron density distributions of the He+ions, H+2molecules, and N2molecules are shown in Figs. 1(a2)–1(c2). One can see that the electron density distributions of He+ions is circular in the(x,y)plane,the electron density of the H+2molecule is elliptical with the σgsymmetry,and the N2molecule has three nodes located along the molecular R axis with the σgsymmetry.

Fig.1. Coulomb potential of(a1)the He+ ion,(b1)the H+2 molecule,(c1)the N2 molecule;and the initial ground states of(a2)the He+ ion,(b2)the H+2 molecule,(c2)the N2 molecule.

The interaction between either ions or molecules and the laser pulse is VL(r,t)=r·E(t)with E(t)being the field vector in the(x,y)plane. The orthogonally polarized laser pulses can be expressed by

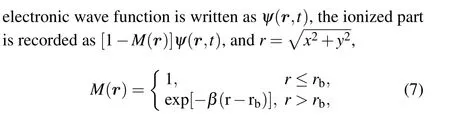
where β = 1 a.u., and the boundary between ionized wave function and bounded wave function is rb=20 a.u. for the He+ion and the H+2molecule,and 30 a.u.for the N2molecule.The photoelectron momentum distributions are acquired by Fourier transforming the ionized wave function into momentum space, the photoelectron angular distribution is obtained from the photoelectron momentum distribution.[29]

3. Results and discussion

Fig. 2. Two-dimensional PMDs and PADs of He+ ions by orthogonally polarized laser pulses at λ =15 nm (ω =3.04 a.u.). The intensity of the pulses is I0 =1×1014 W/cm2 (E0 =5.34×10-2 a.u.) and duration is 20 optical cycles. The results are shown for time delays: (a)Td=0 o.c.,(b)Td=1/8 o.c.,(c)Td=1/4 o.c.,(d)Td=3/8 o.c.,and(e)Td=1/2 o.c.

where σx= σy= 0.00043 are the ionization probabilities along the x and y directions, the ionization probabilities[31]can be obtained from the initial electronic states of the He+ion. A linearly polarized λ =15 nm laser pulse is used to ionize these ions. The intensity and duration of the laser pulses are the same as those in Fig. 2. When the field polarized direction is parallel to the x axis,the ionization probabilities σxalong the x direction is obtained. Similarly,we can obtain the ionization probabilities σyalong the y direction. The scalar products are fx(θ)=cos(θ) and fy(θ)=sin(θ). The wave function ψ1sof the He+ion is circular in the(x,y)plane. The interference term of the x and y directions is

Fig.3. Predictions of photoelectron angular distributions for He+ ions obtained from the ultrafast photoionization models in Eq.(11).

The similar phenomenon can be observed in the photoionization process of a linearly molecular system H+2. The molecule is aligned along the x axis. The same orthogonally polarized laser pulses with wavelength λ = 15 nm is used. We present the results from the TDSE simulations in Figs. 4(a1)–4(a3) and the prediction results in Figs. 4(b1)–4(b3). In Fig. 4(a1), at the time delay Td=0 o.c., two radiation peaks with larger amplitudes are mainly localized at angles 80?and 260?,two radiation peaks with smaller amplitudes are located at angles 8?and 188?as well. At the time delay Td=1/4 o.c.,the PMDs show that two radiation peaks with larger amplitudes are mainly localized at angles 95?and 275?,two radiation peaks with smaller amplitudes are located at angles 8?and 188?in Fig. 4(a2), and a small tilted angle with respect to the laser polarization axis appears. At the time delay Td=3/8 o.c., two radiation peaks with larger amplitudes are mainly localized at angles 100?and 280?,two radiation peaks with smaller amplitudes are located at angles 172?and 352?in Fig. 4(a3). The wave function of highest occupied molecular orbital(HOMO)for H+2can be simply written as ψ1sσg=ψ1s(r-Re/2)+ψ1s(r+Re/2),which illustrates a linearly combination of 1s atomic orbitals that are located at ±R/2. For an intense laser field, the wave function of the molecules in momentum space is

In order to further understand the effects of the time delays on photoelectron angular distributions of multi-electron molecules,the N2molecule is used as a benchmark system in orthogonally polarized laser fields.The N2molecule is aligned along the x axis. In Fig.5(a1),at time delay Td=0 o.c.,PAD is mainly localized at angles 135?and 315?,from Figs.5(a1)–5(c1) we can see that the PADs for N2molecule has four radiation peaks located at angles 38?, 135?, 217?, 315?, and as the time delay increases, the distribution in first and third quadrants in the (x,y) plane becomes weaker, whereas after Td=1/4 o.c. (as shown in Fig.5(c1)),the distribution in first and third quadrants becomes broader.

Fig.4. Two-dimensional PADs of aligned H+2 at equilibrium Re =2.0 a.u. by orthogonally polarized laser pulses at wavelength λ =15 nm(ω =3.04 a.u.). The intensity of the pulses is I0=1×1014 W/cm2 (E0=5.34×10-2 a.u.) and duration is 20 optical cycles. The numerical results are shown for time delays:(a1)Td=0 o.c.,(b1)Td=1/4 o.c.,(c1)Td=3/8 o.c. The prediction results of angular nodels obtained from Eq.(18): (a2)Td=0 o.c.,(b2)Td=1/4 o.c.,(c2)Td=3/8 o.c.

Fig. 5. Two-dimensional PADs of aligned N2 at equilibrium RN-N =2.08 a.u. by orthogonally polarized laser pulses at λ =15 nm (ω =3.04 a.u.). The intensity of the laser pulses is I0=1×1014 W/cm2 (E0=5.34×10-2 a.u.) and duration is 20 optical cycles. The numerical results are shown for time delays:(a1)Td=0 o.c.,(b1)Td=1/4 o.c.,(c1)Td=3/8 o.c. The prediction results of angular nodels obtained from Eq.(22): (a2)Td=0 o.c.,(b2)Td=1/4 o.c.,(c2)Td=3/8 o.c.

Fig. 6. The electron wavepackets for the N2 molecules at different times by orthogonally polarized laser pulses at wavelength λ =15 nm(ω =3.04 a.u.) with four time delays: [(a1), (a2), (a3)]Td =0 o.c., [(b1), (b2), (b3)]Td =1/4 o.c. and[(c1), (c2), (c3)]Td =3/8 o.c. The results are shown at four different times: [(a1),(b1),(c1)]t=7.26 o.c.,[(a2),(b2),(c2)]t=12.10 o.c. and[(a3),(b3),(c3)]t=16.94 o.c.

In order to describe the intensity of the PADs for N2molecules from the TDSE simulations, the evolution of the electron wavepackets by orthogonally polarized laser pulses with different time delays are shown in Fig.6. In Figs.6(a1–6(c1), at t = 7.26 o.c., the electrons are not ionized and the electrons distributed around the molecular nucleus. In Figs. 6(a2)–6(c2), at t =12.10 o.c., the electrons have been mainly ionized in four directions, and the electrons distribute in the range from 26?to 58?, from 118?to 167?, from 204?to 238?and from 295?to 338?, which are in agreement with the PADs of N2molecules in Fig. 5. In Figs. 6(a3)–6(c3),at t = 16.94 o.c., more electrons have been ionized in the(x,y) plane. The electron wavepacket by orthogonally polarized laser pulses with the time delay Td=0 o.c. at time t =16.94 o.c. is presented in Fig. 6(a3), which shows that there are more electrons distributed in the range from 108?to 167?in the second quadrant and from 292?to 342?in the fourth quadrant rather than the range from 18?to 58?in the first quadrant and from 197?to 241?in the third quadrant. Thus the radius of the PAD for N2molecules located at angles 135?and 315?is longer and wider than the radius located at angles 38?and 217?in Fig. 5(a). The electron wavepacket by orthogonally polarized laser pulses with the time delay Td=1/4 o.c. at time t =16.94 o.c. is presented in Fig.6(b3),which shows that there are much more electrons distributed in the range from 118?to 164?in the second quadrant and from 298?to 340?in the fourth quadrant rather than the range from 25?to 61?in the first quadrant and from 206?to 243?in the third quadrant. Thus the radius of the PAD for N2molecules located at angles 138?and 318?is much longer than the radius located at 42?and 222?in Fig.5(b). The electron wavepacket by orthogonally polarized laser pulses with the time delay Td=3/8 o.c.at time t=16.94 o.c. is presented in Fig. 6(c3), which shows that there are more electrons distributed in the range from 121?to 164?in the second quadrant and from 301?to 342?in the fourth quadrant rather than the range from 22?to 63?in the first quadrant and from 203?to 243?in the third quadrant. Thus the radius of the PAD for N2molecules located at 142?and 322?is longer than the radius located at 45?and 224?in Fig.5(b).

4. Conclusions

The ionic and molecular photoionization in orthogonally polarized laser fields for different time delays is investigated theoretically. Simulations are performed on the He+ions,H+2molecules and N2molecules by numerically solving corresponding 2D TDSEs. The PMDs and PADs are dependent on the time delays between the orthogonally polarized laser pulses, which comes from the interference between coherent electron wave packets. For the He+ions, the interference of the coherent electron wave packets is created by the time delay of two orthogonally polarized laser pulses. For H+2molecules and N2molecules, the interference of the coherent electron wave packets is created by the time delay of two orthogonally polarized laser pulses and two-center ionization. The ultrafast photoionization model[25]is adopted to describe these results given above. The PADs of He+ions and H+2molecules can be well described by the ultrafast photoionization model,and the angles of the PADs for N2molecules from the TDSE simulations are in good agreement with the prediction from the ultrafast photoionization model. The evolution of the electron wavepackets is employed to describe the intensity from TDSE simulations for N2molecules.

Acknowledgment

We are thankful to Hongdan Zhang for helping us with the corrections of the article.