Suresh BASNET, Atit DEUJA and Raju KHANAL

Central Department of Physics, Tribhuvan University, Kirtipur, Kathmandu 44613, Nepal

Abstract Kinetic theory has been employed to investigate the magnetized plasma-sheath structure and its characteristics in the presence of more than one species of negatively charged particles:hot electrons,cold electrons, and negative ions.The cold electrons and negative ions are considered to obey a Maxwellian distribution, whereas the hot electrons follow a truncated Maxwellian distribution.The Bohm sheath condition has been extended for the case of more than one species of negatively charged particles, in which the concentration of hot electrons has a crucial role in achieving the Bohm velocity.The thermal motion of hot electrons is much higher compared to cold electrons and negative ions,such that the variation of hot electron concentrations and the temperature ratio of hot to cold electrons play a key role in the determination of the plasma-sheath parameters:particle densities,electrostatic potential, the flow of positive ions towards the wall, and sheath thickness.We have estimated the deviation of the resultant drift velocity of positive ions on the plane perpendicular to the wall from the parallel component at the presheath-sheath interface.It is found that the deviation between the two velocity components increases with an increase in the obliqueness of the magnetic field.Furthermore, the results obtained from the kinetic trajectory simulation model are compared with the results obtained using a fluid model; the results are qualitatively similar, although the potential varies by less than 4% in terms of the magnitude at the wall.

Keywords: Bohm velocity, fluid theory, plasma sheath, electronegative plasmas

1.Introduction

The plasma-wall transition (PWT) is one of the oldest problems in plasma physics[1];however,it is very important and of growing interest nowadays, as many surface treatment techniques use plasma technology [2, 3].The PWT is the region between a quasineutral plasma and the material surface that exists when plasma is confined using any material surface or by a surface to be treated.The PWT has a significant influence on the flow of particles and energy fluxes towards the wall and hence affects the plasma-wall interaction mechanisms[4].It consists of two distinct regions:the sheath and presheath regions.Sheaths are positive or negative space charged regions formed in the vicinity of a material wall to maintain the losses of ion and electron fluxes.In plasmas,the thermal velocity of electrons is comparatively higher than in their positive or negative ionic counterparts, thus the population of electrons reaching the wall is higher,and a negative potential is developed on the wall with respect to the core plasma [5].This negative potential repels negatively charged particles and attracts positive ions,thus the positive ions form a layer near the boundary surface known as a plasma sheath.This is a thin non-neutral layer that extends over several electron Debye lengths from the wall and is characterized as a region with sharp gradients of physical parameters such as potential, electric field, and density.

Plasma with more than one species of negatively charged particle with different temperatures is commonly found in experimental devices [6-9].For example, slow and fast electron components are present in sputtering magnetron plasma [10], and at the edges of fusion devices such as tokamaks, in which the fast electrons (high-temperature or energetic electrons) can significantly affect the transport properties of the edge plasma and the energy flow towards the divertor plate that determines the lifetime of the plasmafacing components[11].In the presence of negative ions,the plasma sheath has markedly different properties compared to ordinary plasma containing positive ions and electrons.On this basis,this type of plasma has a wide range of applications in diverse fields such as the enhancement of dry etching, the fabrication of semiconductor devices in the electronics industry, thin film deposition, and the negative ion sources used in magnetic fusion devices to produce highly energetic neutral beams [12-15].Besides these, it is crucial in the understanding of the Earth's ionosphere [16] and astrophysical plasmas [17].In the past few decades, many works have been devoted to the study of plasma-sheath characteristics with two or more populations of negatively charged particles (e.g., two groups of electrons, or those containing negative ions) and this is still an attractive subject in plasma physics[18-22].Sheridan et al[10]experimentally observed the existence of two-temperature groups: hot and cold electrons in magnetron sputtering plasma.It was found that the density of hot electrons was higher than that of cold electrons in the magnetic trap.?er?ek et al [23] studied the effect of energetic electrons on plasma-sheath characteristics by using an electrostatic particle-in-cell simulation method.It was suggested that the electron composition ratio affected plasmasheath characteristics and the potential variation of the presheath region as well.Gyergyek et al[24,25]investigated the plasma-sheath structures in front of an electron-emitting surface in the presence of two-temperature groups of electrons using kinetic and fluid models.The potential, electric field,and particle density profiles obtained from the numerical solution of Poisson’s equation were compared with the results obtained by particle-in-cell simulation.It was found that the results were in good agreement.Ou et al [26] and Sharma et al[27]studied the properties of magnetized plasma sheaths containing low-temperature Maxwellian electrons and hightemperature truncated Maxwellian electrons.It was found that the sheath structure and energy flux towards the wall were influenced by the concentration of high-temperature electrons.

Oudini et al [28] and Chabert [29] investigated electronegative discharges using particle-in-cell simulation and fluid approaches.The effects of electronegativity on sheath formation, negative ion flux towards the wall or biasing electrodes,and the velocity of positive ions at the sheath entrance have been investigated.Moreover, the h1factor (the ratio of positive ion density at the edge to the center), which determines the flux of positive ions reaching the wall for lowpressure electronegative discharges,is systematically presented.Borgohain et al [22] investigated collisionless non-magnetized plasma-sheath profiles in the presence of a two-temperature distribution of electrons.They systematically presented the effect of nonextensive two-temperature electrons on electrostatic plasma-sheath profiles such as potential, Bohm velocity,and particle densities.

Due to imperfect shielding of the plasma sheath, the residual effect of the negative wall potential penetrates beyond the sheath entrance deep into the quasineutral plasma.In the presheath region, the electrostatic potential and other physical parameters have weak gradients; however, positive ions are accelerated towards the sheath entrance by the residual field and satisfy Bohm's criterion as [30]

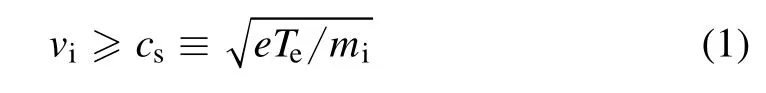
where viis the velocity of the monoenergetic positive ions(PIs),csis the ion acoustic velocity,miis the mass of an ion,Teis the electron temperature in eV and e=1.6×10?19.

In the presence of an oblique magnetic field, the scale length of the magnetic presheath LMPSis determined by the ion gyroradius and the obliqueness of the magnetic field.The spatial extension of the magnetic presheath is estimated as[1]

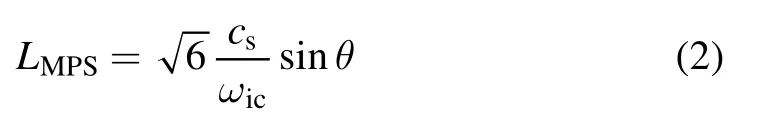
where ωicis the ion cyclotron frequency and θ is the obliqueness of the magnetic field.

In our previous work [31], we presented the effect of negative ions and cut-off distribution on electronegative magnetized PWT properties.In that case, the plasma was composed of positive ions, negative ions, and a single group of electrons.Based on previous works [10, 22-27], twotemperature groups of electrons are often found in experimental devices and the study of this type of plasma is of great practical interest.In this work, we have focused on the study of collisionless magnetized PWT with more than one species of negatively charged particle [two-temperature groups of electrons: cold electrons (CEs) and hot electrons (HEs) with singly charged negative ions (NIs)] via the kinetic trajectory simulation (KTS) method.The Bohm sheath condition that ensures the formation of a plasma sheath has been extended.The effects of the concentration of HEs, the concentration of NIs, the temperature ratio of hot to cold electrons, and the obliqueness of the magnetic field on the electronegative plasma sheath and the presheath-sheath interface are systematically presented.In addition,the kinetic results obtained are compared with the results from the corresponding fluid model and it is found that the results are in qualitative agreement,but quantitatively vary by less than 4%in terms of magnitude.

2.KTS method and basic equations

2.1.Model and basic equations

In contrast to the fluid model, the KTS method is based on self-consistent kinetic theory which is useful in the study of spatially bounded plasmas.In this method, we trace the particle trajectories in phase space by solving collisionless kinetic equations for the given distribution functions.The new velocity distribution of particles is obtained by performing a trajectory integration that gives the new density of the particles.Once we obtain the particle densities, we can calculate the space charge density, which is used further in Poisson’s equation to obtain the new potential distribution in the Ithtime step φnew(I).The new re-adjusted potential distribution φ(I)is obtained by a straightforward relaxation scheme [32];

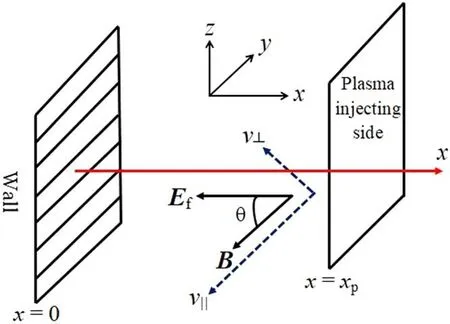
Figure 1.Schematic diagram of the magnetized plasma-wall transition region.

where ω is the relaxation parameter and the choice of this parameter determines the convergence of the system.The numerical stability conditions adopted in the KTS method are:

(1) The ratio of mesh size (Δx) and electron Debye length(λDe) is less than unity i.e., Δx/λDe＜1.

(2) To resolve the motion of ions in the timescale of electrons, the product of the numerical time step (Δt)and the electron plasma frequency (ωpe) is taken to be unity.

(3) The relaxation parameter is taken to be ω=0.08 for the present case.

Detailed explanations of the KTS method, including the discretization of phase space and the iteration scheme are discussed in our earlier works [31, 33, 34].

The electronegative plasma consists of singly charged positive ions(argon),negative ions(oxygen)and hot and cold electrons.The region of interest is bounded by two parallel planes between x=xpand x=0,which are designated as the presheath-sheath interface(on the particle injection side)and a perfectly absorbent material wall,as shown in figure 1.The external magnetic field B lies in the xz-plane,which makes an angle θ with the direction of the electric field Ef.In the presence of an oblique magnetic field,the velocity of the positive ions can be resolved into two components: the velocity parallel to the magnetic field(v‖)provides the forward motion of the charged particles, and the velocity perpendicular to the magnetic field (v⊥) produces gyration around the magnetic field.

In this work, we assign the subscripts ‘ce’ to cold electrons (CEs), ‘he’ to hot electrons (HEs), ‘i’ to positive ions(PIs) and ‘n’ to negative ions (NIs).In the presence of twotemperature groups of electrons, the effective temperature of the electrons Teffis given by [35]

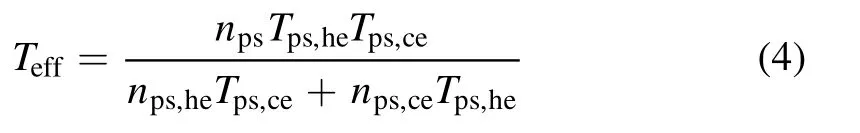
in which npsis the plasma density, Tps,he, Tps,ce, nps,he, and nps,ceare the temperatures and densities of the hot and cold electrons at the presheath-sheath interface, respectively.

As we are dealing with a time-independent PWT mechanism, the time-independent Boltzmann equation for the collisionless plasma becomes the Vlasov equation and is written as;

in which ms, qsandare the mass, charge, and the distribution function of the particle species s,respectively and the termis the macroscopic acceleration of particle species s.

The electrostatic potential distribution φ(r)is obtained by solving Poisson's well-known equation:

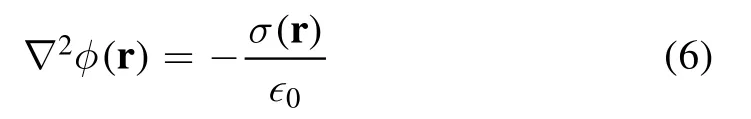
where ?0is the electric permittivity for free space and σ(r) is the net charge density.

The electric field Efcan be expressed in terms of electric potential as

In this 1d3v case, the PIs’ velocity distribution function is

The thermal motion of the HEs is greater than the motions of the CEs and NIs.Due to reflective nature of the wall potential,the HEs follow the truncated Maxwellian velocity distribution function, which is written as;

The CEs and NIs are in thermal equilibrium and they obey a Maxwellian velocity distribution [9, 36]

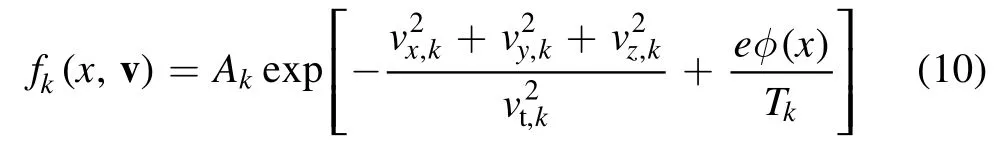
where Akis the amplitude of the distribution function related to their respective particle densities at the presheath-sheath interface,vMiis the Maxwellian maximum velocity of the PIs,H(x)is the Heaviside step function defined asH(x)=0 for x ＜0 and ( )H x=1, for x ≥0,is the truncated velocity of the HEs,is the thermal velocity of particle species s with k=ce and n for CEs and NIs, respectively.

The density of the particle species s is

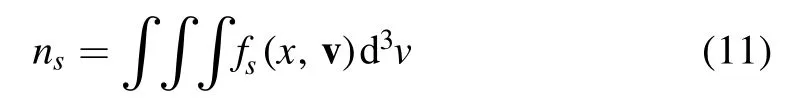
which yields a particle density at the presheath-sheath interface of

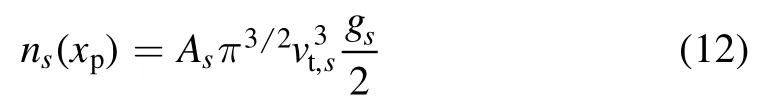
in which the factor gsis defined as;

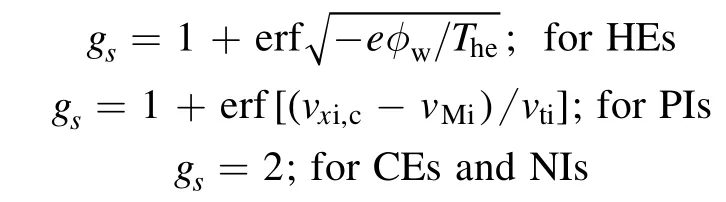
where vxi,cis the cut-off velocity of positive ions.

The average fluid velocity of particle species s is

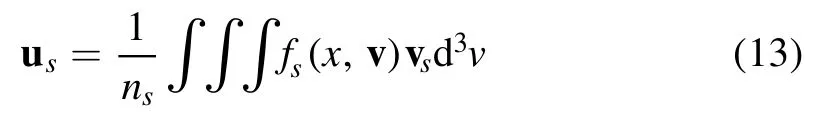
which yields average fluid velocities at the presheath-sheath interface of:

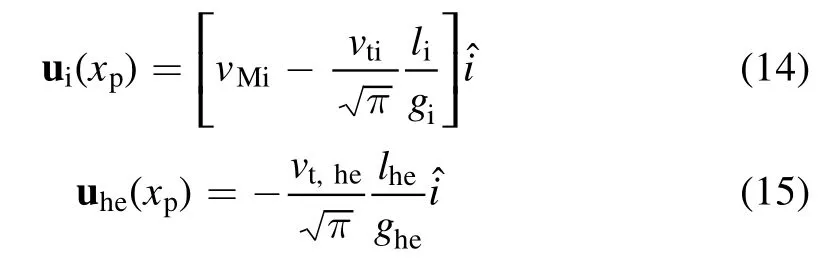
and

The fluid temperature distribution of particle species s is

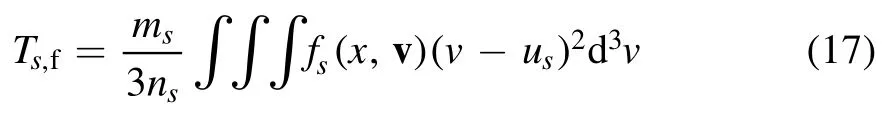
which yields an average fluid temperature at the presheathsheath interface of:

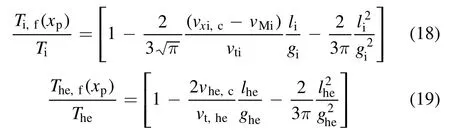
and

2.2.The Bohm condition

The formation of a non-neutral plasma sheath near to the material wall demands that positive ions must enter the plasma-sheath region at a sufficiently high speed.This criterion for the formation of the plasma sheath is known as the Bohm sheath condition and it is modified if the plasma consists of more than one species of negatively charged particles.In this section, we extend the kinetic Bohm sheath condition for electronegative plasmas containing cold and hot electrons.The generalized kinetic Bohm sheath condition is

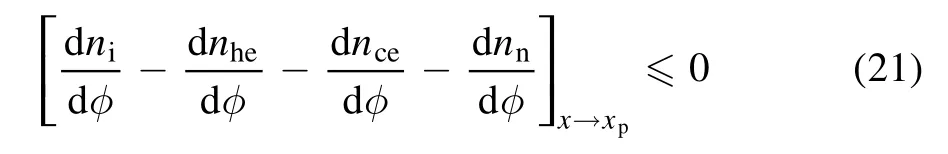
which yields:

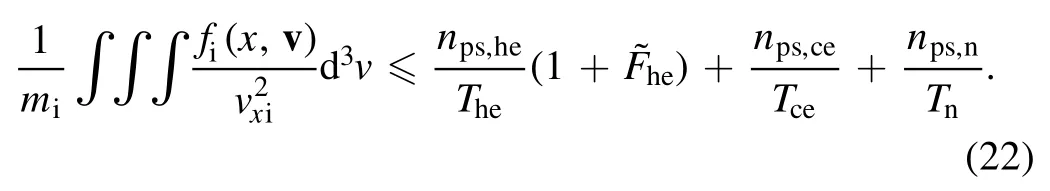
In a simplified form, the kinetic Bohm sheath condition equation (22) becomes:

in which u‖is the average ion velocity parallel to the magnetic field which is averaged over the positive ion velocity distribution function.The various other terms appearing in equation (23) are defined as:

where the term Δsis equal to δps,1,andfor HEs, CEs, and NIs, respectively.

Equation (23) is the Bohm sheath condition for an electronegative plasma containing more than one species of negatively charged particles.In the absence of hot electrons,i.e., nps,he=0 and=1, equation (23) becomes

Equation (24) is the well-known Bohm sheath condition for an electronegative plasma and the condition is similar to that of a previous work [37].

The fluid equations relating the macroscopic variables can be obtained by taking the moments of the Vlasov equation i.e.the velocity moments of the distribution such as density,average velocity,etc.The set of equations for the macroscopic quantities is called the fluid equation.To study the dynamics of an ion fluid, steady-state continuity and momentum equations are used.On the other hand, in lowtemperature electronegative plasma, the fluid velocity of negatively charged particles is very small, compared to their random thermal motion.Therefore, the distribution of the negatively charged particles in the PWT region can be modeled by the Boltzmann relation [9, 15, 26,36-38].

The zeroth-order moment yields the continuity equation,which describes the conservation of particle flux, and is written as;

The first-order moment yields the momentum transport equation that describes the conservation of momentum,which is written as;

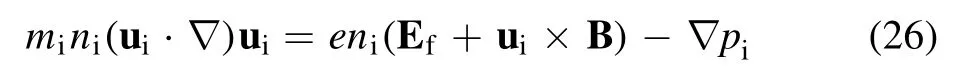
where ?piis the pressure gradient force due to the random motion of the ions.

Poisson’s equation, which connects the electric potential and particle densities is

The spatial variation of the negatively charged particle density is

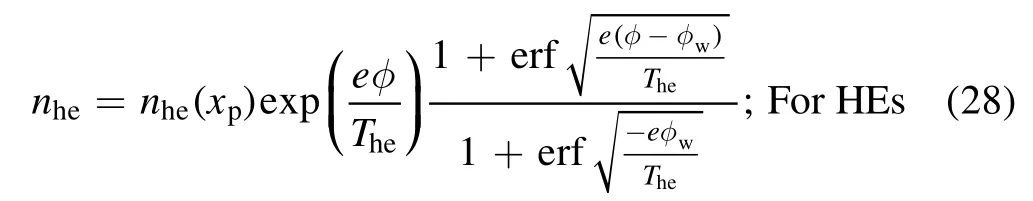
and

3.Results and discussion

The kinetic equations are solved for the specified field and particle boundary conditions.The field boundary conditions are related to the potential distribution.The electric potential at the presheath-sheath interface (x=xp) is taken to be zero,being plasma quasineutral, and another boundary wall (at x=0) has a negative constant value i.e., φ(x=xp)=0 and φ(x=0)=φw＜0.The particle boundary conditions are related to the choices of distribution functions, where we have assumed that particles enter the simulation domain from the injection side with a cut-off Maxwellian distribution.At the right-hand boundary (the particle injection side), the distribution function of positively and negatively charged particles satisfies the following boundary conditions:

and

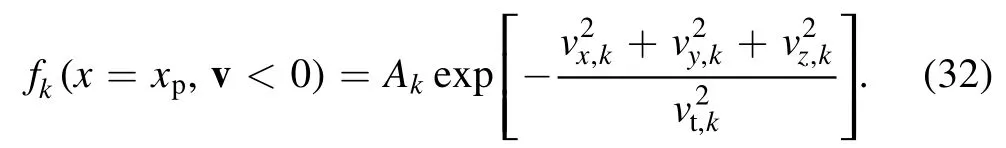
The distribution functions of particle species s satisfy the boundary conditions at the left-hand boundary (wall)

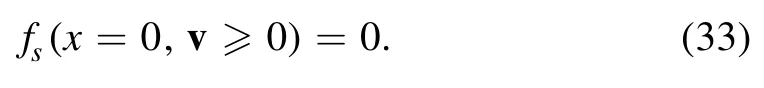
To solve the related kinetic and fluid equations, the physical parameters considered are: the length of region of interest=20λDe(1.5 cm),the plasma density nps=1014m?3,the presheath cold electron temperature Tps,ce=1.0 eV, the electron temperature ratio βps=(4.5-7.5), the negative ion temperature Tps,n=0.3 eV,the ion temperature Tps,i=0.1 eV,the magnitude of the magnetic field B=500 mT, and the obliqueness of the magnetic field θ=(1°-30°).The choice of these physical parameters are consistent with previous works[14,26,28,38].While we vary the concentration of HEs,the concentration of NIs, and the temperature composition of the hot and cold electrons,the obliqueness of the magnetic field is kept constant throughout the simulations i.e., θ=5° and the distance to the wall is expressed in terms of the electron Debye length λDe.

The presence of HEs in an electronegative plasma affects the variation of particle densities in the PWT region,which is depicted in figure 2.At the presheath-sheath boundary, the plasma always tends to preserve its quasineutral property.The concentration of HEs has no significant effect on the positive ion density profile at the presheath-sheath interface;however,the density of positive ions continues to decrease towards the wall [figure 2(a)].When the concentration of HEs increases,the rate of decrease of positive ions towards the wall is much faster and thus, the density of PIs reaching the wall also decreases.The density distributions of negatively charged particles decrease towards the wall, as shown in figures 2(b),(c) and (d).The amplitude of the HEs’ density distribution is increased with an increase in the concentration of HEs,whereas the amplitude of the CEs’ density distribution decreases.In the same scenario,the amplitude of the negative ions’ distribution remains constant at the presheath-sheath interface, but the rate of decrease of the NIs is faster for a higher concentration of HEs.Also,the NIs’minimum density point shifts towards the sheath entrance, indicating a lengthening of the sheath region.The variation of particle densities in the sheath region for different compositional values of the electron temperature is shown in figures 3(a)-(d).It is found that the particle densities decrease towards the wall in all cases and that the process of the decrease is much faster with an increase in the temperature ratio of hot to cold electrons.The effect of negative ion concentration on the particle density profile in the PWT region is shown in figures 4(a)-(d).With an increase in the concentration of NIs, the rate of decrease of PIs becomes slower, and the population of PIs reaching the wall increases [figure 4(a)].The density of HEs reaching the wall decreases [figure 4(b)] and the rate of decrease of the CEs and NIs becomes slower with the increase in negative ion concentration [figures 4(c) and (d)].

Figure 2.Effects of hot electron concentrations on particle density profiles for constant= 0.12and βps=4.5 for(a)PIs,(b)HEs,(c)CEs,and (d) NIs.

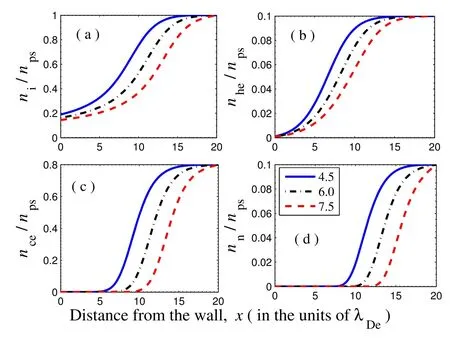
Figure 3.Particle density profiles for different values of the temperature ratio of hot to cold electrons βps at a constant ?=δps= 0.12for (a) PIs, (b) HEs, (c) CEs, and (d) NIs.

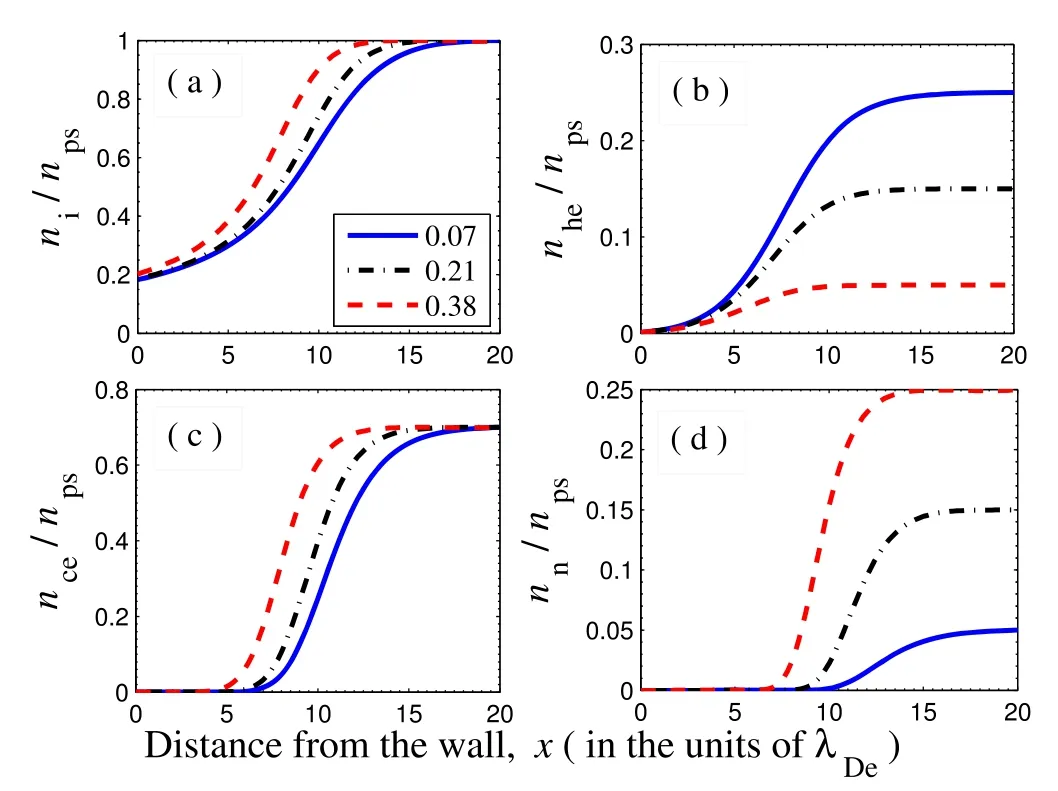
Figure 4.Particle densities profile for the different concentrations of NIs at constant δps=0.12 and βps=4.5 for (a) PIs, (b) HEs,(c) CEs, and (d) NIs.

Figure 5.Electrostatic potential profiles for different values of(a)HE concentration, (b) NI concentration and (c) temperature ratio of hot to cold electrons.

The thermal velocities of CEs and NIs are so much lower than the thermal velocity of HEs that the populations of CEs and NIs reaching the wall are almost negligible, and hence,the population of negatively charged particles reaching the wall determines the magnitude of the wall potential, which is depicted in figure 5.The slope of the potential distribution curve is steeper when the concentration of HEs is increased,and its magnitude increases towards the wall.As the population of HEs reaching the wall increases, the wall becomes more negative with respect to the core plasma.Therefore,the magnitude of the potential is at a minimum at the presheathsheath boundary and does not even change sharply in this region.The magnitude of the potential at the wall increases from about 15.7 to 23.5 when the concentration of HEs is changed from 0.06 to 0.38 [figure 5(a)].When the concentration of NIs increases at the presheath-sheath interface,it reduces the volumetric composition of the electrons and the population of energetic electrons reaching the wall.Therefore,the magnitude of the potential at the wall reduces for an increase in the concentration of NIs [figure 5(b)].This decrement of electric potential is qualitatively consistent with our previous work [31] and the experimental work done by Boruah et al[38].The effects of the temperature composition of electrons on the potential profile are shown in figure 5(c).It can be seen that the magnitude of the normalized potential increments sharply with an increase in the temperature ratio of hot to cold electrons.The magnitude of the potential increases at the wall from about 18.7 to 33 for an increment of the temperature ratio from 4.5 to 7.5.

Figure 6 shows the variation of PI velocities in the PWT region, in which a negative sign in the plots represents the motion of ions towards the wall.The thermal motion of the ions is very low compared to that of the electrons and also the electric field is weak at the presheath-sheath boundary.Thus, the ion velocity components do not change abruptly at the presheath-sheath interface, as shown in figures 6(a)-(c).However, the magnitude of the PI velocities increases at the injection side with an increase in the concentration of the HEs.Once the positive ions enter the sheath region, they accelerate towards the wall due to the sharp gradient of electric potential in the sheath region.For PIs, the x-component velocity is a major component of the velocity with which they strike the wall and transfer energy to the surface.The magnitude of the x-component velocity with which the PIs strike the wall increases from 5.50Csto 6.10Cs[Figure 6(a)], whereas the magnitude of the z-component velocity decreases from 0.13Csto 0.11Cs[figure 6(b)] as the concentration of HEs increases from 0.06 to 0.38.With same increment of the HEs’ concentration, the y-component velocity of the positive ions increases from about 0.11Csto 0.17Cs.The velocity profiles of PIs for varying electron temperature compositions are depicted in figure 7.It can be seen that the x-component velocity of the PIs increases sharply towards the wall, and its magnitude at the wall is found to increase from about 5.80Csto 7.76Cs[figure 7(a)]with an increase in the temperature ratio of hot to cold electrons from 4.5 to 7.5.For the same increment of temperature ratio, the y-component velocity of the PIs increases from about 0.11Csto 0.21Cs[figure 7(c)].The velocity profiles of PIs for varying concentrations of NIs are depicted in figure 8.The magnitude of the velocity increases towards the target surface in all cases, but the incremental rates of the x and y-components decrease with an increase in the concentration of NIs,since the intensity of the electric field at the presheathsheath interface region becomes weaker for higher concentrations of NIs, which causes a reduction in the x- and y-components of the velocity of the PIs[figures 8(a)and(c)].For the same increment to the concentration of the NIs, the z-component velocity increases insignificantly.

The obliqueness of the externally applied magnetic field determines the scale length of the magnetic presheath, which increases with an increase in the obliqueness of the magnetic field; the result is experimentally confirmed [39].In their work, the magnetic presheath was defined as the layer where the velocity of ions was not parallel to the magnetic field.In this work, we have also studied the deviation of the resultant drift velocity of PIs in the xz-planefrom the parallel component (v‖).The x-component velocity of PIs makes a major contribution to the resultant drift velocity(vxz)in the xz-plane.In figure 9, we present the effect of the obliqueness of the magnetic field on the numerical deviation of the resultant drift velocity of PIs on the xz-plane(vxz)from the parallel component(v‖)at a constant concentration of HEs and NIsFor a small obliqueness of the magnetic field, it is found that the resultant drift velocity of the PIs is almost parallel to the magnetic field at the presheath-sheath interface region; however, the deviation between the two components of the ions’ velocity increases with an increase in the obliqueness of the magnetic field.When we increase the obliqueness of the magnetic field from 1°, 10°, 20°, and 30°, it is found that the deviations in percentage terms are: 0.013%, 1.27%, 4.84% and 10.02%respectively.Therefore, it also true in our case that the velocity of the PIs is not parallel to the magnetic field in the magnetic presheath region.

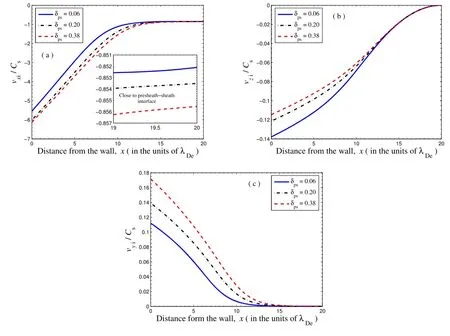
Figure 6.Effects of the concentration of HEs on positive ion velocity profiles at constant= 0.12and βps=4.5.(a) The x-component,(b) the z-component, and (c) the y-component.

Figure 7.Effect of the temperature ratio of hot to cold electrons on PI velocity profiles at a constant= δps= 0.12.(a) The x-component, (b) the z-component, and (c) the y-component.

The presence of a residual electric field at the presheathsheath boundary and a magnetic field in the xz-plane induces the E×B drift on PIs, which acts in the positive y-direction.This drift depends on the magnitudes of the electric and magnetic fields and their obliqueness.The magnitude of the electric field increases towards the wall,and the sheath region has such a strong electric field that we can clearly observe the increment of the E×B drift velocity in figure 10.The increment in the rate of drift velocity of PIs increases with an increase in the obliqueness of the magnetic field.The magnitude of the drift velocity increases from about 0.27Csto 7.75Cswith an increase in the obliqueness of the magnetic field from 1° to 30°.

Due to the negative wall potential, we have assumed a truncated hot electron distribution,as defined in equation(9),since the population of HEs reaching the wall is higher than those of CEs and NIs.The presence of HEs makes a more significant contribution to the plasma-sheath parameters than those of CEs and NIs,so we present a plot of the related fluid variables in figure 11.The truncated velocity of HEs depends on the potential drop in the sheath region,which decreases as the particles flow towards the wall.The thermal velocity of HEs is reduced towards the wall; however, the energetic electrons that overcome the reflective wall potential can reach the wall.Therefore,the density of HEs decreases towards the wall[red solid line in figure 11].The average velocity of HEs increases with an increase in the potential drop in the sheath region [black dashed line in figure 11], although its temperature distribution decreases [blue dash-dot line in figure 11].

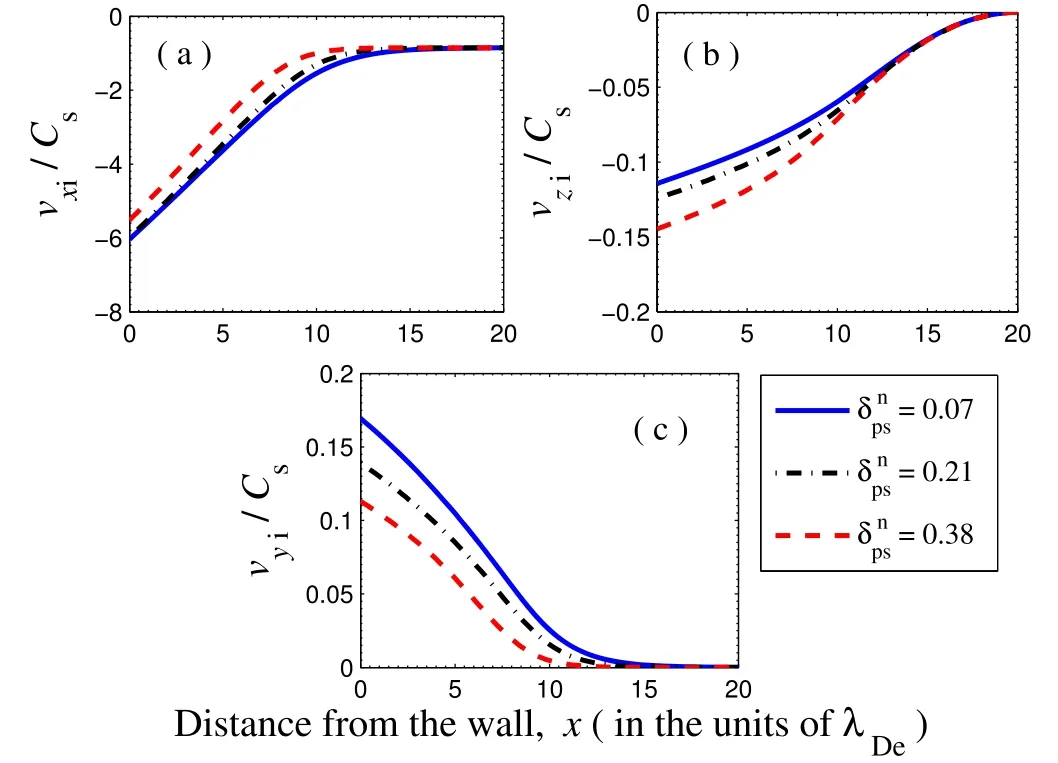
Figure 8.Effect of NI concentrations on positive ion velocity profiles at constant δps=0.12 and βps=4.5.(a) The x-component, (b) the z-component and (c) the y-component.

The thermal velocity of positive ions is so much lower in the sheath entrance that it is not sufficient to provide the Bohm velocity for PIs.A residual electric field penetrates away from the sheath entrance deep into the bulk plasma due to the imperfect shielding of the plasma sheath.Therefore,the magnitude of the wall potential has a key role in accelerating PIs towards the sheath region, so that PIs still satisfy the Bohm condition.Figure 12 depicts that the magnitude of the wall potential increases with an increase in the concentration of HEs [blue dashed line figure 12] and that the residual electric field penetrating beyond the plasma sheath is more intense, which increases the Bohm velocity of the PIs at the sheath entrance [red dotted line figure 12].This result obtained for the present case is qualitatively in agreement with the previous theoretical work [26].

In the presence of two-temperature groups of electrons,the calculation of effective temperature and its fluctuation is an important parameter in the study of plasma sheaths.To study its effect on sheath formation, we present the plot in figure 13,where the graph conveys the information about the wall potential[blue dashed line]and the sheath thickness[red dotted line] at constant βps=4.5 andδpsn=0.12.As the effective temperature of the electrons increases,the number of energetic electrons collected by the wall becomes higher and the wall becomes more negative, which is depicted in figure 13[blue dashed line].With an increase in the effective temperature of the electrons, the minimum value in the density profiles of both CEs and NIs shifts toward the sheath entrance, and consequently the accumulation of net space charge density occurs towards the entrance side.Based on the Child-Langmuir law, the wall potential and sheath thickness are directly proportional to|φw|3/4.Therefore,the scale length of the sheath region lengthens with an increase in the effective temperature of the electrons.It is found that the sheath thickness further lengthens up to about 9 electron Debye lengths when the temperature ratio of hot to cold electrons increases from 4.5 to 7.5.

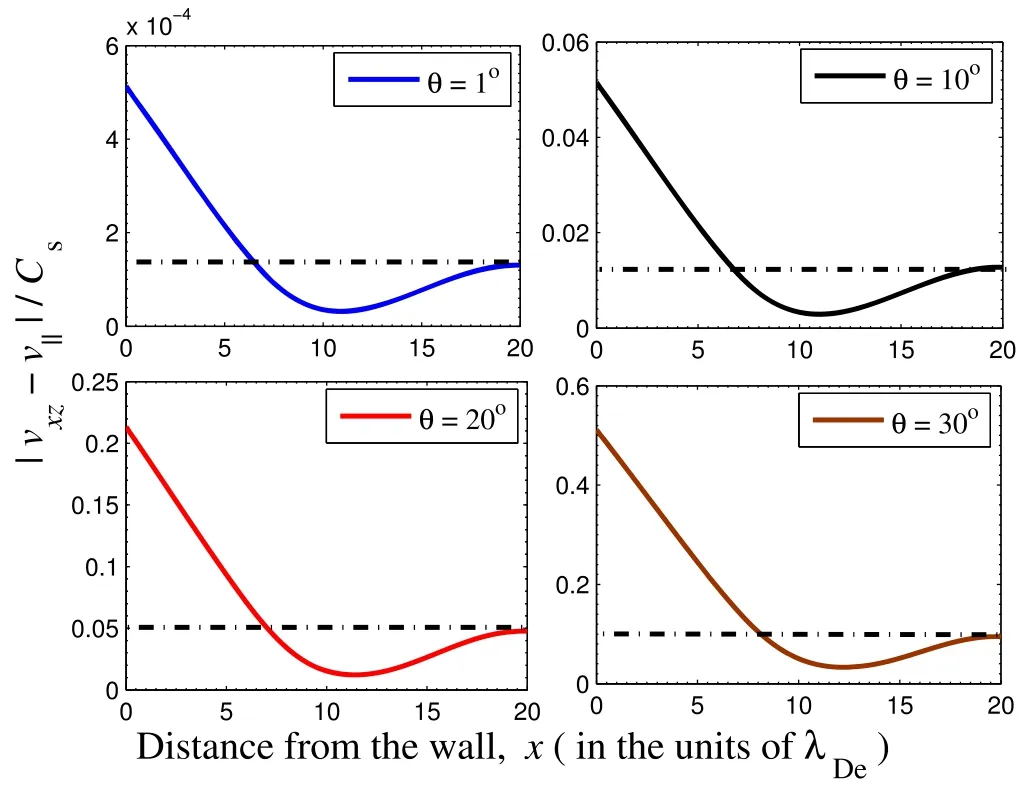
Figure 9.Deviations of the resultant drift velocity of positive ions on the xz-plane from the parallel component for different values of the obliqueness of the magnetic field.

Figure 10.Drift velocity of PIs for different obliquenesses of the magnetic field at a constantδ p s= = 0.12.

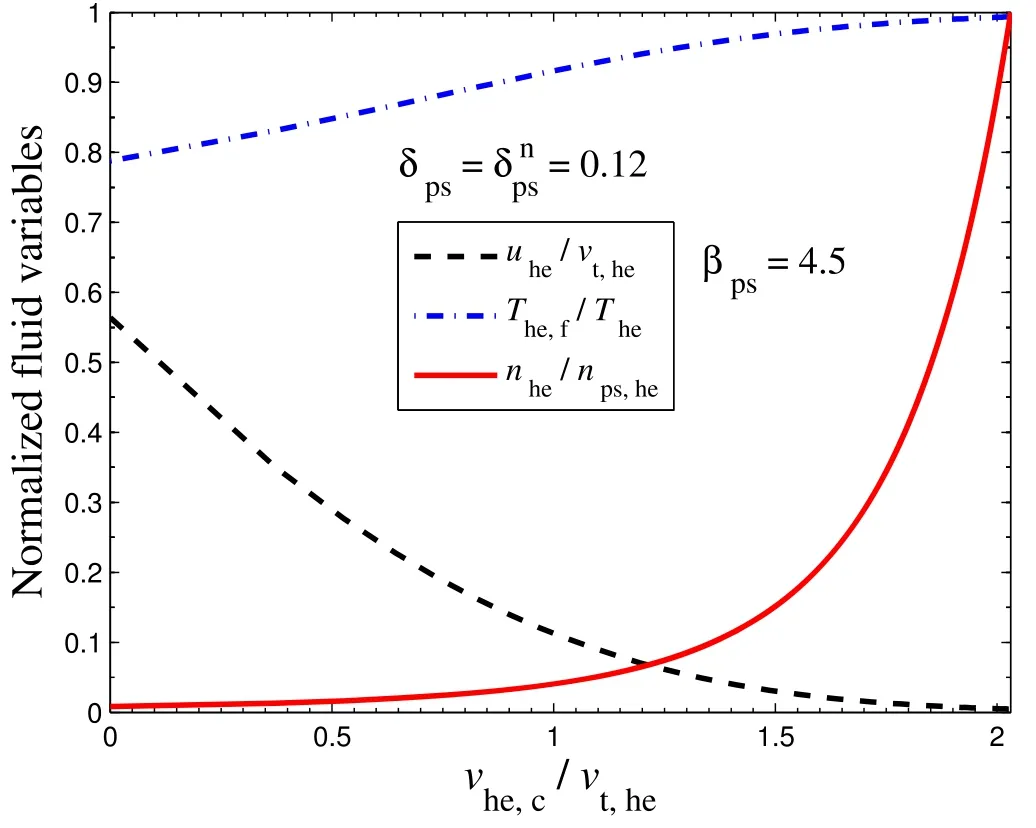
Figure 11.Variation of normalized fluid variables of HEs versus normalized truncated hot electron velocity.

Figure 12.Kinetic Bohm velocity and wall potential as the function of the concentration of HEs at constant= 0.12and βps=4.5.

In this section,we have numerically solved the compiled set of fluid equations (25)-(29) and compared the kinetic results obtained.This comparative study of the results from the kinetic and fluid models emphasizes the validity of the kinetic results.To obtain a numerical solution to the fluid equations, the following boundary conditions, considered at the presheath-sheath interface are: φ(x=xp)=0, Ef(x=xp)=0.01kBTps,ce/eλDe.In the above boundary conditions,the electrostatic potential at the presheath-sheath interface region is considered to be zero;however,a small electric field is assumed to prevent a divergence of the numerical results.Moreover, this ensures that the plasma approximation holds and the result is case insensitive[40].A comparative study of plasma-sheath parameters using kinetic and fluid models at constantand βps=4.5 is depicted in figures 14-16.The potential profile is qualitatively similar and monotonically decreasing towards the wall;however,the magnitudes of the potential at the wall obtained by the kinetic and fluid approaches are found to be 18.67 and 17.92,respectively[figure 14(a)].Therefore,the results obtained are quantitatively similar.A comparative study of the net charge density profile in the PWT region shows a qualitatively similar nature [figure 14(b)], with slight differences in the region close to the wall.The net charge density increases towards the wall and it reaches a maximum at about 13 electron Debye lengths from the presheath-sheath interface region, after which it decreases again towards the wall.The density profiles are more or less similar, and in terms of magnitude, the results do not vary significantly, as shown in figures 15(a)-(d).Figures 16(a)-(c) depict a comparative study of PI velocity profiles using kinetic and fluid models.The profiles are similar to the previous plots,as the results are similar in terms of quality and quantity.

Figure 13.Wall potential and sheath thickness as a function of the effective electron temperature at constant= 0.12and βps=4.5.

4.Conclusions

Using the kinetic trajectory simulation method based on kinetic theory, we have investigated the collisionless 1d3v electronegative magnetized plasma-sheath properties in the presence of more than one species of negatively charged particles: hot electrons, cold electrons, and negative ions.The fundamental Bohm sheath condition has been modified for electronegative plasma discharges consisting of two-temperature groups of electrons, which depend on the concentration of hot electrons and the magnitude of the wall potential.It was found that the concentration of hot electrons, the concentration of negative ions,and the temperature ratio of hot to cold electrons affected the particle density variation, the potential fluctuation and the ion velocity in the plasma-wall transition region.The normal component velocity of positive ions made a major contribution to the energy flow towards the wall.The presence of an oblique magnetic field and a residual electric field produced a drift of positive ions, acting in the positive y-direction.This drift increased with an increase in the obliqueness of the magnetic field.The presheath-sheath interface was dominated by the magnetic field, i.e., the motion of charged particles was governed by the magnetic force rather than the electric force.The velocity of the positive ions was not parallel to the magnetic field in the magnetic presheath region.We have estimated the deviation of the resultant drift velocity of the positive ions on the xz-plane from the parallel component in the presheath-sheath interface region.With an increase in the obliqueness of the magnetic field from 1° to 30°, the deviation between the two components at the sheath entrance increased from 0.013% to 10.02%.The temperature distribution of hot electrons decreased towards the wall,whereas its average velocity increased.In the presence of two-temperature groups of electrons in plasma, the estimation of effective electron temperature is crucial, as it determines the initial Bohm flux and the sheath thickness.Finally, we have compared the kinetic results with the corresponding fluid results, and it was found that the results agreed qualitatively, but in terms of magnitude, the potential varied by less than 4%close to the wall.This comparative study of electronegative discharges using both kinetic and fluid approaches shows that both models are appropriate for studying the presheath and sheath structures; however, the kinetic approach yields higher-accuracy results, especially when the gradients are sharp close to the wall.The understanding of these electronegative plasma-sheath characteristics has useful applications in dry etching,in changing the surface properties of materials, and in cleaning a target surface by sputtering.For the formation of a stable plasma sheath, the fluxes of positive ions and negatively charged particles towards the wall must be equal.In this work,we have not considered the loss of particle fluxes along magnetic field lines, which has a vital role in the flux balance.This work can be extended further by considering the losses of flux along magnetic field lines,active walls,and also the effects of secondary electron emission.

Figure 14.Spatial variation of (a) electrostatic potential and (b) net charge density in the plasma-wall transition region obtained from kinetic and fluid models.

Figure 15.Particle density profiles obtained from kinetic and fluid models for (a) PIs, (b) HEs, (c) CEs, and (d) NIs.

Acknowledgments

S Basnet would like to acknowledge the University Grants Commission, Nepal for the PhD fellowship PhD/075-76-S&T-16.