Aohua MAO (毛傲華), Zhibin WANG (王志斌), Xianglei HE (何向磊) and Xiaogang WANG (王曉鋼)

1 School of Physics, Harbin Institute of Technology, Harbin 150001, People’s Republic of China

2 Laboratory for Space Environment and Physical Sciences, Harbin Institute of Technology, Harbin 150001, People’s Republic of China

3 Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082,People’s Republic of China

Abstract Double tearing modes (DTMs), induced by double current sheet configurations or two neighboring rational surfaces with the same safety factor in tokamaks, are widely observed in solar, space, and fusion plasmas.In this paper, the evolution of DTMs without a guide field is investigated numerically using a hybrid model(electron fluid + ion PIC).The overall evolution processes of DTMs are qualitatively consistent with previous works using other models.The particle dynamics during the evolution of DTMs is analyzed in detail.Behaviors of ions and electrons present different characteristics around the reconnection region which gives rise to Hall effects producing the out-of-plane quadrupole magnetic field.In the explosive reconnection process with interactions between two DTMs islands, the asymmetric drive and the thin current layer feature lead to the emergence of secondary magnetic islands which develop with the late evolution of the DTMs.

Keywords: double tearing mode, hybrid-PIC simulation, fast reconnection, secondary islands

1.Introduction

Double tearing modes (DTMs) and related fast magnetic reconnection processes have been extensively studied in recent years due to their crucial importance in space and fusion plasmas [1-4].In space plasma, double (multiple)current sheets are widely observed, such as in adjoining coronal helmet streamers [5], the solar wind [6], the solar photosphere[7],the Earth’s bow shock[8]and so on,leading to the double, triple, or even multiple tearing modes, in general with the weak or zero guide field [9-11].In fusion plasmas, reversed magnetic shear (RMS) configurations are widely applied for advanced scenarios in tokamak operations[12], leading to the double tearing modes induced by two neighboring rational surfaces with the same safety factor,resulting in an off-axis sawtooth oscillation or even a major disruption [13-16].In the latter case of tokamak plasmas,there is always a strong guide field component due to the toroidal magnetic field with a periodic condition in the toroidal direction, which gives the toroidal mode numbern.

As a DTM excited in tokamak plasmas, with the strong guide field, the reduced model can be applied [17, 18].Pritchett and Lee first analyzed the linear growth processes of the DTMs in 1980 by theory analysis and magnetohydrodynamics (MHD) simulations [19].It was found that the linear growth rate of the DTMs was proportional toS?1/3with S being the Lundquist number, if the distance between the two resonant surfaces,Δrs, was sufficiently small.On the other hand,ifΔrswas sufficiently large,the linear growth rate scaled asS?3/5,the same as that of the single tearing mode(STM) in the constant-ψapproximation.In nonlinear studies in the resistive MHD regime, the DTM islands for the large Δrswere found to grow linearly with time in the Rutherford regime[20].However,for the smallΔrs, four different phases during the nonlinear evolution of the DTMs were observed after the linear growth phase, i.e., an early Sweet-Parker phase scaled by ～S?1/2,a slow Rutherford transition phase of～S?1, a very explosive growth phase scaled by ～S?1/5presenting the merging of separatrices of two islands, and the final decay phase to end the reconnection process [14].Furthermore, for the DTMs with a strong guide field, various influences such as external shear flows [21], bootstrap currents [1], and different nonideal effects such as hyper-resistivity due to anomalous electron viscosity [22], and electron inertia[23,24],have been extensively studied.With a strong guide field, the electron inertial [25] and pressure gradient[26, 27] effects in Ohm’s law play an important role.The nondiagonal components of the electron pressure tensor due to the finite larmor radius (FLR) effect become dominant[28, 29], particularly with anisotropy caused by the guide field in the reconnection region.In reduced treatments, such effects can be approximated by a two-field model of the velocity stream function and the magnetic flux function[30, 31], where the FLR effect is characterized by the ion-sonic gyroradiuswith the ion-acoustic speedcs≈and the ion gyro-frequency

However, in space and astrophysical plasmas, the guidefield effect is usually weak.In this regime,instead of the ionsonic gyroradiusρs, the FLR effect is characterized by the‘Alfvénic’ gyroradiuswith the Alfvén speedand the ion inertial lengthwhere the ion plasma frequency[32, 33].The property presented by such adiscaling is usually called the Hall effect due to the clear decoupling of ion and electron motions in the ion inertial length scale[33,34].The nonlinear evolution of the DTMs is actually a typical multi-scale process, where the interface between different plasma regions is implemented through the thin reconnection region from the fluid to the kinetic scale.In particular, with the development of the DTMs, when the thickness of current sheets,δc,becomes comparable to the ion inertial lengthdi,due to the Hall effect, the ion gets unmagnetized and the magnetic field line carries the electron only and moves faster [34, 35].Previous studies of the Hall effect on the DTMs with a zero guide field were usually in two-fluids or Hall MHD models[36-38].However, without the strong guide field, in the reconnection diffusion region commonly concerned, the particles are distinguishably demagnetized, and the applicability of the fluid assumption needs to be discussed.Furthermore, the kinetic behaviors of particles, which can be significant as the scale length is comparable to, or even smaller than, the ion inertial length, cannot be obtained in the fluid model.Thus, hybrid models, either with a Vlasov treatment of ions or particle-incell (PIC) ions, should at least be applied.

In this paper,the nonlinear evolutions of the DTMs with a zero guide field are revisited in a hybrid model with PIC ions and fluid electrons.The paper is organized as follows.After the introduction,the model and equilibrium profiles for the DTMs are introduced in section 2.The energy evolution and conversion of the DTMs,as well as dynamics of particles,are analyzed in section 3.Moreover, we further show the behavior of electrons and the out-of-plane quadrupole magnetic field produced by the Hall currents in section 4.Furthermore, the generation and merging of the secondary islands during the explosive growth phase are also presented.The work is then summarized in section 5.

2.Model and equations

In this section,the hybrid simulation model with a PIC solver for fully kinetic ions and a fluid treatment for massless electrons in a 2D configuration with the quasi-neutrality assumption, similar to that in previous works [39-41], is briefly described.

Similar to [41], the variables are normalized as follows,

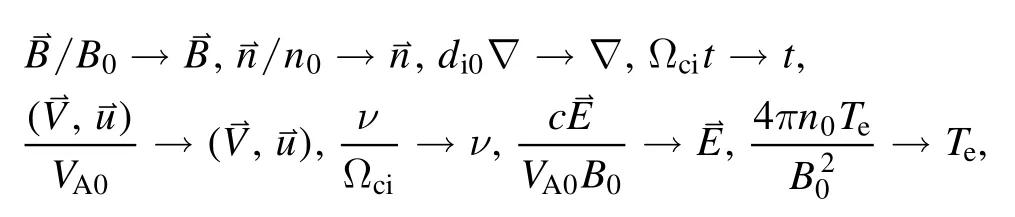
wheren0andB0are the asymptotic density and magnetic field,respectively, and v is the collision rate applied for modeling resistivity.The characteristic quantities, Alfvén speedVA0≡ion gyro-frequency Ω ≡and ion inertial lengthare also used for normalization.Then,the dimensionless dynamic equation for an individual ion can be written as

where the electron is assumed isothermal as the normalizedwhereβe0is the electron beta, and the quasi-neutrality conditionis also applied.Here,by the isothermal assumption for the electrons,we have ignored the Biermann battery effect and the nondiagonal contributions of the pressure to simplify the electron pressure gradient to the density gradient, as shown in the last term on the RHS of equation (2).Under such simplifications, with also the massless electron assumption to eliminate the electron inertia contribution,only the resistivity effect,the second term on the RHS of equation(2),can break the field lines at the X-point.Nevertheless,the gradient of the scalar pressure can still feature the FLR effect by introducing the ‘Alfvénic’ gyroradius scale ofdi,and by more rapidly bringing the feild lines into the ion inertial region to speed up reconnection [26, 42].

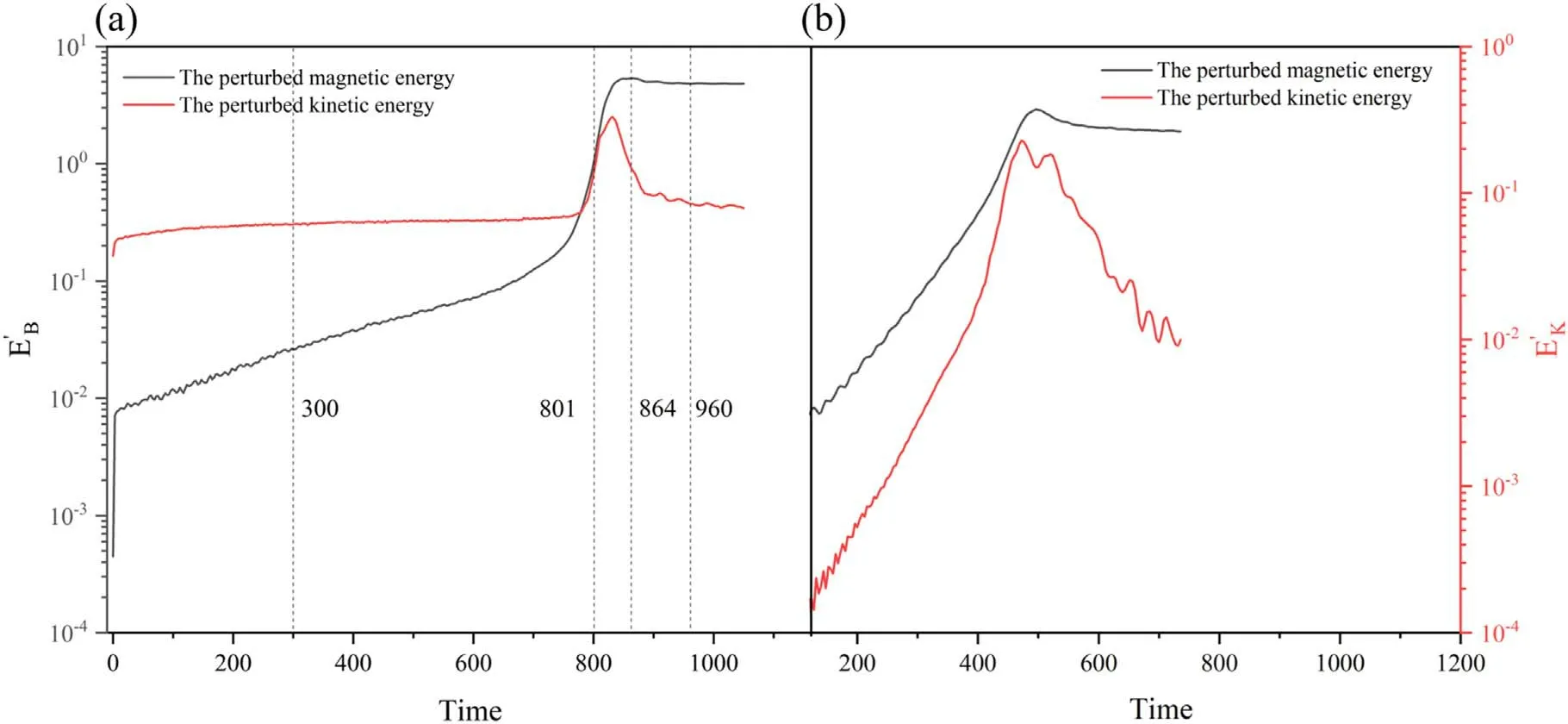
Figure 1.The temporal evolution of the perturbed kinetic and magnetic energies in (a) the hybrid, and (b) the MHD simulations.

The electron flow velocity can then be obtained from Ampere’s law,

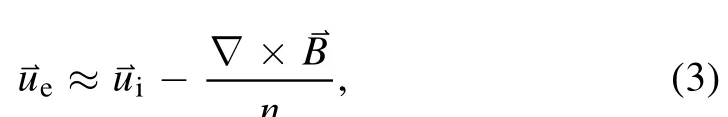
and the magnetic field is advanced temporally by Faraday’s law

with the electric field calculated by equation (2).

The simulation domain is a rectangular box in thex zplane withThe initial equilibrium is a 2D double current sheet configuration created by a magnetic field of

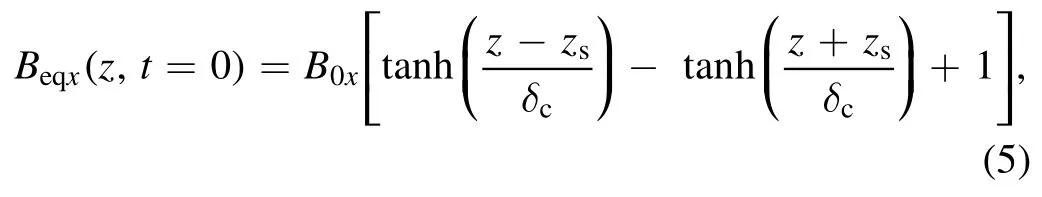
where = ±zzsare the positions of the resonant surfaces,andδcis the half width of each current sheet.Besides, the equilibrium guide field is assumed to be vanishing, i.e.,

while, however, the Hall effect, i.e., the decoupling of the electron and ion motions, can generate an out-of-plane component ofBywith a quadrupole distribution during the evolution of the DTM.

To trigger the double tearing mode, a small perturbation of the magnetic field is applied to the double current sheet system withwhereεis chosen to be 0.01 in this paper so that the system can reach the nonlinear stage quickly.The initial distribution of the ion thermal velocity is set in such a way to make the initial ion temperature uniform and satisfy the pressure balance by the initial number density distribution

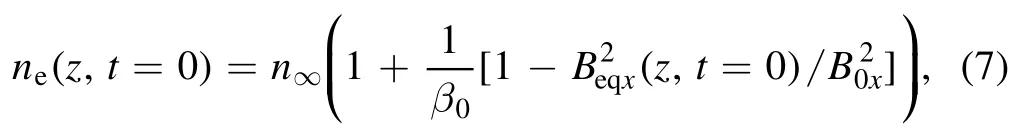
where the asymptotic plasma betain the normalized form withconst.being assumed, according to the observed ratio ofor bigger in general in geospace plasmas [43, 44].

In the simulation, a set of typical normalized parameters withzs=5,Lx=Lz=40,β0= 0.2(βe0= 0.033),ν=0.01,Δrs=2zs=10,δc= 2,andn∞=n0=1are chosen as the reference case to discuss the characteristics of the DTMs evolution.At the boundariesx= ±Lx/ 2,the periodic condition is applied, while the open boundary condition is assumed atz= ±Lz/ 2.Also in the simulation,a total of 1.27 million particles are loaded.

3.Energy conservation and fast reconnection

Based on previous studies [14, 19, 20, 36], the DTMs evolution includes a linear phase, a slow growth early nonlinear phase, an explosive growth phase, and a final decay phase.Figure 1(a)shows the temporal evolution of the magnetic(the solid black curve) and kinetic (the solid red curve) perturbation energies,for the reference case with the typical parameters introduced in the previous section.Here,〈...〉 denotes the spatial average.As a comparison, in figure 1(b), we also show the energy perturbations for an MHD simulation with the same parameters as in the hybrid case, except for the Hall terms being replaced by the resistivity with the Lundquist numberS=104.For better insights into the evolution of the DTMs,the temporal development of the island width in both cases is supplemented in figure 2.

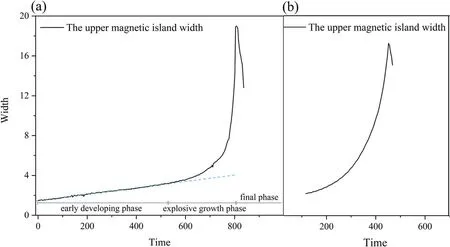
Figure 2.The temporal evolution of the magnetic island width in (a) the hybrid, and (b) the MHD simulations.

It can be seen that from figure 1(a),the magnetic and the kinetic perturbation energies increase moderately in the early stage, and a dramatic increase of the perturbation energies appears later.After that, the kinetic perturbation energy decays and the perturbation magnetic energy saturates in the final stage.As shown in figure 2(a), three phases can be clearly observed, (A) the early developing phase of the islands with dw/dt=const.,in good agreement with the Rutherford reconnection regime, (B) the explosive growth phase with very fast reconnection, and (C) the final phase with decayed islands until their complete disappearance.For the MHD simulation, however, the growth of the perturbations in the early stages is more significant than that for the hybrid case due to the dissipation.Nevertheless, a sudden transition to the explosive growth phase in figure 1(a)is much more clearly shown than that in the MHD simulation(figure 1(b)), indicating a smaller scale and thinner current sheet corresponding to the ion inertial length due to the Hall effect.It has been found that, though there is also an explosive growth phase where the fast reconnection process is almost independent of resistivity (the Lundquist number)[14,20,21,37],the explosive growth due to the Hall effect is even faster.During the reconnection, the ions are demagnetized and the whistler waves take the place of the Alfvén waves, which drives the magnetic reconnection presenting a faster growth rate than that in the MHD regime [32, 34].It can be further shown in figure 2 that the growth of the island size in the hybrid simulation (figure 2(a)) is much more steepened than that in the MHD simulation (figure 2(b)).

Accordingly, structures of magnetic field lines with the ion density distribution in the various phases are illustrated in figure 3 with corresponding moments being marked in figure 1 in dashed lines.As shown in figure 3(a)(t=300),in the early growth phase, reconnection occurs between open field lines with the two islands growing on each resonant surface respectively.Then,as shown in figure 3(b)(t=801),as the two inner separatrices between the islands merge into one, reconnection between the outer open field lines and the early reconnected field line inside the other island takes place.Thus, the fully grown island brings its closed field lines onto the other resonant surface leading to an inflow forced reconnection process[45]to drive the DTMs to the explosive stage [2, 14].The process then makes the current layer thin around the X-point and generates secondary islands in the region, as shown in figure 3(c) (t=864).Eventually, two islands are decayed and then vanished with all field lines being reconnected in the final stage, as shown in figure 3(d)(t=960).Such processes are similar to those seen in resistive and Hall MHD simulations except for the secondary island formation with significant sizes (see figure 3(c)).

The energy evolution during the development of the DTMs is also investigated and shown in figure 4.Clearly, the total energy(the solid green curve)almost remains constant with only a slight loss due to the collision with the rateν,as investigated in detail by Swift [46].In our reference case, the characteristic mean free time can be estimated aswhile the characteristic time of total energy loss calculated from figure 4 isIn other words, the total energy loss is only ～1% in ～5000 field sub-cycle time steps,small enough to ensure the process‘energy conserved’[46].The energy conversion is also clearly shown, as in the explosive phase the magnetic energy decreases obviously and converts to the thermal and the kinetic energies.

Accordingly,the dramatically increased kinetic energy in the explosive phase indicates that the bulk flow of ions is crucial for the DTM development.Thus, the temporal evolution of the ion flow in the x and z directions is calculated by ion dynamics and then illustrated in figure 5.

Figure 3.The magnetic field lines with the ion density in color at(a)t=300,(b)t=801,(c)t=864,and(d)t=960 marked in figure 1.

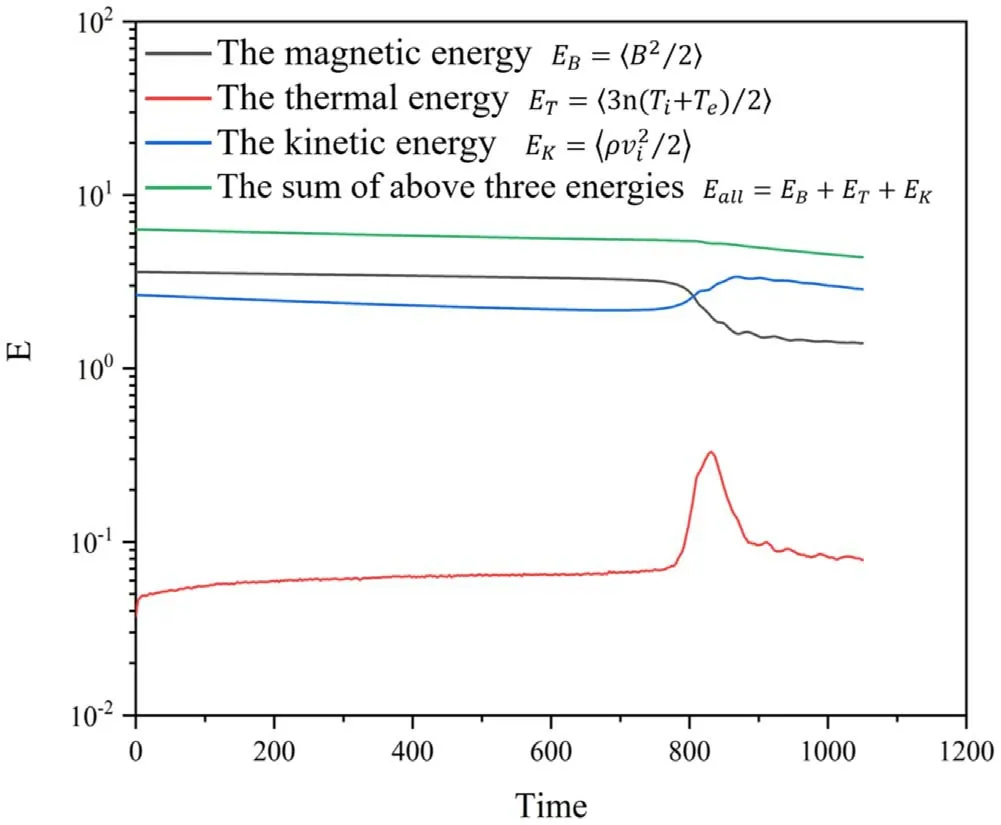
Figure 4.The temporal evolution of the system energy.

Figure 5.Snapshots of the x and z components of the ion flow velocity in color at (a) t=300, (b) t=780, (c) t=807, and (d) t=837.

Figure 7.The configuration of the out-of-plane field at t=807.

It is shown that in figure 5(a) (t=300), the ion flow is very faint in the early developing phase and the flow structure of each island is separated rather than interacting with each other until approaching the explosive phase.As the island width increases, the flows are enhanced, as shown in figure 5(b) (t=780).With the further growth of the island width, the inflow (in the z-direction), driven by the other island size increases, gets stronger and stronger to trigger the onset of the explosive phase, as shown in figure 5(c)(t=807), and the structures of both outflow and inflow become global.Especially as seen in the red box in figure 5(c2) surrounding the upper X-point, the ion inflow onto the inner side of the upper X-point is distributed in the lower island and enhanced obviously, indicating a strong inflow driven due to the growth of the lower island.Thus, it can be seen that the explosive growth of the DTMs is similar to the inflow forced reconnection process [45] due to the intensive coupling between the two islands.As reconnection goes on further, the islands exchange their relative positions,as shown in figure 5(d) (t=837).Moreover, secondary islands are excited around the former X-point position and the distorted O-point region,weakening the drive of the enhanced inflows.Then, all antiparallel field lines are reconnected and the reconnection process is completed.

It has been found that the formation of secondary islands is due to current sheet thinning in the reconnection region[47-51].In this simulation, the current is mostly carried by electrons, while the ions almost have no contribution to the reconnection current sheets but only for quasi-neutrality.Thus, the transition to the whistler mediated process acting together with the island coupling leads to a faster explosive growth than that in the MHD regime where the current carried by ions and electrons is comparable [34].We then further investigate the distribution of electron flows and their relation to the secondary island formation.

4.The electron flow and secondary islands formation

The electron flow shows different characteristics from the ion flow.As shown in figure 6,the electron flow mainly concentrates along the separatrices.The Hall effect,i.e.,decoupling of ions and electrons, can then be clearly observed in such a different flow structure.It is found that the ions are diverted into a relatively wide outflow in the ion inertial region, while the electrons continue to move mostly along the separatrix and toward the X-point.In the process,the magnetic field seen by the electrons decreases gradually.Therefore,due to the condition ofB/ne=const.in a flux tube, the electron density in the reconnection region drops eventually.The electrons are thus accelerated by the parallel electron pressure gradient along the field line.Then as they get into the electron diffusion region close to the X-point, the electrons are decoupled from the magnetic field lines and diverted to the outflow direction, and further accelerated.

The different flow structure of the electrons and ions then produces current loops around the separatrices to generate the out-plane magnetic field component with a quadrupole pattern, as shown in figure 7 (t=807) during the explosive growth phase for the DTM islands.At the moment, the electron inflow and outflow move on the various sides along the separatrix, as shown in figure 6(c) (t=807).Clearly,such a shear flow distribution by the electron inflow and outflow generates the quadrupole distribution along the separatrix for the out-of-plane magnetic field component.

We then further investigated the in-plane current distribution.Although both the electron and ion flows contribute to the current, it can be seen, however, that the in-plane current distribution pattern is highly consistent with the electron flow structure, as shown in figure 8, also in comparison with figure 6.In other words, the in-plane current is mostly carried by the electrons in the reconnection region,and particularly along the separatrices.

Interestingly, in the late explosive phase of the DTMs,starting at approximately t ～ 810,multiple secondary islands are formed.As seen in figure 9(a) (t=813), such tiny secondary islands are generated at the thin current sheet near the X-point of the primary DTMs island along the separatrices and are deformed as reconnection continues.As the evolution of the secondary islands and the primary DTMs,the reconnection geometry turns from a single X-point of the main DTM island on a large scale to the multiple X-points of the secondary and splintered islands on a small scale, as shown in figures 9(b)-(e) (t=837-894).In the process, the multiple X-point structure leads to the magnetic energy relaxation with an oscillation as exhibited in figure 10.Finally, the reconnection finishes and all antiparallel magnetic field structure disappears as shown in figure 9(f) (t=936).

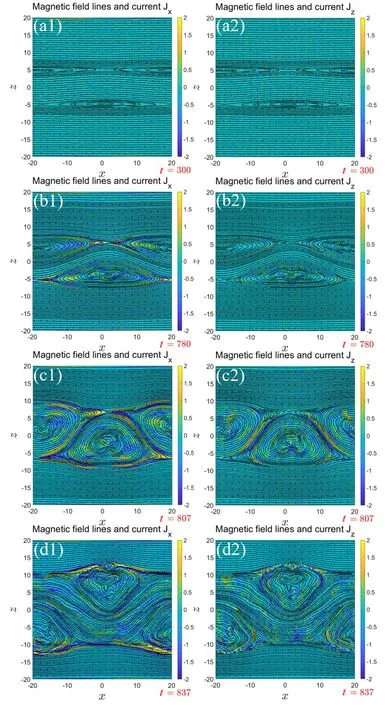
Figure 8.Snapshots of the x and z components of the current at (a) t=300, (b) t=780, (c) t=807, and (d) t=837.

Figure 9.Snapshots of the y components of the current at (a) t=813, (b) t=837, (c) t=855, (d) t=870, (e) t=894 and (f) t=936.

5.Conclusions

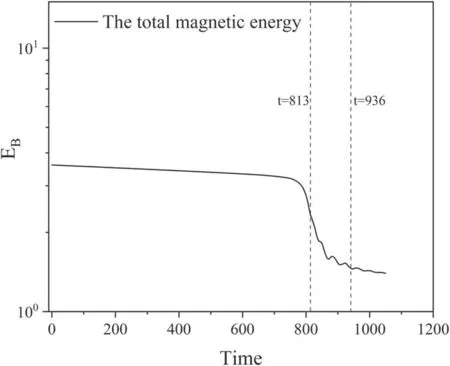
Figure 10.The relaxation of the total magnetic energy.

In this paper, the Hall effects on the DTMs and the corresponding particle behaviors are studied in numerical simulations in a hybrid model with the PIC ions and the fluid electrons.From the temporal evolution of the energy and the island width, three different development phases of the DTMs are observed: the early developing phase, including a linear and an early nonlinear part, the explosive growth phase, and the final relaxation phase.The energy conversion mainly occurs in the explosive growth phase.Moreover, the pattern of ion and electron flows in the different phases shows decoupling characteristics.The ion flow of each island is almost selfdeveloping rather than them interacting with each other in the early developing phase.Approaching the explosive phase,reconnection on the X-point of each island gets strengthened by the enhanced inflow driven by the other island,resembling a forced reconnection pattern with the intense asymmetric inflow.For the electron flow,both the inflow and the outflow are concentrated along the separatrices to make a shear flow layer in the explosive phase.The decoupling of the ions and the electrons is then clearly shown by the flows.One can also see that the current is found to be almost carried by the electrons.Thus, a quadrupole out-of-plane Hall field is formed by the electron flow shear, i.e., a current circuit formed on different sides of the separatrix.Furthermore, the secondary islands are found on the current sheets and inside the primary DTM islands in the onset phase.The emerging and developing secondary islands lead to the reconnection process turning from the large-scale single X-point geometry to the small-scale multiple X-points geometry with the secondary and splintered islands.This indicates a possible mechanism [47-49] for the fast explosive onset with a much steeper growth than that in the MHD simulation.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Nos.11705039, 11975087, and 42011530086), the China Postdoctoral Science Foundation (No.2018M631918),and the Heilongjiang Postdoctoral Foundation (No.184744).