HIGH-ORDER NUMERICAL METHOD FOR SOLVING A SPACE DISTRIBUTED-ORDER TIME-FRACTIONAL DIFFUSION EQUATION?
(李景)(楊瑩瑩) (姜英軍)
School of Mathematics and Statistics,Changsha University of Science and Technology,Changsha 410114,China
E-mail:lijingnew@126.com;1720719892@qq.com;jiangyingjun@csust.edu.cn
Libo FENG(封利波)
School of Mathematical Sciences,Queensland University of Technology,Brisbane,QLD 4001,Australia
E-mail:fenglibo2012@126.com
Boling GUO(郭柏靈)
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
E-mail:gbl@iapcm.ac.cn
Abstract This article proposes a high-order numerical method for a space distributed-order time-fractional diffusion equation.First,we use the mid-point quadrature rule to transform the space distributed-order term into multi-term fractional derivatives.Second,based on the piecewise-quadratic polynomials,we construct the nodal basis functions,and then discretize the multi-term fractional equation by the finite volume method.For the time-fractional derivative,the finite difference method is used.Finally,the iterative scheme is proved to be unconditionally stable and convergent with the accuracy O(σ2+τ2?β+h3),where τ and h are the time step size and the space step size,respectively.A numerical example is presented to verify the effectiveness of the proposed method.
Key words Space distributed-order equation;time-fractional diffusion equation;piecewisequadratic polynomials;finite volume method;stability and convergence
1 Introduction
In recent years,more and more mathematicians and natural scientists have paid attention to fractional partial differential equations,due to their wide applications in many areas[1–11]such as physics,biology,chemistry,finance,dynamics,etc..Meanwhile,it has been found that compared with single and multi-term fractional differential equations,the distributed-order differential equations are more suitable for describing accelerating sub-diffusion and decelerating super-diffusion without power-law scaling over the whole time-domain.After Caputo[12]first put forward distributed-order fractional differential equations,a growing number of specialists have concentrated on how to solve them.
Generally,distributed-order fractional equations are divided into time distributed-order fractional equations and space distributed-order fractional equations.The time distributedorder fractional equations can be used for the kinetic description of anomalous diffusion and relaxation phenomena[13].Many scholars have focused on the numerical solutions of time distributed-order fractional equations,and have investigated the finite difference method[14–17],the reproducing kernel method[18],the alternating direction implicit approach with the element-free Galerkin method[19],the discrete energy method[20],the Chebyshev collocation method[21],the linearized compact difference scheme[22],the RBF based meshless method[23],the Legendre operational matrix method[24],the Chelyshkov wavelets method[25],the Legendre-Gauss collocation method[26],the spectral tau method[27],the spline approximation method[28],and so on.
By contrast,the space distributed-order fractional equation shows a more flexible representation of the effect of the medium and its spatial interactions with the fluid.There are also a few papers on the space distributed-order fractional equations.Li and Liu[29,30]put forward a finite volume method to solve the space distributed-order fractional advection-diffusion equation,and proved that the method was stable and convergent with second-order accuracy in time and space.Based on the unstructured mesh method for the irregular convex domain,Fan and Liu[31]proposed the finite element method to solve the two-dimensional distributedorder space-fractional diffusion equation,and proved that the space convergence order can reach the second order.Combining this with the implicit Galerkin-Legendre spectral scheme,Zhang and Liu[32]presented a Crank-Nicolson alternating direction method for the two-dimensional Riesz space distributed-order advection-diffusion equation.They also got a second-order convergence rate in space.Wang and his coauthors developed a fast finite difference method for the distributed-order space-fractional partial differential equation in a general convex domain in multidimensional space[33].In addition,with the help of an efficient biconjugate gradient stabilized method,they adopted the Crank-Nicolson fast finite volume approximation to solve the nonlinear distributed-order space fractional diffusion equations in three-dimensional space,and proved that the space accuracy can reach to minorder[34],whereare the fractional orders in the x,y,z directions,respectively.Shi and Liu[35]proposed an unstructured mesh finite element method for solving the Riesz space distributed-order wave equation in an irregular convex domain,and obtained the stability and convergence of the method.Making use of the fractional backward differential formulas and the Grünwald difference method,Javidi et al.[36]studied the Riesz space distributed-order advection-diffusion equation.Then,they achieved the Crank-Nicolson scheme and proved that the scheme was convergent with second-order accuracy in space.Abbaszadeh[37]investigated a finite difference scheme for solving the Riesz space distributed-order diffusion equation and concluded that their iteration scheme was convergent with second-order accuracy in space.
According to the authors’knowledge,in the existing literature for solving space distributedorder equations,all authors can only prove that their iterative methods are convergent with no more than second-order accuracy in space.Therefore,in this paper,we investigate a high-order numerical method for the space distributed-order diffusion equation.Based on the piecewisequadratic basis fuctions,we apply the finite volume method to discretize the space distributedorder term,and then we obtain the third-order spacial convergence.
In what follows,based on the model introduced by Sokolov et al.[38],we consider the space distributed-order time-fractional diffusion equation
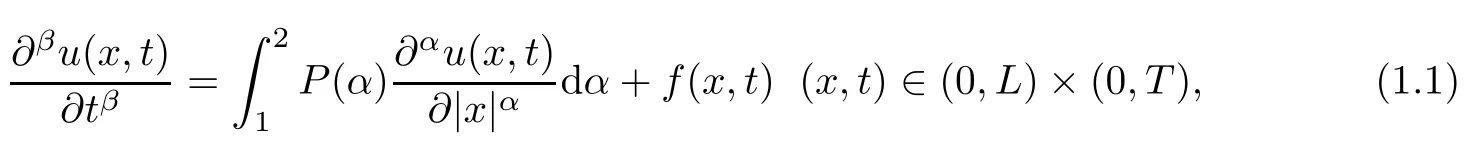
with boundary data
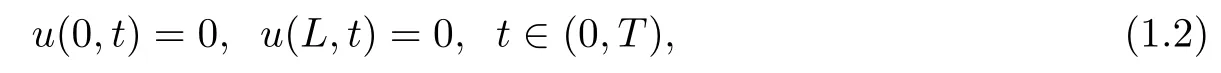
and initial data

The structure of this paper is as follows:in Section 2,we employ the finite difference approximation for a time-fractional derivative,then transform the space distributed-order equation into a multi-term space fractional equation by the mid-point quadrature rule.We take piecewise quadratic polynomials as our basis functions,and use the finite volume method to solve the multi-term space fractional equation;thus we can derive the Crank-Nicolson iteration scheme.In Section 3,we prove the stability and convergence of the discretization scheme.Finally,we present a numerical example to show the validity of our numerical method in Section 4.Some conclusions are given in Section 5.
2 Crank-Nicolson Iteration With Finite Volume Method for the Space Distributed-Order Time-Fractional Diffusion Equation
Discretize the domain[0,L]×[0,T]by tn=nτ,n=0,1,2,...,N,xi=,i=0,1,2,...,2M and h=L/M,τ=T/N.
Adopting the discrete scheme in[39],the time-fractional derivative term can be approximated by the following scheme:

Defining the space Vhas the set of piecewise-quadratic polynomials on the mesh{[xi?1,xi]}i=1,...,2M,the nodal basis function φi,0≤i≤2M of Vhcan be expressed in the following form:for 1≤i≤M?1,ifiis odd,
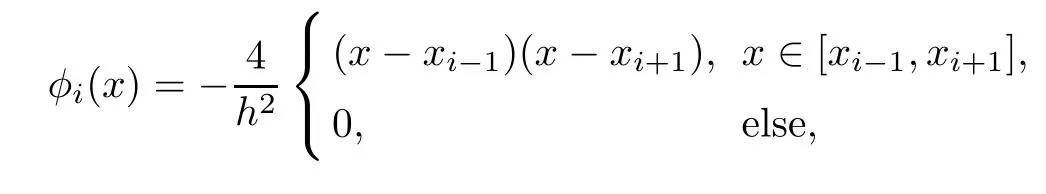
and ifiis even,
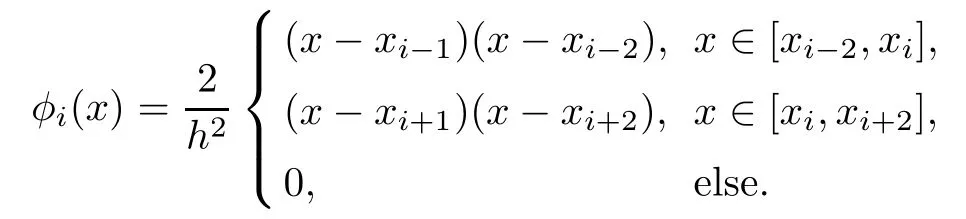
In addition,

Then the approximate solution uh(x,tn)can be expressed as
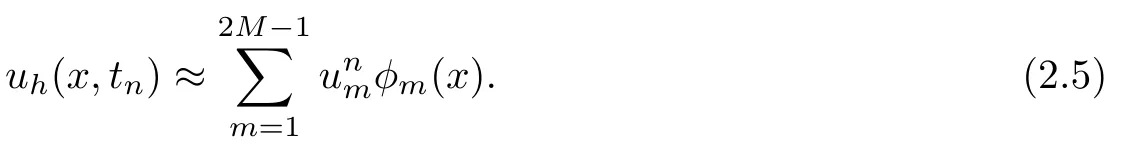
Thus,we obtain
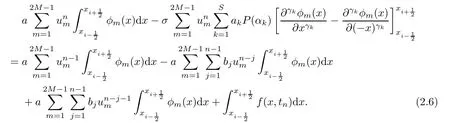
By direct calculation,for 1≤i,m≤2M?1,this yields that if m is odd,then

and if m is even,
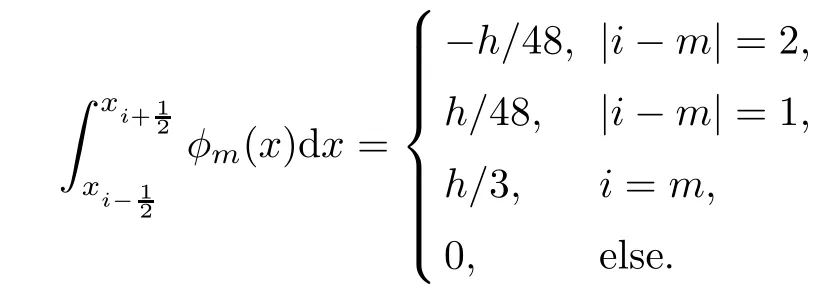
Similarly,if m is odd,then

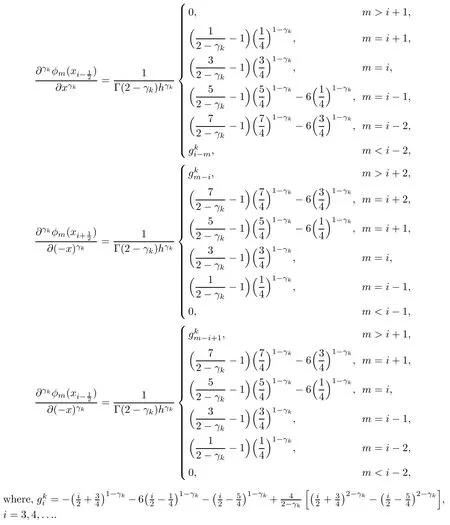
Therefore,(2.6)can be rewritten as follows:
?Ifiis odd,

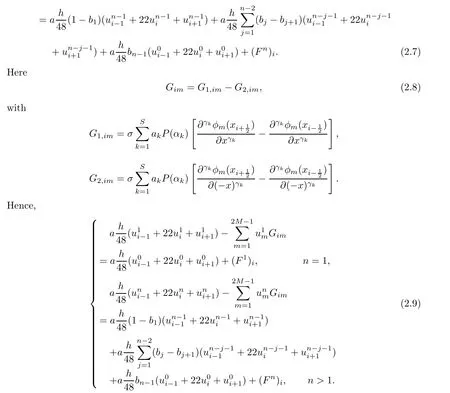
?Ifiis even,
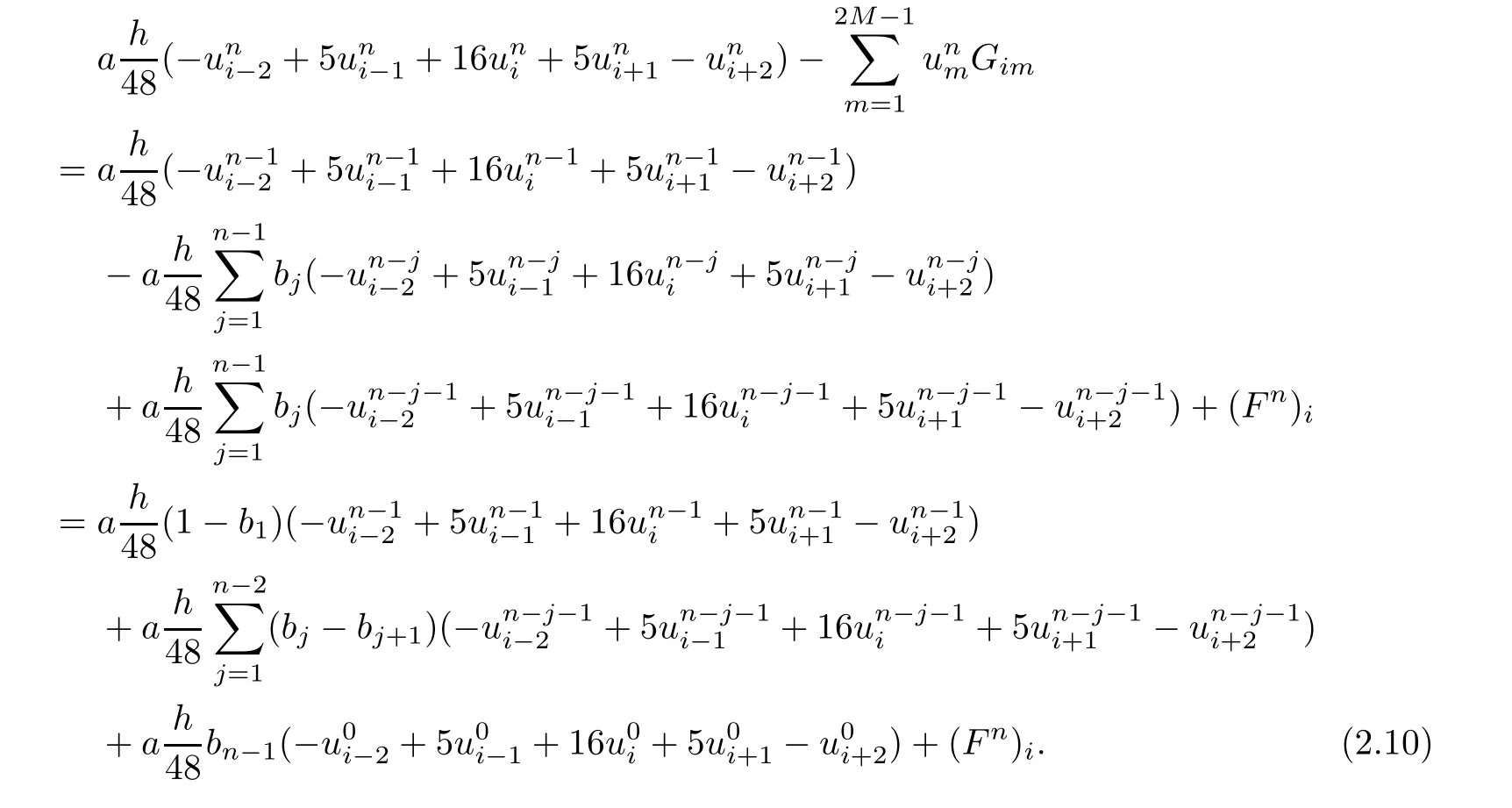
Thus,

3 Stability and Convergence of the Iterative Method
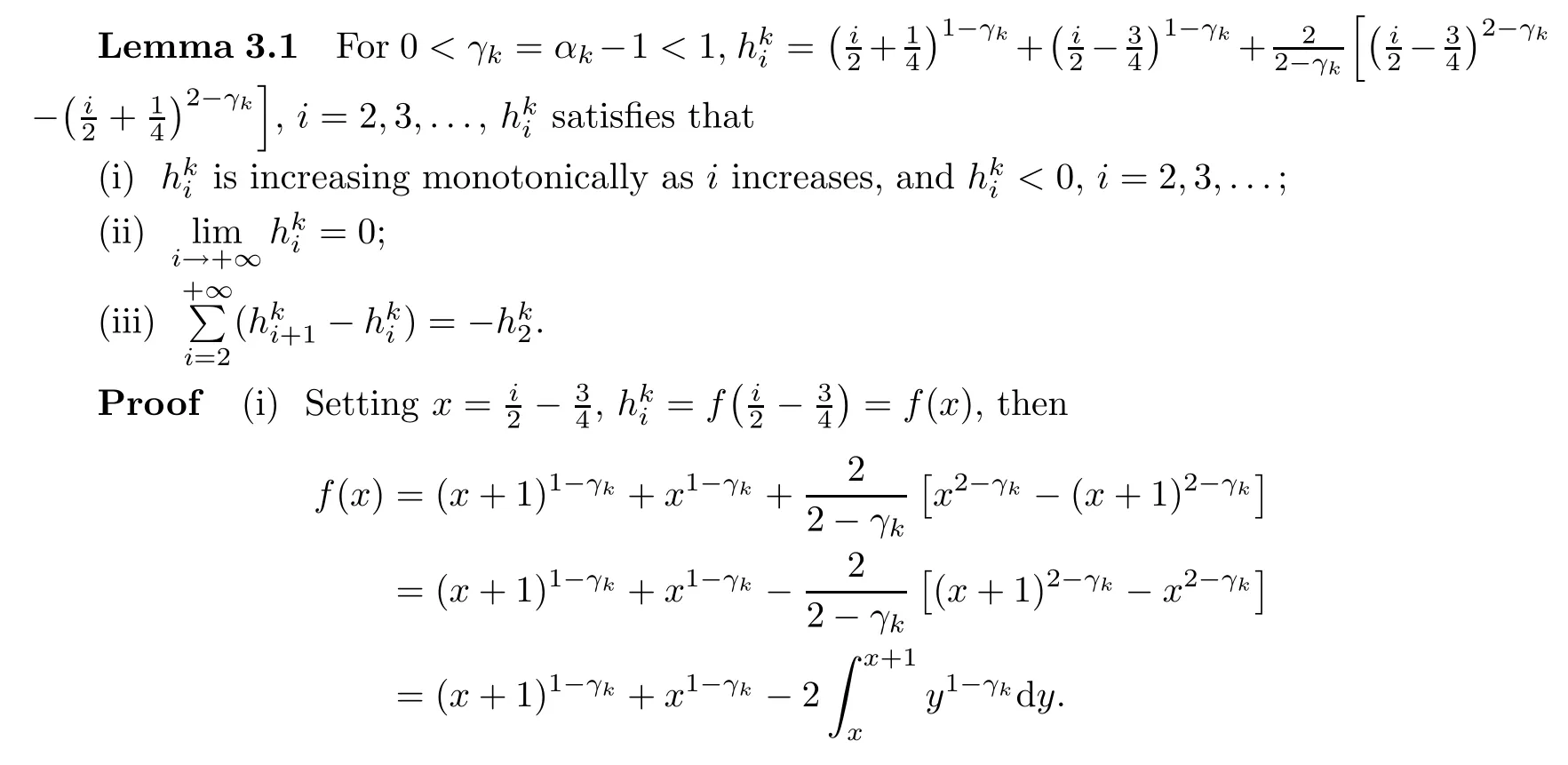
First,we shall prove that f(x)<0 for all x>0.
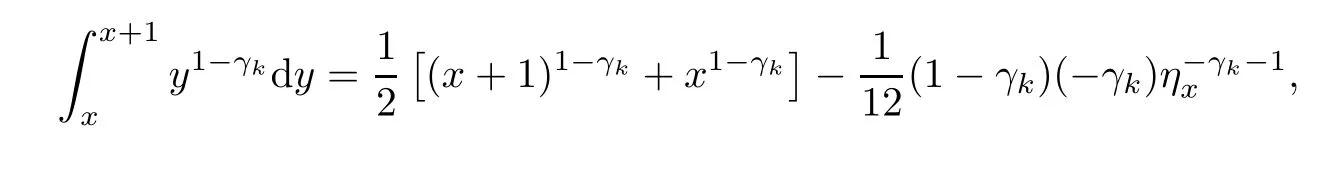

By using the Trapezoidal quadrature formula,there exists ηx∈(x,x+1),such that Consequently,?′′′(t)is monotonically increasing for all t∈(0,1).Since ?′′′(0)<0 and ?′′′(1)<0,?′′′(t)<0 in t∈(0,1),which implies that ?′′(t)is monotonically decreasing.Because ?′′(0)=0,?′′(t)<0 in t∈(0,1).Along the same lines as the above proof,we also know that ?(t)is monotonically decreasing and that ?(t)<0 in t∈(0,1).Therefore F(x)is monotonically increasing and F(x)<0,thusis monotonically increasing as i increases and<0.
(ii)According to the proof of(i),it can be concluded that
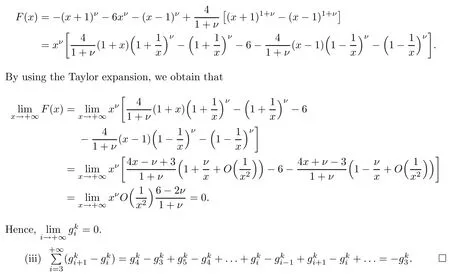
Lemma 3.3([41]) For 0<β<1,bj=(j+1)1?β?j1?β,dj=bj?1?bj,j=1,...,n,bj,djsatisfies
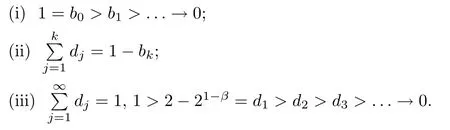
Theorem 3.4Let the element Gimof the matrix G be defined by(2.8).Then,for 0<γk<1,it holds that
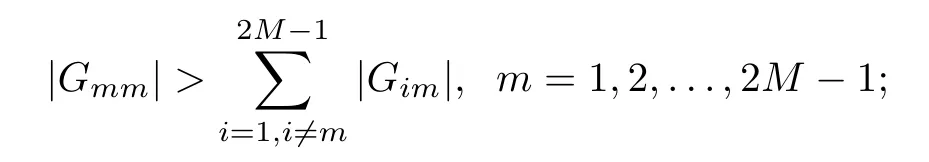
that is,G is strictly diagonally dominant.
ProofNotice that if m is odd,
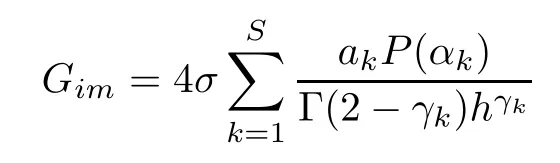
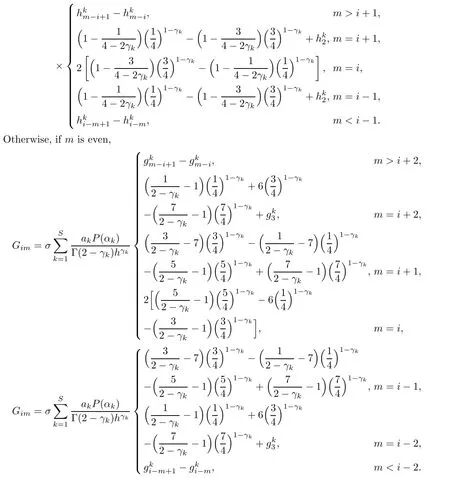
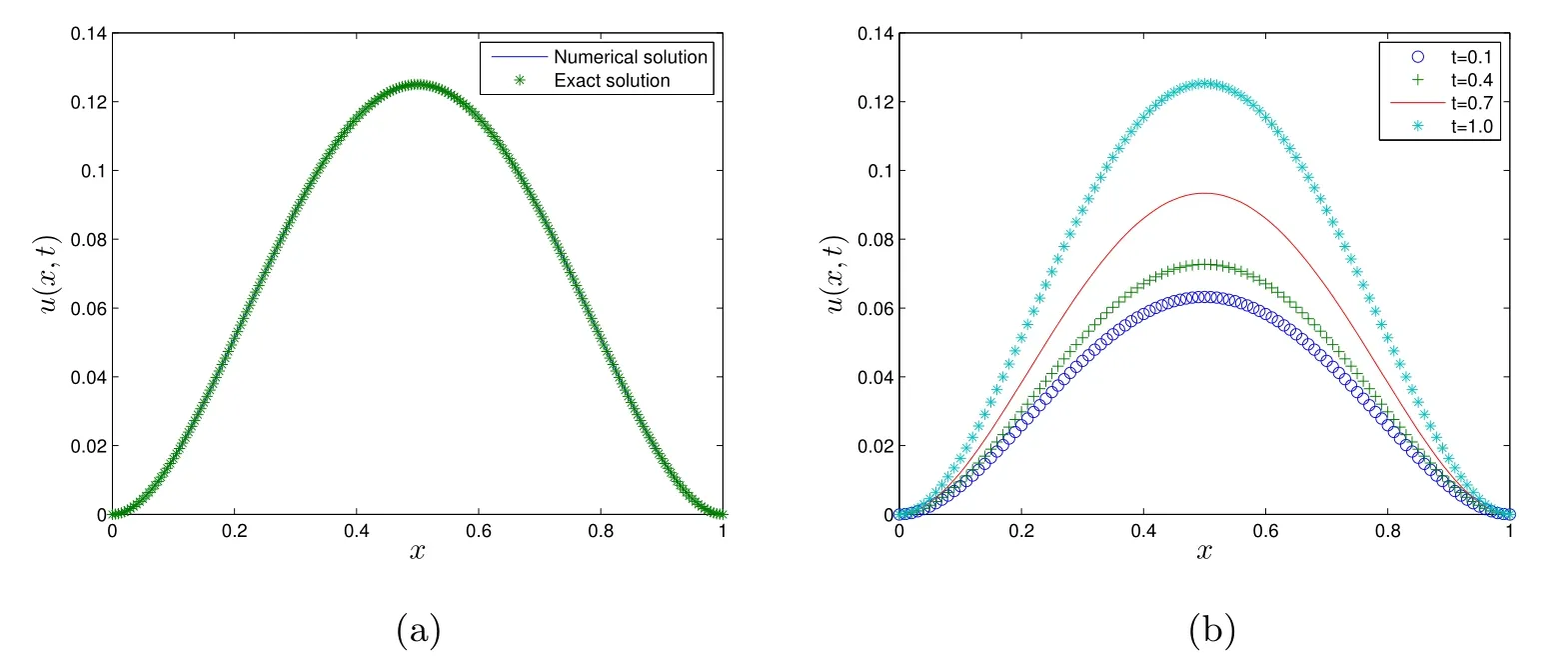
(I)When m is odd,since ak>0,P(αk)≥0,from Lemma 3.1 we know that Gim>0 for m>i+1 and m Hence, (II)When m is even,since ak>0,P(αk)≥0,from Lemma 3.2 we know that Gim>0 for m>i+2 and m Hence, This completes the proof. □ Theorem 3.5Let B=A?rG.Then for 0<γk<1,B is strictly diagonally dominant and the spectral radius of B?1fulfills ProofNote that if m is odd, otherwise,if m is even, ? When m is odd,according to the proof of Theorem 3.4,it yields that Bmm>0 and Bim<0 for all m>i+1 and m ?When m is even,Theorem 3.4 indicates that Bmm>0 and Bim<0 for all m≥i+2 and m≤i?2.Consequently, Therefore, From the above inequalities,we know that B is strictly diagonally dominant,so B is nonsingular and reversible.Let λ0be the eigenvalue of the matrix B.Then,by Gerschgorin’s circle theorem,we have that that is, Henceforth, which completes the proof. □ Theorem 3.6Defining D=(λ?1)A?λrG,for 0<γk<1,if λ>1 or λ ProofWhen m is odd, and when m is even, (1)If λ>1,then (i)When m is odd,from Theorem 3.4,we know that Dim<0 for m>i+1 and m (ii)When m is even,according to the proof of Theorem 3.4,we can obtain that Dim<0 for m≥i+2 and m≤i?2,Dmm>0.Thus, Therefore, (2) If λ1,we can conclude that The proof is complete. □ Theorem 3.7The spectral radius of B?1A satisfies that ρ(B?1A)<1. ProofNote that B and A are strictly diagonally dominant.Assuming that λ is an eigenvalue of B?1A,then Since B is nonsingular and invertible,det(B?1)/=0,thus det(λB?A)=0.Let D=λB?A=(λ?1)A?λrG.Then, (i)if λ±1 or 0,then D is diagonally dominant; (ii)if λ>1 or λ Henceforth,det(D)/=0 for all|λ|≥1 and λ=0.According to the above analysis,as the roots of the equation det(λB?A)=0 exist,λ must satisfy 0<|λ|<1,so the eigenvalue of B?1A satisfies|λ|<1.Thus,ρ(B?1A)<1,which completes the proof. □ Theorem 3.8Suppose that(i=1,2,...,2M?1,n=0,1,...,N)are the approximate solution and the numerical solution of(2.12),respectively.LetThen‖Yn‖≤‖Y0‖,which implies that the scheme(2.12)is unconditionally stable. ProofWe will use mathematical induction to prove the stability. Now assume that for all n≤k?1,we have that‖Yk?1‖≤‖Y0‖. Then,for n=k, Thus,we can get‖Yn‖≤‖Y0‖,which completes the proof. □ Lemma 3.9We suppose that the solution u(x,t)is smooth enough.Then, Lemma 3.10For 0<γk<1, ProofFollowing along the same lines as Corollary 1 in[42],we can assert that this lemma holds. □ Theorem 3.11Let unbe the exact solution of problem(1.1).Then the numerical solution Ununconditionally converges to the exact solution unas σ,τ and h tend to zero.Moreover, and when i is even, According to Theorems 3.5 and 3.7,we know thatand ρ(Q)<1,so there exists a vector norm and induced matrix norm‖·‖such that‖Q‖<1 and‖B?1‖ Now assume that for all n≤k?1,we can obtain that‖Ek?1‖≤O(τβ(τ2?β+σ2+h3)). Then,when n=k,we get that Therefore,‖En‖≤C(τ2?β+σ2+h3),which completes the proof. □ Consider the distributed-order equation with boundary data u(0,t)=0,u(1,t)=0,and initial data u(x,0)=x2(1?x)2,where The exact solution of the above equation is u(x,t)=(t2+1)x2(1?x)2. Figure 3(a)shows a comparison of the exact solution and the numerical solution for this example.It is apparent from Figure 3(a)that the numerical solution is in excellent agreement with the exact solution.Figure 3(b)displays the evolution of u(x,t)at different times,which increases with increasing time.In addition,Table 1 shows the error and convergence order for our method with respect to σ,for τ=h=1/400.With decreasing σ,the convergence order of σ can reach second order.Table 2 shows the error and convergence order with respect to τ for σ=h=1/500 at t=1.It can be seen that with τ decreasing,the convergence order of τ is close to 2?β.Table 3 shows the error and convergence order with respect to h,for σ=τ=1/1000.From Table 3,the convergence order of h can reach the third order very accurately.According to the error and convergence rate in all the tables below,we can conclude that the numerical method is efficient and stable,as expected. Figure 1 (a)Function S1(x)with x∈(0,1);(b)Function S2(x)with x∈(0,1) Figure 2 (a)Function S3(x)with x∈(0,1);(b)Function S4(x)with x∈(0,1) Table 1 The error and the convergence order of σ for Table 2 The error and the convergence order of τ for Table 3 The error and the convergence order of h for Figure 3 In this paper,we have proposed a high-order numerical method for solving the space distributed-order time-fractional diffusion equation and obtained the convergence with thirdorder accuracy in terms of the step size in space.However,due to the nonlocality of the fractional operator,the discretization of equation(1.1)leads to a dense stiffness matrix which has an O(M)memory requirement and an O(M3)computational complexity,where M is the total number of spatial unknowns.This makes the computation costly.Thus,in the future,combined with the fast Fourier transformation and the finite volume method introduced by Wang[43,44],we will discuss the numerical solution for the space distributed-order time-fractional diffusion equation in two dimensional space.Consequently,the overall computational cost and the memory required can be reduced to O(M logM)and O(M),respectively.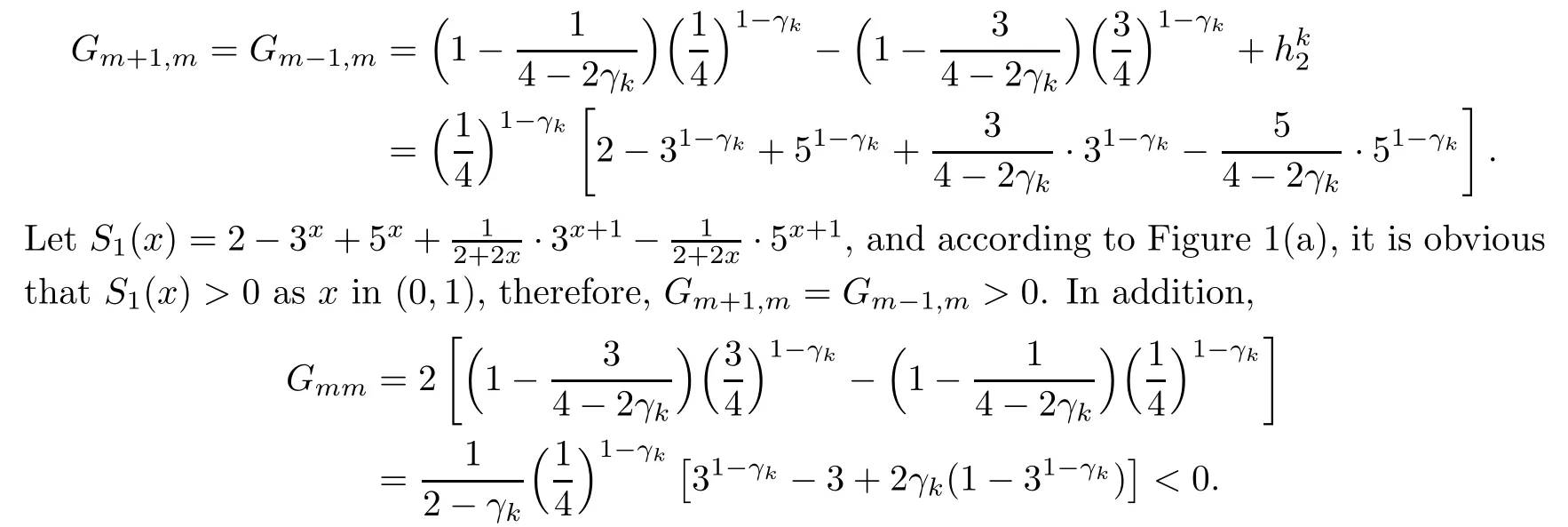

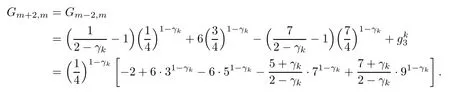

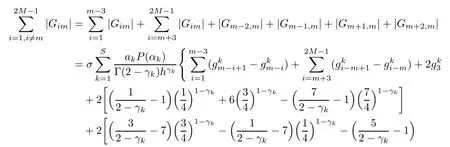
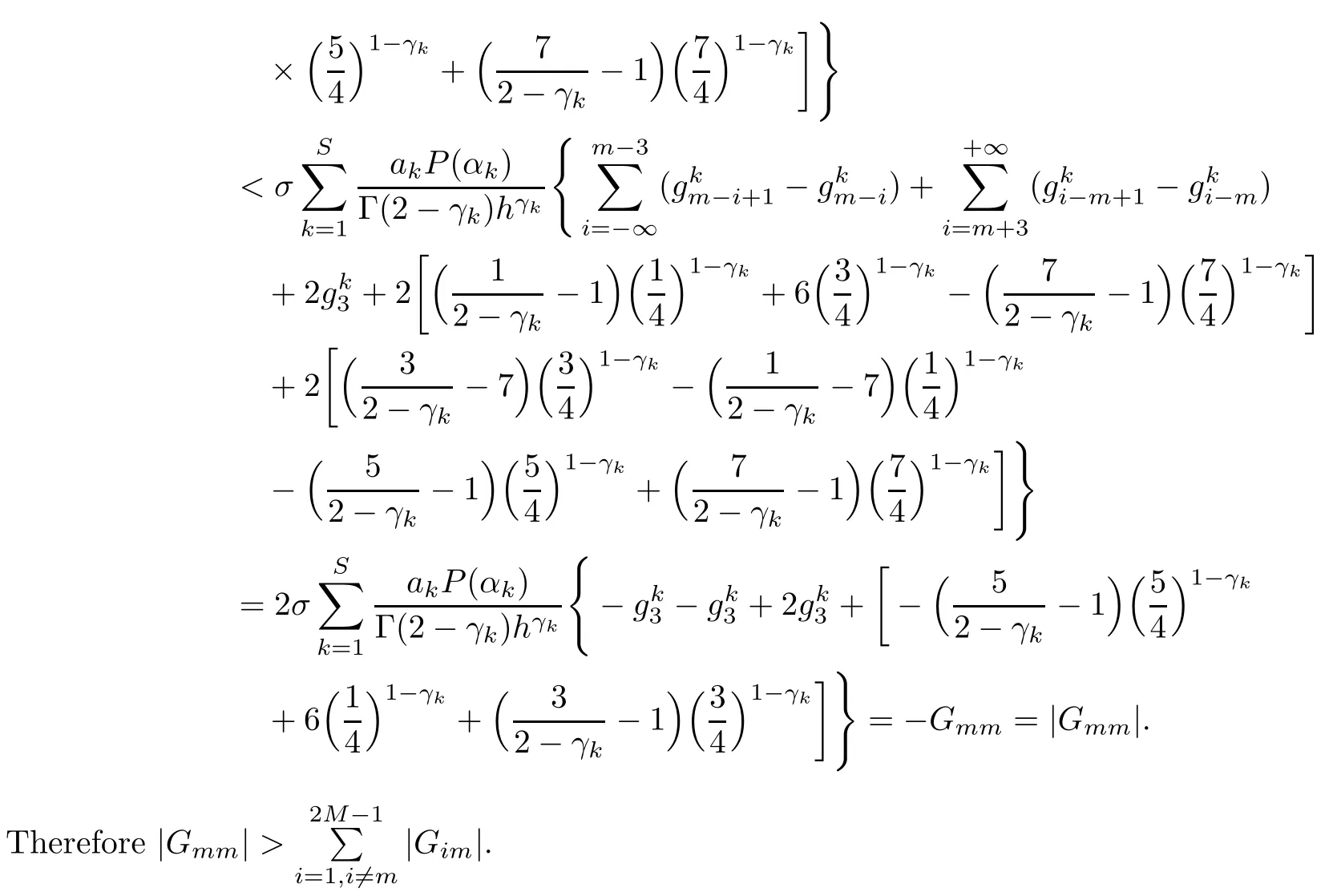



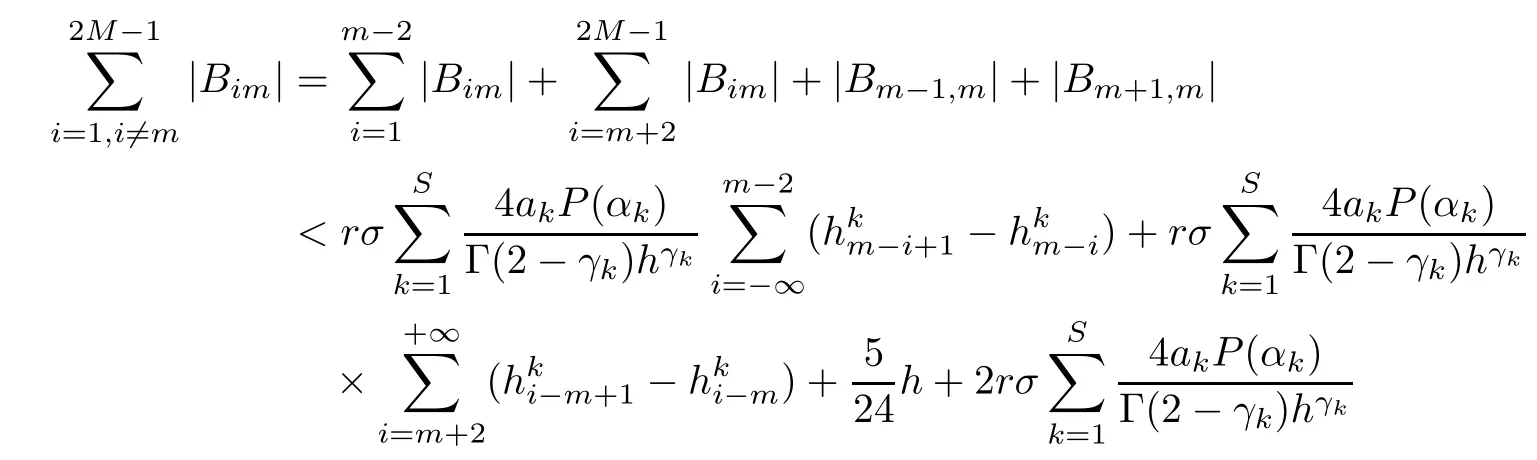
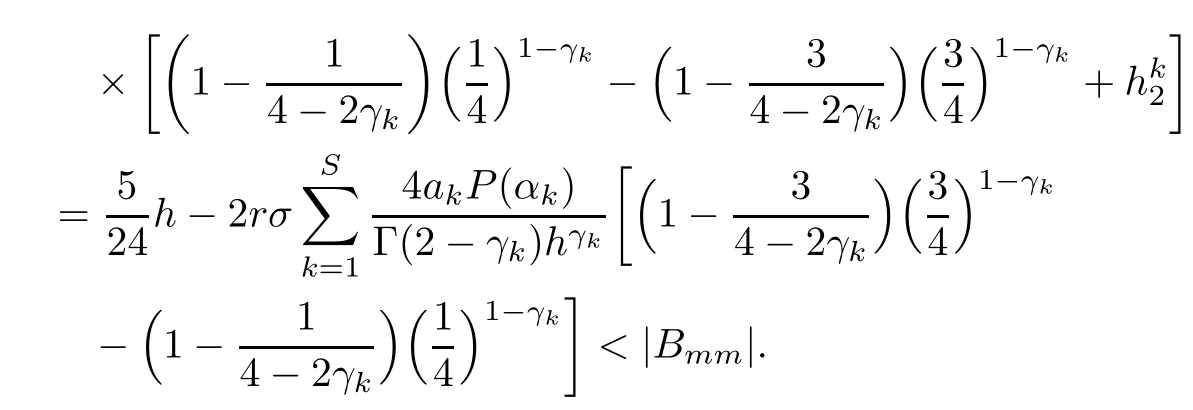

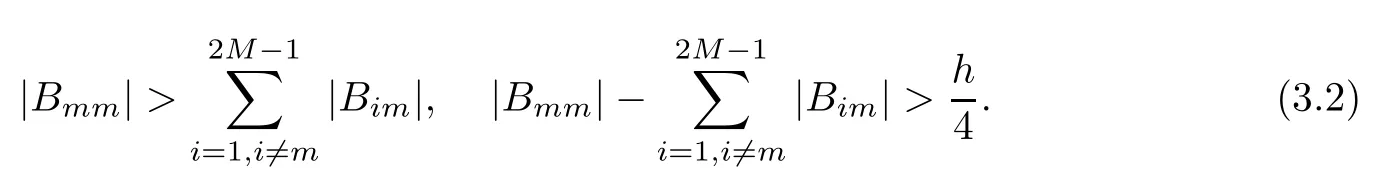
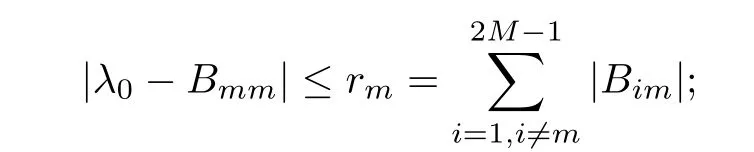
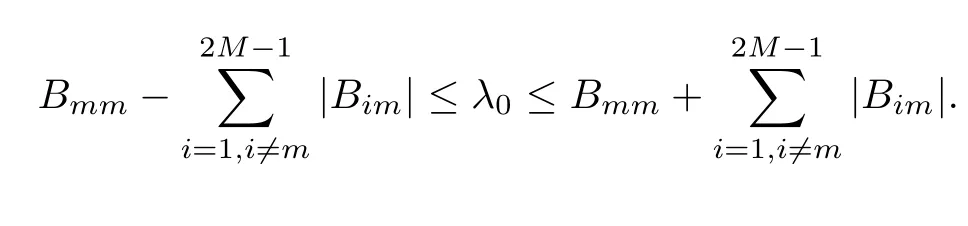

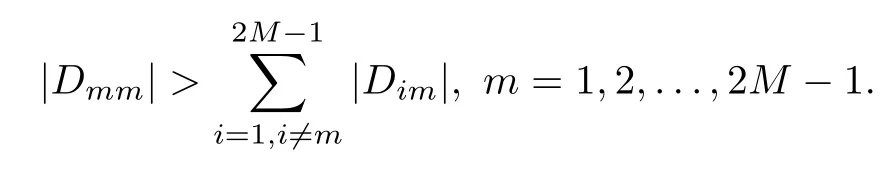

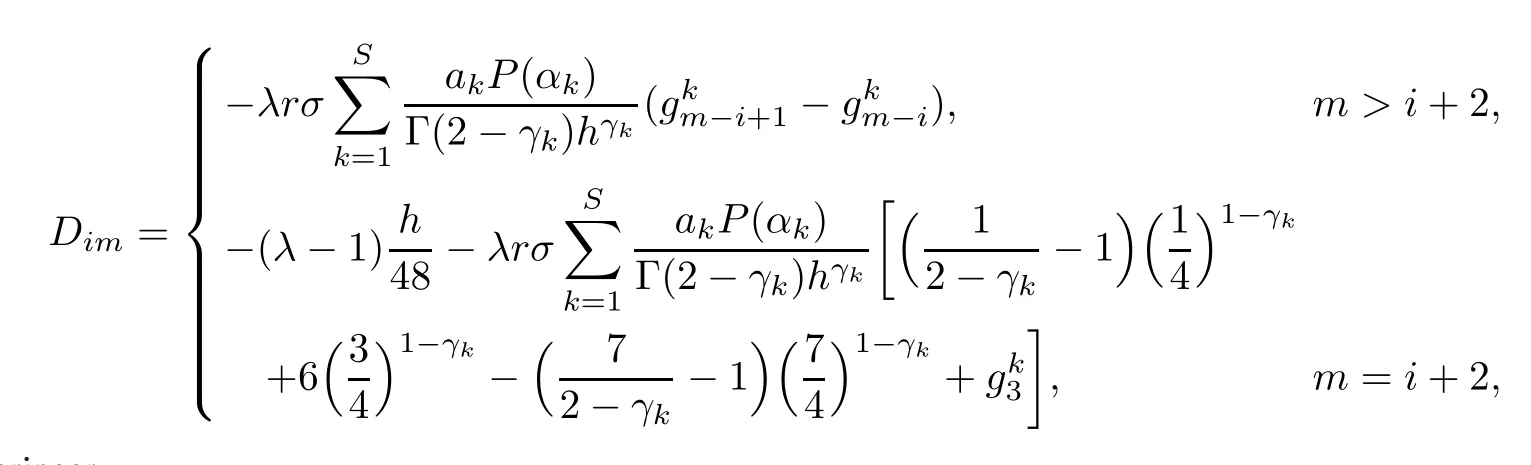

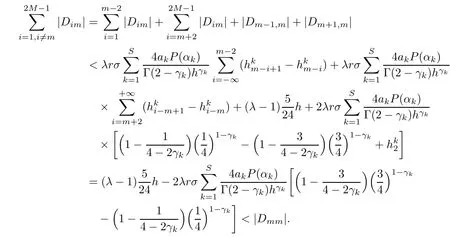
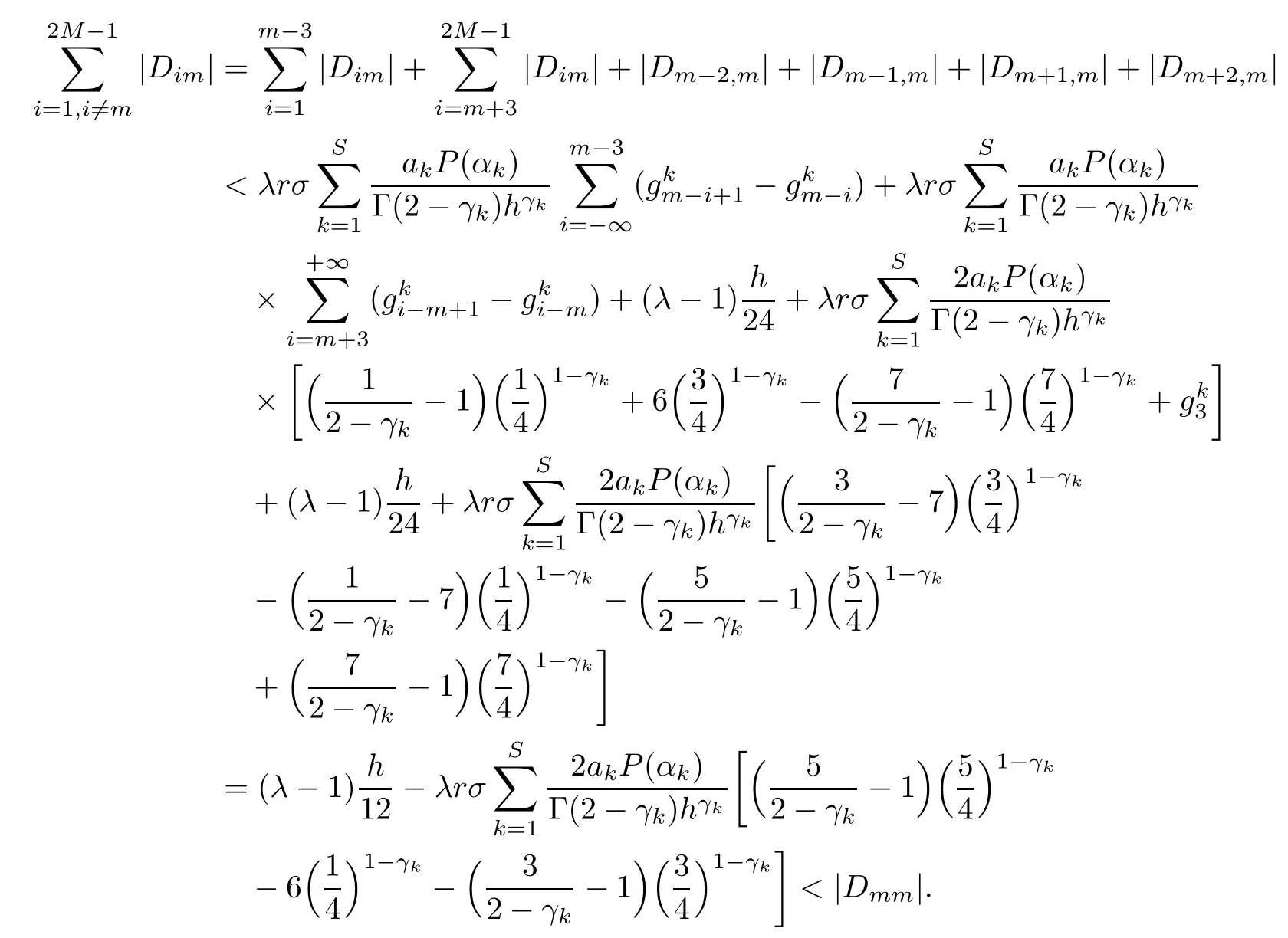
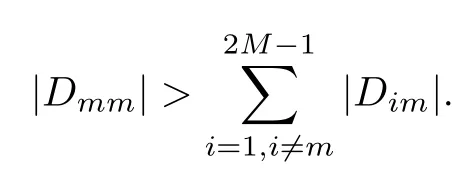
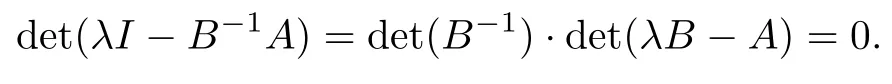
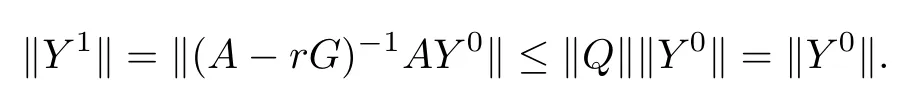
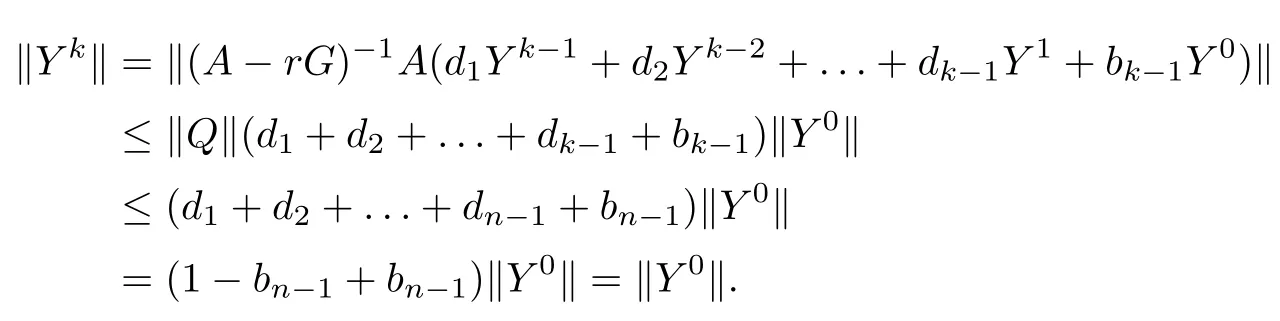
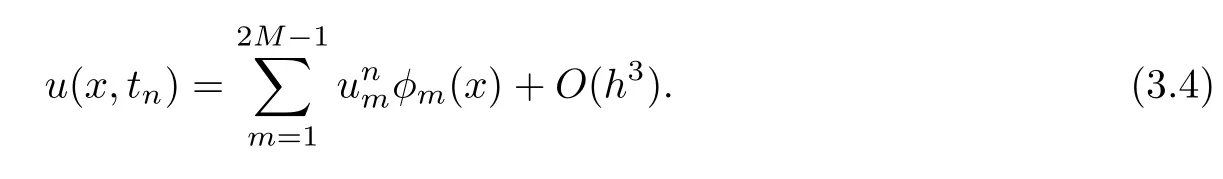

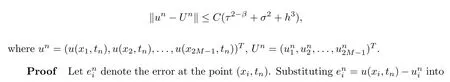
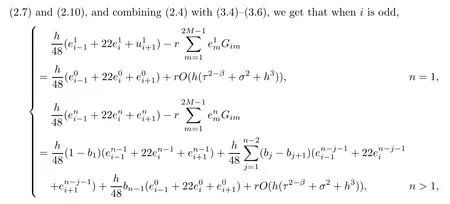

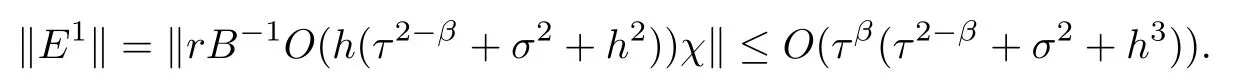

4 Numerical Example
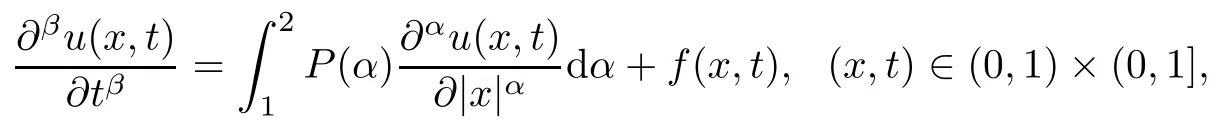
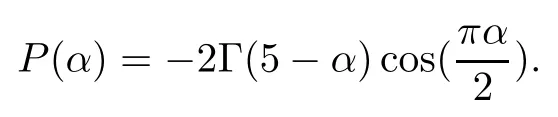



5 Conclusion
 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
