徐碧云, 姜坤, 曹煒

(寧波大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院, 浙江 寧波 315211)

1 引言

Markoff-Hurwitz 類型的方程是指如下形式的丟番圖方程

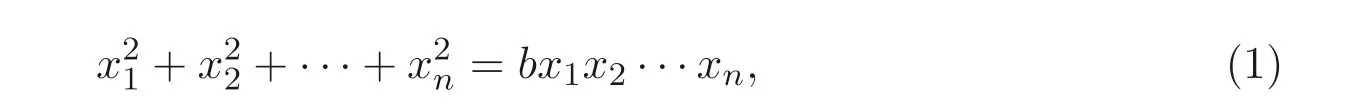
其中n,b均為正整數(shù). 由于它與丟番圖逼近理論的緊密聯(lián)系, 文獻[1] 首先研究了它在n=3,b=3 情形時的解數(shù)公式; 文獻[2] 考察了它的一般形式, 這是此類方程命名的由來.

設(shè)Fq是一個特征為p且含有q個元素的有限域, 其中q=pr,r ≥1,p是一個奇素數(shù), F?q= Fq{0}. 對于多項式f ∈Fq[x1,x2,··· ,xn], 用Nq(f) 表示方程f(x1,x2,··· ,xn)=0 在Fq中的解數(shù). 尋找Nq(f) 的具體表達式是有限域中的一個重要課題. 一般來說, 給出Nq(f) 的具體表達式是比較困難的, 所以需要限制一些特殊條件(參見文獻[3-10]).

文獻[3] 研究了有限域Fq上的Markoff-Hurwitz 類型的方程

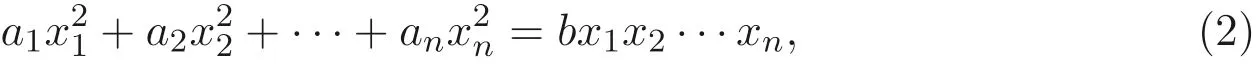
其中a1,··· ,an,b ∈F?q, 文獻[3] 給出了當(dāng)n=3 和n=4 時在某些特殊情況下的具體解數(shù)公式, 并提出了尋找此類方程解數(shù)公式的問題.

文獻[4] 推廣了文獻[3] 的上述結(jié)果, 得到了n ≥5 時, 其在某些特殊情況下的具體解數(shù)公式; 文獻[5] 研究了如下廣義的Markoff-Hurwitz 類型方程

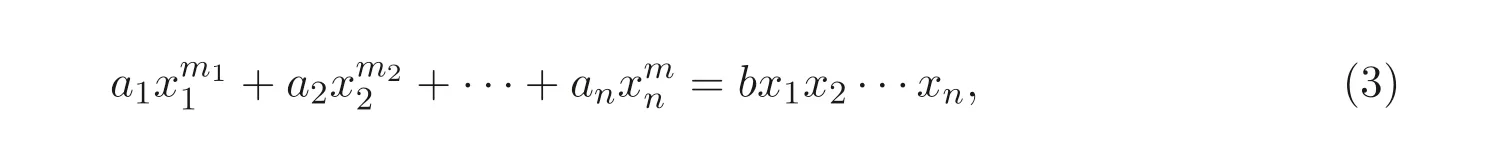
其中ai,b ∈F?q,mi(i=1,2,··· ,n) 為正整數(shù), 利用指數(shù)和的工具, 在文獻[6] 研究成果的基礎(chǔ)上給出了它在某些限制條件下的解數(shù)公式.

文獻[7] 研究了廣義的Markoff-Hurwitz 類型方程

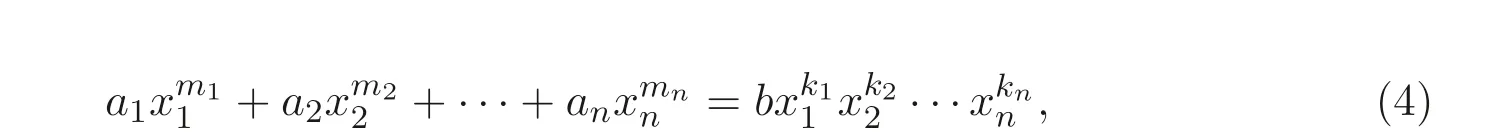
其中ai,b ∈F?q,mi,ki,i= 1,2,··· ,n,n ≥2 為正整數(shù), 利用剩余類環(huán)Z/(q ?1)Z 上增廣次數(shù)矩陣的Smith 標準型給出了其在特殊條件下的解數(shù)公式, 推廣并簡化了文獻[5]的相關(guān)結(jié)果.

文獻[9] 考慮了更為廣義的Markoff-Hurwitz 類型方程

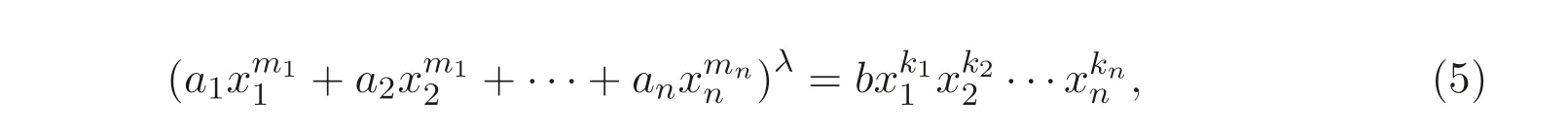
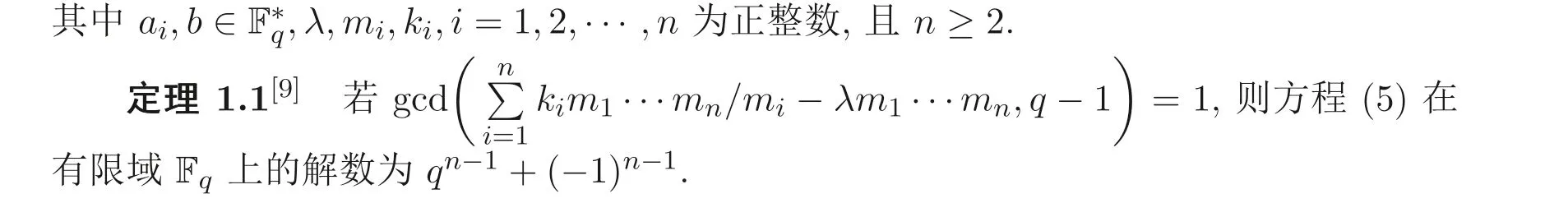
本文將給出定理1.1 的另一種組合證明方法, 并進一步研究如下廣義Markoff-Hurwitz 類型方程的解數(shù)問題:

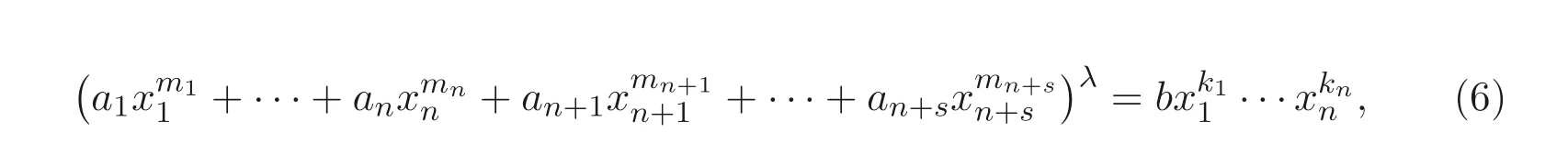
其中ai,b ∈F?q,λ,mi,kj,i=1,2,··· ,n+s,j=1,2,··· ,n, 且n ≥2,s ≥0 均為整數(shù).

本文的結(jié)構(gòu)安排如下: 在第二節(jié), 介紹一些預(yù)備知識; 在第三節(jié), 給出定理1.1 的另一種組合證明; 方程(6) 的解數(shù)公式及推論和例子在第四節(jié)中給出.

2 預(yù)備知識

設(shè)f(X) 是Fq上的n元多項式, 記為

對一個給定的向量l= (l1,l2,··· ,lm)∈Ωm, 定義σ(l) 為向量l中非零元的個數(shù).記(v1,v2,··· ,vm)T=l1?D1+l2?D2+···+lm?Dm, 定義s(l) 為(v1,v2,··· ,vm)T中非零元的個數(shù).

設(shè)ξp是p次復(fù)本原單位根,χ是乘法群F?q上的Teichm¨uller 特征, 即對任一a ∈F?q, χ(a) 是q ?1 次復(fù)本原單位根, 滿足χ(a)(modp) =a. 定義Fq上的(q ?2) 個高斯和為

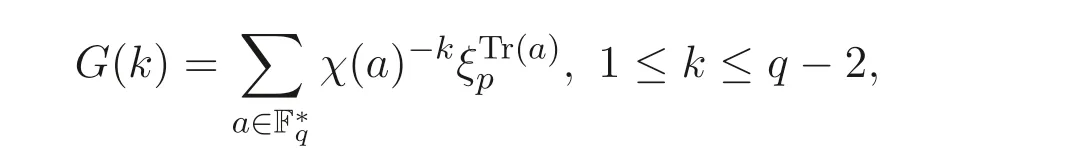
為Fq上的二次高斯和.

引理2.1[12]對q=pr, 有

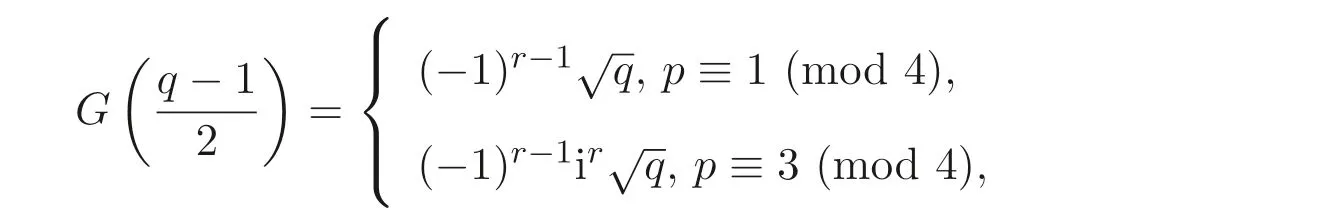
其中i 是虛數(shù)單位.

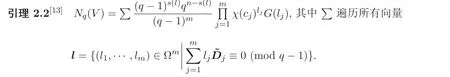
3 定理1.1 的證明

設(shè)代數(shù)簇V由下列方程組確定:

令(v1,··· ,vn+3)T=?D(l1,··· ,ln+3)T滿足(v1,··· ,vn+3)T≡0 (modq ?1), 即

由于條件

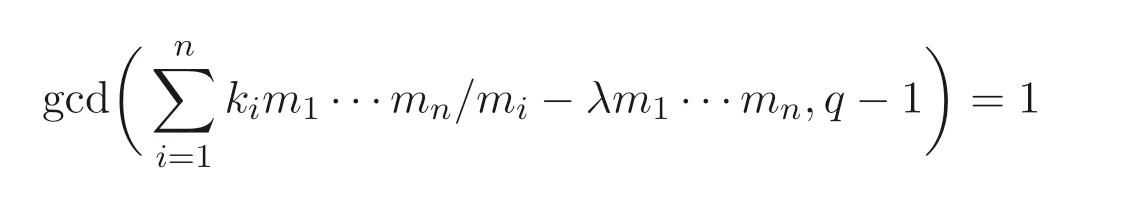
等價于V的增廣次數(shù)矩陣?D在剩余類環(huán)Z/(q ?1)Z 中可逆, 因此由Cramer 法則, 同余方程組?Dl ≡0(modq ?1)只有零解,即(l1,l2,··· ,ln+3)≡(0,0,··· ,0)(modq ?1),注意這里l ∈Ωn+3,Ω={0,q ?1}.

下面根據(jù)(7) 式對σ(l) 和s(l) 的具體情形進行分類討論.

當(dāng)σ(l) = 0 時, 即(l1,··· ,ln+3) = (0,··· ,0), 有(v1,··· ,vn+3) = (0,··· ,0),故s(l)=0.

當(dāng)σ(l)=1 時, 即l1,··· ,ln+3中有1 個不為0, 分兩種情形討論:

(i) 若從l1,··· ,ln+2中任選1 個不為0, 則s(l)=2;

(ii) 若ln+3?=0 , 則s(l)=n+1.

當(dāng)σ(l)=2 時, 即l1,··· ,ln+3中有2 個不為0, 分三種情形討論:

當(dāng)3≤σ(l)≤n+1 時, 即l1,··· ,ln+3中有σ(l) 個不為0, 分三種情形討論:

當(dāng)σ(l)=n+2 或σ(l)=n+3 時,s(l)=n+3.

對上述情形進行合并歸納, 結(jié)果見表1.

表1 σ(l), s(l) 及對應(yīng)個數(shù)

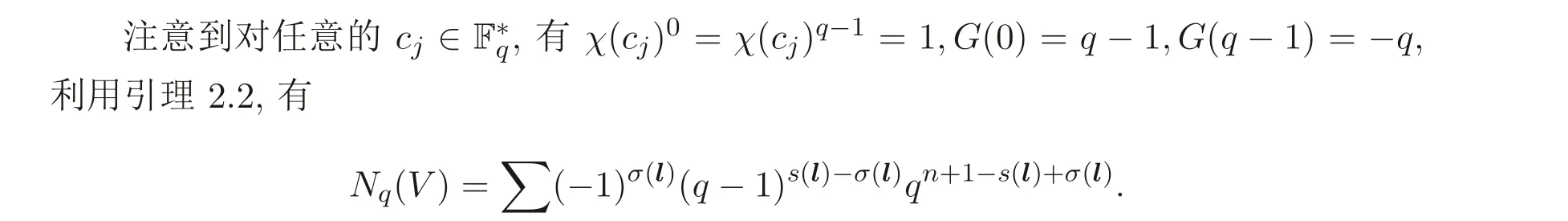
其中∑遍歷所有向量l= (l1,··· ,ln+3)∈Ωn+3, 且滿足?DlT≡0 (modq ?1). 由此可得

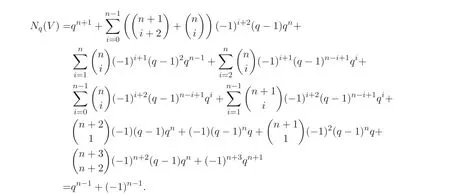
4 推廣的Markoff-Hurwitz 方程

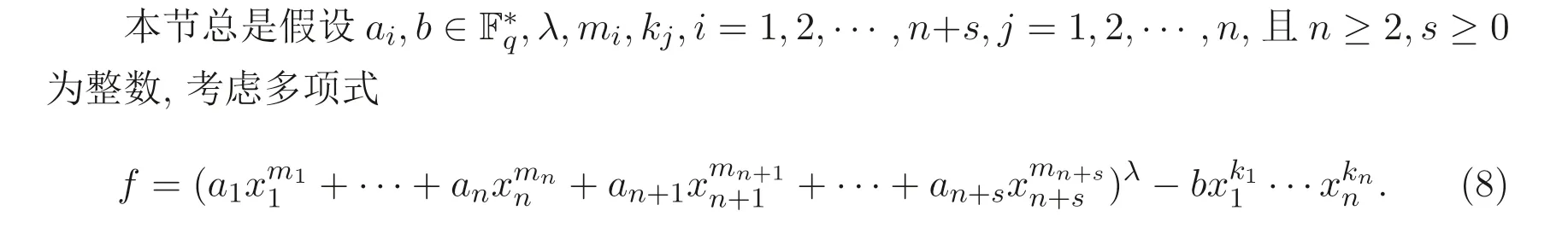
設(shè)代數(shù)簇V′由下列方程組確定

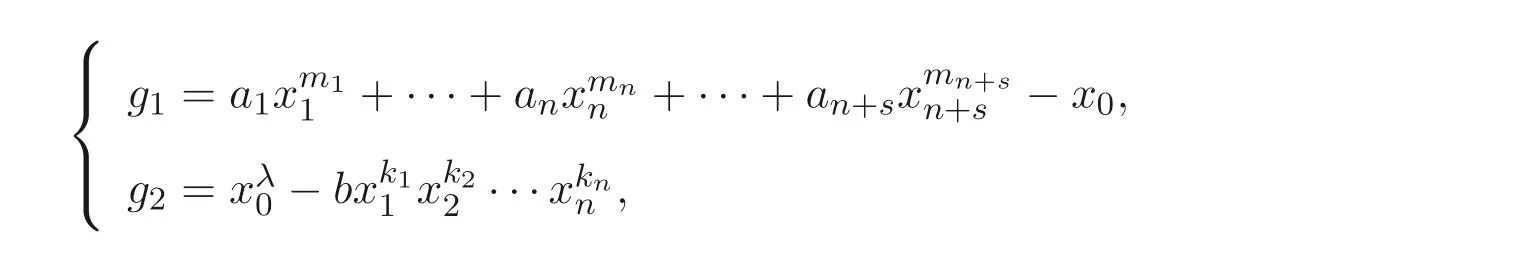
有Nq(f)=Nq(V′).

因此只需要計算Nq(V′). 設(shè)V′的增廣次數(shù)矩陣為?DV′= (?D1,?D2,··· ,?Dm). 注意到確定V′的多項式組中有n+s+1 個變量. 因此, 由引理2.2 可得

(ii) 當(dāng)p ≡3 (mod 4) 時,

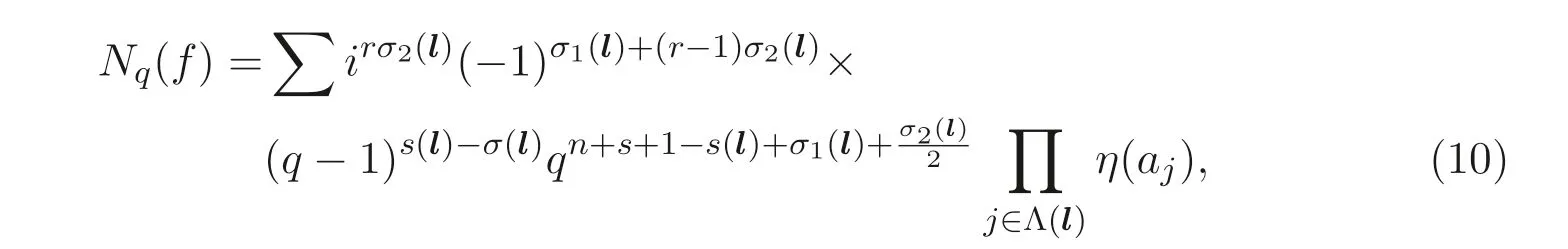
其中(9) 式-(10) 式中的∑遍歷所有向量l=(l1,l2,··· ,lm)∈Ωm, 這里其中∑遍歷所有向量l=(l1,··· ,ln+3)∈Ωn+3, 且滿足?DV′lT≡0 (modq ?1). 利用引理2.1 即可得證. 由Nq(f)=Nq(V′) 可得結(jié)論.

推論4.1若gcd(N,q ?1)=1, 則

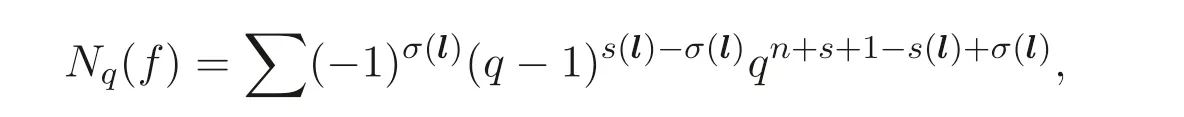
其中∑遍歷所有向量l=(l1,l2,··· ,ln+s+3), 使得?DV′lT≡0 (modq ?1).

證明若gcd(N,q ?1)=1, 則Ω={0,q ?1}, 即σ2(l)=0,Λ(l)=?,σ1(l)=σ(l),由定理4.1 即可得證.

推論4.2若det(N,q ?1)=1 且s=0, 則

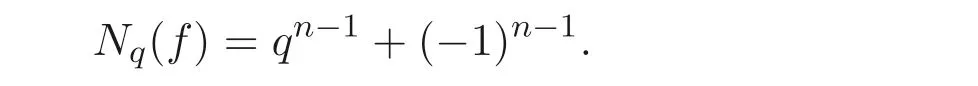
證明由推論4.1 有Nq(f)=∑(?1)σ(l)(q ?1)s(l)?σ(l)qn+1?s(l)+σ(l), 其中∑遍歷所有向量l=(l1,··· ,ln+3)∈Ωn+3, 且滿足?DV′lT≡0 (modq ?1). 再由定理1.1 的證明過程即可得證.

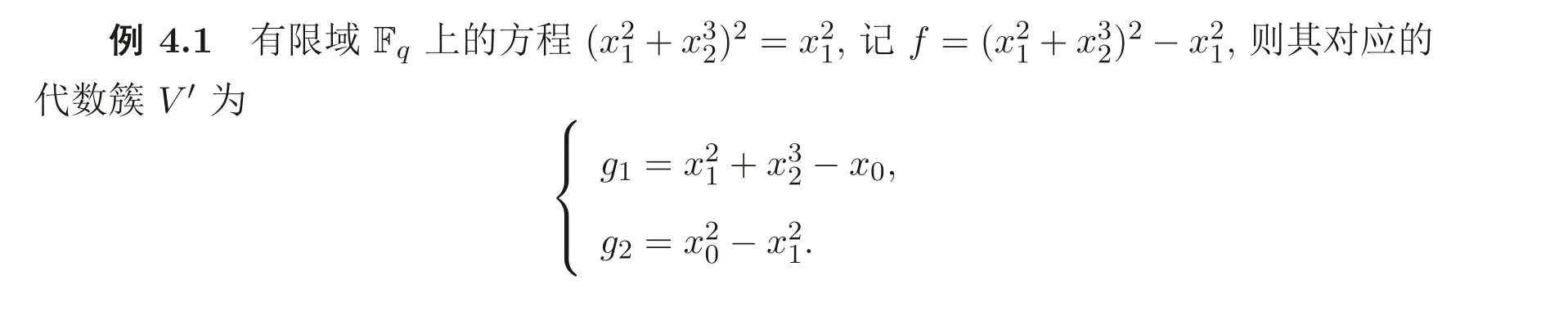
因此V′的增廣次數(shù)矩陣為

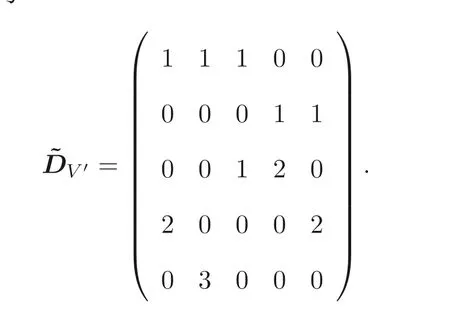
易得, det(?DV′)=?6, 即N=6.

在剩余類環(huán)Z/(q ?1)Z 中解同余方程組?DV′lT≡0 (modq ?1), 對滿足條件gcd(N,q ?1)| 2 的q來說,l的解共有40 種情形. 以q= 3 為例, 每種情形下的σ1(l),σ2(l) 和s(l) 的值列表如表2.

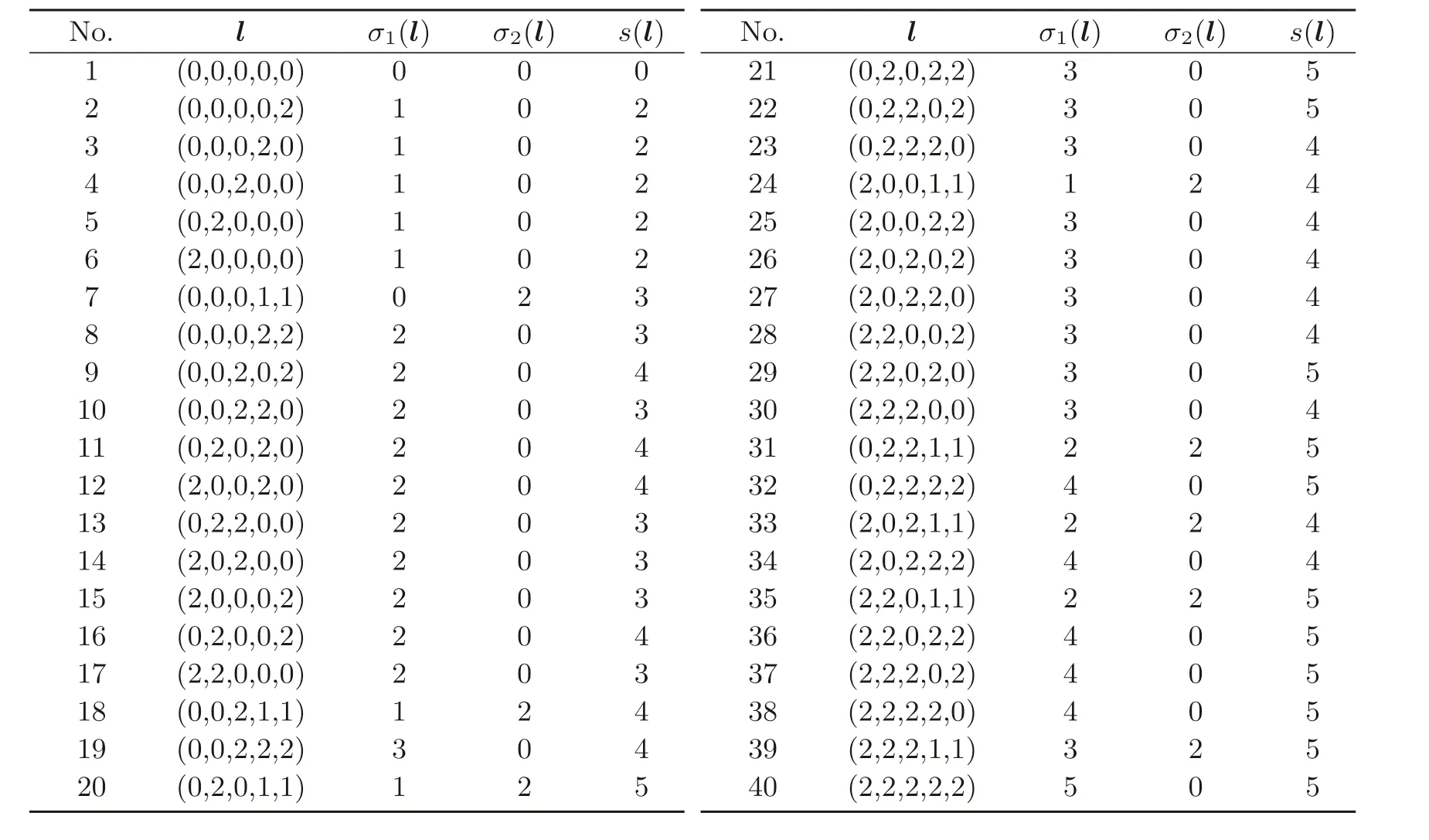
表2 l 及其對應(yīng)的σ1(l),σ2(l) 和s(l) 的值

由定理4.1 得Nq(f)=5. 對于q=5, 顯然也滿足條件gcd(N,q ?1)| 2, 可用類似方法, 由定理4.1 得Nq(f)=9. 以上結(jié)果均與用Matlab 驗算的方程實際解數(shù)一致.