王軍濤, 肖佳平, 王申橋, 郭靜賢, 陳鵬英, 程頌

(西安石油大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系, 陜西 西安 710065)

1 引言

在經(jīng)典邏輯推理中, 已知前提所使用的概念和提供的信息都是精確的, 就能保證推得的結(jié)果也是準(zhǔn)確無誤的, 這種精確的, 嚴(yán)格的邏輯推理是人工智能科學(xué)及相關(guān)研究中普遍采用的方法, 形成了傳統(tǒng)計(jì)算機(jī)的理論基礎(chǔ). 然而傳統(tǒng)計(jì)算機(jī)通常只能按照經(jīng)典邏輯進(jìn)行識(shí)別, 對(duì)模糊概念卻無能為力. 為了克服經(jīng)典邏輯在計(jì)算機(jī)應(yīng)用中的不足, 文獻(xiàn)[1] 提出了模糊邏輯的概念, 從而使計(jì)算機(jī)不但可以對(duì)模糊概念進(jìn)行處理, 還可以在信息有限的情況下, 提供精確的答案. 模糊邏輯主要采用代數(shù)邏輯的研究方法, 而后者則以邏輯代數(shù)為工具來進(jìn)行研究, 由此可知, 邏輯代數(shù)在模糊邏輯的研究中起著十分重要的作用[2-7]. 在模糊邏輯對(duì)應(yīng)的代數(shù)系統(tǒng)研究中, MV- 代數(shù)是一類最重要的邏輯代數(shù). MV- 代數(shù)最初是由文獻(xiàn)[8] 提出, 隨后不少學(xué)者對(duì)MV- 代數(shù)的性質(zhì)進(jìn)行了研究, 得到了一些重要的結(jié)論[8-9]. 導(dǎo)子理論來源于分析學(xué), 將它引入代數(shù)系統(tǒng)中有助研究代數(shù)系統(tǒng)的結(jié)構(gòu)和性質(zhì). 一些學(xué)者在環(huán)和近似環(huán)上研究了微分算子的性質(zhì)[10-11]. 文獻(xiàn)[12]將環(huán)上的微分算子理論引用到BCI- 代數(shù)中, 得到了一些重要的結(jié)果. 文獻(xiàn)[13] 將導(dǎo)子的理論應(yīng)用到格上, 并利用保序?qū)ё涌坍嬃四８瘛⒎峙涓竦慕Y(jié)構(gòu). 文獻(xiàn)[14] 嘗試研究了MV- 代數(shù)上的(⊙,⊕) 導(dǎo)子, 得到了基本的結(jié)論; 文獻(xiàn)[15] 深入研究了MV- 代數(shù)上的(⊙,⊕)- 導(dǎo)子和(?,⊙)- 導(dǎo)子, 并刻畫了保序(⊙,⊕)- 導(dǎo)子. 文獻(xiàn)[16] 在MV- 代數(shù)中引入了(⊙,⊕)- 導(dǎo)子, 討論了這類導(dǎo)子與MV- 代數(shù)上其它導(dǎo)子之間的關(guān)系, 得到了一些重要的結(jié)論. 2014 年, 辛小龍教授通過利用MV- 代數(shù)上的自同態(tài)映射將文獻(xiàn)[17] 中的兩類導(dǎo)子進(jìn)行了推廣, 得到了MV- 代數(shù)的f和g導(dǎo)子, 討論了兩者之間的聯(lián)系, 研究了其不動(dòng)點(diǎn)之集與理想之間的關(guān)系.

本文借助于MV- 代數(shù)上的自同態(tài), 引入并研究了其上的廣義(⊙,⊕)- 導(dǎo)子, 給出其等價(jià)刻畫, 并利用廣義(⊙,⊕)- 導(dǎo)子得到了MV- 代數(shù)成為Boole 代數(shù)的等價(jià)條件, 推廣了現(xiàn)有文獻(xiàn)中的相關(guān)結(jié)論, 進(jìn)一步刻畫了MV- 代數(shù)的結(jié)構(gòu).

2 預(yù)備知識(shí)

定義2.1一個(gè)MV-代數(shù)是(2,1,0)型代數(shù)(A,⊕,?,0)滿足如下公理:?x,y,z ∈A,

(MV1)x ⊕(y ⊕z)=(x ⊕y)⊕z;

(MV2)x ⊕y=y ⊕x;

(MV3)x ⊕0=x;

(MV4)x??=x;

(MV5)x ⊕0?=0?;

(MV6) (x?⊕y)?⊕y=(y?⊕x)?⊕x.

在MV- 代數(shù)A中記0?=1 并定義二元運(yùn)算⊙,∧,∨,→,?如下:

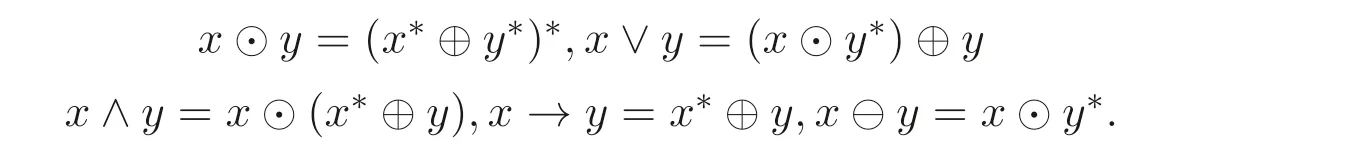
顯然(A,⊙,1) 是一個(gè)可換含幺半群, 且(A,∧,∨,0,1) 是一個(gè)有界分配格. 在MV-代數(shù)中定義偏序關(guān)系≤為x ≤y當(dāng)且僅當(dāng)x ∧y=x. 定義x?=x →0. 若A中任意兩個(gè)元素都存在偏序關(guān)系, 則稱A是線序的. 此外, 集合

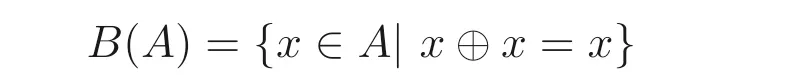
為A的布爾中心, 則(B(A),⊕,?,0) 是一個(gè)布爾代數(shù).

命題2.1設(shè)A是MV- 代數(shù), 則下列結(jié)論成立:?x,y,z ∈A,

(1)x ⊕x?=1,x ⊙x?=0;

(2)x ≤y當(dāng)且僅當(dāng)x ⊙y?=x ?y=0 當(dāng)且僅當(dāng)x →y=1;

(3) 若x ≤y, 則y →z ≤x →z,z →x ≤z →y,y?≤x?;

(4)x ⊙y ≤x ∧y ≤x,y ≤x ∨y ≤x ⊕y;

(5)x ∨y=(y →x)→x=(x →y)→y;

(6)x ⊕y=y當(dāng)且僅當(dāng)x ⊙y=x;

(7) (x ?y)⊕y=x ∨y,x ?(x ?y)=x ∧y;

(8) (x ?z)?y=(x ?y)?z;

(9)x ∧(y ⊕z)=(x ⊕z)∧(x ⊕y).

定理2.1設(shè)A是MV- 代數(shù), 下列結(jié)論等價(jià):

(1)x ∈B(A);

(2)x ⊕y=x ∨y,?y ∈A;

(3)x ⊙y=x ∧y,?y ∈A.

定義2.2設(shè)A是MV- 代數(shù),I是A的子集, 滿足以下條件:?x,y ∈A,

(1) 0∈I;

(2) 若x ∈I,y ∈A, 且x ≤y, 則x ∈I;

(3) 若x,y ∈I, 則x ∨y ∈I, 則稱I是A的理想.

定義2.3設(shè)A是MV- 代數(shù),F是A的子集, 若F滿足以下條件:?x,y ∈A,

(1) 1∈F;

(2) 若x ∈F,y ∈A, 且x ≤y, 則y ∈F;

(3) 若x,y ∈F, 則x ∧y ∈F, 則稱F是A的格濾子;

(4) 若?x,y ∈F,x ∨y ∈F, 則x ∈F或y ∈F, 則稱F是A的格素濾子.?a ∈A,(a] 表示由a生成的濾子, 稱(a] 為主濾子, 容易驗(yàn)證(a]={x ∈A|x ≥a}.

定義2.4設(shè)P是偏序集,P上的二元運(yùn)算⊕和?互為余伴隨, 若以下條件成立:

(1)⊕:P×P →P是單調(diào)遞增的;

(2)?:P×P →P是關(guān)于第一變量不減, 關(guān)于第二變量不增;

(3)c ≤a ⊕b當(dāng)且僅當(dāng)c ?b ≤a.

定義2.5設(shè)M,N是MV- 代數(shù),f:M →N是映射, 若f滿足以下條件:

(1)f(0)=0;

(2)f(x ⊕y)=f(x)⊕f(y);

(3)f(x?)=(f(x))?,?x,y ∈A, 則稱f是MV- 代數(shù)的同態(tài).

定義2.6設(shè)A是一個(gè)MV- 代數(shù),d:A →A是映射. 若存在A的自同態(tài)f使得d滿足:?x,y ∈A,d(x ⊙y)=(d(x)⊙f(y))⊕(f(x)⊙d(y)), 則d是A上的f導(dǎo)子.

定義2.7設(shè)A是一個(gè)MV- 代數(shù),d:A →A是映射. 若存在A的自同態(tài)g使得d滿足:?x,y ∈A,d(x ?y)=(d(x)?g(y))⊕(g(x)?d(y)), 則d是A上的g導(dǎo)子.

定義2.8設(shè)A是一個(gè)MV- 代數(shù),d:A →A是映射. 若d滿足:?x,y ∈A,

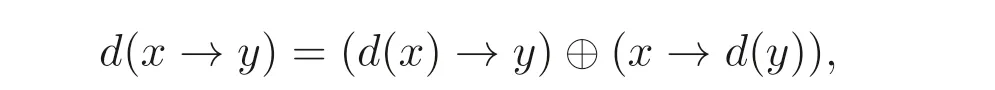
則d是A上的(→,⊕) 導(dǎo)子.

3 MV- 代數(shù)的廣義(→,⊕)- 導(dǎo)子

本文引入了MV- 代數(shù)的廣義(→,⊕)- 導(dǎo)子, 并研究它的一些代數(shù)性質(zhì).

定義3.1設(shè)A是一個(gè)MV- 代數(shù),d:A →A是映射,f:A →A是A上的自同態(tài). 若d滿足:?x,y ∈A,d(x →y)=(d(x)→f(y))⊕(f(x)→d(y)), 則稱d是A的廣義(→,⊕)- 導(dǎo)子.

例3.1設(shè)A是一個(gè)MV- 代數(shù), 定義映射d:A →A為d(x) = 1,?x ∈A,f:A →A是A上的自同態(tài), 由于

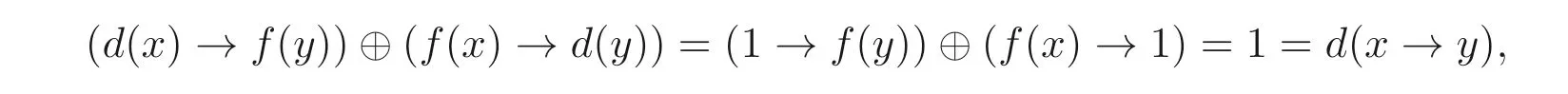
顯然,d是A的廣義(→,⊕)- 導(dǎo)子, 稱d為平凡廣義(→,⊕)- 導(dǎo)子.

例3.2設(shè)A={0,a,b,1}, 其中0≤a ≤b ≤1. 定義二元運(yùn)算⊕和?如下:

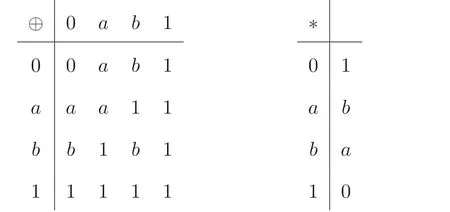
則(A,⊕,?,0,1) 是MV- 代數(shù). 分別定義映射d:A →A, 映射f:A →A為

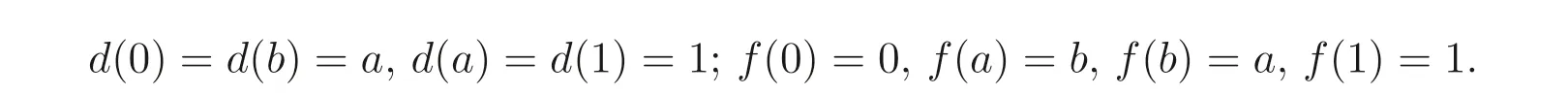
容易驗(yàn)證d是A的廣義(→,⊕)- 導(dǎo)子, 然而

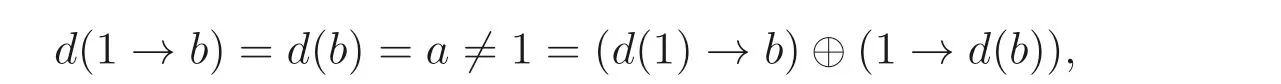
因此,d不是A的(→,⊕)- 導(dǎo)子.

注3.1例3.2 中的(→,⊕)- 導(dǎo)子d, 其定義中d(0)?= 0, 因此d不是文獻(xiàn)[17] 中的f,g導(dǎo)子.

命題3.1設(shè)d是MV- 代數(shù)A的廣義(→,⊕)- 導(dǎo)子, 則下列結(jié)論成立:?x,y ∈A,

(1)d(1)=1;

(2)d(x)=f(x)⊕d(x);

(3)f(x)≤d(x);

(4)x ≤y蘊(yùn)涵d(x)≤d(y);

(5)d(x)→f(y)≤f(x)→d(y);

(6)d(x)→d(y)≤d(x →y).

證明(1)d(1)=d(1→1)=(d(1)→f(1))⊕(f(1)→d(1))=1.

(2)d(x)=d(1→x)=(d(1)→f(x))⊕(f(1)→d(x))=f(x)⊕d(x).

(3) 由(2) 可知f(x)≤f(x)⊕d(x)=d(x).

(4) 若x ≤y, 則y=x ∨y, 因此

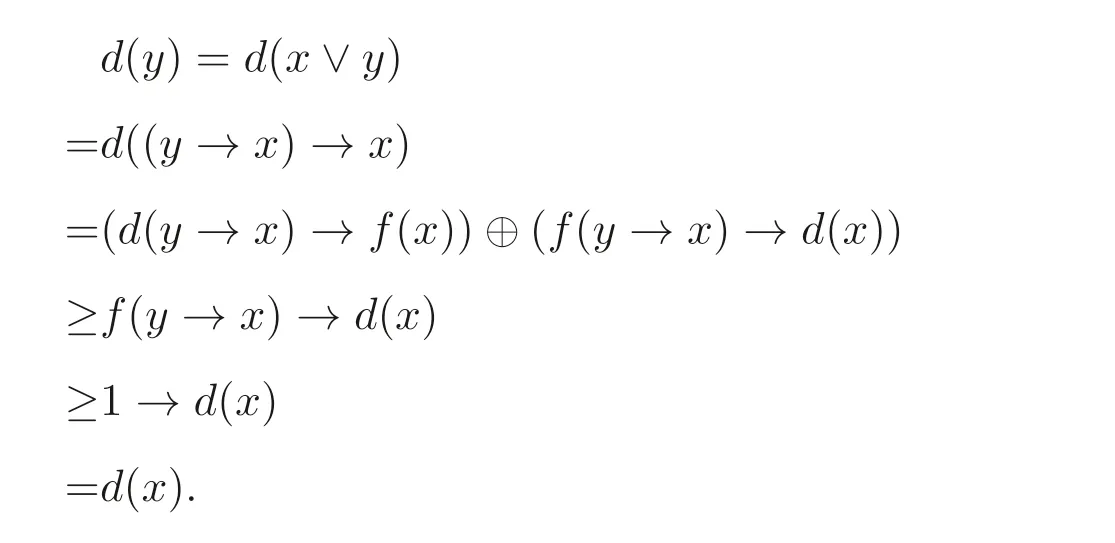
(5) 由命題2.1(3) 和命題3.1(3) 可得.

(6) 由定義3.1, 命題2.1(3) 和命題3.1(3) 可得

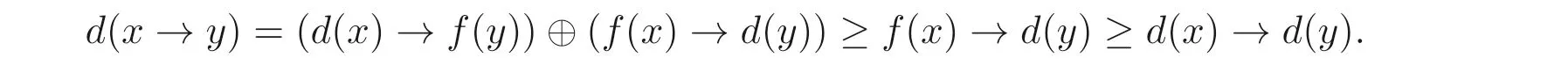
定義3.2設(shè)d是MV- 代數(shù)A的廣義(→,⊕)- 導(dǎo)子. 若d(0)=0, 則稱d是MV-代數(shù)A的正則廣義(→,⊕)- 導(dǎo)子.

例3.3設(shè)A是例3.2 中的MV- 代數(shù), 分別定義映射d:A →A, 映射f:A →A為

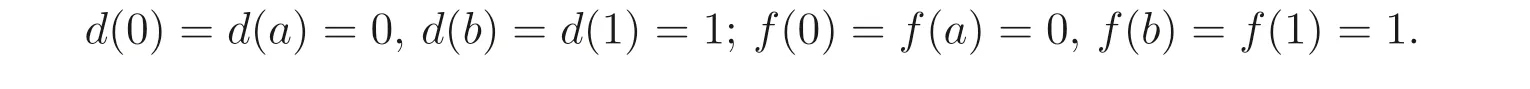
則容易驗(yàn)證d是A的正則廣義(→,⊕)- 導(dǎo)子.

命題3.2設(shè)d是MV- 代數(shù)A的正則廣義(→,⊕)- 導(dǎo)子, 則下列結(jié)論成立:?x,y ∈A,

(1) (d(x))?≤d(x?);

(2)d(x ⊕y)≤d(x)⊕d(y);

(3)d(x)?d(y)≤d(x ?y).

證明(1) 根據(jù)命題2.1(6) 和d(0)=0 可得.

(2) 由定義3.1 和命題3.2(1) 知

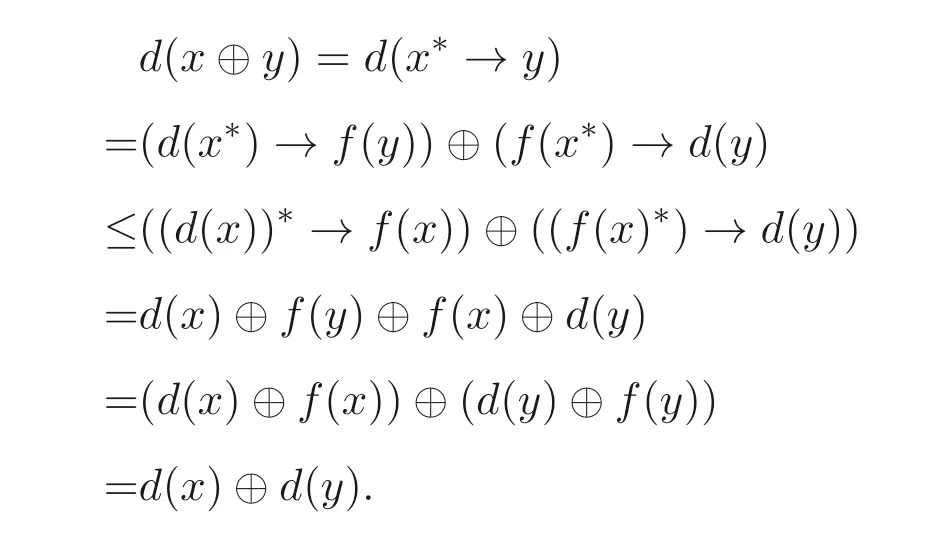
(3) 由命題2.1(8), 命題3.1(4) 和命題3.2(2) 可知

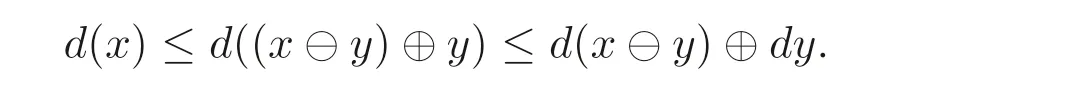
下面討論MV-代數(shù)A上布爾中心上的廣義(→,⊕)-導(dǎo)子的一些性質(zhì),并給出MV-代數(shù)A上布爾中心上的廣義(→,⊕)- 導(dǎo)子的等價(jià)刻畫.

命題3.3設(shè)d是MV- 代數(shù)A的廣義(→,⊕)- 導(dǎo)子, 則下列結(jié)論成立:?x,y ∈B(A),

(1)d(B(A))?B(A);

(2)d(x →y)=(d(x)→f(y))∨(f(x)→d(y));

(3)d(x →y)=f(x)→d(y);

(4)d(x ∨y)≤d(x)∨d(y);

(5) 若d(0)=0, 則d(x?)=f(x?);

(6) 若d(0)=0, 則d(x ∧y)=f(x)∧f(y).

證明(1) 設(shè)x ∈B(A), 由于f是自同態(tài), 則f(x)∈B(A), 進(jìn)而由命題2.1(2) 和定理2.1 可知

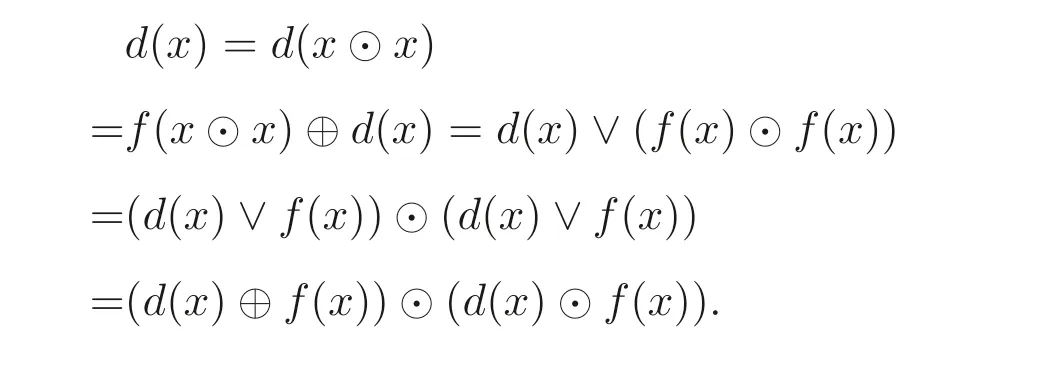
因此

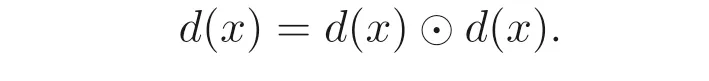
(2) 設(shè)x,y ∈B(A), 由(1) 和定理2.1(2) 可知

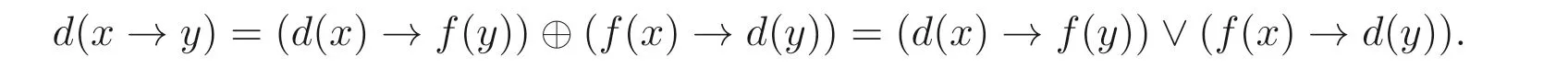
(3) 由(2) 和命題2.1(5) 可得d(x →y)=f(x)→d(y).

(4) 由命題2.1(2) 可得d(x ∨y)=d(x ⊕y)≤d(x)⊕d(y)=d(x)∨d(y).

(5) 由(3) 和d(0)=0 可知d(x?)=d(x →0)=f(x)→d(0)=(f(x))?=f(x?).

(6) 由(5) 可知

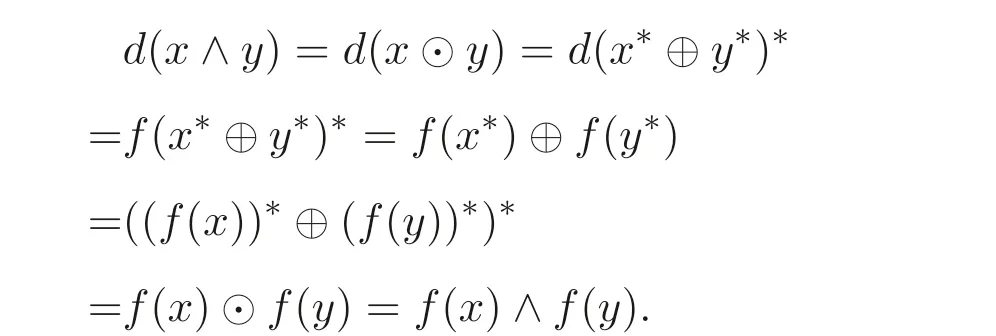
推論3.1設(shè)d是MV- 代數(shù)A上的一個(gè)映射, 則以下結(jié)論等價(jià):

(1)d是B(A) 上的廣義(→,⊕)- 導(dǎo)子;

(2)d(x →y)=f(x)→d(y),?x,y ∈B(A).

證明(1)?(2) 由命題2.1(5) 和命題2.3(2) 可得.

(2)?(1) 假設(shè)d是B(A) 上的映射且滿足?x,y ∈B(A),d(x →y) =f(x)→d(y),則

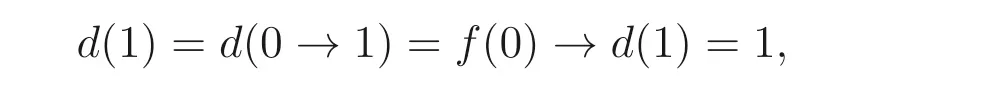
又

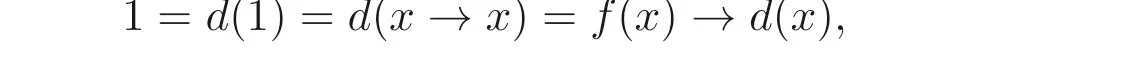
因此?x ∈B(A),f(x)≤d(x), 進(jìn)而由命題2.1(3) 可知d(x)→f(y)≤f(x)→d(y). 因此,

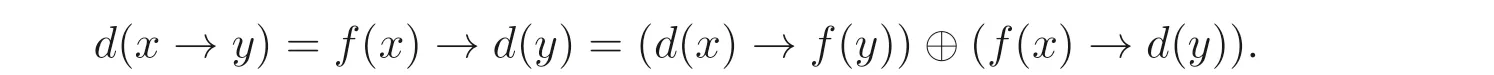
設(shè)A是MV-代數(shù),d:A →A是一個(gè)映射,f:A →A是A上的一個(gè)自同態(tài). 定義

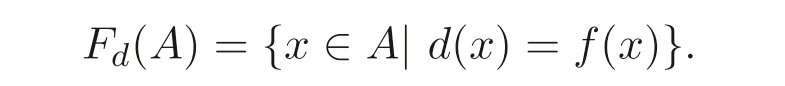
命題3.4設(shè)d是MV- 代數(shù)A的廣義(→,⊕)- 導(dǎo)子, 則Fd(A)?B(A).

證明設(shè)x ∈Fd(A), 由命題2.1(2) 可知d(x)=f(x)⊕d(x), 則

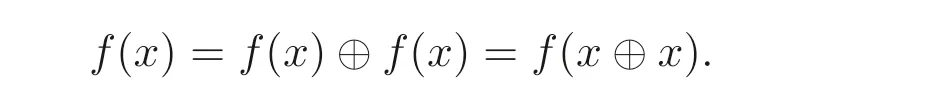
又由于f是自同態(tài), 所以x ⊕x=x, 因此x ∈B(A).

注3.2命題3.3 的逆命題一般不成立. 設(shè)A是例3.2 中的MV-代數(shù), 分別定義A上的映射d和單同態(tài)f為?x ∈A,d(x) = 0;f(0) = 0,f(1) = 1,f(a) =b,f(b) =a.則易驗(yàn)證Fd={0}?{0,a,b,1}?B(A), 但是d不是A上的廣義(→,⊕)- 導(dǎo)子. 因?yàn)?/p>

定理3.1設(shè)A是MV- 代數(shù),f:A →A是A上的單同態(tài), 則以下結(jié)論等價(jià):

(1)A是Boole 代數(shù);

(2) 映射d=f是廣義(→,⊕)- 導(dǎo)子.

證明(1)?(2) 假設(shè)A是Boole 代數(shù)且映射d=f, 則d(x →y) =f(x)→d(y).由推論3.1 可知,d是Boole 代數(shù)A的廣義(→,⊕)- 導(dǎo)子.

(2)?(1) 假設(shè)映射d=f是A上的廣義(→,⊕)- 導(dǎo)子, 由命題3.4 可知

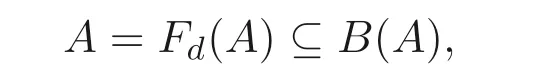
因此A是Boole 代數(shù).

由定理3.3 可知, 若A是Boole 代數(shù),f:A →A是A上的單同態(tài), 則映射d=f是A上的廣義(→,⊕)- 導(dǎo)子. 下面這個(gè)定理給出了Boole 代數(shù)上的映射d=f時(shí)廣義(→,⊕)- 導(dǎo)子的等價(jià)刻畫.

定理3.2設(shè)d是Boole 代數(shù)A上的廣義(→,⊕)- 導(dǎo)子,f:A →A是A上的單同態(tài), 則以下結(jié)論等價(jià):

(1) 映射d=f;

(2)?x,y ∈A,f(x)→d(y)=d(x)→f(y).

證明(1)?(2) 顯然.

(2)?(1) 假設(shè)?x,y ∈A,f(x)→d(y)=d(x)→f(y). 由推論3.1 可知

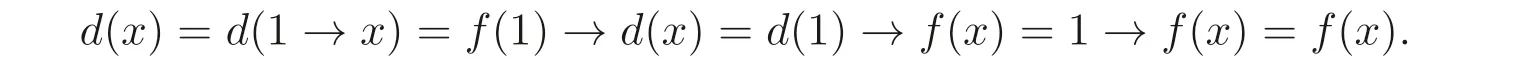
因此映射d=f.

命題3.5設(shè)A是MV- 代數(shù),f:A →A是A上的自同態(tài),a ∈A,

(1) 定義da:A →A為?x ∈A,da(x) =a ⊕f(x). 若da(A)?B(A), 則da是A的廣義(→,⊕)- 導(dǎo)子.

(2) 若f滿足f(a)=a, 定義

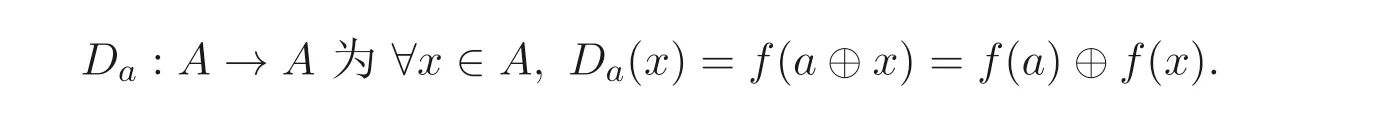
若Da(A)?B(A), 則Da是A的廣義(→,⊕)- 導(dǎo)子.

證明由定義2.1, 命題2.2 知,?x,y ∈A,

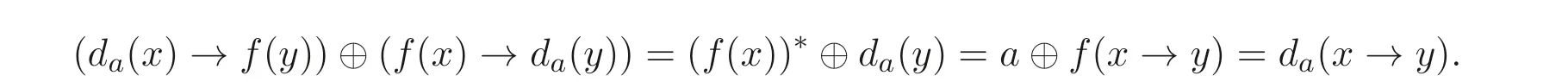
由定義2.8 知,da是A的廣義(→,⊕)- 導(dǎo)子.

注3.3由于da是MV- 代數(shù)A的布爾中心上的廣義(→,⊕)- 導(dǎo)子, 稱da是MV-代數(shù)A的中心主微分; 由于Da是MV- 代數(shù)A的布爾中心上的強(qiáng)廣義(→,⊕)- 導(dǎo)子,稱Da是MV- 代數(shù)A的強(qiáng)主中心廣義導(dǎo)子.

命題3.6設(shè)A是MV- 代數(shù),f:A →A是A上的自同態(tài), 則存在A上的自映射

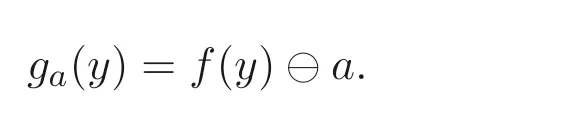
使得(da,ga) 是A上的一對(duì)余伴隨.

證明顯然⊕是單調(diào)不減的,?是關(guān)于第一變量不增, 關(guān)于第二變量不減并且?x,y,a ∈A,

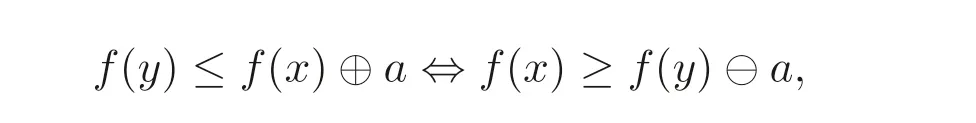
由定義2.4 可知(da,ga) 是A上的一對(duì)余伴隨.

命題3.7設(shè)A是MV- 代數(shù). 如果ga(A)?B(A), 則ga是g導(dǎo)子.

證明設(shè)ga(A)?B(A). 設(shè)?x,y ∈A,g:A →A是A的自同態(tài), 由命題2.1(8) 知

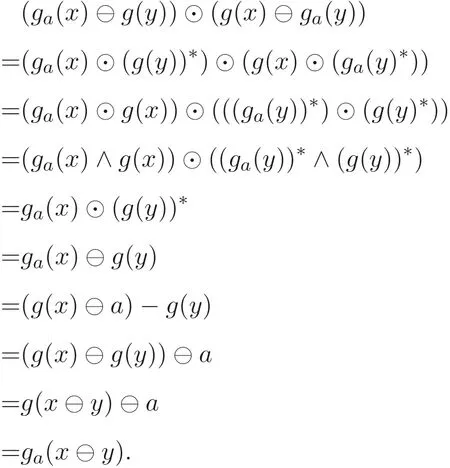
由定義2.7 可知ga是MV- 代數(shù)的g導(dǎo)子.

命題3.8設(shè)A是MV- 代數(shù). 如果ga(A)?B(A), 則ga是f導(dǎo)子.

證明設(shè)ga(A)?B(A). 設(shè)?x,y ∈A,g:A →A是A上的自同態(tài),

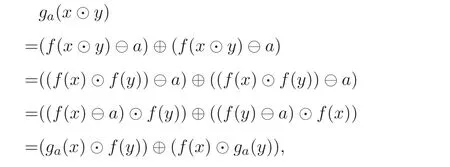
由定義2.6 可知ga是f導(dǎo)子.

引理3.1設(shè)d是MV- 代數(shù)A的f導(dǎo)子, 則下列結(jié)論等價(jià):

(1)d是保序的;

(2)?x ∈A,d(x)=f(x)⊙d(1).

命題3.9(1) 設(shè)A是MV- 代數(shù),d是A上的保序f導(dǎo)子. 若存在A上的自映射f滿足f(A)?B(A), 且(d,f) 是A上的一對(duì)余伴隨對(duì), 則f是A上廣義(→,⊕)-導(dǎo)子.

證明由命題3.5- 命題3.6, 命題3.8 可證.

(2) 設(shè)A是Boole 代數(shù),g是A上的g導(dǎo)子. 若存在A上的自映射f滿足(g,f)是A上的余伴隨對(duì), 則f是A上廣義(→,⊕)- 導(dǎo)子.

證明由命題3.5- 命題3.7 可證.

定理3.3設(shè)d是MV- 代數(shù)A上的正則廣義(→,⊕)- 導(dǎo)子, 則以下結(jié)論等價(jià):

(1)A是Boole 代數(shù);

(2)Fd(A) 是A的格濾子.

證明(1)?(2) 假設(shè)A是Boole 代數(shù)且d是A上的正則廣義(→,⊕)- 導(dǎo)子, 由于f(1)=d(1)=1, 故1∈Fd(A). 若x,y ∈Fd(A), 則d(x)=f(x),d(y)=f(y), 由命題2.1(6) 可得d(x ∧y)=d(x)∧d(y)=f(x)∧f(y)=f(x ∧y), 則x ∧y ∈Fd(A). 下面證明Fd(A) 是A的上集. 若x ∈Fd(A),y ∈A且x ≤y, 則

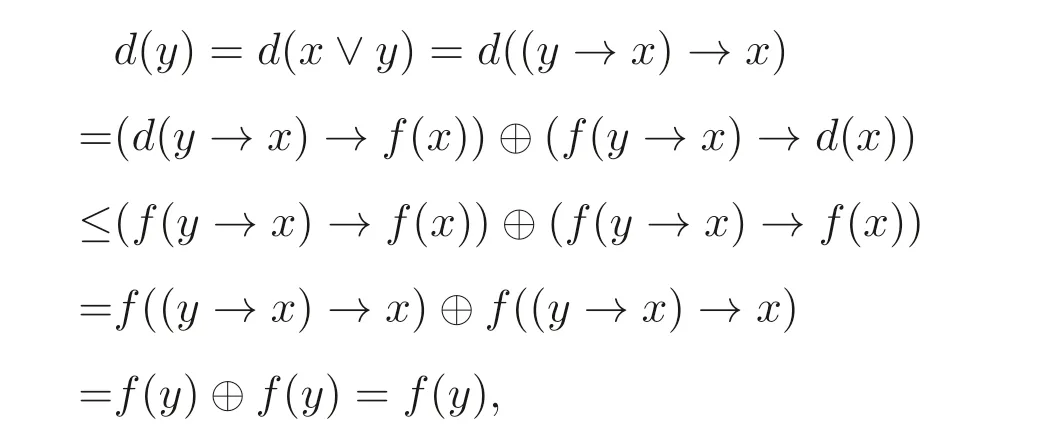
從而d(y)≤f(y). 另一方面, 由命題2.1(3)知f(y)≤d(y), 故f(y)=d(y). 因此Fd(A)是A的格濾子.

(2)?(1) 假設(shè)Fd(A) 是A的格濾子, 由正則廣義(→,⊕)- 導(dǎo)子的定義可知

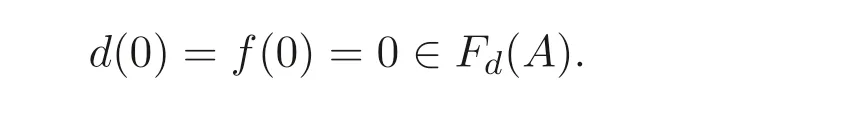
從而Fd(A)=A. 由命題3.4 知,A ?B(A), 故A是Boole 代數(shù).

定理3.4設(shè)d是A的廣義(→,⊕)- 導(dǎo)子,f:A →A是A的保序單同態(tài), 則以下結(jié)論等價(jià):

(1)A是Boole 代數(shù);

(2) 每一個(gè)強(qiáng)主中心廣義導(dǎo)子Da滿足FDa(A)=(a].

證明(1)?(2) 假設(shè)A是Boole 代數(shù), 則?x ∈A,x ⊕x=x成立. 由于

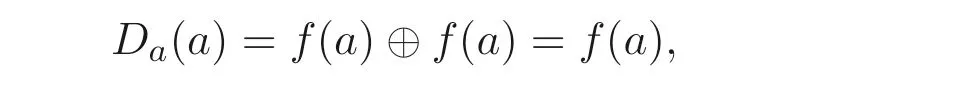
則a ∈FDa(A). 根據(jù)定理3.3 得Fd(A) 是A的上集, 因此對(duì)?a ≤x, 有x ∈FDa(A),從而(a]?FDa(A).

另一方面, 設(shè)x ?FDa(A), 則Da(x)=f(x)=f(a)⊕f(x)≥f(a), 由于f是保序的, 則有x ≥a. 這就證明了x ∈(a]. 因此FDa(A)=(a].

(2)?(1) 由(2) 知?a ∈A,FDa(A) = (a]. 由于a ∈(a], 則a ∈FDa(A), 從而有f(a)⊕f(a) =Da(a) =f(a),?a ∈A成立. 由于f是保序單同態(tài), 則a ⊕a=a,?a ∈A成立, 即A是一個(gè)Boole 代數(shù).

4 結(jié)束語(yǔ)

利用MV- 代數(shù)的自同態(tài), 將MV- 代數(shù)的(→,⊕)- 導(dǎo)子進(jìn)行了推廣, 引入了廣義(→,⊕)- 導(dǎo)子, 研究了它們的性質(zhì). 此外, 定義并研究了正則廣義(→,⊕)- 導(dǎo)子, 并討論了MV- 代數(shù)的布爾中心上的廣義(→,⊕)- 導(dǎo)子的一些性質(zhì). 最后, 利用廣義(→,⊕)-導(dǎo)子給出了MV- 代數(shù)成為Boole 代數(shù)的等價(jià)刻畫.