Thermodynamic properties of massless Dirac-Weyl fermions under the generalized uncertainty principle*
Guang-Hua Xiong(熊光華), Chao-Yun Long(龍超云), and He Su(蘇賀)
Department of Physics,Guizhou University,Guiyang 550025,China
Keywords: T3 lattice, massless Dirac-Weyl fermions, generalized uncertainty principle, thermodynamic
1. Introduction
It is well known that in well-known Heisenberg uncertainty principle, we can separately measure the position or momentum of a test particle with arbitrary accuracy in principle. However,various approaches to unifying quantum theory with gravity support the idea that near the Planck scale,the standard Heisenberg uncertainty principle should be replaced by the so-called generalized uncertainty principle that implies the existence of a minimal length.[1-9]Since Kempf and co-workers developed the theoretical framework of quantum mechanics based on a generalized uncertainty principle, the studies of Schr¨odinger equation, the Dirac equation and the DKP equation under the minimal length uncertainty have received much attention.[1,2,4,6,10]Some phenomena in black hole remnants,[11]the trans-Planckian problem of inflation,[12-14]and the cosmological constant problem[15-17]can be explained by generalized uncertainty relations. On the other hand, in recent years, many fields of physics have been influenced by the rapid development of topology,and a variety of lattices can be designed for utilizing.[18-23]In particular, research of the Kagome,[24-26]the Lieb and Perovskite lattices,[27]the honeycomb,[28]the square,[29,30]the checkerboard,[31]the pyrochlore,[32]the diamond,[33]the square-octogon[34]and the T3 lattice[23,35,36]have become one of the most active fields in condensed-matter physics. In such lattices, quasi-particles are characterized by the Dirac-Weyl equation. However, for Dirac-like particles with pseudo spin in these lattices, we haves=1, rather than ass=1/2 for graphene[23,36,37]and the algebraic properties of matrix in the Dirac-Weyl equation are different from Dirac matrix in the usual Dirac equation. The main purpose of this work is to obtain the exact energy levels of the Dirac-like particles under external magnetic field and the generalized uncertainty principle and to study the corresponding thermal properties including the partition function and mean internal energy, etc. This paper is organized as follows: In Section 2, we first use the Nikiforov-Uvarov(NU)method to solve the energy spectrum and the wave function of T3 lattice under the generalized uncertainty principle(GUP).Based on the energy spectrum,the partition function of T3 lattice is obtained and other thermodynamic functions of the system are further obtained. The variation curves of energy spectrum and thermodynamic functions of T3 lattice under the GUP are drawn and analyzed briefly.Section 3 is our summary.
2. Thermodynamic properties of the T3 lattice under the GUP
Considering the effect of the gravitation, in more than one dimension, the minimal measurable distance emerges inevitably, which can be encoded in the following form of the GUP:[1-8]
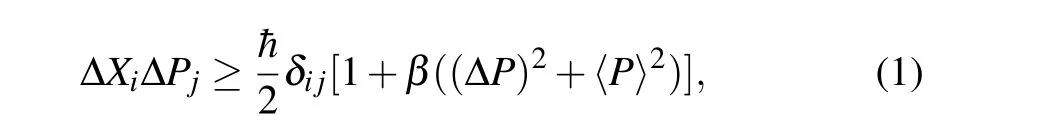
whereβis the GUP parameter. The above inequality follows from the modified Heisenberg algebra
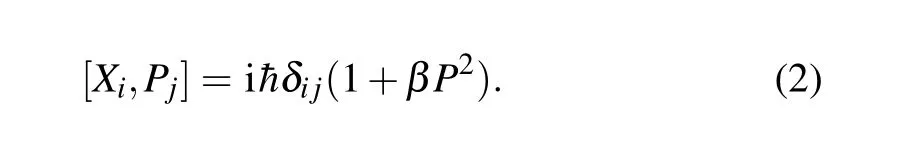
In the absence of the second term on the right-hand side, the commutation relation(2)reduces to the usual Heisenberg’algebra. However, the above algebra does not admit a simple representation in position space. In momentum space representation,if we define

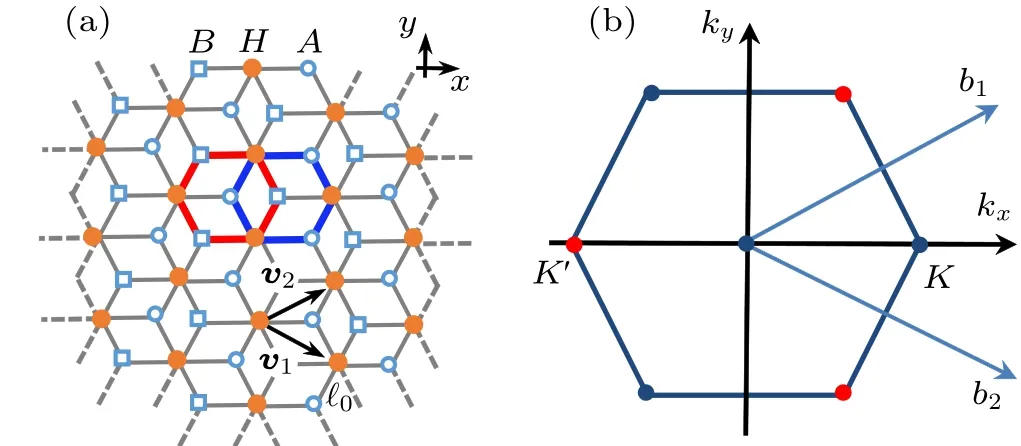
Fig. 1. (a) The T3 lattice, characterized by translation vectors, v=(3/2,-/2)?0 and v2=(3/2,/2)?0,with lattice constant ?0. Rim sites A and B have a lower connectivity of 3 compared to 6 of the hub site. (b)In the reciprocal space of T3 lattice,inverse lattice base vector, where ?0 is the distance between two adjacent lattice points. Moreover,the two non-equivalent Dirac points K and K′are located at and

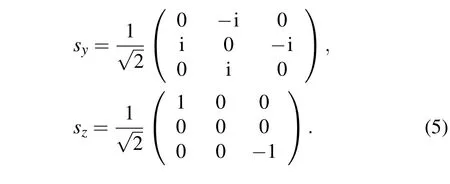
These matrices satisfy angular momentum commutation relations. The corresponding eigenvalue equation of Hamiltonian in Eq.(4)reads


Using of Eq. (7) and considering magnetic fieldB=B0ezwhose magnetic vector potential is chosen as the symmetric gaugeA=(-B0Y/2, B0X/2,0), we can obtain the following equation satisfied byψH:

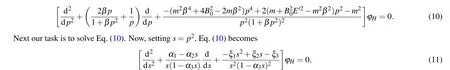
where
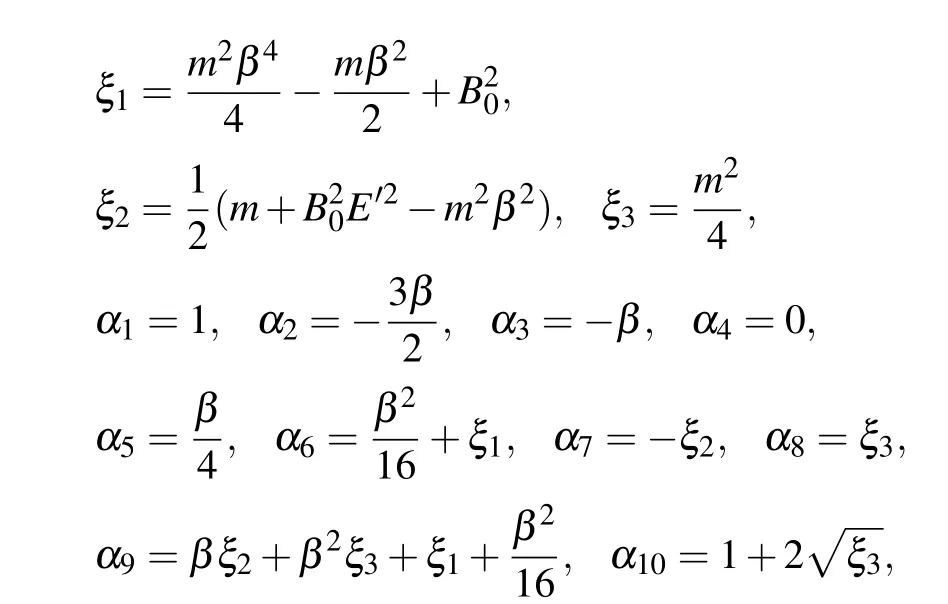
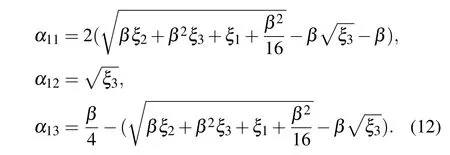
It can be easily found that Eq.(11)is of the form basic equation of the NU method.[38,39]Thus,we can straight-forwardly obtain the corresponding energy and wave function using the NU method (also see Appendix). Then the corresponding mathematical expression satisfied by energy spectra can be expressed as

From Eq.(14),it is not difficult to find that in the case ofβ=0,the Dirac particles in the T3 lattice still show a limited energy value even ifn=m=0,which is consistent with the conclusion in the T3 optical lattice under the condition of external magnetic field.[23]Now let us focus on the characteristic wave functions of the T3 lattice under the GUP. According to the NU method,[38-43]we can obtain the wave functions of any state of the T3 lattice:
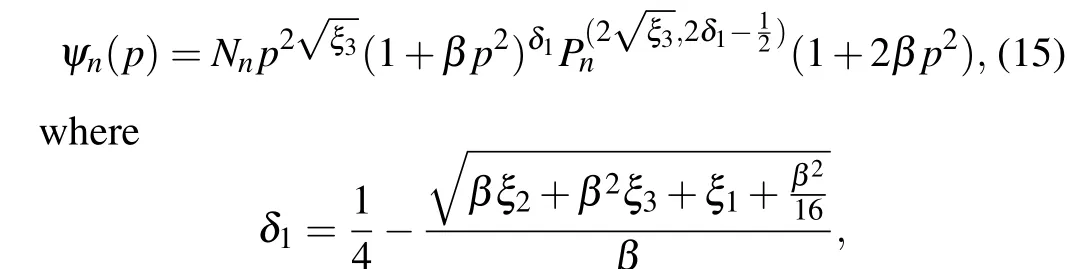

Further,the characteristic wave functionψn(p)of any state of the T3 lattice in Eq.(15)is expressed as[38-44]
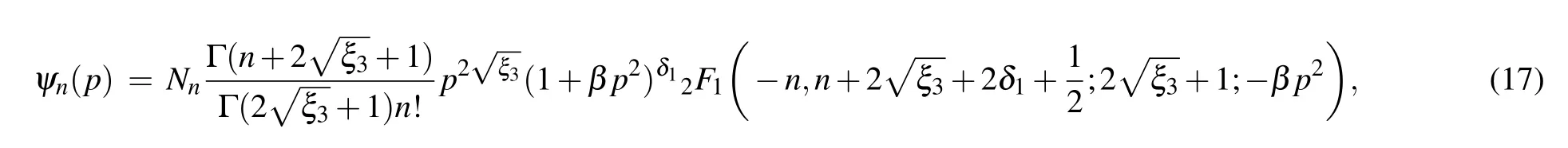
where Γ is the Gamma function. Using Eq. (15) in Ref. [38], we obtain the analytic expression of normalized constantNnas follows:
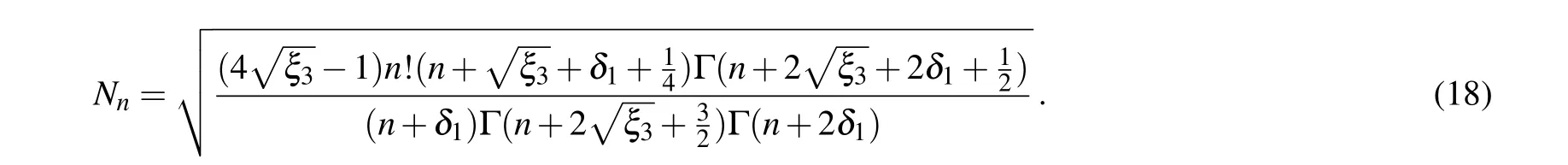
In particular,whenn=0,the corresponding ground state wave function of the T3 lattice is
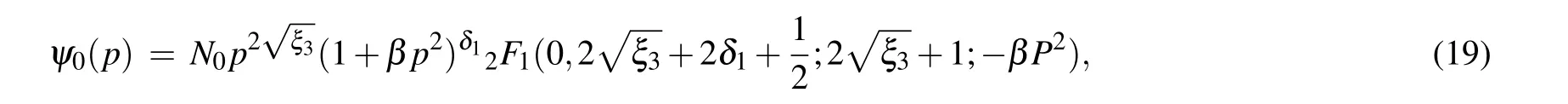


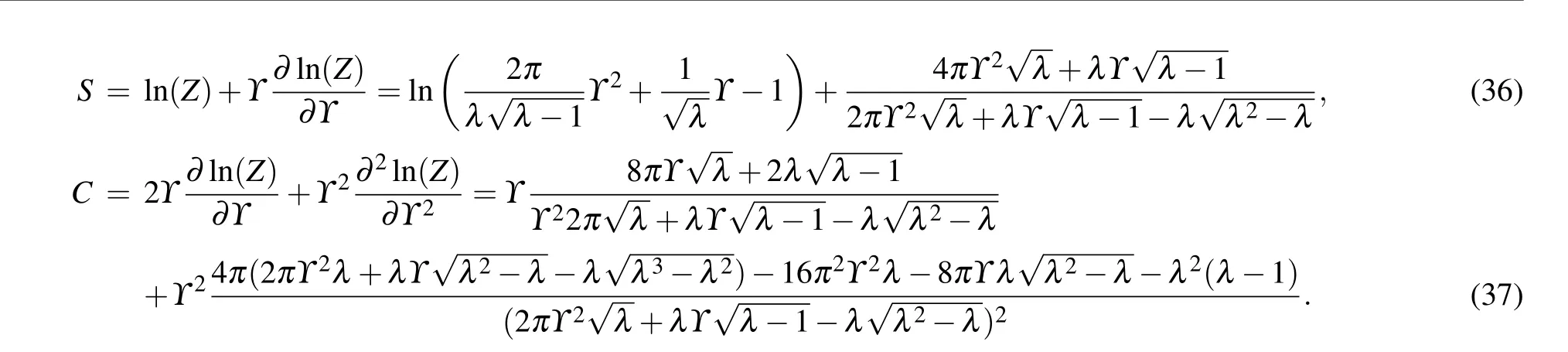
Before drawing the curves of energy spectrum and thermodynamic functions of the T3 lattice under the GUP,we first make a brief numerical analysis of the analytical expression of the thermodynamic functions. For the asymptotic behavior, we consider two special cases,namely high temperature and low temperature:[50-52]
(1) For a very high temperature range, the modified canonical partition function in Eq.(33)is approximately
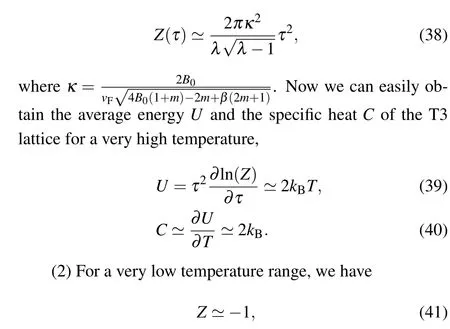
and consequently both average energyUand specific heatCtend to zero:
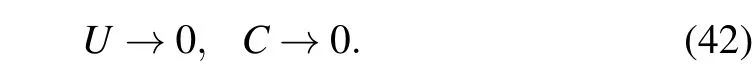
Next,we draw a curve in Fig.2,which is the variation of the energy spectrumEof the T3 lattice under the GUP with the principal quantum numbernat different values ofβ. The variation curves of thermodynamic functions with variableτ(kBT) under different values ofβandmare plotted from Figs.3-7.
Figure 2 presents the reduced spectrum of energyEand quantum numbernof the T3 lattice under different values ofβ.The results show that the energy of T3 lattice increases with the increasingn. In addition,the GUP parameter has a significant influence on the energy spectrum,which is mainly shown as the energy spectrum increases with the increase ofβ.When the GUP is absent(β=0),even ifn=m=0,the particles still display a limited energy value,which is similar to the energy spectrum of T3 optical lattice under the condition of external magnetic field in Ref.[23].
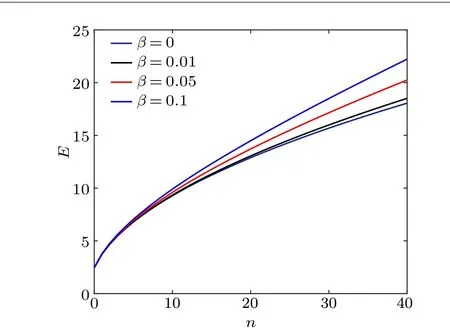
Fig. 2. The energy E of the T3 lattice in the context of the GUP as a function of the principal quantum number n for different values of β(B0=vF=m=c=ˉh=1).
It can be seen from Figs.3 and 4 that the partition functionZand free energyFare negatively correlated withτ,βandm. Furthermore, at extremely low temperature, the partition function satisfies the asymptotic behaviorZ ?-1.
Fig. 3. The partition function Z of the T3 lattice in the context of the GUP as a function of τ (kBT)for different values of β and m(B0=0.1,vF=c=ˉh=1).
According to Fig. 5, we can know that there is a positive correlation between the average energyUandτ. Whenτremains constant,the larger thembecomes,the smaller the average energy is. On the other hand, whenβis different,the average energy variation curve tends to be almost the same straight line, which shows that the influence ofβon the average energy is very small. In addition, the average energy tends toU=2kBTin a very high temperature range and to zeroU →0 in a very low temperature range.
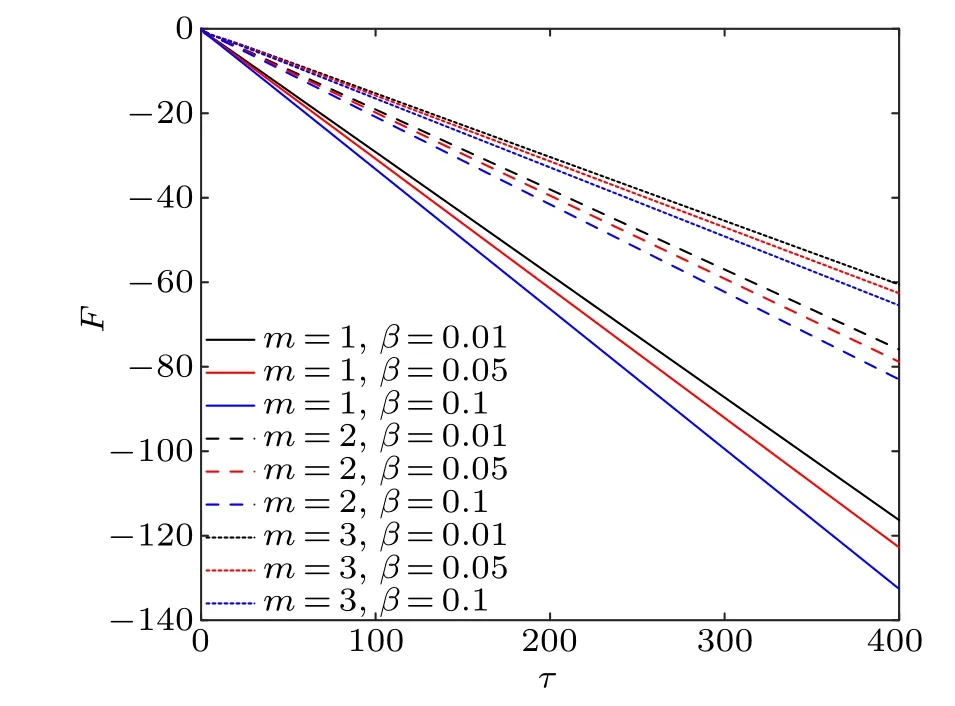
Fig. 4. The free energy F of the T3 lattice in the context of the GUP as a function of τ (kBT) for different values of β and m (B0 =0.1,vF=c=ˉh=1).
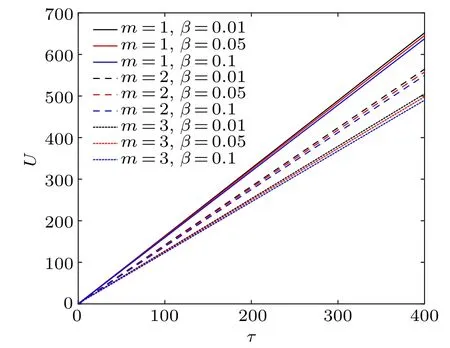
Fig. 5. The average energy U of the T3 lattice in the context of the GUP as a function of τ (kBT) for different values of β and m(B0=vF=c=ˉh=1).
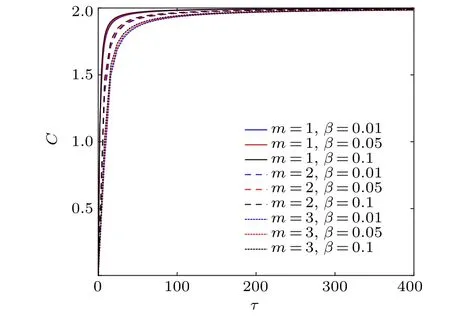
Fig.6. The specific heat C of the T3 lattice in the context of the GUP as a function of τ (kBT)for different values of β and m(B0=vF=c=ˉh=1).
Figures 6 and 7 show the relationship between specific heatCand entropySwithτ, respectively. It is not difficult to see that they all increase with the increase ofτ. We find that the specific heat and entropy vary unobviously whenβchanges. It is worth mentioning that in Fig.6,when the temperature is extremely high, all the specific heat curves coincide with each other and reach a fixed valueC=2kB,which is completely consistent with the asymptotic expression of specific heat in the extremely high temperature range. However,the heat capacity tends to zeroC →0 in the extremely low temperature range,which satisfies the asymptotic behavior of specific heat at low temperature.
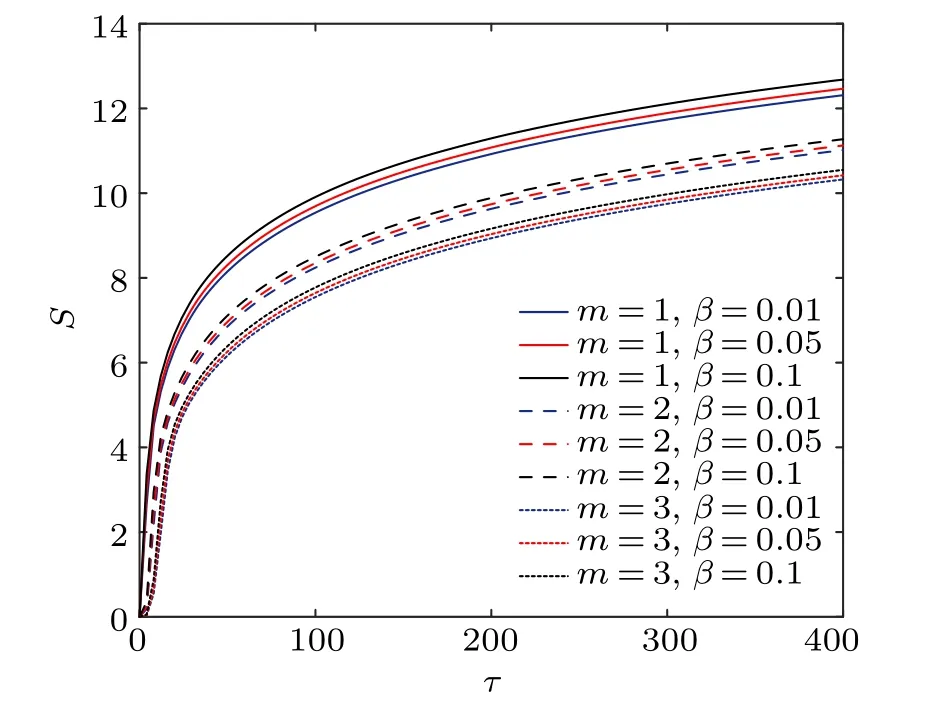
Fig. 7. The entropy S of the T3 lattice in the context of the GUP as a function of τ (kBT) for different values of β and m (B0 =0.1,vF=c=ˉh=1).
3. Conclusion
In the framework of the modified version of quantum mechanics due to the generalized uncertainty principle (GUP),the Dirac-Weyl equation characterized quasi-particles in the T3 lattice are studied under external magnetic field using the GUP. The corresponding eigenvalue equation is analytically solved by the Nikiforov-Uvarov(NU)method,then the corresponding energy spectrum is extracted. By computing the modified canonical partition function,the thermodynamic properties of the system have been investigated. The influence of GUP parameter on thermodynamic properties of the T3 lattice is analyzed theoretically and numerically.
Appendix A

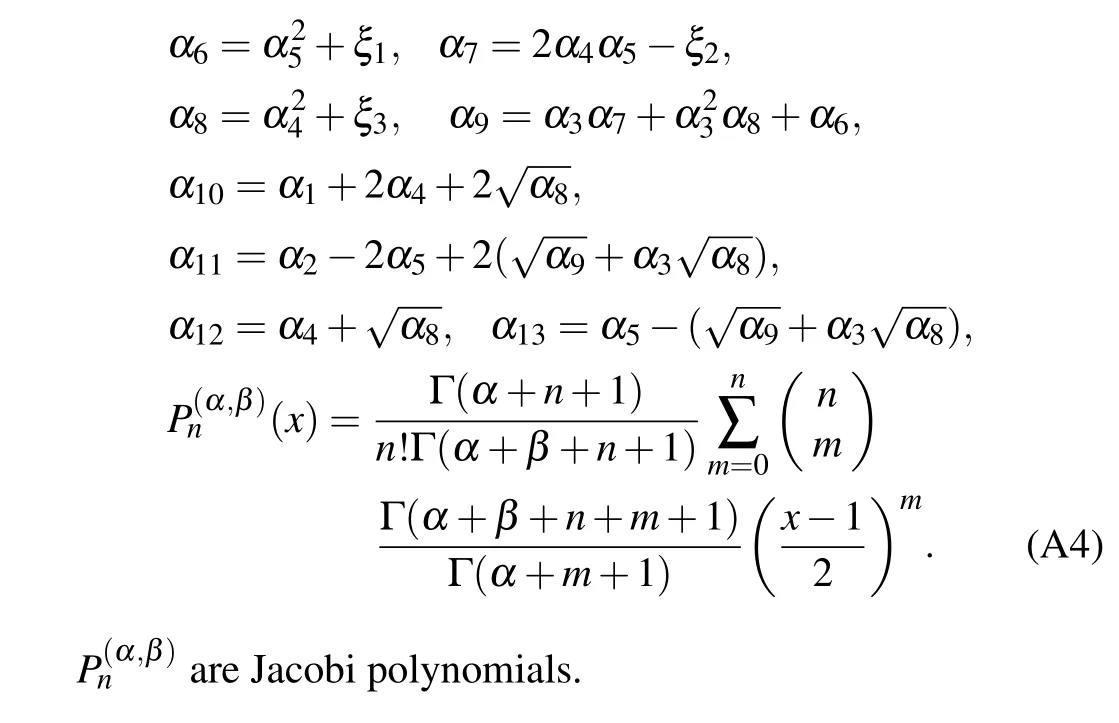
——呼光華
——記全國勞動模范楊光華同志
- Chinese Physics B的其它文章
- Projective representation of D6 group in twisted bilayer graphene*
- Bilayer twisting as a mean to isolate connected flat bands in a kagome lattice through Wigner crystallization*
- Magnon bands in twisted bilayer honeycomb quantum magnets*
- Faraday rotations,ellipticity,and circular dichroism in magneto-optical spectrum of moir′e superlattices*
- Nonlocal advantage of quantum coherence and entanglement of two spins under intrinsic decoherence*
- Universal quantum control based on parametric modulation in superconducting circuits*

