SHOCK DIFFRACTION PROBLEM BY CONVEX CORNERED WEDGES FOR ISOTHERMAL GAS?
(王欽)
Department of Mathematics,Yunnan University,Kunming 650091,China E-mail:mathwq@ynu.edu.cn
Kyungwoo SONG?
Department of Mathematics,Kyung Hee University,Seoul 02447,Korea E-mail:kyusong@khu.ac.kr
Abstract We are concerned with the shock diffraction con figuration for isothermal gas modeled by the conservation laws of nonlinear wave system.We reformulate the shock diffraction problem into a linear degenerate elliptic equation in a fixed bounded domain.The degeneracy isofKeldysh type—the derivative of a solution blows up at the boundary.We establish the global existence of solutions and provethe-regularity of solutions near the degenerateboundary.We also compare the difference of solutions between the isothermal gas and the polytropic gas.
Key words Nonlinear wave system;isothermal gas;shock diffraction;degenerate elliptic equation;Riemann problem;regularity
1 Introduction
When we consider the well-known two-dimensional(2-D)compressible Euler system for isentropic flow,if the nonlinear velocity terms are ignored,we can derive the nonlinear wave system

t>
0,(x,y
)∈R,ρ
=ρ
(t,x,y
)is the density,u
=u
(t,x,y
)andv
=v
(t,x,y
)are thex
andy
component of velocity respectively,the pressurep
=p
(ρ
)is given as a function ofρ
,and(m,n
)=(uρ,vρ
)are momentum.We refer the readers to[4,23]and the references therein for more information on this system.We are interested in the shock re flection-diffraction problem for the nonlinear wave system.The shock re flection-diffraction con figurations are not only important in gas dynamics,but also fundamental in the structure of global entropy solutions of the 2-D Riemann problems for hyperbolic conservation laws.It is well known that the mathematical theory of 1-D Riemann problems for hyperbolic system of conservation laws has been understood well([5,15,17]),while not much is known about the mathematical results on the multi-dimensional Riemann problems.In particular,for 2-D Riemann problems,one of the main mathematical difficulties is that the governing equation changes its type between a hyperbolic equation and an elliptic equation.Moreover,the elliptic equation turns out quasilinear and degenerates on its boundary which is composed of shocks and sonic lines.The study on transonic shocks and sonic lines has been essential in the research on the 2-D Riemann problems.There has been much effort in the study of 2-D Riemann problems with various simpli fied models,including the potential flow equation[7,25],the unsteady transonic small disturbance equation(UTSD)[3,19,21],the pressure gradient system[29,30,33,34],the nonlinear wave system[4,6,22]and the references cited therein.The researches on these models can inspire new ideas and techniques to deal with the related problems for the Euler equations.
In[35],Zheng constructed the transonic shock solutions for the regular re flection problem of a shock hitting a wedge of large angle with the pressure gradient system which is similar to the nonlinear wave system.Recently Yang et al.[32]extended the result in[35]to the case in which the wedge angle is allowed to across the sonic angle to the detachment angle.The shock regular re flection by wedges for the potential flow equation was studied in a series of works[1,7–10]by Chen et al.The shock diffraction problem for a shock interaction with the wedge of angleπ/
2 using the nonlinear wave system was considered by E.Kim in[22].Kim established the global existence of subsonic solutions.Later,Chen,Deng and Xiang[6]extended the previous result into a global subsonic existence result on the shock diffraction by any convex cornered wedge for the nonlinear wave system.Another important con figuration in 2-D Riemann problem is the Prandtl-Meyer re flection of unsteady global solutions for supersonic flow impinging onto a solid wedge.In 1936,Prandtl[27]first employed the shock polar analysis to show that there are two possible steady con figurations:the steady weak shock solution and strong shock solution if the wedge angle is less than a critical angle,which is called a detachment angle.The steady weak shock solution is more believed to be physically admissible.The first rigorous unsteady analysis was due to Elling and Liu[16]for the wedge angle less than the sonic angle.Later,Bae,Chen and Feldman[2]established the existence theorem for the Prandtl-Meyer re flection for unsteady potential flow allowing all the physical parameters up to the detachment angle.
In this paper,we are concerned with the mathematical analysis of shock diffraction by convex cornered wedges for the nonlinear wave system of isothermal gas.The relation betweenp
andρ
for isothermal gas is given by
The shock diffraction problem with system(1.1)for polytropic gas was considered in[6],where the state of equation is

γ
→1in(1.3)for polytropic gas([8]).
W
be a convex cornered wedge in Rsuch that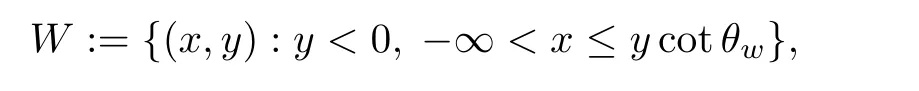
θ
∈(?π,
0)is given as in Figure 1.LetS
be a vertical planar shock separating two constant states which are the left stateU
:=(ρ
,m
,
0)and the right stateU
:=(ρ
,
0,
0).WhenS
passes the wedge,the shock diffraction occurs.The shock diffraction problem can be formulated as follows: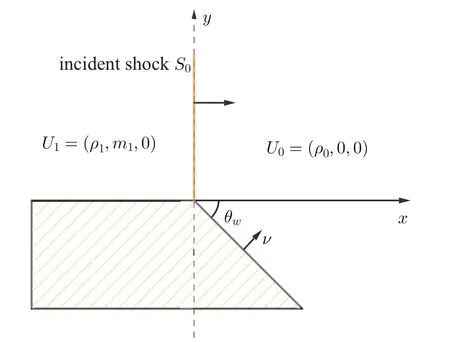
Figure 1 Initial data
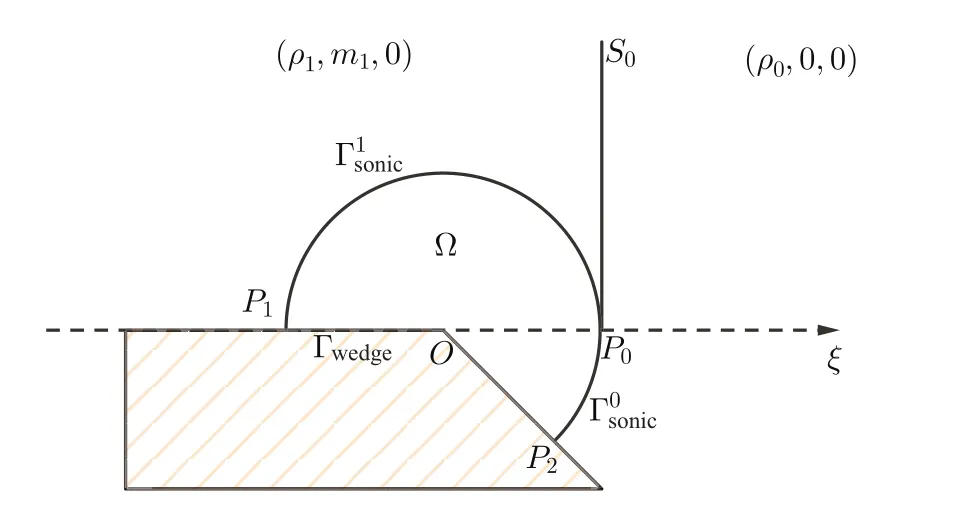
Figure 2 Shock diffraction con figuration for isothermal gas
Problem 1.1
(Initial-boundary value problem)Seek a solution of system(1.1)with the initial condition: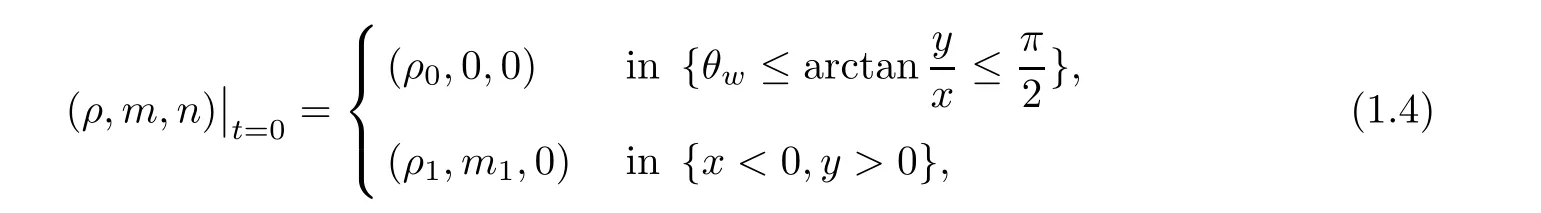
?W
: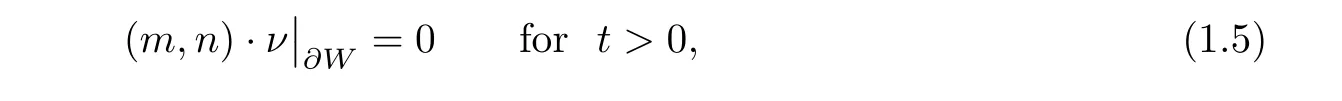
ν
is the outward unit normal vector to?W
.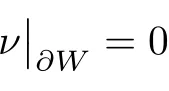
2 Mathematical Reformulation and the Main Theorem
Since Problem 1.1 is invariant under the scaling(t,x,y
)→(αt,αx,αy
)forα>
0,we seek self-similar solutions of Problem 1.1 with the following form: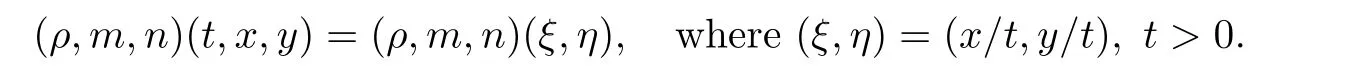
ξ,η
)-coordinates,the nonlinear wave system(1.1)becomes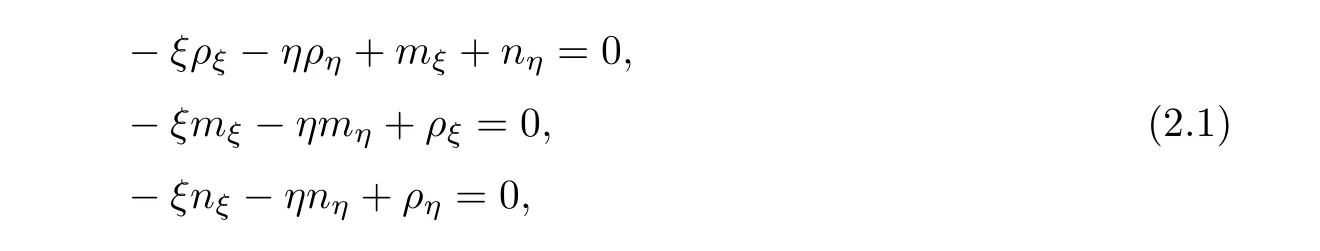
ρ
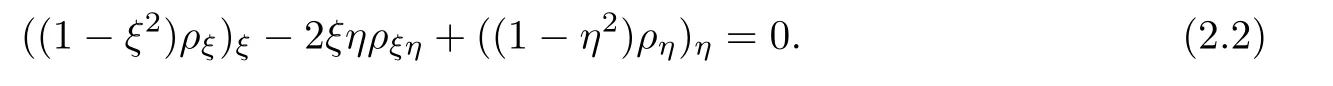
The non-divergence form of(2.2)is
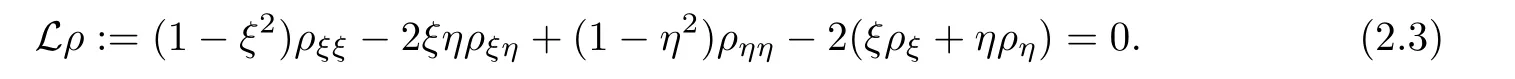
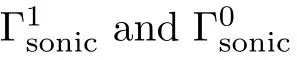
In the self-similar coordinates,Problem 1.1 can be restated as a boundary value problem in an unbounded domain.
Problem 2.1
(Boundary value problem)Find a solution of system(2.1)with the boundary condition,asξ
+η
→∞,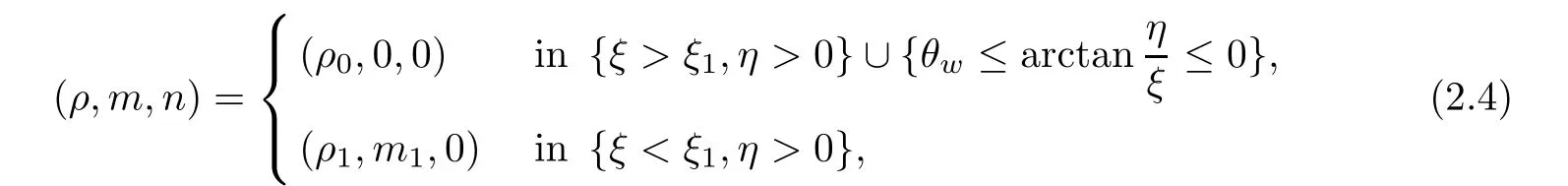
?W
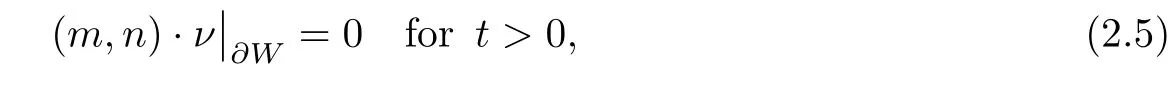
ν
is the outward unit normal to?W
.Hereξ
=1 is the location of the incident planar shockS
in the self-similar coordinates.We note that(2.1)can be expressed by a conservation form of
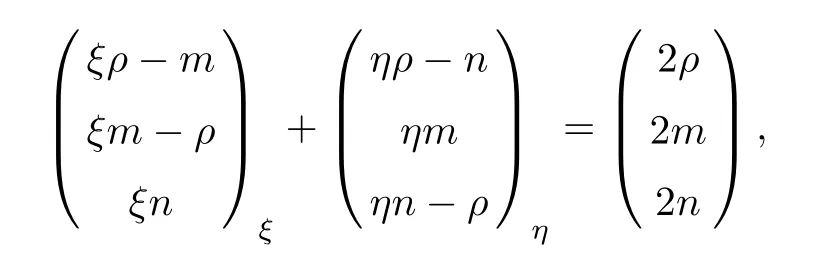
which produces the following Rankine-Hugoni ot conditions:
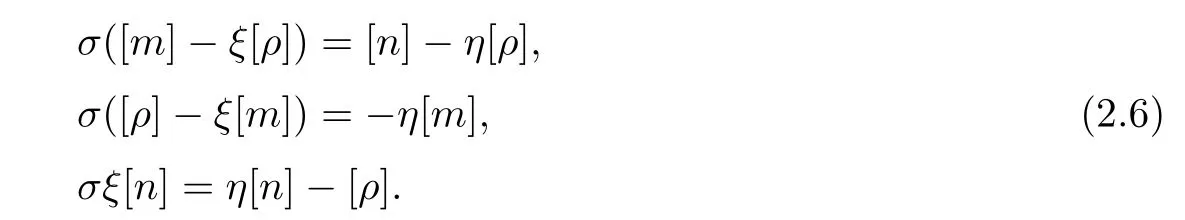
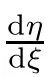
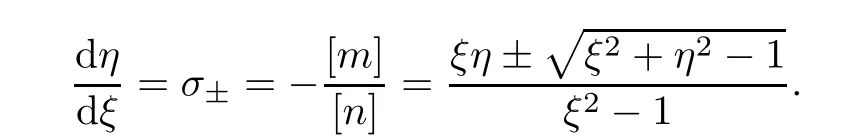
It can also be derived that
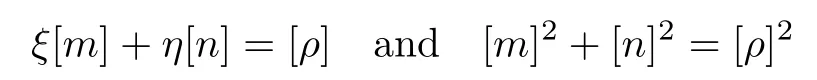
ρ
increases across the discontinuity in the relative flow direction.Hence,from the given initial dataU
,U
and the relation[m
]+[n
]=[ρ
],we know that the initial condition should satisfy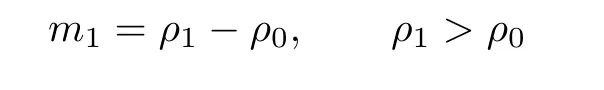
S
.Moreover,since the location of the incident shockS
is{ξ
=1}in the self-similar coordinates,it is easy to see thatS
is tangent to the sonic circle at pointP
.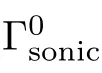
Problem 2.2
(Fixed boundary problem)Seek a solution of the second-order linear equation(2.3)for the density functionρ
in the domain ?,satisfying the following boundary conditions: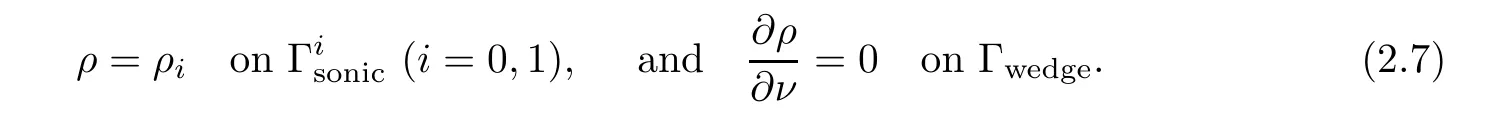
S
coming from in finity is tangent to the sonic circle and terminates atP
.On the other hand,for polytropic gas the incident shockS
intersects with the sonic circle of the left stateU
and then becomes a transonic shock Γ,which is a free boundary and terminates atP
on the wedge(see Figure 3).Then the shock diffraction problem for polytropic gas can be further reformulated as a free boundary problem for nonlinear degenerate elliptic equations of second order with a degenerate oblique derivative boundary condition on Γ.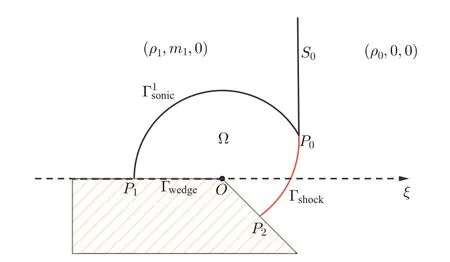
Figure 3 Shock diffraction con figuration for polytropic gas
Remark 2.3
We notice the property that the shock is tangent to the sonic circle for isothermal gas modeled by the nonlinear wave system also appears in the 2-D Riemann problem of Euler equations for Chaplygin gas.In[28],Serre proved that a shock line between two constant states must be tangent to the both sonic circles.More researches on Riemann problems for Chaplygin gas can be referred to[12–14,31]and the references cited therein.For the fixed boundary problem,Problem 2.2,we establish the following results,which form the main theorem of this paper.
Theorem 2.4
(Main theorem)Let the angleθ
in Figure 1 be between?π
and 0.Then there exists a global solution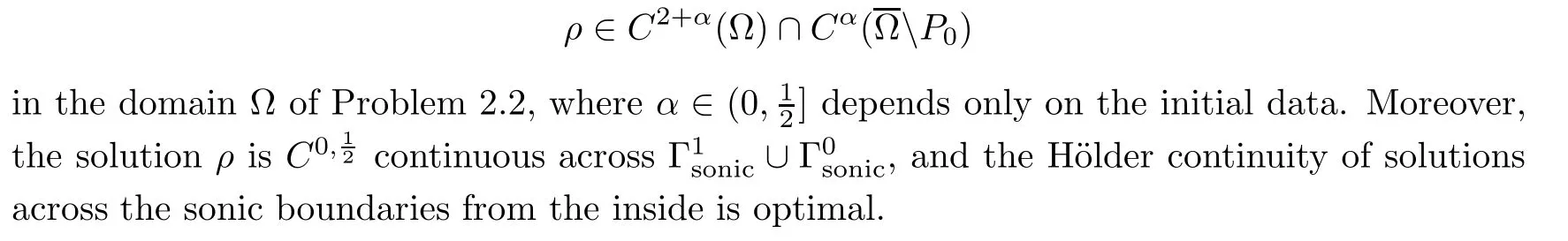
3 Proof of Main Theorem
3.1 Existence of solutions
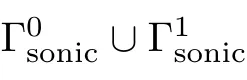

?
.Lemma 3.1
For fixed?>
0,there exists a solutionρ
∈C
(?)∩C
(?P
)to the linear uniformly elliptic equation(3.1)with the boundary conditions in(2.7).Moreover,ρ
is uniformly bounded:ρ
≤ρ
≤ρ
in ?.Proof
To prove this lemma,only the cornerP
needs a new treatment.Sinceρ
is not continuous atP
along the sonic boundary,we first modify the boundary conditions on{r
=1}as follows:
Proof
By the local ellipticity and the standard interior Schauder estimate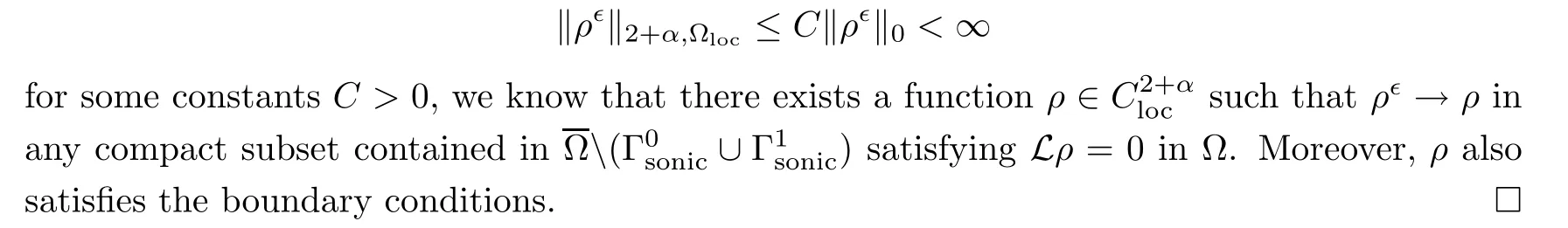
3.2 Optimal regularity near the sonic boundary

and consider the domain
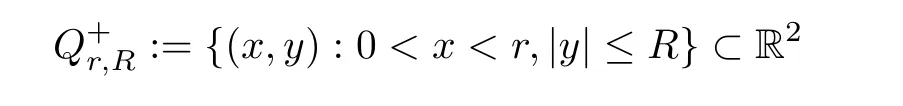
R>
0.If we let?
=ρ
?ρ
,then it follows from(3.2)that?
satis fies that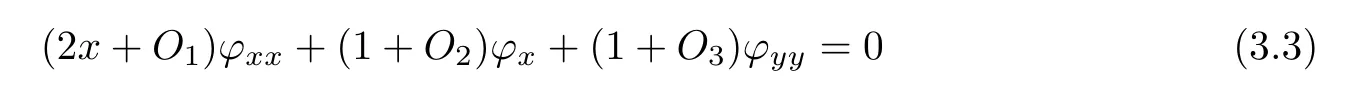
x,y
)-coordinates,where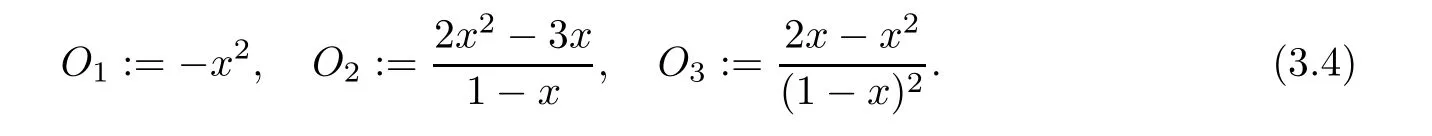
?
satis fies that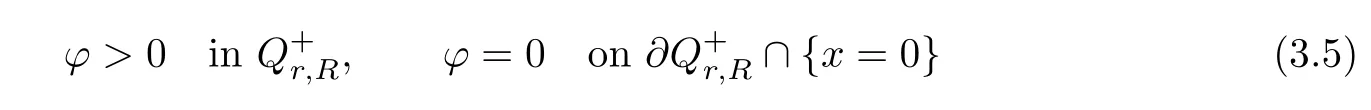
r
∈(0,τ
).It is easy to see that the termsO
(x
)(j
=1,
2,
3)are continuously differentiable and satisfy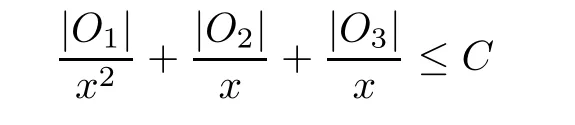

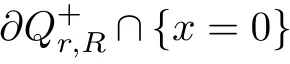

α>
0 andv
(0,y
)/=0.Equation(3.3)yields an equation forv
: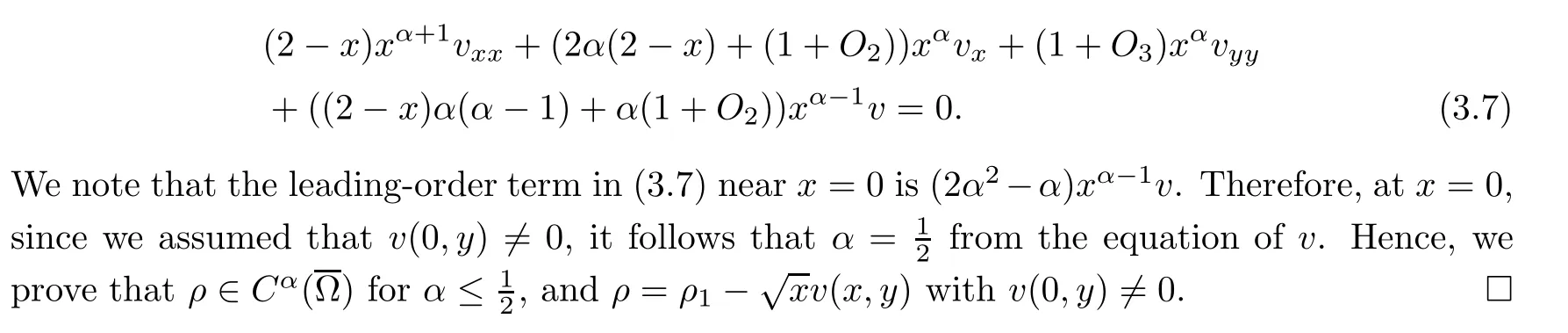
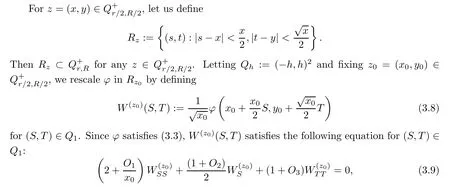
O
(i
=1,
2,
3)are de fined as in(3.4).It is obvious that the coefficients of equation(3.9)are bounded so that equation(3.9)is uniformly elliptic for(S,T
).By the classical theory,for uniformly elliptic equations we have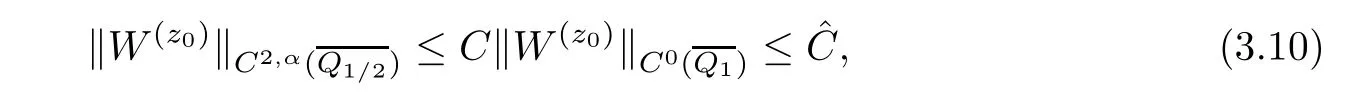
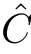
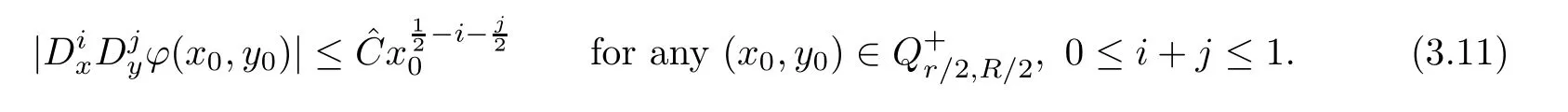
Hence,we prove the regularity of solutions as follows:
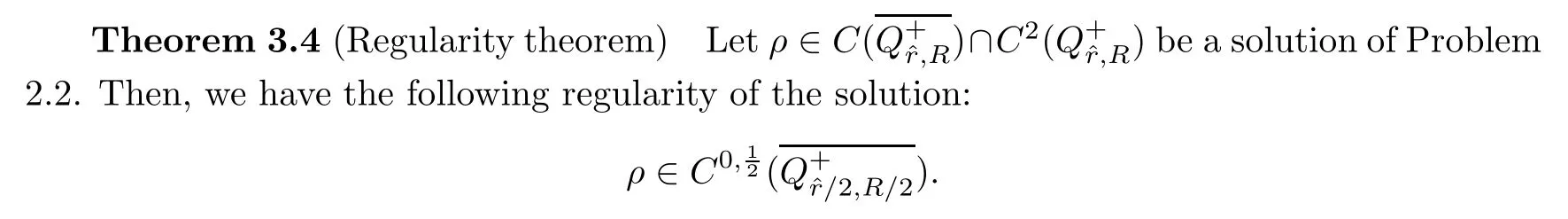
c
(ρ
)=p
(ρ
)=Aγρ
withA>
0 andγ>
1.In[6]the governing second-order quasilinear equation forρ
was given by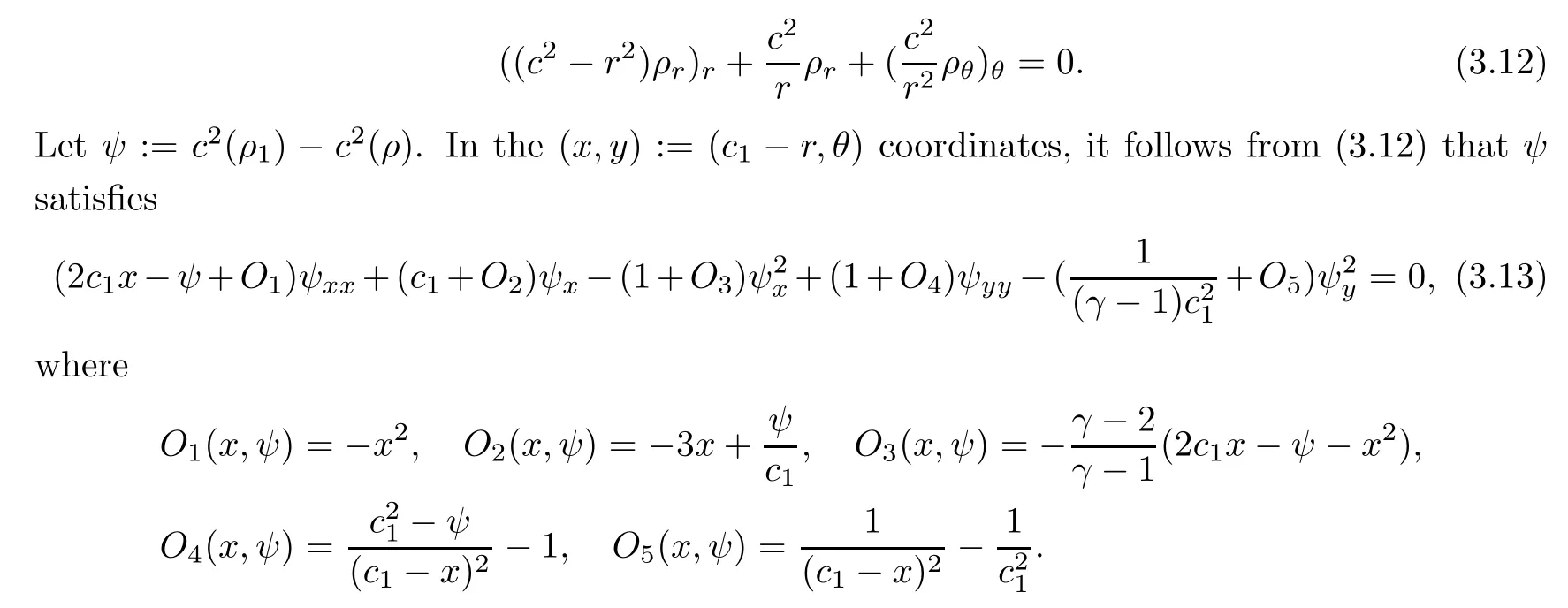
The main terms of(3.13)form the following equation:
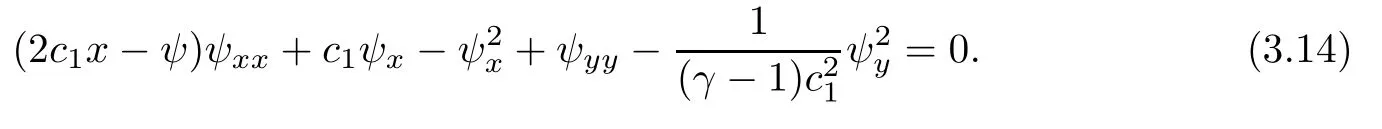
x
=0}.In[6]Chen et al.proved thatC
is the optimal regularity ofψ
across the boundary{x
=0}.This implies that the nonlinear terms can improve the regularity of solutions.The conclusion that the regularity for nonlinear degenerate elliptic equations may be higher than that for linear equations is also shown in[1]for the shock re flection problem for potential flow.4 Existence and Regularity of Global Solutions of the Nonlinear Wave System

In conclusion,we have proved the following theorem:
Theorem 4.1
Let the angleθ
in Figure 1 be between?π
and 0.Then,there exists a global solution(ρ,m,n
)of Problem 2.1 such that
 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- CONSTRUCTION OF IMPROVED BRANCHING LATIN HYPERCUBE DESIGNS?
- LIMIT CYCLE BIFURCATIONS OF A PLANAR NEAR-INTEGRABLE SYSTEM WITH TWO SMALL PARAMETERS?
- SLOW MANIFOLD AND PARAMETER ESTIMATION FOR A NONLOCAL FAST-SLOW DYNAMICAL SYSTEM WITH BROWNIAN MOTION?
- DYNAMICS FOR AN SIR EPIDEMIC MODEL WITH NONLOCAL DIFFUSION AND FREE BOUNDARIES?
- A STABILITY PROBLEM FOR THE 3D MAGNETOHYDRODYNAMIC EQUATIONS NEAR EQUILIBRIUM?
- THE GROWTH AND BOREL POINTS OF RANDOM ALGEBROID FUNCTIONS IN THE UNIT DISC?
