Department of Mathematics,Eastern Mediterranean University,Famagusta,North Cyprus via Mersin 10,Turkey E-mail:mehmetali.ozarslan@emu.edu.tr;banuyilmazgm@gmail.com

Abstract In this paper,we introduce the?h-Gould-Hopper Appell polynomials An(x,y;h)via h-Gould-Hopper polynomials(x,y).These polynomials reduces to?h-Appell polynomials in the case y=0,?-Appell polynomials in the case y=0 and h=1,2D-Appell polynomials in the case h→0,2D?-Appell polynomials in the case h=1 and Appell polynomials in the case h→0 and y=0.We obtain some well known main properties and an explicit form,determinant representation,recurrence relation,shift operators,difference equation,integro-difference equation and partial difference equation satis fied by them.Determinants satis fied by?h-Gould-Hopper Appell polynomials reduce to determinant of all subclass of the usual polynomials.Recurrence,shift operators and difference equation satis fied by these polynomials reduce to recurrence,shift operators and difference equation of?h-Appell polynomials,?-Appell polynomials;recurrence,shift operators,differential and integro-differential equation of 2D-Appell polynomials,recurrence,shift operators,integro-difference equation of 2D?-Appell polynomials,recurrence,shift operators,differential equation of Appell polynomials in the corresponding cases.In the special cases of the determining functions,we present the explicit forms,determinants,recurrences,difference equations satis fied by the degenerate Gould-Hopper Carlitz Bernoulli polynomials,degenerate Gould-Hopper Carlitz Euler polynomials,degenerate Gould-Hopper Genocchi polynomials,?h-Gould-Hopper Boole polynomials and?h-Gould-Hopper Bernoulli polynomials of the second kind.In particular cases of the degenerate Gould-Hopper Carlitz Bernoulli polynomials,degenerate Gould-Hopper Genocchi polynomials,?h-Gould-Hopper Boole polynomials and?h-Gould-Hopper Bernoulli polynomials of the second kind,corresponding determinants,recurrences,shift operators and difference equations reduce to all subclass of degenerate socalled families except for Genocchi polynomials recurrence,shift operators,and differential equation.Degenerate Gould-Hopper Carlitz Euler polynomials do not satisfy the recurrences and differential equations of 2D-Euler and Euler polynomials.

Key words ?h-Appell polynomials;determinant;recurrence;difference equation

1 Introduction

Recently,there has been an active research on Appell polynomials.Many authors have studied on Appell polynomials because they have some useful applications in pure and applied mathematics.

Appell polynomials are de fined by

For some special choices of

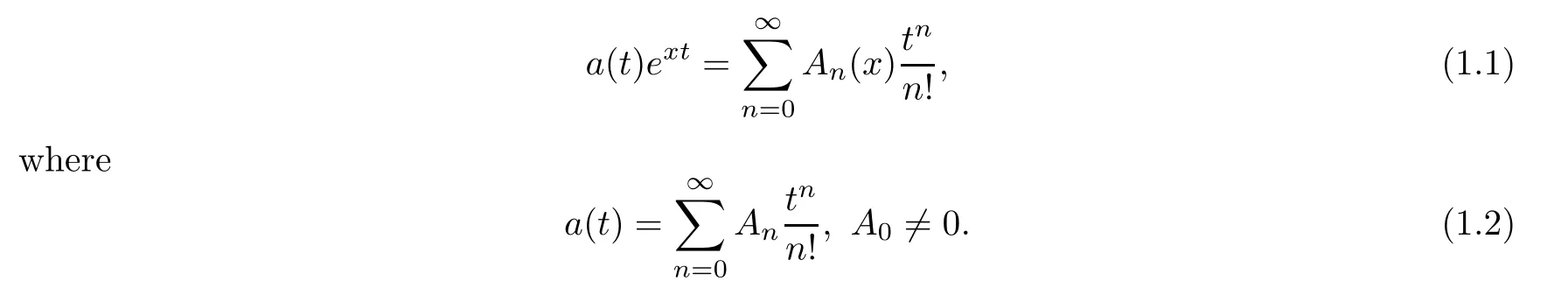
a

(

t

)

,

we have the well known Bernoulli and Euler polynomials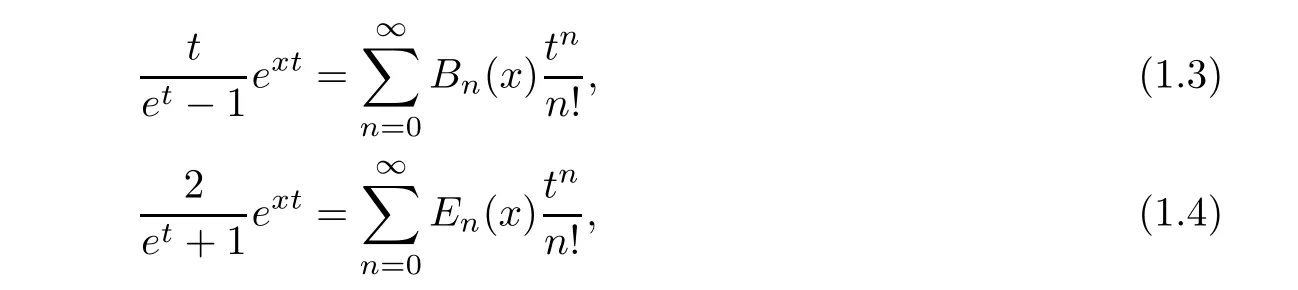

respectively. The recurrence relations and differential equations of the above polynomials were studied in[21].Besides,differential equation satis fied by Frobenius-Euler and Frobenius-Genocchi polynomials were obtained[58].Bivariate Appell polynomials were de fined by

and corresponding differential equations were obtained in[3].Besides,some extensions of the above family were introduced and differential,integro-differential and partial differential equations satis fied by the extended 2

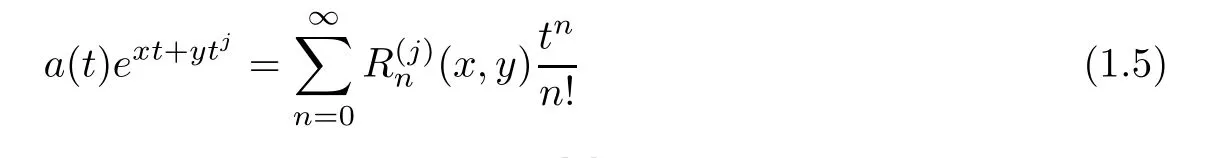
D

Bernoulli and Euler polynomials were obtained in[57]as a special cases.Moreover,some main properties of the Apostol type extensions of the above polynomials were studied in[38,40,42].Also,

q

-extensions of the Apostol type polynomials were introduced and some addition theorems were obtained in[39].Differential,integro-differential and partial differential equations for the Hermite-based Appell polynomials were obtained in[51].Furthermore,uni fication of the Hermite-based Apostol Bernoulli,Euler and Genocchi polynomials was introduced,and some properties such as symmetry identities and generalized sum of integer powers were obtained in[41].The common property of the Appell polynomial sequence{

A

(

x

)}is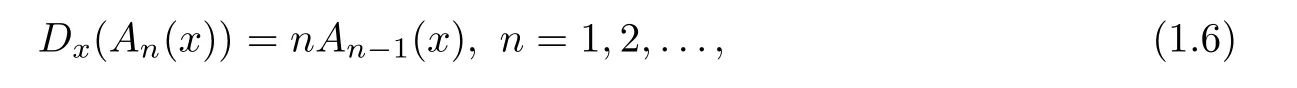

where

D

is the derivative operator.Replacing

D

by difference operator?

,

the polynomial sequence A(

x

)that arises satisfying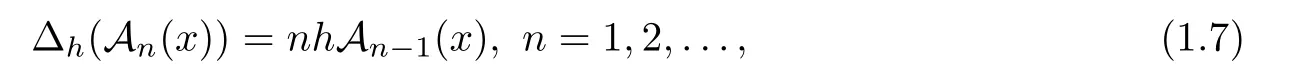

were de fined in[15]and called by?-Appell sequences.

Here,?is the finite difference operator which is

Finite difference operator of order

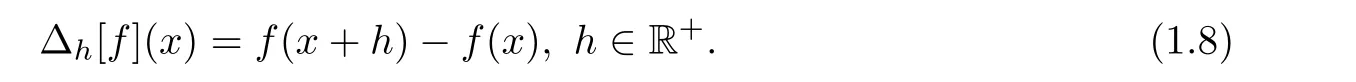
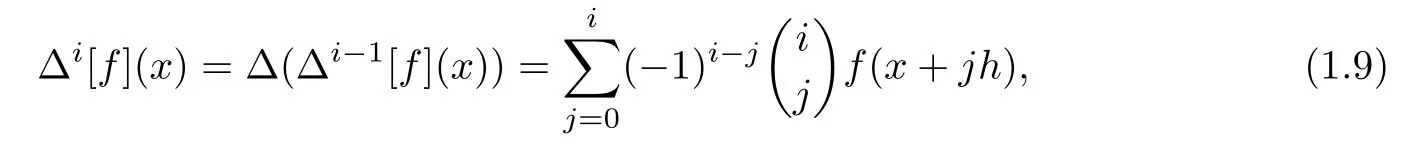
i,i

∈N

,

is given by where?=

I

,?=?and

I

is the identity operator.Related interpolation problem of?-Appell sequences was handled in[15].In[15],?-Appell sequences{A(

x

)}were de fined by the power series of the product of

a

(

t

)(1+

ht

)hby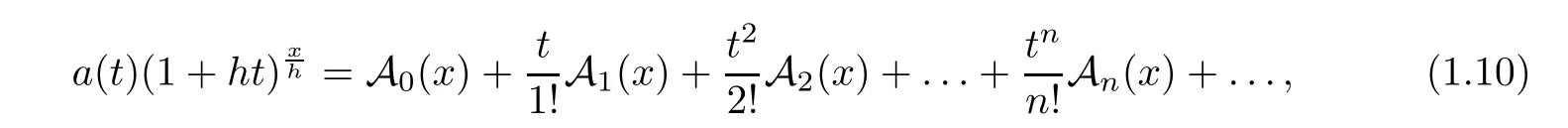

where

a

(

t

)was given by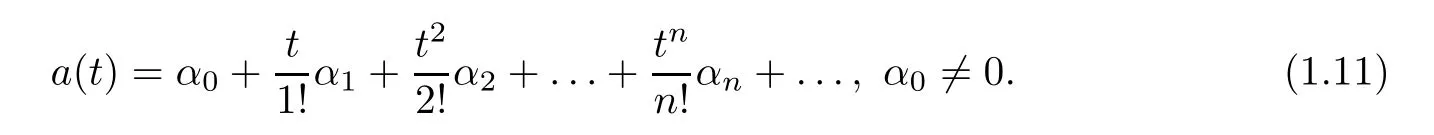

Twice iterated?-Appell polynomials were introduced and difference equations for a class of twice iterated?-Appell polynomials were obtained in[52].Very recently,the Hahn-Appell polynomials which include the usual,?and

q

-Appell polynomials were introduced and analyzed,corresponding difference equations and

d

-orthogonality problem has been solved for Hahn-Appell polynomials in[54].

On the other hand,Carlitz introduced the degenerate Bernoulli polynomials in[5]

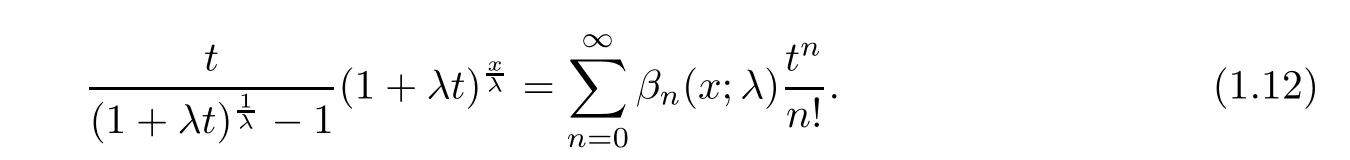
Degenerate Euler polynomials were introduced in[6,27,32],

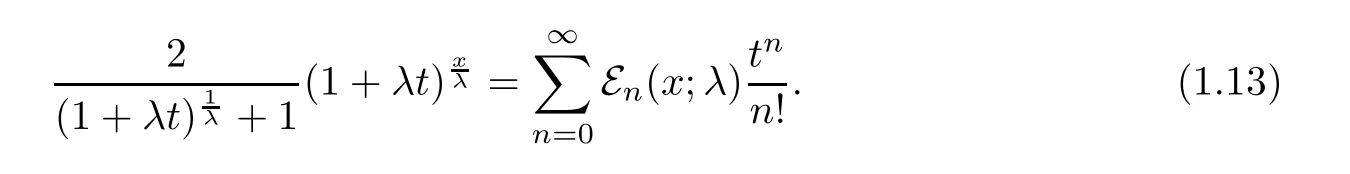
Degenerate Genocchi polynomials were de fined in[27,37],

Recently,Khan et al.[27]de fined a uni fied class of degenerate Apostol-type polynomials.In the special case

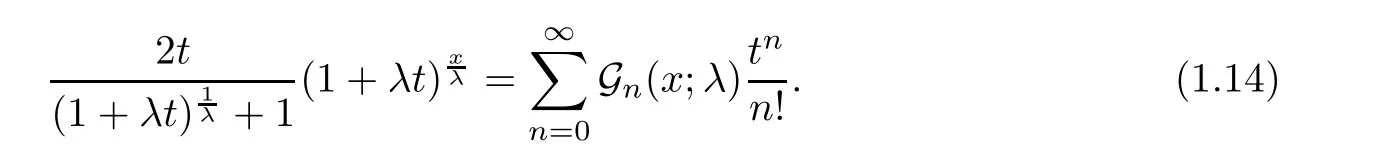
λ

→0

,

uni fied degenerate family reduce to uni fied family satis fied by the Apostol polynomials of order

α.

By monomiality principle,uni fied degenerate Apostol-type polynomials were investigated.Some recurrence relations and explicit representations were obtained.Also,some authors worked on degenerate Bernoulli,Euler and Genocchi polynomials[32,37].The results that are satis fied by the degenerate Bernoulli,Euler and Genocchi polynomials reduce to the results that are satis fied by the usual Bernoulli,Euler and Genocchi polynomials when

λ

→0

.

We observe that the possible de finition of the degenerate Appell polynomials can be the same as the?-Appell polynomials.That is

where

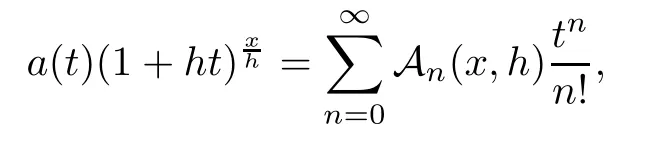
a

(

t

)is given by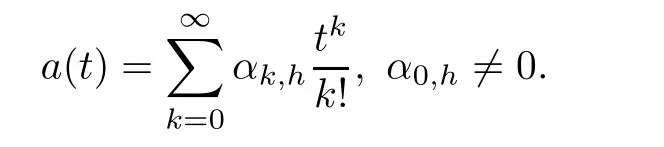

This observation motivate us to introduce and study on the?-Gould-Hopper Appell polynomials,since the results will also be reduced to the newly de fined bivariate degenerate versions of many known polynomials.

Gould-Hopper polynomials are given by

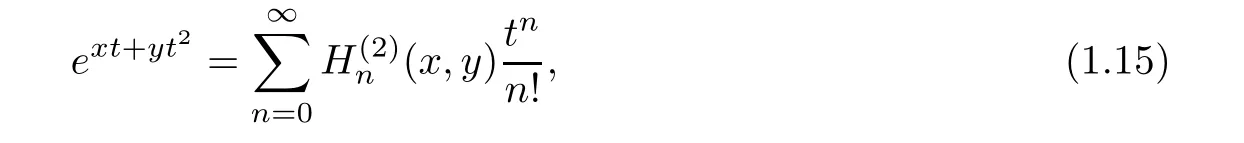
which are solutions of the heat equation

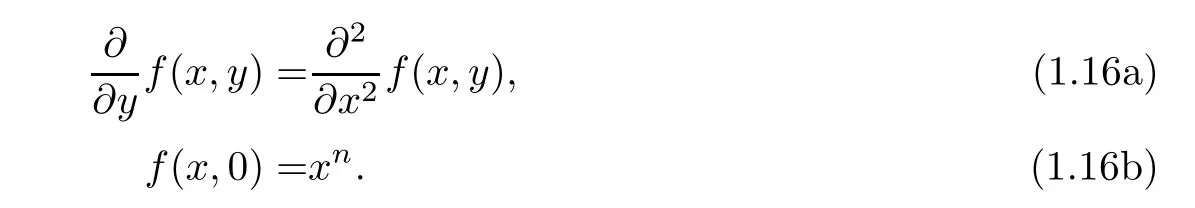
Explicitly,they are given by

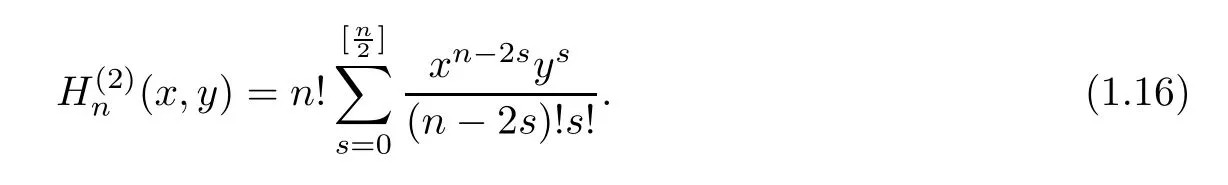
Degenerate Hermite(or Gould-Hopper)polynomials were introduced in[25]

They reduce to usual case when

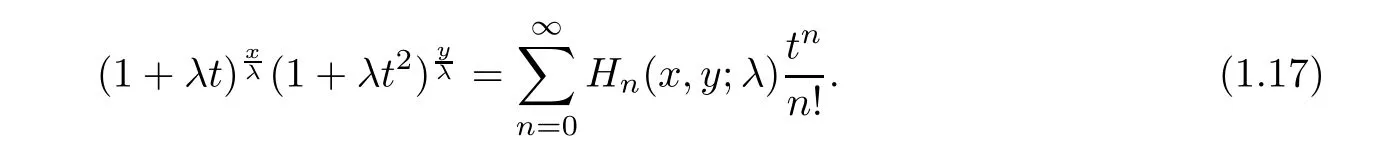
λ

→0

.

The explicit form of the degenerate Gould-Hopper polynomials was given in[25]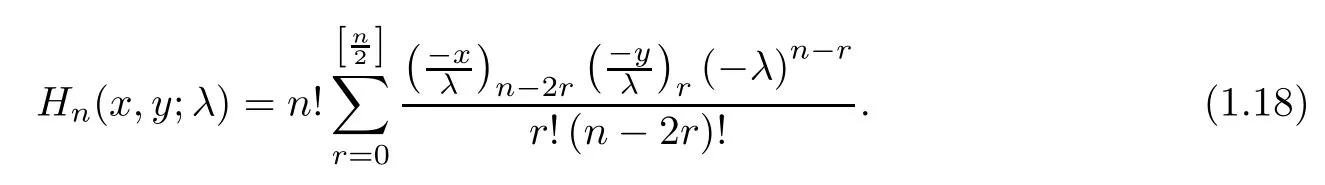

Because of the same intention that we point out about the motivation of this paper,we will call the polynomials,de fined by

as

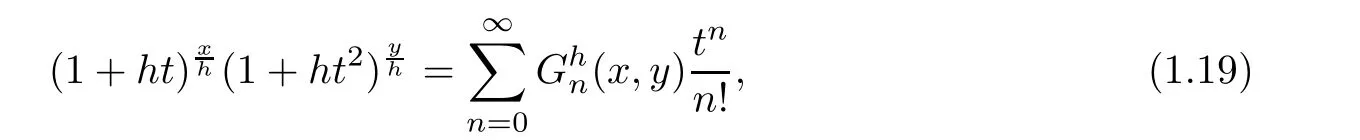
h

-Gould-Hopper polynomials.By means of the above polynomials,we de fine?-Gould-Hopper Appell polynomials A(

x,y

;

h

)as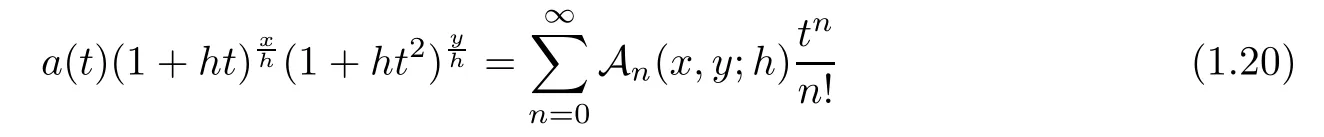

and the?-Gould-Hopper Appell numbers as

In this paper,we introduce degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind by

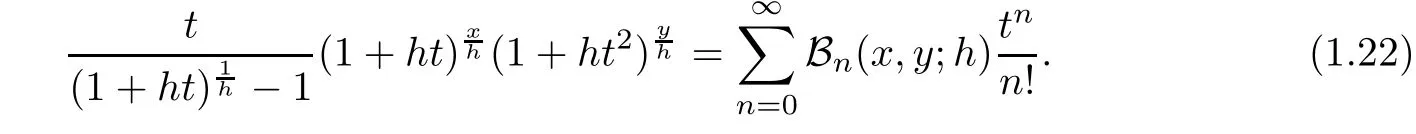
Degenerate Gould-Hopper Carlitz Euler polynomials are introduced as

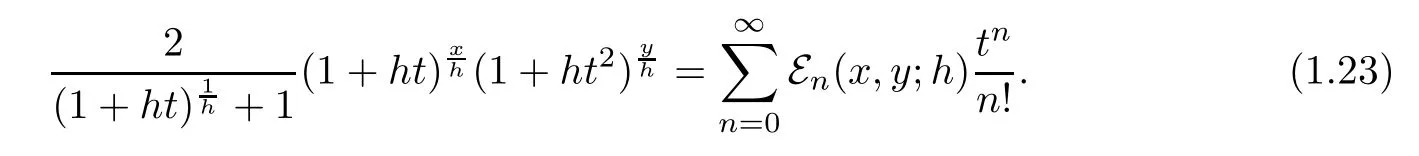
Degenerate Gould-Hopper Genocchi polynomials are de fined as

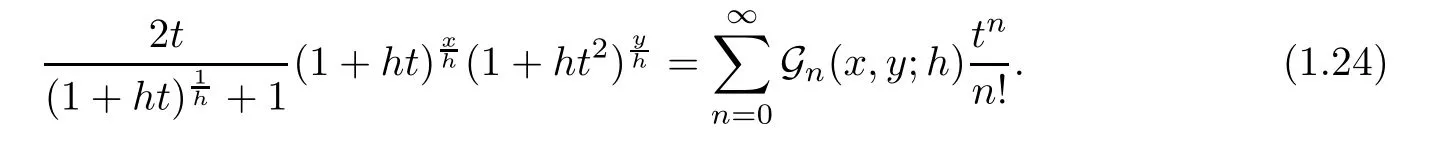
Degenerate Gould-Hopper Boole polynomials are de fined as

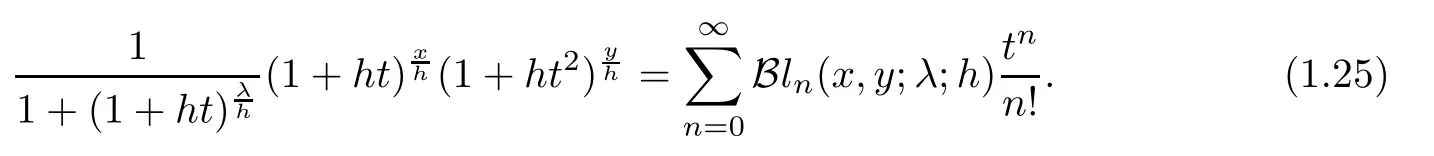
?-Gould-Hopper Bernoulli polynomials of the second kind are de fined as

By fully degenerating the Gould-Hopper polynomials with a

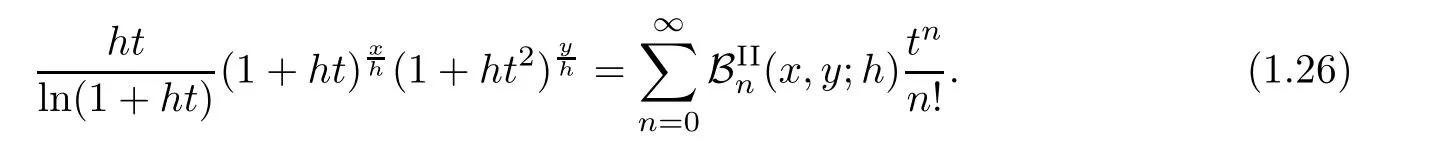
q

-parameter,Gould-Hopper based fully degenerate poly-Bernoulli polynomials with a

q

-parameter were introduced and addition and difference rule properties were analyzed in[18].Generalized degenerate Gould-Hopper based fully degenerate Bell polynomials were introduced and some representations were obtained for generalized degenerate Gould-Hopper based degenerate Bernoulli,Euler and Genocchi polynomials[17].Note that some properties satis fied by the higher order Boole type polynomials and numbers were obtained.Also,some derivative formulas,recurrence relations and finite combinatorial sums including the Apostol-Euler polynomials,the Stirling numbers and Daehee numbers were given in[53].Degenerate Hermite-Bernoulli polynomials of the second kind[24]were introduced and in the case

λ

→0

,

they reduce to the Hermite Bernoulli polynomials(2

D

Bernoulli polynomials).Some explicit formulas for the higher order degenerate Bernoulli numbers of the first kind and the second kind were obtained and some recurrence formulas were proved.Also,some formulas related with the degenerate Genocchi numbers,degenerate tangent numbers and the coefficient of the higher order degenerate Euler polynomials were deduced in[7].In[15]generalized Bernoulli polynomials of the second kind(?-Bernoulli polynomials of the second kind)were de fined.Some interpolation properties satis fied by these polynomials were obtained.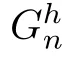

2 Degenerate Hermite Polynomials

Since the

h

-Gould-Hopper polynomials are de fined by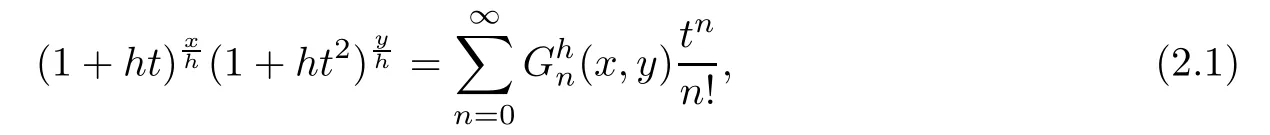

it can be directly seen that they satisfy the following equations:

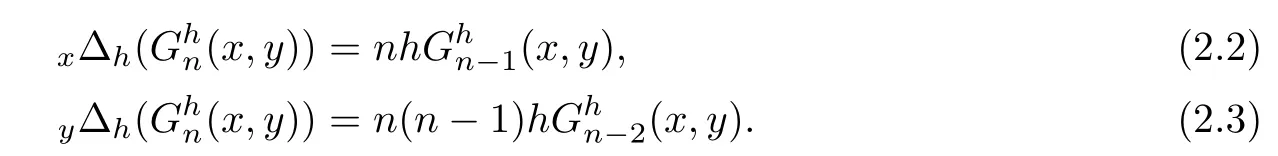
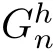
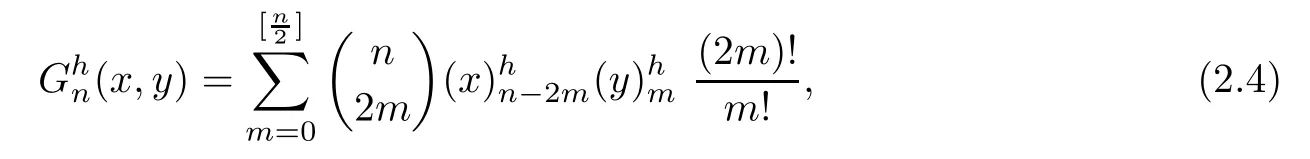
where

and satis fies the discrete heat equation

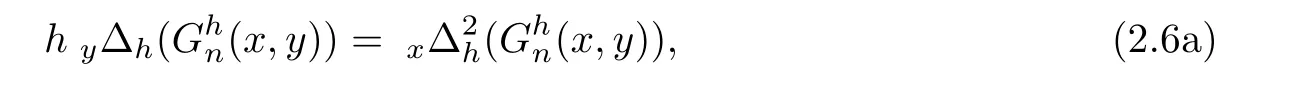
with the initial condition

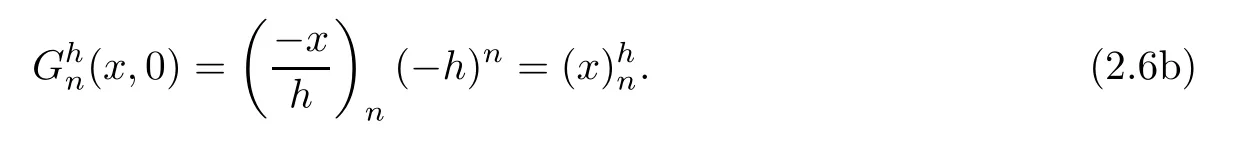
Proof

Using series expansion of(2.1)and applying the Cauchy product,

with the fact that

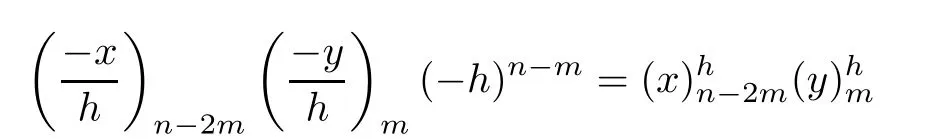
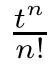
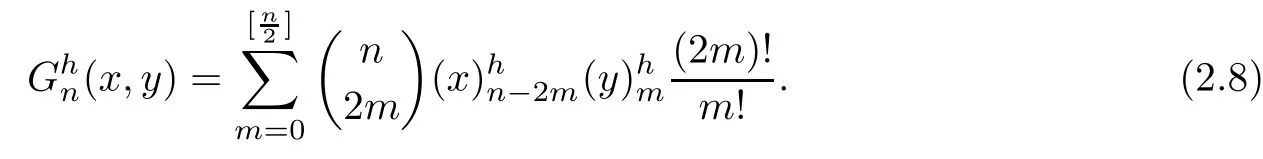
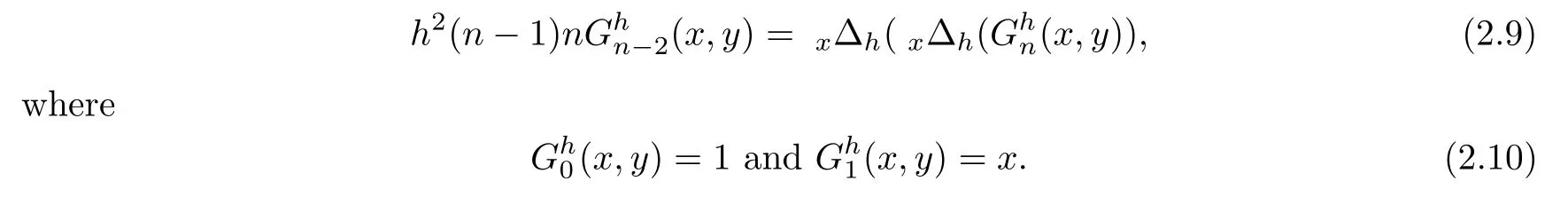
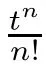
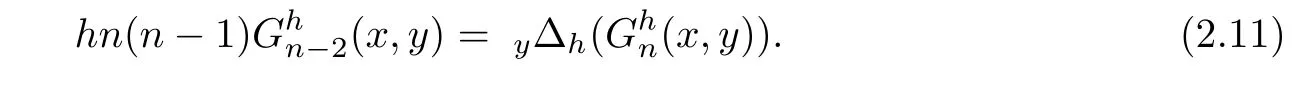
Comparing equations(2.9)and(2.11),we get the discrete heat equation

Substituting

y

=0 in(2.4),we get the following initial condition: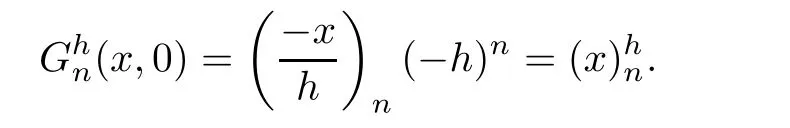

3 An Explicit and Determinantal Forms of?h-Gould-Hopper Appell Polynomials

In this Section,we introduce the?-Gould-Hopper Appell polynomials and obtain an explicit form and the determinantal form of the?-Gould-Hopper Appell polynomials.First,we de fine the?-Gould-Hopper Appell polynomials.

De finition 3.1

?-Gould-Hopper Appell polynomials are de fined by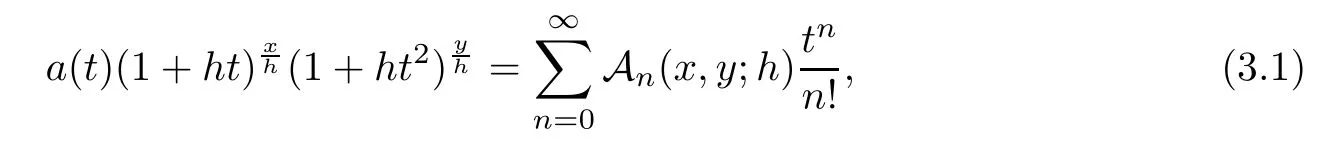

where the degenerate numbers A(0

,

0;

h

):=

α

(

n

=0

,

1

,

2

,...

)are given by the series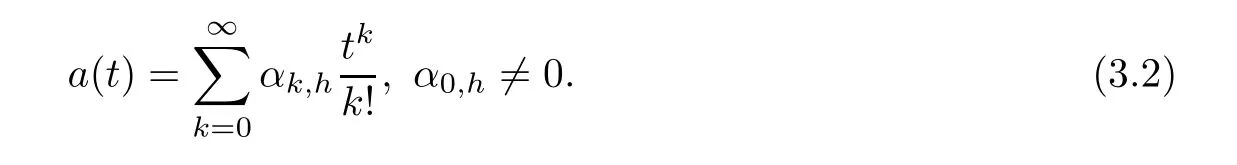

Remark 3.2

?-Gould-Hopper Appell polynomials reduce 2

D

?-Appell polynomials in the case

h

=1;?-Appell polynomials[15]in the case

y

=0;?-Appell polynomials in the case

y

=0 and

h

=1;2

D

-Appell polynomials in the case

h

→0[3];Appell polynomials in the case

h

→0 and

y

=0[21].In some special cases of the?-Gould-Hopper Appell polynomials,we have 2

D

Bernoulli polynomials,2

D

Euler polynomials,2

D

Daehee polynomials of order

k,

Daehee polynomials of order

k

[31],2

D

Peters polynomials(generalized 2

D

Boole polynomials),2

D

Boole polynomials,Boole polynomials[4,35,36,48],2

D

Changhee polynomials,Changhee polynomials[33],2

D

Poly-Cauchy polynomials of the first kind,2

D

Poly-Cauchy polynomials of the second kind,and Poly-Cauchy polynomials of the first kind and second kind.We should also note that some recurrence relations,differential,integro-differential and partial differential equations were obtained for the 2

D

Bernoulli polynomials and for the 2

D

Euler polynomials[3,57],respectively.Note that some explicit formulas for the Bernoulli polynomials of the second kind(in one variable)were obtained in[44].Moreover,general order of the Bernoulli polynomials of the second kind was introduced in[43].An explicit formula for the higher order Bernoulli polynomials of the second kind was obtained in[55].Note that some new matrix representations for the higher-order Daehee numbers and polynomials were obtained in[19].The case

k

=1 was investigated in[34].Some mixed-type polynomials like Barnes-type Daehee polynomials of the second kind and the Poly-Cauchy polynomials of the second kind were introduced in[30].Some properties of the Poly-Cauchy and Peters mixed-type polynomials were investigated in[29].

Theorem 3.3

The following properties are satis fied by?-Gould-Hopper Appell polynomials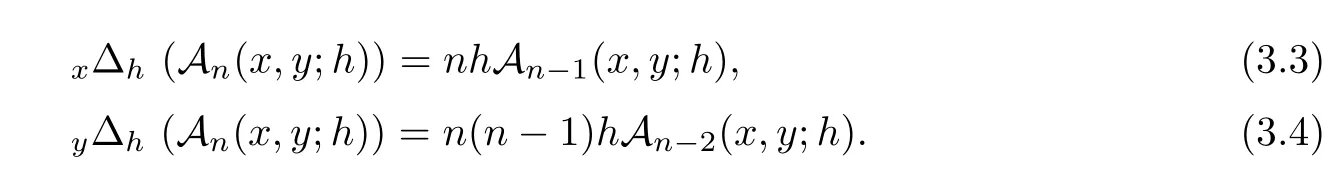

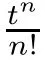
Theorem 3.4

A polynomial sequence{A(

x,y

;

h

)}is a?-Gould-Hopper Appell polynomial sequence if and only if it has an explicit form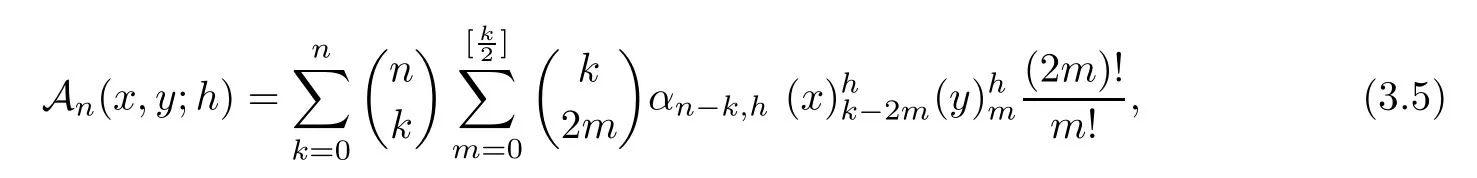

where

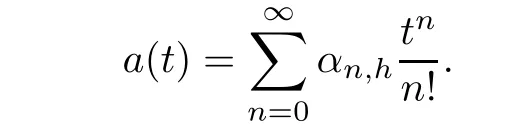
Proof

Multiplying both sides of(2.1)by

a

(

t

)and applying the Cauchy product,then inserting the generating function of?-Gould-Hopper Appell polynomials and using(3.1)on the right sides of the equality,we have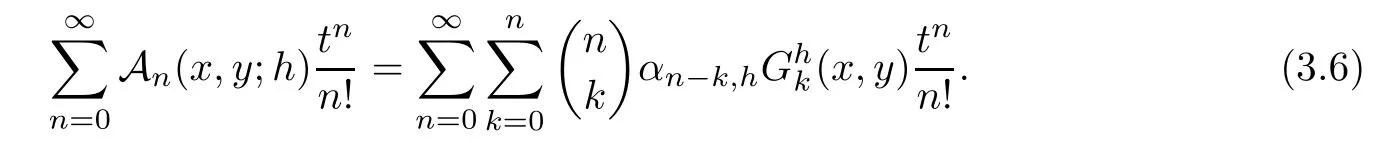

Using(2.4)in(3.6),we have

Theorem 3.5

?-Gould-Hopper Appell polynomials are de fined for each

n

=0

,

1

,

2

,...

by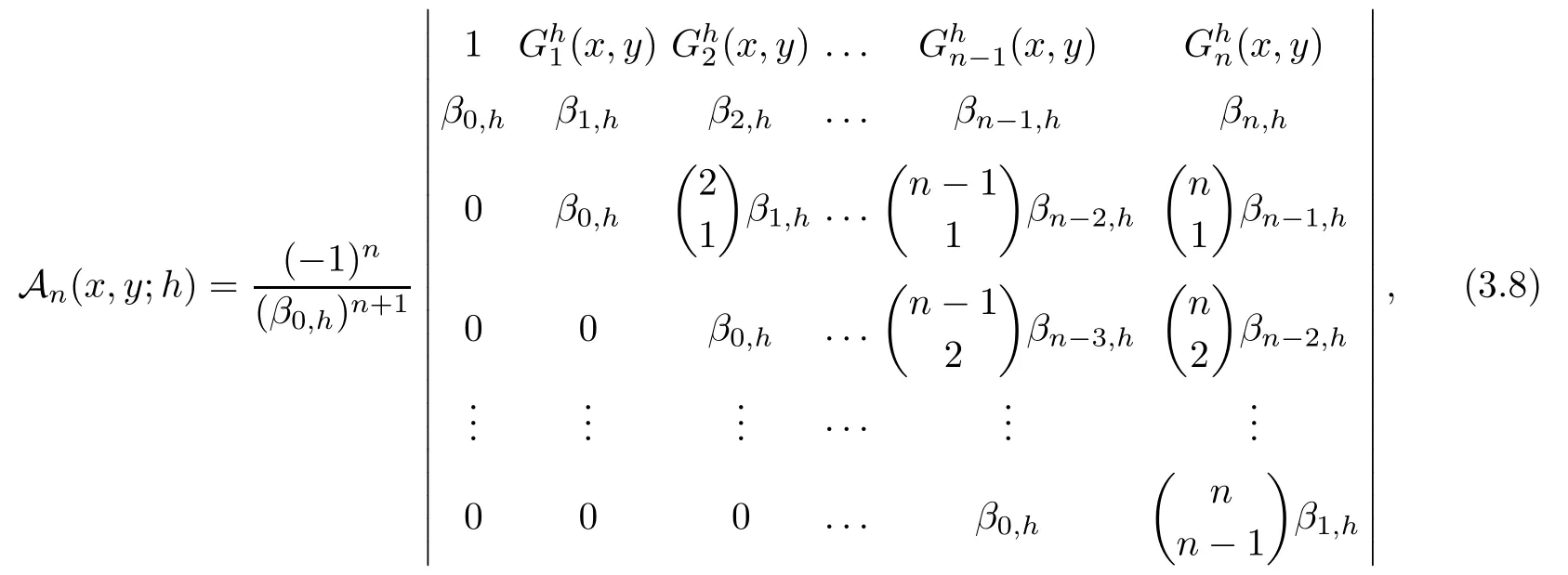

where the numbers

β

(

k

=0

,

1

,

2

,...

)are the coefficients of the Maclaurin series of 1

/a

(

t

)

.

Proof

Inserting the series forms of the

h

-Gould Hopper polynomials in the generating function of the?-Gould Hopper Appell polynomials,we have

Multiplying both sides by

Applying Cauchy product in(3.11)gives This equality leads to the system of

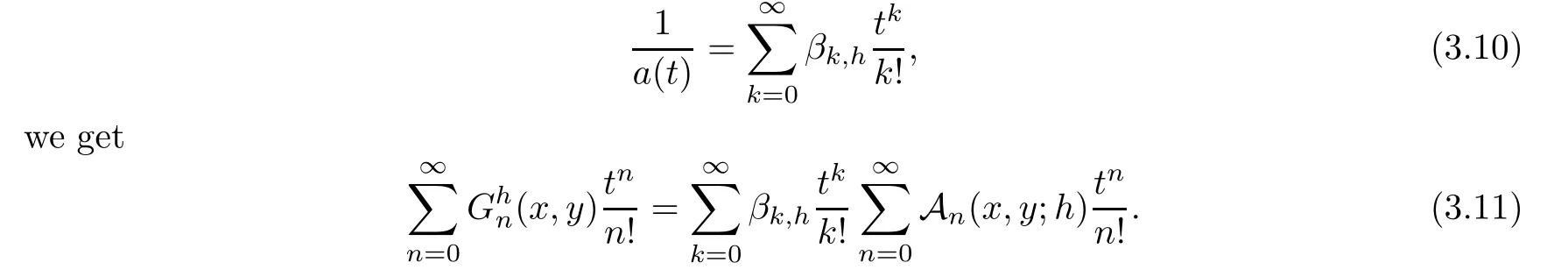
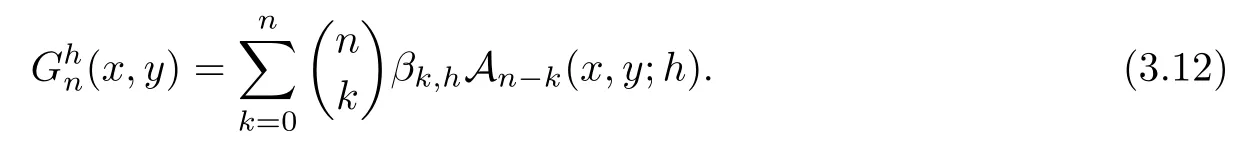
n

-equations with unknown A(

x,y

;

h

)

,n

=0

,

1

,

2

,....

Solving this system using Cramer’s rule and using the fact that denominator is the determinant of lower triangular matrix with determinant(

β

)and by taking transpose of the numerator,then replacing the

i

-th row by(

i

+1)-th position,for

i

=1

,

2

,...,n

?1

,

gives the desired result.

Determinants of?-Appell polynomials and Appell polynomials were obtained in[15]and[14],respectively.

Corollary 3.6

Determinant satis fied by?-Gould-Hopper Appell polynomials reduces to the determinant of?-Appell polynomials[15]in the case

y

=0;?-Appell polynomials in the case

y

=0 and

h

=1;2

D

-Appell polynomials in the case

h

→0;2

D

??-Appell polynomials in the case

h

=1;Appell polynomials[14]in the case

h

→0 and

y

=0

.

4 Recurrence Relation,Difference Equation,Integro-Difference Equation and Partial Difference Equation Satis fied by the?h-Gould-Hopper Appell Polynomials

In this Section,we obtain recurrence relation,lowering operator,raising operator,difference equation,integro-difference equation and partial difference equation satis fied by?-Gould-Hopper Appell polynomials.

Theorem 4.1

Recurrence relation satis fied by?-Gould-Hopper Appell polynomials is given by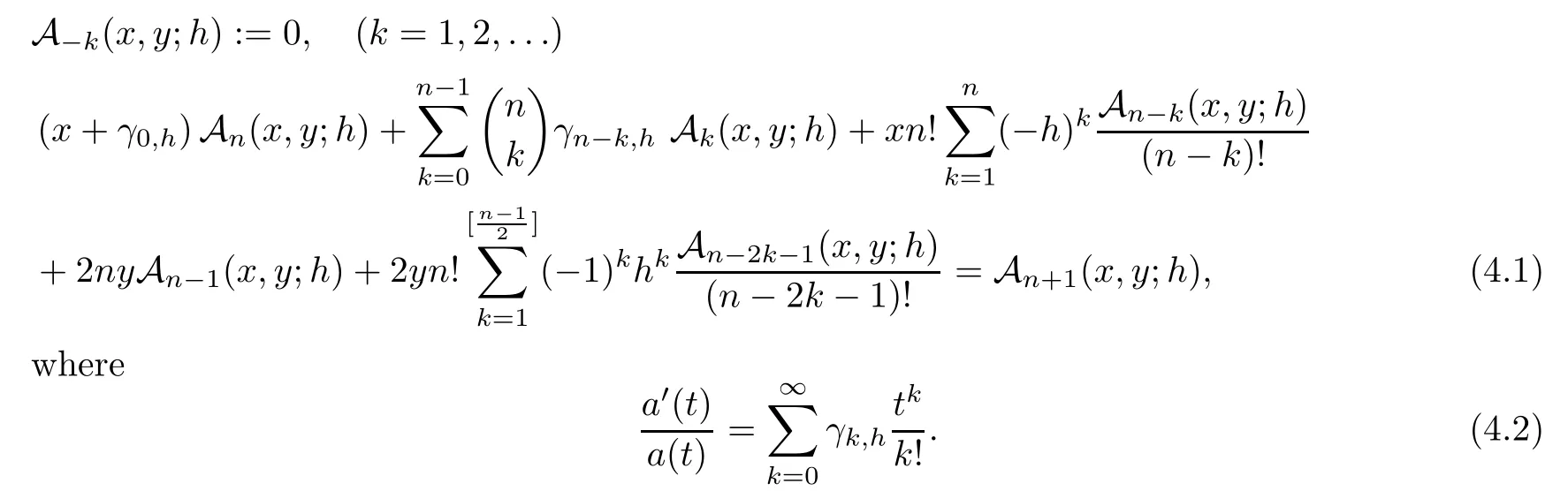

Proof

Taking derivative with respect to

t

on both sides of(3.1),we have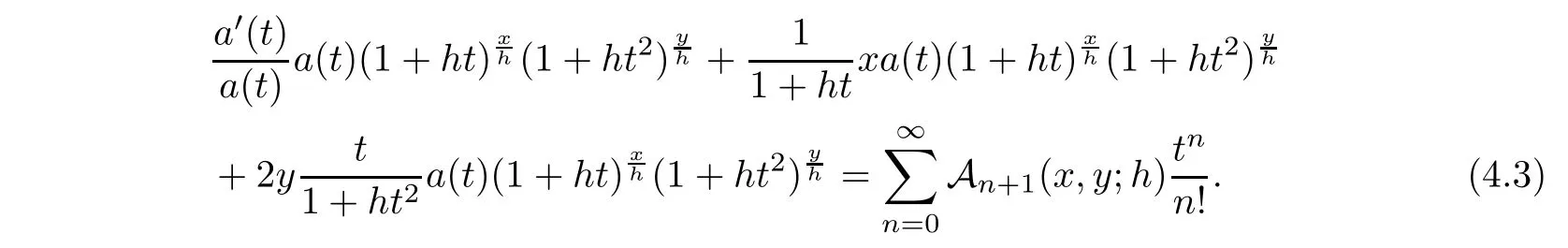

Now,substituting(3.1),(4.2)and series forms of

in(4.3),we have

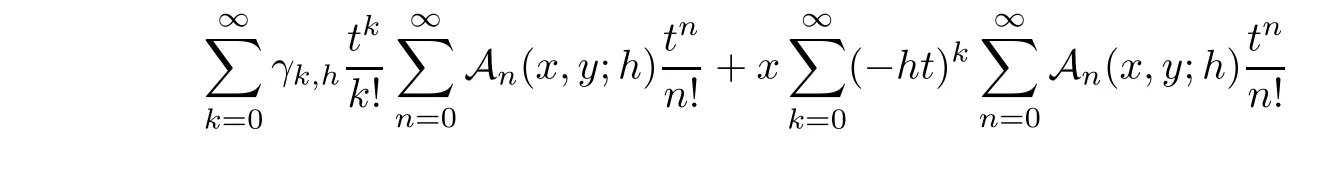
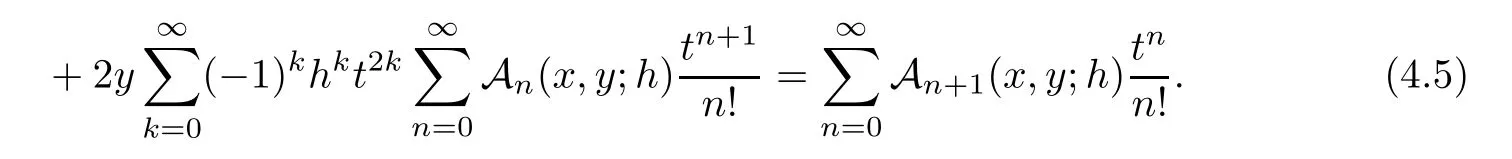
Applying the Cauchy product in(4.5)and writing all summations from 1 to∞,we have

On the other hand,by(3.5)we have A(

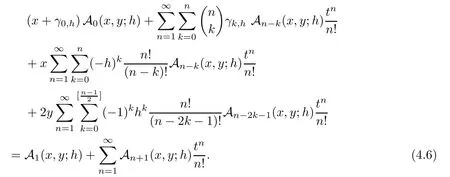
x,y

;

h

):=

α

and A(

x,y

;

h

):=

α

+

α

x

.Inserting(3.2)into(4.2)and after some series manipulations and Cauchy product,we have

γ

α

=

α

.

Hence,we can write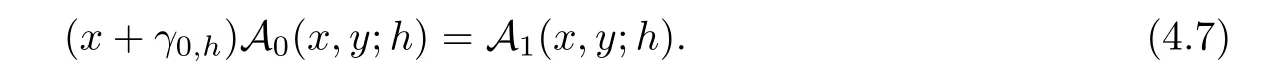

Recurrence relation satis fied by 2

D

-Appell and Appell polynomials were obtained in[3]and[21]respectively.

Theorem 4.2

Lowering operator,raising operator and difference equation satis fied by?-Gould-Hopper Appell polynomials are given by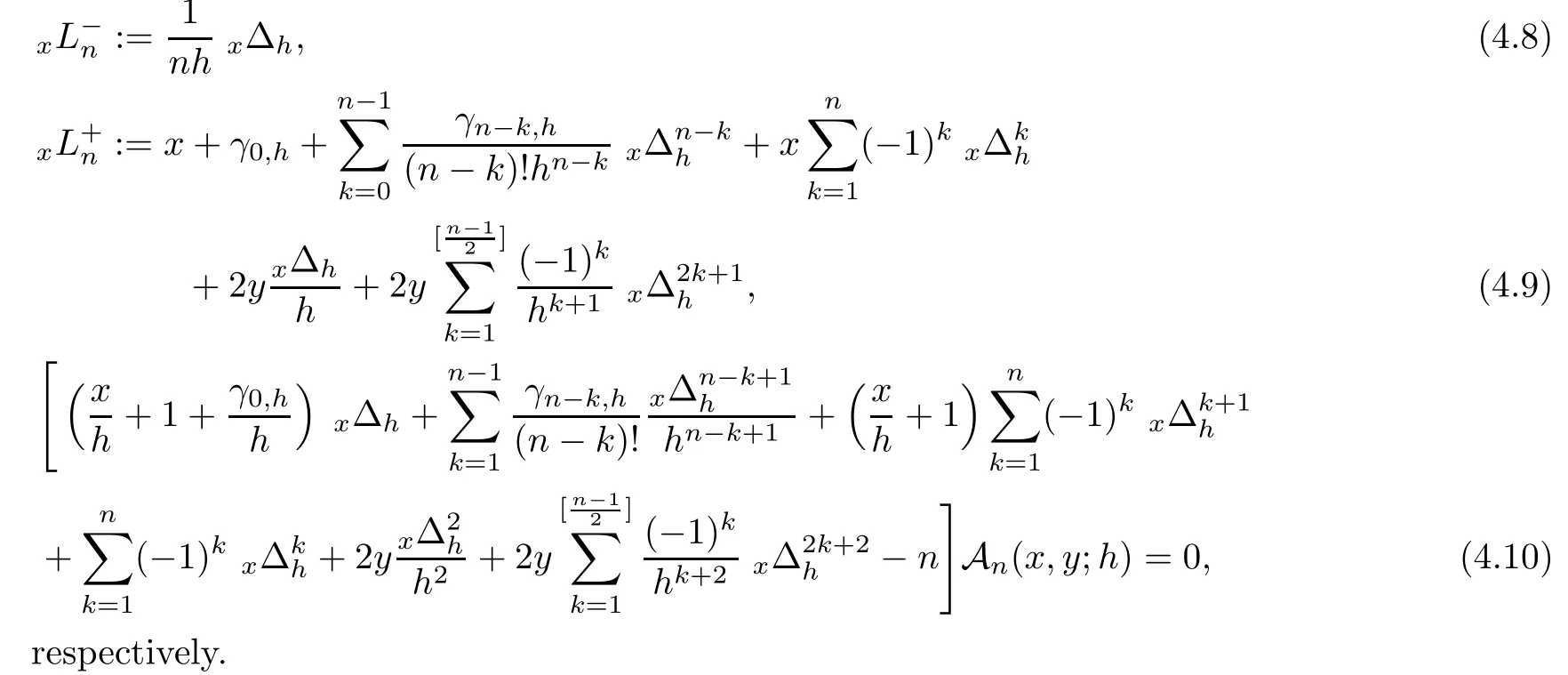

Proof

By(1.7),it can be seen that the lowering operator is given by(4.8).To obtain the difference equation satis fied by?-Gould-Hopper Appell polynomials,we need to find the raising operator.First,we write A(

x,y

;

h

),A(

x,y

;

h

)

,

A(

x,y

;

h

)and A(

x,y

;

h

)in terms of the lowering operator as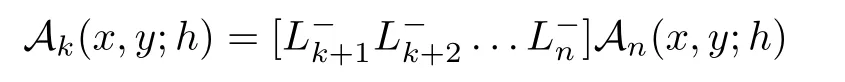

with the fact that

then dividing both sides by

h

,we get the result.Lowering operator,raising operator and differential equation satis fied by 2

D

-Appell polynomials were obtained in[3].Lowering operator,raising operator and differential equation satis fied by Appell polynomials were obtained in[21].

Theorem 4.3

Integro-lowering operator,integro-raising operator and integro-difference equation satis fied by?-Gould-Hopper Appell polynomials are given by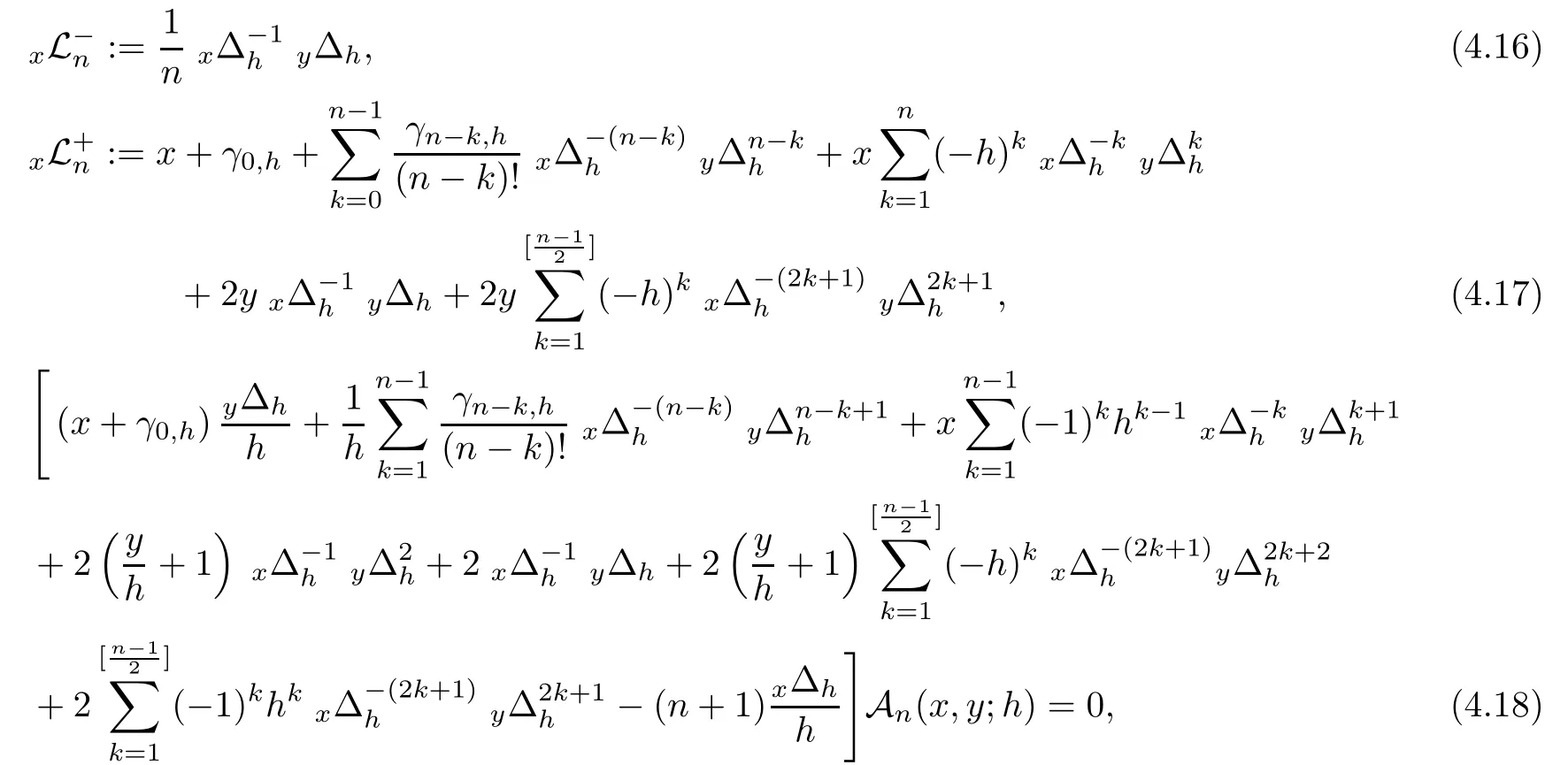

respectively.

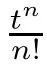
We introduce the inverse forward difference operators by

Inserting the terms

into the recurrence relation satis fied by?-Gould-Hopper Appell polynomials and taking into brackets of A(

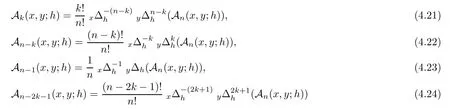
x,y

;

h

),we get the integro-raising operator(4.17).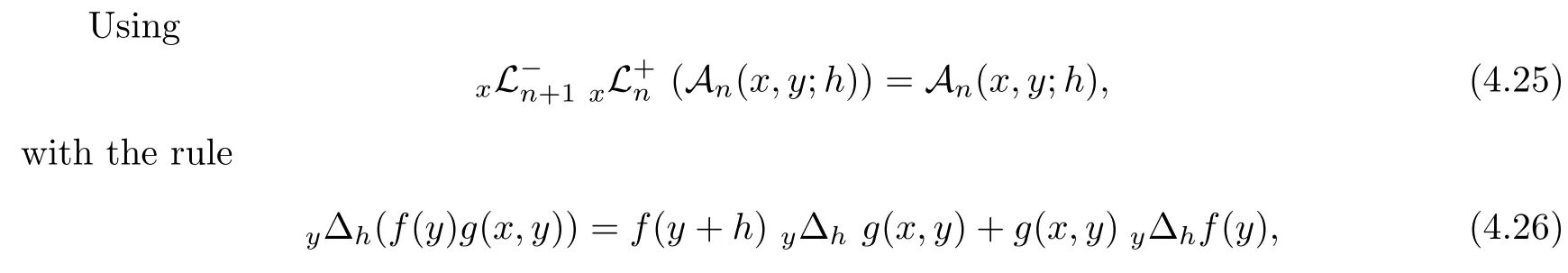

then dividing both sides of the equation by

h

,we get the integro-difference equation satis fied by?-Gould-Hopper Appell polynomials.

Theorem 4.4

Partial difference equation satis fied by?-Gould-Hopper Appell polynomials is given by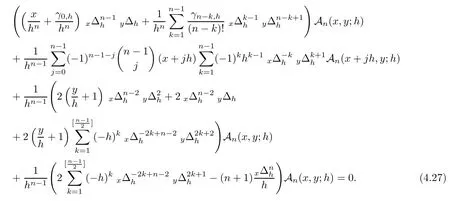

Proof

Applying forward difference operator with respect to

x

,(

n

?1)-times in the integrodifference equation satis fied by?-Gould-Hopper Appell polynomials and using the fact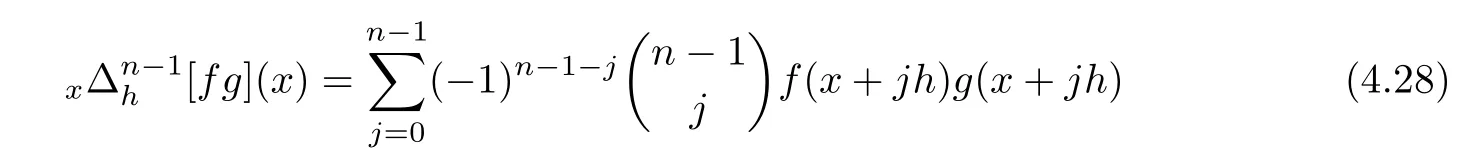

introduced in[15]and then dividing both sides of the equation by

h

,we get the partial difference equation satis fied by?-Gould-Hopper Appell polynomials.

Corollary 4.5

Recurrence relation,lowering and raising operators,difference equation and integro-difference equation satis fied by?-Gould-Hopper Appell polynomials reduce to recurrence relation,lowering and raising operators,difference equation satis fied by?-Appell polynomials in the case

y

=0;?-Appell polynomials in the case

y

=0 and

h

=1;recurrence relation,lowering and raising operators,differential equation and integro-differential equation of 2

D

-Appell polynomials[3]in the case

h

→0;recurrence relation,lowering and raising operators,differential equation of Appell polynomials[21]in the case

h

→0 and

y

=0

.

In the case

h

=1,recurrence relation,lowering and raising operators,difference equation and integro-difference equation satis fied by?-Gould-Hopper Appell polynomials reduce to recurrence relation,lowering and raising operators,difference equation and integro-difference equation satis fied by 2

D

??-Appell polynomials.

5 Explicit Forms,Determinants,Recurrence Relations and Difference Equations of Special Cases of the?h-Gould-Hopper Appell Polynomials

In this Section,as a special case of our main theorems,we derive explicit forms,determinants,recurrence relations,shift operators and difference equations for degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind,degenerate Gould-Hopper Carlitz Euler polynomials,degenerate Gould-Hopper Genocchi polynomials,?-Gould-Hopper Boole polynomials and?-Gould-Hopper Bernoulli polynomials of the second kind,in Subsections respectively.

5.1 Explicit Forms,Determinants,Recurrence Relations and Difference Equations Satis fied by Degenerate Gould-Hopper Carlitz Bernoulli Polynomials of the First Kind

In this Subsection,we present the corresponding explicit forms,determinants,recurrence relations,shift operators and difference equations satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind.

Corollary 5.1

A polynomial sequence{B(

x,y

;

h

)}is a degenerate Gould-Hopper Carlitz Bernoulli polynomial sequence of the first kind if and only if it has an explicit form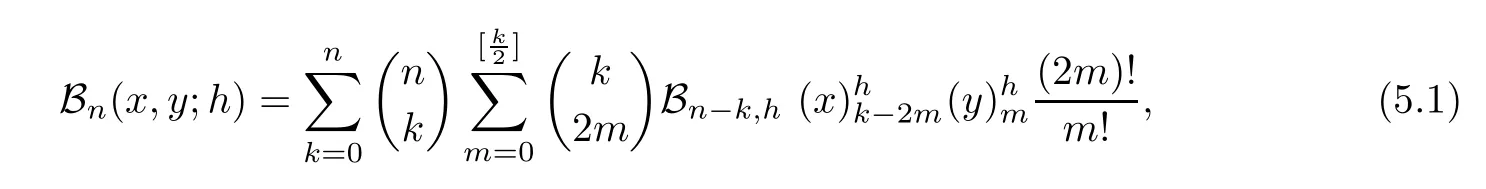

where degenerate Gould-Hopper Carlitz Bernoulli numbers B(0

,

0;

h

):=Bare given by the series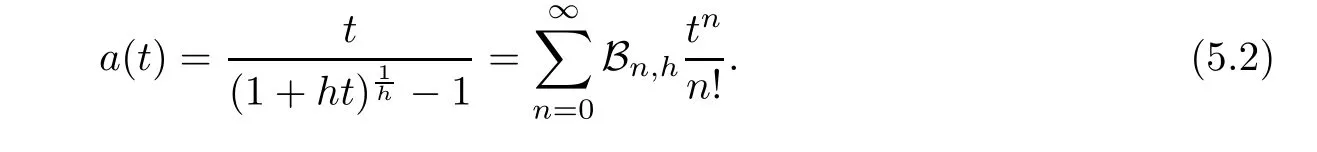

Some degenerate Gould-Hopper Carlitz Bernoulli numbers of the first kind are given by

In the case

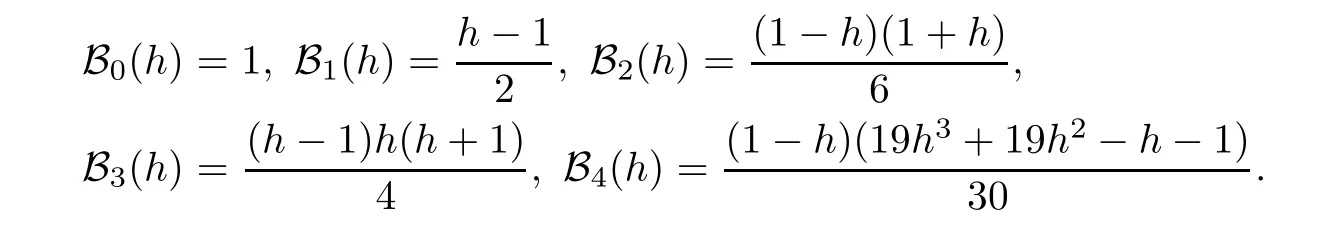
h

→0

,

degenerate Gould-Hopper Carlitz Bernoulli numbers of the first kind reduce to the Bernoulli numbers of the first kind.

Some degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind are given by

In the case

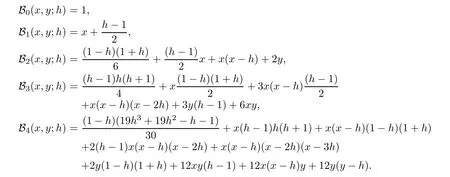
h

→0 and

y

=0

,

degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind reduce to the Bernoulli polynomials of the first kind.

Corollary 5.2

Determinant satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind is given by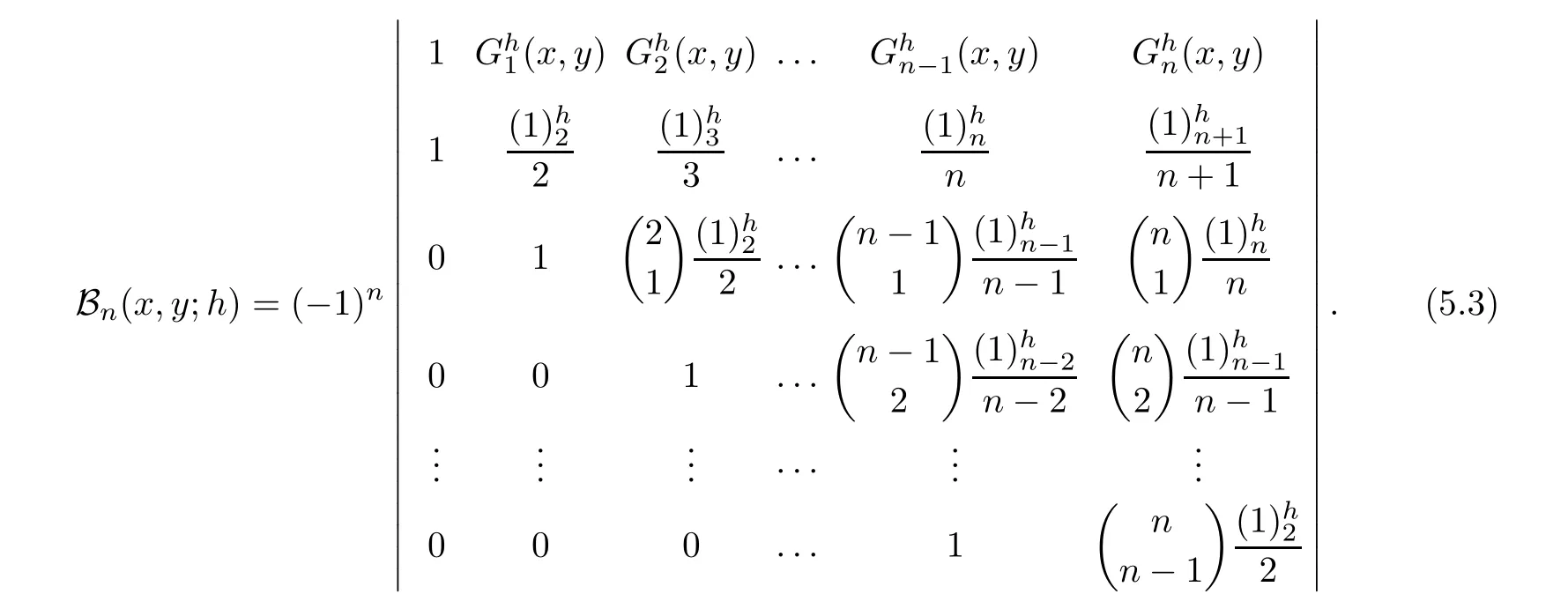

Corollary 5.3

Determinant satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind reduces to determinant satis fied by degenerate Carlitz Bernoulli polynomials in the case

y

=0;?-Bernoulli polynomials in the case

y

=0 and

h

=1;determinant of 2

D

-Bernoulli polynomials in the case

h

→0;Bernoulli polynomials[10–12,45],in the case

h

→0 and

y

=0

.

In the case

h

=1,determinant satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind reduces to determinant satis fied by 2

D

??-Bernoulli polynomials of the first kind(2D-falling factorials).

Corollary 5.4

Recurrence relation satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind is given by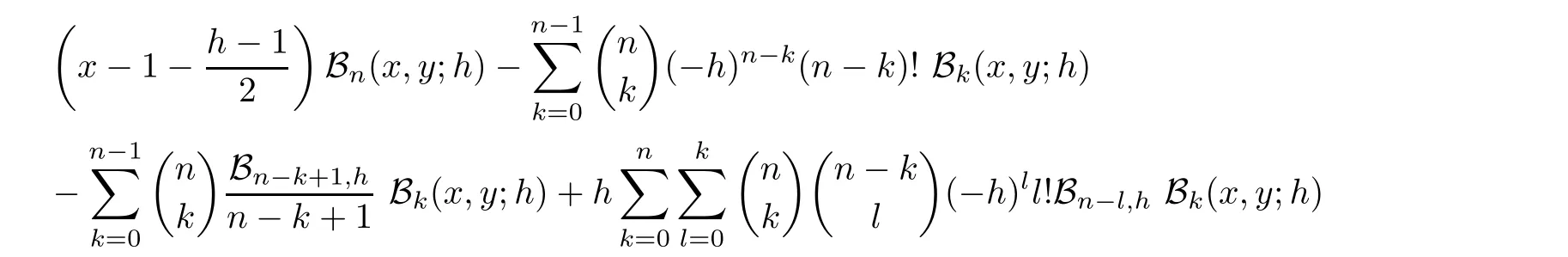

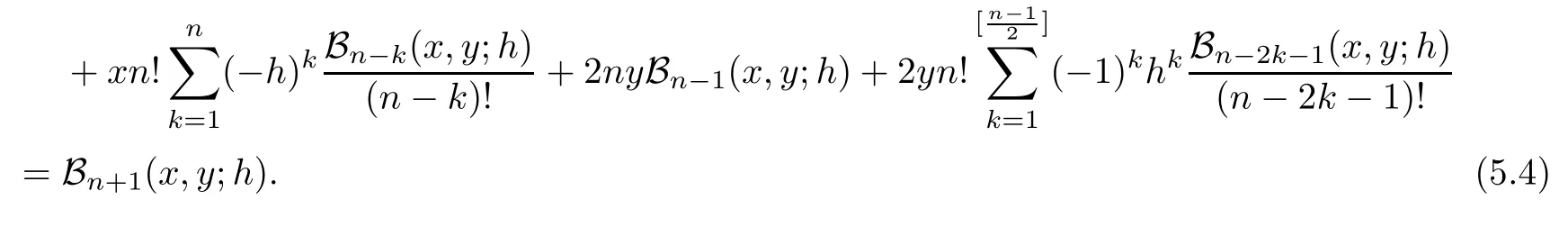
In the following Corollary,we present the lowering operator,raising operator and difference equation satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind.

Corollary 5.5

Lowering operator,raising operator and difference equation satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind are given by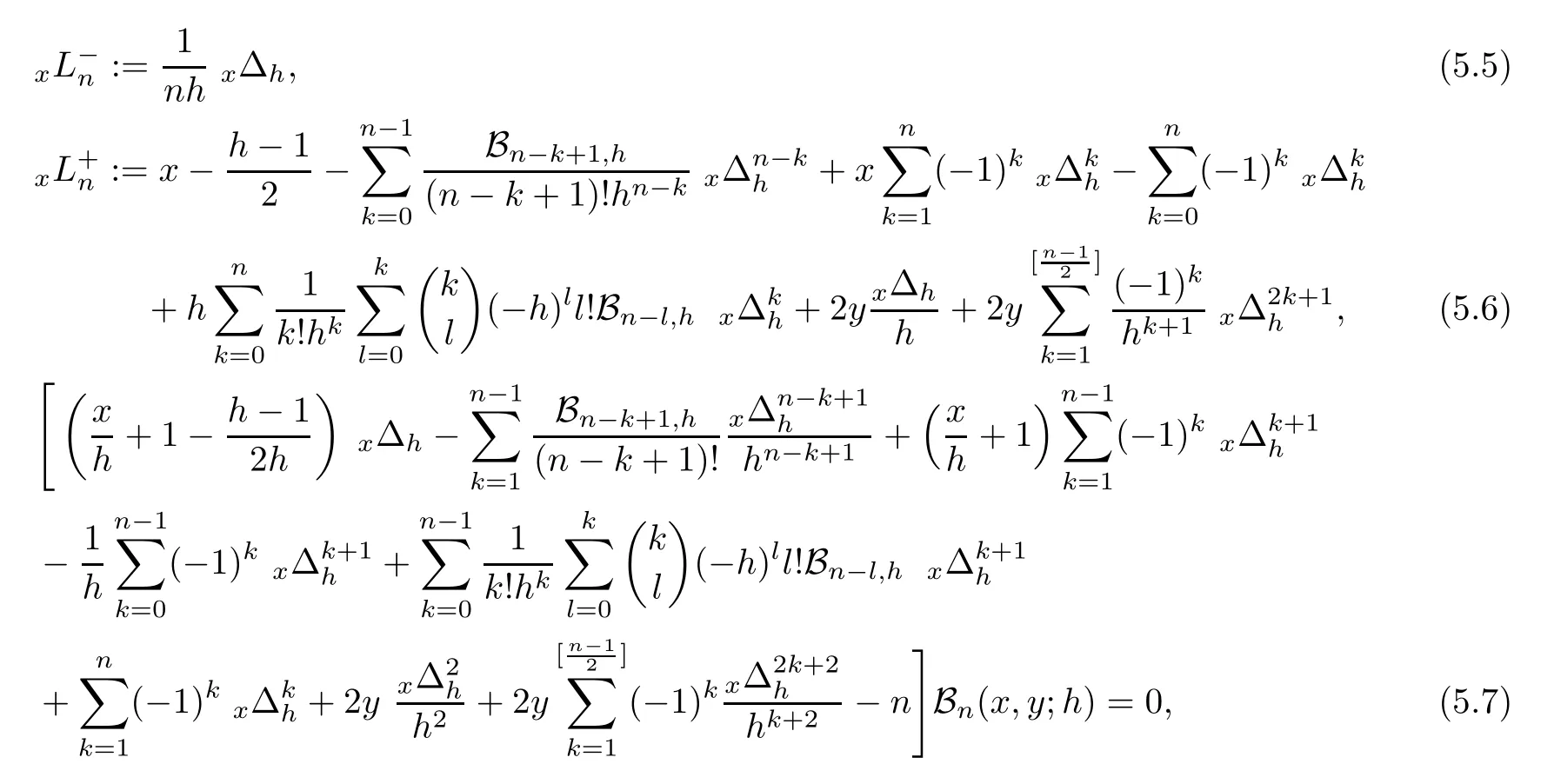

respectively.

Corollary 5.6

Recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind reduce to recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Carlitz Bernoulli polynomials in the case

y

=0;?-Bernoulli polynomials in the case

y

=0 and

h

=1;recurrence relation,lowering and raising operators,differential equation of 2

D

-Bernoulli polynomials[3,57]in the case

h

→0;Bernoulli polynomials[10,21,57]in the case

h

→0 and

y

=0

.

In the case

h

=1,recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Gould-Hopper Carlitz Bernoulli polynomials of the first kind reduce to recurrence relation,lowering and raising operators,difference equation satis fied by 2

D

???Bernoulli polynomials of the first kind(2

D

-falling factorials).

5.2 Explicit Forms,Determinants,Recurrence Relations and Difference Equations Satis fied by the Degenerate Gould-Hopper Carlitz Euler Polynomials

In this Subsection,we present the corresponding explicit forms,determinants,recurrence relations,shift operators and difference equations satis fied by the degenerate Gould-Hopper Carlitz Euler polynomials.

Corollary 5.7

A polynomial sequence{ε(

x,y

;

h

)}is a degenerate Gould-Hopper Carlitz Euler polynomial sequence if and only if it has an explicit form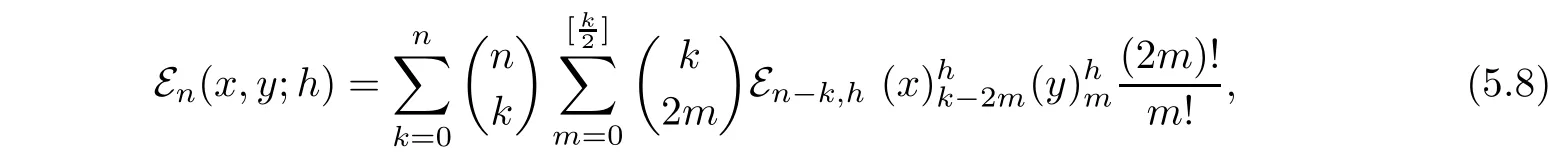

where degenerate Gould-Hopper Carlitz Euler numbers ε(0

,

0;

h

):=εare given by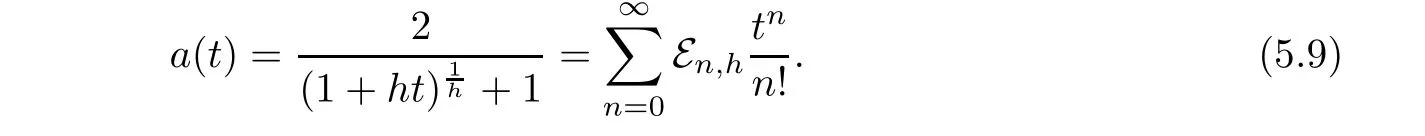

Some degenerate Gould-Hopper Carlitz Euler numbers are given by

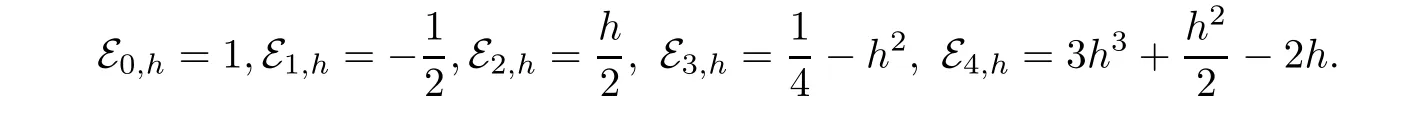
Some degenerate Gould-Hopper Carlitz Euler polynomials are given by

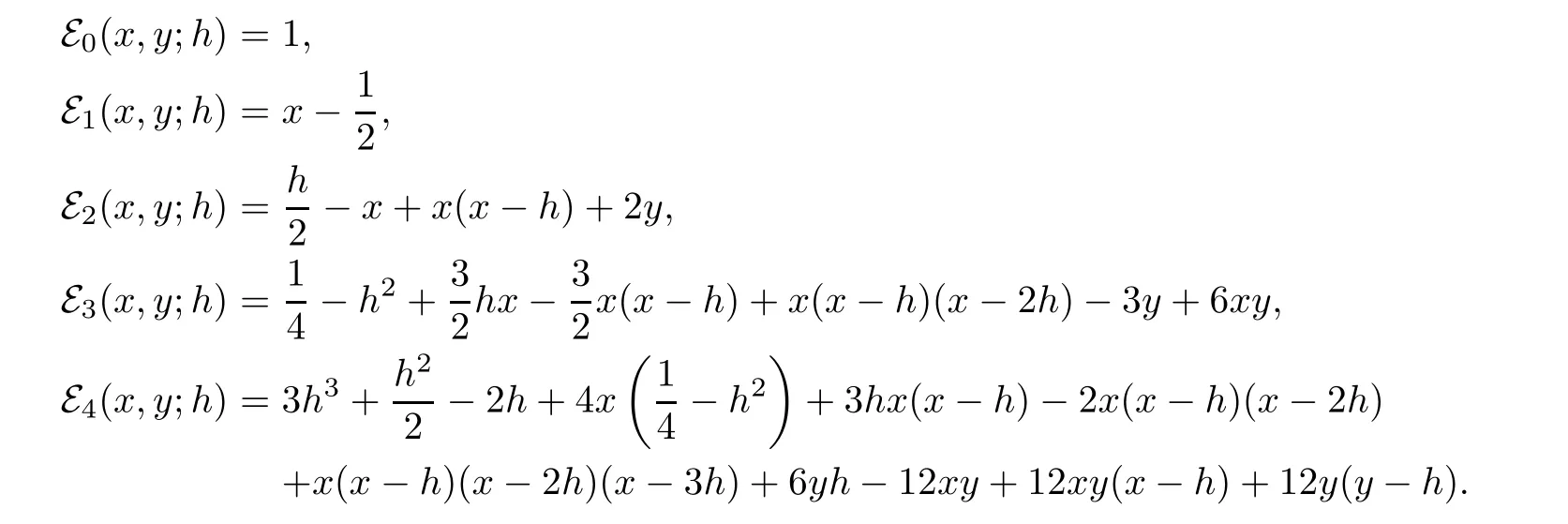
Corollary 5.8

Determinant satis fied by the degenerate Gould-Hopper Carlitz Euler polynomials is given by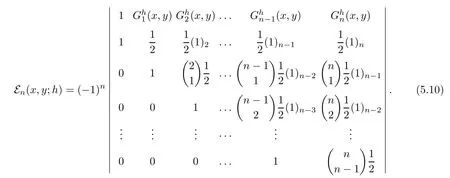

Corollary 5.9

Determinant of degenerate Gould-Hopper Carlitz Euler polynomials reduces to the determinant of Euler polynomials[46]in the case

h

→0 and

y

=0

.

In the case

h

=1,determinant of degenerate Gould-Hopper Carlitz Euler polynomials reduces to the determinant of 2

D

-Changhee polynomials.

Corollary 5.10

Recurrence relation satis fied by the degenerate Gould-Hopper Carlitz Euler polynomials is given by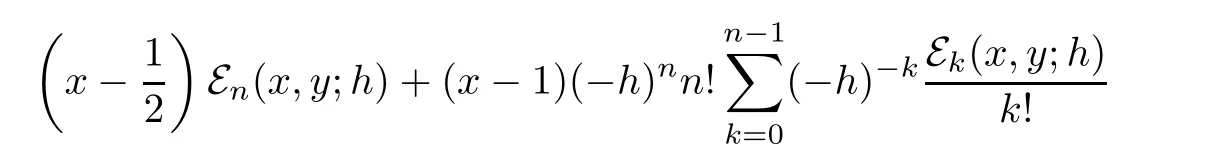

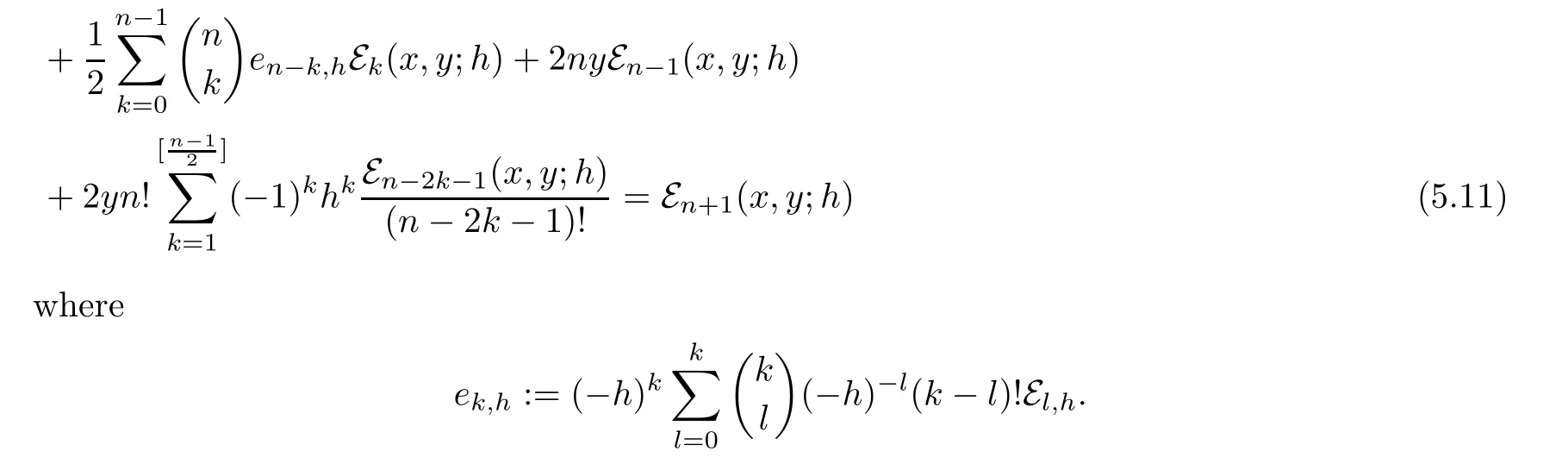
Corollary 5.11

Lowering operator,raising operator and difference equation satis fied by degenerate Gould-Hopper Carlitz Euler polynomials are given by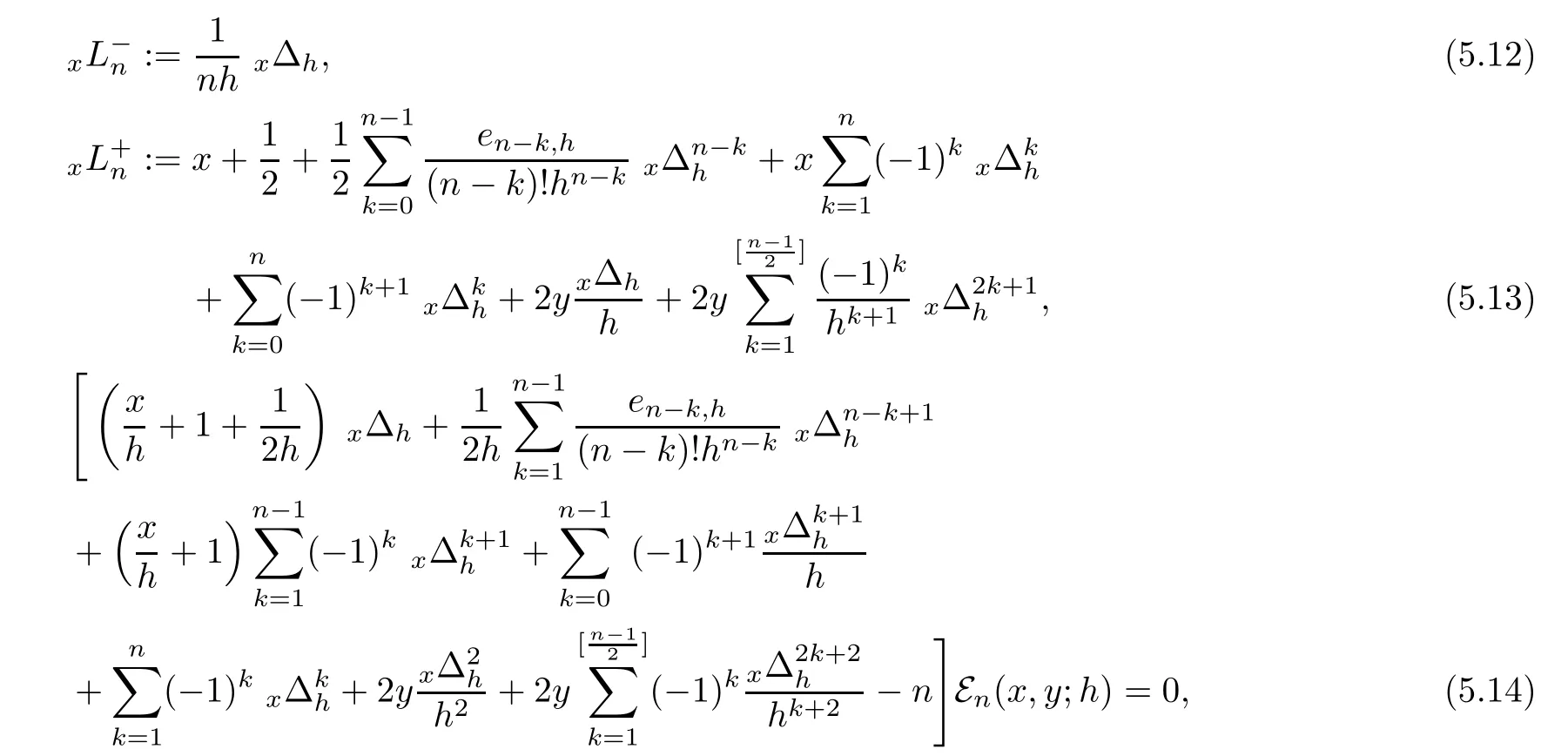

respectively.

Recurrence relation satis fied by Euler polynomials was obtained in[10,21].

Corollary 5.12

Recurrence relation,lowering operator and raising operator,difference equation satis fied by degenerate Gould-Hopper Carlitz Euler polynomials reduce to recurrence relation,lowering operator and raising operator,difference equation of degenerate Carlitz Euler polynomials in the case

y

=0

.

In the case

h

=1,recurrence relation,lowering operator and raising operator,difference equation satis fied by degenerate Gould-Hopper Carlitz Euler polynomials reduce to recurrence relation,lowering operator and raising operator,difference equation of 2

D

-Changhee polynomials.

5.3 Explicit Forms,Determinants,Recurrence Relations and Difference Equations Satis fied by the Degenerate Gould-Hopper Genocchi Polynomials

In this Subsection,we present the corresponding explicit forms,determinants,recurrence relations,shift operators and difference equations satis fied by degenerate Gould-Hopper Genocchi polynomials.

Corollary 5.13

A polynomial sequence{G(

x,y

;

h

)}is degenerate Gould-Hopper Genocchi polynomial sequence if and only if it has an explicit form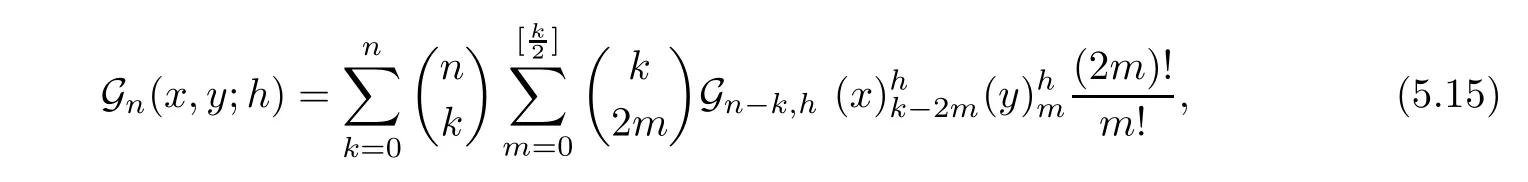

where degenerate Genocchi numbers G(0

,

0;

h

):=Gare given by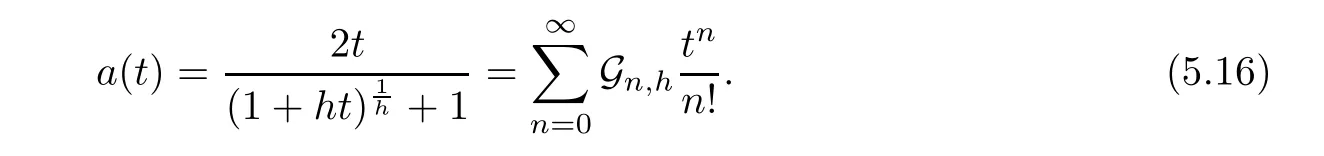

Some degenerate Gould-Hopper Genocchi numbers are given by

In the case

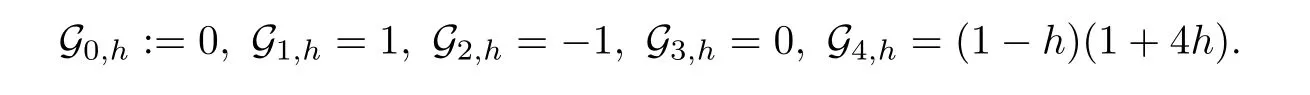
h

→0

,

degenerate Gould-Hopper Genocchi numbers reduce to the Genocchi numbers.

Some degenerate Gould-Hopper Genocchi polynomials are given by

In the case

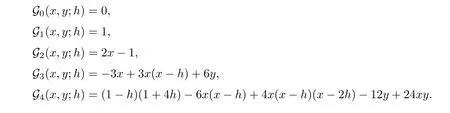
h

→0 and

y

=0

,

degenerate Gould-Hopper Genocchi polynomials reduce to the Genocchi polynomials.

Corollary 5.14

Determinant satis fied by the degenerate Gould-Hopper Genocchi polynomials is given by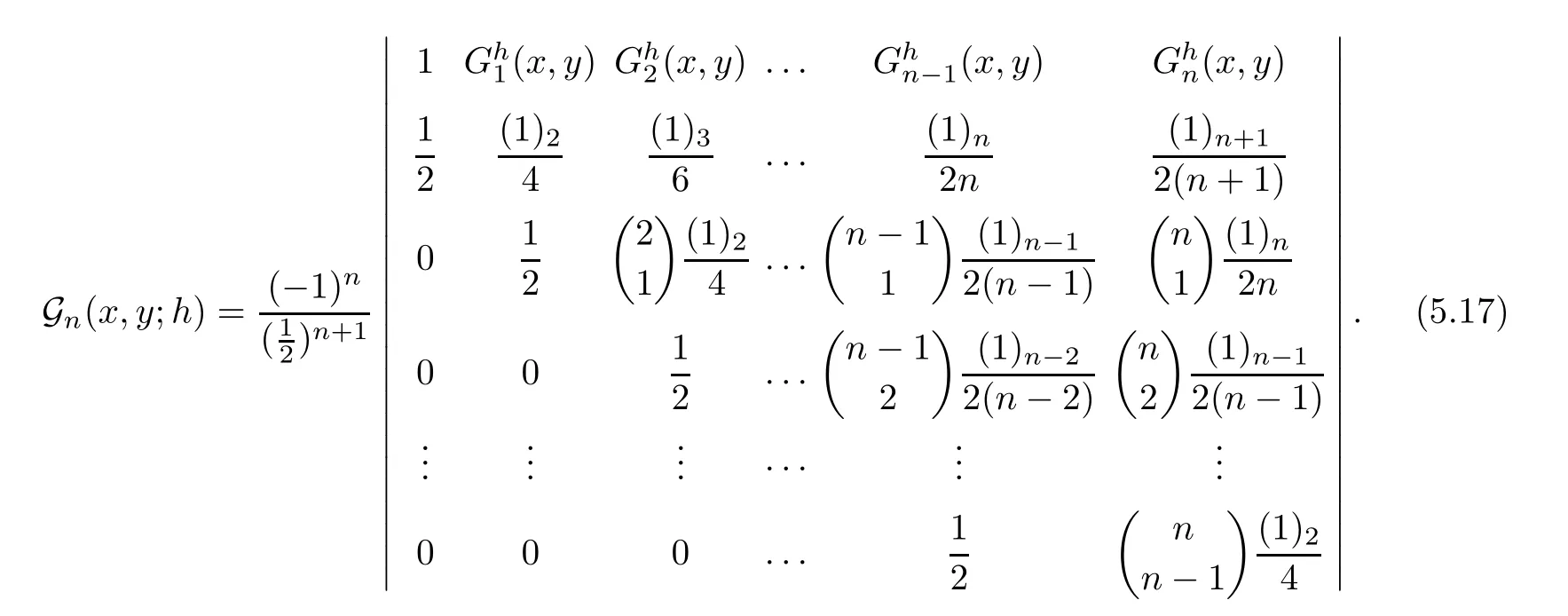

Corollary 5.15

Determinant satis fied by degenerate Gould-Hopper Genocchi polynomials reduce to determinant satis fied by degenerate Genocchi polynomials in the case

y

=0;?-Genocchi polynomials in the case

y

=0 and

h

=1;determinant of 2

D

-Genocchi polynomials in the case

h

→0;Genocchi polynomials[10,13]in the case

h

→0 and

y

=0

.

In the case

h

=1,determinant satis fied by degenerate Gould-Hopper Genocchi polynomials reduce to determinant satis fied by 2

D

??-Genocchi polynomials.

Corollary 5.16

Recurrence relation satis fied by the degenerate Gould-Hopper Genocchi polynomials is given by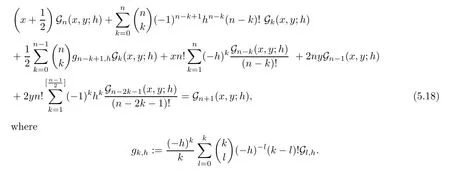

Corollary 5.17

Lowering operator,raising operator and difference equation satis fied by the degenerate Gould-Hopper Genocchi polynomials are given by

respectively.

Differential equations for classical and non classical polynomial sets were obtained in[47].For the classical case,differential equations satis fied by Bernoulli,Euler and Genocchi polynomials were obtained.

Corollary 5.18

Recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Gould-Hopper Genocchi polynomials reduce to recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Genocchi polynomials in the case

y

=0;?-Genocchi polynomials in the case

y

=0 and

h

=1;recurrence relation,lowering and raising operators,differential equation of 2

D

-Genocchi polynomials in the case

h

→0.In the case

h

=1,recurrence relation,lowering and raising operators,difference equation satis fied by degenerate Gould-Hopper Genocchi polynomials reduce to recurrence relation,lowering and raising operators,difference equation satis fied by 2

D

??-Genocchi polynomials.

5.4 Explicit Forms,Determinants,Recurrence Relations and Difference Equations Satis fied by the?h-Gould-Hopper Boole Polynomials

In this Subsection,we present the explicit forms,determinants,recurrence relations,shift operators and difference equations satis fied by?-Gould-Hopper Boole polynomials.

Corollary 5.19

A polynomial sequence{B

l

(

x,y

;

h

)}is a?-Gould-Hopper Boole polynomial sequence if and only if it has an explicit form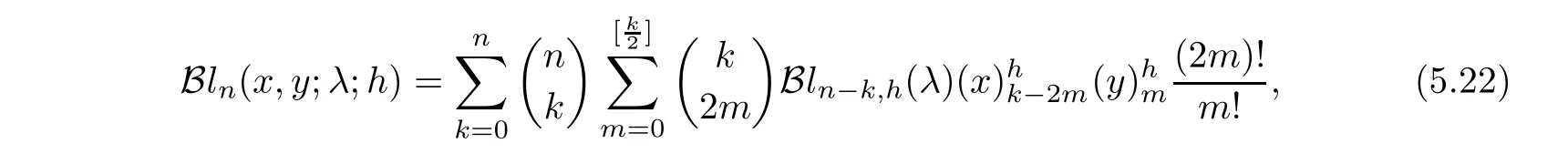

where?-Boole numbers B

l

(0

,

0;

h

):=B

l

(

λ

;

h

):=B

l

are given by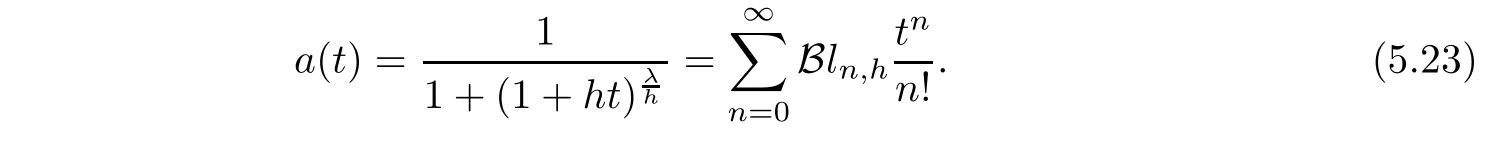

Some?-Boole numbers are given by

In the case

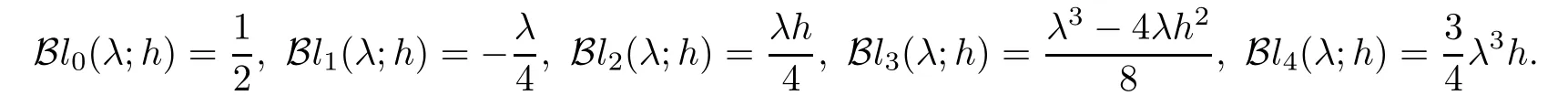
h

=1 and

y

=0

,

?-Gould-Hopper Boole numbers reduce to the Boole numbers.

Some?-Gould-Hopper Boole polynomials are given by

In the case

h

=1 and

y

=0

,

?-Gould-Hopper Boole polynomials reduce to the Boole polynomials.

Corollary 5.20

Determinant satis fied by the?-Gould-Hopper Boole polynomials is given by

Corollary 5.21

Determinant satis fied by?-Gould-Hopper Boole polynomials reduces to determinant satis fied by?-Boole polynomials in the case

y

=0;Boole polynomials in the case

y

=0 and

h

=1;determinant of 2

D

-Boole polynomials in the case

h

=1.

Corollary 5.22

Recurrence relation satis fied by?-Gould-Hopper Boole polynomials is given by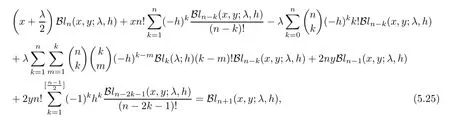

where B

l

(

λ

;

h

)are the?-Boole numbers.

Corollary 5.23

Lowering operator,raising operator and difference equation satis fied by the?-Gould-Hopper Boole polynomials are given by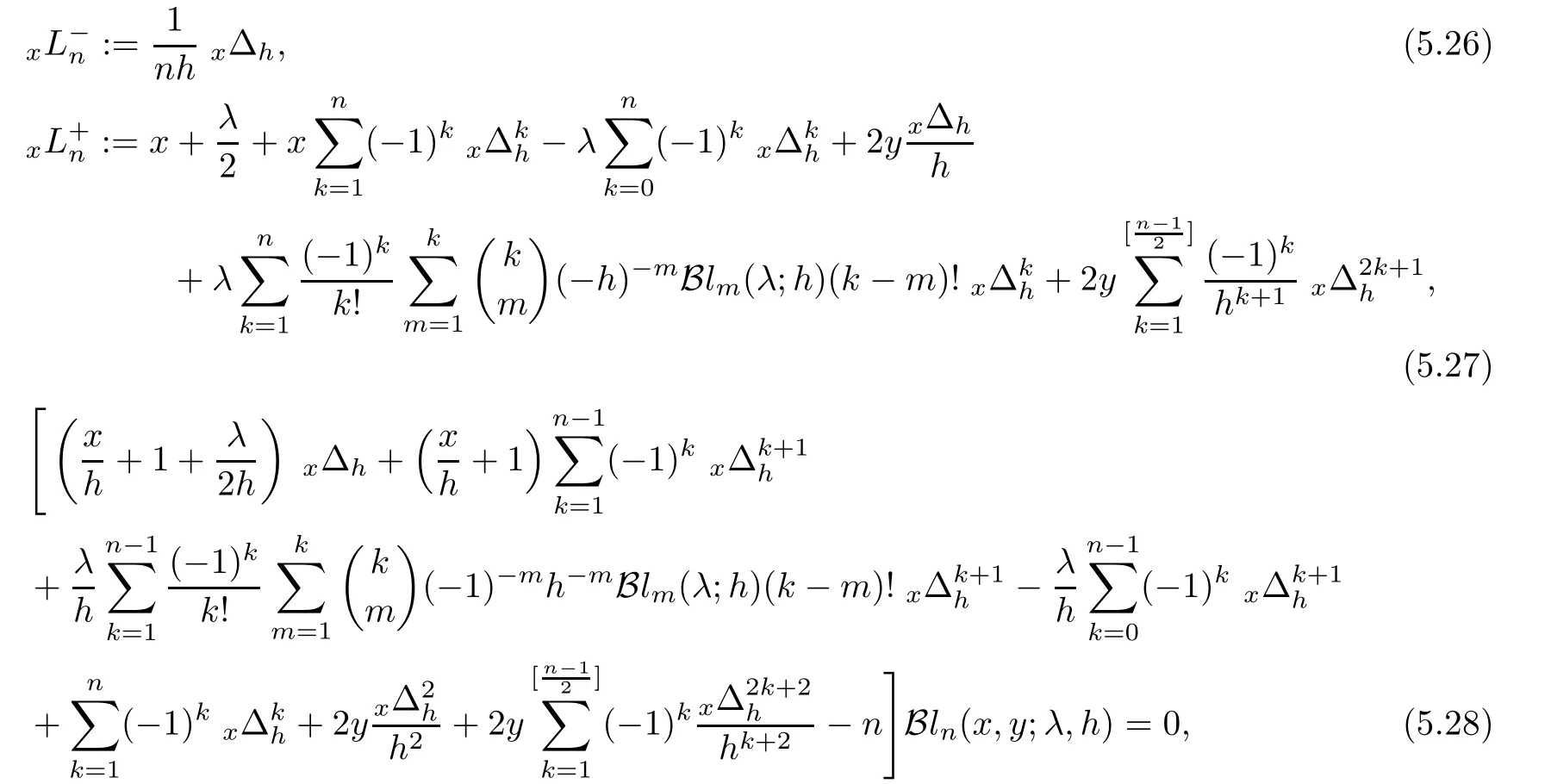

respectively.

Corollary 5.24

Recurrence relation,lowering and raising operators,difference equation satis fied by?-Gould-Hopper Boole polynomials reduce to recurrence relation,lowering and raising operators,difference equation satis fied by?-Boole polynomials in the case

y

=0;Boole polynomials in the case

y

=0 and

h

=1;recurrence relation,lowering and raising operators,differential equation of 2

D

-Boole polynomials in the case

h

=1.

5.5 Explicit Form,Determinants,Recurrence Relation and Difference Equation Satis fied by the?h-Gould-Hopper Bernoulli Polynomials of the Second Kind

In this Subsection,we present the explicit form,determinant,recurrence relation and difference equation satis fied by the?-Gould-Hopper Bernoulli polynomials of the second kind.

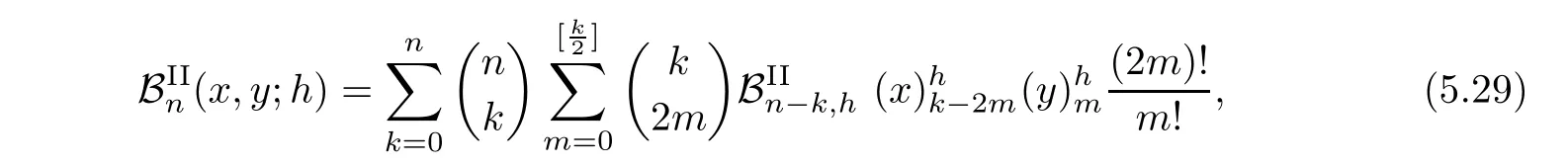
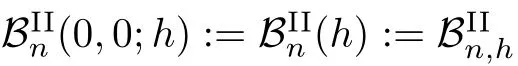
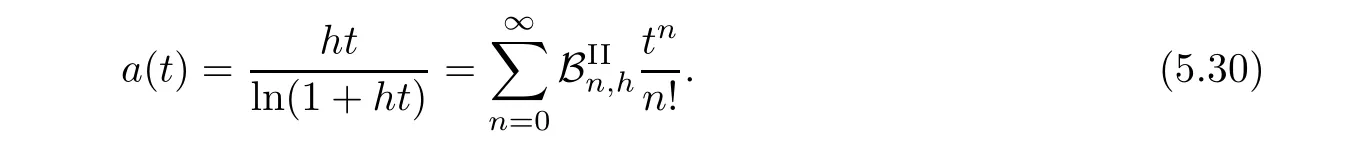
Some?-Gould-Hopper Bernoulli numbers of the second kind are given by

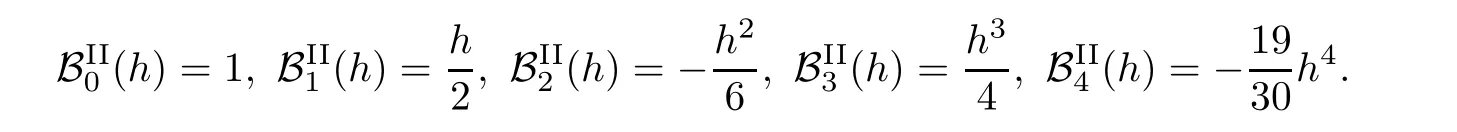
Some?-Gould-Hopper Bernoulli polynomials of the second kind are given by

In the case

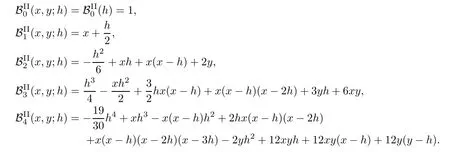
h

=1 and

y

=0,?-Gould-Hopper Bernoulli numbers of the second kind reduce to Bernoulli numbers of the second kind and in the case

h

=1 and

y

=0,?-Gould-Hopper Bernoulli polynomials of the second kind reduce to Bernoulli polynomials of the second kind.

Corollary 5.26

Determinant satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind is given by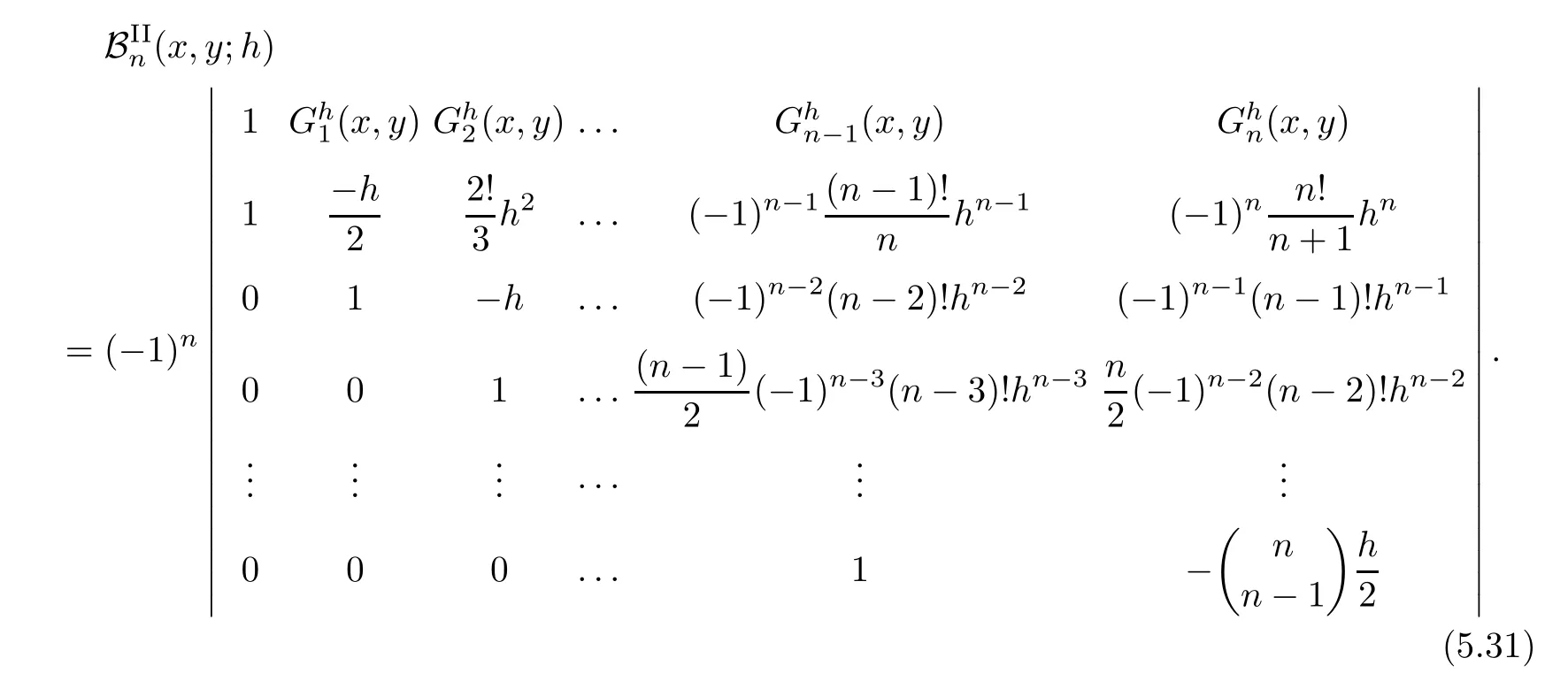

Corollary 5.27

Determinant satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind reduces to determinant satis fied by?-Bernoulli polynomials of the second kind in the case

y

=0;Bernoulli polynomials of the second kind in the case

y

=0 and

h

=1;determinant of 2

D

-Bernoulli polynomials of the second kind in the case

h

=1.In the case

h

→0,determinant satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind reduces to determinant of Gould-Hopper polynomials.

Corollary 5.28

Recurrence relation satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind is given by

Corollary 5.29

Lowering operator,raising operator and difference equation satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind are given by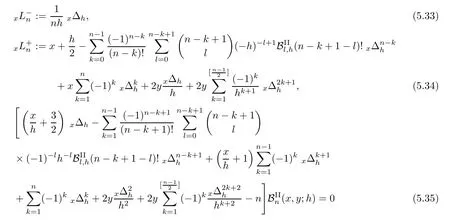

respectively.

Corollary 5.30

Recurrence relation,lowering and raising operators,difference equation satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind reduce to recurrence relation,lowering and raising operators,difference equation satis fied by?-Bernoulli polynomials of the second kind in the case

y

=0;Bernoulli polynomials of the second kind in the case

y

=0 and

h

=1;recurrence relation,lowering and raising operators,differential equation of 2

D

-Bernoulli polynomials of the second kind in the case

h

=1.In the case

h

→0,recurrence relation,lowering and raising operators,difference equation satis fied by?-Gould-Hopper Bernoulli polynomials of the second kind reduce to recurrence relation,lowering and raising operators,differential equation satis fied by Gould-Hopper polynomials.

6 Concluding Remarks

Some identities and relations involving the modi fied degenerate Hermite-based Apostol-Bernoulli and Apostol-Euler polynomials were obtained in[49].A new uni fied class of degenerate Apostol-type polynomials was introduced.By series de finition and within the context of monomiality principle,degenerate Apostol-type polynomials were investigated.Some recurrence relations and explicit representations were obtained in[27].Taking into consideration of the generating functions satis fied by the?-Gould-Hopper Appell polynomials and using the degenerate uni fied Hermite based exponential function[41,42],the generalized uni fied Hermite-based degenerate Apostol polynomials can be introduced.