A GENERALIZATION OF BOYD’S INTERPOLATION THEOREM?
Department of Mathematics and Information Technology,the Education University of Hong Kong,Hong Kong,China E-mail:vkpho@eduhk.hk
Abstract Boyd’s interpolation theorem for quasilinear operators is generalized in this paper,which gives a generalization for both the Marcinkiewicz interpolation theorem and Boyd’s interpolation theorem.By using this new interpolation theorem,we study the spherical fractional maximal functions and the fractional maximal commutators on rearrangement-invariant quasi-Banach function spaces.In particular,we obtain the mapping properties of the spherical fractional maximal functions and the fractional maximal commutators on generalized Lorentz spaces.
Key words Interpolation of operator,quasilinear operator,rearrangement-invariant function space,spherical fractional maximal function,fractional maximal commutator,generalized Lorentz space
1 Introduction
This paper extends Boyd’s interpolation theorem for quasilinear operators to rearrangement-invariant quasi-Banach function spaces.
The interpolation of operators is one of the important tools in analysis for studying the mapping properties of operators.There are a number of celebrated results on the interpolation of operators,such as the Riesz convexity theorem,the Marcinkiewicz interpolation theorem,and the Stein-Weiss interpolation theorem.Several important results in analysis can be derived from these interpolation theorems,such as the Hausdorff-Young theorem,Young’s inequality,and the boundedness of the Hardy-Littlewood maximal function.It is impossible to review the complete results and trace the whole of the development of the interpolation theory for operators in this paper,therefore,for simplicity,we refer readers to[4,5,29].
This paper aims to extend Boyd’s interpolation theorem.Roughly speaking,Boyd’s interpolation theorem assures us that for any quasilinear operatorTwhich is of strong type(p,p)and(q,q),1≤p≤q≤∞,soTis a bounded operator on a rearrangement-invariant Banach function spaceXif the Boyd indices ofXare strictly in betweenpandq.Recall that an operatorTis of strong type(p,p)ifT:Lp→Lpis bounded.
The main result of this paper gives the mapping properties of those quasilinear operators onXwhenT:Lp0→Lq0andT:Lp1→Lq1are bounded wherepi/=qi,i=0,1.Two typical examples of this type of operator are fractional integral operators and the Fourier transform.
We see that Boyd’s interpolation theorem is a generalization of the Marcinkiewicz interpolation theorem to rearrangement-invariant Banach function spaces.Do note though that the Marcinkiewicz interpolation theorem covers the casepi/=qi,i=1,2[4,Chapter 4,Theorem 4.13],while Boyd’s interpolation theorem is for the casepi=qi,i=1,2 only.This is the main motivation for us to investigate the extension of Boyd’s interpolation theorem.
For wheneverTis linear,the mapping properties forTon rearrangement-invariant quasi-Banach function spaces can be found in[16,18,20,22].A number of concrete linear operators are studied in[16,18,20,22,30],such as Fourier integral operators,oscillatory integral operators and thek-plane transform.Moreover,for the interpolation of operators on rearrangement-invariant martingale Hardy spaces,the reader is referred to[21].
In this paper,we extend the results in[16]to the quasilinear operators of joint weak type on a rearrangement-invariant quasi-Banach space.We obtain the result of this paper by studying the mapping properties of the Caldern operator.
Notice that the method given in[16]also applies to Triebel-Lizorkin spaces,Sobolev spaces[16,Sections 6-8]and Hardy spaces[17],while the result obtained in this paper only applies to rearrangement-invariant quasi-Banach spaces.
This paper is organized as follows:Section 2 gives some de finitions and preliminary results on rearrangement-invariant quasi-Banach function spaces.We review the Caldern operator,the quasilinear operator of joint weak type,and Boyd’s interpolation theorem in Section 3.The generalized Boyd’s interpolation theorem is established in Section 4.The application of the generalized Boyd’s interpolation theorem for the spherical fractional maximal functions and the fractional maximal commutators on generalized Lorentz spaces is given in Section 5.
2 Preliminaries and De finitions
Let(R,μ)be aσ-finite measure space.Let M(μ)and M0(μ)be the set ofμmeasurable functions and the set ofμ-measurable functions that are finiteμa.e.Let m be the Lebesgue measure on(0,∞).
For anyf∈M(μ),de fine
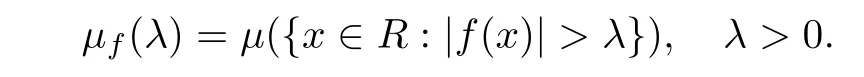
The decreasing rearrangement offis de fined as
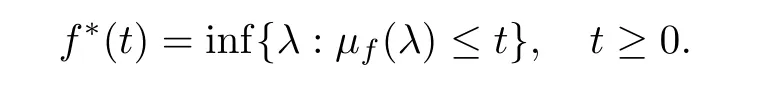
For any pair ofμmeasurable functionsf,g,these are equimeasurable if for anyλ>0,μf(λ)=μg(λ).
We recall the de finition of rearrangement-invariantquasi-Banach function spaces(r.i.q.B.f.s.)from[16,18,22].
De finition 2.1A quasi-Banach spaceX?M(m)is called a rearrangement-invariant quasi-Banach function space if there exists a unique quasi-normρX:M(m)→[0,∞]satisfying that
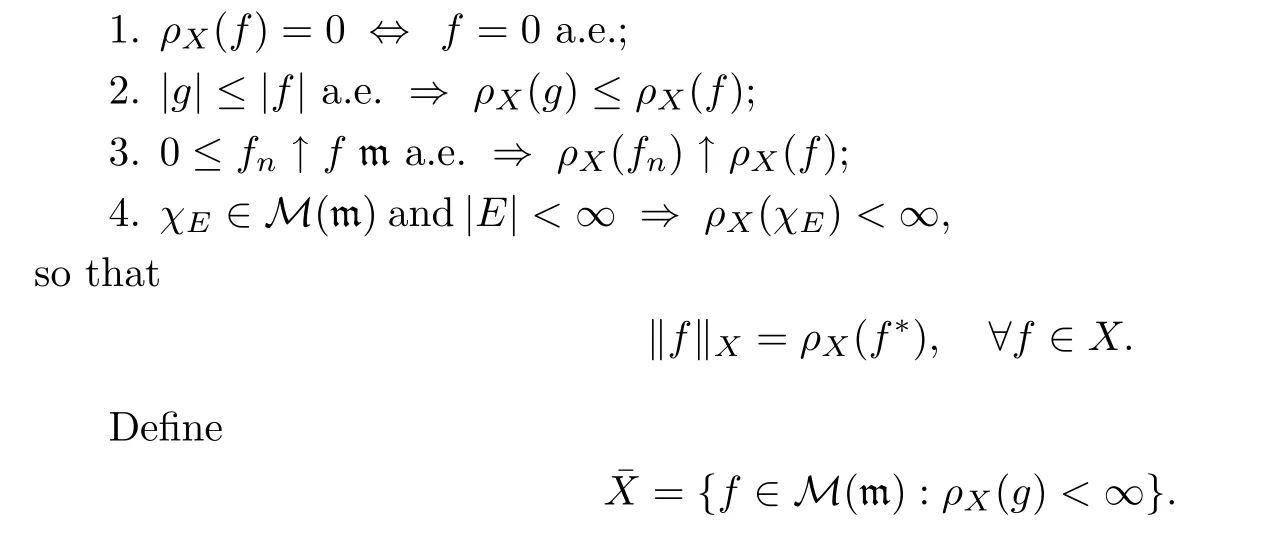
It is easy to see thatXˉ is a r.i.q.B.f.s.on[0,∞).
We callXa Banach function space[4,Chapter 1,De finitions 1.1 and 1.3]if‖·‖Xis a norm and satis fies Items(1)-(3)of De finition 2.1 with m replaced byμsuch that
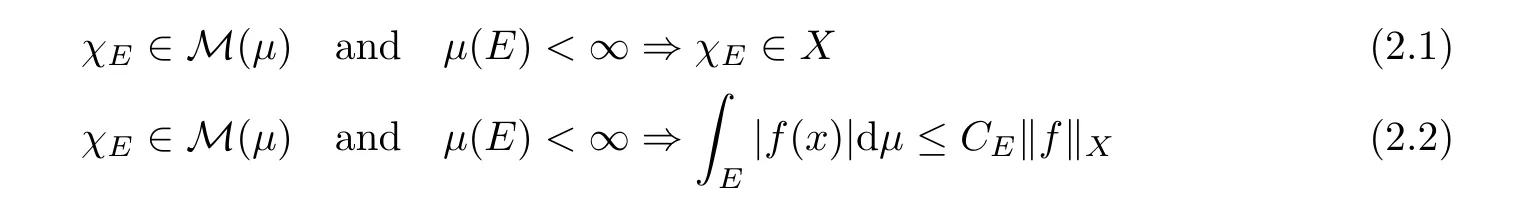
for someCE>0.
A Banach function spaceX?M(μ)is called as a rearrangement-invariant Banach function space(r.i.B.f.s.)if for any pair of equimeasurable functionsf,g∈M(μ),‖f‖X=‖g‖X.
The reader is referred to[4,Chapter 1,De finition 1.1 and Chapter 2,De finition 4.1]for the de finition of r.i.B.f.s.
WheneverXis a r.i.B.f.s,the existence ofρXis guaranteed by the Luxemburg representation theorem[4,Chapter 2,Theorem 4.10]when the underlying measure space is resonant.Recall that a totallyσ-finite measure space is said to be resonant if it is non-atomic or completely atomic with all atoms having equal measure[4,Chapter 2,Theorem 2.7].
In addition,in view of[4,p.64],ρXis uniquely de fined when the underlying measure space is non-atomic and has in finite measure.
Next,we recall the de finition of Boyd’s indices for r.i.q.B.f.s.from[6,7,25].For anys>0 andf∈M(m),de fine(Dsf)(t)=f(st).
De finition 2.2LetXbe a r.i.q.B.f.s.De fine the lower Boyd index ofX,pX,and the upper Boyd index ofX,qX,by
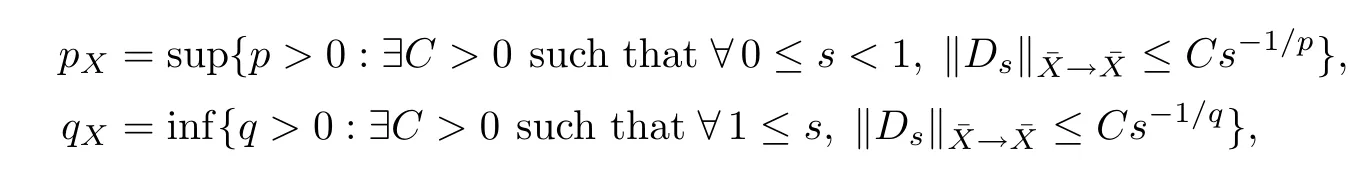
respectively.
WhenXis a r.i.B.f.s.,Boyd’s indices as de fined above are the reciprocals of the ones de fined in[4,Chapter 3,De finition 5.12].
3 Caldern Operator and Boyd’s Interpolation Theorem
We recall the de finitions of the Caldern operator,the quasilinear operators of joint weak type,and Boyd’s interpolation theorem from[4,Chapter 3,Section 5].We begin with the de finition of the Caldern operator.
De finition 3.1Let 0 Letmbe the slope ofσ.For any Lebesgue measurable functionfon(0,∞)andt>0,de fine We callSσthe Caldern operator associated withσ. Next,we have the de finition for quasilinear operators. De finition 3.2Let(R0,μ0)and(R1,μ1)be totallyσ-finite measure spaces.LetTbe an operator with its domain being a linear subspace of M0(μ0),and taking values in M(μ1).We say thatTis quasilinear if there exists ak≥1 such that for allfandgin the domain ofTand all scalarλ. Whenk=1,Tis a sublinear operator.For the interpolation of sublinear operators by general interpolation methods such as the complex interpolation method,the reader is referred to[19]. The following is the de finition of quasilinear operators of joint weak type: De finition 3.3Let 0 We say thatTis of joint weak type(p0,q0;p1,q1)if there exists a constantC>0 such that The notion of joint weak type was introduced by Caldern[8].WheneverT:Lpi→Lqi,i=1,2 is bounded,Tis of joint weak type(p0,q0;p1,q1)[1].Thus,the Hardy-Littlewood maximal operator and the fractional maximal operators are examples of nonlinear operators of joint weak type.In addition,in view of[4,Chapter 4,Theorem 4.11],whenever a quasilinear operatorTis of weak type(p0,q0)and(p1,q1),thenTis of joint weak type(p0,q0;p1,q1).The reader is referred to[4,Chapter 4,De finition 4.9]for the de finition of weak type operators. We are now ready to state Boyd’s interpolation theorem from[4,Chapter 3,Theorem 5.16]. Theorem 3.1Let 1≤p≤q≤∞andXbe a r.i.B.f.s.on an in finite,non-atomic,totallyσ-finite measure space.If the Boyd indices ofXsatisfy then every quasilinear operatorTof joint weak type(p,p;q,q)is bounded onX. IfTis of strong type(p,p)and(q,q)with 1≤p In the next section,the main result of this paper extends Boyd’s interpolation to those quasilinear operators with the interpolation segments which are not subsets of the diagonalD;that is,the case where the interpolation segmentσhas a nonempty intersection withUD. Furthermore,we also extend Boyd’s interpolation theorem to r.i.q.B.f.s. In this section,we have the main result of this paper:the extension of Boyd’s interpolation theorem for quasilinear operators of joint weak type with an interpolation segmentσthat has nonempty intersection withUDon r.i.q.B.f.s. We first introduce a new functional for our main result. De finition 4.1Letα,β∈R withβ/=0 andXbe a r.i.q.B.f.s.de fined on an in finite and non-atomic measure space(R,μ).De fine‖·‖Xα,β:M(μ)→[0,∞]by We consider the example of whenXis the Lorentz space where 1≤p,q<∞.For anyα>?(p)1andβ>0,we find that where we use the substitutionu=tβat the last equality. In other words,we have that On the other hand,for a general r.i.q.B.f.s.X,the setXα,βis not necessarily a linear set.Furthermore,‖·‖Xα,βis also not necessarily a quasi-norm.For instance,the generalized Lorentz space is not necessarily a linear space[12]. There are a number of results in[16,18,22]guaranteeing that‖·‖Xα,βis a quasi-norm and thatXα,βis a r.i.q.B.f.s.Those results are based on conditions satis fied by Boyd’s indices ofX. The function spacesXα,βhave been used in[16,18]for studies of the mapping properties of the Fourier transform,the Fourier integral operators and the oscillatory integral operators on r.i.q.B.f.s.Roughly speaking,we find that when we study the Fourier type transform,we useXα,βwithβ<0[18],while for the fractional integral type operator,we useXα,βwithβ>0[22].Notice that thoseXα,βthat appeared in[16,18,22]are r.i.q.B.f.s. We now present the main result of this paper in the following theorem: Theorem 4.1Let 0 If the Boyd indices ofXsatisfy then there is a constantC>0 such that for any non-negative decreasing functiong∈Xˉ,we have IfTis a quasilinear operator of joint weak type(p0,q0;p1,q1),then we have a constantC>0 such that the estimate is valid for allf∈X. ProofIn view of(3.1),we have that By using the substitutionut=s,we find that According to the de finition ofm,we have that Therefore,the de finition ofαyields that Sincegis decreasing,we find that According to Aoki-Rolewicz theorem[23,Theorem 1.3],there is aκ>0 such that for any non-negative functions, Item 3 of De finition 2.1 assures us that for any non-negative functions,we have Asgis non-negative,by applyingρκXon both sides of(4.5),(4.6)guarantees that The de finition of the Boyd indices yieldsr0,r1satisfying thatp0 According to De finitions 2.1 and 4.1,we have Therefore,we establish estimate(4.3). We say that(4.4)is an estimate instead of the boundedness fromXtoXα,βbecauseXα,βis not necessarily a linear set and‖·‖Xα,βis not necessarily a quasi-norm. IfXis a r.i.B.f.s.andTis of strong type(p,p)and(q,q)with 1≤p Theorem 4.1 is also a generalization of the Marcinkiewicz interpolation theorem.Suppose thatT:Lpi→Lqi,i=0,1 are bounded with 1≤p0 Applying Theorem 4.1 toTwithX=Lp,r,we find that According to(4.1),(4.2)and(4.8),we have(Lp,r)α,β=Lw,rwith Consequently,Theorem 4.1 yields the boundedness ofT:Lp,r→Lq.,r,which recovers the result guaranteed by the Marcinkiewicz interpolation theorem. Therefore,Theorem 4.1 is a generalization of the Marcinkiewicz interpolation theorem to r.i.q.B.f.s.,and a generalization of Boyd’s interpolation theorem. We apply Theorem 4.1 to study the mapping properties of the spherical fractional maximal functions.Letθ≥0.For any locally integrable functionf,de fine where Hn?1is the(n?1)-dimensional Hausdorff measure.Obviously,Sθis a quasilinear operator withk=1. We have the following boundedness result for Sθon Lebesgue spaces: Theorem 4.2Letn≥2.Ifp,q,θsatisfy then we have a constantC>0 such that,for anyf∈Lp, For the proof of the above theorem,see[14,27,28].Theorem 4.2 ensures that Sθis of joint weak type(p0,q0;p1,q1)when(p0,q0)and(p1,q1)satisfy the conditions in Theorem 4.2. The following result presents the mapping properties of the spherical fractional maximal functions on r.i.q.B.f.s: ProofAccording to the conditions satis fied bypXandqX,there existp0andp1satisfying(4.9)-(4.10)and Theorem 4.2 guarantees that Sθ:Lpi→Lqi,i=0,1 are bounded where Consequently,Sθis a quasilinear operator of joint weak type(p0,q0;p1,q1)[4,Chapter 4,Theorem 4.11]. In view of(4.11),we find thatm=1 andα=?.Therefore,Theorem 4.1 yields a constantC>0 such that We have another application of Theorem 4.1 on the fractional maximal commutator.Let 0<θ where the supremum is taken over all ballsBcontainingx. Let 0<γ<1.the Lipschitz spaceΛ˙γconsists of all Lebesgue measurable functionsfsatisfying for someC>0. In view of[15,Corollary 4.7],we have the following result: What follows are the mapping properties for the fractional maximal commutator on r.i.q.B.f.s. Theorem 4.5Let 0<γ<1,0≤θ andb∈,then there exists a constantC>0 such that The proof of the above result is similar to the proof of Theorem 4.3,therefore,for brevity,we skip it and leave it to the reader. In this section,we apply our main result to the generalized Lorentz spaces.We begin with the de finition of the generalized Lorentz spaces[2,9,10,24,26]. De finition 5.1Let 0 The generalized Lorentz space was introduced by Lorentz[24].Moreover,whenp≥1,Lorentz showed thatis a norm if and only ifwis non-increasing.For the conditions for whichis equivalent to a Banach space,the reader is referred to[2,9,26]. satis fies the△2condition for someC>1. Therefore,whenever the fundamental functionWis finite a.e.and satis fies the△2condition,is a r.i.q.B.f.s. We are going to present a formula for the Boyd’s indices of[1]. When there exists0,s∞,p0,p1>0 andC0,C∞>0 such that (5.1)assures us thatp0 Taking into account of(5.2)and(5.3),the following interpolation theorem for generalized Lorentz spaces follows from Theorem 4.2: IfTis a quasilinear operator of joint weak type(p0,q0;p1,q1),then we have a constantC>0 such that the estimate is valid for allf∈. SinceWis increasing and satis fies(5.2)–(5.3),Wsatis fies the△2condition.Therefore,is a r.i.q.B.f.s. For anyα∈R,β∈R{0}and non-negative Lebesgue measurable functionf,there is a constantC>0 such that where we use the substitutiont=uβ1on the above equality. Therefore,for anyα∈R,β∈R{0},we have is finite a.e.and satis fies the△2condition.WheneverVsatis fies the above conditions,Theorem 5.1 guarantees the boundedness ofT:→. Wheneverθand the Boyd’s indices ofsatisfy the conditions in Theorem 4.3,we obtain the boundedness of the spherical fractional maximal functions on the generalized Lorentz space.There exists a constantC>0 such that,for anyf∈, wherev(t)=t?θp/nw(t). Similarly,we also have the boundedness of the fractional maximal commutators.Suppose that 0≤θ wherev(t)=t?(θ+γ)p/nw(t). Notice that according to[16,Proposition 3.1],is a r.i.q.B.f.s. In this paper,we have considered the spherical fractional maximal functions and the fractional maximal commutators as examples for the boundedness of operators on.We can also obtain the boundedness of the Fourier integral operators,the oscillatory integral operators,thek-plane transforms,the Fourier transform,and the Hankel transform on,but for brevity,we skip the details and refer the reader to[16,18,22].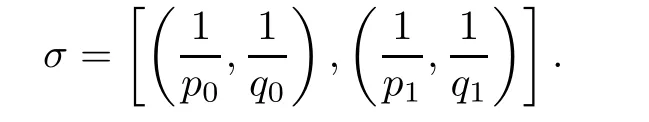
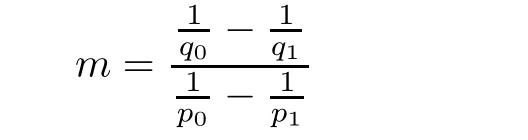
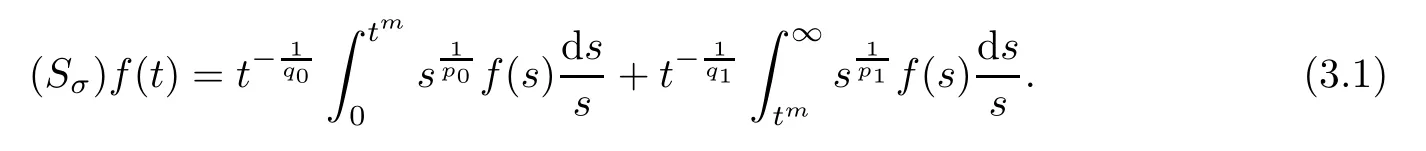
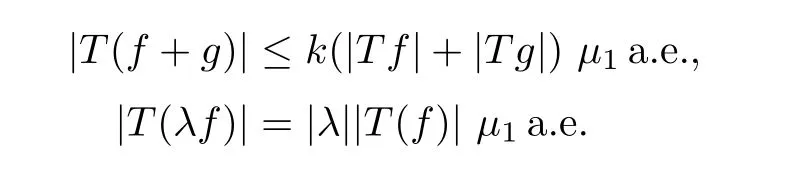
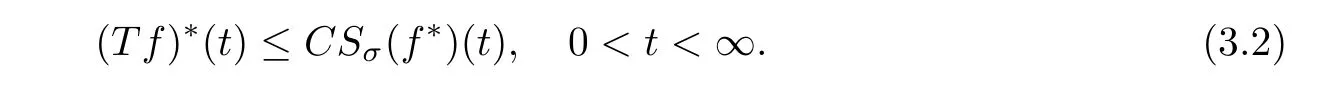
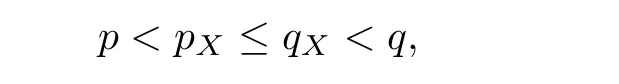
4 Generalized Boyd’s Interpolation Theorem
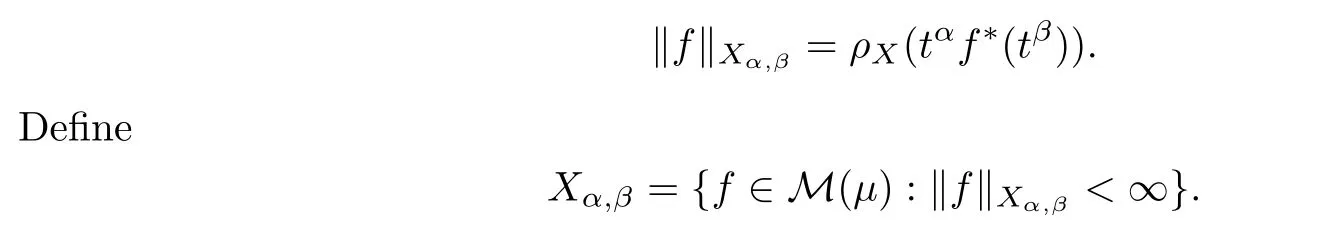
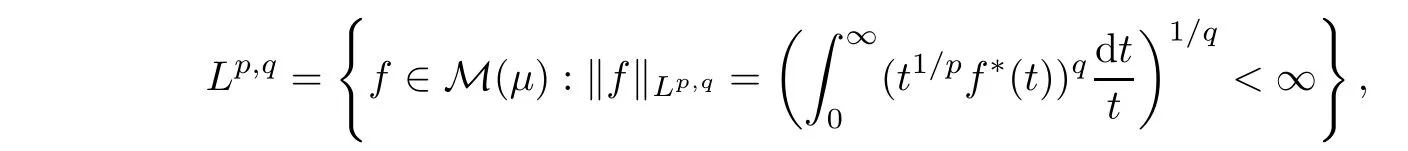
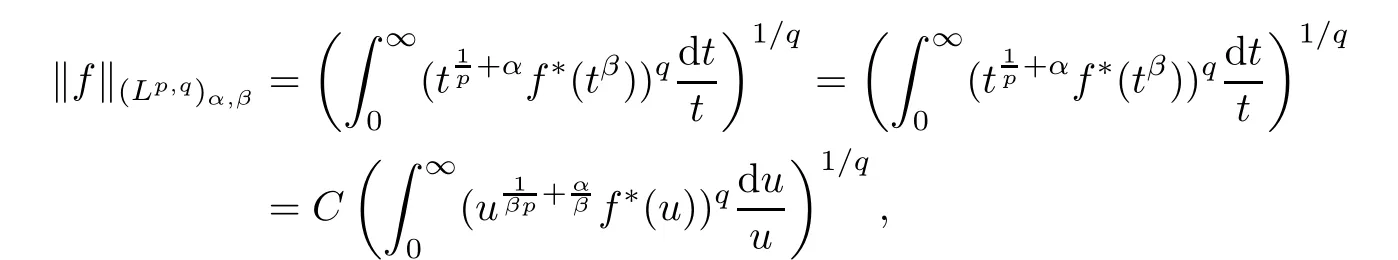
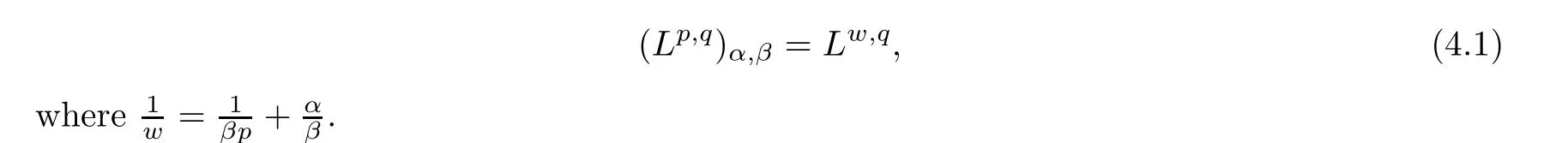
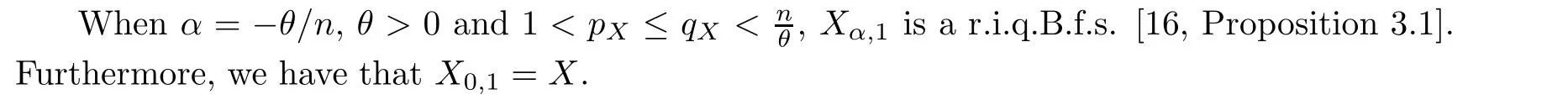
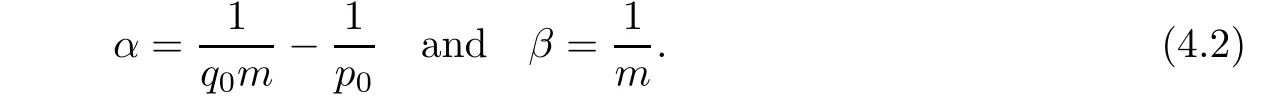
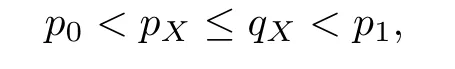


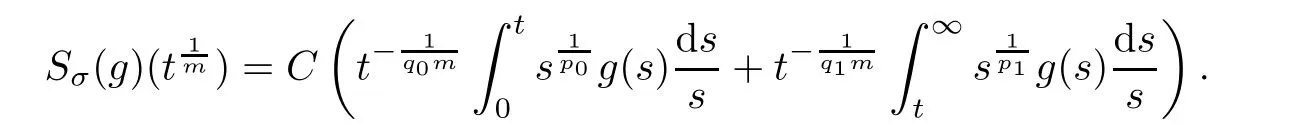
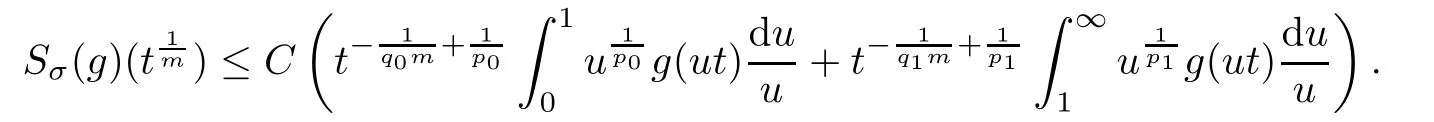
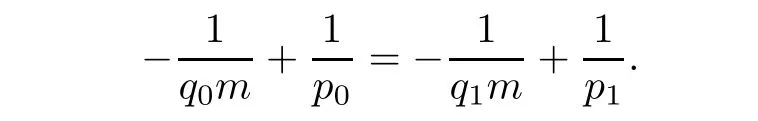
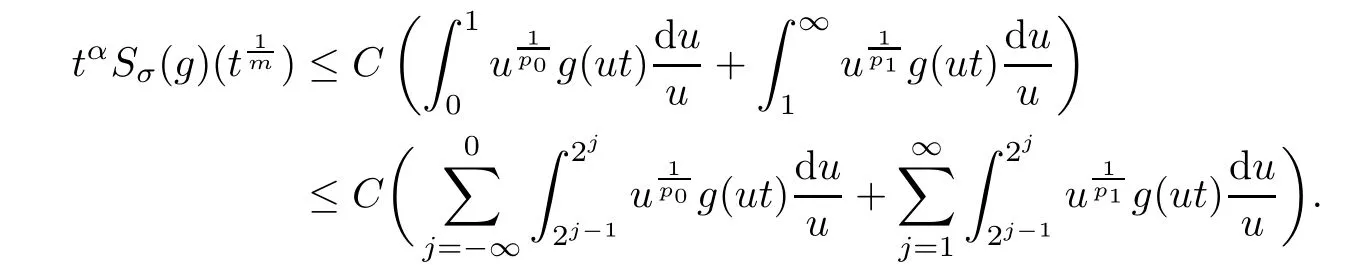
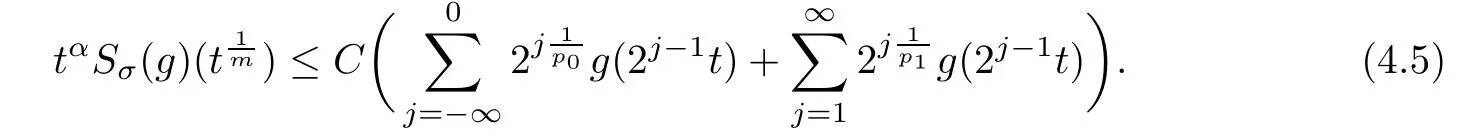
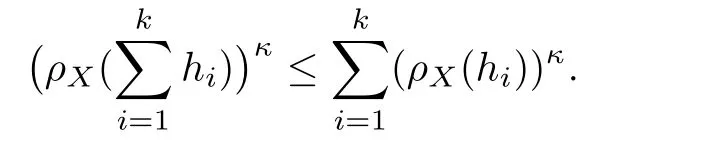
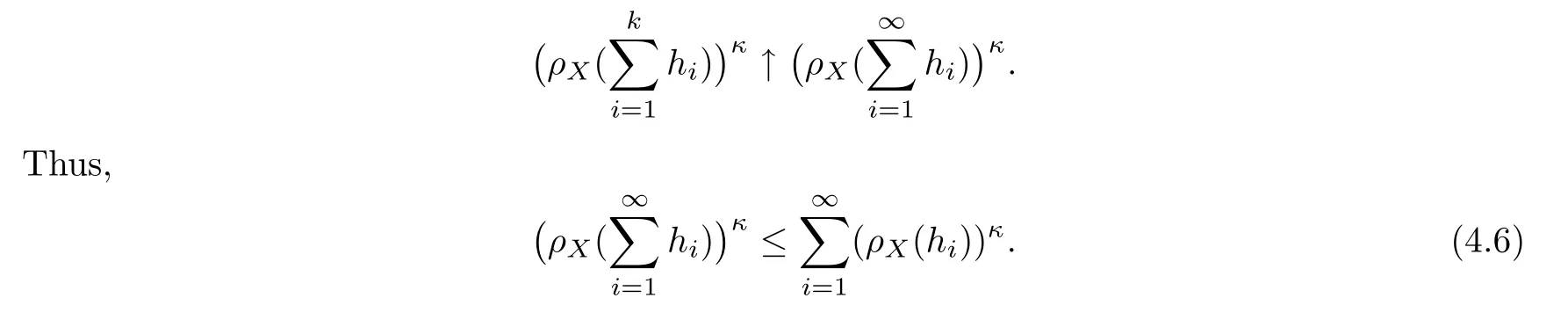
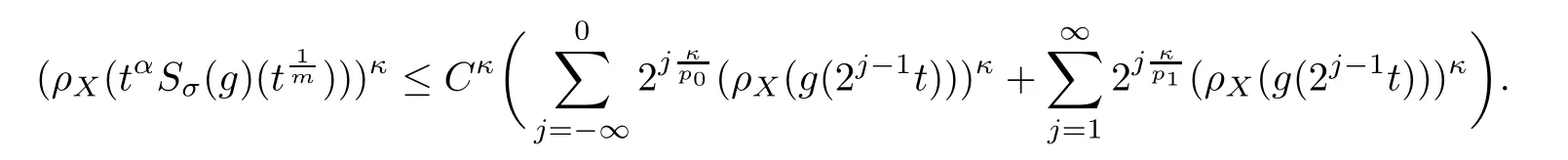
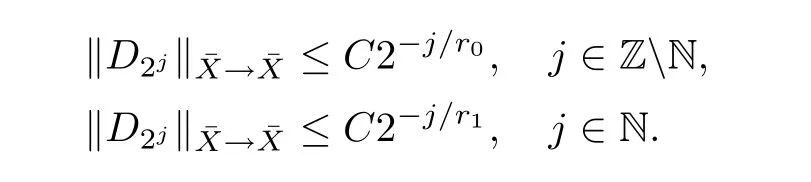
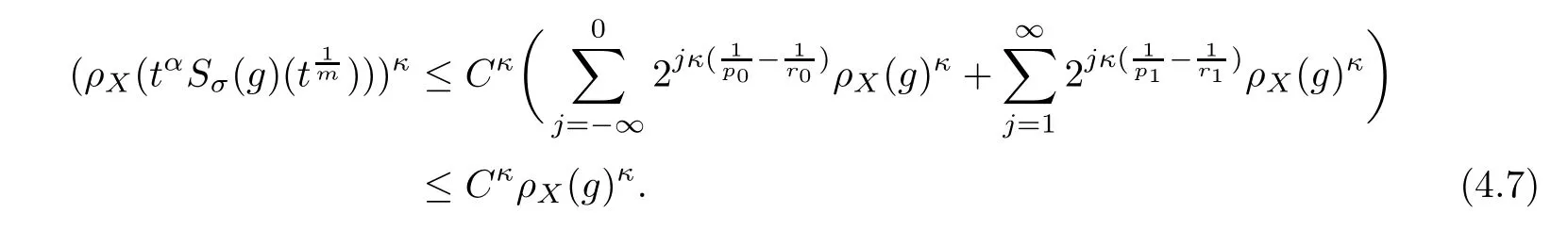
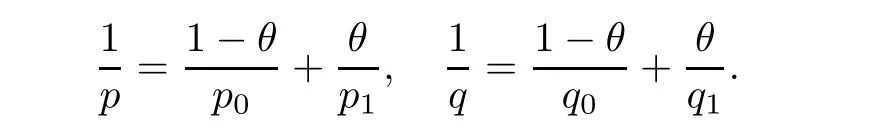
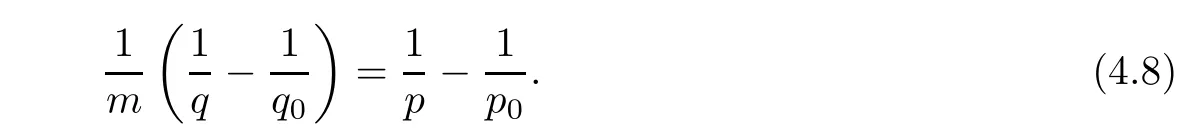
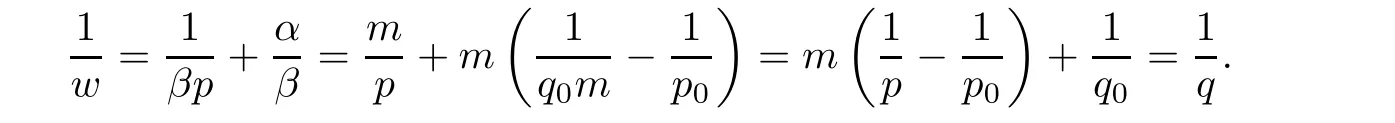
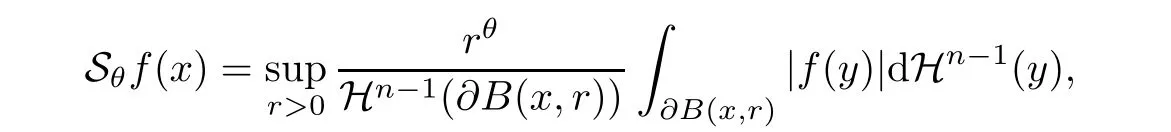

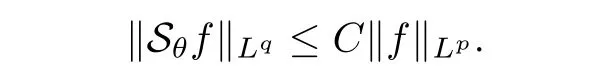
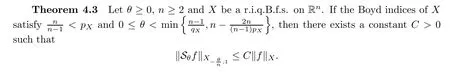
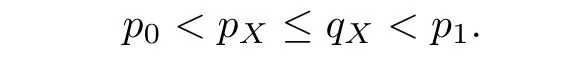
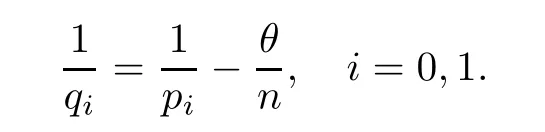
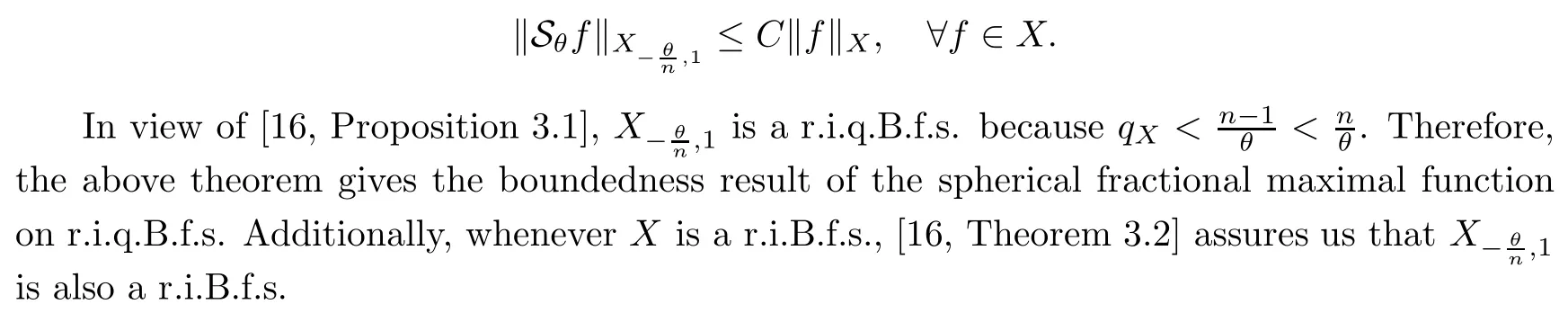
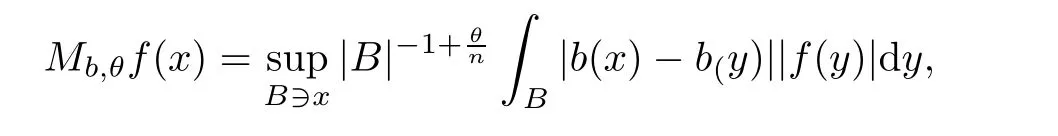
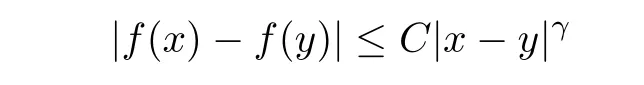
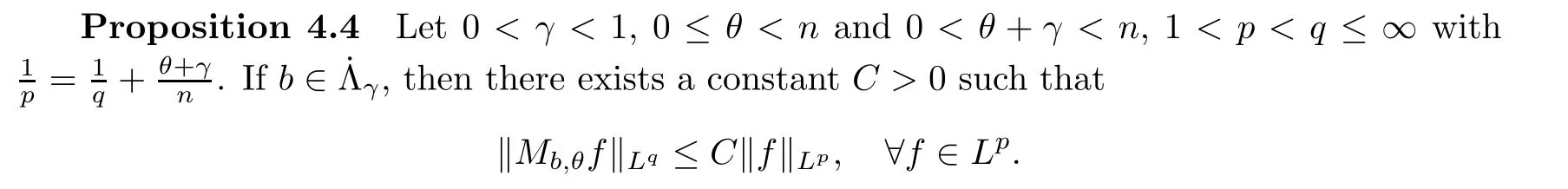

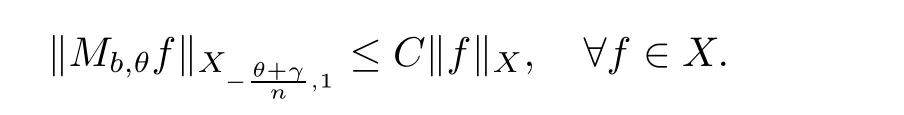
5 Generalized Lorentz Spaces
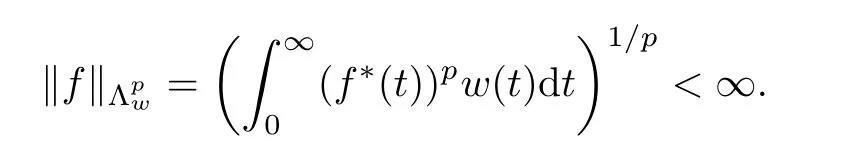
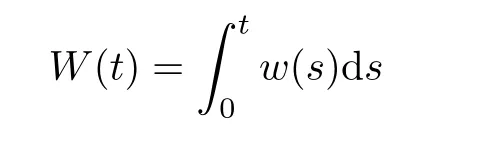
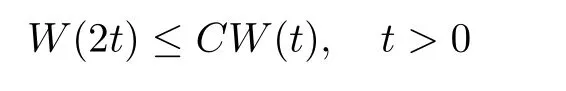
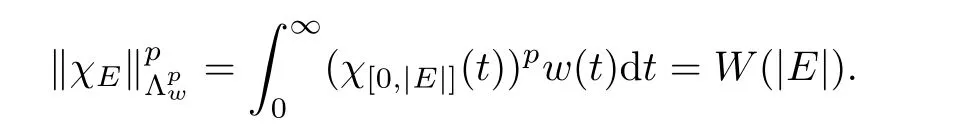

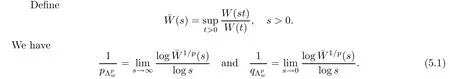
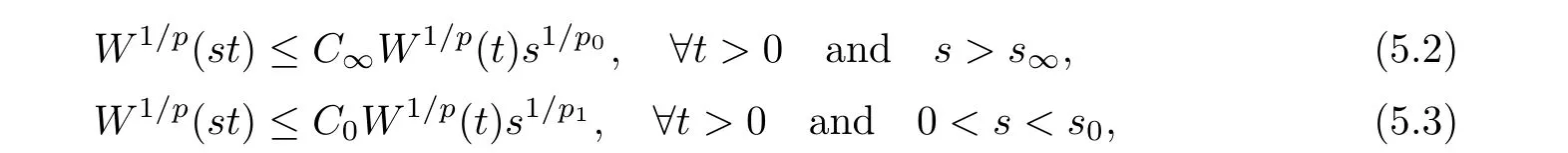
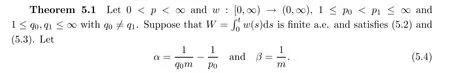
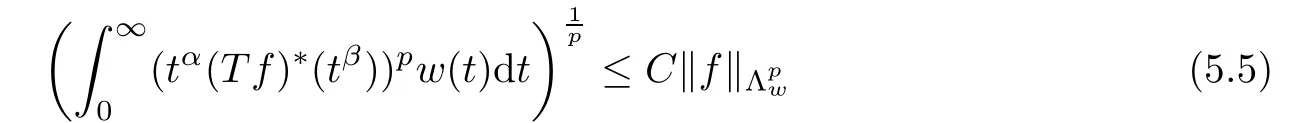
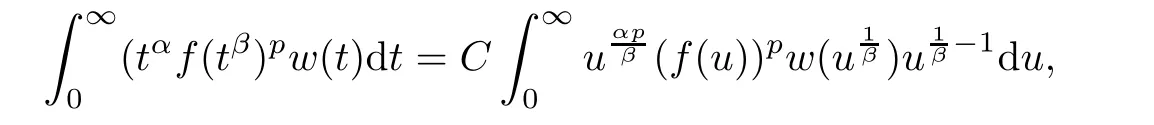
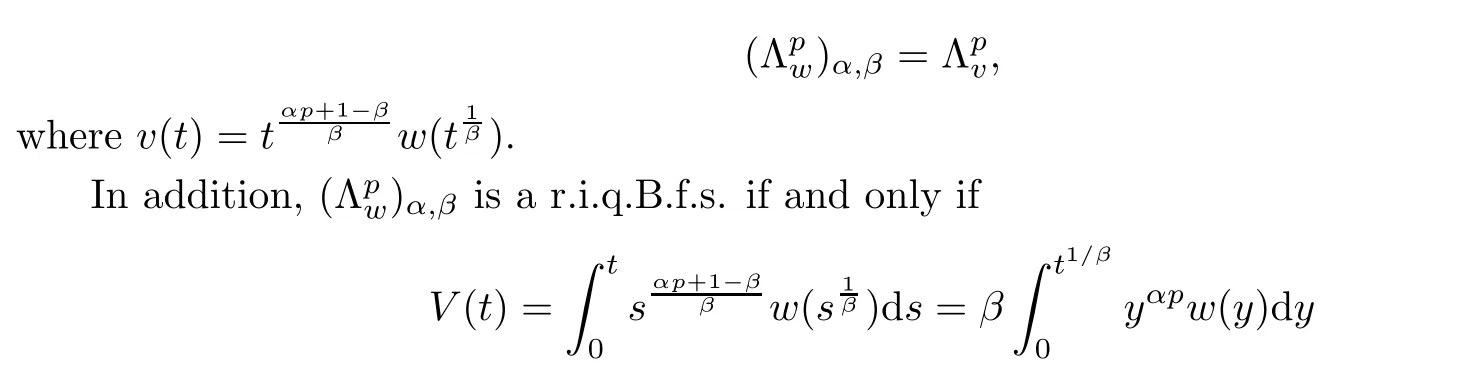
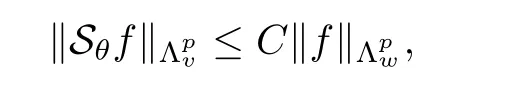
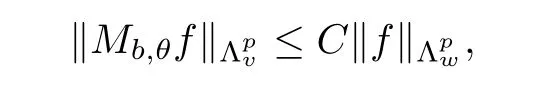
 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
