AN OPTIMAL DIVIDEND STRATEGY IN THE DISCRETE MODEL WHEN PAYMENTS ARE SUBJECT TO BOTH TRANSACTION COSTS AND TAXES
WANG Shao-feng,YIN Chuan-cun
(1.School of Mathematics and Computer Application Technology,Jining University,Qufu,Shandong 273155,China)
(2.School of Statistics,Qufu Normal University,Qufu,Shandong 273165,China)
Abstract:In this paper,we study the optimal dividend problem in the discrete risk model in which transaction costs and taxes are required when dividends occur.Moreover assume that dividends are paid to the shareholders according to an admissible strategy with dividend rates bounded by a constant.The company controls the amount of dividends in order to maximize the cumulative expected discounted dividends prior to ruins.We show that the optimal value function is the unique bounded solution of a set of discrete Hamilton-Jacobi-Bellman equations.In addition,the optimal image functions are approximately obtained by solving the HJB equation.
Keywords:discrete model;optimal strategy;value function;image function
1 Introduction
Over the past decades,the optimal dividend problem has been a hot issue and a large number of papers in this field have came out.The study of dividend problem has a realistic sense:for a joint-stock company,it has responsibility to pay dividends to its shareholder,therefore choosing a divided strategy is important for this company.The research of dividend problem stems from the work of De Finetti[1].He is the first to suggest that a company should maximize the expected discounted dividend payout.In earlier research of this field,scholars focused on two kinds of dividend strategies.The first one is the constant barrier strategy.In this model,we have a barrier b,splitting region into two parts.Under such policy,the surplus cannot cross the barrier b at any time t>0,and when it hits the barrier,it will either stay at the barrier b or decrease below the barrier(see for example Gerber and Shiu[2],Albrecher et al.[3],Albrecher and Kainhofer[4],Li and Garrido[5],Loeffen et al.[6]).The second one is threshold strategy,specifically,dividends can be paid out at certain rate if the surplus exceeds a threshold(see for example Gerber and Shiu[2],Lin and Pavlova[7]).Stochastic control theory has been introduced to solve the optimal dividend problem.HJB equation,QVI,and singular control as tools were used to deal with dividend problem from different aspects.Asmussen and Taksar[3]considered optimal continuous dividend for diffusion model.In the paper Azcue and Muler[8],the author not only studied the optimal continuous dividend strategy but also considered the reinsurance policy in the compound Poisson model.Impulsive dividend and reinsurance strategies for diffusion model can be found in paper Cadenillas et al.[9].
Compared with continuous time risk models,obviously discrete time risk models with the dividend payment strategies have not attracted much attention,although De Finetti[1]gave the problem first in a discrete time model.However,discrete time models also have their merits,for example,they are closer to reality and they can be seen as the approximations of continuous time models.For the optimal dividend payment problem in discrete models,see[1]and[10]for the classic results.In addition,several recent contributions can be found.Gerber et al.[11]modeled the surplus of an insurance company(before dividends)as a time-homogeneous Markov chain with possible changes of size+1,0,?1,?2,...in one period,and showed that the optimal dividend-payment strategy is band strategy irrespective of the penalty at ruin.Tan et al.[12]considered the discrete Sparre Andersen risk model and its derivative models by anew setting up the initial times,and showed that the optimal value function is the unique bounded solution of a set of discrete Hamilton-Jacobi-Bellman equations.
However,in these papers,it is assumed that there are not any transaction costs when dividends are paid out.Practically,transaction costs cannot be neglected.Here,to make the dividend analysis even more realistic,we take into account fixed transaction cost K>0 which is incurred each time the dividend is paid out.In addition to transaction costs,we assume that the shareholders are required to pay taxes with a tax rate 1?k(0 Therefore,it is necessary to look for an optimal dividend strategy when dividend payments are subject to both transaction costs and taxes in discrete risk model. In this paper,we study the optimal dividend problem in the discrete model.Transaction costs and taxes are required when dividends occur.The outline of this paper is as follows.In Section 2,we give a rigorous mathematical formulation of the problem.In Section 3,we heuristically derive the set of discrete HJB equations for the optimal value functions and introduce the transformation method.Section 4 firstly gives properties of the optimal image functions and then by solving the HJB equation,the optimal image functions are approximately obtained. Consider the discrete Andersen surplus process where U(0)=u is the initial surplus,which is a non-negative integer.c is the premium received in each time period,which is a positive integer.The counting process N(t),t=0,1,2,···denotes the number of claims up to time t and is defined as N(t)=max{n:T1+T2+ ···+Tn≤ t},where claim inter-occurrence times Tiare assumed i.i.d.positive and integer-valued random variables with common probability function p(k)=Pr(Ti=k),k=1,2,···and ETi< ∞.Therefore,N={N(t)}is an ordinary renewal process.The random variable Xirepresents the ith claim,independent of{N(t)}.The random variables Xi,i=1,2,...are i.i.d random variables with common probability function f(k)=Pr(Xi=k),k=1,2,....Denote the filtration by{Ft}(t=0,1,2,···),where Ftcomprises all the information before time t. We do not need positive safety loading condition in this paper.We say the company ruins if the surplus becomes negative.Put σk=T1+T2+ ···+Tk(k=1,2,...)and σ0=0.Let We now enrich the model.Let the company pay dividends to its shareholders according to some dividend strategies.To make the dividend analysis even more realistic,we take into account fixed both transaction costs K and transaction taxes with tax rate 1?k which are incurred each time that dividends are paid out(no matter how much). A strategy is described by where τnand ξndenote the times and amounts of dividends.Thus,when applying strategy2 Problem Formulation

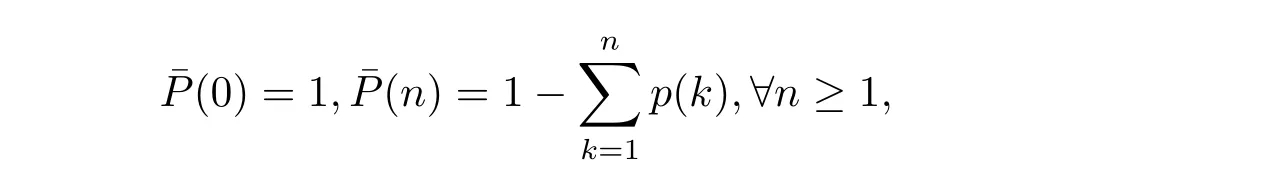



3 Optimal Value Functions and Their Transformations




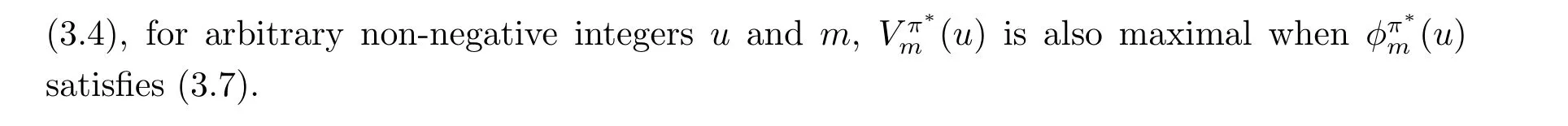
4 Properties of Image Functions and Bellman’s Recursive Algorithm


- 數(shù)學(xué)雜志的其它文章
- SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS
- APPROXIMATIONS OF THE IDENTITY ADAPTED TO CONTINUOUS ELLIPSOID COVER
- THE REPRESENTATION CATEGORIES OF DIAGONAL CROSSED PRODUCTS OF INFINITE-DIMENSIONAL COFROBENIUS HOPF ALGEBRAS
- DIFFERENTIAL MIXED EQUILIBRIUM PROBLEMS IN BANACH SPACE
- 阿貝爾方程的兩個(gè)周期解的存在性
- 一類非線性隨機(jī)微分方程的統(tǒng)計(jì)性質(zhì)

