Effects of module number and firing condition on charge thermal safety in gun chamber
Hun-yu Qin ,Yong-gng Yu ,* ,Jing Liu
aSchool of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing,210094,China
b Academy of Opto-Electronic,China Electronics Technology Group Corporation (AOE CETC),Tianjin,300308,China
Keywords:Thermal safety Modular charge Cook-off Firing condition
ABSTRACT Thermal safety of modular charge which is fed into and retained in the chamber after gun fires consecutively is first investigated with cook-off method.A two-dimensional cook-off model of modular charge in gun chamber is established and the cook-off process of modular charge in gun chamber is numerically simulated.Then the effects of module number and firing condition on charge thermal safety are evaluated by researching the cook-off response characteristics of modules.The results show that,under conditions of different module numbers the cook-off responses all occur on the module closest to the boundary of missile,and the single-base propellants located at the inner surface of cartridge ignite first.When the number of loaded module changes from 1 to 6,the cook-off response temperatures vary little,only in a small range of 478.1 K-482.4 K.The cook-off response times decrease logarithmically in the range of 211.2 s-166.7 s with the increasing length of residual air gap in gun chamber.The simulation results are well matched with the experimental data.Furthermore,different firing conditions have great influence on the cook-off response time,minor influence on the initial response position and little influence on the response temperature.Under the three conditions of consecutive 32 launches with 5 rounds/min,43 launches with 1 round/min,and 41 launches with different firing frequencies,the cookoff response temperatures are 479.2 K,481.1 K and 479.9 K respectively and the response times are 709.2 s,211.2 s and 214.4 s respectively.The response position is near the middle area of the inner cartridge surface in the former condition and near the right area in the latter two conditions.
1.Introduction
Modular charge is one of the most promising charge methods for large caliber howitzers,which features both rigidity of charge and modularization of structure,achieving the convenience of loading artillery automatically,the rapid firing and the intelligent service management of ammunition.However,during consecutive firings the temperature of gun chamber surface keeps rising due to the thermal shock of high temperature gas.The gun chamber becomes overheated when a series of firings are finished[1].Thermal spontaneous combustion or unexpected thermal safety accidents may occur if the module is continued to be fed into chamber at this time.Consequently,it’s necessary to predict thermal safety characteristics of modular charge retained in the chamber,such as the cook-off response time and temperature.
As an effective approach,the cook-off method has been widely adopted to solve thermal problems in many fields.It’s usually combined with other experimental and numerical methods to study thermal safety of ammunition systems,mainly involving energetic materials such as explosives and propellants.In slow cook-off test,Deng et al.[2]found that the melt-cast composition B explosive featured strong reaction intensity and shorter delay time with the enhance of tightness under different constraints and would explode under full enclosed constraint.Similarly,the cookoff test of LX-04 explosive indicates that lower confinement will act to lower cook-off pressure and overall burning rate,achieving lower overall violence and higher relative safety[3],and the LX-04 at 190C is more shock sensitive than that at 150C or 170C [4].Additionally,the explosive performance of CL-20 is found to be greater than that of HMX and its sensitivity is moderate as determined by cylinder expansion and tantalum plate acceleration experiments[5].Another test of CL-20 suggests that the higher the pressure,the stronger the reaction intensity and the worse the thermal safety [6].Thermal stability of explosives RDX,HMX,TNT and the responses to thermal stimuli at different heating rates were analyzed numerically.It’s found that the cook-off response temperature of HMX presents a function of heating rate under rapid cook-off [7].Similar results were obtained when simulating the behavior of HMX in response to external heat flux[8].By means of slow cook-off device,Aydemir et al.[9] measured the cook-off response time,position and temperature of explosive PBCN-110.Zemana et al.[10] investigated the PBXs explosive strength in relation to heat of combustion and thermal reactivity of PBXs versus the heats of formation.
Besides explosives,thermal safety of propellants is also widely studied.Zhu et al.[11] examined the influence of humid environment on the thermal safety and mechanical property of RDX/APNEPE propellant.Thermal explosion tests of NEPE propellant grains in different sizes at 90C,100C,110C and 120C indicate that at the same temperature the larger the grain size,the larger the reaction rate constant,and the smaller the specific grain surface area,the larger the activation energy [12].Similarly,in different flame environments and at different heat fluxes,cook-off tests of AP/HTPB composite propellants were executed on small-scale experimental apparatus to discuss the thermal security [13,14].A two-dimensional cook-off model of AP/HTPB composite propellant was adopted to evaluate the thermal security problem of base bleed device and large-scale solid rocket motor [15-17].By DSC and TG test,Sun et al.[18] observed that sulphur-free propellants performed better than the black powder for its low sensitivity.Gross et al.[19] established a one-dimensional transient model of HMX and found that small changes in the heat path such as air gaps changed the predicted ignition time significantly for fast cook-off but slightly for slow cook-off.By researching the thermal safety of SF-3 propellants in cook-off experiment,Chen et al.[20] indicated that the environmental temperature had a great influence on spontaneous combustion delay time and intensity,and the thermal safety of modified SF-3 propellant became worse with the increase of environmental temperature.Jia et al.[21] studied the thermal safety of a new DB propellant SZQu-1 by ARC method.The results showed that compared with SF-3,SZQu-1 had poor performance in thermal stability and strong explosiveness.Research on the thermal behavior and thermal safety of BTATz-CMDB propellants [22]showed that with the substitution of 26% RDX by BTATz and the help of CMDB propellants formulation,the gun safety would be improved.
Thermal safety researches also involve the field of explosives.The initial decomposition temperature range of the compound NTO was 249.4-271.2C when the heating rate was 2-20C/min [23].Zhang et al.[24]obtained the kinetic equation of NNHT thermal decomposition reaction and the kinetic parameters of NNHT chemical reaction at different heating rates to evaluate the thermal safety of NNHT.Thermal safety of nitrocellulose with different nitrogen content was studied,and the results showed that main pyrolysis temperature of nitrocellulose was 192-209C and the decomposition temperature decreased as the nitrogen content increased [25].Under the condition of external heating rate of 1-10 K/min,the cook-off response characteristics of modules made of nitrocellulose suggested that the cook-off response time decreased exponentially with the increase of heating rate [26].Cook-off analysis of propellants in a 7.62 mm rifle was conducted experimentally and numerically and the temperature distribution of gun barrel was obtained [27].
Though remarkable progress has been made in the past,extensive researches reported only considered the thermal safety problem of ammunitions under controllable linear heating conditions.However,in the consecutive firings process of gun,the heating rate is non-linear and uncontrollable.Additionally,under actual circumstances the gun usually shots according to different requirements.Under these conditions thermal safety of ammunitions has rarely been studied,especially the thermal safety of modular charge.That is exactly the point the present study sought to research.A 155 mm gun after multiple consecutive firings is taken as the research object,and a two-dimensional unsteady cookoff model of modular charge in the chamber is established to numerically simulate the cook-off process and to evaluate the thermal safety characteristics when modules are loaded and retained within gun chamber after the gun finishes firings.On this basis,the effect of module number from 1 to 6 on cook-off characteristics of modular charge is evaluated.Finally,different firing conditions are compared when six modules are loaded.
2.Physical model
The structure sketch of module is shown in Fig.1.The cartridge made of combustible material is filled with single-base propellants nitrocellulose and in the shape of thin-walled cylinder.The module is equipped with a central fire tube in where a serpentine igniter packet is placed.Both of the ends of the tube are sealed with cardboard baffles.
The structure sketch of gun chamber is shown in Fig.2(when one module is loaded).The chamber is approximately seemed as a cylinder with equal wall thickness.The module is located on the left side within chamber,leaving a clearance to the boundary of breech.The outer wall of the cartridge contacts the inner surface of the annular chamber,ignoring the clearance.
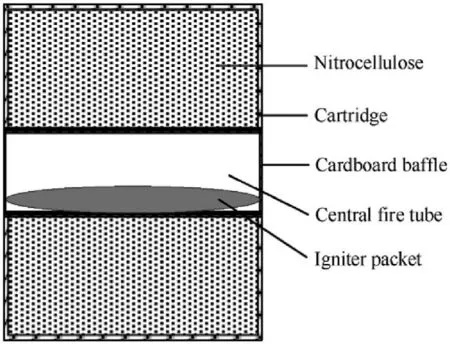
Fig.1. Structure sketch of module.
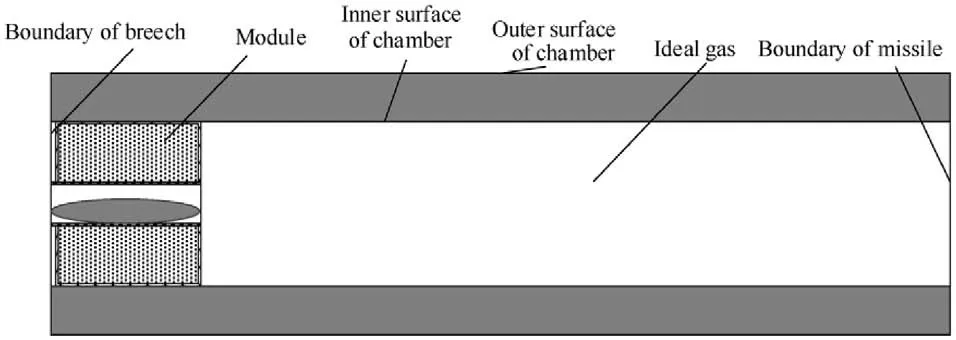
Fig.2. Structure sketch of gun chamber with one module loaded.
Modules are fed into gun chamber after consecutive firings.Due to the heat accumulation during firing process,the inner surface temperature of gun chamber keeps rising and reaches a high value,and the cook-off process starts immediately when the modules are fed in place.Taking the gun chamber and internal modules as the research object,the chamber acts as the heat source at high temperature.In the subsequent cook-off process four parts of heat transfer are considered:(1)Heat conduction occurs between every two solid materials from gun chamber to the central fire tube.(2)Heat convection goes on between the inner surface of chamber and the gas in chamber.(3) Heat convection occurs between the outer surface of chamber and the external environment.(4) Heat convection exists between the cartridge and gas (including the gas in central fire tube) in chamber.
Considering the consecutive firings process of gun and the structure characteristics of gun chamber with modules,a twodimensional unsteady cook-off model of modular charge in chamber is established,and the following simplified assumptions are adopted:
(1) The thermal decomposition reaction of combustible cartridge and single-base propellants abide by Arrhenius law.
(2) The cartridge and single-base propellants are assumed as homogeneous and isotropic materials,which maintain solid during the entire cook-off process without phase transition.
(3) The physical and chemical parameters of the materials keep constant.
(4) The chamber is sealed and the air in chamber is assumed as ideal compressible gas.
(5) The propellants are evenly distributed in the cartridge and the mixed state of air and single-base propellants in the cartridge is described by porous charge.
(6) Thermal radiation from the inner surface of metal chamber,thermal effect of breechblock and thermal effect of serpentine igniter packet are neglected.
3.Mathematical model
3.1.Basic equation
3.1.1.Dynamic equation
Thermal decomposition reactions of combustible cartridge and single-base propellants can be described by one-step chemical reaction.According to Arrhenius Law and Mass Action Law,the chemical reaction rates W、Ware expressed as

where subscripts 1,2 represent cartridge and single-base propellants.Aand Aare pre-exponential factors.Eand Eare activation energy.ρa(bǔ)nd ρa(bǔ)re density.R is the Molar gas constant.
3.1.2.Solid phase energy equation
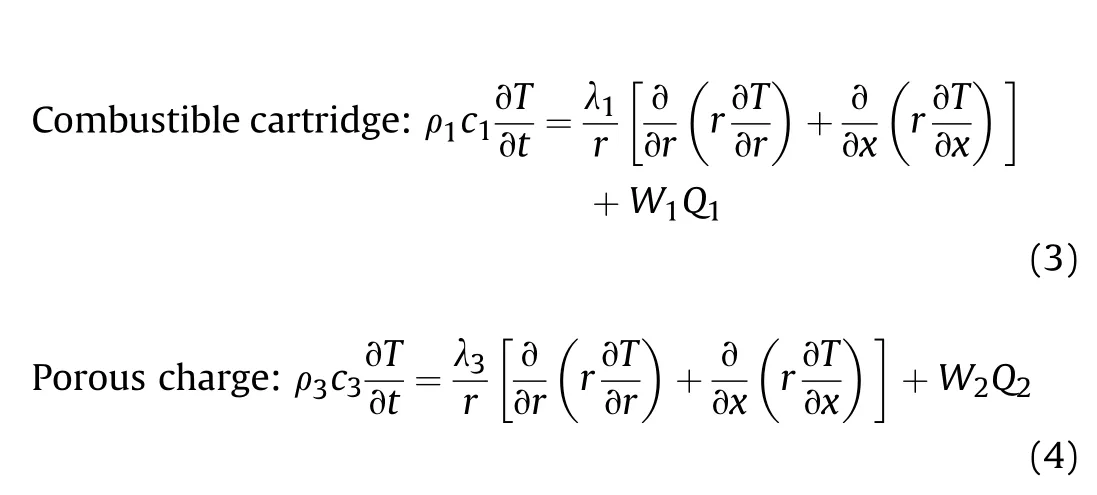
where the calculation methods of ρ,cand λof the porous charge [28] are given as
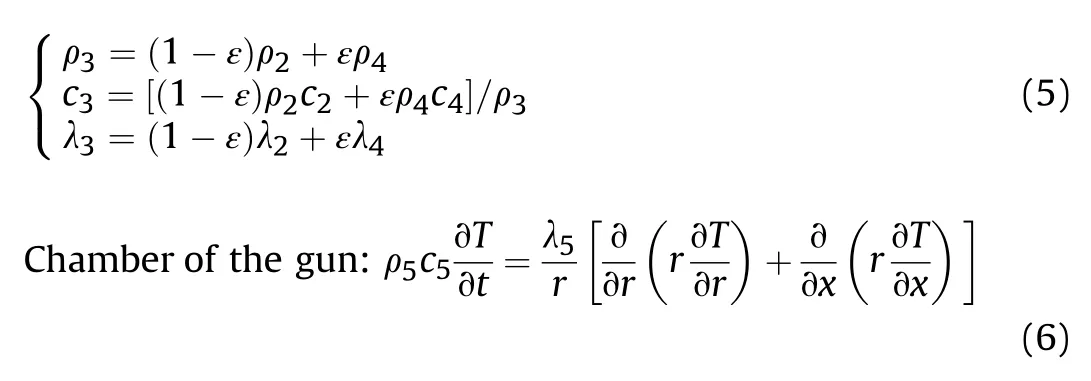
where subscripts 1,2,3,4,5 represent cartridge,single-base propellants,porous charge,air and chamber of the gun respectively.ρ,c and λ represent density,specific heat capacity and thermal conductivity respectively.εis the porosity of porous charge.Qand Qare the reaction heat of Eq.(1) and Eq.(2).
3.2.Boundary conditions
The boundary conditions for solving Eqs.(3),(4) and (6) are given as follows.
The solid interfaces between adjacent areas meet the conditions of continuous temperature and continuous heat flow,
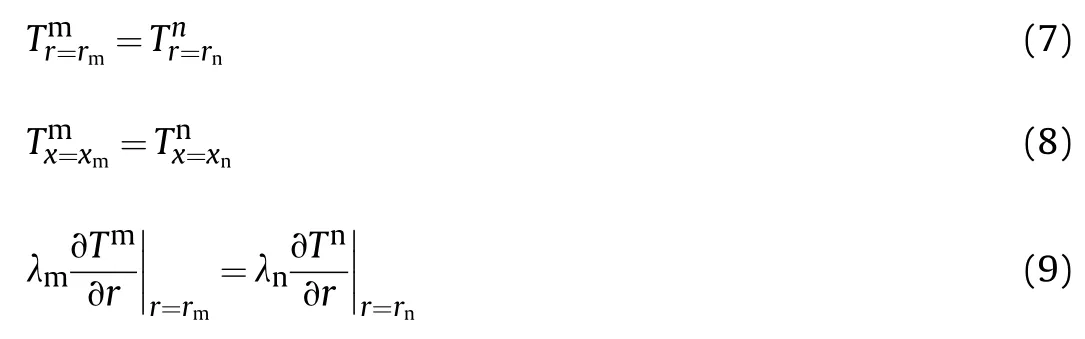
where,subscripts m and n represent different kinds of solid materials adjacent to any interface.
Heat convective between the inner chamber surface and gas inside:

Heat convective between the outer chamber surface and the external environment,

Heat convective between the outer surface of cartridge and the gas in chamber:

The boundary of breech and boundary of missile are regarded as adiabatic boundaries.
3.3.Initial conditions
At initial time,the pressure in gun chamber is 1atm.The temperature in gun chamber and outer atmospheric environment is 293 K.Supposing that the multiple consecutive firing of gun has been finished and then the modules are fed into the chamber.
Here three consecutive firing conditions are considered.Attention should be paid that each firing condition is corresponding to specific initial cook-off temperature condition.
a.Consecutive firings for 32 rounds with 5 rounds/min.
b.Consecutive firings for 43 rounds with 1 round/min.
c.Mixed firings for 41 rounds:Firing for 3 min with 5 rounds/min in the first stage,firing for 5 min with 3 rounds/min in the second stage,and consecutive firings with 1 round/min in the third stage.
In the early simulation experiments,the module was placed on the plate heated to about 170C.After a few minutes,the module would catch fire.Therefore,170C was taken as the critical temperature which may cause the module to have a cook-off response.This is the experimental basis of the temperature boundary conditions [29].In Ref.[29],the inner and outer wall temperatures of gun chamber under three firing conditions were obtained by calculation,as listed in Table 1.The calculated results are used as the initial boundary conditions of temperature for cook-off in this study.

Table 1 Initial temperature of the inner/outer chamber surface.
4.Computational model
The calculation model is shown in Fig.3(unit:mm).The symbol i is the module number.Here taking i=1 as an example,the module is located at the left end of gun chamber,with a clearance of 5 mm to the boundary of breech,and the space on the right side of module is full of gas.Cook-off process begins when the module is loaded in place.The kinetic and physical parameters[30-32]used for calculation are shown in Table 2 and Table 3.In order to observe the temperature changing of module,points A,B,Cand Eare set as characteristic points in each module and the temperatures are monitored.Coordinates of characteristic points are shown in Table 4.In the coordinate system(x,r)(unit:mm)shown in Fig.3,point A(75,52.5) is the center of single-base propellants within cartridge,point B(75,67.5)and point C(75,82.5)are directly above point A,and point E(147.5,82.5) is at the upper right corner of cartridge.Typically point F marked in Fig.3(a) is the calculated cook-off response center where the cook-off response occurs first.Actually the coordinate of point F can’t be determined before the first calculation is completed.After that,the first position-to-ignite is set as point F,and the temperature characteristics need to be calculated again.It’s believed that the cook-off response center is the point whose temperature profile rises steeply and generates the inflection point at certain time.Then the temperature corresponding to the inflection point is the cook-off responsetemperature,and the corresponding time of the inflection point is the cook-off response time.

Table 2 Kinetic parameters of module.

Table 3 Physical parameters of module and chamber.
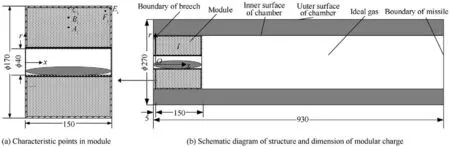
Fig.3. Schematic diagram of calculation model (when loading one module).

Table 4 Coordinates of characteristic points(unit:mm).
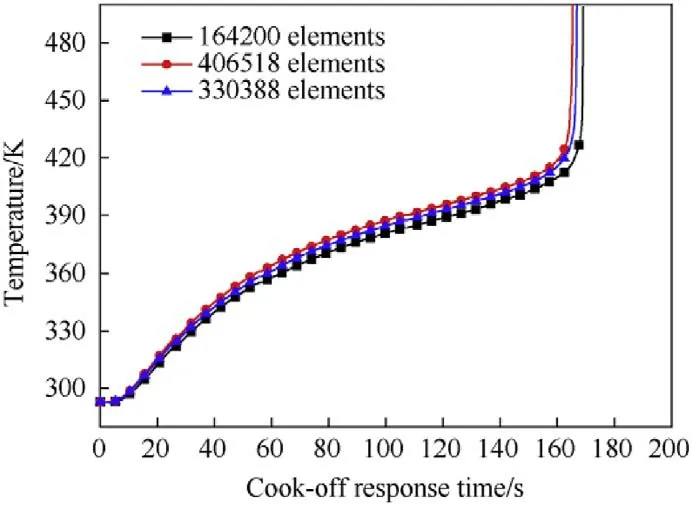
Fig.4. Cook-off response curve under different element numbers.
The cook-off process of modules in chamber is simulated by computational fluid dynamics software FLUENT.For simplicity the 1/2 structure model is employed to calculate the two-dimensional axisymmetric problem.The computational domain is divided by structural grid and is refined at the boundaries and interface areas to improve the accuracy of calculation.Under condition-b,164200,330388 and 406518 elements are adopted for calculation respectively when one module is loaded.The temperature curves of the cook-off response points are shown in Fig.4.The difference of the calculated results between 164200 elements and 330388 elements is about 1.45%,and that of 406518 elements and 330388 elements is less than 0.84%.Then 330388 elements are selected to carry out the calculation for the higher accuracy and efficiency.After verifying the grid independence,the schemes of 330388,351830,374178,396224,418572 and 441222 elements are adopted to carry out the calculation when the module number varies from 1 to 6,respectively.Source terms of the energy equation in Eq.(3)and Eq.(4)are compiled and introduced by user-defined function.A solver of Pressure-Based Type,Absolute Velocity Formulation,Transient Times and Axisymmetric 2D Space is employed.Velocity-pressure coupling is achieved by SIMPLE arithmetic in calculation,and second-order upwind difference condition is adopted in density,pressure,momentum and energy equations.The time step is taken as 0.1 s after verifying the time step independence.
5.Results and analyses
5.1.Effect of module number on charge thermal safety
5.1.1.Temperature contours of module
Under firing condition-b,after 43 rounds of consecutive firings at 1 round/min,the inner surface temperature of gun chamber is 443.2 K,and the outer surface temperature of gun chamber is 435.2 K.The temperatures are taken as the initial temperature for cook-off.Then numerical simulations are performed to discuss the effect of module number on charge thermal safety which increases from 1 to 6.
Temperature distribution of modules at different time are shown in Fig.5(1),(2) and (3) when loading 1,3 and 6 module(s),respectively.For conciseness only the three cases are listed here,and Fig.5(1) corresponding to loading 1 module is taken as an example for analysis.The cook-off process is simply divided into three stages:The initial stage,the intermediate stage and the response stage.As shown in Fig.5(1),the image at the left upper corner describes the whole temperature distribution and the relative position of modules in gun chamber.Under that are three representative contours corresponding to the three stages in turn.In addition,a partial enlarged image from the last contour located at the right upper corner is given to illustrate the detail of the cookoff response center clearly.
According to Fig.5(1),in the initial stage of cook-off (t=23.6 s),areas at high temperature appear on the outer surface of cartridge and the right end of central fire tube.Structurally the outer surface of cartridge is adjacent to the inner gun chamber surface,so heat conduction exists between two of them and heat is directly imposed to the outer surface of cartridge,making the temperature rising gradually.Later on,the heat transfers to the single-base propellants within cartridge.Meanwhile,the temperature of gas in the right space of module increases through heat convection with the inner chamber surface,and then the heat transfers to the left direction from the right end of cartridge and central fire tube layer by layer.Therefore,the temperature at the right end of cartridge increases slowly and is higher than that at left,so does it in central fire tube.It can be noticed that temperatures at the rest parts remain nearly the initial value of 293 K,due to far distance to the high temperature heat source,no heat conducted and no selfthermal reaction.Additionally,the left side of cartridge is close to the boundary of breech whose thermal effect has been ignored as the simplified assumption,and the temperature is treated as the ambient temperature of 293 K.The clearance between the left end of cartridge and the boundary of breech is only 5 mm.Although gas in the clearance transfers heat as possible through natural convection among the inner chamber surface,the left end of cartridge and the boundary of breech,the temperature difference and the amount of gas are too little to make sense.So the heat transfer by gas here merely gives a minor contribution and basically there is no temperature change at the left end of cartridge or central fire tube.
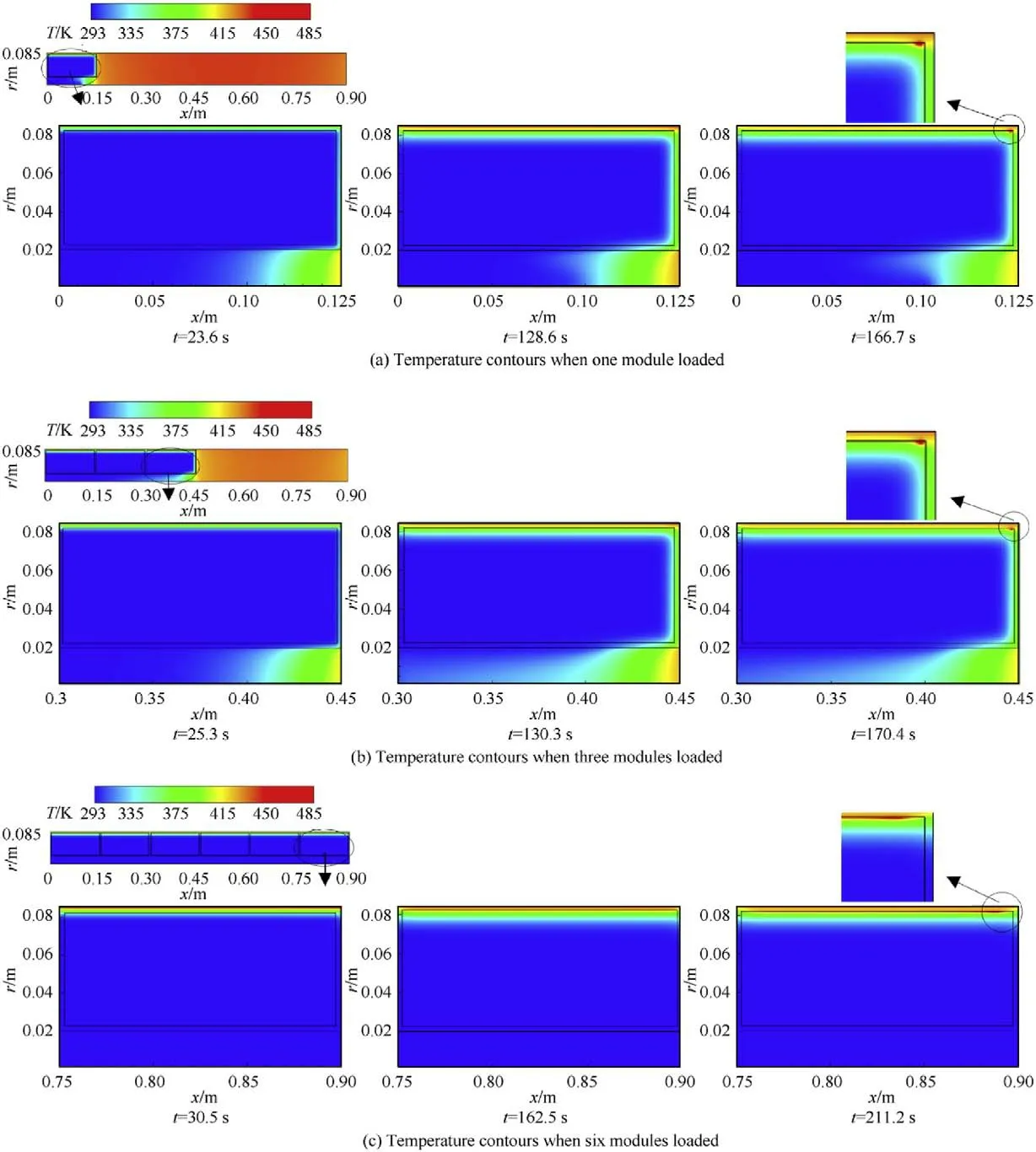
Fig.5. Temperature contours of modules with different module numbers.
In the intermediate stage(t=128.6 s),it can be clearly observed from the temperature contour that the outer surface of cartridge dominates the highest temperature.The temperature of singlebase propellants within cartridge increases a little,especially the propellants close to the inner surface of cartridge,and the heat transfer from the cartridge to the internal propellants is relatively uniform.In this stage,single-base propellants within the cartridge which receive more and more heat begin to undergo a slow selfthermal reaction when the temperature grows high enough to make it.Subsequently,the heat generated by self-thermal reaction and transferred by the cartridge is accumulating and continues transferring to the inner propellants at lower temperature.As a result,the temperature at the outer surface and the right end of cartridge increases continuously,and a uniform temperature gradient is formed.The left side of central fire tube is still at low temperature,so the high temperature gas on the right side continues transferring heat to the left,layer by layer.Due to the larger thermal conductivity of cartridge than gas,the temperature rising at the outer surface of cartridge through contact with high temperature inner chamber surface is higher than that at the right end of cartridge,and the temperature at the inner surface of central fire tube is slightly higher than that at central axis of central fire tube.It lasts a long time for module to undergo the slow self-thermal reaction in the intermediate stage of cook-off.
As shown in Fig.5(a),cook-off response occurs when t=166.7 s.A partial enlarged image details the position and shape of cook-off response center clearly.The initial cook-off response position is near the inner surface of cartridge,where the single-base propellants within the cartridge ignite first.Taking a comprehensive consideration of the three temperature contours in Fig.5(a),it can be deduced that the single-base propellants located at the initial ignition position are subject to the heat transfer from both the outer surface of cartridge and the right end of cartridge,and the singlebase propellants have a stronger thermal capacity than that of cartridge,so the single-base propellants present a much higher temperature rising than cartridge when receiving the same quantity of heat.What’s more,the density of the single-base propellants is higher than that of cartridge,making it difficult for heat to dissipate and resulting in mutual promotions of self-thermal reaction and heat accumulation.As time goes on,the temperature of single-base propellants keeps rising and the rising rate grows faster,forming a gradually expanding high temperature area until the temperature value exceeds the ignition temperature range at 166.7 s.At that time the cook-off response occurs,and the coordinates (x,r) of the annular area center of cook-off response is about(146.1,82.1)mm.
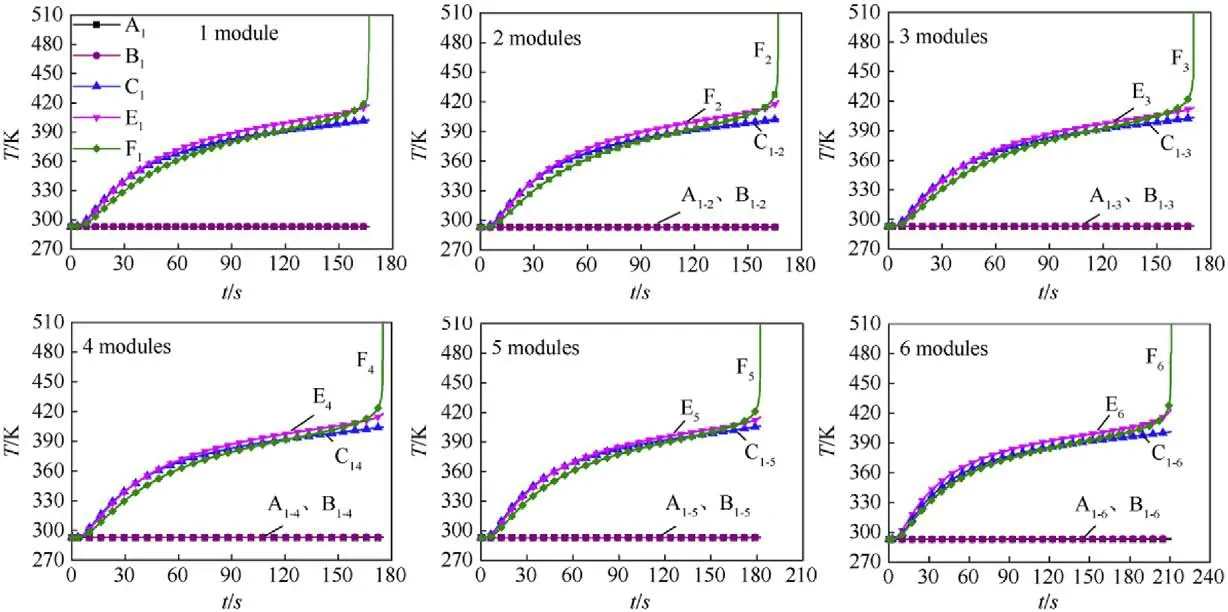
Fig.6. Temperature profiles of characteristic points when module number i=1,2,3,4,5,6.
In Fig.5(b),the three contours belong to the third module as indicated,and in Fig.5(c)those belong to the sixth one.The results demonstrate that the cook-off response occurs on the third module when loading three modules and on the sixth module when loading six ones.It’s observed that the response positions move a little to the left in the cook-off module.Also,similar temperature distributions in modules at each stage are found in Fig.5(a),(b)and(c).It can be concluded that whereas the module numbers are different,cook-off processes and heat transfers of modules are similar under the three cases.Actually,it has been calculated and verified (but not fully presented in this study) that when the number of module,i,increases from 1 to 6,it is the i-th module,namely,the module closest to the boundary of missile,that occurs cook-off response first.And the six sets of temperature contours all display similar temperature distributions,which indicates that the cook-off processes of the modules are similar to each other when different numbers of module are loaded into the chamber after consecutive firings.As the module number increases from 1 to 6,the single-base propellants near the inner surface of cartridge ignite first and then the annular cook-off response areas are formed.The coordinates (x,r) of the cook-off response centers are(146.1,82.1) mm,(296.1,82.1) mm,(446.1,82.1) mm,(596.0,82.1)mm,(745.5,82.1) mm and(887.9,82.1)mm,respectively.The response temperatures are 478.1K,481.9K,482.4K,481.6K,481.7K and 481.1K respectively,with a small difference.
5.1.2.Temperature profiles of the characteristic points
Temperature profiles of the characteristic points at different times under all six cases of i=1,2,3,4,5,6 are expressed in Fig.6 visually.The image of one module loaded,which corresponds to Fig.5(a),is taken as an example for analysis.As shown in Fig.5(a)and the first image of Fig.6,the temperature at point Aremains almost unchanged during the whole cook-off process,indicating that only small amount of heat is transferred to the center of propellants within cartridge.The temperature at point Bincreases slightly because it is far from the high temperature chamber surface,so there is only a small temperature rising.For point Cand point E,the temperature profiles increase greatly and rapidly in the initial stage of cook-off due to the locations at the edge of cartridge and close to the high temperature surface,and then follow by a stable rising in the subsequent cook-off process.Especially,point Eis almost directly in contact with the high temperature surface so the temperature increases much more along with the cook-off process.Attention should be paid that point Fis the calculated cook-off response position,which is located in the propellants contained in cartridge and near the inner surface of cartridge.Under the thermal effect of inner surface of the high temperature chamber,as well as the reaction heat accumulation of propellants and cartridge,the temperature of point Fkeeps rising.As shown in the first image of Fig.6,it rises faster in the initial stage(the temperature rising rate is lower than that of point Cand point E),slows down to some extent but maintains a higher value due to going through the slow thermal accumulation in the intermediate stage,and then accelerates sharply in the response stage.When the temperature profile at point Fturns obviously and rapidly,the inflection point comes into being,which indicates that the cook-off response occurs.The occurrence of the thermal runaway shows the single-base propellants within the cartridge igniting afterwards.The temperature and delay time corresponding to the inflection point are adopted as the cook-off response temperature and the cook-off response time.
The curves in Fig.6 show that the temperature risings of characteristic points in the module are similar to each other under all six situations,which repetitively illustrates that the cook-off processes of modules are approximately the same even if the loading number changes.As shown in Fig.7,the temperature-time curves of the six cook-off response centers are summarized and compared.
In the above analyses from Figs.5,Figs.6 and 7,it can be deduced that cook-off processes of module are similar under different module numbers.The more the module loaded,the longer the cook-off response time,which are 166.7 s,167.0 s,170.4 s,175.1 s,182.2 s and 211.2 s,respectively.In particular,a more complex and long-term heat transfer,heat accumulation and selfthermal reaction process of modules occurs when six modules are loaded,so the cook-off response time displays a significant increase.
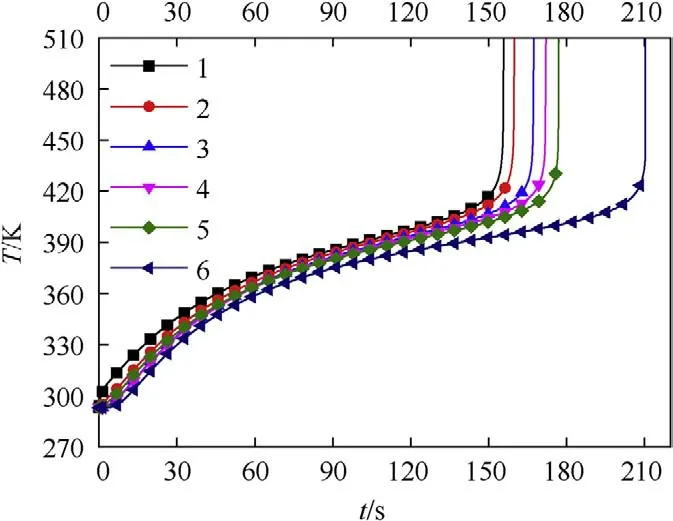
Fig.7. T-t curves of cook-off response centers.
It can be inferred that the shift-to-left of the cook-off position,the differences in temperature distribution and in the cook-off response times are related to the thermal effect of gas within chamber,which is in minor amount but the influence cannot be ignored.When loading one module,the gas quantity in chamber is relatively larger,so the thermal effect is stronger,with a display of higher temperature at both the right face of cartridge and the right side of central fire tube.When three modules are loaded,the thermal effect decreases slightly,with a display of lower temperature than that of one module.When six modules are loaded,most of the chamber space is occupied and there is only a small amount of gas left in chamber,playing minimal thermal effects.Therefore,as shown in Fig.5(3),the temperatures at the right surface of cartridge and the right side of central fire tube almost remain unchanged.What’s more,under different loading numbers,the temperatures of the outer and inner chamber surface are different after the heat transfer process,resulting in different temperature differences,which affect the flow and heat transfer of gas in chamber and finally make the cook-off response positions and the cook-off response time different.Whereas the small amount of gas and tiny heat transfer,there is only a slight deviation to the cook-off response position.Here,the relationship between the relative length of air gap after loading module(s)and the cook-off response time can be expressed as t=Aln(x/L)+B,where t is the cook-off response time,x is the length of the residual air gap in the chamber after loading module(s),L is the total length of the chamber.A and B are coefficients(unit:s),A=-13.34,B=161.89.Here the Goodness of Fit R=0.99.The fitting curve is shown in Fig.8.
5.2.Experimental verification
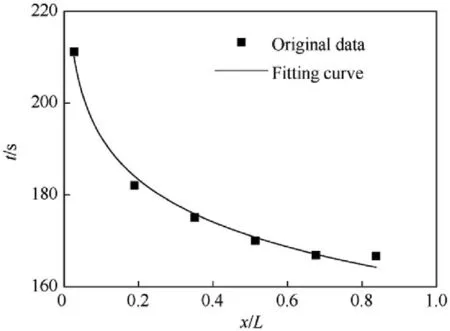
Fig.8. Curve of cook-off response time and relative length of air gap.
Fig.10 displays the numerical results.Calculated temperature curve of the specific monitoring point A within the single module in the chamber is in good agreement with the experimental one,which verifies the correctness of the models.
Furthermore,according to the experiment in Ref.[34],the ignition temperature of the single-base propellants is about 472 K-485 K.In the above six cases,the result obtained by numerical simulation is 478.1 K-482.4 K,which is consistent with the experimental results well and confirm the model again.
5.3.Effect of firing condition on charge thermal safety
Three firing conditions are used here to assess the effect of firing condition on charge thermal safety in gun chamber.Six modules are loaded under all conditions.The initial temperature for cook-off under three firing conditions have been listed in Table 1.
It has been known from the above that it’s the sixth module that occurs cook-off response first when loading six modules.Therefore,the characteristic points A,Band Care taken from the sixth module.Points D,E,F are recorded as the cook-off response center positions under firing condition-a,condition-b and condition-c,respectively.As what have been stated,only after the first calculation finishes can the positions be ascertained.The schematic diagrams of calculation model are shown in Fig.11.
The temperature distribution of all six modules within chamber at different times are shown in Fig.12.The right ones are temperature images of the sixth module in detail.Fig.13 gives the temperature curves of characteristic points on the sixth module under firing condition-a,condition-b and condition-c.
As shown in Figs.12 and 13,the cook-off processes of modules under condition-b and condition-c are similar and the numerical simulation results are basically the same,while the cook-off process under condition-a shows significant differences from the other two.The results show that the cook-off response temperatures are 479.2 K,481.1 K and 479.9 K,and the response times are 709.2 s,211.2 s and 214.4 s under three firing conditions respectively.The response position is near the middle position of the inner surface of cartridge with the shape as a long and narrow strip in condition-a,while they are both near the right position of the inner surface of cartridge and the shapes are approximately flat ovals under condition-b and condition-c.The calculated results under three conditions are listed in Table 5.
Fig.9. Corresponding diagram of the module and the computational domain grid.
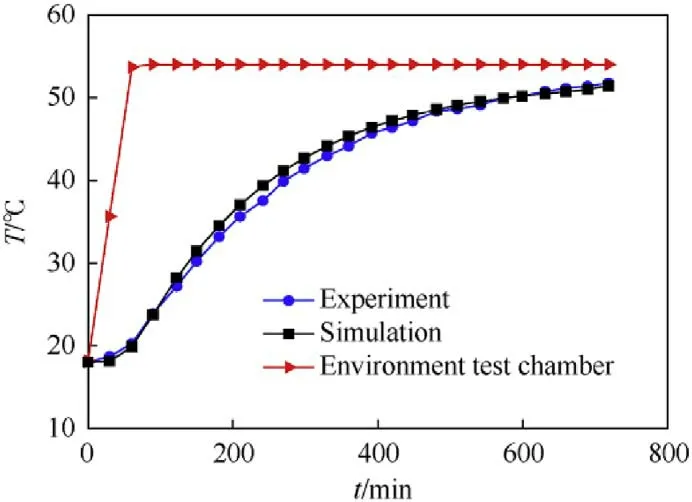
Fig.10. Simulation and experiment results of temperature at point A.
According to the initial conditions of simulation,the initial temperature differences between the inner and outer chamber surfaces for three conditions are ΔT=62.8 K,ΔT=ΔT=8 K.As for the initial temperature difference in inner surface,condition-a distinguishes itself from condition-b and condition-c with a value ΔT≤1.6 K on the inner chamber surface,and that in the outer chamber surface is ΔT≈56 K.Taking a comprehensive analysis of Figs.12 and 13,the differences of the cook-off response time,cook-off response temperature and cook-off response position under three firing conditions are definitely caused by the initial temperature difference between the inner and outer chamber surfaces.The initial temperature difference between the inner and outer surfaces of condition-a is larger,which directly leads to the difference of heat transfer,heat accumulation,gas convection and temperature rising within the chamber.Therefore,the cook-off results under condition-a are different from those under condition-b and condition-c,acting a longer cook-off response time and shift-to-left of response position when the other conditions are the same.It can be concluded that different firing conditions lead to different initial temperatures of the inner and outer chamber surfaces,then affect the cook-off response characteristics.The firing condition has a great effect on the cookoff response time,minor effect on the cook-off response position,and nearly little effect on the cook-off response temperature.
6.Conclusion
The actual cook-off process of modules which are continued to be loaded and retained in gun chamber after consecutive firings are simulated.Then the effects of module number and firing condition on the cook-off response characteristics of modules are analyzed.The simulation results are well matched with experimental data.Conclusions can be drawn as follows:
(1) Under condition-b of firings for 43 rounds with 1 round/min,the module number mainly affects the cook-off response time.The times are 166.7 s,167.0 s,170.4 s,175.1 s,182.2 s and 211.2 s respectively as the number increases from 1 to 6.Under all six conditions the cook-off responses occur on the module closest to the boundary of missile.And the singlebase propellants located at the inner cartridge surface ignite first at nearly the same position on the module in which the cook-off response arising.The response position slightly moves to the left on the cook-off module with the module number increasing.The cook-off response temperatures are 478.1 K,481.9 K,482.4 K,481.6 K,481.7 K and 481.1 K respectively.
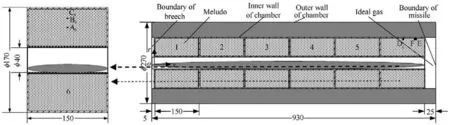
Fig.11. Calculation model and structure sketch of chamber with six modules loaded.
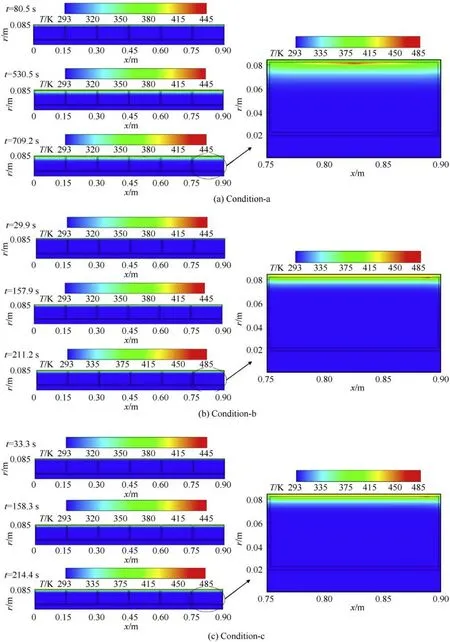
Fig.12. Temperature contours of modules at different times under condition-a,condition-b and condition-c.
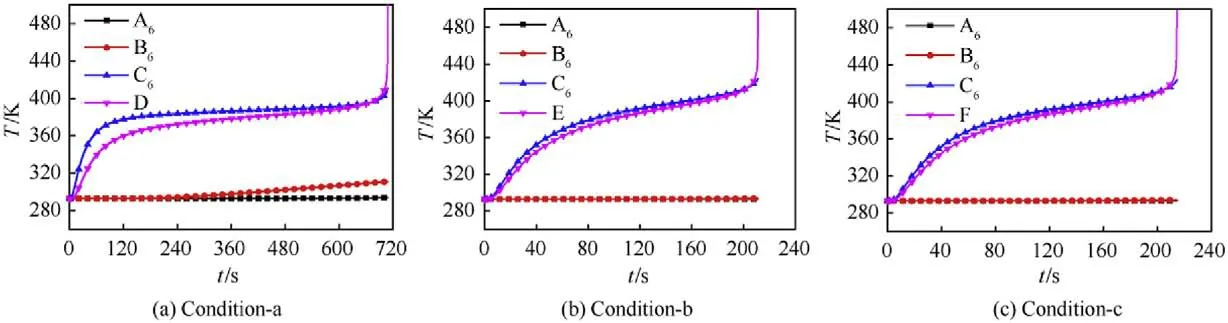
Fig.13. Temperature profiles of characteristic points under firing condition-a,condition-b and condition-c.

Table 5 Calculated results under three conditions.
(2) Different firing conditions have great influence on the cookoff response time,minor influence on the initial cook-off response position and little influence on the cook-off response temperature.The cook-off response time of modules under condition-a is 709.2 s,longer than that under condition-b and condition-c which are 211.2 s and 214.4 s respectively.The cook-off response area is near the middle position of the inner cartridge surface and is a long and narrow strip under condition-a,while the areas are near the right position of inner surface and shapes as flat ovals under condition-b and condition-c.The cook-off response temperature is 479.2 K,481.1 K and 479.9 K,respectively.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
- Defence Technology的其它文章
- Defence Technology
- A study on the surface overpressure distribution and formation of a double curvature liner under a two-point initiation
- Performances and direct writing of CL-20 based ultraviolet curing explosive ink
- One-step synthesis of FeO(OH) nanoparticles by electric explosion of iron wire underwater
- Driving force coordinated control of an 8×8 in-wheel motor drive vehicle with tire-road friction coefficient identification
- Monitoring and Prediction of the Vibration Intensity of Seismic Waves Induced in Underwater Rock by Underwater Drilling and Blasting

