An analytical model for cross-Kerr nonlinearity in a four-level N-type atomic system with Doppler broadening
Dinh Xuan Khoa, Nguyen Huy Bang, Nguyen Le Thuy An, Nguyen Van Phu, and Le Van Doai
Vinh University,182 Le Duan Street,Vinh City,Vietnam
We present an analytical model for cross-Kerr nonlinear coefficient in a four-level N-type atomic medium under Doppler broadening.The model is applied to 87Rb atoms to analyze the dependence of the cross-Kerr nonlinear coefficient on the external light field and the temperature of atomic vapor.The analysis shows that in the absence of electromagnetically induced transparency (EIT) the cross-Kerr nonlinear coefficient is zero, but it is significantly enhanced when the EIT is established.It means that the cross-Kerr effect can be turned on/off when the external light field is on or off.Simultaneously,the amplitude and the sign of the cross-Kerr nonlinear coefficient are easily changed according to the intensity and frequency of the external light field.The amplitude of the cross-Kerr nonlinear coefficient remarkably decreases when the temperature of atomic medium increases.The analytical model can be convenient to fit experimental observations and applied to photonic devices.
Keywords: electromagnetically induced transparency,Kerr nonlinear effect,Doppler effect
1.Introduction
As is well known, the Kerr nonlinear effects play a crucial role in nonlinear and quantum optics.[1]The selfphase modulation (SPM) refers to the phenomenon in which a light beam propagating in a medium interacts with the medium and produces an optical phase modulation on itself.The cross-phase modulation (XPM) is a change in the optical phase of a light beam caused by another light beam in a Kerr nonlinear medium.The self-Kerr effect can be found in many applications such as optical bistability,[2]generation of optical solitons,[3]and frequency conversion.[4]In contrast,the cross-Kerr effect has some useful applications in optical communications,[5]optical Kerr shutters,[1]quantum phase gates,[6]quantum entanglement of single photons,[7]quantum non-demolition measurements,[8]spontaneous chirality,[9]photon blockade for nonreciprocal devices,[10]and so on.In all of these applications,a large Kerr nonlinear coefficient is desirable to reduce laser intensity and to increase the sensitivity of nonlinear optical processes.
In recent years, the discovery of electromagnetically induced transparency(EIT)[11]has yielded a simple solution to obtain large Kerr nonlinear coefficients with small absorption in the vicinity of atomic resonance.[12]Indeed,Xiaoet al.[13]firstly measured giant self-Kerr nonlinear coefficient (about 10?6cm2/W)in a three-level lambda-type atomic system.In addition to three-level atomic schemes, the enhancement of self-Kerr nonlinearity has also been done in four-level[14–16]and five-level[17–19]atomic systems.
Besides, Schmidtet al.[20]firstly obtained a giant cross-Kerr nonlinear coefficient in a four-level N-type system without Doppler broadening.Later, this scheme was experimentally verified by Kanget al.in cold Rb atoms.[21]Similar to the case of self-Kerr, several other configurations have also been proposed to get giant cross-Kerr nonlinear coefficient via EIT effect such as five-level M-type,[22]four-level inverted-Y type,[23]four-level tripod-type,[24,25]and four-level tripodtype systems.[26]More recently, giant cross-Kerr nonlinearity achieved at multiple frequencies in a six-level inverted-Y atomic system has been proposed.[27,28]In addition,the influences of cross-Kerr nonlinearity on light propagation in transparency media were also performed.[29–32]
Although the cross-Kerr nonlinear effect has been implemented in an ultra-cold four-level N-type atomic system,most applications of Kerr nonlinearity often use hot atomic gas media that is always governed by the Doppler effect.Therefore, the study of the Kerr nonlinear effect in the presence of Doppler broadening is necessary to be applied to photonic devices working under different temperature conditions.
In order to meet the above need,in this work,we develop an analytical model for the cross-Kerr nonlinear coefficient in the four-level N-type atomic system including Doppler broadening.The analytical model is applied to87Rb atoms to study the dependence of the cross-Kerr nonlinear coefficient on the intensity and the frequency of laser fields and the temperature of the atomic vapor.
2.Theoretical model
The level scheme of a four-level N-type atomic system interacting with three laser fields is depicted in Fig.1.A weak probe laser field (with angular frequency ωpand Rabi frequency Ωp) drives the transition |1〉?|3〉, while a strong coupling laser field(with angular frequency ωcand Rabi frequency Ωc) couples the transition |2〉?|3〉.A signal laser field (with angular frequency ωsand Rabi frequency Ωs) applies to the transition|2〉?|4〉.In these excitations, the role of the coupling laser field is to generate the EIT effect while the signal field is to cause the cross-Kerr effect for the probe field.
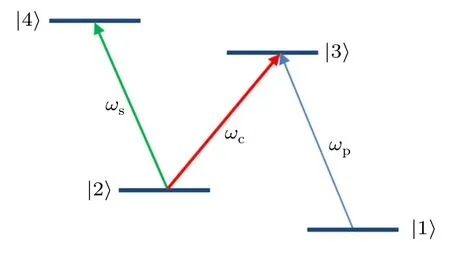
Fig.1.Four-level N-type atomic system interacting with three laser fields.
The evolution of the atomic system in the laser fields can be represented by the following Liouville equation:
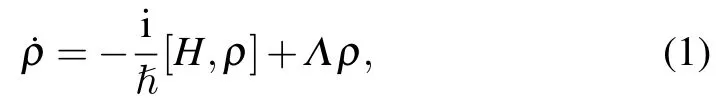
whereHand ρ are, respectively, the total Hamiltonian and density matrix operator, and Λρ presents the relaxation process.In the rotating-wave and electric-dipole approximations,the density matrix equations can be obtained as follows:
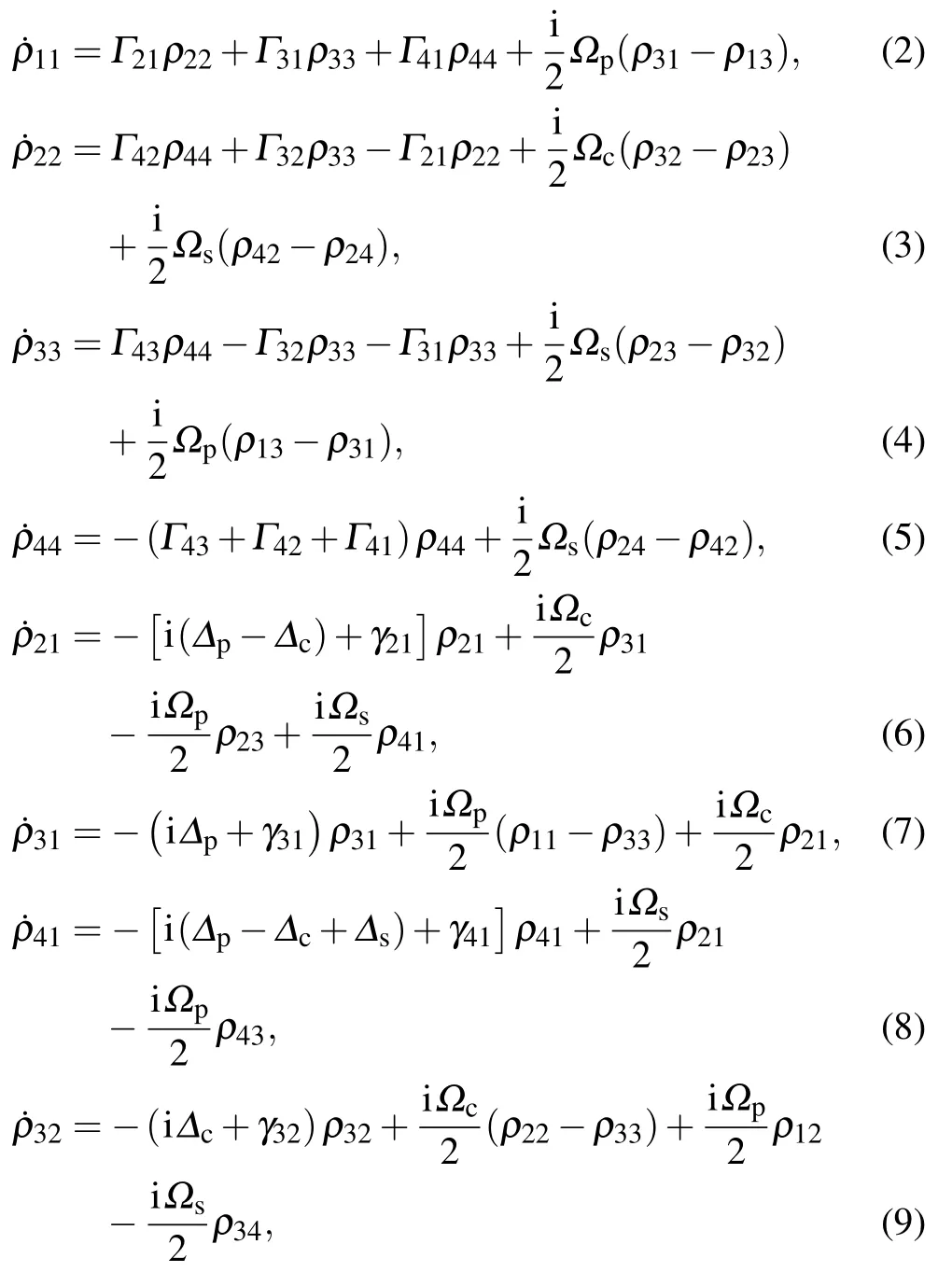
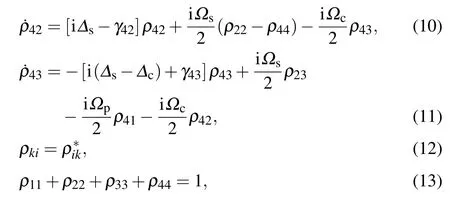
where the frequency detunings of the probe,coupling and signal fields are, respectively, defined as Δp=ωp?ω31, Δc=ωc?ω32and Δs=ωs?ω42.Ωp=d31Ep/, Ωc=d32Ec/and Ωs=d42Es/are Rabi frequencies that are induced by the probe,coupling and signal fields,respectively,wheredkiis a dipole moment of the|k〉–|i〉transition, γkiis the coherence decay rate,while Γkiis the population decay rate from the level|k〉to the level|i〉.
Now, we solve the density-matrix equations under the steady-state condition to find the solution for density matrix element ρ31related to the probe response up to third order perturbation.From Eqs.(6)–(8),we obtain
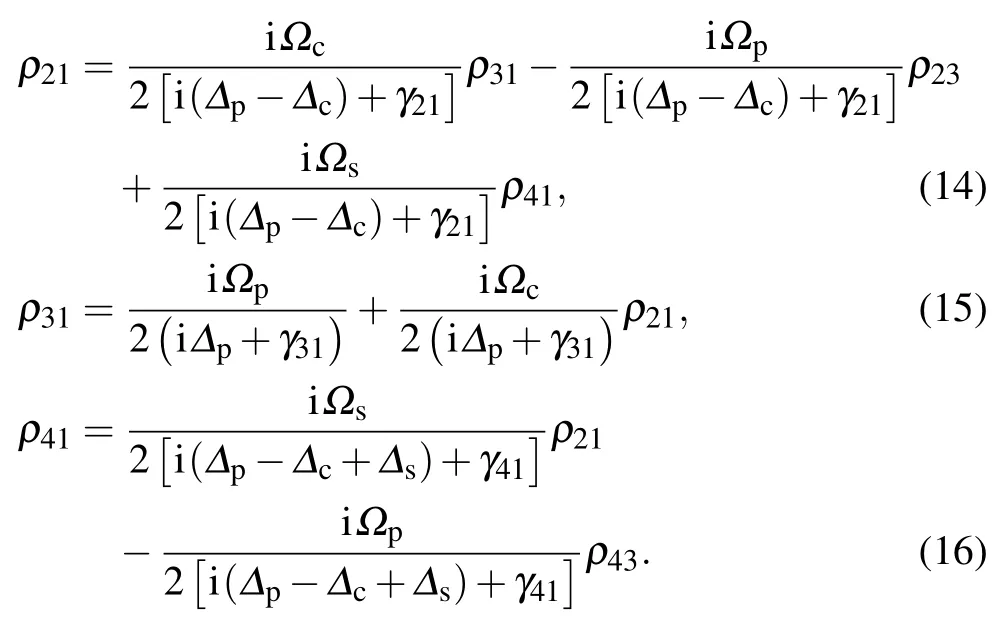
Under the assumption that the probe light intensity Ωpis much weaker than the coupling light intensity Ωcand signal light intensity Ωs,therefore from Eqs.(14)–(16),we find the solution for density matrix element ρ31up to third order in Ωcand Ωsas

where
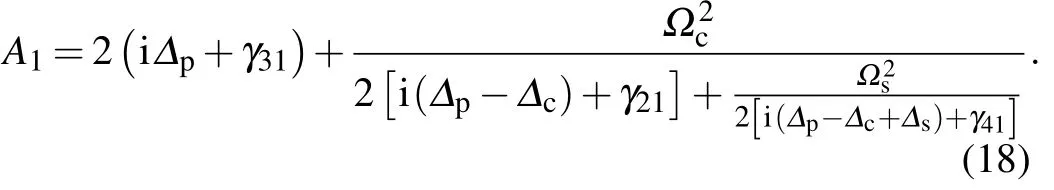
The total susceptibility for the probe field can be determined by the following relations:[18]
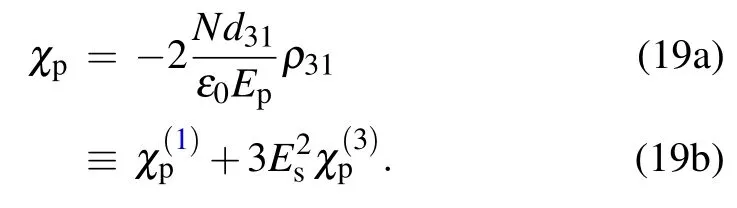
Performing a Taylor expansion in Ωsof Eq.(19a) and then identifying it with Eq.(19b), we obtain expressions of first-and third-order susceptibilities for the probe light field as follows:
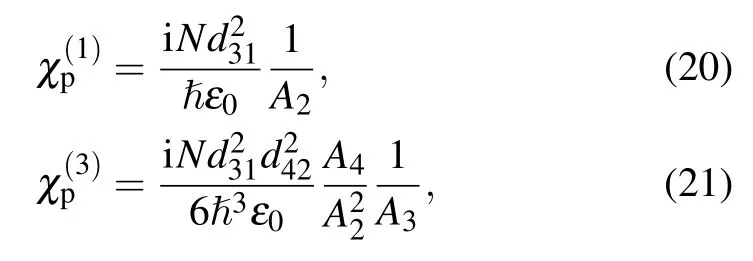
where
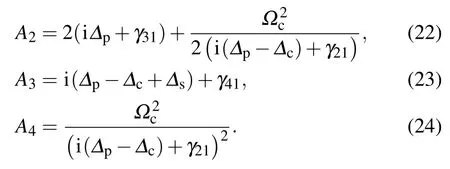
In order to introduce the Doppler effect, we assume that the coupling laser field is co-propagating with the probe laser field while the signal laser field is counter-propagating with the probe laser field into the atomic medium,which can eliminate the first-order Doppler effect.[13]Therefore, when an atom is moving with velocity ν towards the propagation direction of the probe beam, the frequency detunings of probe and coupling beams are upshifted to ωp+(v/c)ωpand ωc+(v/c)ωc,respectively,while the frequency detuning of the signal beam is downshifted to ωs?(v/c)ωs.The numbers of atoms having velocityvwhich lie along the beams obey a Maxwellian distribution

whereu=is the root mean square atomic velocity andN0is the total atomic density of the atomic medium.Therefore,the expressions of the first-and third-order susceptibilities for the probe field must be changed as
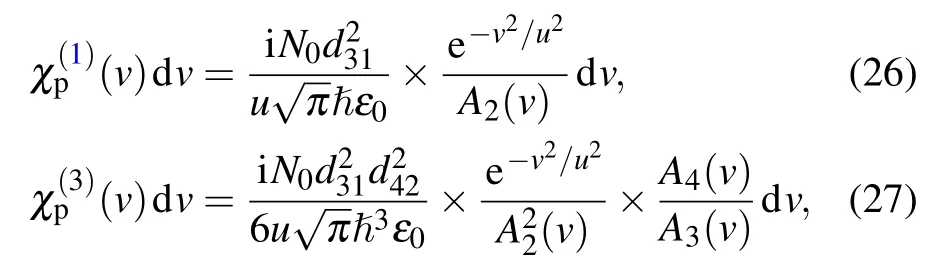
where

The integration of Eqs.(26)and(27)over the velocityvfrom-∞to+∞can easily be performed in Mathematica,which leads to the following results:
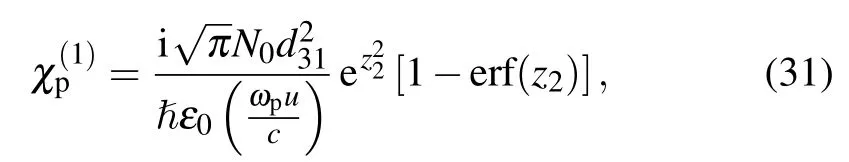
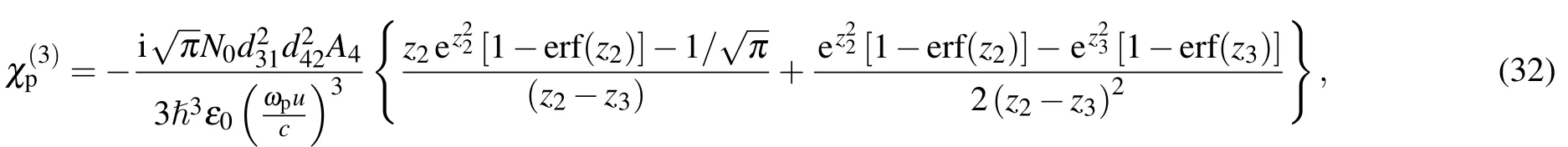
where
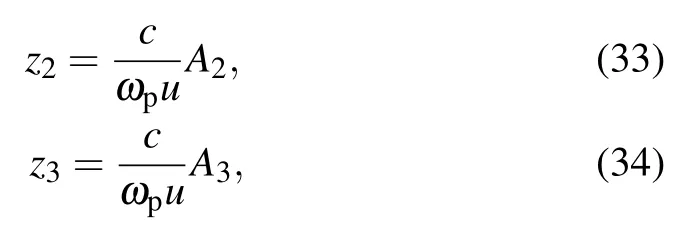
and erf(z)is the error function encountered in integration that has the normalized Gaussian function form
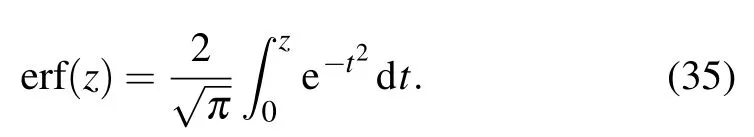
From the first-order susceptibility,the absorption(α)and dispersion(n0)coefficients are calculated by
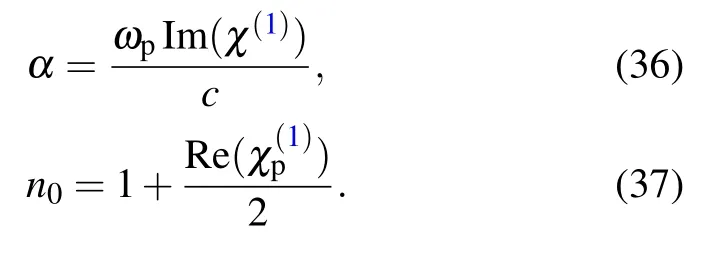
From the third-order susceptibility, the cross-Kerr nonlinear coefficient of the four-level N-type atomic system for the probe field under Doppler broadening is determined by
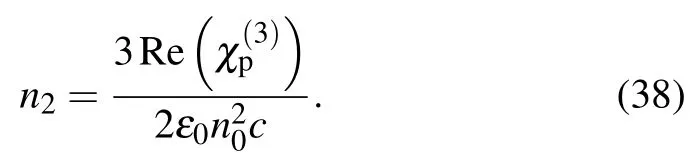
Thus, Eq.(38) combined with Eq.(32) represents the cross-Kerr nonlinear coefficient as a function of the laser and atomic parameters,and the temperature of atomic vapor.In Section 3,we use these expressions to study the influences of the detunings and intensities of the applied fields as well as the temperature of atomic vapor on cross-Kerr nonlinear coefficient in four-level N-type atomic system.
3.Results and discussion
In this section, we apply the analytical model to87Rb atom,where|1〉and|2〉are two hyperfine levels of the ground state |1〉 = |5S1/2,F= 1〉 and |2〉 = |5S1/2,F= 2〉, while|3〉and|4〉are two hyperfine levels of the excited state|3〉=|5P3/2,F′=2〉and|4〉=|5P3/2,F′=3〉.The atomic parameters are[30,33]N=3.5×1017atoms/m3, Γ42=Γ32=Γ31=6 MHz,d31=1.6×10?29C·m and ωp=3.77×108MHz.
Firstly, we consider the dependence of cross-Kerr nonlinearity on the coupling intensity by plotting the cross-Kerr nonlinear coefficient with the probe detuning Δpat different values of the coupling Rabi frequency Ωc=0 (dotted line),Ωc=20 MHz (solid line), Ωc=40 MHz (dashed line) and Ωc= 60 MHz (dash-dotted line), as seen in Fig.2(a).We can see that when the coupling field is absent, i.e., Ωc=0,the cross-Kerr nonlinear coefficient is equal to zero (see the dotted line).This can be explained that when the coupling field is absent, the probe and signal fields become independent (see Fig.1) and therefore they are not induced to create the cross-Kerr nonlinear effect.When the coupling field is present, the cross-Kerr nonlinear effect for the probe field is also established with a pair of negative-positive values ofn2around the probe resonant frequency.By increasing the Rabi frequency of the coupling field, the amplitude of the cross-Kerr nonlinear coefficient also considerably increased.To explain these phenomena, we plotted the absorption coefficient with the probe detuning Δpfor the different values of coupling Rabi frequency Ωcas described in Fig.2(b).It is shown that the width and depth of the EIT window increase with the growth of the coupling Rabi frequency which leads to enhancement of the nonlinear refractive index.
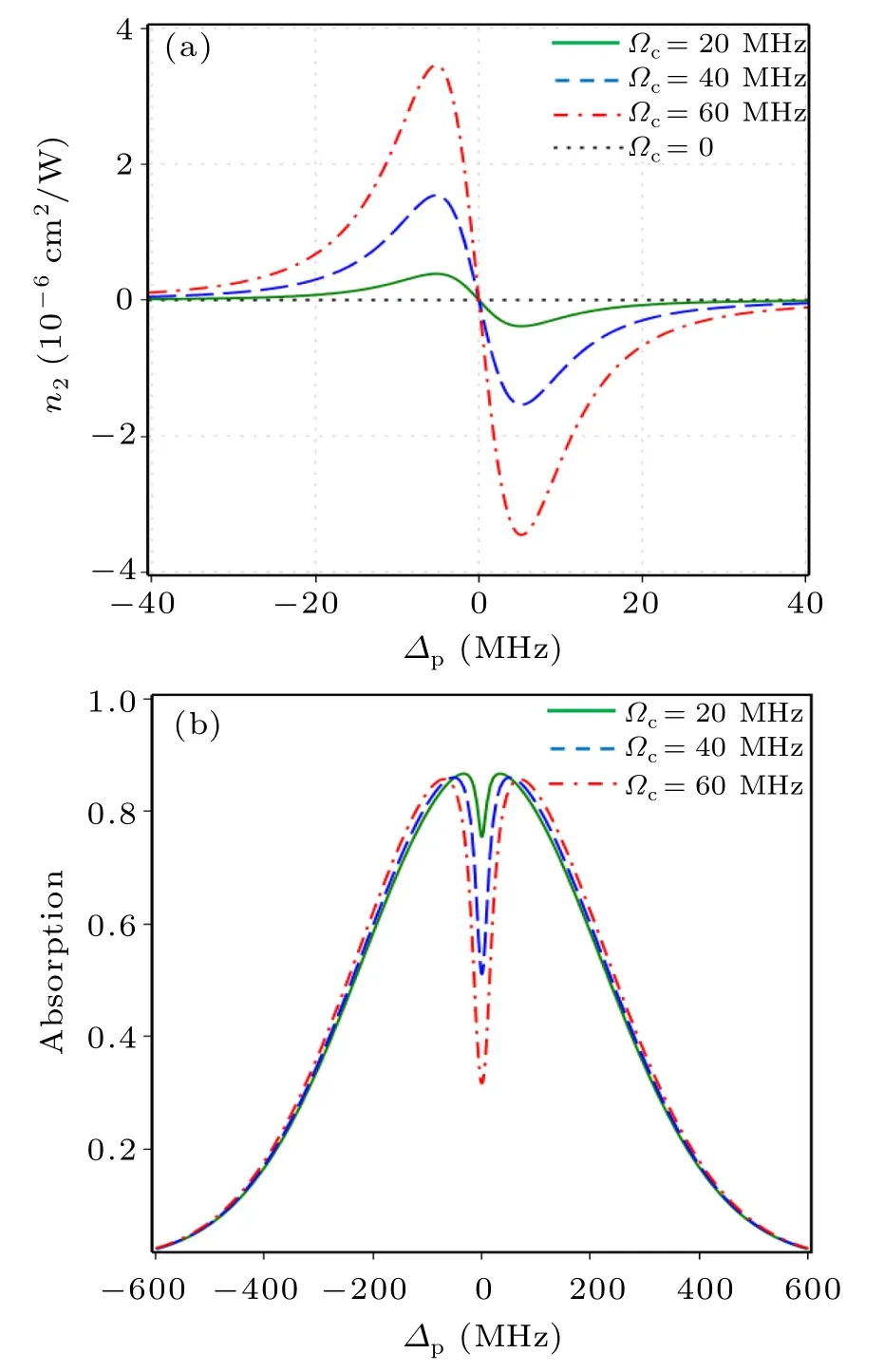
Fig.2.Variations of cross-Kerr nonlinear coefficient(a)and absorption coefficient(b)with probe detuning Δp for the different values of coupling Rabi frequency Ωc when Δc=0 and T =300 K.
In order to see more clearly the coupling intensity dependence of the cross-Kerr nonlinear coefficient, we plot the cross-Kerr nonlinear coefficient with the coupling Rabi frequency Ωcas in Fig.3.Again, it is clear that the magnitude of the Kerr nonlinear coefficient increases with increasing the coupling field intensity.

Fig.3.Variations of cross-Kerr nonlinear coefficient with the coupling Rabi frequency Ωc for the several values of the probe detuning Δp when Δc =0 and T =300 K.
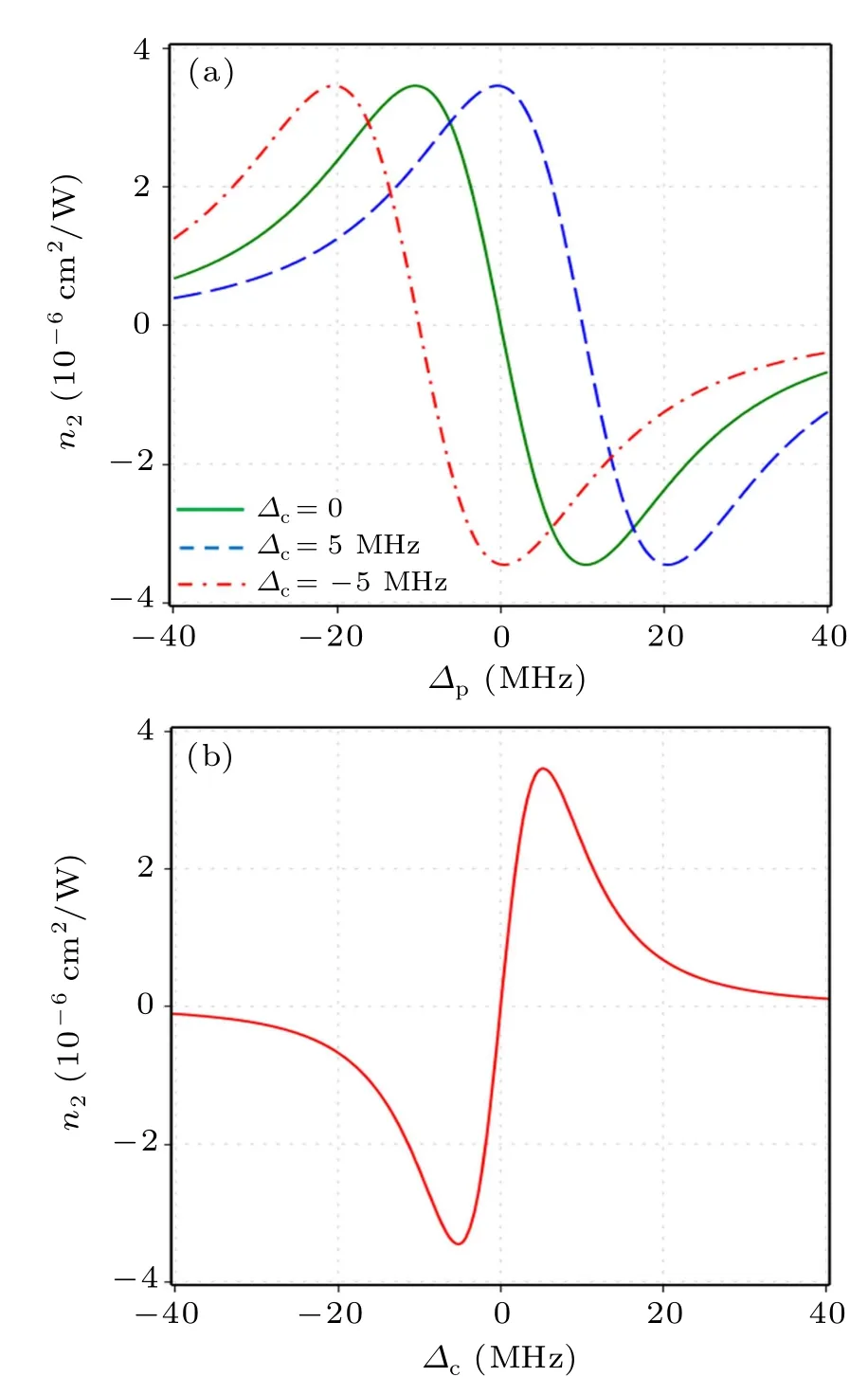
Fig.4.(a)Variations of cross-Kerr nonlinear coefficient with the probe detuning Δp for the different values of coupling detuning Δc.(b)Variations of cross-Kerr nonlinear coefficient with the coupling detuning Δc when Δp=0.Other parameters are Ωc=60 MHz and T =300 K.
Next, we consider the dependence of cross-Kerr nonlinear coefficient on the coupling field frequency by plotting the Kerr nonlinear coefficient with the probe detuning Δpat different values of the coupling detuning Δc= 0 (solid line),Δc=5 MHz (dashed line) and Δc=?5 MHz (dash-dotted line), as seen in Fig.4(a).It is found that at the probe resonant frequency Δp=0, the Kerr nonlinear coefficient is zero when Δc= 0, but it is turned into a negative peak when Δc= ?5 MHz or a positive peak when Δc= 5 MHz.It is because the position of the EIT window changes with the coupling laser frequency to satisfy the two-photon resonance condition(between coupling and probe fields).[12]Figure 4(b)presents the variation of the Kerr nonlinear coefficient versus the coupling detuning when fixed other parameters at Δp=0 and Ωc=60 MHz.It is easy to see that the cross-Kerr nonlinear coefficient is also enhanced around the coupling resonant frequency Δc=0.The amplitude of the cross-Kerr nonlinear coefficient decreases rapidly to zero when the coupling frequency is adjusted far from the atomic resonant frequency.Thus, the value of the nonlinear coefficient can change from negative to zero and to positive when adjusting the coupling laser frequency around the atomic resonant frequency.
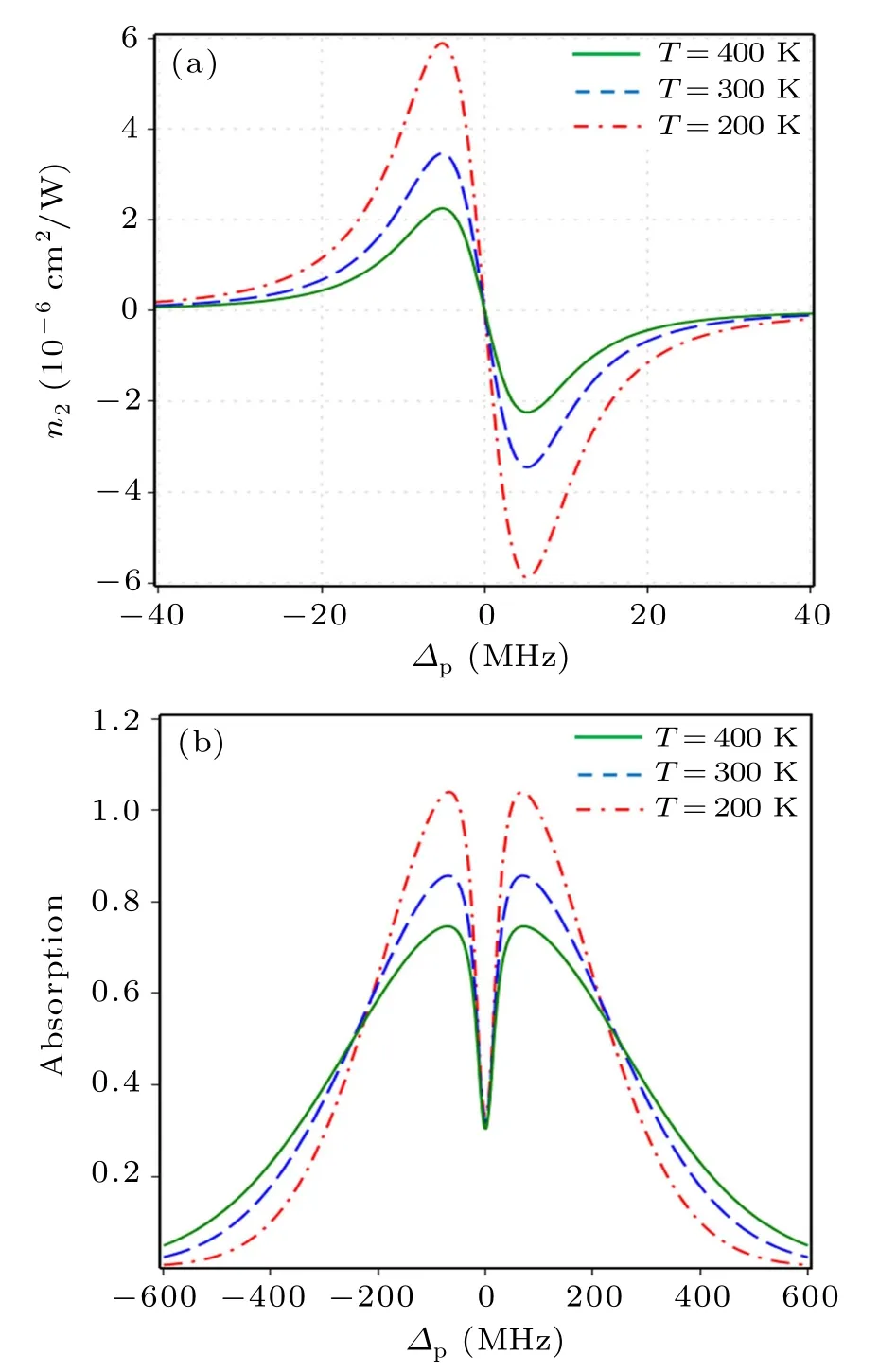
Fig.5.Variations of cross-Kerr nonlinear coefficient(a)and absorption coefficient(b)with the probe detuning Δp for the different values of temperature T when Ωc=60 MHz and Δc=0.
Finally,in Fig.5(a)we examine the influence of Doppler broadening (or temperature) on cross-Kerr nonlinear coefficient by plotting the Kerr nonlinear coefficient versus the probe detuning Δpfor the different values of temperatureT=200 K (dash-dotted line),T=300 K (dashed line) andT=400 K (solid line).An investigation of Fig.5(a) shows that the amplitude of the Kerr nonlinear coefficient considerably reduces when the temperature increases.Also,to explain these phenomena,we plotted the absorption coefficient versus the probe detuning Δpfor the different values of the temperature of atomic vapor as displayed in Fig.5(b).It is clear that the depth of the EIT window decreases significantly with increasing the temperature, therefore the amplitude of the Kerr nonlinear coefficient is greatly reduced.
4.Conclusion
Solving the density matrix equations to the third-order perturbation under the weak probe field approximation, we have derived the expression for cross-Kerr nonlinear coefficient in Doppler broadened four-level N-type atomic medium.Under EIT condition, cross-Kerr nonlinear coefficient of the system is controlled by laser parameters.We found that, the cross-Kerr nonlinear coefficient can be turned on/off when the external light field is on or off.When adjusting the intensity and/or frequency of the coupling laser,the depth and the width as well as the position of the EIT window are also changed.They change the amplitude and the sign of the Kerr nonlinear coefficient.In addition,EIT efficiency decreases with increasing temperature,so the amplitude of the cross-Kerr nonlinear coefficient also remarkably decreases.The analytical model can be convenient to fit experimental observations and study related applications under different temperatures.
Acknowledgement
This work was supported by Vietnam’s Ministry of Education and Training under Grant No.B2018-TDV-01SP.
- Chinese Physics B的其它文章
- A broadband self-powered UV photodetector of a β-Ga2O3/γ-CuI p-n junction
- High-sensitive terahertz detection by parametric up-conversion using nanosecond pulsed laser
- High efficiency,small size,and large bandwidth vertical interlayer waveguide coupler
- High-fidelity resonant tunneling passage in three-waveguide system
- Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves
- Estimation of co-channel interference between cities caused by ducting and turbulence