Long-time evolution of charged grains in plasma under harmonic external force and after being withdrawn
Miao Guan(管苗) Zhi-Dong Chen(陳志東) Meng-Die Li(李夢(mèng)蝶)Zhong-Mao Liu(劉忠茂) You-Mei Wang(汪友梅) and Ming-Yang Yu(郁明陽(yáng))
1Department of Physics,School of Science,Hangzhou Dianzi University,Hangzhou 310016,China2College of Engineering Physics,CAMDT,Shenzhen Key Laboratory of Ultraintense Laser and Advanced Material Technology,Shenzhen Technology University,Shenzhen 518118,China3Institute for Fusion Theory and Simulation,Zhejiang University,Hangzhou 310007,China4Theoretical Physics I,Ruhr University,Bochum D-44780,Germany
Evolution of the charged grains in a two-dimensional dusty plasma under a spatially harmonic external force, in particular,their long-time behaviors after the force has been withdrawn,is studied by using molecular dynamics simulation.Under an external force and a grain–grain interaction force,initially homogeneously distributed grains can reach a quasistationary state in the form of a disk crystal. After the external force is withdrawn,the disk moves initially with its size and shape nearly unchanged until it rapidly stops moving,and eventually the disk grain rotates like a vortex. The time needed to reach the final state increases with the strength of the initial external force increasing.
Keywords: dusty plasma,external force,long-time behavior,molecular dynamics(MD)simulation
1. Introduction
Dusty plasmas have received much research attention in the past few decades. Besides electrons, ions and neutrals,a dusty plasma contains a large number of dust grains.[1,2]Owing to the much higher mobility of the plasma electrons,the dust grains are usually highly negatively charged,for they inelastically collide much more frequently with the plasma electrons.[3]Dusty plasmas are present in space, semiconductor manufacturing,material coating and modification,and many other environments.[4–9]Dust grains in plasma can be produced by chemical reaction, molecular aggregation, or by external injection.[1–5]In laboratory plasma discharges,charged grains of different mass values and charges are usually separately suspended as vertical two-dimensional(2D)layers through balance between a vertical electric field and gravity field,and horizontally confined by a radial electric field.[1,6–10]As a result,when the electric field is turned off,the grains fall to the bottom,an effect that is detrimental in the fabrication of microelectronic devices.[1]The grain–grain interaction force,which is attractive at larger distances due to a unique grain–grain shadowing effect,and repulsive at smaller distances due to electrostatic repulsion,plays an important role in the growing and evolving of dust grains, and can lead to many interesting, unusual, as well as practical phenomena.[3,4,11–26]Recently it has been shown that by tailoring the external force one can obtain controllable compact structures such as dust-grain crystals,[26,27]and the time required to reach the cluster state decreases with external force increasing.[28–33]Although what happens after the external force has been withdrawn can be important in many applications,[1]it has not been investigated.In this paper,we use molecular dynamics(MD)simulation to investigate the evolution of charged grains in a 2D dusty plasma under an external force, particularly the long-time evolution of the resulting grain crystal after it has been withdrawn. It is found that after the external force is withdrawn, the rotating grain crystal will be displaced inertially along the direction of the force for a certain distance and then come to a stop moving.Our results should lead to more detailed theoretical investigation of such an evolution process.
2. Formulation
In our simulation,the dust grains are of the same mass and charge. Initially they are homogeneously distributed. Periodic boundary conditions are used, so the system in fact models a much larger one, but phenomena larger than the simulation box are precluded. The MD simulation runs in the NVT(constant temperature) mode.[34]The external force is spatially harmonic, and the grain number, charge, momentum, and the total energy are conserved.
The massive dust grains are affected by the background electrons and ions, as well as the other grains. Since the electrons and ions are much lighter, on a time scale of dustgrain dynamics they can be treated as in thermal equilibrium.Thus, they provide Debye shielding for the grains’ Coulomb repulsion force. However, because they are finite in size and highly charged, the grains can also block, or shadow mutualinfluence by the background electrons and ions,leading an attractive regime in their effective interaction potential to occur.There are several grain–grain interaction models,[10,12,13,19–21]but they all describe interaction potentials with the same general profile: namely possessing both repulsive and attractive regimes. The differences among the models lie in the ranges and magnitudes of the two regimes. In our simulation, the grain–grain interaction is governed by a modified-Yukawa potential[19,20,28–31,33]
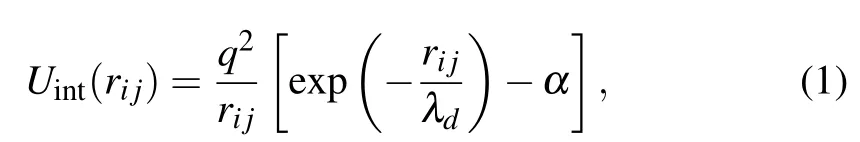
whereλd,q,ri jare the Debye length, the grain charge, and the distance between the grainsiandj,respectively. As mentioned, the grain–grain interaction includes a long-range attractive part,here governed by the constantα,where 0<α<1.[12,20,21]Thus,when the distance between the grains is large(small), the interaction force is attractive (repulsive).[16–21]It should be mentioned that other grain–grain interaction models[3,4,12,13]can also lead to qualitatively similar results,as long as the model includes both attractive and repulsive interaction regime.
The space-dependent harmonic external force is given byFext(r)=?br,wherebis a constant and,whereandare unit vectors. The grains are assumed to be point charges. The momentum equation for the grainiwith massmiis
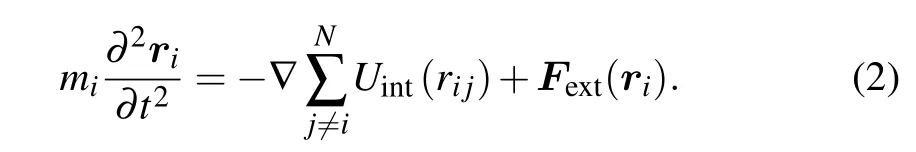
For convenience of the MD simulation and comparison with the existing results, the momentum equation can be rewritten as
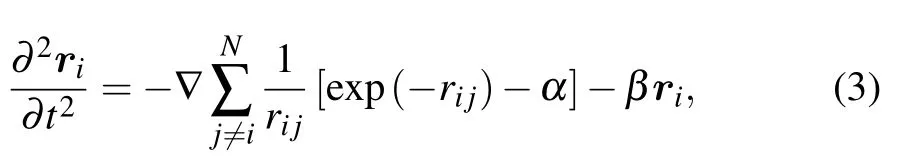
whereriandrijare normalized byλd,tis normalized by
The one hundred (N=100) charged grains are initially homogeneously distributed in the form of a 10×10 square matrix. The initial density of the charged grainsndis normalized by the plasma densityn0,which implicitly determines the initial grain–grain separation distance. The average initial(Maxwellian distributed)grain velocities are characterized by their temperatureTd=2〈Ek〉/3Nk,where〈Ek〉is the total kinetic energy of all charged grains(in units of eV).For definitiveness, in the simulation we setTd=5×10?5,nd=0.004,andα=0.5. The simulation time step is Δt=0.03.
The grain evolution contains two stages. In the first stage,the grains gradually aggregate and eventually reach a statistically stationary state in the form of a disk crystal.In the second stage,the external force is stepwise withdrawn untilβ=0.We are interested mainly in the evolution of the disk crystal,especially its long-time behavior after the external force has been fully withdrawn.
3. Methods and results
We first consider the evolution of the charged grains forβ=3×10?4. The grains are initially uniform in space but their velocities are of Maxwellian distribution as shown in Fig. 1(a). The external force is already present in the initial stage, nearby grains aggregate and form small clusters under the action of the external force and grain–grain interaction force as shown in Fig. 1(b). The clusters and individual grains continue to combine until the system reaches a statistically quasi-stationary state in the form of a rotating disk-like crystal in the center of the simulation box as shown Fig.1(c).Figure 1(d)is an elongated near-center region of the disk crystal. It can be seen that the grains in the crystal experience external-force driven harmonic oscillations in the direction of the force, with the oscillation periodTf=390. Fluctuations due to macroscopic grain–grain interactions also exist, but their amplitudes are much smaller than the counterpart in the case of the external-force driven harmonic oscillations and difficult to be distinguished from the numerical fluctuations.
We now consider what happens after the external force has been withdrawn. Fromt= 15000 on, the strengthβof the external force gradually decreases, namely in steps of Δβ=0.0001 in time steps of Δt=3000 untilβ=0. The oscillation period of the grains in the disk cluster increases asβdecreases as expected.[31]
As shown in Fig. 2, after the external force vanishes att=2.4×104,the grain disk first moves diagonally across the simulation box along the direction of the withdrawn external force at nearly constant speed. The grain’s exterior,i.e., size and shape, rather than its internal dynamic behavior, also remains almost unchanged. This can be attributed to the fact that although the external force conduces to the disc formation process(for the parameters chosen, no such single-disk crystal is formed if the external force is absent),after its formation the overall structure of the grains is mainly determined by the grain–grain interaction potential, since the distance between the grains is now restricted. On the other hand,as long as the external force is still present, it dominates the grain oscillations. With each decrease in the value ofβ,the grain oscillation inside the disk relaxes to less external-force driven state and more grain–grain interaction driven state. The grain disc moves at nearly constant speed untilt=54150,when it rather rapidly slows down and becomes stationary.
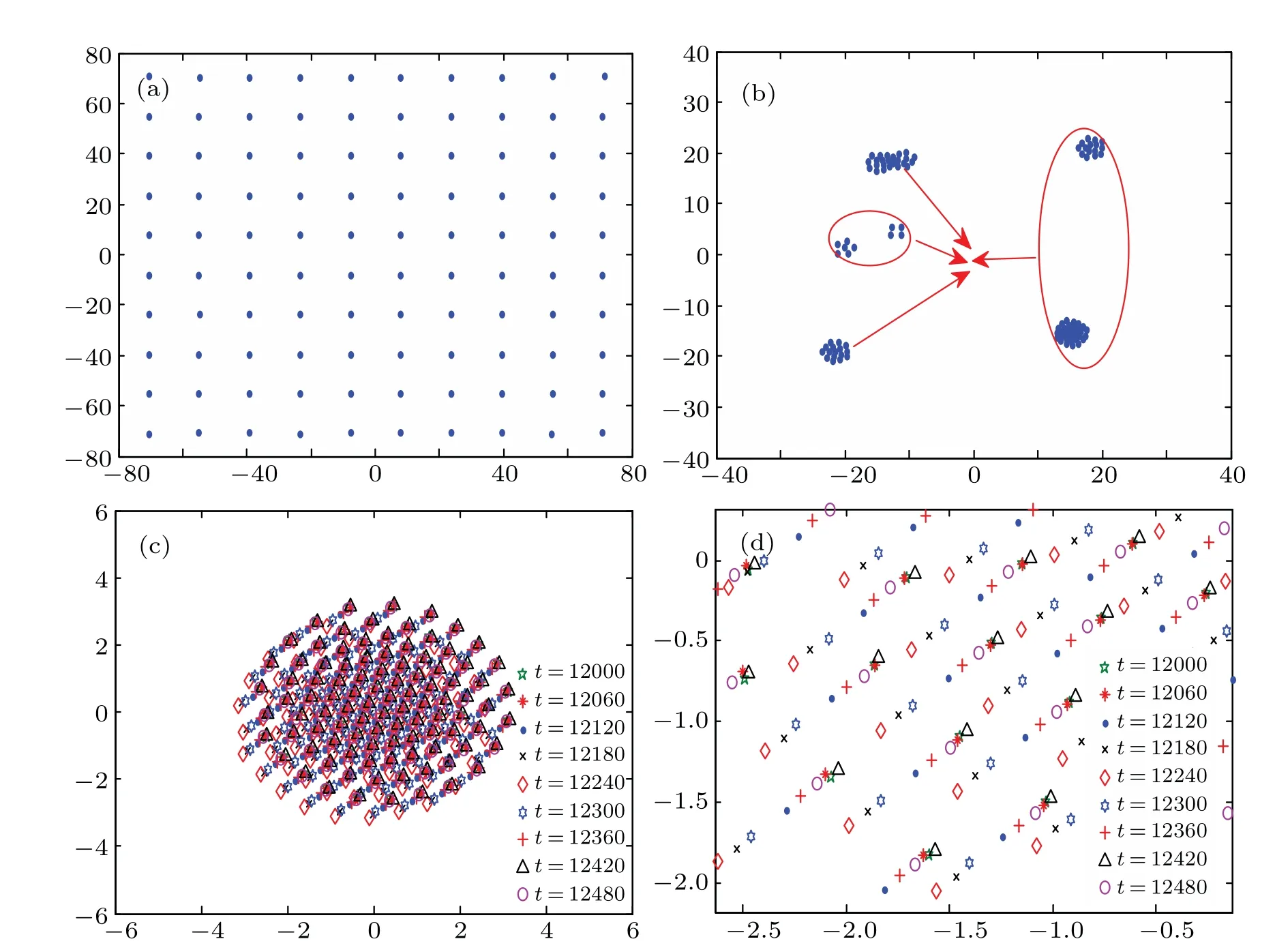
Fig.1. Evolution of the charged grains for β =3×10?4. (a)Initial grain distribution,(b)intermediate stage in clustering process,where red arrows roughly show the movement of the already-formed small clusters,(c)formation of disk-like crystal,(d)enlargement of near-center region in panel(c),synchronized external-force driven grain oscillations can be clearly seen. Here and in the following figures,Td=5×10?5,nd=0.004,and α =0.5.
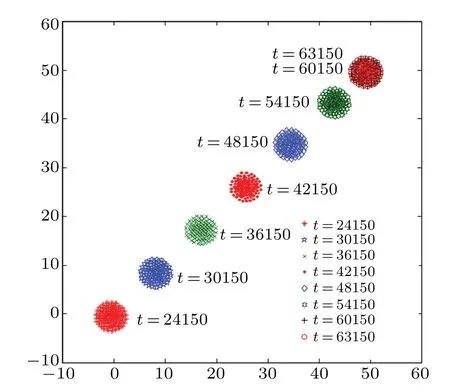
Fig. 2. Trajectory of disk crystal formed in the center of the simulation box after the external force β = 3×10?4 has been fully withdrawn at t =2.4×104. The disk first moves forward initially in the direction of the external force, and then stops at t =60150. Before that, it also slows down rather rapidly,starting at t=54150.
We now consider the self-organization of the grains after the external force has been completely withdrawn. Figure 3(a)shows that the onset time of rapid velocity decrease depends on the translational disk velocity at the instant when the external force vanishes. For example, with the initial external force strengthβ=3×10?4, the disk speed is 2.1×10?3att=2.4×104,which is greater than the value 1.4×10?3att=2.61×104and less than the value 3.7×10?3att=2.55×104.The disk speed depends more on the instant when the external force is fully extinguished than on the initialβ: the larger the disk speed,the earlier the disk becomes stationary.Figure 3(b)for an enlarged region of Fig. 3(a) shows that the time of the rather rapid speed change is almost the same if the disk speed is the nearly the same at the time when the external force vanishes. In general, the time of the speed drop depends more on the speed of the disk than on the initial strength of the external force, and the time needed for the disk to stop moving decreases with its speed increasing.
Figure 4 shows that after the rapid slowing down and stopping of the disk motion, the rotation of the grains is also redistributed (in addition to their oscillations). That is, after withdrawing the external force,part of the oscillation energy is converted into rotational energy,and part of it into directional energy,with the corresponding momentum converted into that in the azimuthal direction and radial direction respectively.In fact, figure 5 for still longer times shows that the grains eventually become circularly distributed. They also move azimuthally,as well as oscillate weakly as shown in Figs.5 and 6.
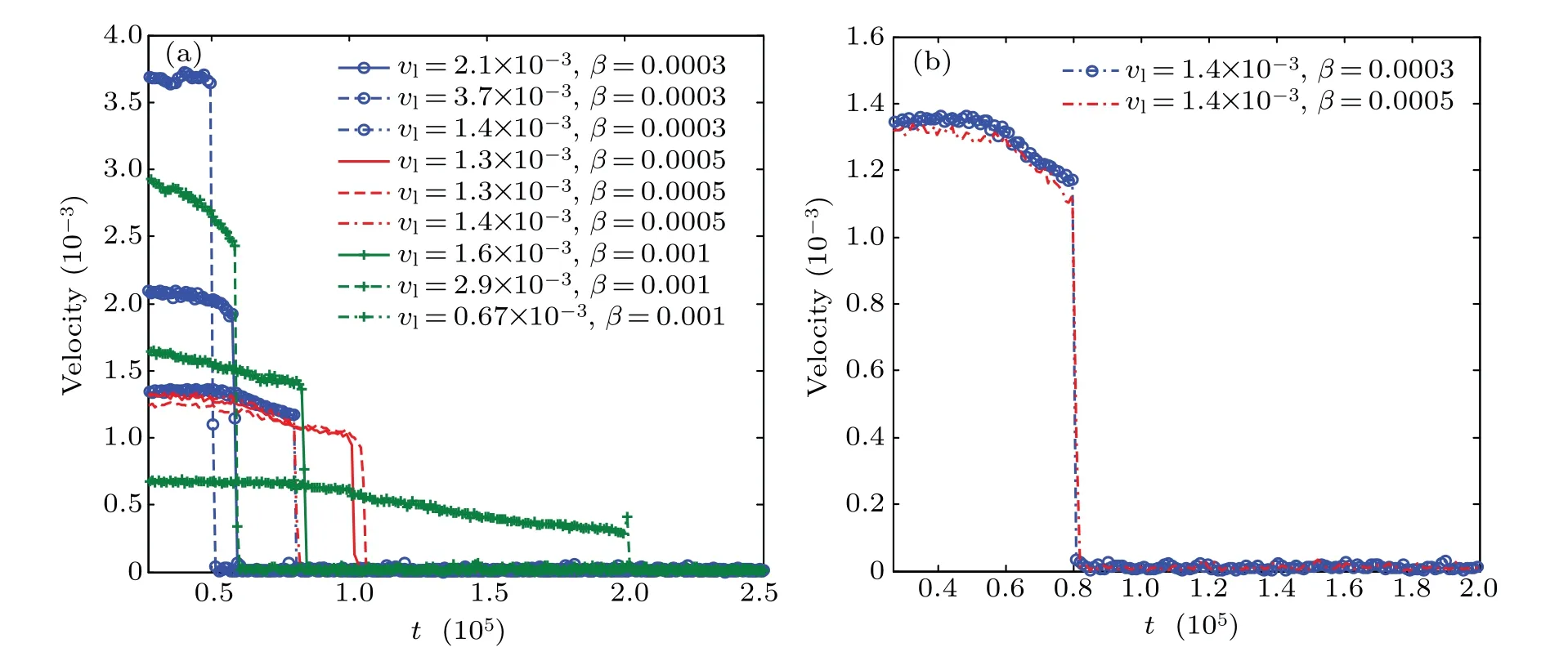
Fig.3. Evolution of speed of disk crystal after the external force has been fully withdrawn(occurring at different times)for different values of force strength β. Here,vl is the linear or translational disk velocity,and the solid,dashed,and dash-dot curves are for the instant t=2.4×104,2.55×104,and 2.61×104,respectively,at which the external force is fully withdrawn. (b)Details of rather rapid speed-reduction stage for two closely related cases,showing that this change depends more on the instant of withdrawing the external force,rather than on its initial magnitude.
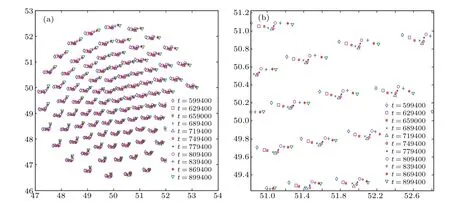
Fig. 4. (a) Motion of dust grains during and after the rapid decrease of the linear velocity and stop of the disk for the initially β =3×10?4 case. (b)Enlargement of a region in panel(a). In the self-organization process,besides the oscillations of the grains,their rotational motion is redistributed.
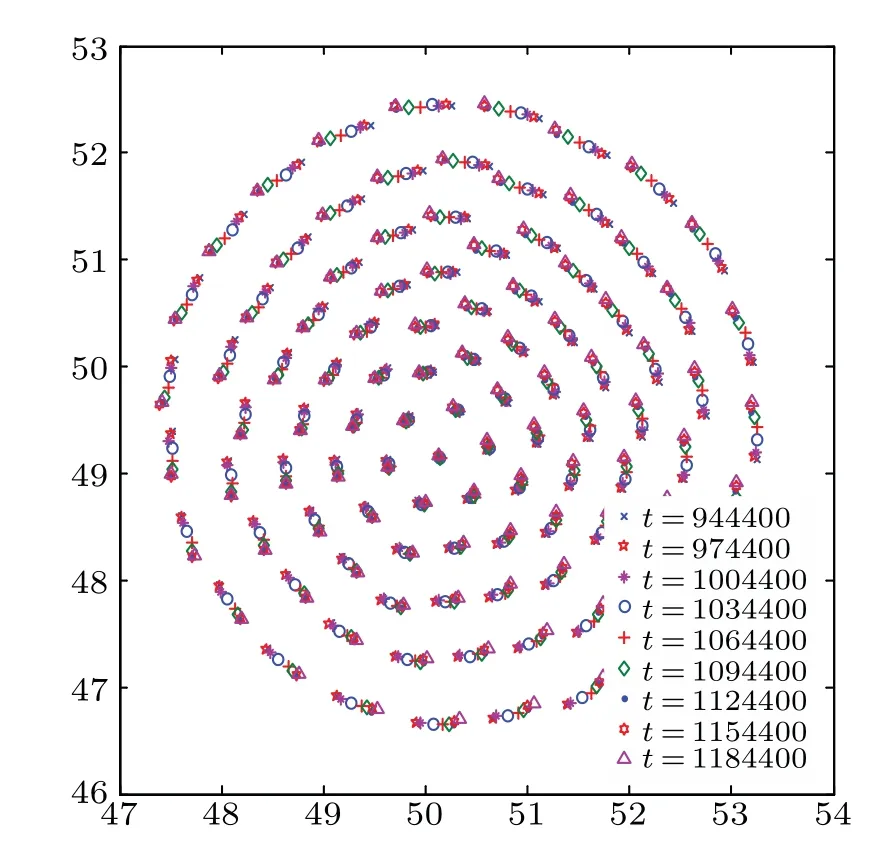
Fig.5.Motion of charged grains at long times for(initial)β =3×10?4.The grains are now radially distributed, and rotate azimuthally like a vortex rotating slowly,and fluctuate as well(also see Fig.6).
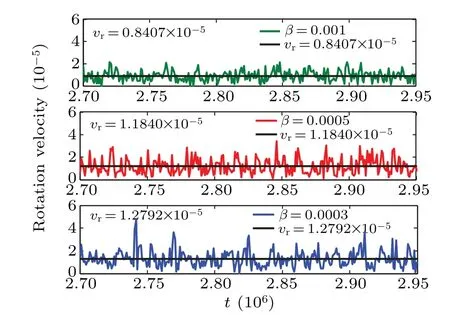
Fig.6. Evolution of the rotation speed vr versus t for different initial values of β,with black solid line denoting average velocity.
In the final, or longtime, quasi-stationary state, all the charged grains in the disk rotate and also fluctuate azimuthally.The average rotation speed decreases with the initial external force increasing as shown in Fig.6. As mentioned above,thetime needed to reach a quasi-stationary state after the external force has been withdrawn increases with the force strengthβincreasing.
For completeness,figure 7 shows the velocity autocorrelation function[32]
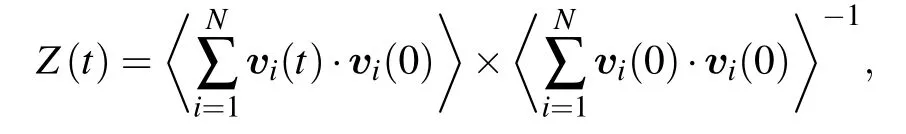
of the final state of the grains for different initial values ofβ, withtdenoting the correlation time. The crystal-like short-time correlation and lack of long-time correlation can be clearly seen. We can see that the fluctuation frequency increases with the value ofβincreasing,and that the VACF decays faster for larger initialβvalues.
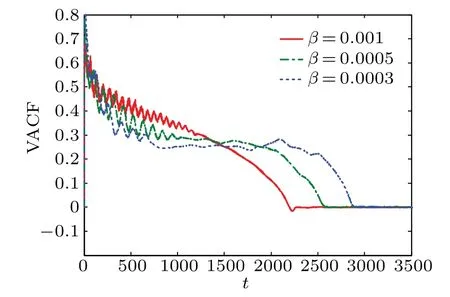
Fig.7. Long-time behaviors of VACF for different initial values of β,with t denoting the correlation time.
4. Summary and discussion
We have phenomenologically considered the evolution of charged grains in a 2D dusty plasma during applying and after withdrawing a harmonic external force. Small grain clusters are first formed, which then merge into a circular disk-like crystal in the center of the simulation box. The oscillations of the charged grains inside the disk are driven mainly by the external force,and their period depends on the force strength.After the external force is withdrawn in a stepwise manner,the grain disk moves inertially along the direction of the extinct external force at nearly constant speed. The grain exterior,i.e.,size and shape,rather than its internal dynamic behavior,remains almost unchanged until it stops moving rather rapidly.In the process, the original external-force driven coherent oscillations are gradually converted into the rotational motion.In the final long-time quasi-stationary state,the charged grains rotate around the center of the disk like a vortex rotating, accompanied with the incoherent small fluctuations. The time needed to reach this state depends on the strength of the initial external force. The larger the force, the longer the time needed to reach the asymptotic state, and the slower the final rotation speed. The withdrawing of the external force apparently provides the free energy that causes the eventual rapid stop moving of the grain disk and redistribution of the grain momenta. However, the physics of the observed phenomena,especially the rapid stop moving of the inertially moving disk,is still unclear and open for more rigorous,especially theoretical, investigation. It should also be noted that the stepwise manner in which the external force is withdrawn here may be physically nonequivalent to invoking a time-dependent external force that decreases smoothly,which would make the system nonconservative from the very beginning.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11975088 and 11705041) and the Natural Science Foundation of Zhejiang Province, China(Grant No.LY15A050001).
- Chinese Physics B的其它文章
- High sensitivity plasmonic temperature sensor based on a side-polished photonic crystal fiber
- Digital synthesis of programmable photonic integrated circuits
- Non-Rayleigh photon statistics of superbunching pseudothermal light
- Refractive index sensing of double Fano resonance excited by nano-cube array coupled with multilayer all-dielectric film
- A novel polarization converter based on the band-stop frequency selective surface
- Effects of pulse energy ratios on plasma characteristics of dual-pulse fiber-optic laser-induced breakdown spectroscopy