Color-image encryption scheme based on channel fusion and spherical diffraction
Jun Wang(王君) Yuan-Xi Zhang(張沅熙) Fan Wang(王凡) Ren-Jie Ni(倪仁杰) and Yu-Heng Hu(胡玉衡)
1Sichuan University,School of Electronics and Information Engineering,Chengdu 610065,China
2Department of Electrical and Computer Engineering,University of Wisconsin-Madison,Madison,WI 53706,USA
Keywords: channel fusion,hyper-chaotic system,asymmetric encryption,spherical diffraction
1. Introduction
In the past few decades, information security has been widely discussed in the military field and civilian field. As one of the most common information carriers, encryption research on the image has always been a concern of scientific researchers. Unlike traditional digital encryption, optical encryption has attracted more and more attention due to its high-speed transmission,parallel processing,and large capacity. The earliest optical encryption system can be traced back to the double random phase encryption scheme proposed by Refregier and Javadi in 1995,[1]which can encrypt the image into stationary white noise in the 4f optical system. However, this symmetry system was later proved to be vulnerable to known-plaintext[2]and chosen-plaintext attacks.[3]To overcome the shortcoming,the fractional Fourier transform,[4,5]fractional Mellin transform,[6,7]phase-shifting interferometry,[8,9]Fresnel transform,[10]ghost image,[11]and cylindrical diffraction[12,13]have been proposed. Moreover,as an important branch of image encryption,a lot of colorful image encryption schemes[14-20]have been proposed based on previous researches.
Nevertheless, most of color image optical encryption schemes at present which convert color plaintext into color ciphertext suffer the problem of information leakage.[21-23]The red-green-blue (RGB) channels of the color image are encrypted independently first in these encryption schemes.Then,encrypted channels are fused into a color image again. In this case, the attacker only needs to know part of the ciphertext and private key to obtain most of the partial information of the plaintext image. There are two feasible schemes to solve this problem. One is to reduce the strong correlation between separate RGB channels and the color image,[24-26]such as changing the pixel values or position of one channel through another channel.[24]However, like the parallel processing scheme, this scheme usually requires optical modulations more than once to obtain the ciphertext. Moreover,since the existing hardware usually discretizes the image,this scheme will lead to more errors in optical encryption and reduce the quality of the decrypted image. Therefore, researchers proposed another scheme[27-29]whose idea is similar to multi-image encryption.[30]Dissimilarly, the second scheme tries to transform a color image into a grayscale image. A common method to transform a color image into a single channel image is to perform the convolution operation on all three channels together.[28,29]Compared with the first scheme, the second scheme is more suitable for optical encryption. However, the second scheme usually requires more private keys to separate the merged images during decryption.And the second scheme does not solve the problem of information leakage well since the attackers can still obtain the complete information about a particular channel if they know the full ciphertext and part of the private keys. Therefore, considering the problems of existing schemes, it is necessary to develop a more secure and efficient color image encryption scheme. The proposed encryption scheme should integrate the advantages of first and second schemes and avoid their disadvantages.
In this paper, a color-image encryption scheme based on channel fusion and spherical diffraction is proposed. In this scheme, a color image is first transformed into a grayscale image by channel fusion technology based on a hyperchaotic system and discrete wavelet transform (DWT). Here, the hyperchaotic system is to reduce the correlation between the RGB channels and colorful original image, and the DWT is to transform the color image into a grayscale image. Then,the grayscale image is modulated by a mask generated by the hyperchaotic system. The modulation result is input into an asymmetric spherical diffraction system which is more secure than the symmetric system. Finally, the improved equal module decomposition (IEMD) is used to hide the complexvalued result of diffraction into two real-values masks which are more valuable for the actual data transmission. The proposed scheme can solve the problem of information leakage well in optical encryption. The simulation results and safety analysis prove the effectiveness of our scheme.
2. Principle of encryption and decryption
Here in this section, some basic principles related to our proposed scheme are introduced.
2.1. Encryption in spherical diffraction domain
Owing to the asymmetric property of spherical diffraction, the shortcomings of symmetry of the plane diffraction encryption schemes can be overcome. Therefore,it can resist ciphertext attack, plaintext attack, and phase-retrieval attack.Meanwhile, the diffraction parameter can also be used as a private key to improve the security of the encryption scheme.
According to spherical holographic theory,[31-35]the object surface and observation surface of spherical diffraction are the surfaces of concentric spheres with radii ofrandR.Hence,there are two propagation models which are inside-tooutside propagation(IOP)model and outside-to-inside propagation(OIP)model as shown in Figs.1(a)and 1(b).
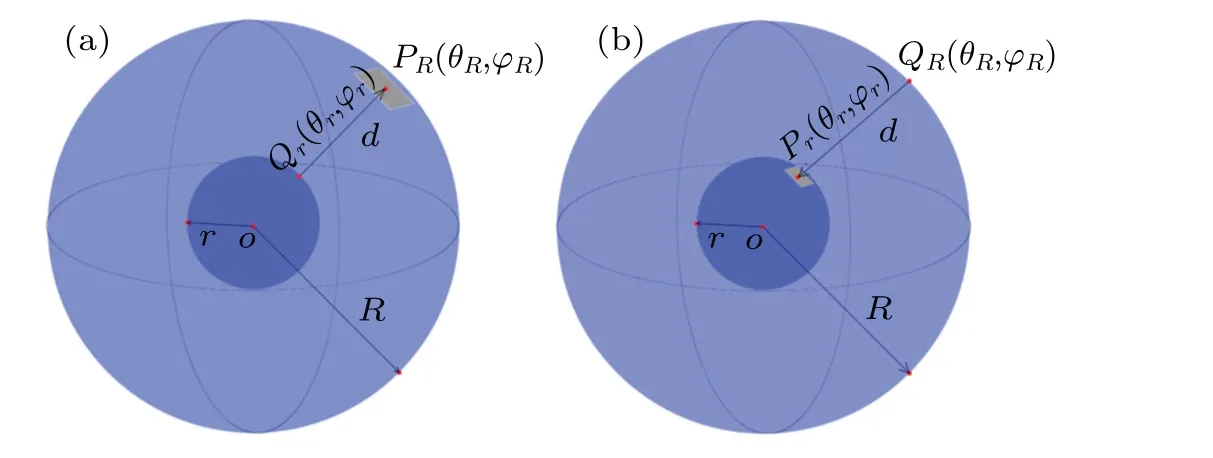
Fig.1. Spherical diffraction of(a)inside-to-outside propagation model and(b)outside-to-inside propagation model.
For the IOP model,Qr(θr,φr)andPR(θR,φR)represent the object point and observation point in the spherical coordinate,respectively. For the OIP model,QR(θR,φR)andPr(θr,φr)denote the object point and observation point in the spherical coordinate,respectively. TheθrandθRare in a range from-πtoπ,andφRandφrare in a range from-π/2 toπ/2. If we denote the diffraction distributions on inner surfaces and outer surfaces asur(θr,φr)anduR(θR,φR),the diffraction integral equations based on the Rayleigh-Sommerfeld integral equation of the two models can be written as
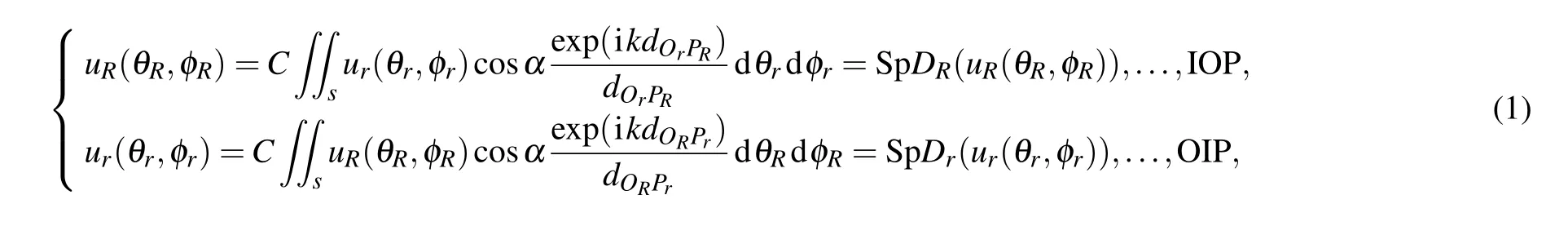
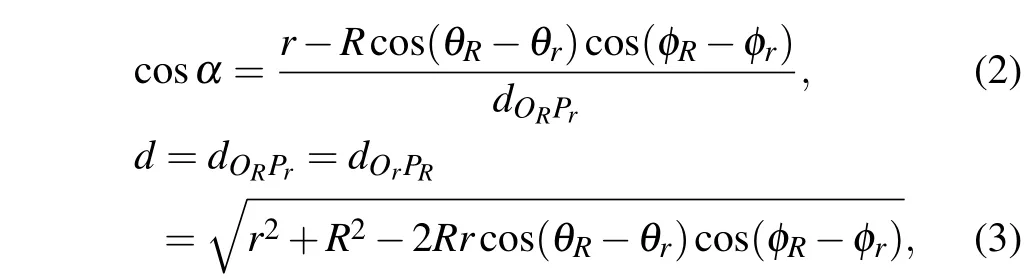
whereCis a constant andkdenotes the wavenumber of the incident light,drepresents the distance between the observation pointPand the object pointQ, andsrefers to the object surface.
2.2. Improved equal module decomposition
In conventional equal module decomposition(EMD),[36]a complex amplitudeUcan be represented by two equal module masksP1andP2. The new distribution of complex amplitude can be rewritten as
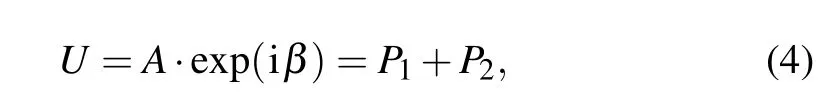
whereAis the amplitude ofU, andβis the phase ofU. If a random phase mask (RPM) (in the following text, RPM is denoted byR)distributed uniformly in the interval[0,2π],R2is expressed as

where rand(M×N)means a random number matrix ofMrows andNcolumns,and the value range of element is[0,1]. Here,P1will be gained byA,andP2byβandR2.
However,P1andP2are expressed as two complex-valued masks and they are not convenient to transmit. Therefore,an IEMD scheme is used[37]to solve the problem. Here in the IEMD the output ofP1andP2are replaced byCandPKwhich are both real valued. Under the IEMD,the decomposition equation of complex amplitudeUis as follows:
U=C·[exp(iR2)+exp(iPK)],
C=0.5A·[cos(β-R2)]-1, PK=2β-R2=arg(P2),(6)
whereCis ciphertext, andPKis the private key. In our scheme,R2is generated from the hyperchaotic system controlled by private key. Therefore, it is not necessary to transmitR2. Hence,Uis hidden into two real-valued masks [C,PK]successfully.
3. Proposed scheme
3.1. Encryption process
Step 1 First, we need to generate several sequences or masks. In this step, Chenet al.’s four-dimensional (4D) hyperchaotic system[38]is used to generate the sequences and masks for subsequent encryption. The hyperchaotic system is as follows:
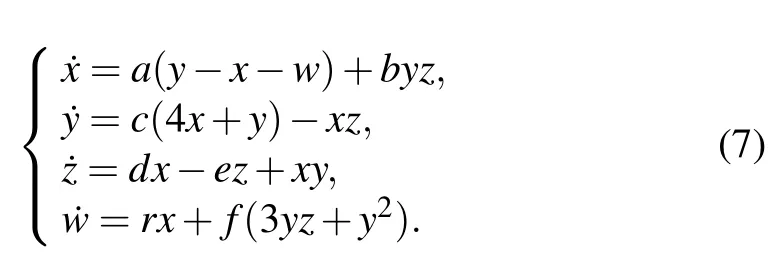
Here, the parameters of the system are set to bea=80,b=45,c=22,d=5,e=21,f=8,andr=78,and they are broadcasted as public keys.
The initial conditions used as private keys are determined by different plaintexts. The initial value ofx,y,z, andware determined by variance and mean of the color plaintext, respectively. The generated four sequences are used as key1,key2,R1,andR2for subsequent encryption. The key1 and key2 are used in the channel fusion process.R1is a random phase mask which forms a complex amplitude with the fused image in spherical diffraction.R2is the random mask in IEMD.
In the actual transmission,the only private keys we need to transmit are the initial values of the hyperchaotic system.
Step 2 In this step, the color plaintext is processed by channel fusion based on DWT and the keys generated by the hyperchaotic system. The channel fusion will change the distribution and values of the plaintext pixels through key1 and key2 and finally resulting in a grayscale image.
Firstly,the RGB channels of colorful image are separated,and they are processed by as follows:
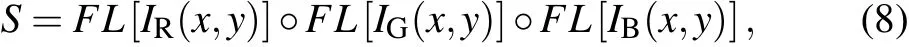
whereIR,IG, andIBrepresent the corresponding RGB channels of the original image,FL[·]denotes the progress of transforming a two-dimensional (2D) image matrix into a onedimensional(1D)pixel sequence,°refers to the matrix splicing operation,andSis the spliced sequence.
Secondly, the sequenceSis diffused and permuted by key1 and key2 which are obtained in step 1, and expressed as
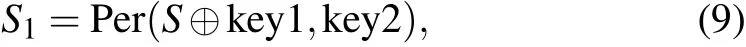
where Per(a,b) denotes usingbto permutea, and⊕is the operation of XOR.
After that,S1is reshaped from a sequence to three matrices. Each of the three matrices contains part of the information about the three RGB channels, which means that the strong correlation between the RGB channels is weakened. In this way, the corresponding color plaintext cannot be recovered well while missing any matrix.After reshaping the fusion sequence back to three gray-scale images, they will perform inverse DWT[39]together with the interfering image to finally get a grayscale image

where IDWT[·]is the inverse discrete wavelet transform,Re(·)is the operator of reshaping.Itis the interfering image, andf(x,y) is the grayscale image after fusion. The process of channel fusion is shown in Fig.2,and the intermediate and the final results of channel fusion are shown in Fig.3. The size of final fused image is four times that of the original image.

Fig.2. Channel fusion process.

Fig.3. Channel fusion results,showing(a)original image,(b)interfering image,IDWT without(c)and with(d)permutation and diffusion,and(e)fusion image.
Step 3 After the channels are fused, the phase mask RPM(x,y)=exp(jR1) generated by the hyperchaotic system andf(x,y) together form the complex amplitude distribution to be diffracted.
According to the theory of Eq.(1),the result of diffraction in IOP mode is expressed as a complex distribution
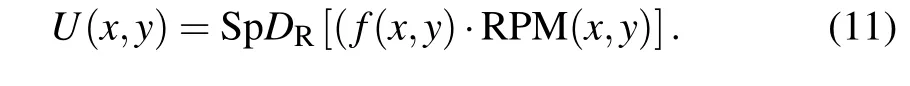
Step 4 Owing to the fact that the result of spherical diffraction is a complex distribution, it is necessary to make it more convenient to the actual data transmission. Compared with the traditional EMD, the IEMD can hide complex amplitude into two real-value masks while improving security.According to Eq.(6),the result of spherical diffraction can be rewritten as
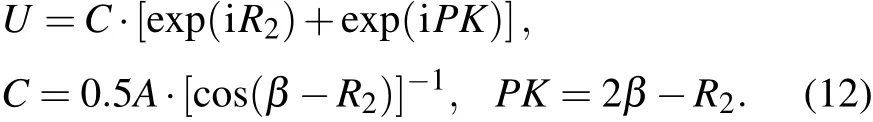
The whole encryption progress is shown in Fig.4.
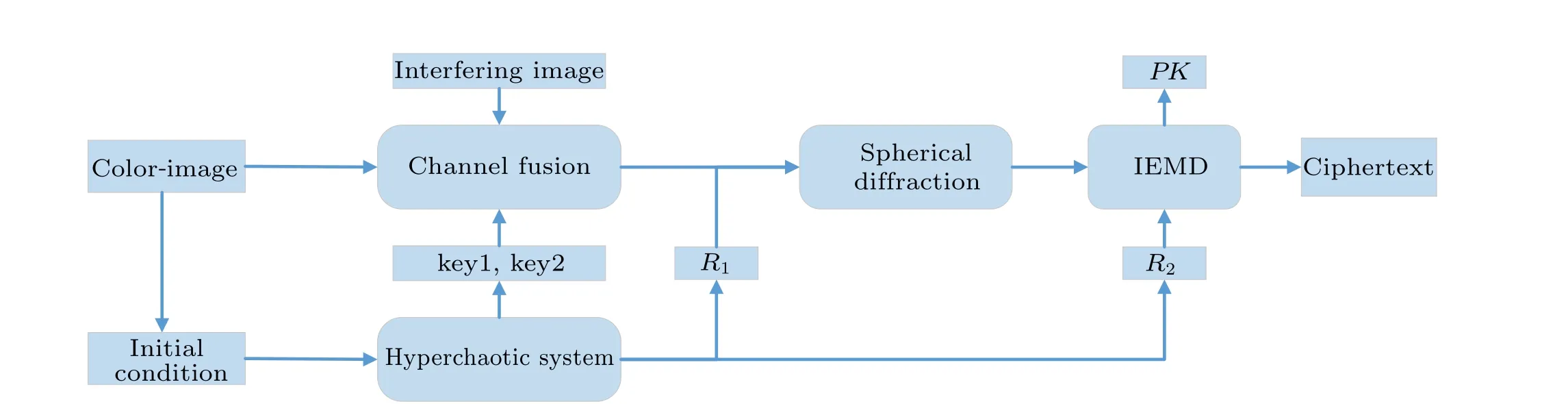
Fig.4. Encryption process.
3.2. Decryption progress
Step 1 Firstly,according to Eq.(12),we can obtain the complex amplitudeU. TheUis modulated by RPM*after spherical diffraction. The fused imagef(x,y)can be obtained from

where LH corresponds to the red channel, HL denotes the green channel,and HH refers to the blue channel. The correspondence between subbands and channels will be determined by the encryption process.
Step 3 Then,S2is inversely permuted and inversely diffused to restoreS. According to Eqs. (8) and (15), the onedimensional sequenceSwith complete RGB three-channel information is then reshaped into three two-dimensional matrices corresponding to RGB. Finally, the RGB channels are merged and the colorful plaintext is restored as shown below:
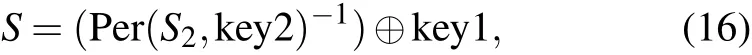

where Per(a,b)-1is the inverse process of Per(a,b), and merge{·}means RGB channels’mergence.
4. Simulation results
4.1. Encryption and decryption result
The simulation is performed with Python 3.8.2 to analyze the performance of the proposed scheme on a 64-bit computer. In the simulation, the radius of the outer sphereR, the radius of the inner spherer, and the wavelengthλare set to be 500 mm,50 mm,and 0.25 mm. According to the spherical holographic sampling theory,[34,35]the above parameters require that the number of sampling points in the horizontal and vertical directions of the image should be at least 2513 pixels and 1257 pixels. However, if we select only 1/5 of the sphere surface, the minimum number of sampling points required will be 503 pixels and 252 pixels in the corresponding direction. To achieve this goal, the size of the original image is select as 256×256×3, and the corresponding size of the ciphertext is 512×512. Figure 5 shows the result of encryption and decryption with plaintext ‘baboon’. The parameters related to spherical diffraction and the hyperchaotic system are listed in Table 1.

Fig.5. Encryption and decryption results,showing(a)original image,(b)cipher-text,(c)private key PK,(d)decryption result with correct PK,and(e)decryption result with the wrong PK.

Table 1. Parameters of spherical diffraction and Chen’s 4D hyperchaotic system.
To better evaluate the quality of encryption and decryption,we introduce PSNR and SSIM as reference indexes. The corresponding equation is as follows:


whereμIoandμIdrepresent the mean values of the original image and the decryption result image respectively;σIo,σId,σIoIdrepresent the variance of the original image and the decrypted image and the co-variance between them,respectively;c1andc2are constants to avoid division by 0;Ldenotes the dynamic range of pixel values. Usually,k1=0.01 andk2=0.03.
4.2. Histogram
The histogram shows the effectiveness and security of the encryption scheme.The histograms of ciphertext and plaintext should be completely different in the ideal encryption scheme.Figure 6 shows the histograms corresponding to RGB channels of color images‘a(chǎn)irplane’and‘baboon’,and their respective ciphertext histograms,which shows that the histogram of the ciphertext is different from that of any channel.
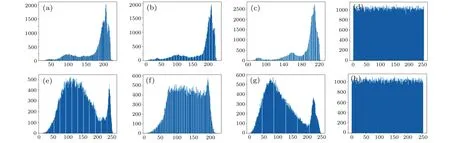
Fig. 6. (a)-(c) RGB channels’ histograms of ‘a(chǎn)irplane’, (d) ciphertext histogram of ‘a(chǎn)irplane’, (e)-(g) RGB channels’ histograms of ‘baboon’, and (h)ciphertext histogram of‘baboon’.
4.3. Key sensitivity and key space analysis
Key sensitivity is usually used to test the reliability of an encryption scheme. Figures 7(a)and 7(b)show the sensitivity sensitivities of spherical diffraction parameters and initial values of hyperchaotic systems, respectively. Here, ‘baboon’ is selected as the plaintext.
The dependence of SSIM on the change ofr,R,λare shown in Fig. 7(a). Whenr,R, andλchange 1% , 1%, 3%,the SSIM value would change dramatically.
The initial condition of the chaotic sequence is also used as a private key. Figure 7(b) shows the decryption effects of changes in initial conditions, indicating that the initial condition changing by 0.25% will have a significant influence on the decryption result when the initial condition is 4 decimal places. With the increase of the decimal places of the initial condition,the spatial sensitivity of the initial condition becomes stronger.

Fig.7. (a)Key sensitivity of spherical diffraction,and(b)key sensitivity of initial conditions of 4D hyperchaotic system.
4.4. Noise and occlusion attacks
Usually, the ciphertext may be polluted during transmission. Therefore,it is very important to ensure that the encryption scheme is robust to noise attack. In this part, multiplicative Gaussian noise is used to test the anti-noise performance of the image.The additive Gaussian noise model is as follows:

wherePandP′represent ciphertext and ciphertext with noise,respectively,Gdenotes the Gaussian noise with a mean value of 0 and a standard deviation of 0.01,andkrefers to the signalto-noise ratio.Figures 8(a)-8(d)show the decryption results of the plaintext‘baboon’under different strengths of multiplicative Gaussian noise attack. The strengths of the four images arek=0.01,0.05,0.1,and 0.5,and the corresponding PSNR values are 28.16 dB, 21.58 dB, 18.51 dB, and 11.45 dB, respectively.
In the process of transmission, the occlusion of ciphertext is also one of the possible pollutions. Figure 9 shows the decryption effects under different occlusion ratios: 50×50 pixels (1%), 100×100 pixels (4%), 150×150 pixels (8%),and 200×200 pixels(15%),respectively. The corresponding PSNR values are 17.79 dB,14.68 dB,12.81 dB,and 11.61 dB,respectively. Table 2 shows the decryption quality of the proposed scheme and Ref.[36]under the same clipping ratio. It shows that the proposed scheme is more resistant to ciphertext occlusion than the counterpart in Ref.[36].
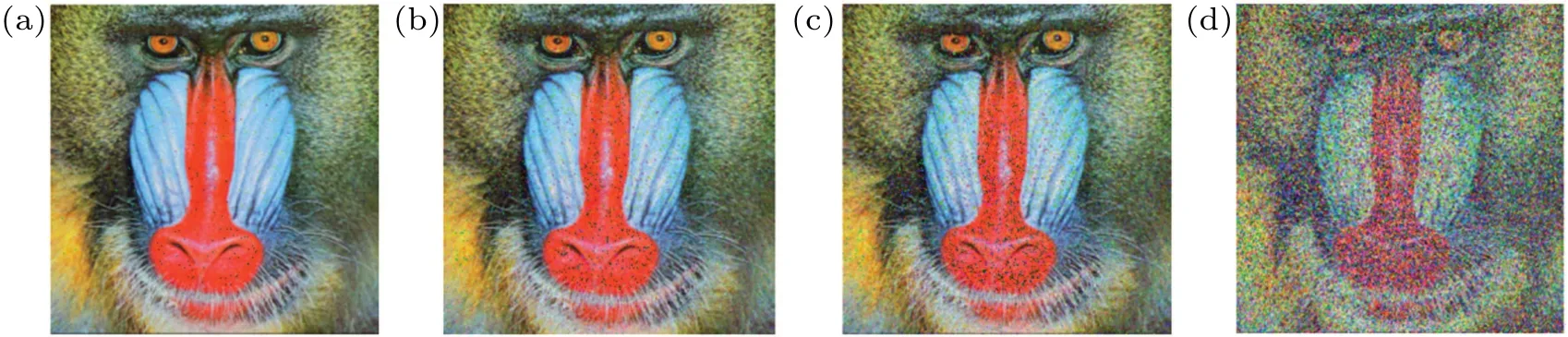
Fig.8. Decryption results of encryption image with noise strengths: k=0.01(a),0.05(b),0.1(c),and 0.5(d).

Fig.9. Decryption results of encryption image with occlusion of(a)50×50 pixels(1%),(b)100×100 pixels(4%),(c)150×150 pixels(8%),and(d)200×200 pixels(15%).

Table 2. Comparison of t ability to resistocclusion between Ref.[36]and proposed scheme,with‘baboon’chosen as plaintext.
4.5. Error analysis of spatial light modulator
Since spatial light modulator carries out the numerical quantization of the image on the target plane,quantization errors are regarded as a main error in optical encryption.To simulate an actual optical decryption,we will test this error to approach to the simulation results of real optical experiments.[40]
Figures 10(a)-10(d) show the decryption effects of the images at different quantization levels: 22levels, 24levels,28levels, 216levels, and the corresponding PSNR values are 10.25 dB,15.28 dB,26.34 dB,and 29.02 dB,respectively.Under the introduction of this error,the proposed scheme is better than Ref.[21].Figure 11 shows the difference between the two schemes. The corresponding PSNR values are 11.54 dB and 27.63 dB,and SSIM values are 0.69 and 0.79,respectively.

Fig.10. Decryption results at(a)22,(b)24,(c)28,and(d)216 quantization levels.

Fig.11. Decryption results with quantization level 28,showing(a)original image,(b)decryption result of Ref.[21],and(c)decryption result of the proposed scheme.
4.6. Resisting information leakage
The current partial color image encryption adopts three channels parallel processing method,[21-23]which has the risk of information leakage in the process of transmission. Unlike these schemes,the single-channel grayscale ciphertext and the low correlation among the three channels in our scheme can significantly reduce the possibility of information leakage during transmission. To test the ability to resist information leakage, we assume that the information leakage has occurred.That is, the attacker has obtained the information about one of the three RGB channels,which means that for our scheme,the attacker has obtained a subband completely. Meanwhile,we assume that the attacker knows all the private keys and the encryption scheme.
Figure 12 shows the comparison of the decryption effect between the two schemes under the condition of only knowing channel B information,taking the result in Ref.[23]as the comparison. The corresponding SSIM values of Figs. 10(c),10(g),10(d),and 10(h)are 0.99,0.99,0.09,and 0.09,respectively, showing that the ciphertext security of our scheme is much higher than the parallel processing scheme.

Fig.12.Comparison of anti-information leakage ability between the literature and the proposed scheme,with channel B taken for example,displaying((a),(e))plaintext,((b),(f))B channel of plaintext,((c),(g))decryption result of Ref.[23],((d),(h))decryption of the proposed scheme.
4.7. Potential attack analysis
Phase iterative attack is a common way to attack optical encryption.[41]Here,we compare the resistance to phase iterative attack between Ref. [23] and our scheme. To compare the result better, the black edge is padded around the image.Figure 13 shows the phase recovery of the image after 500 iterations,and figure 14 shows the relation between the number of iterations and the SSIM of the recovered image.

Fig.13. Result of phase iterative attack: (a)plaintext,(b)result of Ref.[23],(c)result of the proposed scheme.
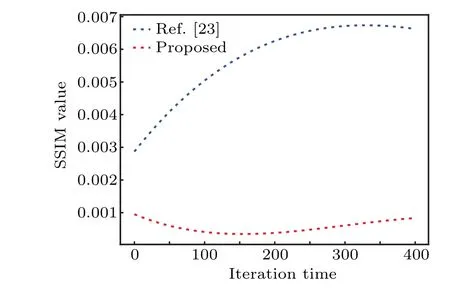
Fig.14. Comparison of phase attack results between Ref.[23]and the proposed scheme.
Compared with linear optical system, nonlinear optical system has better resistance to phase attack. And since spherical diffraction is just one kind of nonlinear optical system,our scheme has a better performance against phase attack.
An encryption system with high security should be able to resist differential attacks. In general, the number of pixel change rate (NPCR) and unified average changing intensity(UACI)are used to evaluate the ability to resist differential attacks,and defined as
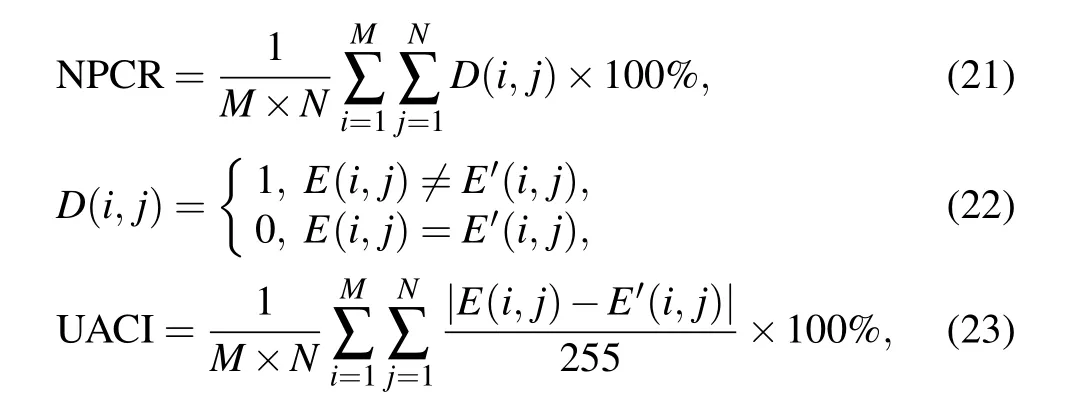
whereEandE′represent the ciphertext and the ciphertext with only one pixel changed,respectively.
The corresponding NPCR and UACI values under different plaintexts are shown in Table 3 as compared with those in Refs. [24,42-44]. The result from the characteristics of chaotic systems shows that the difference in result caused by small changes in initial values is widely divergent. And since the initial value is determined by the colorful plaintext,a small change in the plaintext will make the key completely different.Therefore it has a strong ability to resist differential attacks.

Table 3. Values of NPCR and UACI of different schemes.
5. Conclusions
In this paper,an efficient and secure color image encryption scheme based on channel fusion and spherical diffraction is proposed. Especially,channel fusion technology can effectively solve the problem of information leakage in color image encryption and reduce the loss of encryption. Compared with the symmetric system, the asymmetric spherical diffraction system used in this paper can significantly improve the antiattack ability and security of the scheme. Besides,the IEMD also solves the problem that the diffraction result is complexvalued. The simulation results and the comparison show the high security and robustness of the proposed scheme. Therefore,the proposed scheme may be used as a reference to resisting the risk of information leakage in color image encryption.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No. U1933132) and the Chengdu Science and Technology Program, Sichuan Province, China(Grant No.2019-GH02-00070-HZ).
- Chinese Physics B的其它文章
- Measurements of the 107Ag neutron capture cross sections with pulse height weighting technique at the CSNS Back-n facility
- Measuring Loschmidt echo via Floquet engineering in superconducting circuits
- Electronic structure and spin-orbit coupling in ternary transition metal chalcogenides Cu2TlX2(X =Se,Te)
- Characterization of the N-polar GaN film grown on C-plane sapphire and misoriented C-plane sapphire substrates by MOCVD
- Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics
- Quantum partial least squares regression algorithm for multiple correlation problem

