王 寵 陳 超

(中國(guó)人民大學(xué)附屬中學(xué)豐臺(tái)學(xué)校)

在證明不等式的過(guò)程中,將不等式中的變量進(jìn)行適當(dāng)代換,使不等式得以證明,這種方法稱(chēng)為不等式證明中的換元法.不等式證明中的換元法是換元思想的重要體現(xiàn).

換元法沒(méi)有固定模式,常用的方法是三角換元法和代數(shù)換元法,其中三角換元法有一定的規(guī)律性.若問(wèn)題中含有“x2＋y2＝r2,x2＋y2≤r2,”,可以考慮用“sinα,cosα”進(jìn)行代換,尤其是r＝1時(shí),這樣代換的優(yōu)勢(shì)更為明顯,進(jìn)行這些代換的理論依據(jù)是sin2α＋cos2α＝1以及圓x2＋y2＝r2的參數(shù)方程為y＝rsinα,x＝rcosα;若問(wèn)題中含有“|x|≤a”,可以考慮設(shè)“x＝asinα”或“x＝acosα”,其理論依據(jù)是|sinα|≤1,|cosα|≤1;類(lèi)似地,對(duì)于“和“”可分別進(jìn)行“x＝rtanα”和“x＝rsecα”代換.需要特別指出的是,當(dāng)時(shí),tanα可取全體實(shí)數(shù),所以tanα可以代換任意實(shí)數(shù).

對(duì)于代數(shù)換元法,雖然它的規(guī)律性不像三角換元法那么強(qiáng),但是也有一些可以遵循的規(guī)律.如果題目中出現(xiàn)類(lèi)似“已知a＞b＞c＞0”的條件,這時(shí)可以令x＝a－b,y＝b－c,z＝c,從而將原來(lái)關(guān)于a,b,c的式子轉(zhuǎn)化為關(guān)于x,y,z的式子,并且此時(shí)x,y,z只需為正實(shí)數(shù)即可.如果題目中出現(xiàn)類(lèi)似“a,b,c是三角形的三邊”的條件,此時(shí)可以令x＝,從而得到a＝y(tǒng)＋z,b＝x＋z,c＝x＋y,并且此時(shí)x,y,z只需為正實(shí)數(shù)即可.

盡管換元法沒(méi)有固定的模式,但有一個(gè)原則是必須遵守的,那就是進(jìn)行變量代換時(shí),新變量的變化范圍必須確保原來(lái)變量的變化范圍不發(fā)生變化,這是換元法的重點(diǎn),也是難點(diǎn).下面結(jié)合一些具體的題目,談一談?chuàng)Q元法在不等式證明中的應(yīng)用.

例1求證:函數(shù)f(x)＝在x∈[0,1]上的最小值是1,最大值是

分析看到x和,注意到二者的平方和等于1,所以可以進(jìn)行三角換元,令x＝cosα.因?yàn)轭}中要求x∈[0,1],所以α∈[0,],從而sinα,那么接下來(lái)就需要利用三角函數(shù)的相關(guān)知識(shí)來(lái)處理問(wèn)題了.

證明令x＝cosα,α∈那么sinα,從而

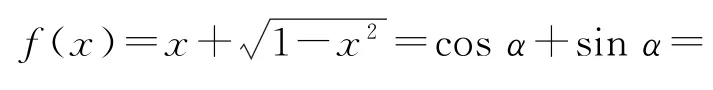
例2已知x2＋y2≤1,求證:

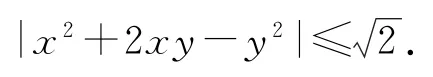
分析x2＋y2≤1可理解為它所確定的平面區(qū)域?yàn)閳A形區(qū)域{(x,y)|x2＋y2≤1},這樣的x和y可以表示為x＝rcosα,y＝rsinα,其中r∈[0,1],α∈[0,2π).

證明令x＝rcosα,y＝rsinα,其中r∈[0,1],α∈[0,2π).于是

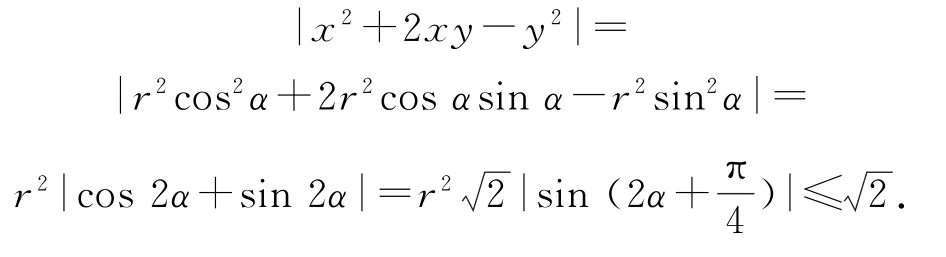
例3已知0＜x＜1,求證:

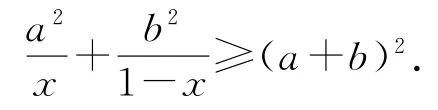
分析注意到當(dāng)0＜x＜1時(shí),0＜1－x＜1,并且x＋(1－x)＝1.聯(lián)想到sin2α＋cos2α＝1,作變換x＝cos2α或sin2α,簡(jiǎn)化運(yùn)算.

證明考慮到0＜x＜1,令x＝sin2α,α∈(0,,則1－x＝cos2α,從而

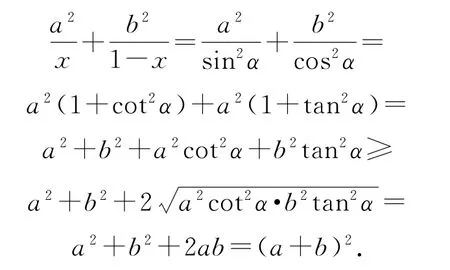
例4已知|x|≤2,求證:|3x－x3|≤2.

分析由|x|≤2,可知||≤1,因此可以考慮對(duì)作“sinα,cosα”代換.

證明考慮到|x|≤2,令x＝2sinα,α∈[0,2π).從而

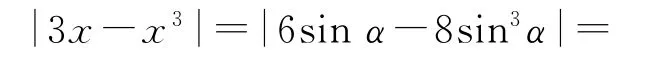
2|3sinα－4sin3α|＝2|sin3α|≤2.

例5已知a＞b＞c,求證:

分析因?yàn)閍－c＝(a－b)＋(b－c),并且a＞b＞c,這時(shí)可以考慮設(shè)x＝a－b,y＝b－c,此時(shí)x和y均為正實(shí)數(shù).

證明因?yàn)閍＞b＞c,所以a－b＞0,b－c＞0,a－c＞0.令x＝a－b,y＝b－c,則x＞0,y＞0,并且a－c＝x＋y.從而原不等式轉(zhuǎn)化為即(x＋y≥4,亦即≥4.

而上述不等式成立是顯然的,并且當(dāng)且僅當(dāng)x＝y(tǒng),即2b＝a＋c時(shí)取等號(hào).

綜上,原不等式成立.

補(bǔ)充本題所證結(jié)論可推廣為一般情形:若n∈N,n≥2,a0＞a1＞a2＞…＞an,則

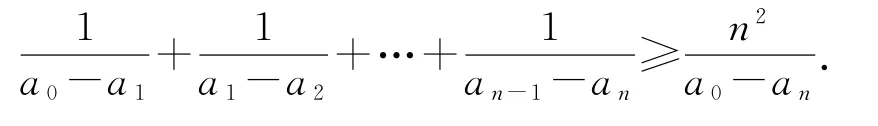
例6已知a,b,c是三角形的三邊長(zhǎng),求證:

而上述不等式成立是顯然的,并且當(dāng)且僅當(dāng)x＝y(tǒng)＝z,即a＝b＝c時(shí)取等號(hào).

綜上,原不等式成立.

例7已知a,b,c為正實(shí)數(shù),并且滿(mǎn)足a2＋b2＋c2＝1,求證:

分析注意到待證不等式形式較為復(fù)雜,考慮通過(guò)代數(shù)換元簡(jiǎn)化其形式.

證明令.因?yàn)閍,b,c為正實(shí)數(shù),所以x＞0,y＞0,z＞0,并且a2＝xz,b2＝xy,c2＝y(tǒng)z,因此xz＋xy＋yz＝1.從而原不等式轉(zhuǎn)化為x＋y＋z≥,而上述不等式成立是顯然的.事實(shí)上,有

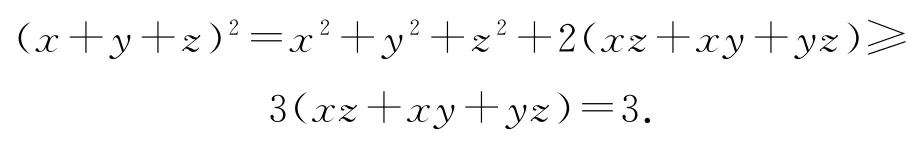
綜上,原不等式成立.

例8已知a,b,c為正實(shí)數(shù),求證:的最小值為

分析對(duì)于分式,通過(guò)換元可以使分母的形式變得簡(jiǎn)單,這樣處理起來(lái)會(huì)方便很多.

證明令x＝a＋2b＋c,y＝a＋b＋2c,z＝a＋b＋3c.因?yàn)閍,b,c為正實(shí)數(shù),所以x＞0,y＞0,z＞0,并且a＝5y－x－3z,b＝x＋z－2y,c＝z－y.從而

綜上,命題得證.

例9求證:

分析由于a∈R,所以可以考慮利用公式1＋tan2α＝sec2α換元.式中里面的“4”提示我們可以令a＝2tanα.當(dāng)然,本題也可以用代數(shù)換元法來(lái)證明.

由函數(shù)的相關(guān)知識(shí)可知函數(shù)f(t)＝t＋在[2,＋∞)上單調(diào)遞增,所以當(dāng)t＝2時(shí),f(t)有最小值為.因此原不等式成立.

通過(guò)以上幾道例題,相信大家對(duì)利用換元法證明不等式有了一個(gè)較為籠統(tǒng)的認(rèn)識(shí).在利用換元法證明不等式的過(guò)程中,我們要善于觀察,通過(guò)引入新的變量,對(duì)題目進(jìn)行轉(zhuǎn)化,使隱含的條件顯露出來(lái),將已知和結(jié)論關(guān)聯(lián)起來(lái),以便迅速找到解題思路.不等式的證明方法繁多,只有不斷總結(jié)和思考,才能融會(huì)貫通.

鏈接練習(xí)

鏈接練習(xí)參考答案

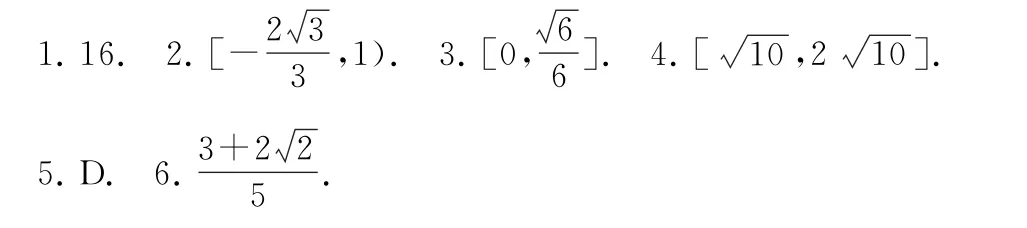
(完)