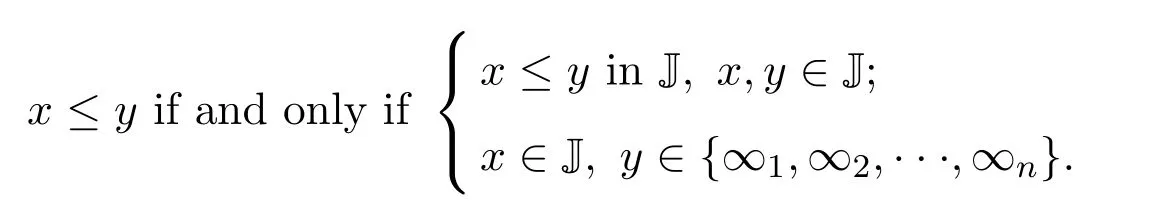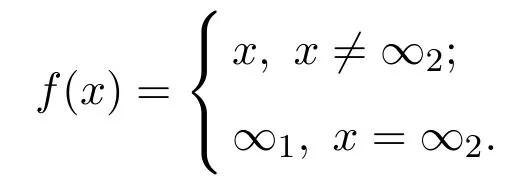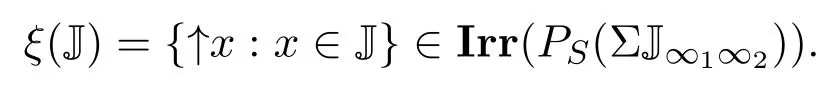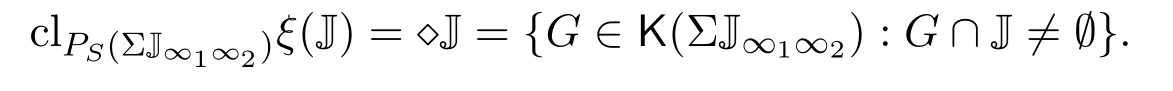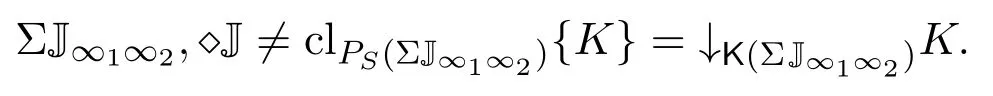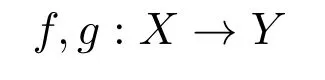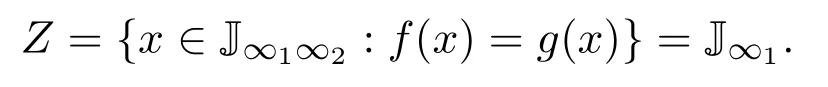Retracts and Smyth power spaces of k-bounded sober spaces
Yang Yi,Bao Meng,Xu Xiaoquan
(1.School of mathematics and statistics,Minnan Normal University,Zhangzhou 363000,China;2.College of Mathematics,Sichuan University,Chengdu 610064,China)
Abstract:This paper mainly investigates hereditary properties,retracts,function spaces and Smyth power spaces of k-bounded sober spaces.It is shown that k-bounded sober spaces are saturated-hereditary but not closed-hereditary,and are not closed under retracts and Smyth power constructions.It is also shown that there exists a k-bounded sober space X for which the function space[X→X]equipped with the topology of pointwise convergence is not k-bounded sober.
Keywords:k-bounded sober space,heredity,retract,function space,Smyth power space
1 Introduction
Sobriety is probably the most important and useful property ofT0spaces[1-22].It has been used in the characterizations of spectral spaces of commutative rings in Reference[23]and theT0spaces which are determined by their open set lattices[1,24].Sober spaces possess many nice properties[2].They are closed under retracts and products,and are closed-hereditary and saturated-hereditary.The function spaces of sober spaces equipped with the topology of pointwise convergence are sober and the equalizers of sober spaces are sober.More importantly,the category of all sober spaces is reflective in the category Top0of allT0spaces with continuous mappings[2-5]and Smyth power spaces of sober spaces are still sober[6-7].
In recent years,a number of kinds of strongly sober spaces and weakly sober spaces have been introduced and extensively studied from various different perspectives[8-10,25-29].Referance[25]introduced and investigated a weak notion of sobriety-kbounded sobriety.One remarkable result about this new kind of weakly sober spaces is that the category ofk-bounded sober spaces with continuous mappings is not reflective in Top0[26-27].
In this paper,we mainly investigate hereditary properties,retracts,function spaces and Smyth power constructions ofk-bounded sober spaces.It is shown thatk-bounded sober spaces are saturated-hereditary but not closed-hereditary,and are not closed under retracts and Smyth power constructions.It is also shown that there exists ak-bounded sober spaceXfor which the function space[X→X]equipped with the topology of pointwise convergence is notk-bounded sober.We present related counterexamples both with Alexandr off topology and with Scott topology on posets.
2 Preliminaries
In this section,we briefly recall some fundamental concepts and notations that will be used in the paper.For further details,we refer the reader to References[2-3,6,30].
For a posetPandA?P,let↓A={x∈P:x≤afor somea∈A}and↑A={x∈P:x≥afor somea∈A}.Forx∈P,we write↓xfor↓{x}and↑xfor↑{x}.A subsetAis called a lower set(resp.,an upper set)ifA=↓A(resp.,A=↑A).For a nonempty subsetAofP,define max(A)={a∈A:ais a maximal element ofA}and min(A)={a∈A:ais a minimal element ofA}.
Let|X|be the cardinality ofXandω=|N|,where N is the set of all natural numbers.LetPbe a partial order set andD?P,Dis called directed if every two elements inDhave an upper bound inD.The set of all directed sets ofPis denoted byD(P).Pis called a directed complete poset,or dcpo for short,provided that∨Dexists inPfor anyD∈D(P).
A subsetUof a posetQis Scott open ifU=↑U,and for any directed subsetDfor which∨Dexists,∨D∈UimpliesD∩U?.All Scott open subsets ofQform a topology.This topology is called the Scott topology onQand denoted byσ(Q).The space ΣQ=(Q,σ(Q))is called the Scott space ofQ.The upper sets ofQform the(upper)Alexandroff topologyα(Q).
A functionf:S→Tbetween dcpos is said to be Scott-continuous iffis continuous with respect to the Scott topologies,that is,f-1(U)∈σ(S)for allU∈σ(T).
For aT0spaceX,we use≤Xto represent the specialization order ofX,that is,x≤Xyiff.In the following,when aT0spaceXis considered as a poset,the order always refers to the specialization order if no other explanation.LetO(X)(resp.,Γ(X))be the set of all open subsets(resp.,closed subsets)ofX.
It is very straightforward to verify the following result.


3 Retracts and Smyth power spaces of k-bounded sober space
In this section,we mainly investigate hereditary properties,retracts,function spaces and Smyth power constructions ofk-bounded sober spaces.It is shown thatk-bounded sober spaces are saturated-hereditary but not closed-hereditary,and are not closed under retracts and Smyth power constructions.It is also shown that there exists ak-bounded sober spaceXfor which the function space[X→X]equipped with the topology of pointwise convergence is notk-bounded sober.
First,we show thek-bounded sober spaces are saturated-hereditary.
Proposition 3.1LetXbe ak-bounded sober andUa nonempty saturated subspace ofX.ThenUisk-bounded sober.
ProofSuppose that.LetC.ThenC∈Irr(X)by Lemma 2.1 anduis an upper bound ofCinX.For any upper boundvofCinX,sinceUis a saturated subset ofXandC?U,we have thatv∈U,and henceu≤vinUor,equivalently,inX.It follows thatu=XC,whenceu=XclXCby Remark 2.1.By thek-bounded soberity ofX,there isx∈Xsuch that clXC=clX{x}.ByC?U=↑UandC?↓x,we havex∈Uand clUC=(clXC)∩U=(clX{x})∩U=clU{x}.Thus as a saturated subspace,Uisk-bounded sober.
Then we show that there exists ak-bounded sober spaceXfor which a certain closed subspace ofXis notk-boundedsober.
Example 3.1LetP={a,b}∪N.Define a partial order≤onPas follows(see Fig.1):

Fig.1 A k-bounded sober space with a non-k-bounded-sober closed subspace
(a)n (b)n (c)aandbare incomparable. It is clear that Irrc(P,α(P))={↓x:x∈P}∪{N}.However,the irreducible closed set N does not have supremum in(P,α(P)),then(P,α(P))is ak-bounded sober space. LetA=N∪{a}.Obviously,A=N∪{a}=↓ais a closet subset of(P,α(P)).ConsiderAas a closed subspace of(P,α(P)).Then↓nis a irreducible closed subset ofA.But for anyx∈A,clAN=NclA{x}=↓x.Therefore,as a closed subspace of thek-bounded sober space(P,α(P)),Ais notk-bounded sober. Definition 3.1[2]A topological spaceYis said to be a retract of a topological spaceXif there are two continuous mapsf:X→Yandg:Y→Xsuch thatf?g=idY. Next,we give an example to show that the class ofk-bounded sober spaces is not closed under retracts. Example 3.2LetX=(P,α(P))andY=(A,α(P)|A)be the two spaces in Example 3.1.Definef:X→Yby and defineg:Y→Xbyg(y)=yfor eachy∈Y,that is,gis the identical embedding ofYinX.It is easy to see thatfis continuous andf?g(y)=yfor eachy∈Y,that is,f?g=idY.Therefore,Yis a retract ofX.It has been proved in Example 3.1 thatXis ak-bounded sober space,butYis notk-bounded sober. Example 3.3LetX=(P,α(P))be the space in Example 3.1.Then LetQ=N∪{a,b,c}and define a partial order≤onQas follows(see Fig.2): Fig.2 A k-bounded sober space with a non-k-bounded-sober Smyth power space (a)n (b)n (c)c (d)aandbare incomparable. Then both the crows bowed, and begged to have a fixed15 appointment, for they thought of their old age, and said it would be so comfortable to feel that they had provision for their old days, as they called it. And then the prince got out of his bed, and gave it up to Gerda,—he could do no more; and she lay down. She folded her little hands, and thought, “How good everyone is to me, men and animals too;” then she closed her eyes and fell into a sweet sleep. All the dreams came flying back again to her, and they looked like angels, and one of them drew a little sledge, on which sat Kay, and nodded to her. But all this was only a dream, and vanished as soon as she awoke. Then it is easy to verify thatPS(X)is homeomorphic to(Q,α(Q)). In(Q,α(Q)),it is clear that.However,for anyx∈Q, Therefore,(Q,α(Q))is not ak-bounded sober space and hencePS(X)is notk-bounded sober. It was proved in Reference[28]that if{Xj:j∈J}is a family ofk-bounded sober spaces,then the product space∏isk-bounded sober.We show the converse is also valid. Proposition 3.2Let{Xi:i∈I}be a family ofT0spaces.If the product spaceis ak-bounded sober space,thenXiisk-bounded sober for eachi∈I. ProofFor eachi∈I,suppose thatAi∈Irrc(Xi)and the supremum ofAiexists.Choosesj∈Xjfor anyj∈I{i}.Put,where It follows from Lemma 2.3 thatA∈Irrc(X).Moreover,we know that∨A=(xi)i∈I,where SinceXisk-bounded sober,there exists a unique pointx=(xi)i∈Isuch that Letpj:X→Xjbe thejth projection(j∈I).Then.Therefore,Xiisk-bounded sober. It is well-known that ifXis aT0space andYis sober,then the function space of all continuous functions equipped with the topology of pointwise convergence(i.e.,the relative product topology)is sober(see Reference[2]).However,the following example shows that the similar result fork-bounded sober spaces does not hold. Example 3.4There exists ak-bounded soberXfor which the function space[X→X]equipped with the topology of pointwise convergence is notk-bounded sober. Indeed,letX=(P,α(P))be the space in Example 3.1.It was proved in Example 3.1 thatXis ak-bounded sober space.Clearly,f:X→Xis continuous ifff:P→Pis order preserving.For eachi∈N,define a mappingfi:X→Xby LetD={fi:i∈N}.It was proved in Reference[8]thatDis a directed subset in[X→X]under the pointwise ordering and↓[X→X]Dis a closed subset in[X→X]with respect to the topology of pointwise convergence.It follows that cl[X→X]D=↓[X→X]D.One readily sees thatgis the only upper bound ofDin[X→X],whereg(x)=bfor anyx∈P,and henceg=[X→X]D.Moreover,↓[X→X]D↓[X→X]g.Therefore,[X→X]of all continuous functions with the topology of pointwise convergence is notk-bounded sober. In Section 3,using the Alexandroff topology,we have shown thatk-bounded sober spaces are not hereditary with respect to closed subspaces and are not closed under retracts and Smyth power constructions.In this section,we give some similar counterexamples with Scott topology. First,we recall the non-sober dcpo J constructed by Johnstone in Reference[12],which is defined as J=N×(N∪{ω}),with the order defined by(j,k)≤(m,n)if and only ifj=mandk≤n,orn=ωandk≤m.The set of maximal elements of J is denoted by Jmax.Clearly,Jmax=N×{ω}={(n,ω):n∈N}. Definition 4.1Forn≥1,let J∞1∞2···∞n=J∪{∞1,∞2,···,∞n}.Define a partial order≤on J∞1∞2···∞nby Example 4.1Consider the Scott space ΣJ∞1∞2.It was proved in Reference[26]that ΣJ∞1∞2is ak-bounded sober space.Clearly,ΣJ∞1is a closed subspace of ΣJ∞1∞2andJ∞1J=∞1,and hence.However,JclJ∞1{x}=↓J∞1xfor everyx∈J∞1.Therefore,as a closed subspace of thek-bounded sober space ΣJ∞1∞2,ΣJ∞1is notk-bounded sober. Example 4.2Consider the two Scott spaces ΣJ∞1∞2and ΣJ∞1in Example 4.1.It has been shown that ΣJ∞1∞2isk-bounded sober and ΣJ∞1is notk-bounded sober.Now we show that ΣJ∞1is a retract of ΣJ∞1∞2. Definef:ΣJ∞1∞2→ΣJ∞1by and defineg:ΣJ∞1→ΣJ∞1∞2byg(y)=yfor eachy∈J∞1.It is straightforward to verify thatfandgare both Scott continuous.Moreover,for anyy∈ΣJ∞1,f?g(y)=y,that is,f?g=idΣJ∞1.Therefore,ΣJ∞1is a retract of ΣJ∞1∞2. Now we show that the Smyth power space of ak-bounded sober Scott space is notk-bounded sober in general. Example 4.3Consider thek-bounded sober Scott space ΣJ∞1∞2.We prove that its Smyth power spacePS(ΣJ∞1∞2)is notk-bounded sober. Defineξ:ΣJ∞1∞2→PS(ΣJ∞1∞2)byξ(x)=↑xfor allx∈J∞1∞2.Thenξis a topological embedding,and hence by J∈Irr(ΣJ∞1∞2)we have However,it was proved in Reference[19]that ifKis a compact saturated subset in ΣJ,thenK=↑Ffor some nonempty finite subset of J or?K?Jmax.From this result we get that for a nonempty upper subsetK?J∞1∞2,K∈K(ΣJ∞1∞2)iffK=↑J∞1∞2Gfor a nonempty finite setG∈(J∞1∞2)(<ω)or a nonempty setG?Jmax.Therefore,for any nonempty compact saturated setKin Therefore,PS(ΣJ∞1∞2)is not ak-bounded sober space. Definition 4.2[25,29]AT0space is said to be bounded sober if every upper bounded closed irreducible set is the closure of a unique singleton. Proposition 4.1[28]LetXbe a bounded sober space,YaT0space and two continuous mappings.Then as a subspace ofX,Z={x∈X:f(x)=g(x)}is a bounded sober space. The following example shows that the similar result does not hold fork-bounded sober spaces. Example 4.4Consider the Scott space J∞1∞2.Then ΣJ∞1∞2is ak-bounded sober space(see Reference[26]or Example 4.2). Letf=idΣJ∞1∞2:ΣJ∞1∞2→ΣJ∞1∞2be the identical mapping.Define It is easy to verify thatgis Scott continuous and It has been proved in Example 4.1 that as a closed subspace of ΣJ∞1∞2,Z= ΣJ∞1is notk-bounded sober. Finally,by the examples above,References[26,Lemma 3.1]and[32,Example 3.1],we have the following result. Proposition 4.2Let J be the Johnstone′s dcpo.Then (1)Irrc(ΣJ)={↓x:x∈J}∪{J}; (2)ΣJ is not well-filtered and hence not sober; (3)ΣJ is bounded sober and hencek-bounded sober; (4)K(ΣJ)={G?Jmax:G?}∪{↑JmaxF:?F∈J(<ω)}; (5)ΣJ∞1is not well-filtered and notk-bounded sober,and hence not bounded sober; (6)For anyn≥2, ΣJ∞1∞2···∞nis not well-filtered and not bounded sober,butk-bounded sober; (7)For anyn≥2,ΣJ∞1is notk-bounded sober as a closed subspace of thek-bounded sober Scott space ΣJ∞1∞2···∞n; (8)For anyn≥2,PS(ΣJ∞1∞2···∞n)is not well-filtered and not bounded sober,butk-bounded sober.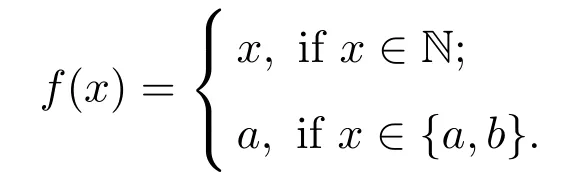
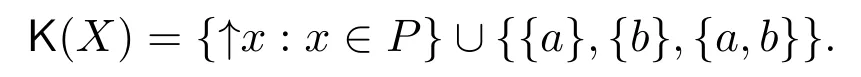

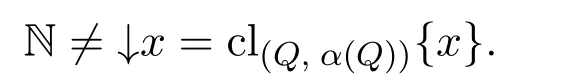

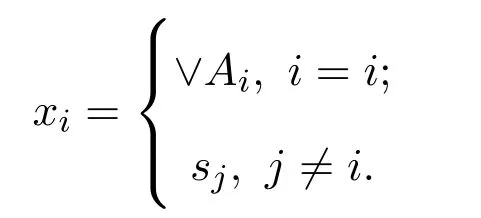
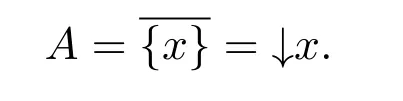
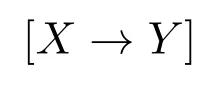
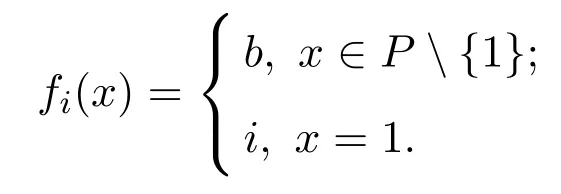
4 Counterexamples with Scott topology