劉合國,趙靜

(湖北大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院,湖北 武漢 430062)

1 引言

為方便計(jì),本文用 diag(a1,a2,···,an)表示對角線元素是a1,a2,···,an的n階對角陣,用Cn表示基本的n階循環(huán)置換矩陣,V(x1,x2,···,xn)表示關(guān)于x1,x2,···,xn的Vandermonde矩陣,即

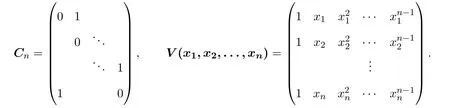
一般地,本文采用的術(shù)語和符號是標(biāo)準(zhǔn)的,參見文獻(xiàn)[1-2].

特殊矩陣在矩陣分析里起著核心的作用.循環(huán)矩陣,Vandermonde矩陣,Hilbert矩陣以及Cauchy矩陣是常常碰到的幾類矩陣,它們在各種數(shù)學(xué)理論里發(fā)揮著重要的作用,見文獻(xiàn)[3].現(xiàn)在用統(tǒng)一的思想來重新處理這些矩陣的幾個基本問題,由此可以看到它們之間的本質(zhì)聯(lián)系,以及它們與多項(xiàng)式理論,線性方程組理論之間的深刻聯(lián)系,這為理解這些經(jīng)典結(jié)果提供了又一種思考方式.

具體說來,運(yùn)用 Cramer法則和 Lagrange插值公式來計(jì)算 Vandermonde矩陣,Hilbert矩陣和Cauchy矩陣的行列式,逆矩陣以及逆矩陣的所有元素之和等問題,用Lagrange插值公式來處理一個涉及循環(huán)矩陣的矩陣分解問題.這種處理問題的思路和方法與文獻(xiàn)[4-5]是一致的,其最核心的工具是插值,這是中國剩余定理的本質(zhì)所在.在理解這點(diǎn)后,本文可以看做是文獻(xiàn)[4-5]的延伸.

本文反復(fù)用到的一些基本事實(shí)如下.

2 關(guān)于一個矩陣分解的定理

熟知每個n階循環(huán)矩陣都可表示為關(guān)于Cn的多項(xiàng)式,這類矩陣在理論和應(yīng)用方面都具有重要性,見文獻(xiàn) [6].從下面的矩陣恒等式可知Cn與 diag(1,ω,···,ωn?1)是相似的,

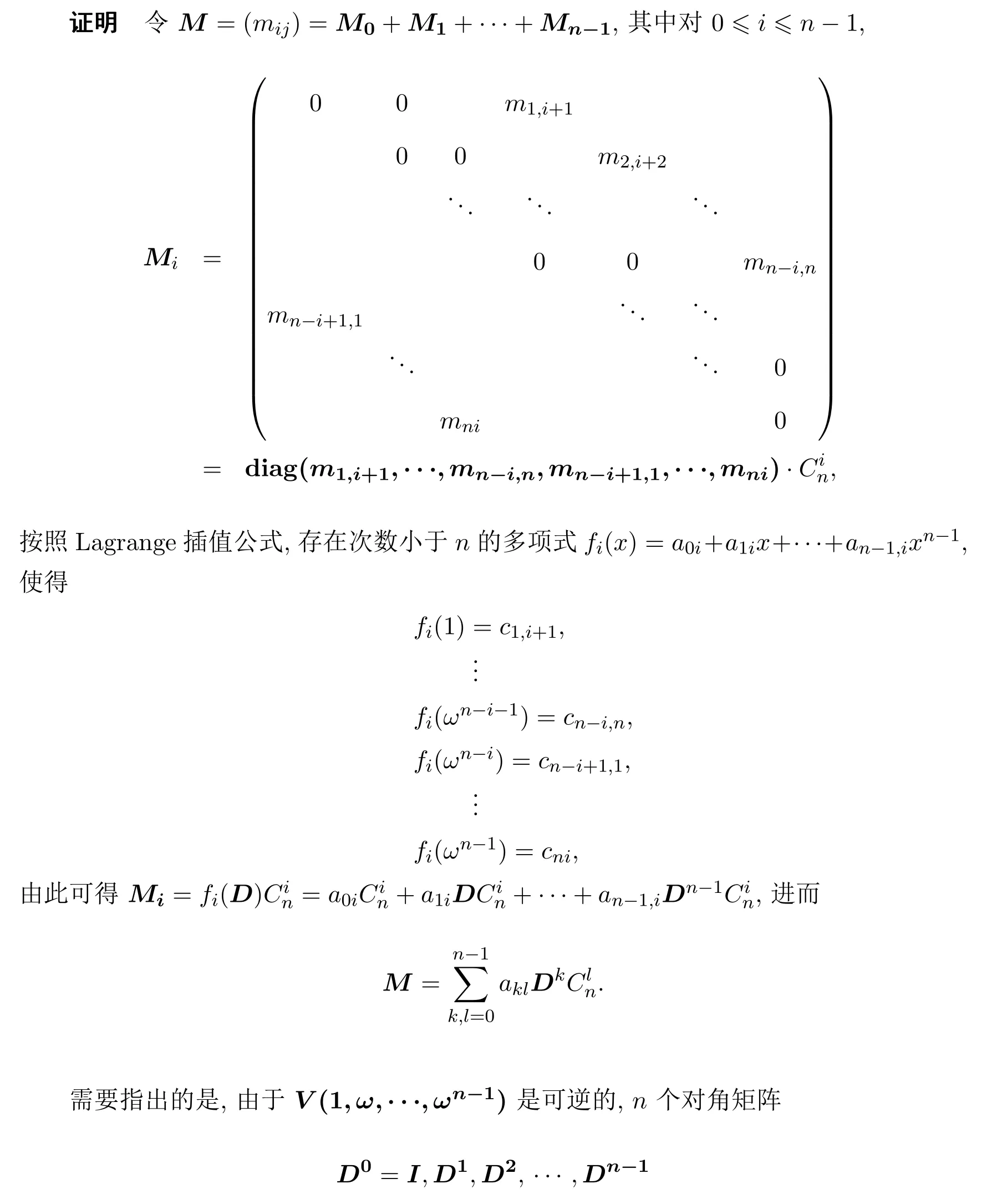
是線性無關(guān)的,故每個對角矩陣都是它們的線性組合,文獻(xiàn)[7-8]由此得到定理2.1的證明.注意到Lagrange插值公式能夠由多種方式推導(dǎo)出來,包括運(yùn)用Vandermonde行列式進(jìn)行證明,參見文獻(xiàn)[4,9],這樣本文的證明與文獻(xiàn)[7-8]的證明在本質(zhì)上是一致的.

定理2.1可推廣成更一般的形式.

3 Vandermonde矩陣

Vandermonde矩陣是最熟悉的矩陣之一,它在線性代數(shù) (高等代數(shù))里時(shí)常出現(xiàn),參見文獻(xiàn)[10-11].下面的結(jié)論是最基本的,這里給出一個多項(xiàng)式證明.

4 Hilbert矩陣

5 Cauchy矩陣

文獻(xiàn)[12-15]處理了某些與Vandermonde矩陣,Hilbert矩陣,Cauchy矩陣相關(guān)的問題.不論是就理論還是就應(yīng)用來說,特殊矩陣都是值得關(guān)注的研究對象.熟練地運(yùn)用基本工具去解決特殊矩陣的基本問題,是研讀矩陣分析的基本功.