Evaluation on performance of MM/PBSA in nucleic acid-protein systems
Yuan-Qiang Chen(陳遠強) Yan-Jing Sheng(盛艷靜) Hong-Ming Ding(丁泓銘) and Yu-Qiang Ma(馬余強)
1Center for Soft Condensed Matter Physics and Interdisciplinary Research,School of Physical Science and Technology,Soochow University,Suzhou 215006,China
2National Laboratory of Solid State Microstructures and Department of Physics,Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China
Keywords: molecular mechanics/Poisson-Boltzmann surface area(MM/PBSA),screening electrostatic inter
1. Introduction
The molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) and the molecular mechanics/generalized Born surface area (MM/GBSA) methods are two popular approaches to estimate the binding free energy of ligandbiomolecule and biomolecule-biomolecule interactions.[1-4]Compared to the alchemical free energy (AFE) methods like free energy perturbation (FEP) and thermodynamic integration (TI),[5-7]the MM/PBSA and MM/GBSA methods require much lower computational cost; moreover, they can also reproduce and rationalize experimental findings better than the molecular docking.[8-11]Thus, the MM/PBSA and MM/GBSA have been widely used in many studies,especially in bio-systems like protein-ligand binding,[1,2,12-16]proteinprotein interactions.[2,17-20]
However,recently more and more studies have shown that the performance of the MM/PBSA or MM/GBSA could be just moderate and even poor in some cases,[1,2,21,22]particularly in highly charged systems. To overcome such problem,the high value of solute dielectric constant in the MM/PBSA and MM/GBSA or the residue-type-dependent dielectric constant in the MM/GBSA was recommended.[2,9,14,17,19,23,24]It is shown the latter one can indeed greatly improve the performance of the MM/GBSA.[19,23,24]Moreover,the enhanced sampling is another possible way,but the improvement is usually limited.[17]Notably, it is still difficult to introduce the residue-type-dependent dielectric constant in the MM/PBSA,thus presently the performance of the MM/PBSA (even if a very large solute dielectric constant was set)is usually worse than that of the MM/GBSA in the highly charged systems.Therefore, it is a challenging problem to improve the performance of the MM/PBSA in such systems.
Recently, we raised a modified approach of MM/PBSA that considers the screening effect of ions on the electrostatic interaction between the proteins. The modified method (i.e.,screening MM/PBSA) showed a good performance on the protein-protein interactions,[25]especially in the SARS-CoV-2 RBD-ACE2 interaction.[26]However, it is still unclear how about its performance on other bio-systems like the nucleic acid-involved systems.
Actually, the nucleic acids (including DNA/RNA) are highly negative-charged biomolecules. For example, the linear charge density of the single strand DNA is about 0.17 e/nm while that of the double strand DNA is about 0.34 e/nm.Thus, there are many counter ions that could condensed on the DNA,namely the well-known Manning condensation,[27]which could greatly decrease the effective charges of DNA molecules. As a result, the DNA/RNA may be compacted closely to form specific structures in nature[28]and can be assembled into various three-dimensional(3D)structures in the experiments.[29-31]Moreover,their interaction with proteins is of great importance in bio-systems like transcription,replication and recombination.[28]For example,the expression level of genes is regulated by transcription-factor proteins, which can recognize a specific sequence of the DNA in the binding domain.[32]
In this work,we take the protein-nucleic acid interaction as an example,and show that the use of the screening electrostatic energy (instead of the coulomb electrostatic energy) in molecular mechanics can greatly improve the performance of the MM/PBSA in the systems,especially when the proteins are also negatively charged. Moreover,the effect of the solute dielectric constant and the salt concentration on the performance of the screening MM/PBSA is also investigated.
2. Model and methods
2.1. Preparation of the datasets for the protein-nucleic acid complexes
In order to systematically assess the performance of the standard MM/PBSA and screening MM/PBSA for the nucleic acid-protein interaction, two different datasets (i.e., dataset I and dataset II) were provided, which were listed in Table S1 and Table S2. The dataset I was mainly selected from the dataset by Houet al.[21]The dataset I covered a broad range of 8 orders of magnitude (experimental binding affinities between 750μM and 2.14 pM).The proteins in dataset I were all positively charged(or charge-neutral),thus there may exist the attractively electrostatic interactions between the proteins and the nucleic acids. On the contrary, the proteins in dataset II were all negatively charged, and were downloaded from the PDBbind database.[33,34]Notably,since the nucleic acids were negatively charged, there may exist the repulsively electrostatic interaction between the nucleic acids and the proteins.Thus, the data points were not easily collected in dataset II.Nevertheless, it also covered a relatively broad range of 6 orders of magnitude (experimental binding affinities between 50μM and 90 pM).
2.2. All-atom molecular dynamics(MD)simulations
Each system(i.e.,the protein-nucleic acid complex)was solvated in TIP3P water[35](the minimum distances from the surfaces of the box to the complex atoms were set to 15 A°)and NaCl to neutralize the systems at salt concentration of 0.15 M. In this work, all-atom MD simulations were carried out by using GROMACS 2019.03 package[36,37]with Amber ff14sb parmbsc1 force field.[38]The LINCS constraints[39]were used to all bonds involving hydrogen atoms. The particle mesh Ewald method was used when calculating the long-range electrostatic interactions,[40]and the Lennard-Jones (LJ) interactions were cut off at a distance of 1.0 nm. The periodic boundary conditions were adopted in all three directions.
During the simulations, the system was first energyminimized by the steepest descent method for about 10000 cycles when the heavy atoms of the protein and the nucleic acid were harmonically restrained with spring constant of 1000 kJ·mol-1·nm-2.Then the system was energy-minimized by the steepest descent method for about 10000 cycles with turning off all the constraints.[19]After that, the system was gradually heated from 0 K to 298 K in the NVT ensemble over a period of 100 ps,and then relaxed by 100 ps in the NPT ensemble,where the temperature was controlled at 298 K by the V-rescale thermostat[41]with a time constant of 0.2 ps and the pressure was kept at 1 atm(1 atm=1.01325×105Pa)by the Parrinello-Rahman barostat[42]with a time constant of 1.0 ps.The protein and the nucleic acid were harmonically restrained with spring constant of 1000 kJ·mol-1·nm-2in the above two stages. Finally,5-ns free NPT simulations were performed for each system.[17]
2.3. MM/PBSA calculation of the protein-nucleic acid binding energy
In the binding free energy calculation, 100 frames (with an interval of 10 ps in the final 1 ns) of the MD trajectories or the minimized structure were used to calculate the binding energy in each system via the MM/PBSA method. All the MM/PBSA calculations were performed by using the modified shell script gmx mmpbsa.[43]
In standard MM/PBSA,the binding free energy ΔGbindis calculated as follows:[1-3]
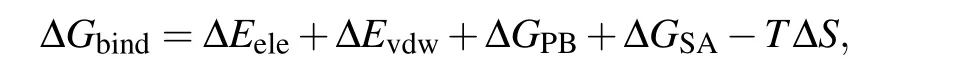
where ΔEeleand ΔEvdware the electrostatic energy and van der Waals energy between the protein and the nucleic acid at the gas-phase,respectively. ΔGPBand ΔGSAare the polar contribution and non-polar contribution of the desolvation free energy,respectively.-TΔSis the entropy change upon binding,and is not considered here due to the high computational cost and low prediction accuracy.[21,22]
Notably, ΔEeleusually has the Coulombic form in the standard MM/PBSA:[1-3]
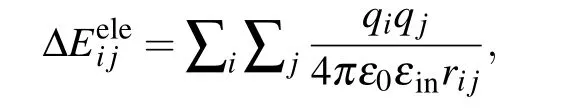
whereqiis the charge of atomiin the protein,qjis the charge of atomjin the nucleic acid,rijis the distance between atomiand atomj,ε0is the dielectric constant in vacuum,andεinis the relative dielectric constant of the solute.
While in the screening MM/PBSA,ΔEelehas the following form:[25,26]
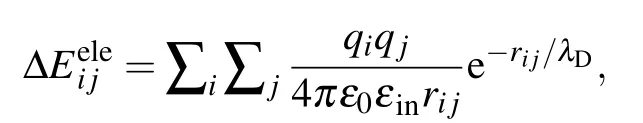
whereλDis the Debye screening length and is about 0.8 nm when the salt(NaCl)concentration is 0.15 M.
The experimental binding energy was estimated as ΔG=kBTlnKd, wherekBis the Boltzmann constant,Tis the temperature,Kdis the equilibrium dissociation constant. Then,the Pearson correlation coefficientrpwas employed to evaluate the linear correlation between the predicted binding free energies and the experimental ones.
3. Results and discussion
3.1. Comparison of accuracy of binding energy between standard MM/PBSA and screening MM/PBSA
The binding free energy of the protein-nucleic acids in dataset I was first calculated using the standard MM/PBSA methods. In terms of the correlation coefficients, the accuracy of the standard MM/PBSA in dataset I was relatively satisfied-the Pearson correlation coefficient(rP)was about 0.69, 0.69, 0.67, respectively when the solute dielectric constants (εin) were set as 2.0, 4.0, and 8.0 (see Figs. 1(a)-1(c)and Figs.S1(a)-S1(c)). Notably, the MM/PBSA calculations based on the minimized structures was nearly the same as the MM/PBSA calculations based on the MD trajectories, which agreed with previous studies.[9,22]Moreover,such results also indicated that hererPwas nearly independent onεin.Nevertheless,whenεinwas small(e.g.,2.0 or 4.0),the predicted binding energy was over thousands of kJ/mol in some cases,which was extremely larger than the experimental value (~dozens of kJ/mol),even though we did not consider the entropy term here. On the contrary, when using a relatively largerεin, the predicted binding energy greatly decreased to tens or hundreds of kJ/mol. However,there existed some positive values in the binding energy (see Fig. 1(c)), meaning that the complex of the protein and the nucleic acid may be dissolved, probably due to the fact that the largerεinmay underestimate the attractively electrostatic interaction between the protein and the nucleic acid.
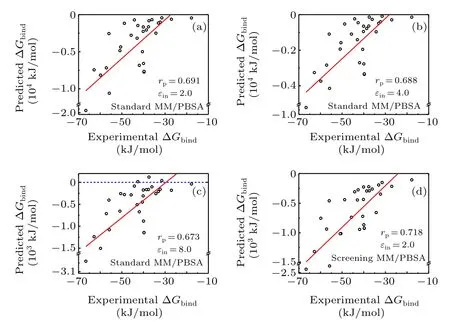
Fig. 1. Pearson correlation coefficient for the dataset I based on the minimized structures in the standard and screening MM/PBSA methods.(a)Standard MM/PBSA under solute dielectric constant 2.0;(b)standard MM/PBSA under solute dielectric constant 4.0;(c)standard MM/PBSA under solute dielectric constant 8.0; (d) screening MM/PBSA under solute dielectric constant 2.0.
The binding energy of the protein-nucleic acid complexes in dataset I was then calculated using the screening MM/PBSA method based on the screening electrostatic energy. As shown in Fig. 1(d) and Fig. S1(d), the Pearson correlation coefficientrP(0.718-0.730) was slightly better that(0.667-0.695) in the standard MM/PBSA using differentεin.Besides, the MM/PBSA calculation based on the minimized structures(rP=0.718)was also similar to the MM/PBSA calculations based on the MD trajectories(rP=0.730).More importantly,the predicted binding energy predicted by screening MM/PBSA was between-100 kJ/mol and-2000 kJ/mol,and no positive values were observed,which was more reasonable than that in the standard MM/PBSA to some extent.
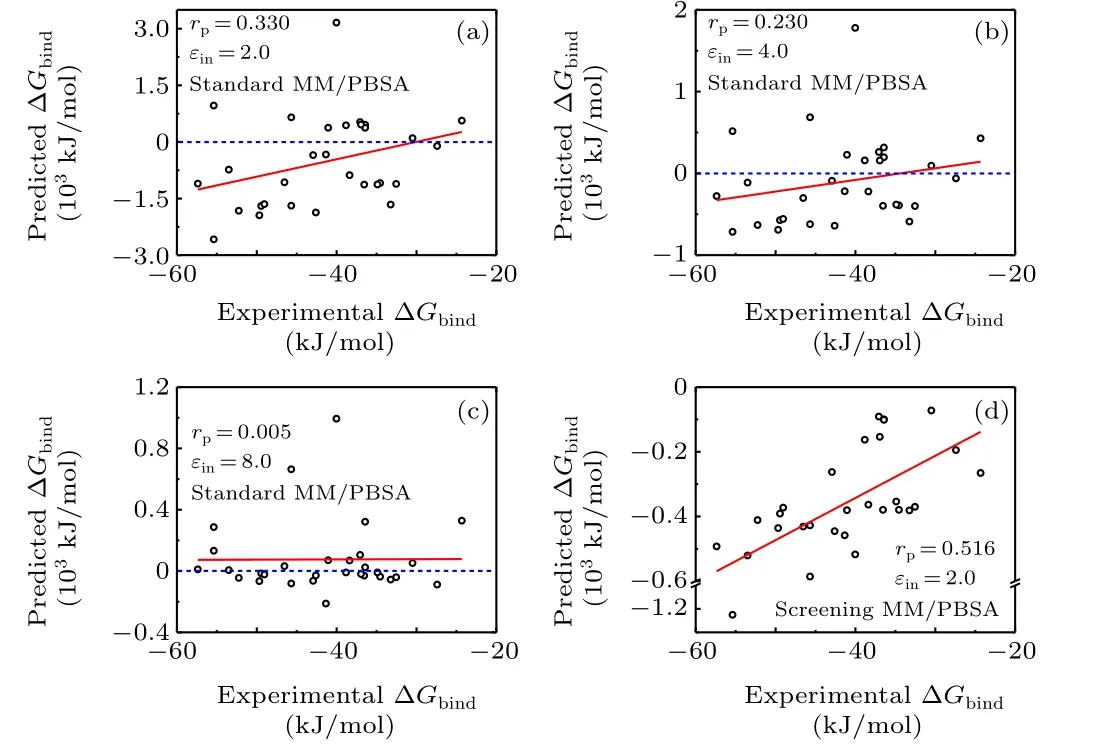
Fig. 2. Pearson correlation coefficient for the dataset II based on the minimized structures in the standard and screening MM/PBSA methods.(a)Standard MM/PBSA with solute dielectric constant 2.0;(b)standard MM/PBSA with solute dielectric constant 4.0; (c) standard MM/PBSA with solute dielectric constant 8.0;(d)screening MM/PBSA with solute dielectric constant 2.0.
The binding energy of the protein-nucleic acid complexes in dataset II was further calculated using the standard MMPBSA and the screening MM/PBSA(Fig.2 and Fig.S2).In terms of the correlation coefficients, the accuracy of standard MM/PBSA in dataset II was quite poor(-0.060<rP<0.330,the average ofrPwas about 0.15),where the MM/PBSA calculations underεin= 8.0 gave the worst prediction and even predicted the opposite trend using the MD trajectories(rP=-0.060). Moreover, there were many positive binding energies predicted by the standard MM/PBSA in dataset II,namely nearly half of the values was positive underεin=8.0 and over one third of the values was positive underεin=2.0 or 4.0. All these results indicated that the performance of the standard MM/PBSA in dataset II was much weaker than that in dataset I,which is mainly caused by the repulsively electrostatic interactions between the proteins and the nucleic acids carrying the charges of the same sign.
On the contrary,the accuracy of the screening MM/PBSA in dataset II was much better than that of the standard MM/PBSA and was in the moderate range (Fig. 2(d) and Fig. S2(d)), where the Pearson correlation coefficient was 0.516 based on the minimized structures and it was 0.528 based on the MD trajectories. Moreover,the predicted binding energies were all negative. We analyzed the electrostatic energy in the cases where the binding energy predicted by the standard MM/PBSA was positive. The electrostatic energy was divided into two parts on the basis of the Debye screening length(0.8 nm),namely,the long-range part(r >0.8 nm)and the short-range part(r <0.8 nm). As shown in Table S3,the long-range electrostatic energy was always positive (i.e.,repulsive) when using the standard MM/PBSA. More importantly, the repulsively long-range energy was comparable to(and even greater than)the attractively short-range energy. As a result, the total electrostatic energy was small and can be even positive. On the contrary, the long-range electrostatic energy was negative or weakly positive, and the attractively short-range electrostatic energy dominated in most cases when using the screening MM/PBSA.On the basis of above discussion, we can conclude that the usage of Coulomb interaction in the standard MM/PBSA may overestimate the repulsively electrostatic energy(especially in the long range)between the proteins and the nucleic acids carrying the charges of the same sign. On the contrary, the screening interaction corrected the overestimated electrostatic energy between the proteins and the nucleic acids in the long range, thus it gave a relatively better result.
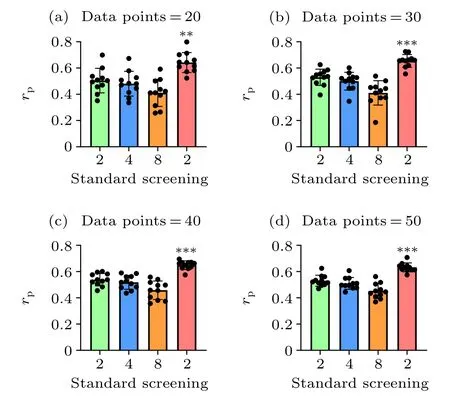
Fig. 3. Overall comparison of the prediction accuracies between the standard and screening MM/PBSA methods using different data points. We randomly selected the data points from dataset I and dataset II for 11 times in each case. The p values were calculated using multiple t tests (??p <0.01,???p <0.001).
Taking dataset I and dataset II together, the screening MM/PBSA method (rP=0.628) still yields the best performance, following with 0.534 (εin= 2.0), 0.516 (εin= 4.0),0.458 (εin=8.0) in the standard MM/PBSA. We also compared the performance of the screening MM/PBSA and the standard MM/PBSA by using different mixtures of dataset I and dataset II. Not surprisingly, the accuracy of the binding energy calculated by the screening MM/PBSA was always the highest, and with the increase of data points, the significant difference between the screening MM/PBSA and the standard MM/PBSA became more obvious(Fig.3),indicating that the usage of the screening electrostatic energy in molecular mechanics can indeed improve the performance of MM/PBSA in highly charged systems.
3.2. The effect of solute dielectric constant in screening MM/PBSA on accuracy of predicted binding energy
The accuracy of the predicted binding energy is usually related to the solute dielectric constantεinin the standard MM/PBSA.Here, we investigated the effect of solute dielectric constant on the performance of the screening MM/PBSA.As discussed above,the results based on the minimized structures was similar to that based on the MD trajectories,thus,for the sake of simplicity, we just used the minimized structures for the MM/PBSA calculation in this subsection.
As shown in Table 1, the accuracy of the screening MM/PBSA in dataset I was nearly independent onεin(rPwas about 0.70)except that the Pearson correlation coefficient was 0.658 whenεin=3.2. The best performance of the screening MM/PBSA(rP=0.728)in this case corresponded toεin=2.4 or 2.6. While in dataset II,the Pearson correlation coefficient decreased with the increase of the solute dielectric constant,but the difference was not obvious whenεin<=2.0. With further increase of the solute dielectric constant,the performance of the screening MM/PBSA became worse, particular whenεin>2.6, indicating that the largeεinmay underestimate the electrostatic energy and was harmful for the prediction accuracy in this case. Actually, when the proteins and the nucleic acids carried the opposite charges in dataset I, there should be a strong polarization at the interface of the protein-nucleic acid complex. Thus a largeεinshould be used to well describe the polarization but this value should not be very large to avoid overestimating the polarization. While in dataset II,the proteins and the nucleic acids carried the like charges,there should be no obvious polarization at their interface. Thus, a smallεin(i.e., 1.0) should be used. Taking the two datasets together,the screening MM/PBSA showed good performance whenεin<=2.6 (see the last column in Table 1), where it(rP=0.628)showed the best performance underεin=2.0.
We also investigated the relationship between the correlation coefficient and the solute dielectric constant in the standard MM/PBSA (Table 2). Similar to that in the screening MM/PBSA,there was also an optimal value ofεinin dataset I while the Pearson correlation coefficient decreased with the increase of the solute dielectric constant in dataset II. However,since such difference in dataset II was much more obvious than that in dataset I, the Pearson correlation coefficient also decreased with the increase of the solute dielectric constant in the whole dataset.

Table 1. Overall prediction accuracies of the screening MM/PBSA under different solute dielectric constants.
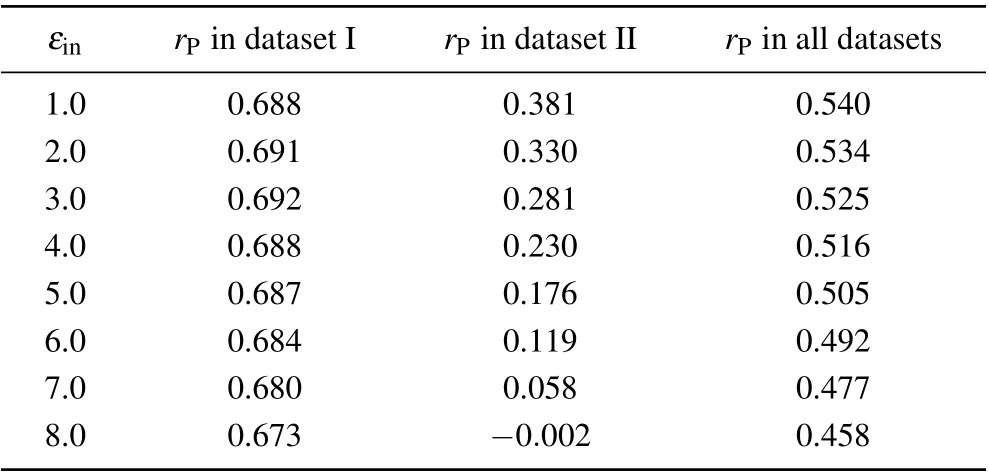
Table 2. Overall prediction accuracies of the standard MM/PBSA under different solute dielectric constants.
3.3. Effect of salt concentration in screening MM/PBSA on accuracy of predicted binding energy
In real experiment, the conditions for measuring the protein-nucleic acid binding affinity could be very different,where the type of salts could be various and the concentration could be in a broad range. Since the Debye length in the screening electrostatic energy and the polar energy was related to the salt concentration,it is of great importance to investigate the effect of the salt concentration on the accuracy of binding energy predicted by the screening MM/PBSA. Here, for the sake of simplicity,three different salt concentrations were considered (0.05 M, 0.15 M, 0.30 M) and the salt type (i.e.,NaCl)was kept the same.
As shown in Fig. 4, when the salt concentration was 0.05 M, most of the predicted binding energy became larger due to the weaker screening effect of the electrostatic interaction, particularly in dataset I. On the contrary, most of the predicted binding energy become smaller due to the stronger screening effect when the salt concentration was 0.30 M.In terms of the correlation coefficients, the accuracy of the screening MM/PBSA at 0.05 M was very similar to that at 0.15 M (i.e., 0.709versus0.718 in dataset I and 0.519versus0.516 in dataset II).However,the accuracy of the screening MM/PBSA at 0.30 M became worse than that at 0.15 M,especially in dataset II (0.291versus0.516), indicating that the high screening effect could be harmful for the prediction, which was similar to the standard MM/PBSA using a very largeεin(e.g., 8.0) or the screening MM/PBSA using a largeεin(e.g., 3.0). As we know, the interaction energy at the interface between the protein and the nucleic acid usually played an important role in total binding energy. The high screening of electrostatic interaction would certainly underestimate the attractively electrostatic energy at the binding interface,particularly in dataset II(the protein was also negatively charged),thereby it would lead the inaccuracy of the screening MM/PBSA.
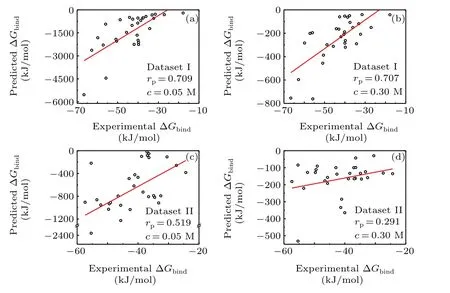
Fig.4.Pearson correlation coefficient for the dataset I and dataset II based on the minimized structures in the screening MM/PBSA methods. (a)Dataset I under the concentration of 0.05 M; (b) dataset I under the concentration of 0.30 M;(c)dataset II under the concentration of 0.05 M;(d)dataset II under the concentration of 0.30 M.
4. Conclusion
In this study, we have applied a modified approach via the screening electrostatic energy within the framework of the MM/PBSA method. Based on 60 protein-nucleic acid complexes in dataset I and dataset II, the screening MM/PBSA shows an excellent performance in dataset I and a moderate performance in dataset II;while the standard MM/PBSA just yields a good performance in dataset I and a poor performance in dataset II (probably due to the overestimated long-range electrostatic energy). Besides, we also evaluated the performance of the screening MM/PBSA under different solute dielectric constantεin, and recommend that a smallεinshould be used. In general,the screening MM/PBSA can indeed provide reasonable predictions on the binding energy in charged bio-systems.
Acknowledgment
Project supported by the National Natural Science Foundation of China(Grant Nos.11874045 and 11774147).
- Chinese Physics B的其它文章
- Helium bubble formation and evolution in NiMo-Y2O3 alloy under He ion irradiation
- Dynamics and intermittent stochastic stabilization of a rumor spreading model with guidance mechanism in heterogeneous network
- Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
- Low-overhead fault-tolerant error correction scheme based on quantum stabilizer codes
- Transmembrane transport of multicomponent liposome-nanoparticles into giant vesicles
- Molecular dynamics simulations of A-DNA in bivalent metal ions salt solution

