Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
Yuhao Zhu(朱宇豪) Rui Jin(金銳) Yong Wu(吳勇) and Jianguo Wang(王建國)
1Key Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
2Center for Free-Electron Laser Science,DESY,Hamburg 22607,Germany
3HEDPS,Center for Applied Physics and Technology,Peking University,Beijing 100084,China
Keywords: eigenchannel R-matrix,oscillator strengths
1. Introduction
Atomic energy levels and optical oscillator strengths,particularly for Rydberg states, are crucial physical parameters in many physics fields, e.g., astrophysical spectroscopy,[1-3]diagnostic analysis of plasma,[4,5]quantum information processing[6-8]and so on. Specifically speaking,optical oscillator strengths between energy states are important for the understanding of energy balance and the rate of radiative decay in various types of astrophysical and laboratory plasma.[9-11]With the determination of line intensity ratios, the electron temperature, electron density and elemental abundances in plasma are indicated. In some special plasma environments,the radiation of Rydberg states cannot be neglected, e.g., the hot dense plasma.[12,13]Higher requirements are put forward for the richness of atomic energy levels and optical oscillator strengths. Although experimental measurements in spectroscopy have already made large promotion, they still cannot completely avoid absolute discrepancies. Therefore, precise theoretical calculations need play an indispensable role in atomic energy levels and optical oscillator strengths.
While traditional atomic structure calculation methods,such as the configuration interaction[14](CI) method and many-body perturbation theory[15](MBPT),are generally believed that the computational costs are too expensive for Rydberg states. Fortunately, there is a correlative relationship between the atomic energy levels and corresponding electronion collision processes in terms of the analytical continuation property of the short-range scattering matrices.[16-18]Depending on this property, the eigenchannel based on a relativistic R-matrix(R-R-Eigen)[19-21]could provide the required atomic data mentioned above with adequate precision. In the scenario of an R-R-Eigen,a half-collision model where it could be regarded as an ion in low-lying excited states combined with an incident electron in the bound orbital or the continuum orbital composes the atomic system.Whatever in the bound or continuum energy regions,the short-range scattering matrices for the multi-channel process can be calculated accurately. One can extract the needed physical parameters in multi-channel quantum defect theory(MQDT)[22-26]from the scattering matrices,i.e.,the eigenchannel phase and transformation matrix. Due to the analytical continuation of the scattering matrices, MQDT parameters vary smoothly as a function of energy. It is sufficient for us to calculate the scattering matrices with a minority of energy points in order to obtain good MQDT parameters for the entire energy of interest. By employing the MQDT,all energy level positions in discrete energy regions will be predicted without missing anyone. Furthermore,various electron dynamics processes in atomic systems can be calculated using MQDT parameters (i.e., scattering matrices) checked by precise spectroscopy measurements, such as those of scatter,optical absorption,and radiation.
Nitrogen is one of the most abundant elements found both on Earth and in the atmospheres of stars with huge demand for spectral line diagnosis. As an open-shell element, nitrogen also is extremely useful for plasma modeling. Previous research works[27-33]on the nitrogen atom have mainly studied the electronic structures and transitions for low-lying energy states because of the correlation effect of electrons. However, we are able to stretch the energy region to the extent of high Rydberg states with high precision and less computational costs using R-R-Eigen. In this work,the nitrogen atom has been investigated for the specific partial waveJπ=1.5+(+represents even parity). The present paper is organized as follows.The MQDT parameters of the selected physical channels are obtained in Subsection 2.1. The discrete energy levels of the major Rydberg series are calculated in Subsection 2.2.In Subsection 2.3,we calculate the optical oscillator strengths for the transition between the ground state and parts of the Rydberg series. The partial theoretical energy levels and corresponding optical oscillator strengths are exhibited in detail.Finally,the paper ends with a short summary.

Table 1. Physical channels with corresponding eigenchannels for N system with Jπ =1.5+ symmetry.
2. Theoretical methods and calculation results
2.1. Calculation of the MQDT parameters
The construction of the nitrogen atom system is from the model of an electron collision with a nitrogen cation. The wavefunction of the N+1 system (i.e., ion with an electron)is solved by a method that seems like a traditional relativistic R-matrix.[34-37]In the inner region, the scattering system is treated as the bound state, i.e., the CI expansion of the internal wavefunction,since there is a strong exchange and correlation effects between the scattering electron and the target electrons. On the other hand, the incident electron is in the long-range multipole potential field of the target in the outer region. We can obtain the exact wavefunction of the electrons by neglecting the exchange and correlation effects. The inner and outer wavefunctions are connected by the R matrix to construct the total wavefunction of the N+1 system.Thus,we can derive the reaction matrices (K matrices) from the N+1 electron wavefunction defined on a certain boundary in the reaction zone. The electron wavefunction in the R-R-Eigen is as follows:
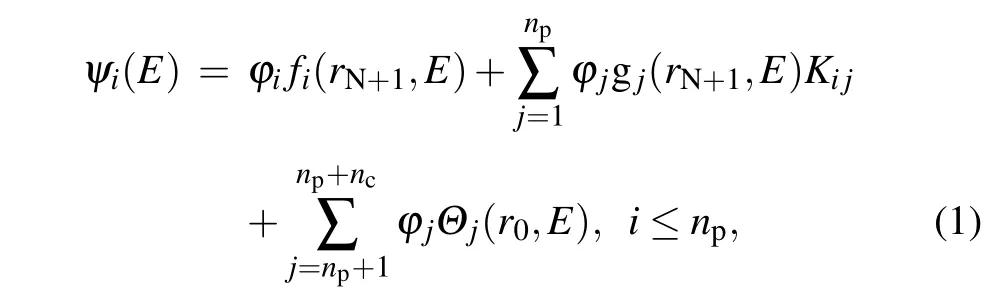
wherenpandncare the number of physical and computational channels, andΘjis the corresponding radial wavefunctions of the N+1 electron system. Note that the definitions of the channels are different from the traditional R-matrix.[38]For theithphysical channel,the regular and irregular Coulomb wavefunctions,fi(rN+1,E)and gj(rN+1,E),modified by the appropriate long-range polarization interactions,cover the entire set of the one-electron orbitals, with both negative and positive energy.[23]The scattering matricesSijare extracted from the reaction matricesKij. We transform the wavefunction into an eigenchannel representation and the short-range scatter matrices with a specific total angular momentum and parityJπare diagonalized as follows:
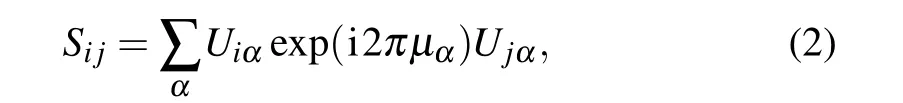
where the eigenchannel phaseμαandnp×nporthogonal transformation matrixUiαare the main parameters in MQDT.The transformation matrix between the eigenchannels and physical channelsUiαcan usually be characterized as Eulertype angles[16,22]θk,k=1,...,np(np-1)/2.
We take account of 12 physical channels in the scattering matrices calculation of N withJπ= 1.5+symmetry.As the scattering energy varies from the bound-state energy region to the continuum-state energy region, the number of physical channels increases gradually rises from the mathematical properties of the Coulomb wavefunctions,[39]i.e., 2,5, 8, and 12 channels are in the four different energy regions, respectively. More specifically, in the energy region of-0.225 Ry to-0.125 Ry, there are two physical channels,namely,N+(3P1)s1/2and N+(3P2)s1/2. In the energy of-0.125 Ry to-0.06 Ry,there are five physical channels with three additional channels,namely,N+(3P0)d3/2,N+(3P1)d3/2,N+(3P1)d5/2. Three extra channels in the eight physical channels energy region of-0.06 Ry to 0.08 Ry are N+(3P2)d3/2,N+(3P2)d5/2, N+(3P2)g7/2, respectively. The 12 physical channels with four additional channels, i.e., N+(1D2)s1/2,N+(1D2)d3/2,N+(1D2)d5/2,N+(1D2)g7/2,are in the final energy region of 0.08 Ry to 0.18 Ry. For better identification of physical channels, we list all 12 physical channels(JJnotation) with their corresponding eigenchannels (LSnotation)in Table 1. Due to the number of physical channels equal to the eigenchannels in each independent energy region,there are four transformation matricesUiαwith the same dimension as the number of eigenchannels,which are represented by 1,10,28, 66 Euler-type angles in the four energy regions respectively.
The MQDT parametersUiαandμαvarying via the energy are shown in Fig. 1(a) and 1(b), respectively. As we see, the MQDT parametersμαandUiαvary as functions of the energy smoothly over the whole energy region, which substantially reflects the analytical continuation property of the scattering matrices. Evidently,all of the connections between the identical channels in the adjacent energy regions belong to the type-I connection with weak interchannel interactions.[20]Based on the analytical continuation property of scattering matrices,all discrete energy levels can be obtained without missing anyone in the framework of the MQDT in the next section.
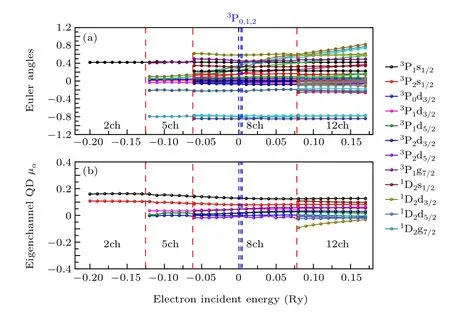
Fig. 1. Eigen-quantum defects μα, Euler angles θk for Uiα matrix in the Jπ =1.5+ symmetry of N.The dashed red lines indicate the connection position of different channel regions. The zero energy of abscissa represents the first ionization threshold of 3P0 and all the ionization thresholds of N are plotted with the dashed blue lines. Note that the labels of channels on the right are only for eigen-quantum defectsμα.
2.2. Calculation of the discrete energy levels
In order to obtain the discrete energy levels,we briefly introduce the MQDT. The energy eigenfunctions are expressed as the linear combination of eigenchannel wavefunctions,i.e.,

whereCiαis the cofactor of the elementFiαof the determinant|Fiα|, and the choice of indexiis arbitrary. The solutions to Eqs.(5)and(6), i.e., discrete sets of the numbersνi, provide discrete energy levels of the perturbed Rydberg series.
Utilizing the smooth MQDT parameters, we can solve Eqs. (5) and (6) to obtain the energy levels that can be compared with the precision spectroscopic measurements to correct scattering matrices. In our case of the nitrogen atom withJπ=1.5+,three thresholds are involved in the interested energy region leading to three principal quantum numbersν3P0,ν3P1,ν3P2.For the atomic system with more than two ionization thresholds,one can adopt a projected high dimensional quantum-defect graph (symmetrized), i.e., JHANGZ plot, to show the results of the graphic method. More precisely, we use the energy constraint from Eq.(5)to project the problem of three-dimensional solution of Eq. (6) (i.e., three unknown variables) to an advisable two-dimensional subspace through selecting arbitrary two of the three principal quantum numbers(ν3P0,ν3P1,ν3P2) as known variables. In this calculation, it is appropriate to select a two-dimensional plot withν3P0versus-ν3P1as a way of physical understanding. Thus, theν3P1is the known variables with unknown variablesν3P0,ν3P2to scan the energy ofν3P1. Effective principal quantum numbers are projected out in Eq.(6)with the following energy constraint:

whereqis the target charge andIis the ionization threshold.
In Fig.2(JHANGZ plot),one can see that the seven differently colored branch curves determined by mixing coefficientAαof the eigenchannel wavefunction represent the different eigenchannel effective phase shifts solved by Eq. (6).There are four quasi-horizontal differently colored branch curves, including black, red, orange and purple, which represent channels with3P0d3/2(4F),3P1s1/2(4P),3P2d3/2(4P),3P2d5/2(2P),respectively. On the other hand,three quasiperiodic resonant colored branch curves,blue,pink and green,represent channels with3P1d3/2(4D),3P1d5/2(2D),3P2s1/2(2P),respectively.The dashed lines are the Rydberg relationship between the projected ionization thresholds3P0and3P1.What is more,the crossing points between the dashed lines of the Rydberg relationship and solid curves of the seven colored branch curves are the theoretical energy level positions for the relevant eigenchannel.We have labeled the theoretical energy levels with various symbols, i.e., black circle, red triangle, blue five-pointed star,pink pentagon,green square,orange inverted triangle and purple rhombus, representing each eigenchannel determined by the corresponding color, respectively. The abscissa is the principal quantum number identified by Eq. (5)for the different eigenchannel. It is noted that discrepancies of tunnel depth in the multi-electronic system result in diverseνof s wave and d wave channels(decided by the different types of the incident continuous electron). For the condition of N withJπ=1.5+symmetry, the 65 experimental values in the NIST[40]and corresponding existing theoretical values under these projection thresholds are labeled in Fig. 2. Compared with available experimental data, the precision of the shortrange scattering matrices is estimated to be within 2%. In this framework, one can systematically obtain all energy levels without missing anyone by employing the MQDT, rather than calculating energy levels one by one like in traditional methods.

Fig.2. Projected high-dimensional quantum-defect graph. Quantum-defect-ν3P0 (mod 1)versus ν3P1 plot of N Jπ =1.5+ partial wave. The dashed cyan lines are the Rydberg relationship between the two ionizations of 3P0 and 3P1. The differently colored solid curves indicate F=0,i.e., Eq.(6). The crossing points between the solid curves and dashed lines are the positions of theoretical energy levels. The corresponding energy level positions are labeled with different types of symbols. i.e.,black circles are d wave4F,red triangles are s wave4P,blue five-pointed stars are d wave 4D,pink pentagons are d wave 2D,green squares are s wave 2P,orange inverted triangles are d wave 4P and purple rhombuses are d wave 2P. All theoretical energies results are indicated as solid symbols, and available experimental energies are presented by the open symbols for comparison. Note that the energy grid at the top is not equidistant,but increasingly dense.
2.3. Optical oscillator strengths
After obtaining the exact eigenchannel wavefunction,optical absorption and radiation of atomic systems can be investigated. The optical oscillator strengths (OOSs) ofn-th state could be derived from the mixing coefficient for the different channel via

We calculate the OOS of N for the transition between the ground state and a portion of the Rydberg series which have the sameLSnotation. It is noted that computational costs of the energy levels and OOSs for highly excited states are considerably less than for conventional methods.[14,15]In Table 2,the calculation results are listed,including the principal quantum number of the projected ionization thresholdν3P1, theoretical energy levels,experiments energy levels from NIST[40]and the length and velocity values of the oscillator strengths for the transition between the ground state4So3/2and Rydberg series with the terms4P3/2and2P3/2. The theoretical energy levels generally coincide with the experiments with a precision of better than one percent. To our knowledge, we only found calculations[27,28,31]that reported OOS for relevant fine structures with the configurations 2s22p23s and 2s22p23d in the transition conditions of4So3/2-4P3/2and4So3/2-2P3/2. As we see, the discrepancies between our theoretical results and others[28,31]in the condition of configuration 2s22p23s with transition of4So3/2-4P3/2are within 10%. However,the conditions of the configurations 2s22p23s and 2s22p23d with transition of4So3/2-2P3/2are more than 10%,which may result from the different expansions of wavefunctions. Precisely,the basis sets in our method are a group of scattering channel wavefunctions, others[28,31]have usually employed the traditional atomic orbital basis sets. We also found that there are few experimental and other theoretical results in highly excited states for comparison. As a matter of fact, it is an enormous challenge for experiments and traditional methods to study the optical oscillator strengths of the Rydberg states near the ionization threshold. Further experimental and theoretical studies on the OOSs of Rydberg states are necessary. As for the scenario of R-R-Eigen, a specific N+1 system channel can be ascertained in advance based on the principle of scattering. We can accurately obtain a series of bound states of this channel and corresponding dynamics conveniently through energy determination. Namely,the complete basis of the total electronic wavefunction is formed by the wavefunctions of different scattering channels.
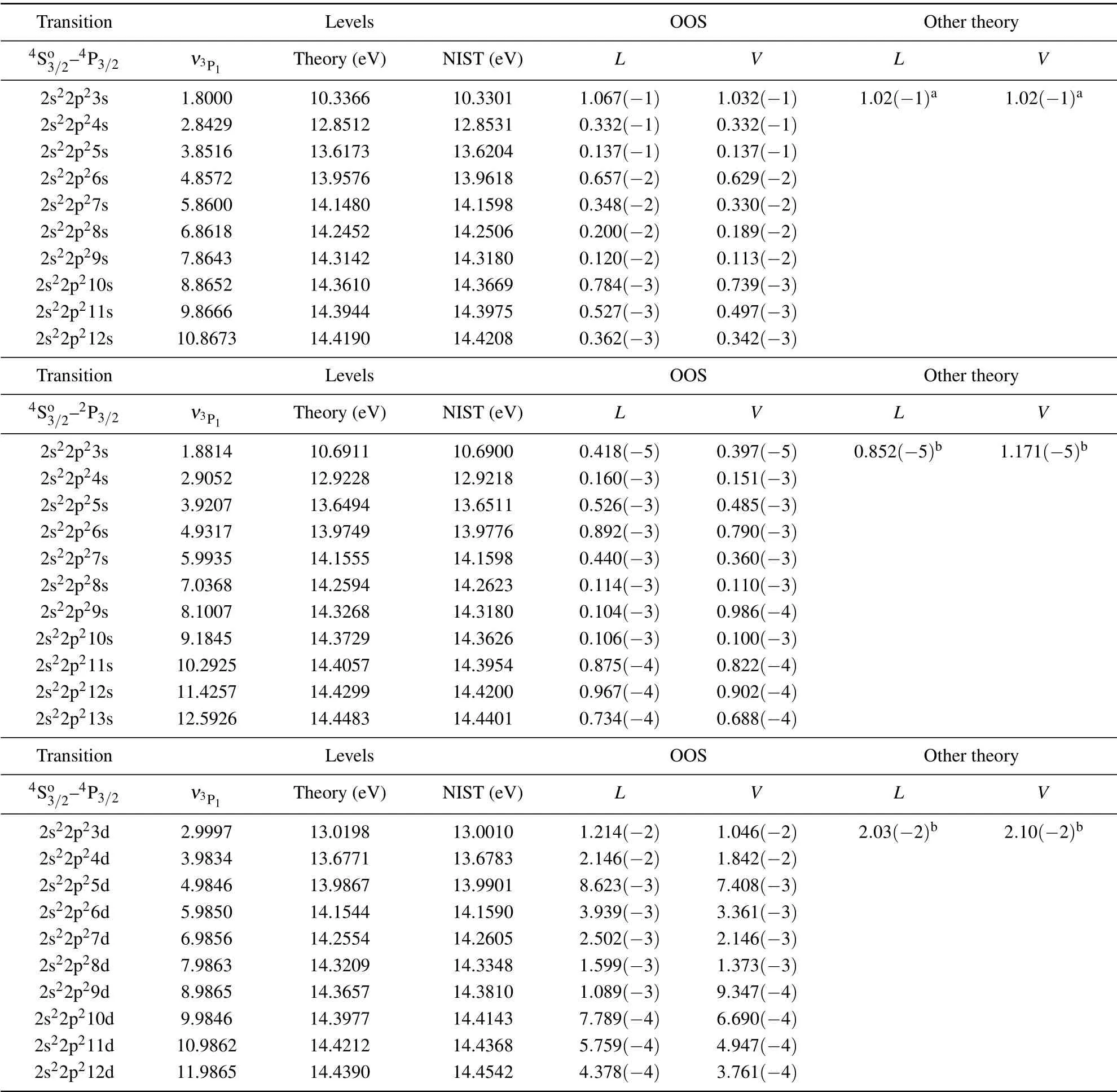
Table 2. Energy levels and the length(L)and velocity(V)values of OOS for the transitions of 4So3/2-4P3/2 and 4So3/2-2P3/2 are listed. The ν3P1 is the principal quantum number for the state of corresponding Rydberg series.
3. Summary
With employing the R-R-Eigen method, we calculate the short-range scattering matrices of the e+N+system forJπ=1.5+symmetry which provided good MQDT parameters(μα,Uiα) in the energy region from-0.225 Ry to 0.18 Ry.The smoothness of the MQDT parameters(i.e.,the analytical continuation of scattering matrices)is guaranteed by selecting the appropriate physical channels in different energy regions.Additionally, the accuracy of our calculated MQDT parameters is determined to be within 2%. All the connections of the MQDT parameters in different energy regions belong to the type-I connection, which has weaker eigenchannels interactions compared with the type-II connection.[20]In the condition for multi-thresholds of the atomic system, we propose the JHANGZ plot to perform the final result of solving the MQDT equations in the discrete energy region. The JHANGZ plot shows theoretical energy level positions and experimental values for each channel systematically. The theoretical energy levels in the current work are within one percent discrepancy compared to the values of the NIST. According to the precise spectroscopy measurements,we could review the MQDT parameters to obtain more accurate results. Namely, given the analytical continuation property of scattering matrices,the smoothness of MQDT parameters in all energy regions is necessary. Thus,in order to ensure the smoothness of the MQDT parameters, the slope of the MQDT parameters varying with energy will not be distorted,only a small translation of the parameters as a whole. In this way,we shall improve the numerical accuracy of the results without destroying the analytical continuation property of scattering matrices.
In our work, the relevant physical channels dipole matrix elementsDαand the mixing coefficient of the eigenchannel wavefunction are calculated to obtain the optical oscillator strengths. The optical oscillator strengths for the transitions between the ground state and Rydberg series with terms4P3/2and2P3/2are exhibited thoroughly. There is good agreement between other theoretical calculations and ours in the condition of the configurations 2s22p23s and 2s22p23d. The optical oscillator strengths could supply abundant information about the optical transition of highly excited states to help us understand the influence of the radiation on the energy balance of high energy levels in hot dense plasma. Moreover, we look forward to more experiments and theoretical calculations in further studies on the optical oscillator strengths of the Rydberg states.
Acknowledgments
Project supported by the Science Challenge Project(Grant No. TZ2016005), the National Key Research and Development Program of China (Grant Nos. 2017YFA0403200 and 2017YFA0402300), and the CAEP Foundation (Grant No. CX2019022). We thank the Institute of Applied Physics and Computational Mathematics for the supercomputing source.
- Chinese Physics B的其它文章
- Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube
- Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs
- Manipulating vortices in F =2 Bose-Einstein condensates through magnetic field and spin-orbit coupling
- Beating standard quantum limit via two-axis magnetic susceptibility measurement
- Neural-mechanism-driven image block encryption algorithm incorporating a hyperchaotic system and cloud model
- Anti-function solution of uniaxial anisotropic Stoner-Wohlfarth model

