Qing Xia(夏清) Ming-Hui Cai(蔡明輝) Liang-Liang Xu(許亮亮) Rui-Long Han(韓瑞龍)Tao Yang(楊濤) and Jian-Wei Han(韓建偉)

1National Space Science Center,Chinese Academy of Sciences,Beijing 100190,China

2School of Astronomy and Space Science,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: lunar dust,south polar region,solar wind,mini-crater

1. Introduction

Lunar dust is a serious threat to lunar exploration.[1,2]The size of lunar dust particles is about 30 nm to 20μm,and more than 95%of particles are＜2μm.[3]Lunar dust particles are small, sharp and insulating, and can be easily charged. They readily adhere to surfaces of spacecraft and invade the mechanical structure,which affects the normal operation of space systems. Lunar exploration during the Apollo era proved that diffusion of lunar dust particles can give rise to visual obstacles, meter reading errors, lunar dust adhesion and pollution,surface skidding, mechanical obstruction, surface wear, thermal control problems and seal failure, and can cause physiological stimulation.[2]The lessons obtained from the Apollo landing program demonstrate that the influence of lunar dust on lunar surface exploration activities is one of the problems that must be solved when human beings return to the moon.

Exploration of the lunar polar region is a strategic goal for many powerful countries.[4]The south polar region of the moon is considered to be of great significance for science and engineering. It is characterized by low temperatures(100 K-160 K),a complex topography(many craters and slopes)and a low solar altitude angle, which at the south pole varies between±1.54°.[5]

A study by Maoet al.showed that the smaller the solar altitude angle (0°and 180°), the thicker the charged sheath and the more likely the lunar dust floating phenomenon is to occur.[6]A study by Alvaezet al.showed that the environmental conditions of low temperature and low solar altitude in the lunar south polar region can make the conductivity of the lunar soil very low.[7]When the solar altitude angle is 30°and the soil conductivity of the moon meter 10-6S/m,the potential of the lunar surface would be 60 V,while at 10-8S/m it would be 170 V,[8]which indicates that the very low conductivity of the lunar soil in the south polar region would cause high potential charging of the local lunar surface,generating large quantities of electrostatically charged floating lunar dust.

Furthermore, the complex topography in the lunar south polar region and the low solar altitude angle will produce a large number of shaded areas. Farrellet al.showed that there may be electron-rich regions in the shaded area of kilometerscale craters. This electron-rich environment could cause a negative potential of magnitude -100 V, which may further produce electrostatic repulsion of negatively charged lunar dust under the action of the surface potential, thus forming a harsh lunar dust environment.[9-11]In conclusion, the special environmental characteristics in the lunar south polar region will lead to much more severe lunar dust environment than in the mid-latitude region.

The purpose of this paper is to work out the possible charged lunar dust atmosphere caused by the characteristics of the south polar region, namely, a low solar altitude angle,low temperature(low soil conductivity)and complex topography. We studied the dusty-plasma atmosphere near the lunar surface in the south polar region of the moon using Spacecraft Plasma Interactions Software (SPIS) developed by the European Space Agency.[12]First, the spatial distribution of lunar dust at different solar altitude angles was simulated,as well as the distribution of photoelectrons,ions and electrons. Second,we studied the spatial distribution of lunar dust, photoelectrons, ions and electrons in the plasma void area created by shielding of the solar wind by a mini-crater. The mechanism of lunar dust distribution was analyzed.Third,the migration of lunar dust at the boundary between light and shade was studied. Finally, the probable dust risk faced by astronauts in the south polar region was simulated using a spacesuit model.

2. Dusty plasma on the lunar surface

Dusty plasma refers to ionized gases consisting of electrons,ions and charged microscopic dust particles. When immersed in space plasma or exposed to sunlight, dust particles start to collect or emit electrons and ions, thus charging the dust particles to a floating potential. In this paper we will discuss the dusty plasma on the lunar surface under a solar wind plasma and sunlit environment.

2.1. Dusts in solar wind plasma

The characteristics of dust in plasma can be divided into those of isolated dusts and non-isolated dusts, distinguished by the dust radiusrd, the average dust intergrain distanceaand the Debye lengthλD.[13,14]λDis given as

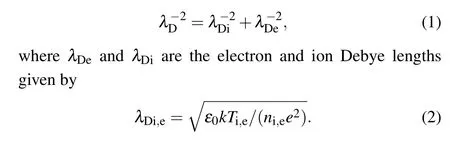
Hereε0is the permittivity of space,kis the Boltzmann constant,Ti,eis the ion (i) and electron (e) temperature andni,eis the ion and electron density. Dust particles in plasma can be dominated by the local electric field when they are charged.Whenrd?λD?a,charged dust in plasma can be regarded as an isolated dust which only interacts with plasma but not with dust particles themselves. The dust charging process can be modeled by the orbital motion limited (OML) theory.[15]On the other hand, whena ?λD?rd, influences between dust particles themselves cannot be ignored. Dust particles interact with each other and also participate in the collective behavior of the local plasma.

Solar wind plasma is a quasi-neutral plasma which consists of a high-speed stream of charged particles with a bulk velocity from 200 km/s to 800 km/s. It is an anisotropic plasma that changes with solar incidence angle. On the lunar surface,the Debye length of the solar wind and photoelectrons is about 10 m and 1 m, respectively, which indicates we should not simplify the dusts as isolated ones. For non-isolated dusts,the Monte Carlo collision (MCC) algorithm was used to describe the collected probability of an interacting cross section between plasma and dust particles(see Section 3).

2.2. The motion of particles

The motion of plasma species is described by the following equations:

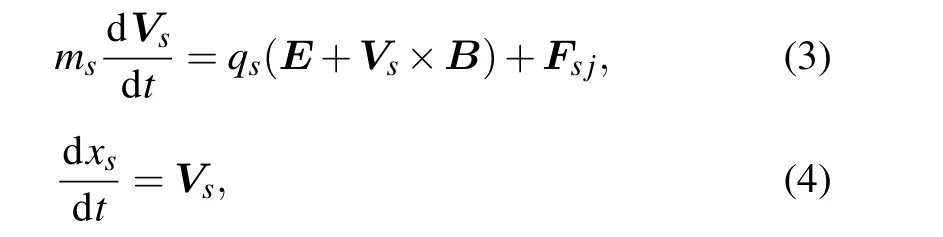
where the subscriptsrefers to ions or electrons,Vsis the velocity of particle s,msis the mass,xsis the position,qsis the charge,EandBare the electric and magnetic fields,respectively,andFs jis the force due to collision with other species.The motion of a charged dust follows the same equation as the plasma species:

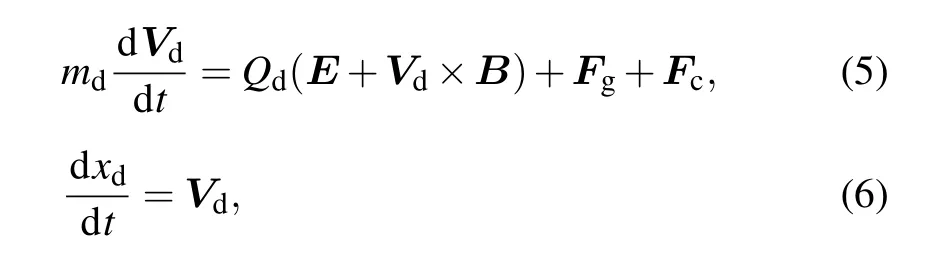
where the subscript d refers to dust,Fgis the gravitational force andFcis the collision force due to collision with neutral and ionized particles. The dust chargeQd(t) is a function of time and is given by

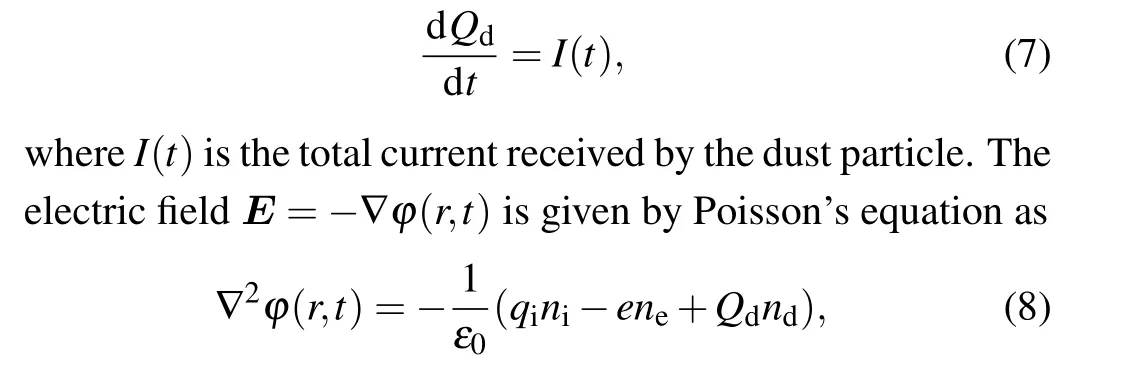
whereni,ne, andndare the ion, electron and dust densities,respectively,qiis the ion charge andQdis the dust charge.Equation(8)shows that the electric field which originates from charged dusts was not ignored.[16]

3. Particle-in-cell with Monte Carlo collision method

The simulation volume was divided into mathematical meshes and nodes which overlay all particles in the simulation volume; this is known as the particle-in-cell (PIC) method.Instead of simulating all particles in the simulation volume,the PIC method uses superparticles which represent many particles with their charge and weight deposited on the nearby nodes. The interaction between plasma and dust particles is simulated via the MCC algorithm,and the multi-step MCC algorithm proposed by Gatsoniset al.was employed to describe different collision frequencies of dust particles, as they can vary with size and charge.[17]

The computational sequence of PIC-MCC is shown in the following.[16]

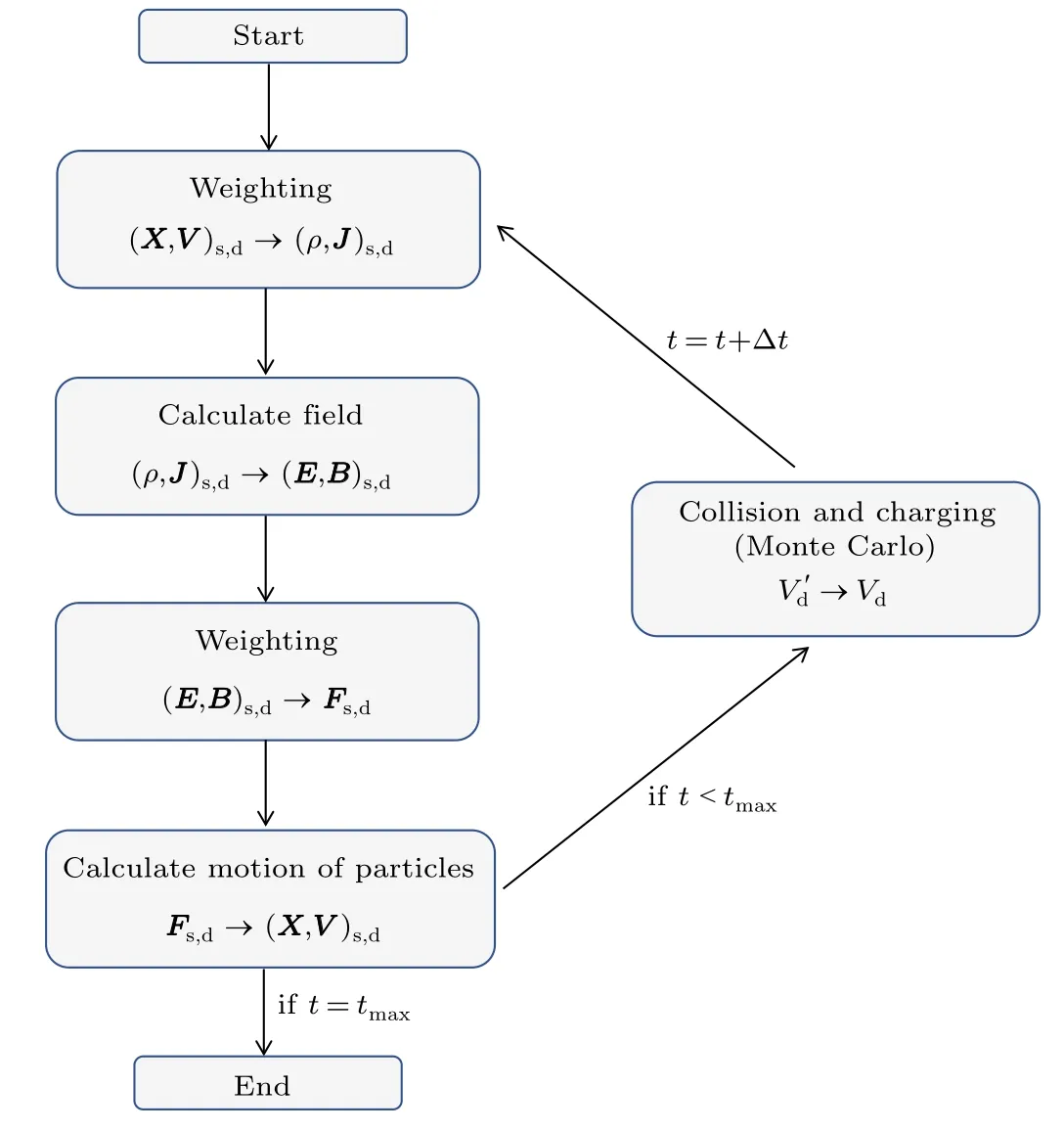
An additional ‘collision and charging’ step was inserted to check for possible collisions between plasma particles and dust particles. When a collision event occurs, a number of plasma particles will be removed from the simulation and their charges assigned to the corresponding dust particle. This is based on the assumption that all collisions are of the absorption type where the colliding plasma particles stick to the dust surface.

The collision possibility is described by the absorption collision frequencyνd,

The calculating cycle will keep repeating for a specific time period.

4. Simulation model

In this paper, interaction of the lunar surface with solar wind plasma was simulated using SPIS-DUST,which includes an ambient environment model, surface charging, dust injection from the lunar surface,dust charging and dust dynamics.Simulation models are shown in Figs.1 and 2.We will discuss two typical environmental situations. In the first situation,described in Fig.1,the distribution of lunar dusts,ions and electrons, as well as the lunar surface potential were simulated with solar altitude angles of 20°and 0°. In the second situation, described in Fig. 2, an environment of lunar dusts and plasma, as well as lunar surface potential and volume potential,were considered in the nightside of a 5 m high mini-crater with a solar altitude angle of 20°. We also consider an astronaut standing on the moon in these two situations and discuss the dust risk to the spacesuit.

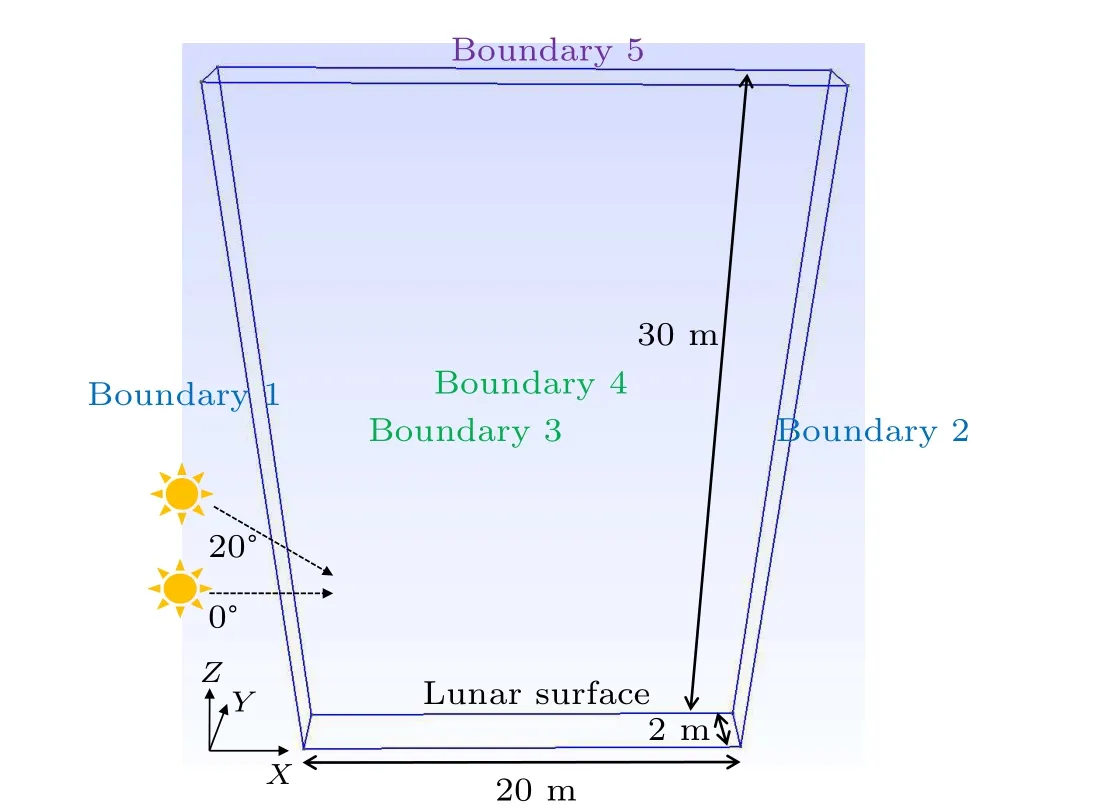
Fig.1. Simulation model 1.

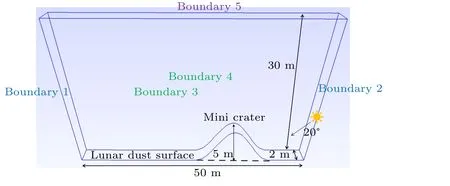
Fig.2. Simulation model 2;the crater is 5 m high.

4.1. Simulation domain

The simulation domain cannot cover the moon entirely.We adopt a ‘box’ to simulate the infinite lunar surface and no current divergence should exist across the side boundaries. Thus, lateral boundaries should be set as either reflecting or periodic to ensure physical rationality.[18]The simulation boxes are shown in Figs. 1 and 2. They were set as 20 m×2 m×30 m and 50 m×2 m×30 m,respectively. The reflecting boundaries return the particles to the simulation box,but the perpendicular component of the particle velocity is reversed.The periodic boundaries return the particles to the simulation box so that if a particle reaches the outer boundary it will be moved to the opposite boundary, keeping the velocity unchanged. The boundary conditions were therefore set as periodic for boundaries 1 and 2, which were passed through by the solar wind, and reflective for boundaries 3 and 4, which were parallel to the solar wind. Boundary 5 was set as an open boundary and the lunar surface was set as an absorbing boundary.

The meshing algorithm was set as Delaunay for twodimensional surfaces and three-dimensional volume. An uneven mesh size was adopted,and 0.4 m was set at the surface and 2 m at the upper boundary.

4.2. Global parameters

The parameters of plasma and lunar dust surface which come from slow solar wind conditions are shown in Table 1 as recommended in SPIS documentation.[12]

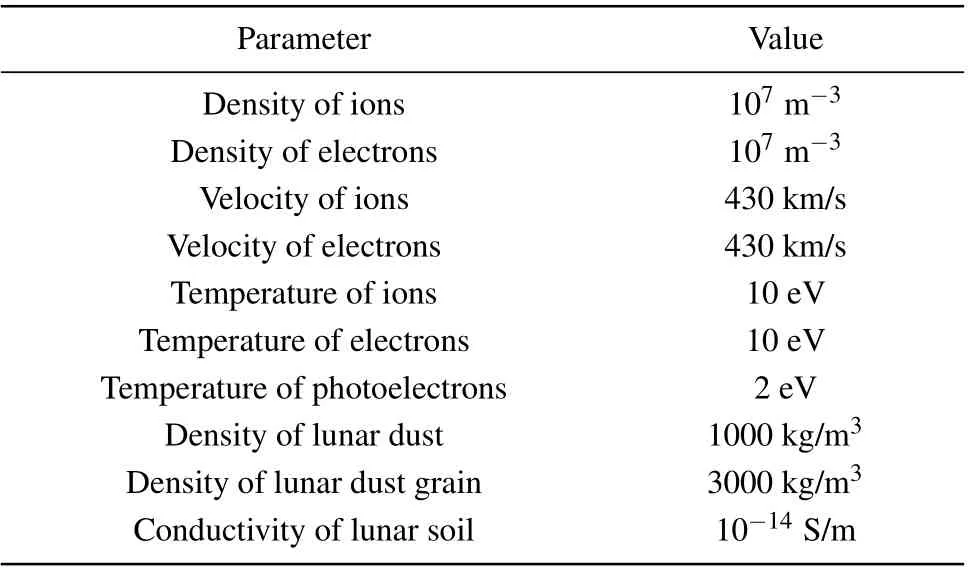
Table 1. Global parameters.

The default dust size distribution is from 1.91×10-9m to 3.2×10-2m radius, referred to as sample 71501,1 Mare,with mean grain sizes mostly between 45μm and 100μm.[19]

In this simulation, solar wind plasma was injected from boundary 5 (open boundary). Solar wind plasma passed through boundary 5 and was absorbed by the lunar dust surface which was set as an absorbing boundary. Solar wind plasma was absorbed and photoelectrons as well as dust particles were emitted by the lunar dust surface. The dusty lunar surface emits dust according to the force balance between all forces acting on the dust. On the lunar surface, the energy distribution function of the photoelectron is Maxwellian by default,with a temperature of 2 eV.Other dusty plasma conditions are default in SPIS.

5. Results and discussion

On the lunar surface,λDis about 1 m due to photoelectrons and about 10 m in the solar wind. Under such a largeλDit is obvious that the collective behavior of dust particles,such as dust density,should be more representative. In this section,we will discuss the density distribution of dust and plasma near the lunar surface in the south polar environment. The solar altitude angle was set as 20°and 0°, values which would be representative of the local environment.[5]The distribution of dusts and plasma in the nightside of a mini-crater caused by shielding of solar wind by craters or rocks was considered. As recommended in the SPIS user manual,[12]a simulation duration of 3000 s was set. The distribution and transport mechanism of dusts near the lunar surface is discussed.

5.1. Distribution of dusts and plasma near the lunar surface in the south polar environment for a solar altitude angle of 20°

The distribution of charged lunar dusts near the lunar surface with a solar altitude angle of 20°is shown in Fig.3. As can be seen in the figure, different colors represent different dust densities (logarithmic scale). The spatial density of lunar dust is 109.15m-3-1010.4m-3near the lunar surface(at a height of about 1 m above the surface). At heights over 1 m from the surface,most of the region is green,which represents a lunar dust density of about 107.91m-3.

Fig.3. Distribution of charged lunar dust for a solar altitude angle of 20°.

The spatial distribution of charged lunar dust depends on the local plasma environment, i.e., the distribution of photoelectrons,ions and electrons from the solar wind and light.

The photoelectric effect is the main mechanism of lunar charging on the dayside of the moon.The lunar soil emits photoelectrons under sunlight and is positively charged. During the simulation,the lunar surface remained positively charged.At the end of the simulation,the potential of the lunar surface was 17.5 V.

The distribution of photoelectrons, ions and electrons near the lunar surface (0 m-30 m above the surface) is presented in Figs.4(a)-4(c). It should be pointed out that the periodic boundary condition caused nonuniformity of particles at the periodic boundaries, so here and later we focus on the results in the middle region of the lunar surface model. As shown in Fig. 4(a), there is a photoelectron sheath within a height of about 1 m from the surface and the density of photoelectrons is 106.95m-3-107.45m-3.The photoelectron density decreases with height. Beyond the photoelectron sheath, the photoelectron density is 105.96m-3-106.46m-3. The distribution of ions is presented in Fig.4(b). The ions near the lunar surface are repelled as the lunar surface is positively charged.The density of ions is 102.24m-3-107.47m-3in the upper region from 18 m-30 m. The electrons can reach the positively charged lunar surface under a Coulomb force and their density is 105.54m-3-106.59m-3.

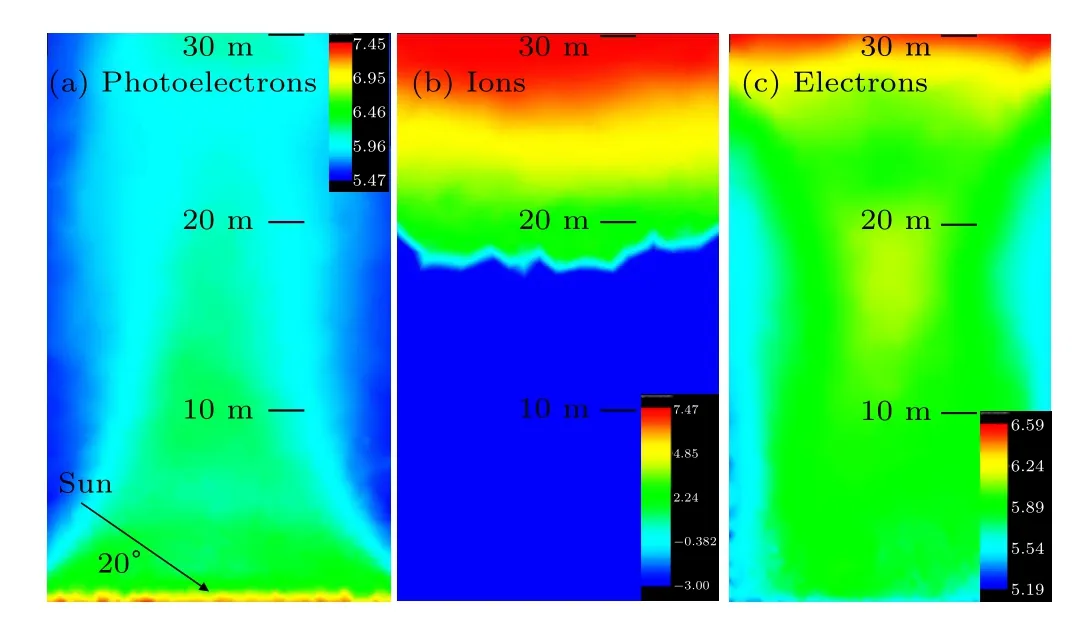
Fig.4.Distribution of(a)photoelectrons,(b)ions,(c)electrons;solar altitude angle=20°.

5.2. Distribution of dusts and plasma near the lunar surface in the south polar environment or a solar altitude angle of 0°

The distribution of charged lunar dust near the lunar surface for a solar altitude angle is 0°is shown in Fig. 5. The spatial density of lunar dust is 1010.9m-3-1011.5m-3near the lunar surface for heights of-1 m above the surface. In regions above 1 m, the lunar dust density is 108.9m-3-1010.2m-3.The lunar dust density is at least an order of magnitude higher than that presented in Fig. 3 where the solar altitude angle is 20°.

The spatial distribution of charged lunar dust is decided by the local plasma environment. For a solar altitude angle of 0°there is no photoelectron emission,as presented in Fig.6(a).The photoemission mechanism is the crucial factor for the formation of lunar surface potential. When the solar altitude angle at the lunar surface is 0°a high potential will not occur,which also means a weak electric field there. After the simulation reaches equilibrium,the potential of the lunar surface is about 0.1 V.As shown in Figs.6(b)and 6(c),the plasma environment is almost quasi-neutral when the solar altitude angle is 0°,with electrons being slightly attracted and ions repelled by the 0.1 V lunar surface.

Fig.5. Distribution of charged lunar dust for a solar altitude angle of 0°.

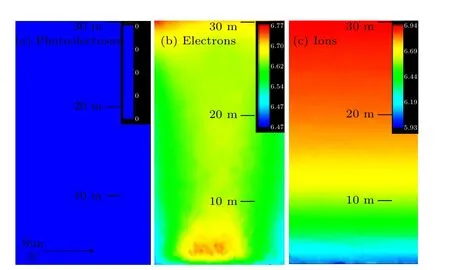
Fig.6.Distribution of(a)photoelectrons,(b)ions and(c)electrons for a solar altitude angle of 0°.

Comparing Subsections 5.1 and 5.2,the difference in the lunar dust density near the lunar surface is caused by the following two factors. Firstly, charged lunar dust which can be lifted up from lunar surface is made up of really small particles from nanometers to micrometers in diameter. Assuming a 20 nm diameter dust particle with a single chargeQ=1.6×10-19C, the gravity is about 1.3×10-8g, which means an electric field of about 0.1 V/m would be able to drag it away. For a solar altitude angle of 20°, there is a stronger electric field than in the 0°situation, so it is much easier for the charged dust particles to attain a high acceleration velocity and be driven away by column force. However,in the 0°situation,the surface potential is much lower,which means there will be less transportation by electric force. This is one reason for the order of magnitude difference in dust density shown in Figs.3 and 5. Secondly,photoelectrons can neutralize positively charged lunar dust, but this neutralization mechanism hardly exists when the solar altitude angle is 0°,thus causing a density difference for charged lunar dust.

5.3. Influences of topography: distribution of dusts and plasma in the plasma void of a mini-crater

The distribution of charged lunar dust around a 5 m high mini-crater is displayed in Fig.7.The density of charged lunar dust in the plasma void of this mini-crater is almost an order of magnitude lower than in other regions, about 106.55m-3in the nightside region compared with 107.78m-3in the other part. This might be due to the charging environment in the nightside of the mini-crater. To make this clearer,we will discuss the plasma and electronic environment and figure out the physical mechanism of dust distribution.

Fig.7. Distribution of charged lunar dust;the crater wall is 5 m high and the solar altitude angle is 20°.

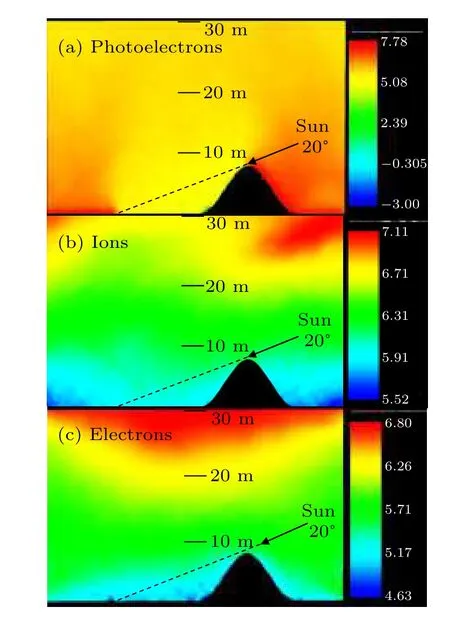
Fig.8.Distribution of(a)photoelectrons,(b)ions and(c)electrons;the crater wall is 5 m high and the solar altitude angle is 20°.

The plasma environment is shown in Figs.8(a)-8(c). The distribution of photoelectrons in Fig.8(a)presents an obvious density difference at the boundary between light and shade.The photoelectron density in the light region is～107.78m-3and～105.08m-3in the shade. The density distributions of ions and electrons displayed in Figs. 8(b) and 8(c) are 105.52m-3-107.11m-3and 104.63m-3-106.80m-3, respectively.

The distribution of ions suggested that ions can reach the plasma void region of a 5 m high mini-crater,unlike kilometerscale craters.[9]This is because the 5 m height cannot prevent the solar wind ions with a thermal temperature of 10 eV from reaching the nightside of the crater. However,the existence of mini-crater does produce a special plasma environment in the shaded region. In the nightside of the mini-crater, there is no photoemission. Thus,the plasma environment is formed only by ions and electrons from the solar wind which do not have the component of solar wind velocity,and the potential of the lunar surface in this region is decided only by the thermal velocity of ions and electrons. Thus,the surface potential of the shaded region is about 3.78 V while it is 23 V-80.6 V in the light region,as shown in Fig.9.

Fig.9. Distribution of surface potential; the crater wall is 5 m high and the solar altitude angle is 20°.

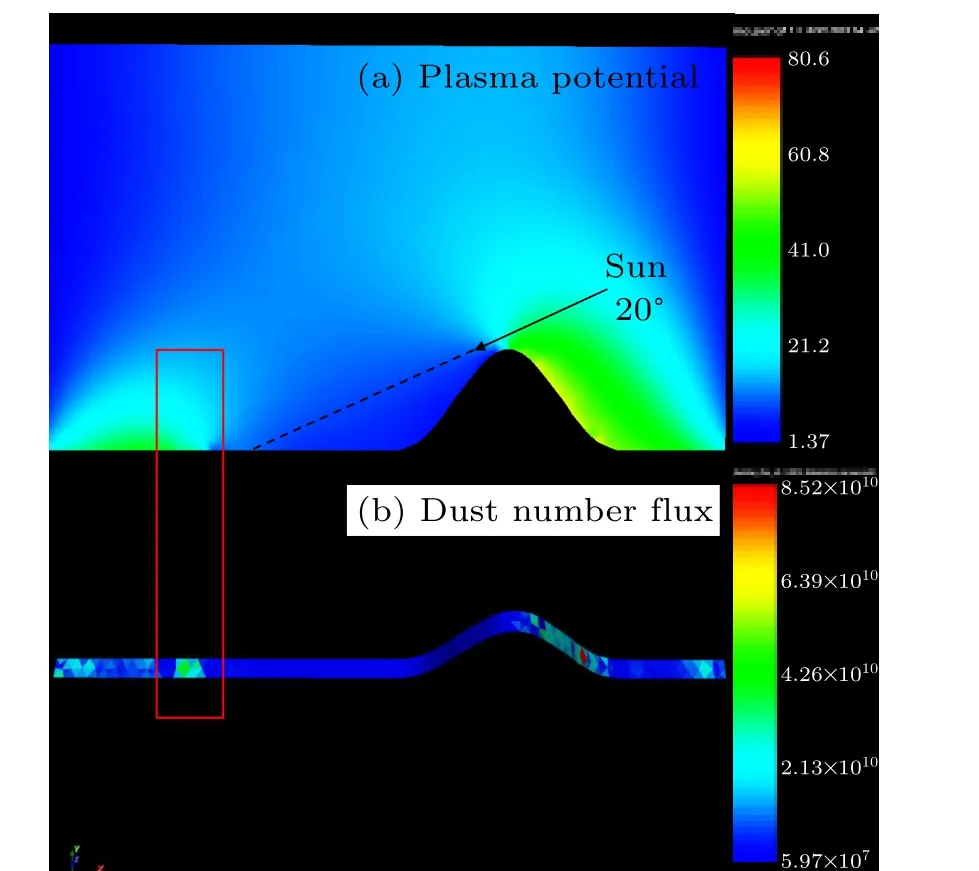
Fig.10. Distribution of(a)plasma potential in volume and(b)dust number flux on the surface;the crater wall is 5 m high and the solar altitude angle is 20°.

The plasma potential is mostly decided by the surface potential and the photoelectrons, as shown in Fig. 10(a). In the light regions, the plasma potential near the lunar surface is about 41 V-60.8 V (green and yellow) while at the nightside of the mini-crater it is about 1.37 V. This will lead to a large potential difference at the boundaries between light and shade. Figure 10(b)presents the dust number flux on the lunar surface. There is a high of dust flux at the boundary between light and shade of about 3×1010m-2·s-1,demonstrating high transport of charged lunar dust at the boundary. On the other hand, figure 10(b) shows that in the nightside region of this crater, the dust number flux is almost three orders of magnitude smaller than in other regions,which means dust levitation activity there is much reduced.

As has been discussed above, the nightside of the 5 m high mini-crater has a quasi-neutral plasma environment that might be a better place for astronauts to shelter from severe dust environments. We built a model of a spacesuit on the plasma void of the mini-crater,as shown in Fig.11.The spacesuit is made of gold(face window),steel(neck ring and chest)and Teflon(arms,legs and life support system).[2]

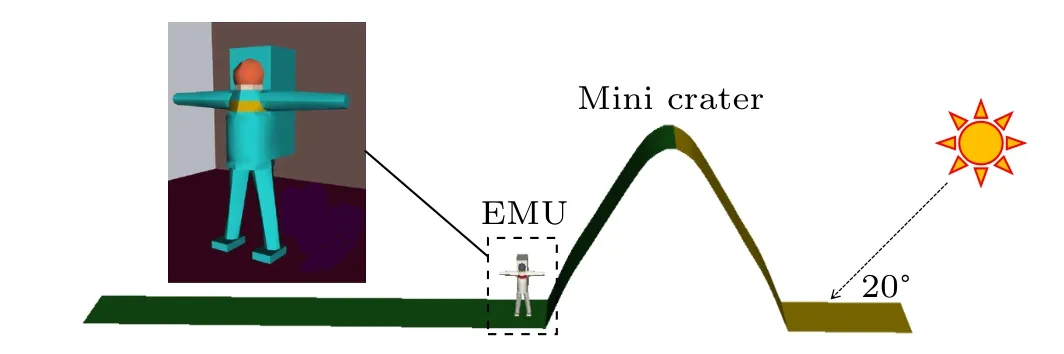
Fig.11. Spacesuit in the nightside; the crater wall is 5 m high and the solar altitude angle is 20°.

The distribution of lunar dust on a spacesuit in the nightside of the mini-crater is presented in Fig. 12(a). To make a comparison, the distribution of lunar dust on a spacesuit in the light region with a solar altitude angle of 20°is presented in Fig.12(b). It is obvious that the risk of dust on the spacesuit is much lower in the nightside than in the light region. The dust density is～1010.5m-3in Fig.12(a)while it is～1012.5m-3in Fig.12(b)and the dust covered area is much smaller in Fig.12(a)(the blue color represents a dust density of 10-3m-3).

Fig.12. Distribution of lunar dust on a spacesuit: (a)spacesuit in the nightside of a mini-crater; (b) spacesuit in the light. The solar altitude angle is 20°.

6. Conclusion and perspectives

In this paper we studied the distribution of charged lunar dust in the specific plasma environment in the lunar south polar region using SPIS.The lunar south polar region has the characteristics of low solar altitude angle and low temperature(low soil conductivity)and has a variety of complex topographies. Three typical situations were simulated to describe the characteristics and mechanism of the charged lunar dust environment in the south polar region of the moon.

Firstly, the distributions of dust and plasma within 30 m of the lunar surface for a solar altitude angle of 20°and 0°were studied. The spatial densities of lunar dust were 107.91m-3-1010.4m-3and 108.9-1011.5m-3,respectively. The difference is caused by the surface potential and photoelectrons. The surface potential was around 17.5 V for a solar altitude angle of 20°and 0.1 V for a solar altitude angle of 0°;a higher surface potential will result in transportation of small dusts. Photoelectrons can also neutralize positively charged dusts.

Secondly,we studied the distribution of dust and plasma in the plasma void of a 5 m high mini-crater for a solar altitude angle was 20°. We obtained a quasi-neutral electric environment in the plasma void region of the mini-crater. This is because the solar wind velocity of ions and electrons was resisted by the 5 m high wall of the mini-crater, but the solar wind plasma can still be affected by the electric field from the nightside of the mini-crater as the Debye length of the solar wind is 10 m. Besides,the dust number flux is almost three orders of magnitude smaller in the nightside region of the crater than in other regions, and causes the dust density there to be an order of magnitude lower in than other regions. There is very high transportation of charged lunar dust in the boundary between light and shade,which is dominated by the difference in surface and plasma potential caused by photoemission.

Finally,we built a model of a spacesuit in the nightside of the mini-crater and compared the lunar dust on the spacesuit in the nightside(plasma void)and dayside(solar altitude angle 20°). The dust density on spacesuit was～1010.5m-3on the nightside and～1012.5m-3on the dayside, and it is obvious that the dust risk is much lower in the nightside than in the dayside.

Acknowledgments

Project supported by the National Key Research and Development Program of China(Grant No.2020YFC2201300),the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA17010301), and the Technical Basic Scientific Research Project (Grant No.JSZL2019903B001).