Min Dai ,Xiao-Dian Chen,2,3 ,Kun Wang ,Yang-Ping Luo ,Shu Wang,2 ,and Li-Cai Deng,2,3

1School of Physics and Astronomy,China West Normal University,Nanchong 637002,China;chenxiaodian@nao.cas.cn

2 CAS Key Laboratory of Optical Astronomy,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China

3 School of Astronomy and Space Science,University of the Chinese Academy of Sciences,Beijing 101408,China

Abstract The development of large-scale time-domain surveys provides an opportunity to study the physical properties as well as the evolutionary scenario of B-type subdwarfs(sdBs)and M-type dwarfs(dMs).Here,we obtained 33 sdB+dM eclipsing binaries based on the Zwicky Transient Facility (ZTF) light curves and Gaia Early Data Release 3(EDR3)parallaxes.By using the PHOEBE code for light curve analysis,we obtain probability distributions for parameters of 29 sdB+dMs.R1,R2 and i are well determined,and the average uncertainty of mass ratio q is 0.08.Our parameters are in good agreement with previous works if a typical mass of sdB is assumed.Based on parameters of 29 sdB+dMs,we find that both the mass ratio q and the companion’s radius R2 decrease with the shortening of the orbital period.For the three sdB+dMs with orbital periods less than 0.075 days,their companions are all brown dwarfs.The masses and radii of the companions satisfy the mass–radius relation for low-mass stars and brown dwarfs.Companions with radii between 0.12 R⊙and 0.15 R⊙seem to be missing in the observations.As more short-period sdB+dM eclipsing binaries are discovered and classified in the future with ZTF and Gaia,we will have more information to constrain the evolutionary ending of sdB+dMs.

Key words:(stars:) binaries:eclipsing–stars:evolution–(stars:) subdwarfs–(stars:) brown dwarfs

1.Introduction

Hot subdwarf stars are located between the main sequence and the white dwarf (WD) sequence in the Hertzsprung-Russell diagram (Heber 2016).They are classified as B-type (sdB,Teff＜40,000 K)and O-type(sdO,Teff＞40,000 K)according to their different spectral types (Hirsch et al.2008).sdB stars are located in the blue tail of the horizontal branch(HB),which is also known as the extreme horizontal branch(EHB;Heber 1986).sdB has a helium-burning core and an extremely thin residual hydrogen envelope (mass ＜0.01 M⊙).Its progenitor is likely an evolved star that loses most of its hydrogen envelope when it ascends the red giant branch.sdB will not enter the asymptotic giant branch phase,instead,it will become a WD directly.The average lifetime on the EHB is on the order of 108yr (Dorman et al.1993).Maxted et al.(2001)suggested the binary ratio of sdB is～60%.About half of these binary systems are close binaries with periods of a few days (Allard et al.1994;Maxted et al.2001),while the others are wider binaries with periods of several years (Stark &Wade 2003;Chen et al.2013;Vos et al.2018).

The evolution of sdB is still controversial (Geier &Heber 2012),although the binary evolution scenario is favored.Han et al.(2002,2003)proposed three binary evolution channels for sdBs (common envelope evolution,stable Roche-lobe overflow and the merger of two He WDs).Subsequently,a number of works tried to test these theories through observations(Luo et al.2019,2020;Kupfer et al.2020;Kramer et al.2020;Pelisoli et al.2020).For single sdB stars,the formation has always puzzled us.About 40%of sdB stars have been found to be single.Although it has been argued that all sdB stars evolved from binary stars(Pelisoli et al.2020),several facts suggest that the merger channel of two He WDs cannot satisfactorily explain single sdB stars(Burdge et al.2020;Van Grootel et al.2021).First,the number of low-mass WD binaries is small (Ratzloff et al.2019b).Second,the predicted broad mass distribution of single sdB stars from the merger channel seems to be inconsistent with observations(Fontaine et al.2012).Third,observations show that most single sdB stars have a very slow rotation,which counters the fast rotation predicted by the merger channel (Geier &Heber 2012;Charpinet et al.2018).Recently,a new channel for the formation of single sdB stars has been proposed (Meng et al.2020,2021).

When an sdB+dM binary system is eclipsed,it exhibits an HW Vir-type light curve (LC).The number of such stars is relatively small,and since they possess a characteristic LC,they provide a direct way to measure the physical properties of components by modeling the LC and radial velocity curve,which helps to test the theory of formation and evolution of such systems.For a more detailed review on HW Vir-type stars,see Heber (2016).Such stars have been studied continuously and extensively over the last few decades,and their number is increasing (see e.g.,Kilkenny et al.1978;Menzies &Marang 1986;Drechsel et al.2001;?stensen et al.2007;For et al 2010;Barlow et al.2013;Schaffenroth et al.2014;Kupfer et al.2015;Almeida et al.2017;Ratzloff et al.2019a;Koen 2019;Ratzloff et al.2020;Sahoo et al.2020a;Baran et al.2021).The orbital periods of HW Vir-type stars are easily obtained from LCs,while the physical parameters such as mass and radius of sdB and the companion stars can be determined based on radial velocity measurements and LC analysis.Based on these parameters,it is possible to constrain the evolution of HW Vir-type stars and the mass–radius relations of two components.The mass–radius relation of brown dwarfs was studied by Baraffe et al.(2003) using the COND model from Chabrier et al.(2000).The mass–radius relation of low-mass stars was studied by Knigge et al.(2011) using cataclysmic variables(CVs).HW Vir-type stars are suitable objects for updating the physical properties of low-mass stars and brown dwarfs.

There are currently about 200 HW Vir-type stars in the database of AAVSO International Variable Star Index4https://www.aavso.org/vsx/index.php(Watson et al.2006,VSX),which are mainly collected from the periodic variable catalog of the Zwicky Transient Facility (Chen et al.2020,ZTF),the fourth phase of the Optical Gravitational Lensing Experiment(Udalski et al.2015,OGLE)and the catalog of the Asteroid Terrestrial-impact Last Alert System (Heinze et al.2018,ATLAS).Schaffenroth et al.(2019)studied a sample of HW Vir-type stars in OGLE and ATLAS.ZTF is a northernsky time-domain survey with limiting magnitudes of 20.8 mag in g band and 20.6 mag in r band (Masci et al.2019).By monitoring the northern sky with several hundred detections for each object over a 3 yr period,ZTF will discover a large number of HW Vir-type stars.The presence of more short-period(P ＜0.2 days) HW Vir-type stars will help constrain the evolutionary timescale and ending of such systems.

In this paper,we analyze the physical and orbital parameters of 29 sdB+dM eclipsing binaries using LCs from ZTF Data Release 5(DR5).By fixing an sdB’s mass and temperature,we obtain the orbital inclination,mass ratio,radius of sdB and dM,and the dM temperature.We also determine the mass–radius relation of dM and investigate how an sdB+dM evolves with the shortening of the orbital period.In Section 2,we describe the selection of sdB+dM eclipsing binaries and their LCs.We explain how to use PHOEBE to obtain orbital parameter solutions from LCs,and the reliability of our determined parameters in Section 3.In Section 4,we present our results and make a comparison with previous works.We also discuss the physical properties and the evolutionary stage of our sdB+dM eclipsing binaries in this section.Finally,we conclude this work in Section 5.

2.Sample and Data Selection

We cross-matched the HW Vir-type stars in the VSX database with the ZTF catalog of periodic variable stars and obtained a sample of 31 HW Vir-type stars.Two other HW Vir-type stars not included in the VSX were identified by eye and added to the sample.About two-thirds of this sample have periods smaller than 0.2 days.We compared them to～900 other short-period variables from the ZTF Catalog of Periodic Variable Stars through the Gaia-band intrinsic color versus absolute magnitude diagram (CMD).This helps determine the type of primary component for HW Vir-type stars.In Figure 1,the red dots represent the 33 HW Vir-type stars,and the gray dots are the ZTF short-period variables with P ＜0.2 days.We adopted the extinction values of Green’s 3D extinction map (Green et al.2019) and converted them to AGand E(GBp-GRp) using the updated extinction law (Wang &Chen 2019).The absolute magnitude and intrinsic color are estimated by MG=G-AG-5respectively.? is the corrected Gaia Early Data Release 3(EDR3) parallax in mas (Lindegren et al.2021).The corrected EDR3 parallax was found to reduce the systematic bias to ＜10 μas (Ren et al.2021).

Figure 1.Gaia-band absolute magnitude vs.intrinsic color diagram.The red dots represent 33 HW Vir-type stars,and the error bars of four brighter HW Vir-type stars are added.The gray dots signify the locations of ZTF shortperiod variables with P ＜0.2 days and distance uncertainty less than 50%.

From Figure 1,we found that HW Vir-type stars concentrate as a clump with an absolute magnitude around MG=5 mag.The clump is bluer than the main sequence variables and brighter than the cataclysmic variables.This means our HW Vir-type stars are sdB+dM eclipsing binaries rather than WD+dM eclipsing binaries.To further confirm that primary components in our sample are all sdB stars,we adopt the method in Gentile Fusillo et al.(2015),where the authors calculated the reduced proper motion defined as H=G +5 logμ+5.G and μ are G band magnitude and proper motion respectively.We found that H values of our sample are all less than 14.5,which demonstrates that they are sdBs rather thanWDs (Schaffenroth et al.2019).The distribution of HW Virtype stars is consistent with constraints of-1.0 ＜MG＜7.0 and(Geier et al.2019;Geier 2020),but more concentrated in MG.Four sdB+dMs are brighter than the others,and these deviations are due to the large uncertainties propagated from Gaia parallaxes.We display their error bars in Figure 1.The 1σ uncertainties of the absolute magnitude for other sdB+dMs are less than 0.35 mag.We also note that in the CMD,there are dozens of gray dots distributed in the location of our sdB+dM eclipsing binaries.By examining their LCs,we found that they are non-eclipsing sdB+dM binaries,and their brightness variations are due to reflection.Reflection occurs when the hot component illuminates part of the spherical surface of the cooler component when the temperature difference between the two components is large.The size of the illuminated surface varies with the projection angle,which leads to an eventual sinusoidal-like LC without eclipse.This suggests that many sdB binaries orbit at such a small inclination that we cannot see the eclipse.The HW Vir-type star is a subtype of detached eclipsing binaries (EA-type) that have similar LC shapes.The specific distribution in the intrinsic color versus absolute magnitude diagram helps to separate HW Vir-type stars from other main sequence eclipsing binaries.With these properties,we expect to find hundreds of HW Vir-type stars in future ZTF-based variable star searches.Moreover,the CMD is useful to separate sdB+dM eclipsing binaries and WD+dM eclipsing binaries when Gaia parallaxes are accurate enough.

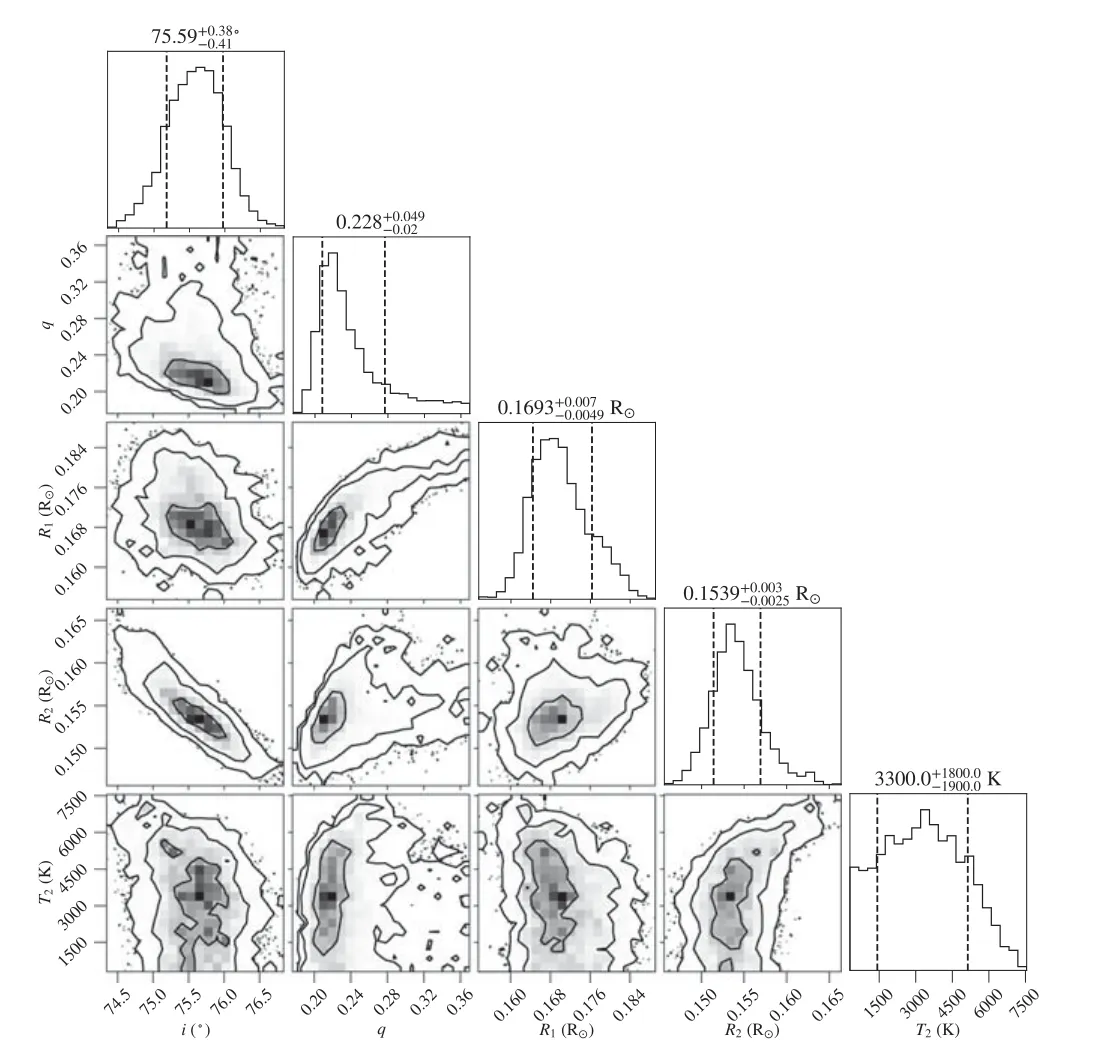
Figure 2.MCMC results for ZTF J204046.56+340702.8.In the diagram,i,R1,R2 and q present a Gaussian-like distribution.

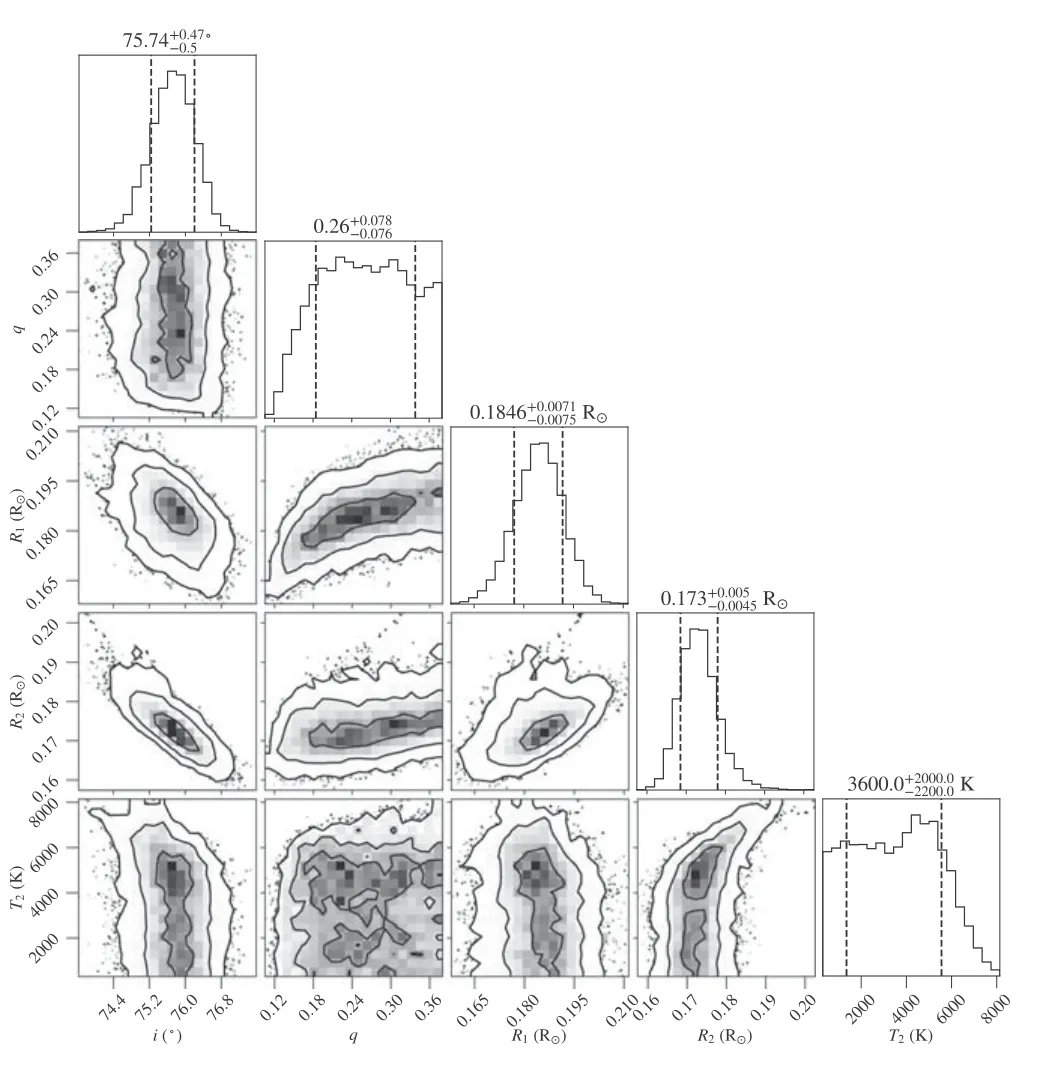
Figure 3.MCMC results for ZTF J224547.36+490824.7.In the diagram,i,R1 and R2 present a Gaussian-like distribution,but q does not obey a Gaussian distribution.

Figure 4.LC analysis of ZTF J204046.56+340702.8.The top and bottom panels are the LC fitting diagram and residual diagram respectively.In the top panel,the green and yellow lines are modeled LCs,and the blue and black dots are photometric measurements in g and r bands,respectively.The error bars represent the uncertainties of the photometry.In the bottom panel,the blue and black dots are the residuals between the modeled and observed LCs respectively.The green and yellow lines indicate the average of the residuals.

We downloaded the g,r band LCs of 33 sdB+dM eclipsing binaries from the ZTF DR5 database.To ensure the quality of LCs,we selected only good photometric data with catflag ＜10’.ZTF DR5 contains photometric data obtained during a twoand-a-half year survey,with more than 200 detections per band for most objects.Given that typical photometric uncertainties are around 0.015 mag,we believe that a reliable analysis can be performed on the ZTF LCs.LCs were folded with periods from Chen et al.(2020),and the ephemeris of the primary minimum T0was estimated by the lc_geometry package in PHOEBE 2.3(Conroy et al.2020).We also performed a careful visual inspection of all LCs to make sure that the period and T0were not significantly biased.We excluded photometric outliers(less than 10) for each LC according to the fit line of the Gaussian processes.Magnitude was converted into normalized flux by assuming the maximum flux in g,r bands is equal to 1.The primary eclipses of four sdB+dMs are fainter than the detection limit of ZTF (r ＞20.5 mag).We excluded them and performed LC analysis on the remaining 29 sdB+dMs.

3.Light Curve Analysis

sdB+dM eclipsing binaries are the best objects to study the physical properties of sdBs and dMs.However,only the radial velocity curve of the primary component is available,so the mass ratio cannot be directly determined from radial velocity curves.One way to solve this problem is to assume a typical mass of sdB,e.g.,M1=0.47 M⊙.Based on this assumption,parameters of two components can be constrained well by analysis of the single-line radial velocity curve and LCs.The shortcoming of this method is that M1cannot be studied.The other way is to constrain the mass ratio q based onloggand fix it in the subsequent analysis(Drechsel et al.2001;Heber et al.2004;Vu?kovi? et al.2007;For et al 2010;Schaffenroth et al.2014;Almeida et al.2017;Barlow et al.2013;Schaffenroth et al.2021).In this method,the accuracy of q depends on the extent to which it is constrained by LCs.When q does not converge in the iterations,the uncertainty is relatively larger.In this work,we used the PHOEBE 2.3 code to study the probability distribution of parameters for 29 sdB+dMs and to evaluate how well q is constrained by LCs.

With some exceptions,most sdB stars have a mass around 0.47 M⊙,which is also known as the typical mass (Han et al.2002,2003;Sahoo et al.2020b).Most sdB stars have a temperature in the range of 27,000–31,000 K (Geier et al.2012).Three of 29 sdB+dMs were studied previously with spectra and an sdB’s temperature is in this range.The three sdB+dMs are ZTF J162256.66+473051.1 with a temperature T1,eff=29,000±600 K(Schaffenroth et al.2014),ZTF J153349.44+375927.8 with a temperature T1,eff=29,230±125 K (For et al.2010) and ZTF J223421.49+245657.1 with a temperature T1,eff=28,500±500 K(Almeida et al.2017) or T1,eff=28,370±80 K (?stensen et al.2007).The companion star of an sdB+dM is an M dwarf or a brown dwarf,and its temperature is around 3000 K (Menzies &Marang 1986;Schaffenroth et al.2014;Vu?kovi? et al.2014).

Our idea is to assume that the primary components of sdB+dMs are all canonical sdB stars with a mass of 0.47±0.03 M⊙,a radius of 0.175±0.025 R⊙and temperature about 30,000 K(Van Grootel et al.2021).We fixed the sdB mass M1to 0.47 M⊙and the sdB temperature T1to 30,000 K in our LC analysis.Small deviations in T1will directly affect the poorly constrained T2(typically with 30% uncertainty),but have little effect on R2and other parameters.With these assumptions,we can still study the properties of the companion star and the evolution stage of the system in terms of statistics.We set the orbital eccentricity e to 0 since all of our sdB+dM eclipsing binaries have a very short period (less than 0.5 days).We set the linear limb-darkening coefficient of sdB to 0.25 and 0.2 in the g band and r band,respectively,while that for the companion is 1.0 in both the g band and r band (Claret &Bloemen 2011).We set the gravity-darkening factor to 1.0 and 0.32 for sdB and the companion,respectively(Claret&Bloemen 2011).The reflection factor of sdB and the companion was set to 1.0.The range of the initial orbital inclination i is 60-90 degrees,and the other parameters are unrestricted.All preset parameters are listed in Table 1.

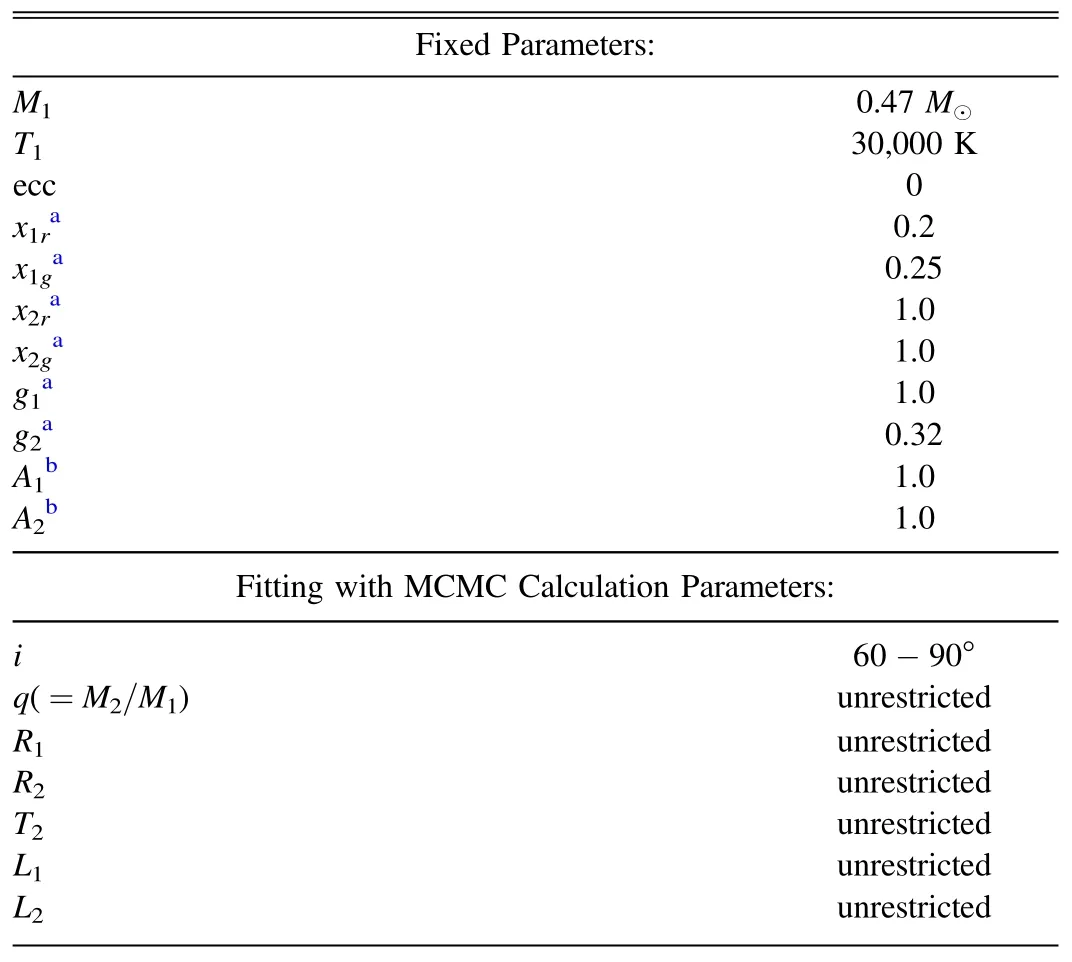
Table 1 Preset MCMC Parameters in PHOEBE 2.3.

We used the Markov chain Monte Carlo (MCMC) sampler based on EMCEE (Foreman-Mackey et al.2013) to determine parameters of 29 sdB+dM eclipsing binaries.For sampling,we relied on 50 walkers and 2000 iterations,and each run cost 30 hours on a 4-core CPU.We also tested 5000 iterations for five sdB+dMs and 20,000 iterations for one sdB+dM and found the results were almost the same as those based on 2000 iterations.In the first run,the mass ratios qiare not well constrained for most of the objects,as it is difficult to obtain the true q from many local optimal mass ratios.In contrast,the radii R1,i,R2,iand inclination iiare constrained well in two-band LC analysis.From the R1,i-q and R2,i-q distributions,R1,iand R2,ionly increase by 20%when q increases from 0 to 1,so we decided to use R2,ito establish a prior distribution of q.According to the mass–radius relationship of dM,the ratio of mass to radius is slightly less than 1 in solar units.Given that q and R2are usually overestimated in the first run(q of the sdB+dM is usually less than 0.3),we assumed a prior distribution of q as [0,R2,i/0.47].We again performed MCMC estimation and obtained reliable parameter distributions for most of the sdB+dMs.Eleven sdB+dM eclipsing binaries that have temperatures T2?3000 K are not consistent with their masses and radii.For these objects,we added another prior T2＜4000 K and performed the MCMC estimation again to obtain the final distributions of parameters.

Figure 2 displays the parameter distributions of ZTF J204046.56+340702.8 as an example of one class.We can see that i,q,R1and R2obey Gaussian-like distributions and the correlations between these parameters are small.Parameters of the other three sdB+dM eclipsing binaries are similarly distributed(see Figures A1–A3 in Appendix A).Figure 3 depicts the parameter distributions of ZTF J224547.36+490824.7.It differs from Figure 2 in that q does not satisfy a Gaussian distribution.For this class,q is uniformly distributed,or has a wide tail,or is biased toward one side in the prior range(see Figures B1–B24 in Appendix B).Considering that the prior range is narrow,i.e.,qiis roughly distributed between 0 and 0.2–0.5,the deviation between the maximum likelihood and the true q is not large.This deviation is already included in the error of q(mean uncertainty is 0.08).In addition,the error in R2hardly increases with the error in q due to the weak correlation between R2and q.Based on multi-band LC analysis,the determined masses and radii of the companions in sdB+dM eclipsing binaries are reliable for studying their statistical properties.Nevertheless,in most cases,uncertainty in q or M2is larger.

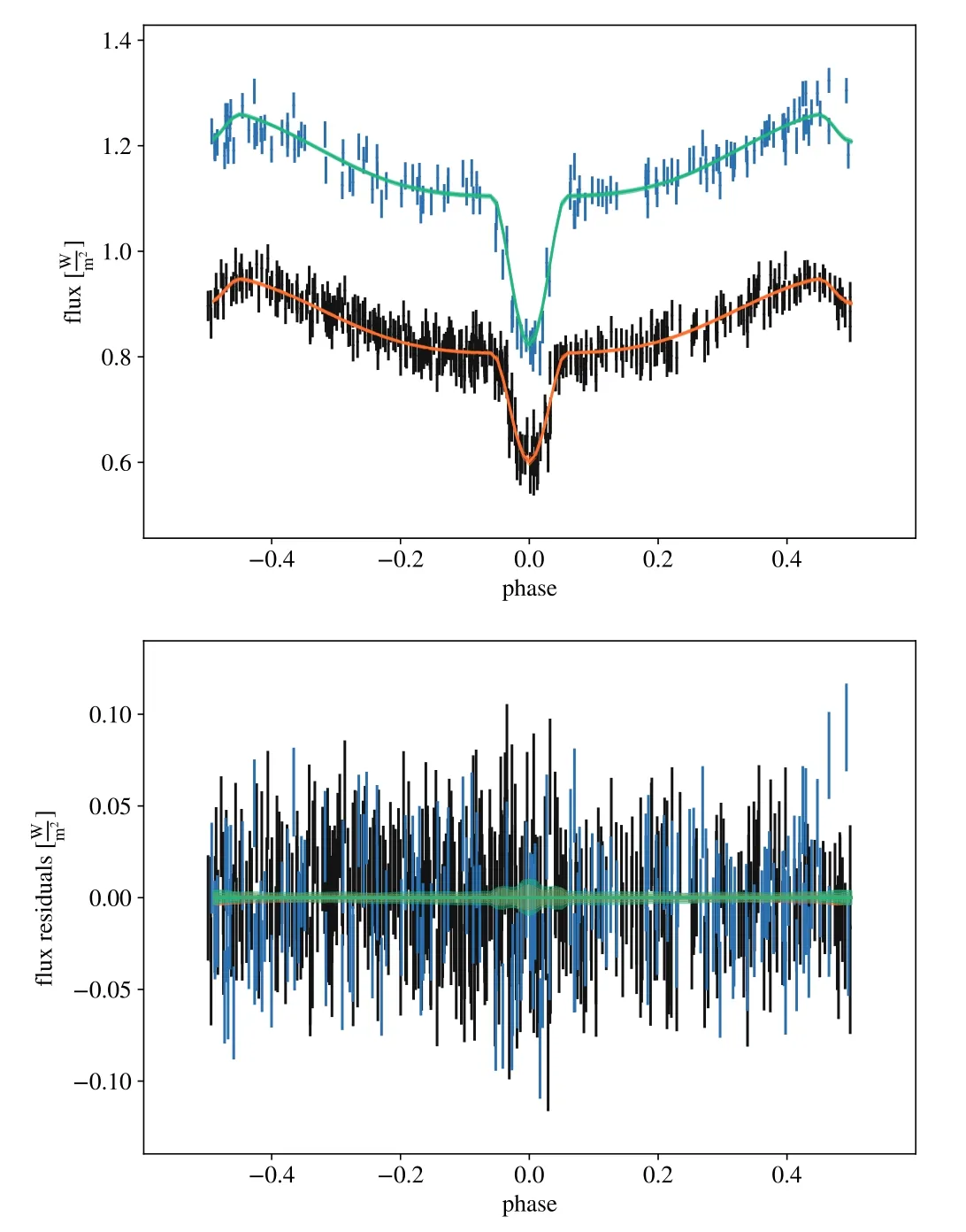
Figure 5.Similar to Figure 4,but for ZTF J224547.36+490824.7.

In both Figures 2 and 3,T2does not exhibit a Gaussian distribution,which means that T2is difficult to be constrained in the LC analysis.The typical uncertainty of 1500 K also indicates that T2is rather uncertain.The upper panels of Figures 4 and 5 feature a comparison of the modeled and observed LCs of ZTF J204046.56+340702.8 and ZTF J224547.36+490824.7,while the lower panels show the residual diagrams.Diagrams for other sdB+dM eclipsing binaries are supplemented in Appendix A and B.

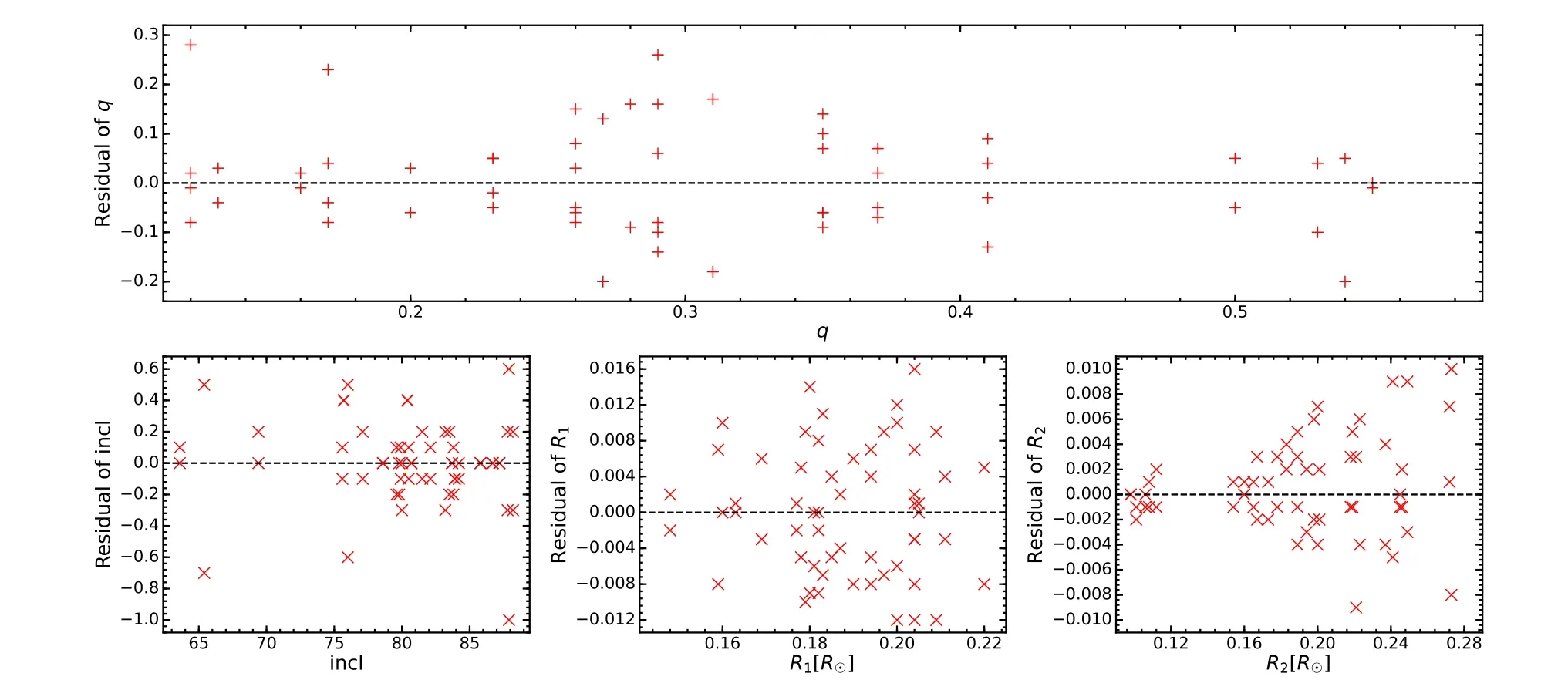
Figure 6.The relationship between the mean values and the residuals when q is fixed to the maximum error and minimum value.The top panel is for q.The leftbottom,middle-bottom and right-bottom panels are similar to the top but for i,r1 and r2,respectively.

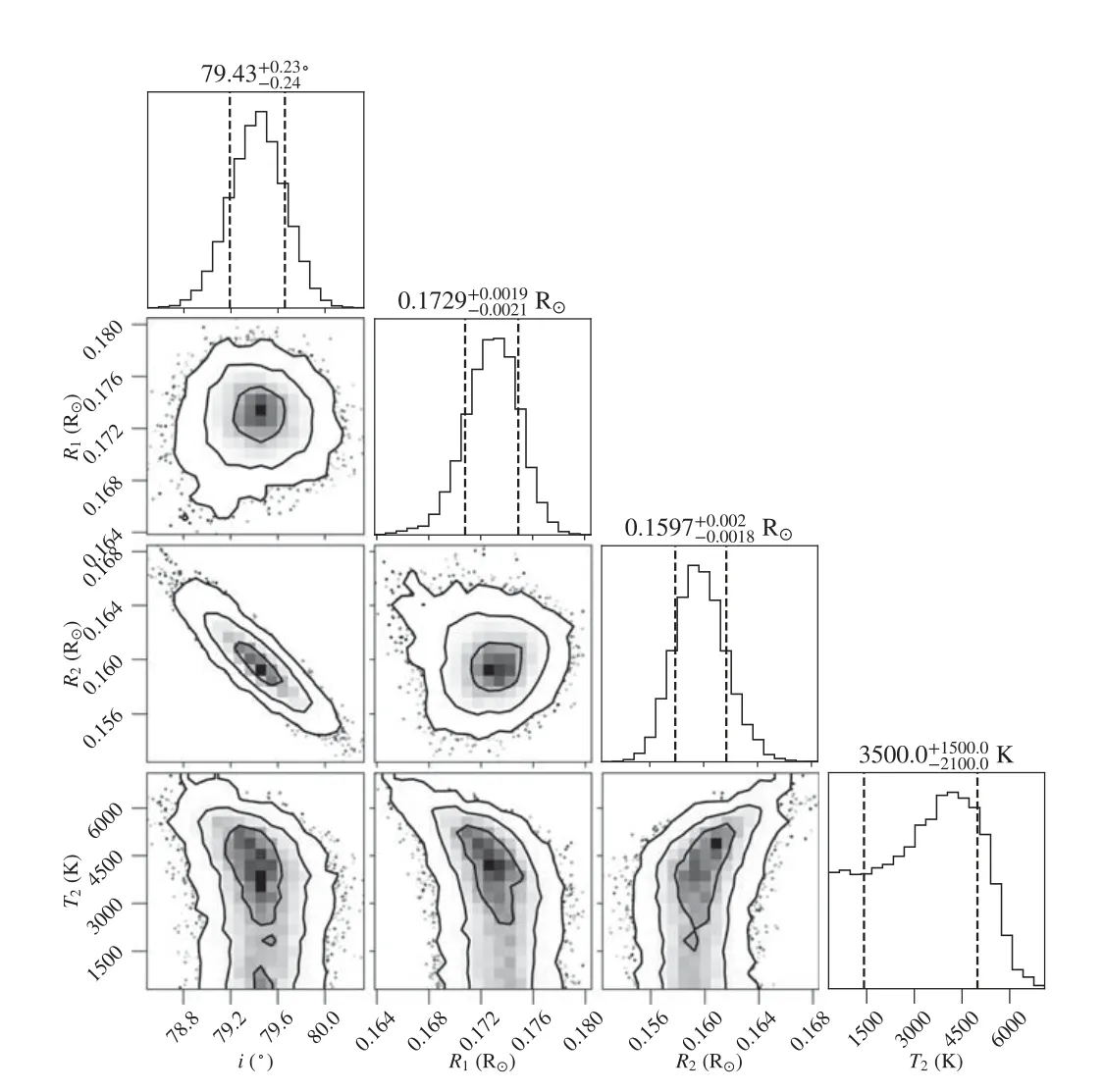
Figure 7.MCMC results for ZTFJ011338.79+431154.9 when fixed q is set to minimum error.

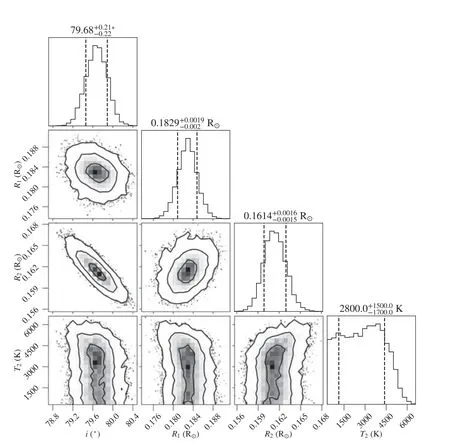
Figure 8.Similar to Figure 7,but fixed q is set to maximum error.

4.Results and Discussions

In this section,we present a table including parameters of 29 sdB+dM eclipsing binaries and make a comparison with previous works.We also discuss how to use our result to constrain the evolutionary stage of sdB+dM eclipsing binaries and the physical properties of companion dM stars.

4.1.Results of 29 sdB+dM Eclipsing Binaries

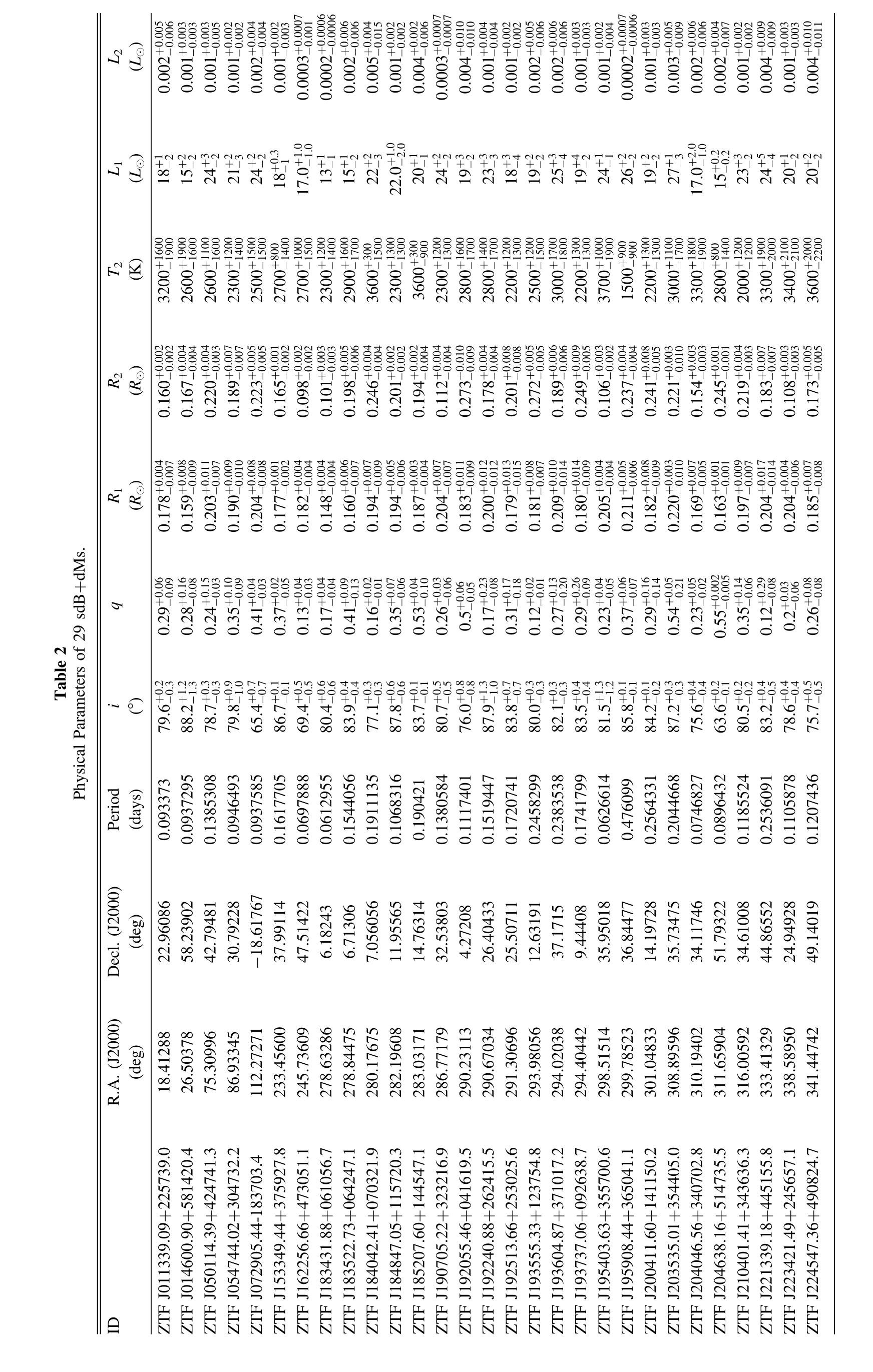
The results of our sample,containing 29 sdB+dMs,were included in Table 2.It contains the ZTF ID,position(J2000 R.A.and decl.),period,physical parameters and the corresponding uncertainties.The physical parameters include i,q,R1,R2,T2,L1and L2.The bolometric luminosities of the sdB and companion are calculated using the PHOEBE code,converted from the passband luminosities.The uncertainty of luminosity is simply estimated based on the propagation uncertainties of the radius and temperature through the equationThe mean radius and luminosity of sdB are R1=0.188±0.018 M⊙and L1=21±4 L⊙respectively,which are consistent with the typical radius and luminosity of sdB (Heber 2016).

4.2.External Errors of Orbital Parameters

Among the obtained orbital parameters,the mass ratio q has the largest error.To check whether the accuracy of the other parameters is affected by q,we fix q to the maximum and minimum valuessee Section 4.1and Table 2) and performed the PHOEBE analysis again,respectively.Figures 7 and 8 display the MCMC results when q is fixed to the minimum and maximum values using ZTFJ011338.79+431154.9 as an example.The residuals of i,r1and r2were estimated by the difference between the new values and the mean values in Table 2.In Figure 6,the top panel shows the relationship between the mean q and the residual values of q,while the left-bottom,middle-bottom and right-bottom panels are similar,but for i,r1and r2respectively.The average percentage error of q is 32.8%,but only 3.1% and 1.4% for r1and r2respectively.These imply that for the sdB+dM system,the radii are reliable even if q has a large error.We also note that i,r1and r2all exhibit Gaussianlike distributions for a fixed q in Figures 7 and 8.

Table 3 ZTF J184847.05+115720.3 as an Example to Test the Effect of Different Initial Values

The selection of initial values in PHOEBE might lead to a bias in the solution of the orbital parameters.Our default initial values of q,r1and r2are 0.3,0.175 and 0.15 respectively,where q obeys a uniform distribution and r1and r2obey Gaussian distributions with a standard deviation of 0.05.To investigate the effect of the initial values on the final results,we also adopted unreasonable initial values of q=0.1,r1=0.05 and r2=0.05.From Table 3,we can see that the choice of the initial value has little effect on our results.

4.3.Comparison with Previous Work

Three of our sdB+dM eclipsing binaries were studied in previous works,which used both the single-line radial velocity curve and LCs to determine parameters.We compared our results with theirs to validate our method.As shown in Table 4,parameters of ZTF J162256.66+473051.1 (PG 1621+476) and ZTF J153349.44+375927.8 (FBS 1531+381) agree well with Schaffenroth et al.(2014) and For et al (2010),respectively.For et al(2010)yielded a relatively small mass for the sdB star,but it does not conflict with the typical mass of an sdB if the error is taken into account.We also confirmed that using a temperature of 30,000 K or temperatures from the literature hardly affect our parameter determination.

As displayed in Table 5,the case of ZTF J223421.49+245657.1 is more complicated.?stensen et al.(2007)suggested that the primary component is an sdB star with a mass of 0.47 M⊙or 0.499 M⊙,while Almeida et al.(2017) suggested that it is a low-mass WD with a mass of 0.19 M⊙or 0.288 M⊙.Our q agrees with these two works while R1and R2do not.It is worth noting that the radii of ?stensen et al.(2007) were given in units of orbital separation not solar radius.Our radius ratio is consistent with Almeida et al.(2017),which means that the reason for the different parameters is due to the difference in the adoption of M1.We prefer the primary component to be a typical sdB when considering its location on the CMD.

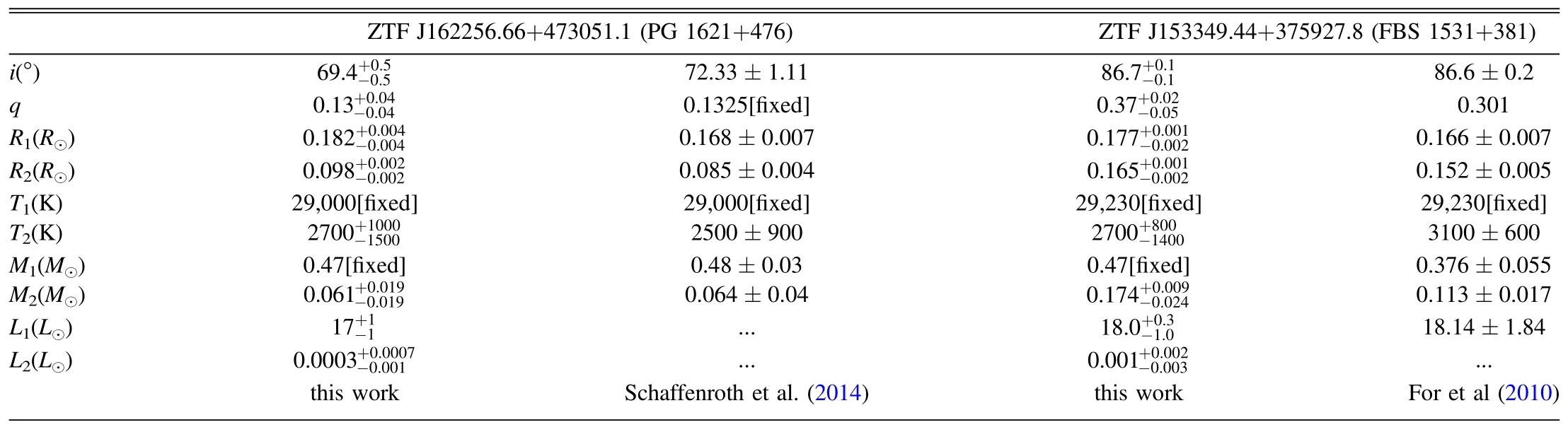
Table 4 Physical Parameters of ZTF J162256.66+473051.1 and ZTF J153349.44+375927.8 Compared to Previous Works.

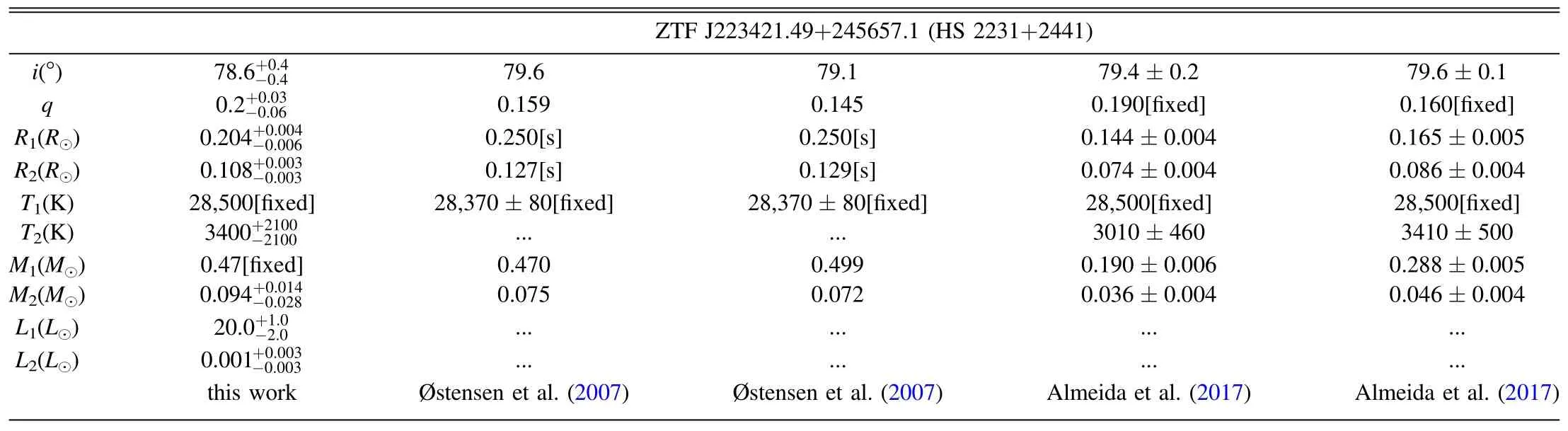
Table 5 Physical Parameters of ZTF J223421.49+245657.1 Compared to Previous Works

In summary,when the primary star is a typical sdB,parameters i,q,R1,R2and M2obtained from only LCs are consistent with those obtained from both LCs and the singleline radial velocity curve.With the single-line radial velocity curve,q and M2can be determined with better precision,especially when the error of the mass ratio based on LCs alone is large.According to the discussion in Section 3 and this section,the mass estimates of sdB stars based on the single-line radial velocity curve have a large uncertainty if q is not constrained well by LCs.

4.4.Evolutionary Stage of sdB+dM

Figure 9 depicts the evolutionary diagram of our sdB+dM eclipsing binaries.In the top panel of Figure 9,the mass ratios are randomly distributed in q=0.1-0.6 when the orbital periods are longer than 0.1 days.However,we only found low mass-ratio(q～0.2) sdB+dM eclipsing binaries when P ＜0.08 days.In the bottom panel of Figure 6,the decrease of R2with the orbital period is more significant than the decrease of q,given the much smaller uncertainty of R2.According to Figure 6,we ascertained that in sdB+dM,the companion stars are found to be less massive as the orbital period shortens.This implies that sdB+dM with more massive companions merge earlier in the orbital decay process.When P ＜0.075 days,the companions of all three sdB+dMs in this work are brown dwarfs.Geier(2015)suggested that the orbital period P ＜～0.2 d and the minimum mass of companion stars M2＜～0.06 M⊙is a critical region where no companion stars would survive in the common envelope phase.Instead they may merge with the sdB or be evaporated(Soker 1998).In the top panel of Figure 9,the blue dashed lines are the period and mass limits of the companion stars,and the absence of stars in this region suggests that our results support Geier’s arguments.More sdB+dM eclipsing binaries with periods shorter than 1 hour will be detected in future data releases of ZTF,and we will gain more knowledge about the evolutionary end of sdB+dMs.

4.5.Physical Properties of Companion Stars

Figure 10 shows the mass–radius relation of the companion stars.The blue,yellow and green solid lines are the theoretical mass–radius relation for brown dwarfs with ages of 1 Gyr,5 Gyr and 10 Gyr (Baraffe et al.2003).The black solid line is mass–radius relation for M dwarfs in CVs from Knigge et al.(2011),and the black dot–dashed line represents the theoretical mass–radius relation for single M-type stars from Baraffe et al.(1998).Most companion stars in our sample agree with the mass–radius relations.The three exceptions are due to underestimation of the mass ratio error or not being a genuine sdB+dM that hosts a 0.47 M⊙sdB.A gap was found between R2=0.12 R⊙and R2=0.15 R⊙and this gap is likely the boundary of low-mass stars and brown dwarfs.Our comparison reveals that the dM mass distribution in our sample is similar to that of Kupfer et al.(2015).Besides,the absolute magnitude and intrinsic color of five companion stars with R2＜～0.12 R⊙are uncharacteristic.These suggest that the gap is not the result of a selection effect.In the future,based on hundreds of sdB+dM eclipsing binaries,it will be possible to update the mass–radius relation for low-mass stars and brown dwarfs.This will help to study the minimum mass of lowmass stars,and the maximum mass of brown dwarfs.

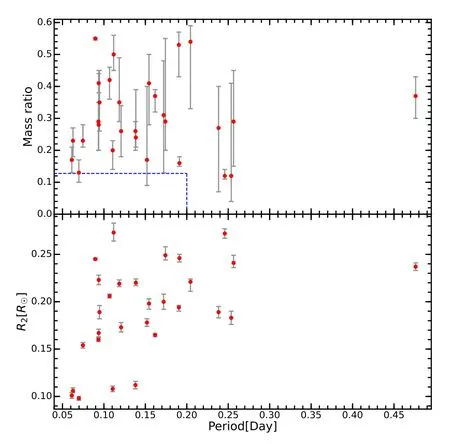
Figure 9.Evolutionary diagram of 29 sdB+dMs.The distribution of mass ratio with period is in the top panel,while the distribution of the companion’s radius R2 with period in the bottom panel.Our sdB+dMs are shown as red dots.The blue dashed lines signify the period and mass limits of companion stars.

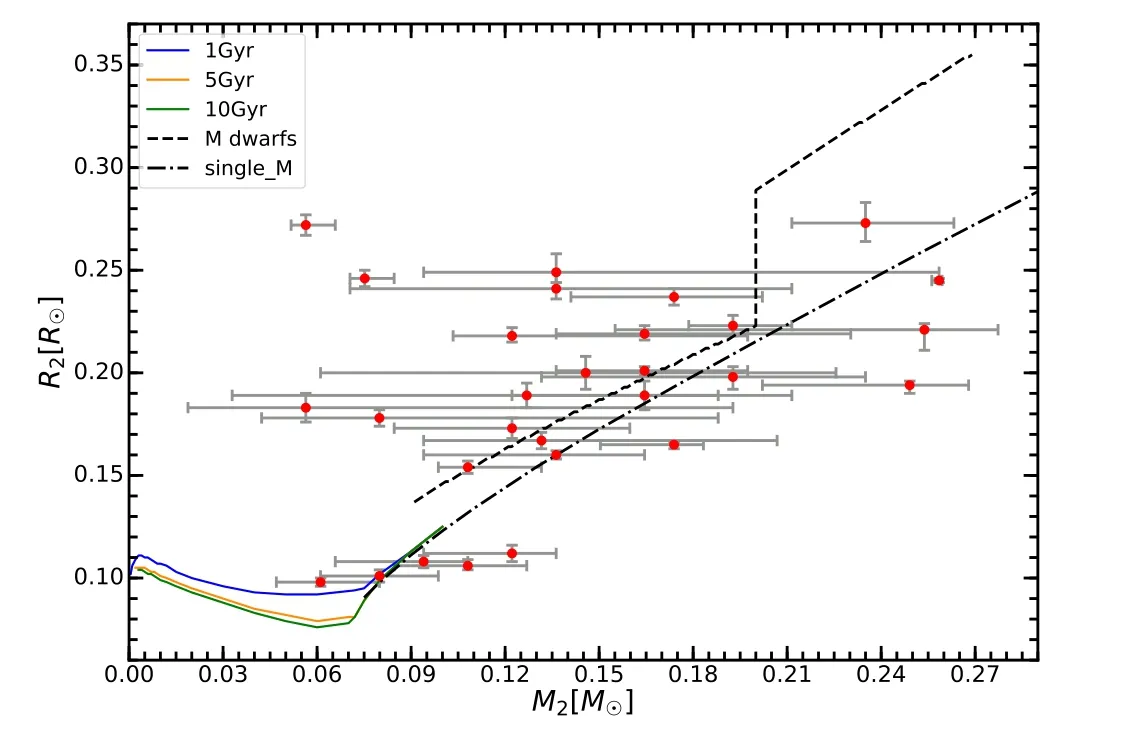
Figure 10.Diagram of the mass–radius relation for the companion stars.The blue,orange and green solid lines signify theoretical mass–radius relations for brown dwarfs with ages of 1 Gyr,5 Gyr and 10 Gyr respectively.The black dotted line is theoretical mass–radius relation for M dwarfs in CVs.The black dot–dashed line represents the theoretical mass–radius relation for single M-type stars.Our 29 sdB+dMs are shown as red dots.

5.Conclusion

In this work,we have selected a sample of 33 HW Vir-type stars in ZTF DR5.Based on Gaia EDR3 parallax and extinction correction,we found that these HW Vir-type stars are concentrated in a clump in the intrinsic CMD.Their locations in the CMD imply that they are sdB+dM eclipsing binaries.By fixing the mass and temperature of sdB to M1=0.47 M⊙and T1=30,000 K respectively and setting the prior of q and T2,we analyzed LCs using the PHOEBE 2.3 code to obtain the probability distributions of parameters q,R1,R2,i and T2.We obtained LC solutions for 29 sdB+dM eclipsing binaries with full primary eclipse detection.R1,R and i obey Gaussian-like distributions and have little correlation with other parameters,which means that they are well constrained by the LC analysis.q does not show a Gaussian distribution in most cases,and the mean uncertainty is 0.08.

Our parameters for three sdB+dMs are comparable with previous works that used both LCs and the single-line radial velocity curve if the mass of sdB is M1=0.47 M⊙.This means that parameters of sdB+dMs determined from LCs are suitable for statistical analysis.Based on 29 sdB+dMs,we found that both q and R2decrease with the decrease of the orbital period.sdB+dMs with larger mass companions are likely to merge early during the shortening of the orbit.It is worth mentioning that companions of all three sdB+dMs are brown dwarfs when the orbital period is less than 0.075 days.The masses and radii of the companion stars are consistent with the mass–radius relation for low-mass stars and brown dwarfs.We found a gap between R=0.12 R⊙and R=0.15 R⊙which can be explained as the boundary between low-mass stars and brown dwarfs.

sdB+dM eclipsing binaries are important objects to study the nature of sdBs and dMs,and their evolutionary endings are very interesting.With deeper photometry and more detections,the ZTF project will detect and classify hundreds of shortperiod sdB+dM eclipsing binaries.Before the availability of large-scale and deep spectroscopic surveys,the statistical properties of sdBs and dMs can be obtained from the LC analysis of large samples.

Acknowledgments

We thank the anonymous referee for the useful comments.This work is supported by Sichuan Science and Technology Program (grant No.2020YFSY0034) and National Natural Science Foundation of China (NSFC) through the projects 12003022,12173047,11903045,12003046,and U1731111.This work is also supported by the Major Science and Technology Project of Qinghai Province 2019-ZJ-A10.

This work has made use of PHOEBE software for the analysis of light curves.PHOEBE is funded in part by the National Science Foundation (NSF #1517474,#1909109) and the National Aeronautics and Space Administration (NASA 17-ADAP17-68).The PHOEBE project website is http://phoebeproject.org/.This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia),processed by the Gaia Data Processing and Analysis Consortium (DPAC,https://www.cosmos.esa.int/web/gaia/dpac/consortium).Funding for the DPAC has been provided by national institutions,in particular the institutions participating in the Gaia Multilateral Agreement.This publication is based on observations obtained with the Samuel Oschin 48 inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project.Z.T.F.is supported by the National Science Foundation under grant AST-1440341 and a collaboration including Caltech,IPAC,the Weizmann Institute for Science,the Oskar Klein Center at Stockholm University,the University of Maryland,the University of Washington,Deutsches Elektronen-Synchrotron and Humboldt University,Los Alamos National Laboratories,the TANGO Consortium of Taiwan,the University of Wisconsin at Milwaukee,and Lawrence Berkeley National Laboratories.Operations are conducted by COO,IPAC,and UW.

Appendix A.Figures for sdB+dMs with Gaussian-like Distributed mass Ratio

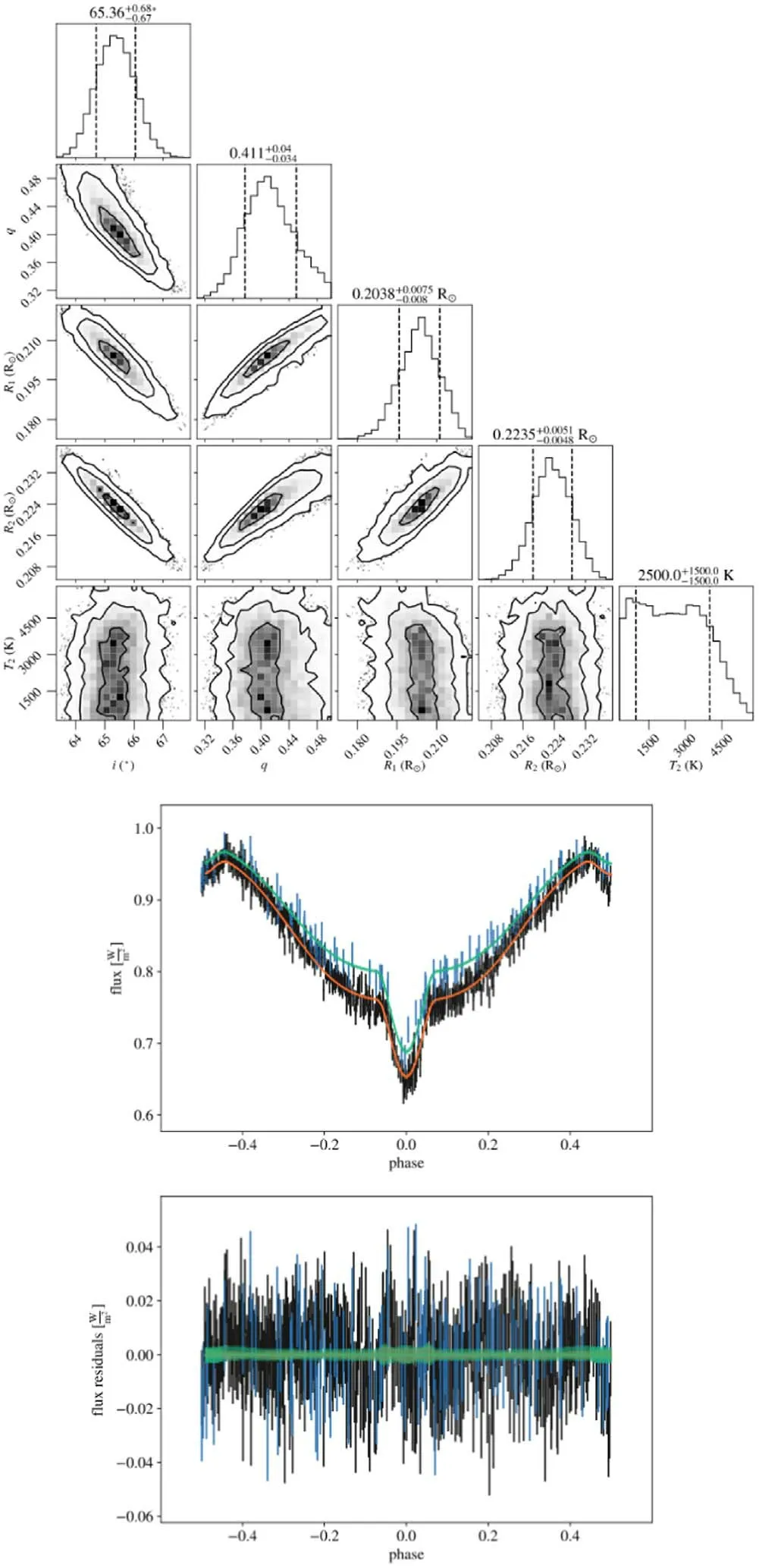
Figure A1.Diagram of MCMC results and LC fitting for ZTF J072905.44-183703.4.

Figure A2.Diagram of MCMC results and LC fitting for ZTF J184042.41+070321.9.

Figure A3.Diagram of MCMC results and LC fitting for ZTF J192055.46+041619.5.

Appendix B.Figures for sdB+dMs with Non-Gaussian Distributed mass Ratio

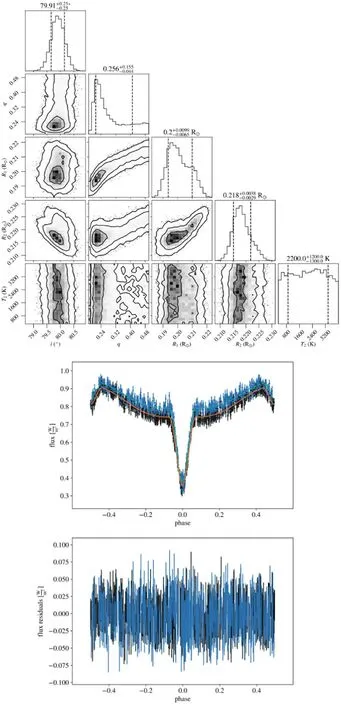
Figure B1.Diagram of MCMC results and LC fitting for ZTF J050114.39+424741.3.

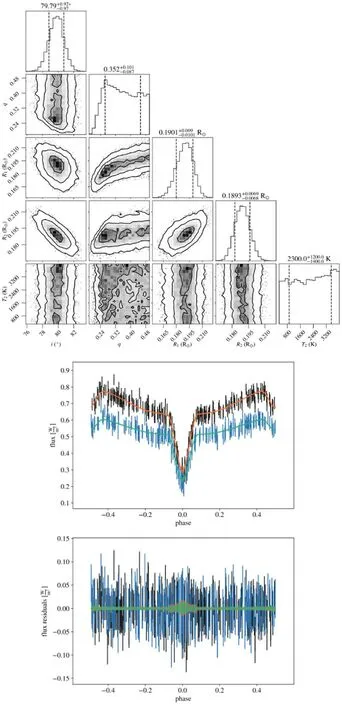
Figure B2.Diagram of MCMC results and LC fitting for ZTF J054744.02+304732.2.

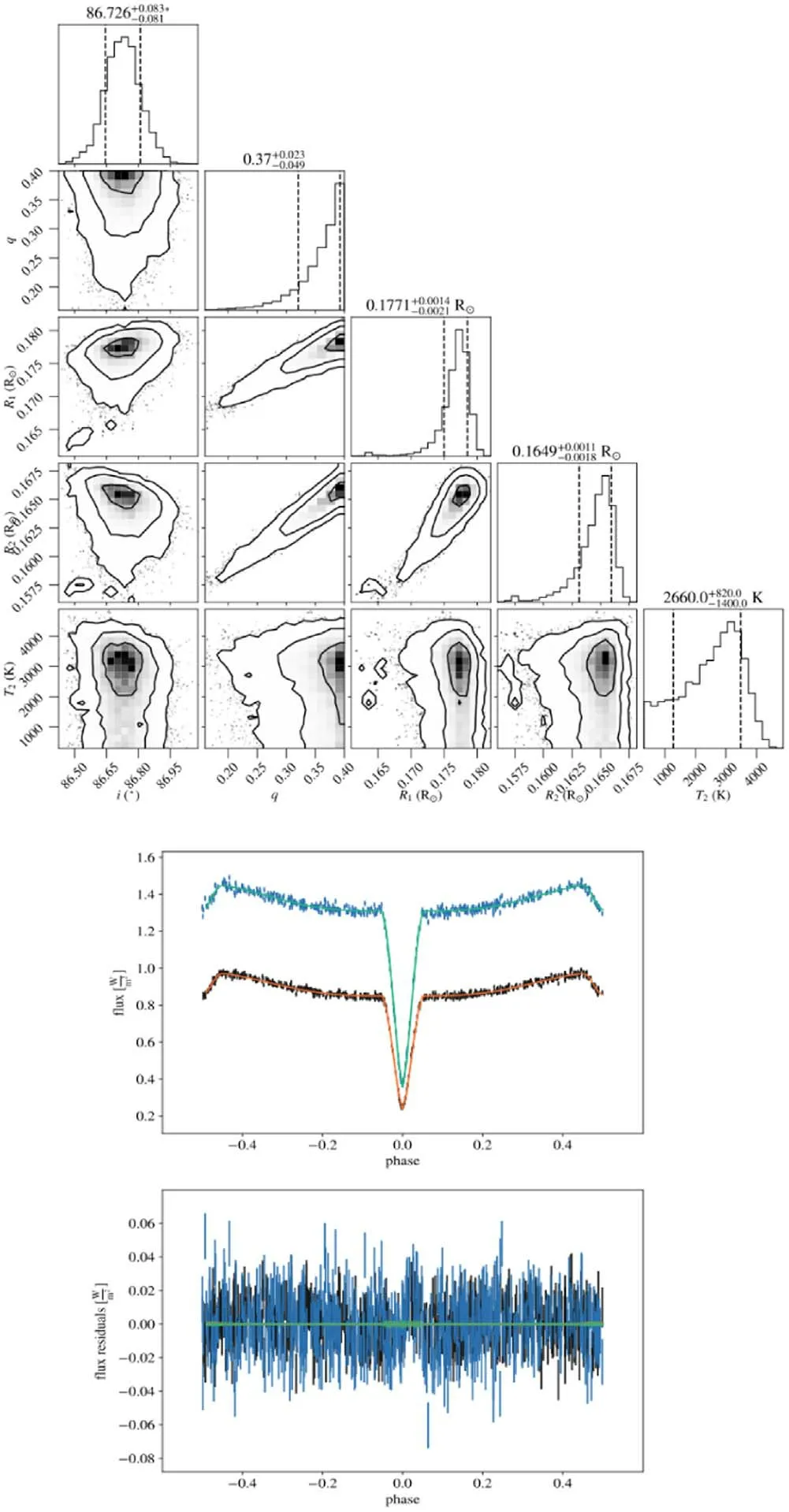
Figure B3.Diagram of MCMC results and LC fitting for ZTF J153349.44+375927.8.

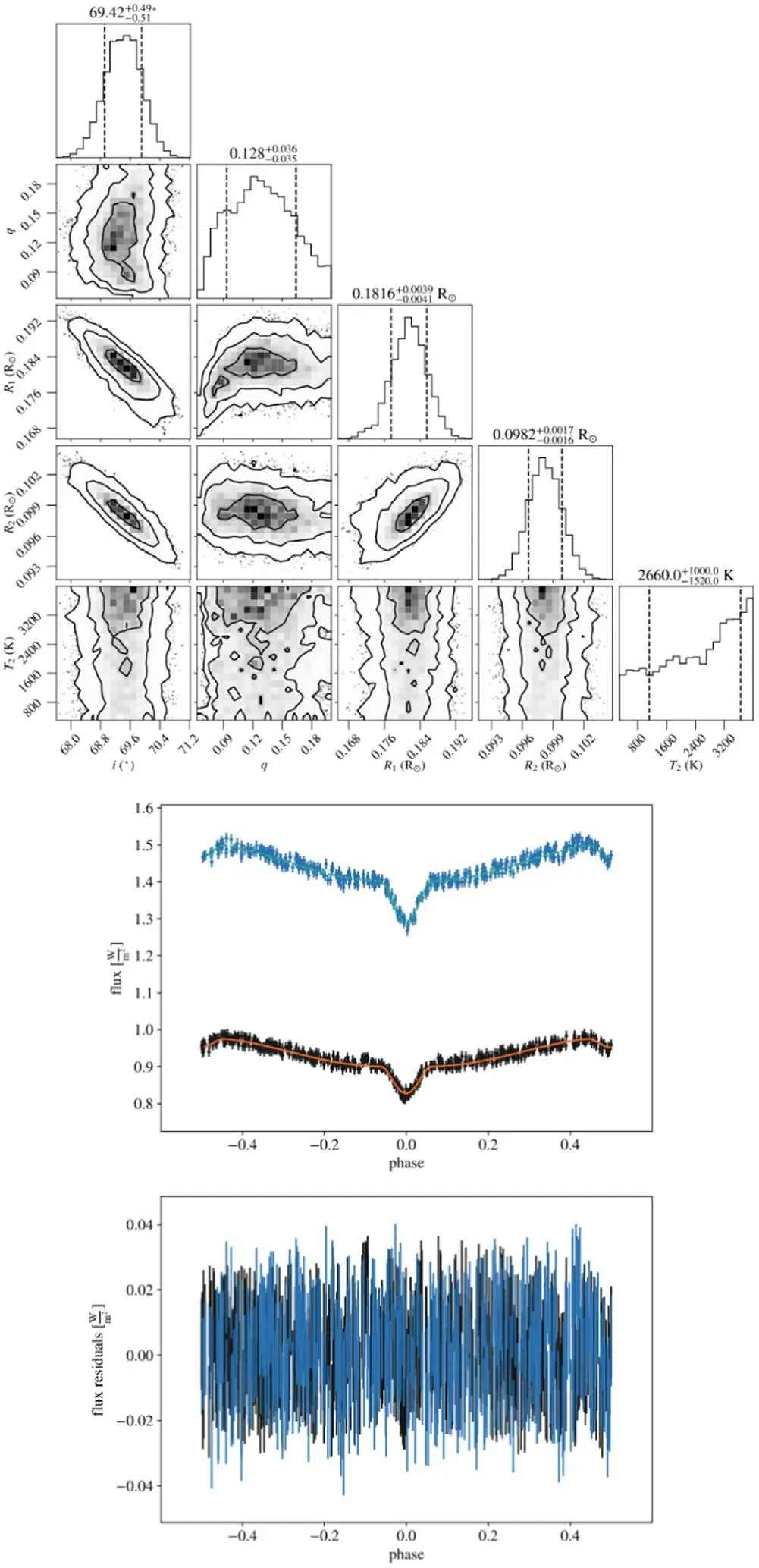
Figure B4.Diagram of MCMC results and LC fitting for ZTF J162256.66+473051.1.

Figure B5.Diagram of MCMC results and LC fitting for ZTF J011339.09+225739.0.

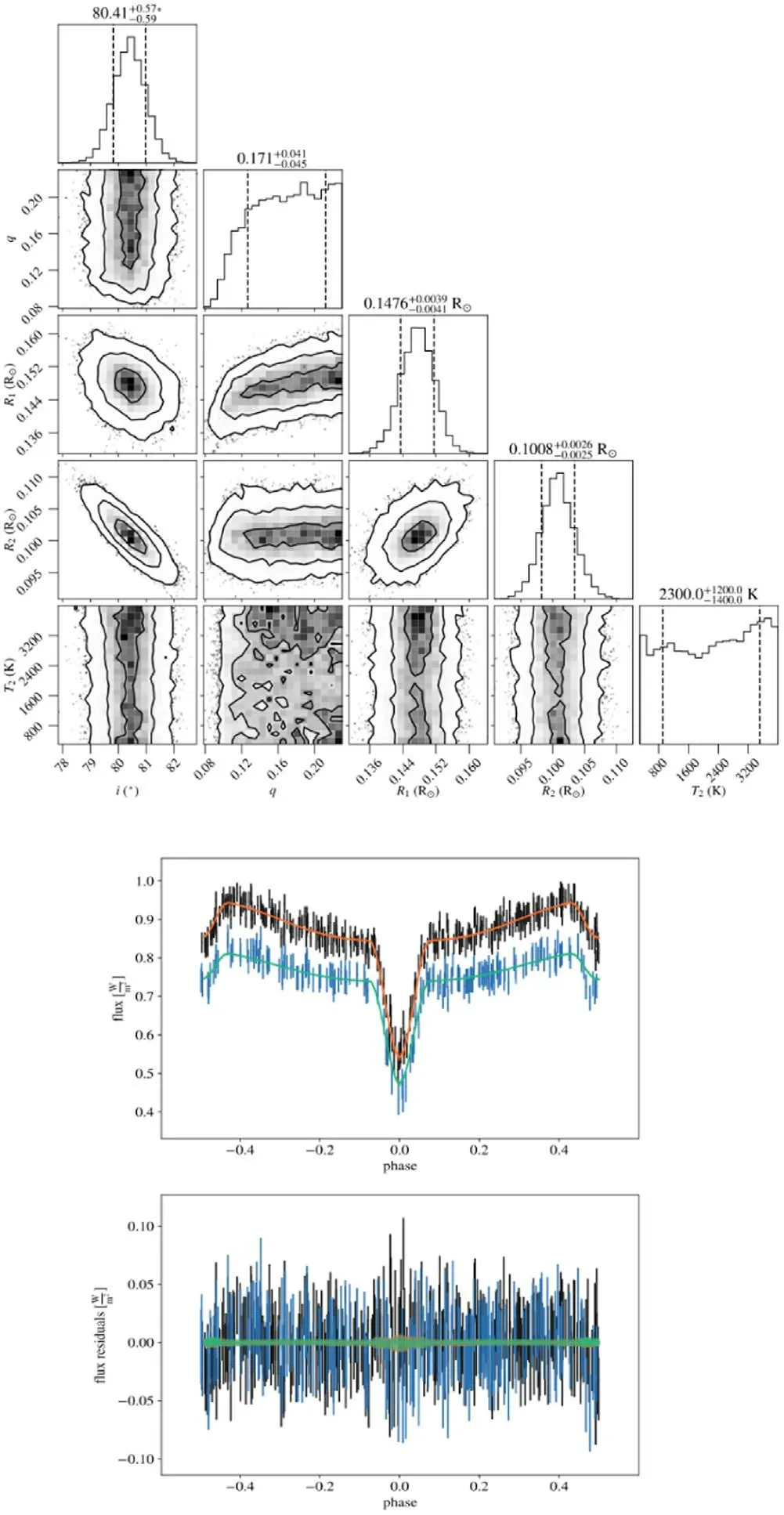
Figure B6.Diagram of MCMC results and LC fitting for ZTF J183431.88+061056.7.

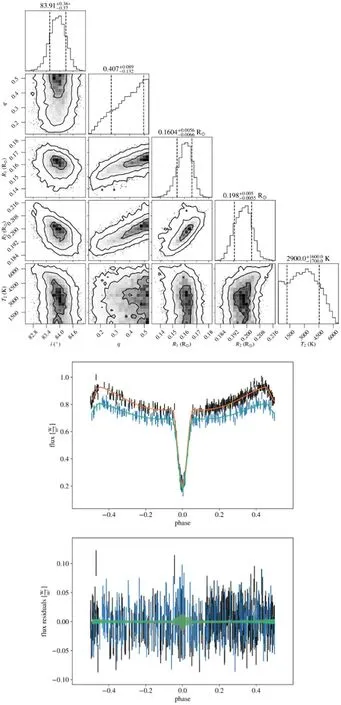
Figure B7.Diagram of MCMC results and LC fitting for ZTF J183522.73+064247.1.

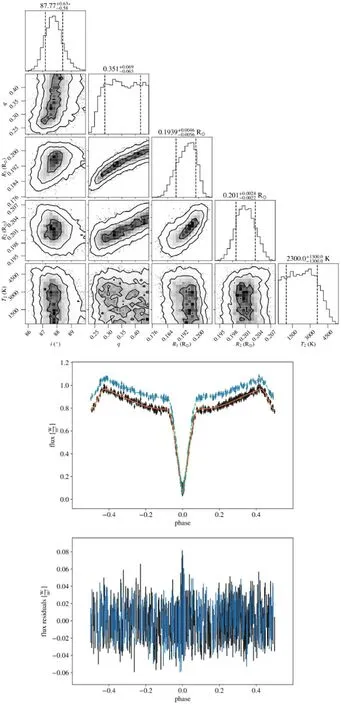
Figure B8.Diagram of MCMC results and LC fitting for ZTF J184847.05+115720.3.

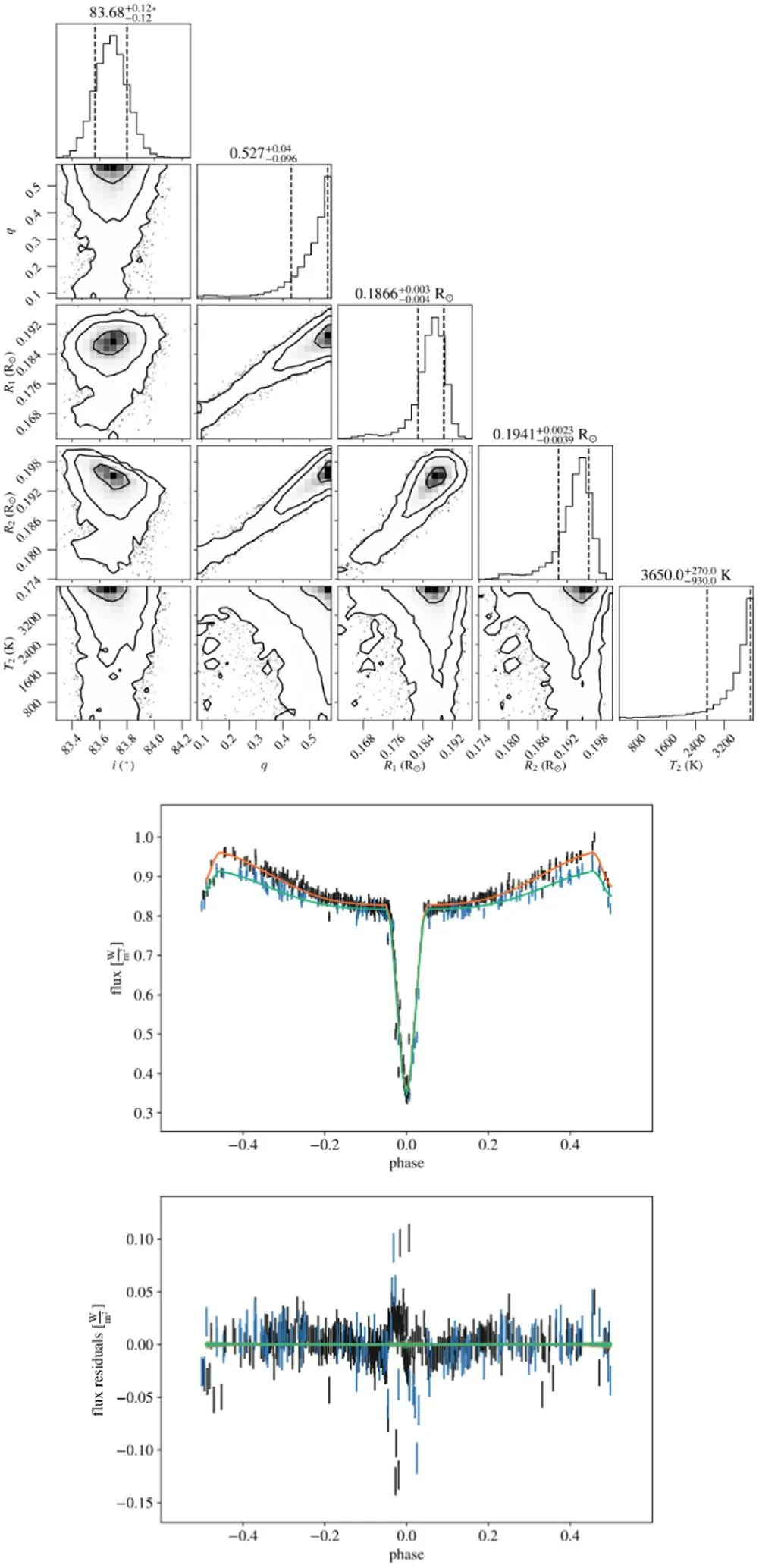
Figure B9.Diagram of MCMC results and LC fitting for ZTF J185207.60+144547.1.

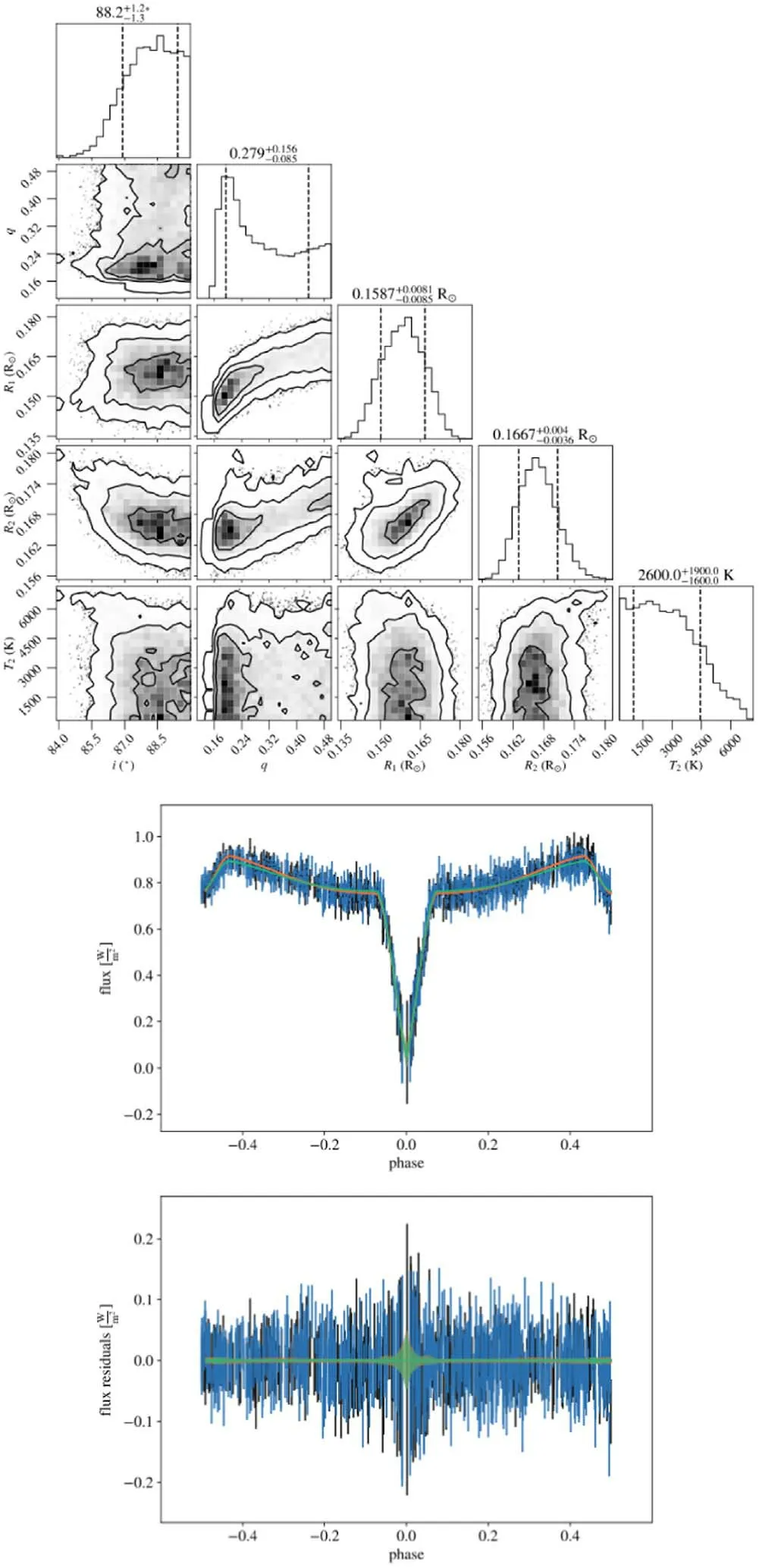
Figure B10.Diagram of MCMC results and LC fitting for ZTF J014600.90+581420.4.

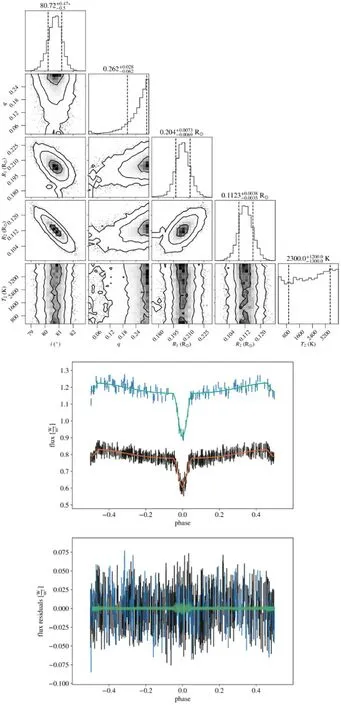
Figure B11.Diagram of MCMC results and LC fitting for ZTF J190705.22+323216.9.

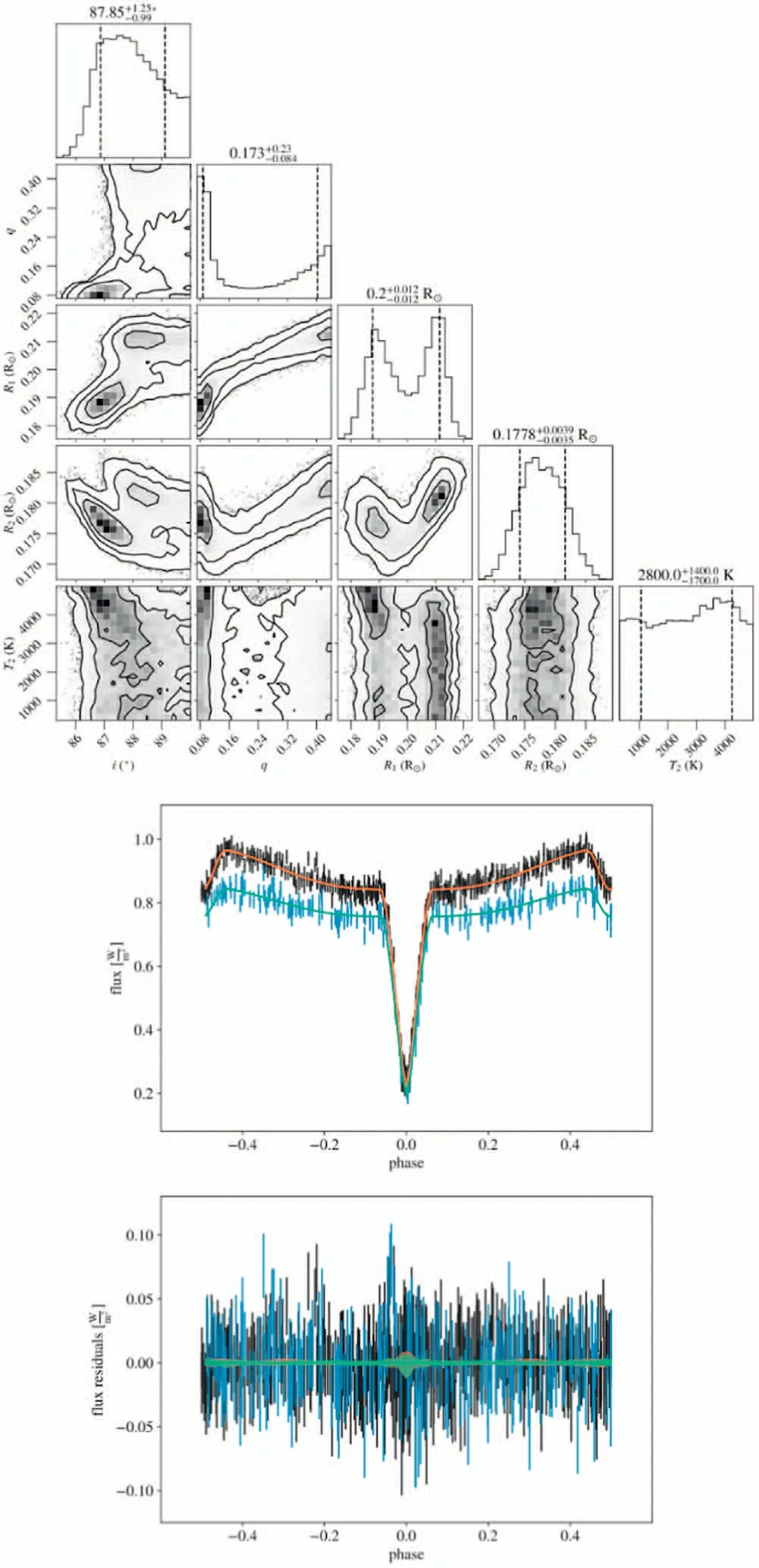
Figure B12.Diagram of MCMC results and LC fitting for ZTF J192240.88+262415.5.

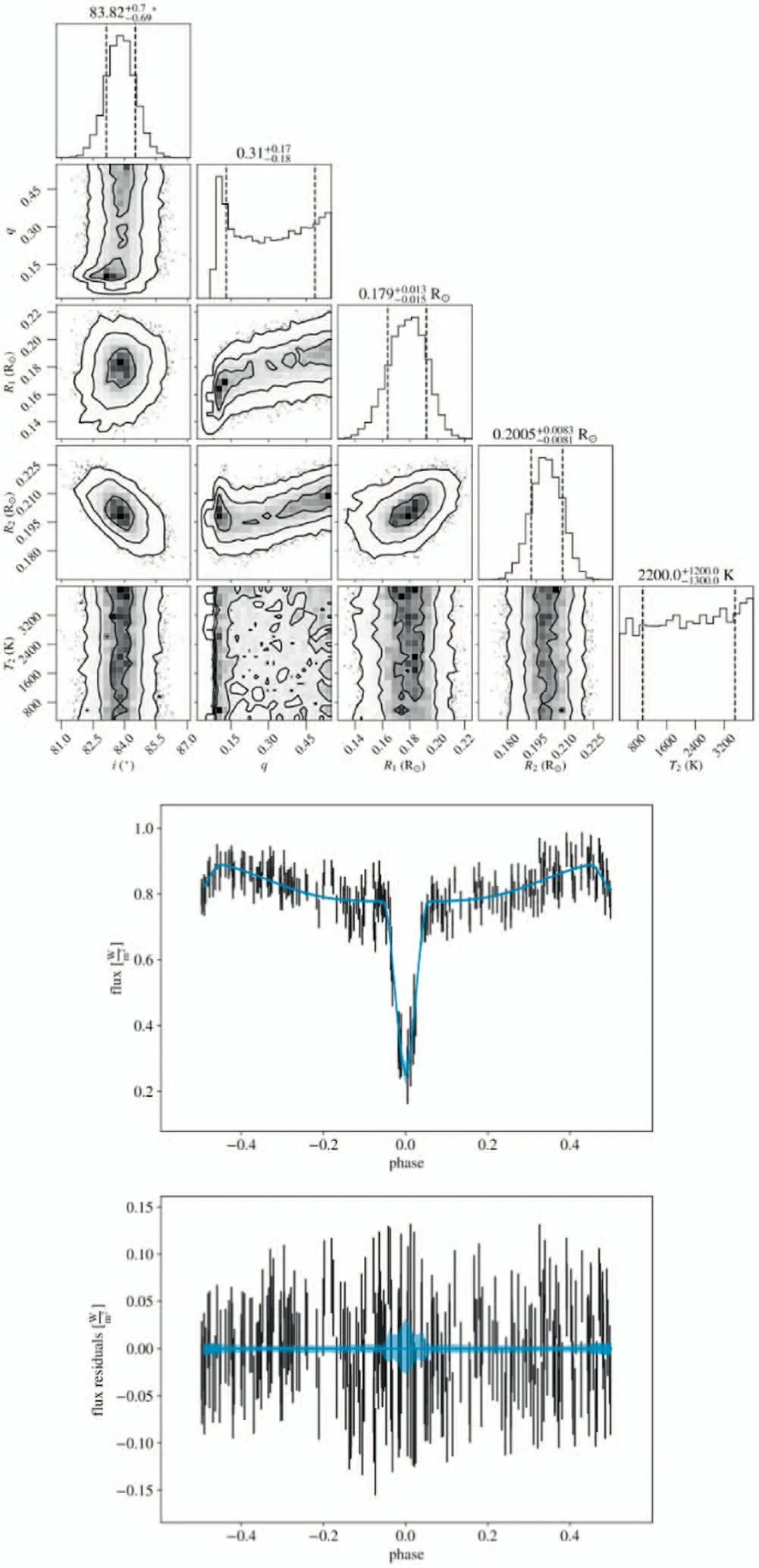
Figure B13.Diagram of MCMC results and LC fitting for ZTF J192513.66+253025.6.

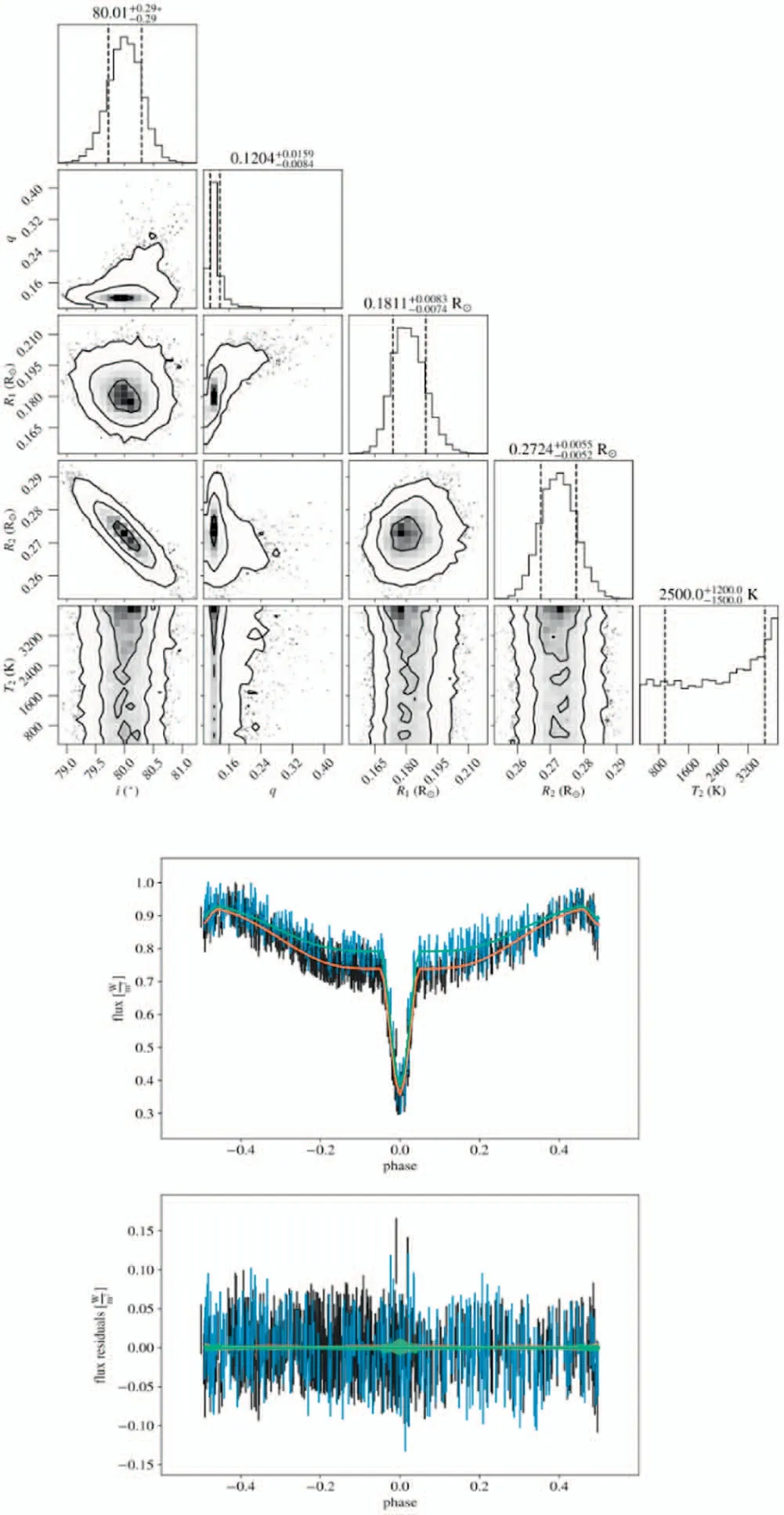
Figure B14.Diagram of MCMC results and LC fitting for ZTF J193555.33+123754.8.

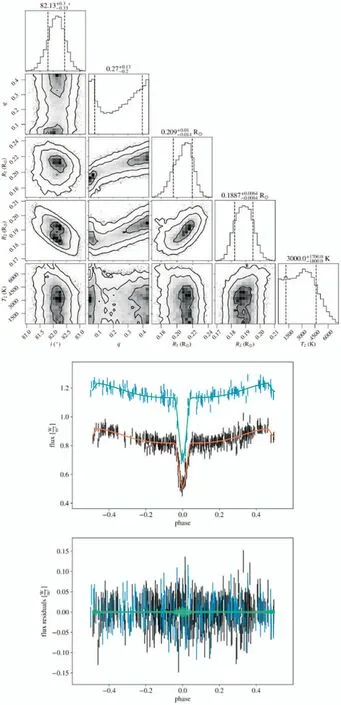
Figure B15.Diagram of MCMC results and LC fitting for ZTF J193604.87+371017.2.

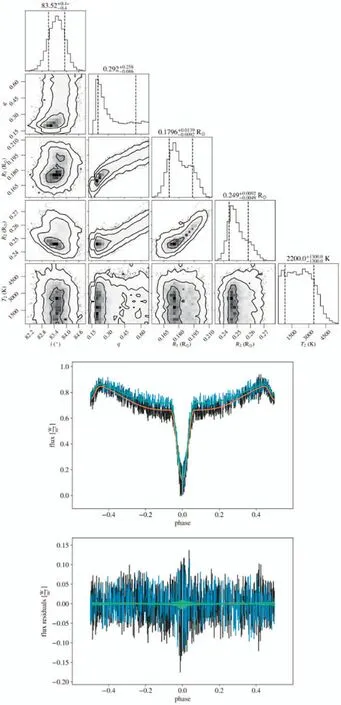
Figure B16.Diagram of MCMC results and LC fitting for ZTF J193737.06+092638.7.

Figure B17.Diagram of MCMC results and LC fitting for ZTF J195403.63+355700.6.

Figure B18.Diagram of MCMC results and LC fitting for ZTF J195908.44+365041.1.

Figure B19.Diagram of MCMC results and LC fitting for ZTF J200411.60+141150.2.

Figure B20.Diagram of MCMC results and LC fitting for ZTF J203535.01+354405.0.

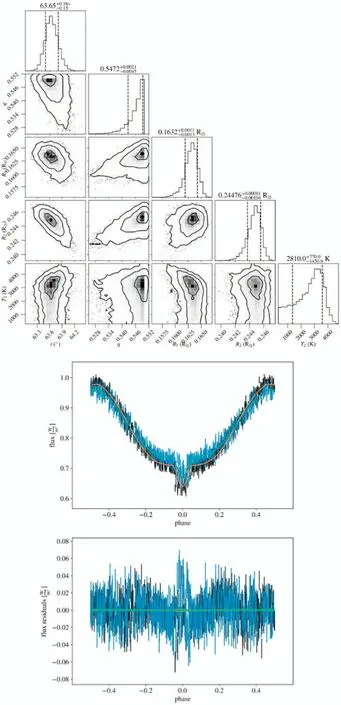
Figure B21.Diagram of MCMC results and LC fitting for ZTF J204638.16+514735.5.

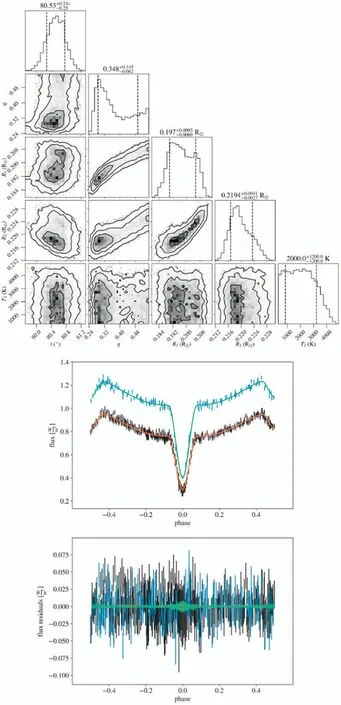
Figure B22.Diagram of MCMC results and LC fitting for ZTF J210401.41+343636.3.

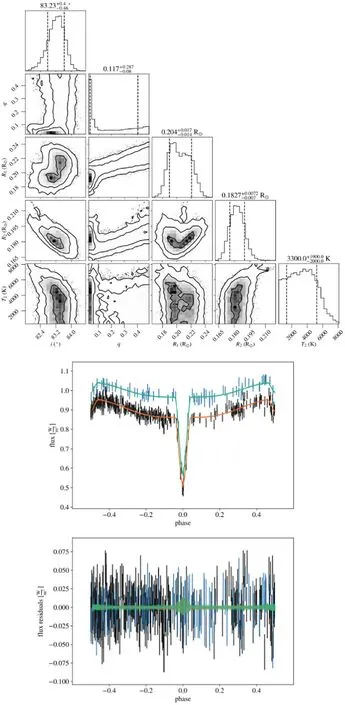
Figure B23.Diagram of MCMC results and LC fitting for ZTF J221339.18+445155.8.

ORCID iDs