Zhiliang Cheng, Wanhuan Zhou, Chen Tian

State Key Laboratory of Internet of Things for Smart City, Department of Civil and Environmental Engineering, University of Macau, Macau, China

Keywords:Global sensitivity analysis (GSA)Multi-gene genetic programming (MGGP)Soil suction response Spatial variation of suction response Uncertainty assessment

ABSTRACT In this study, an intelligent monitoring platform is established for continuous quantification of soil,vegetation,and atmosphere parameters(e.g.soil suction,rainfall,tree canopy,air temperature,and wind speed) to provide an efficient dataset for modeling suction response through machine learning. Two characteristic parameters representing suction response during wetting processes,i.e.response time and mean reduction rate of suction,are formulated through multi-gene genetic programming (MGGP)using eight selected influential parameters including depth, initial soil suction, vegetation- and atmosphererelated parameters. An error standard-based performance evaluation indicated that MGGP has appreciable potential for model development when working with even fewer than 100 data.Global sensitivity analysis revealed the importance of tree canopy and mean wind speed to estimation of response time and indicated that initial soil suction and rainfall amount have an important effect on the estimated suction reduction rate during a wetting process. Uncertainty assessment indicated that the two MGGP models describing suction response after rainfall are reliable and robust under uncertain conditions. Indepth analysis of spatial variations in suction response validated the robustness of two obtained MGGP models in prediction of suction variation characteristics under natural conditions.

1. Introduction

Rapid urbanization increases impervious surface area, potentially worsening flooding and groundwater shortages(Zhang et al.,2019).Additionally,the probability of extreme weather(e.g.heavy rainfall)is increased,likely owing to climate change,which tends to trigger certain natural calamities, such as landslides, debris flow,mountain collapse, and waterlogging (Kim et al., 2012; Sun et al.,2019). The occurrence of some such disasters is closely related to the mechanical behavior of geotechnical engineering infrastructures. Because in the vadose zone of geotechnical engineering infrastructures, soil suction is recognized as an essential parameter dominating the physical properties of unsaturated soil,a comprehensive understanding of the variation properties of soil suction is needed, with the effects of different influential factors under complicated natural conditions. It is noted that soil suction mentioned in this study refers to soil matric suction if there is not special explanation. Soil suction variations consist mainly of two processes: the drying process, which involves removal of water from soil, and the wetting process, which involves water infiltration.Most geotechnical engineering disasters usually occur during wetting when reduction of soil suction destabilizes geotechnical engineering infrastructure.Accordingly,it is essential to explore the effect mechanism of various factors on soil suction reduction during the wetting processes and to reveal the importance of each factor for soil suction reduction. Such studies would provide a reference for evaluating soil mechanical properties and even assessing safety and risk for geotechnical infrastructures.

Under natural conditions, soil suction is greatly affected by certain factors, including vegetation-related parameters as well as weather factors, with vegetation greening having been confirmed as an environmentally friendly solution for water and soil erosion control that has been exploited to some geotechnical infrastructures (Leung et al., 2015; Ni et al., 2018; Zhao et al., 2019).Notable factors related to vegetation and atmosphere parameters are air temperature,air relative humidity,wind speed,rainfall,solar radiation, tree canopy, root water uptake, runoff, and the like(Hemmati et al., 2012; An et al., 2017; Ni et al., 2018). Because a large number of studies seeking analytical or numerical solutions have analyzed soil property variations induced by vegetation and atmosphere, some existing approaches are able to be employed to analyze field-monitored soil suction variations in rooted soil during wetting processes under the influence of vegetation- and atmosphere-related factors. Under natural conditions, atmosphere and vegetation parameters are considered to act on variation of soil moisture in different ways. Accordingly, based on Richards’s equation,certain analytical solutions are developed to express soil water variation by adding various items that take into account the effects of vegetation (Richards,1931; Raats, 2007; Nyambayo and Potts, 2010; Ng et al., 2015, 2016; Zhu and Zhang, 2015). Thus,soil suction variation can be obtained based on the relationship between soil moisture and matric suction known as soil water characteristic curve (SWCC). Analytical solutions are generally convenient and efficient but also tend to require certain assumptions and simplifications, hindering precise analysis of in situ soil suction variations and potentially diverging from the results of actual practice.As a result,some numerical simulation approaches focus on simulating soil property variation under various initial and boundary conditions (Cui et al., 2013). Numerical simulation approaches have become popular since the advent of user-friendly geotechnical software and reliable constitutive modes. Generally,those methods that integrate with finite element or finite difference methods support the input of different types of influential parameters, such as leaf area index, root area index, rainfall, solar radiation, and wind speed, to quantify evaporation, transpiration,root water uptake, and the like for use in analyzing soil-vegetation-atmosphere interactions(Farouk et al.,2004;Hemmati et al.,2012; Kassim et al.,2012; Oh et al.,2016; Rahardjo et al.,2016;An et al., 2017; Ni et al., 2018). Although such numerical approaches can form the basis of a full-scale experiment analyzing soil suction variations in the field, they are generally time-consuming and related to some parameters that are difficult to determine in practice. In recent decades, in addition to common analytical and numerical approaches, machine learning has attracted extensive attention from geotechnical engineers owing to its advantages for use in data analysis, such as no demand for assumptions about model structure and its ability to automatically provide solutions for complicated systems.With further improvements in monitoring technology and the advent of the big data era,machine learning has certainly exhibited marked advantages over typical data mining methods when seeking interesting patterns among the various items of a dataset. Many machine learning methods may be used for analysis of soil suction reduction during a wetting process under the influence of various factors.It is well known that when machine learning is used to formulate relationships among different items,significant challenges can arise in several respects, such as model generalization, interpretability, and repeatability. Compared with most machine learning methods, genetic programming (GP) provides the opportunity to overcome these challenges to model development by automatically evolving an explicit formula (Jain et al., 2004; Johari and Nejad, 2015). Thus, GP has attracted increasing attention and been used to formulate a number of complicated relationships between influential parameters related to the properties of unsaturated soil(Johari et al.,2006;Garg et al.,2014a, 2015; Alemdag et al., 2016; Zhou et al., 2016; Johari and Nejad, 2018). In addition, as a variant of common GP, the multigene genetic programming (MGGP) method holds more potential for model development when the available data are limited and the relationships among different parameters are sophisticated (Garg et al., 2014b; Cheng et al., 2021). To author’s knowledge, few studies have been conducted for in-depth analysis of the variation characteristics of soil suction in a rooted soil using GP method.Additionally, for a rooted soil in the field, spatial variability causes difficulty representing the profile with a deterministic,or precisely defined,set of soil parameters whose variations are closely related to certain meteorological and vegetation parameters.For safety and risk assessment of practical engineering, the characteristics of suction response are necessary to be explored further.For example,the response time of soil suction and suction reduction rate are both important indices related to safety of practical engineering.It is commonly known that field-monitored soil suction suffers great influence from various parameters, which makes the analysis of practical suction response difficult. Therefore, machine learning method is a good choice to be used for exploring the complicated system based on a lot of data collected from field monitoring.Accordingly, performing model development using the MGGP method for soil suction reduction in a rooted soil under the effects of vegetation and atmosphere could offer clear insights into the soil-vegetation-atmosphere interaction mechanism.

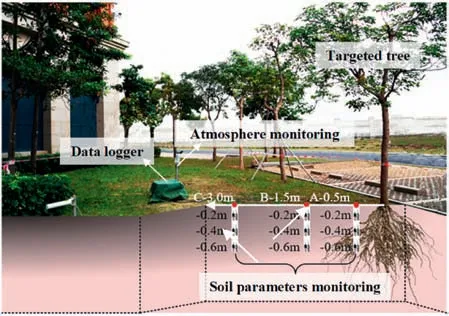
Fig.1. The instrumented field monitoring site.

In this study, multi-dimensional and multi-source data acquisition by a field monitoring test in a vegetated soil is performed for further disclosure of soil suction reduction during the wetting process. Two terms representing the characteristics of soil suction reduction, response time to rainfall and the reduction rate of soil suction, are taken as the output variables in model development using the MGGP method.First,two-dimensional(2D)variations of both two terms are simulated using several selected atmosphereand vegetation-related parameters.Second,based on mathematical models obtained by MGGP,the sensitivity of various vegetation and atmosphere factors to soil suction response during rainfall is illustrated. Then, uncertainty analysis is performed to investigate the models’ uncertainty when estimating soil suction responses during wetting processes. Finally, the spatial variation characteristics of both terms representing soil suction reduction during a rainfall event are explored, with the effects of several important influential parameters determined by sensitivity analysis.

2. Site description and instrumentation

The in situ monitoring was performed in rooted soil on the campus of the University of Macau, located on Hengqin Island,Zhuhai, China. The selected monitoring site is covered with common plants in Macau. The selected target tree named Elaeocarpus Apiculatus Masters is widely distributed in the south of China(e.g.Macau).During the whole monitoring period from September 2016 to March 2019, three trees were selected, near which different types of sensors and equipment were distributed to collect variations in the parameters of unsaturated soil, local weather, and vegetation. During this field monitoring, the effects of slope and grass were ignored, with the study focusing on interactions between monitored characteristic parameters of shallow unsaturated soil,targeted tree,and local weather conditions.The soil with depths ranging from zero to 0.8 m of the study area was classified as well-graded sand(SW)in the Unified Soil Classification System.For detailed information about local climate, monitoring site topography,and monitoring plan,see Zhou et al.(2020)and Cheng et al.(2021).

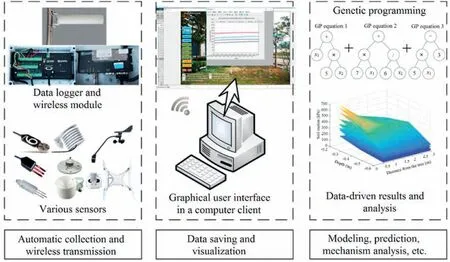
Fig. 2. Composition and workflow of the intelligent monitoring platform.

The soil suction, soil water content, air temperature/relative humidity, solar radiation, rainfall, and wind speed/direction sensors were employed to record and save variations in soil properties and meteorological parameters.An unmanned aerial vehicle(UAV)was used to take images to quantify the variations of tree canopy size. The radius of tree canopy can be quantified through image processing (Cheng et al., 2021). Beyond tree canopy radius, tree’s effect on soil property parameters can also be reflected in the distribution distance of a sensor from the targeted tree. As Fig. 1 shows, total three monitoring points near a targeted tree had sensors installed. Points A, B, and C were distributed at different distances (0.5 m, 1.5 m, and 3 m) and depths (0.2 m, 0.4 m, and 0.6 m) from the targeted tree. Soil suction and volumetric water content sensors were installed at the monitoring points after preparing the boreholes using a drilling machine.The air temperature sensor, air relative humidity sensor and rainfall gauge were installed in the center of the monitoring site to ensure that the monitoring data would not be disturbed by the trees.Data logging equipment was protected using a heat-resistant and water-proof box. The data record interval was 30 min.

Under natural environmental conditions, soil undergoes continuous input and output of various external energies and substances, giving rise to the complexity, multi-formity, indetermination, imperfection, and dynamic evolution that are the hallmark of geotechnical engineering(Zhang and Cai,2012).These soil attributes result in various unpredictable potential safety hazards.Bressani et al. (2018) pointed out that many accidents in geotechnical works, as well as many landslides, have been attributed to communication failures, errors in data interpretation or presentation, and other non-technical factors (e.g. failures of monitoring systems). Additionally, to allow development of better models of soil property variations,a certain amount of data acquired through continuous measurement is required,with record time consistence of multi-source data also needed for model practice in machine learning. Accordingly, an intelligent monitoring system should be established to continuously provide true and reliable data that can be used to investigate soil parameter variations induced by various parameters. In the later stage of field monitoring (start from June 2018), the intelligent monitoring platform (Fig. 2) was introduced to allow collection and transmission of multi-dimensional and multisource data in the soil-vegetation-atmosphere continuum.As a result, data collected from different sensors using the intelligent monitoring system equipped with an antenna could be transmitted timely by wireless network to a computer client.Additionally, a graphical user interface (GUI) was built using the Matlab software to display variations in different parameters with time,so that users could check the variation characteristics of each parameter,based on the data collected from sensors,by clicking the corresponding button in the GUI. Meanwhile, the collected data from the intelligent monitoring platform could be used for further analysis of interactions among soil, vegetation, and atmosphere.

3. Modeling spatial response of soil suction to rainfall

The field monitoring results indicated that soil suction’s response to rainfall can be characterized using two parameters:response time of soil suction reduction,t(the time interval between the beginning of a single rainfall event and the starting of the obvious decrease of soil suction)and mean reduction rate of soil suction vs(Cheng et al.,2021). These two parameters are important indices reflecting the variation characteristics of soil suction during wetting processes.The response time of soil suction is related to the safety duration for which soil suction is not reduced after a rainfall, and the reduction rate of soil suction is used to describe the speed required for suction to drop to the air entry value, which is related to rainfall water infiltration in rooted soil.Monitoring indicated that tree canopy size,rainfall-related parameters (rainfall amount, rainfall intensity, and rainfall pattern)and depth from ground surface could strongly affect soil suction reduction during a rainfall event. Detailed information and quantification of these parameters can be found in Cheng et al.(2021).Some studies have clarified that wind speed plays an undeniably important role in analysis of soil-vegetation-atmosphere interactions (Teng et al., 2014; Lozada et al., 2019). Wind speed usually makes an effect on water evaporation that is correlated with suction reduction rate.Except for that,wind speed may cause a great impact on rainfall water infiltration into soil during a wetting process by changing the air pressure or other parameter(s),which need to be explored further. Therefore, wind speed was also selected as an influential parameter in the model development by MGGP. During data processing,variations in soil suction at the depth of 0.6 m were small,therefore,only data at depths of 0.2 m and 0.4 m were used for model development and analysis.

3.1. Variable selection

In this study,according to statistical analysis of suction variation properties induced by different types of rainfalls, it is found that different rainfalls cause different response times and suction reduction rates.Two characteristic parameters,response time t and mean reduction rate of soil suction vs,at different distances(0.5 m,1.5 m, and 1.5 m) and depths (0.2 m and 0.4 m) from the targeted tree are quantified as the output variables for model development,as shown in Fig. 3. The response time refers to the time to start decent of soil suction when suffering a rainfall, and the mean reduction rate of suction is defined as the mean values of all the slope gradients between two adjacent record data during a wetting process.The quantification of two parameters has been introduced in detail in Cheng et al.(2021).Limited data on soil suction response to rainfall are available for analysis based on the long-term field monitoring. After data filtering, only 91 data are used for model development because limited efficient rainfall events(the number of rainfall events is 149) are separated from total monitoring data.More detailed data processing can be found in the study of Cheng et al. (2021). A total of 91 data are arranged in chronological order for model development. First, 73 data (80% of total data) are planned for use as training data,with the remaining 18 data(20%of the total)as the testing data.In this way,the developed model can be understood as using existing data for model development with a view to estimating future variations in target variables.

After determining the output variables, several influential parameters are selected as input variables for model development.The monitored influential parameters include vegetation-related parameters (tree canopy, distance from the tree), atmosphererelated parameters (air temperature, air relative humidity, rainfall), and soil temperature. However, some influential parameters are strongly correlated, as evident in the multi-collinearity evaluation for each two parameters using variance inflation factors. In addition, some studies have indicated that initial soil suction is an important parameter for model development,because it represents initial stress status, which can strongly influence soil suction reduction. Finally, a total of eight parameters are selected as input variables, including rainfall amount (x1), mean rainfall intensity(x2),normalized value of rainfall pattern(x3),ratio of distance from tree to radius of tree canopy (x4), air temperature (x5), mean wind speed (x6), depth from the ground surface (x7), and initial soil suction (x8), as Fig. 4 shows.

Table 1 gives the results of multi-collinearity evaluation,revealing the correlation between each two selected inputs.Multicollinearity between inputs was evaluated using variance inflation factors (VIF), based on the following criteria: VIF = 1/T < 5 indicating that multi-collinearity problems are unlikely,ensuring good modeling practice,where T is the tolerance value.The relationship among correlation coefficient(R),Tand VIF is expressed as VIF=1/T,and T = 1 - R2.

3.2. MGGP method

3.2.1. Working principle

GP is first introduced to permit better understanding of MGGP,which is a variant of GP.The GP method can automatically create a computer program that represents a model for solving a problem based on the principle of Darwinian natural selection(Johari et al.,2006). As Fig. 5 shows, a typical GP syntax tree consists mainly of internal function nodes and external terminal nodes.The functional nodes can include basic arithmetic operators (e.g. +, -, × , ÷),nonlinear functions (e.g. sin, tan, exp, sqrt), and any other defined functions, with the terminal nodes mainly containing numerical constants and variables,and other arguments.When used to model nonlinear systems, GP offers two main advantages: flexibility and interpretability comparable with other similar machine learning techniques(Faris et al.,2016).Unlike some“black box”approaches,tree models established by GP are explicit and relatively easy to evaluate, with their complexity controllable by setting maximum genes and GP tree depth,among other things.Unlike traditional GP,each symbolic model (and each member of the GP population) in MGGP is a weighted linear combination of the outputs from several GP trees(see Fig.5)by the least square method(Gandomi and Alavi,2012). The MGGP model is linear with respect to its weighted coefficients (W0, W1, …, Wn) despite using nonlinear terms. Accordingly, the basic calculation process is run by the GP program. The working procedures of the GP program can be briefly described as follows. After data preparation, the program generates the initial population (computational models) based on the set GP parameters, such as maximum value of gene, gene tree depth, functional and terminal selections, and constant range (Cheng et al., 2021).The generation of the initial models is random based on user’s settings.After that,individual model component is evaluated by GP algorithm, and new models can be generated by mutation, crossover, and reproduction. The evolutionary process continues by evaluating the fitness of the new models and starting a new round of reproduction,crossover,and mutation.A typical fitness function for evaluating the performance of the generated models is the root mean square error(RMSE) (Cheng et al., 2020).

Fig. 3. Two characteristic parameters describing vegetated soil response.

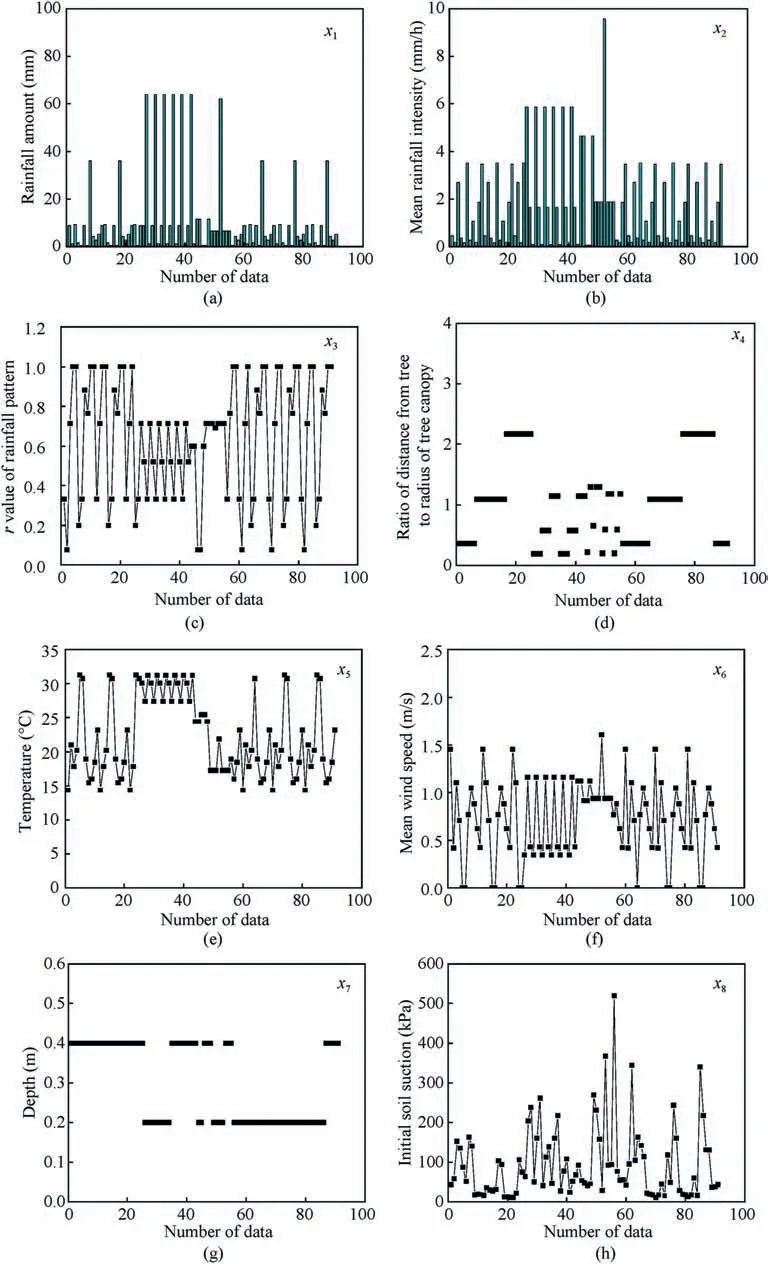
Fig.4. Selected eight input variables for modeling analysis:(a)Rainfall amount,x1;(b)Mean rainfall intensity,x2;(c)Rainfall pattern,x3;(d)Ratio of distance from tree to radius of tree canopy, x4; (e) Air temperature, x5; (f) Mean wind speed, x6; (g) Depth, x7; and (h) Initial soil suction, x8.

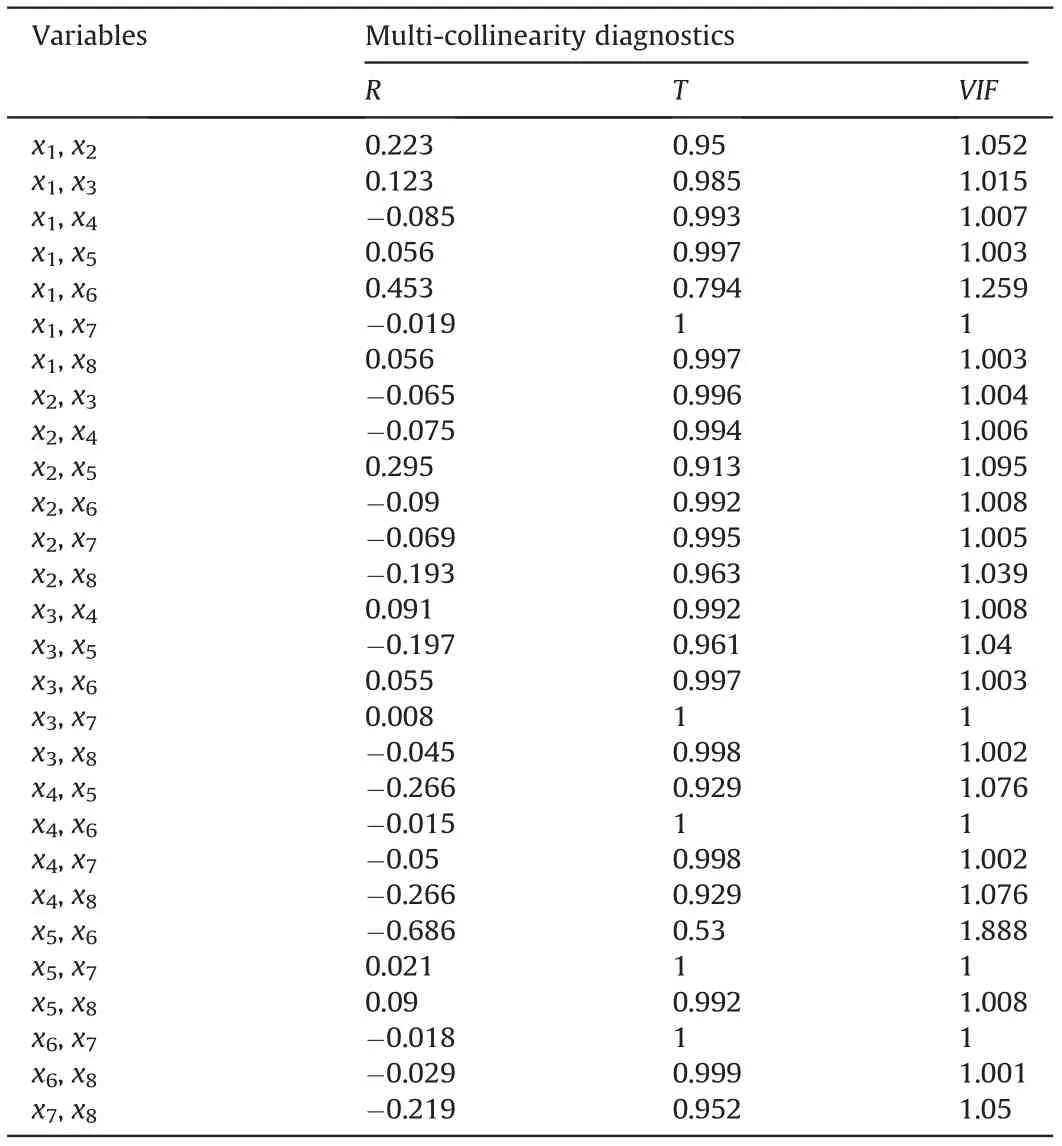
Table 1 Correlation evaluation between each two input variables.

Generally,more complicated parameter settings can contribute to generating an optimal model that produces less error.For a good modeling,it is better to choose simpler parameter settings as far as possible while retaining acceptable performance of the obtained solution, because a simpler structure is more conducive to analyzing relationships between variables. Accordingly, in this study, the simplest parameter settings of MGGP were used for multivariate model development.

3.2.2. Parameter settings for MGGP

Table 2 shows the parameter settings of the MGGP method for model development. The MGGP settings mainly consist of the running number of programs and some parameters related to model structure and complexity.Both models’development in plan uses the same parameter settings as for the MGGP method,ensuring consistent model development and thus allowing simultaneous analysis by the two proposed models. The crossover, mutation,and reproduction probability rates were set at 85%,10%,and 5%, respectively, to produce an optimally efficient model (Ackora-Prah et al., 2015; Danandeh Mehr and Nourani, 2018). Other parameter settings were determined by trial and error, based on the principle of finding an optimal model more efficiently and economically, which is to say a model having better fitness and a simpler structure.

3.3. Modeling results and performance evaluation

Based on the variable selection and parameter settings for the MGGP program, two mathematical models are obtained for formulating the relationships between two characteristic parameters, response time (t) and mean reduction rate of soil suction (vs)and eight dependent variables (see Eqs. (1) and (2)). Two multivariate models generated by the MGGP method have the simplified structures with the acceptable performance:

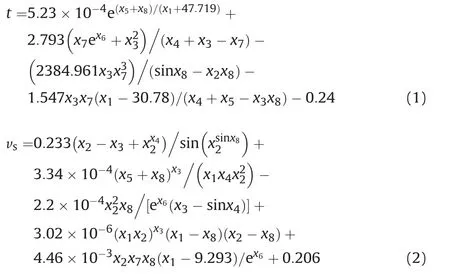
Fig. 6 compares the estimated values from the MGGP models and the measured values obtained through field monitoring of two characteristic parameters representing soil suction response to various influential factors during wetting processes. Table 3 illustrates performance evaluation results of obtained response time t model and mean reduction rate of soil suction vsmodel for training and testing data of the models based on correlation and error analysis.Three metrics are used to estimate the performance of the obtained multivariate models:the coefficient of determination(R2),the root mean square error (RMSE, in %), and the mean absolute percentage error (MAPE, in %). It can be concluded that the two obtained multivariate models, using limited data and the MGGP method, are able to depict the relationships between the two characteristic parameters and eight dependent variables. Two multivariate models are reliable and robust for estimating or predicting soil suction response to various rainfall events within a certain value ranges of selected variables. Additionally, based on those two MGGP models, soil suction response to different influential factors during wetting processes can be explored further.

Fig. 5. Composition of GP syntax tree and working principle of MGGP method.

Table 2 Parameter settings for MGGP program.

Fig. 6. Measured and simulated values of the two parameters t and vs, representing soil suction response during wetting processes.

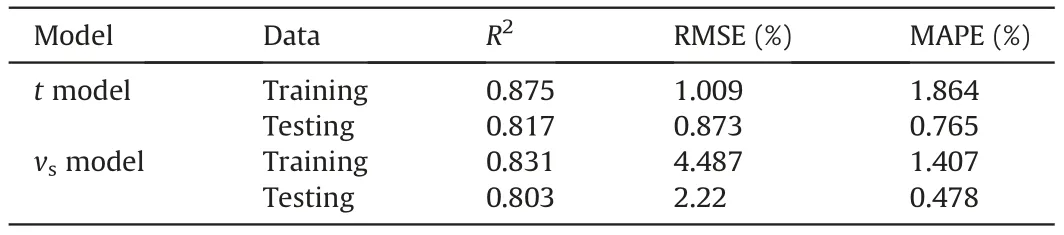
Table 3 Performance evaluation for the two obtained MGGP models.

3.4. Sensitivity analysis

Fig. 7. Effects of input variables on the soil suction response time.

Sensitivity analysis explores the ways in which variations in output variables can be attributed to different input variables,improving understandings of the importance of each input on output. Sensitivity analysis mainly includes local and global sensitivity analyses (LSA and GSA). GSA usually attracts more attention due to its ability of reflecting integrated sensitivity over the whole input variable space (Ni et al., 2018). The variance-based GSA method is recognized as a reliable indicator of parameter sensitiveness as well as quantitative importance indices using which to describe the effect of a single input and the coupled effects of different parameters (Dai and Ye,2015).Two methods,the Fourier amplitude sensitivity test(FAST)and Sobol’sensitivity analysis,can be used to perform variance-based GSA. In this study, these two methods are used to analyze each input variable’s importance to output variables according to two MGGP models, and the analysis results are shown in Figs. 7 and 8.

Based on Fig.7,two GSA methods almost give the same results.It is indicated that ratio of distance from tree to radius of tree canopy (x4) and mean wind speed (x6) strongly influence the response time of field-monitored soil suction in conjunction with a rainfall event.Then,the depth(x7)with a relatively small sensitivity on the response time of suction has a value size like those of other two influential parameters, rainfall amount (x1) and initial soil suction (x8). The remaining three parameters, i.e. mean rainfall intensity (x2), rainfall pattern (x3), and air temperature (x5) with a similar sensitivity have the least influence on the response time(t).The response time of soil suction refers to the time it takes for soil suction to diminish after the beginning of a rainfall event. Clearly,two most primary sensitivity parameters, tree canopy and wind speed, can hinder the rainfall water infiltration into soil by sheltering and wind pressure, respectively. Then, three parameters related to boundary and initial conditions, the depth (x7), rainfall amount(x1)and initial soil suction(x8),have secondary important effect on the response time of soil suction to a rainfall event. The impact of remaining three parameters,mean rainfall intensity(x2),rainfall pattern (x3), and air temperature (x5), may be limited by time. Such findings accord with the general physical law.

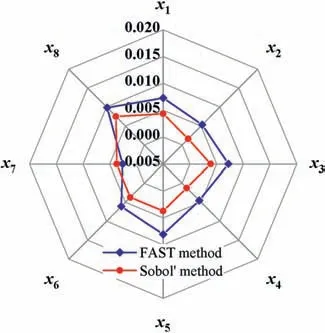
Fig. 8. Effects of input variables on the soil suction reduction rate.

From Fig.8,the sensitivity ranking by FAST method is initial soil suction(x8)>air temperature(x5)>rainfall amount(x1)>rainfall pattern (x3) > mean wind speed (x6) > mean rainfall intensity(x2) > ratio of distance from tree to radius of tree canopy(x4)>depth from ground surface(x7),while that by Sobol’method is initial soil suction (x8) > rainfall amount (x1) > rainfall pattern(x3) > mean wind speed (x6) > air temperature (x5) > depth from ground surface(x7)>mean rainfall intensity(x2)>ratio of distance from tree to radius of tree canopy(x4).It can be seen that,although two GSA methods do not give quite same results, which may be caused by the complexity of obtained MGGP model, the results obtained by two methods behave a certain uniformity in some respects, for example, (i) the most sensitive parameter on suction reduction rate is initial soil suction, x8; (ii) rainfall amount (x1),rainfall pattern(x3),air temperature(x5),and mean wind speed(x6)have similar sensitivity coefficients and play a relatively secondary important role;(iii)the remaining three parameters,mean rainfall intensity (x2), ratio of distance from tree to radius of tree canopy(x4), and depth from ground surface (x7) have the least influence.Initial stress state(referring to initial soil suction in this study)plays the most essential roles in deciding the change speed of stress state with external factors. Then four secondary important parameters are tightly involved in the processes of rainfall water infiltration and evaporation.Especially,as a parameter that is closely related to evaporation, mean wind speed (x6) has an important effect on the reduction rate of soil suction during a wetting process. Some previous studies have indicated the importance of wind speed in analyzing soil-vegetation-atmosphere interactions (Teng et al.,2014; Lozada et al., 2019). The remaining three parameters also have a non-negligible impact on soil suction reduction rate.

3.5. Uncertainty assessment

It is common knowledge that when employing machine learning,various factors can cause uncertainty in a data-driven model,including those related to input data,predictors,model parameters,model structure,and so forth(Solomatine and Shrestha,2009);as a result, it is essential to make the models’ uncertainty clear.Compared with classic methods(e.g.Monte Carlo-based methods),the quantile regression (QR) method has the key advantage of evaluating model residuals and taking into account all sources of uncertainty (Rahmati et al., 2019). In this study, the QR method is used to conduct uncertainty analysis of the two obtained MGGP models. As already mentioned regarding model development, two mathematic models(response time model and suction descent rate model)were developed to evaluate soil suction response to various weather and environmental conditions.As a result,the output values from two MGGP models are collectively referred to as suction response values. Generally, the QR method is carried out by given two quantiles (i.e.τ = 0.05 and 0.95),with a linear relationship between the measured and predicted data assumed. Then, for each selected quantile (i.e. 0.05 and 0.95), the QR model is established using the predicted suction response values (from each obtained MGGP model) as input values and the observed values as output values(Fig.9),where α and β are the slope and intercept of obtained linear QR models, respectively. The established linear QR model for τ = 0.95 means that the data point is below this linear line with a probability of 95%.Finally,the selected quantiles(i.e.0.05 and 0.95)of the suction response values are calculated using the established QR model, using the predicted suction response values (by each obtained MGGP model)as inputs for the whole study area.Based on these linear QR models, a 90% prediction interval between the two boundaries by QR models with the two selected quantiles (i.e. 0.05 and 0.95) can be obtained, as Fig. 10 shows. These uncertainty bounds follow the predicted variations in suction response with an acceptable width. Most of the measured values fall within the prediction interval.In addition,the width of prediction interval for the response time model is larger than that for the suction reduction rate model and indicates greater uncertainty.

Two statistics, mean prediction interval (MPI) and predicted interval coverage probability (PICP), are adopted for validating the performance of the QR method. MPI is the mean width of the prediction interval, with lower values of MPI indicating less uncertainty. PICP indicates the number of measured values that fall within the prediction interval,with higher PICP preferable to lower PICP. MPI and PICP values are calculated as

Fig. 9. Two linear QR models for (a) response time and (b) suction reduction rate.

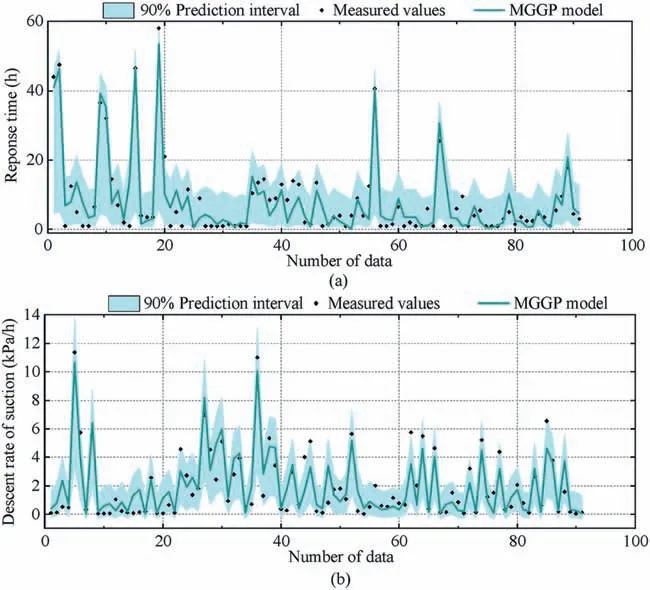
Fig.10. Uncertainty intervals estimated by QR method for two terms representing suction response during wetting processes: (a) t model; and (b) vs model.

Table 4 Uncertainty statistic results by the QR method.

4. Spatial variation of suction response to key parameters

For rooted soil in a field, assessing the spatial variability of soil parameters induced by meteorological and vegetation parameters can offer insights into the soil-vegetation-atmosphere interaction mechanism.In this study,2D spatial response characteristics of soil suction during wetting processes can be obtained after givingvalues for input variables in two obtained MGGP models, because the input variables include ratio of distance from tree to radius of tree canopy (x4) and depth (x7), which represent variations in location along the horizontal and vertical directions, respectively.In addition to those two input variables,the inputs of the proposed MGGP models include other six parameters: rainfall amount (x1),mean rainfall intensity (x2), rainfall pattern (x3), air temperature(x5), mean wind speed (x6), and initial soil suction (x8). For a multivariate model,when output varies with changes in one input variable, other input variables can be set to their average values.Table 5 shows the average values of all input variables except two location parameters (x4and x7) in the proposed MGGP models. In particular, in order to better explore the prediction ability of obtained MGGP models, beyond the depths of 0.2 m and 0.4 m, and the distances from tree of 0.5 m,1.5 m, and 3 m, which are set in field monitoring, depth values of 0.15 m and 0.6 m and distance values of 0.2 m and 5 m are included in this study.In addition,the initial soil suction (x8) differs by depth, therefore, based on the initial suction values at depths of 0.2 m and 0.4 m,the initial suction values at depths of 0.15 m and 0.6 m are calculated using the linear interpolation method.

Table 5 The value settings for input variables in two MGGP models.

Fig.11. Spatial variations in response time induced by two influential parameters: (a) Radius of tree canopy; and (b) Mean wind speed.

Fig.12. Spatial variations in suction reduction rate caused by two influential parameters: (a) Initial soil suction; and (b) Rainfall amount.

Table 6 Initial soil suction values at various depths.

Two methods of GSA,FAST and Sobol’,consistently indicate that among the selected eight influential variables, ratio of distance from tree to radius of tree canopy(x4)and mean wind speed(x6)are the first two important influential parameters for the response time of soil suction under natural conditions.Initial soil suction(x8),air temperature(x5)and rainfall amount(x1)have the greater effect on the reduction rate of soil suction. Accordingly, Fig. 11 shows 2D variations in response time(t)with distance from tree to radius of tree canopy(x4)and mean wind speed(x6),whereas Fig.12 plots 2D variations of suction reduction rate(vs)with initial soil suction(x8)and rainfall amount(x1).It is noted that according to the results of trial, the suction reduction rate has a little change with air temperature,and the results are not shown in this study.Four groups of values within their measured value range are selected for each variable, with the setting values for initial soil suction at different depths indicated in Table 6.According to Fig.11,for locations nearer the tree and deeper depths, response time increases. It also increases with increases in radius of tree canopy and wind speed,consistent with commonly understood physics, which means that the increases in radius of tree canopy and wind speed make the interruption for the rainfall water infiltration greater.Fig.12 shows that soil suction reduces more quickly at locations farther from a tree and at shallower depths. A threshold value is seen, approximately 1.5 m from a tree, beyond which variations in suction reduction rate are inverted,a phenomenon probably related to the presence of the tree’s canopy. The reduction rate of soil suction increases with increases in initial soil suction and rainfall amount.It can be concluded that the obtained MGGP models behave a reliable and robust prediction ability within a certain range.It is noted that the analysis results are based on obtained MGGP models established using limited field-monitored data, and they need to be validated further by more testing and theoretical analysis.

5. Conclusions

Based on data quantification from an intelligent field monitoring platform,the MGGP method is used for model development to depict variations in two characteristic parameters, response time (t) and mean reduction rate of suction (vs), that represent the soil suction response during wetting processes.Eight parameters related to soil,vegetation,and atmosphere are picked as the dependent variables for model development, including rainfall amount (x1), mean rainfall intensity(x2),rainfall pattern(x3),ratio of distance from tree to radius of tree canopy(x4),air temperature(x5),mean wind speed(x6),depth(x7), and initial soil suction (x8). Based on the two obtained MGGP computational models,two GSA methods,FASTand Sobol’sensitivity analysis,are employed to investigate the contribution of each input influential parameter to soil suction response. Uncertainty assessment is then performed to analyze the reliability of two MGGP models.Finally,spatial variations in suction response are given that are represented by two characteristic parameters,induced by several important influential parameters that are themselves determined by sensitivity analysis, revealing variation mechanisms of suction response.Several conclusions can be drawn:

(1) The MGGP method is particularly good for formulating mathematic models of complicated systems using limited data. Two proposed MGGP models produced robust estimations of suction response based on selected input variables within an acceptable range of error.

(2) GSA using FAST and Sobol’method indicated the importance of ratio of distance from tree to radius of tree canopy(x4)and mean wind speed(x6)in estimating response time,revealing that initial soil suction (x8) and rainfall amount (x1) are particularly important when estimating suction reduction rate during a wetting process.

(3) Uncertainty assessment indicated that the two MGGP models developed for estimating suction response are reliable and robust under uncertainty. Comparison with prediction of suction reduction by MGGP model, that of response time shows a larger uncertainty. Most of the measured values fell within the prediction interval. All PICP values for both the response time model and the suction reduction model exceeded 0.781,indicating that most of the measurements were located in or near the corresponding prediction interval.

(4) For locations nearer a tree and at deeper depths, response time was larger owing to the interruption of tree canopy.Response time increased with increases in radius of tree canopy and wind speed, indicating that soil suction is reduced more quickly farther from trees and at shallower depths. The increases of initial soil suction and rainfall amount can cause a larger reduction rate of soil suction.

The two proposed MGGP models have a robust ability to represent suction response under various weather and vegetation factors within a certain range.Additionally,the two obtained MGGP models revealed the suction response caused by different parameters,which can offer insights into suction variations during natural rainfall events and then provide a reference for conducting risk assessment of geotechnical infrastructures. However, they are limited by the dataset and tree types involved,among other things.Perhaps some findings are not universal. More experiments and methods are needed to increase the generalizability and reliability of the obtained MGGP models. Especially, it should be noted that the estimation/prediction of a highly nonlinear state variable(fieldmonitored suction)by machine learning method generally requires a large amount of data. Machine learning modeling for a complicated system using limited data may bring us some results that are locally optimal or are against common sense, which requires experienced experts to judge they are right or wrong.Therefore,it is necessary and significant to carefully consider the potential problems of data sufficiency on the application of machine learning for a complicated system.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors gratefully acknowledge the financial support funded by the Science and Technology Development Fund of Macau SAR(Grant Nos. 0026/2020/AFJ and SKL-IOTSC(UM)-2021-2023), and the Funds for University of Macau(Grant No.MYRG2018-00173-FST).