Hojie Li, Honghu Zhu,b,*, Yunhi Li, Chunxin Zhng, Bin Shi

a School of Earth Sciences and Engineering, Nanjing University, Nanjing, 210023, China

b Institute of Earth Exploration and Sensing, Nanjing University, Nanjing, 210023, China

c State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou, 221116, China

Keywords:Pipe-soil interaction (PSI)Upheaval buckling Distributed strain sensing Image analysis Uplift resistance prediction Interfacial behavior

ABSTRACT Reliable assessment of uplift capacity of buried pipelines against upheaval buckling requires a valid failure mechanism and a reliable real-time monitoring technique.This paper presents a sensing solution for evaluating uplift capacity of pipelines buried in sand using fiber optic strain sensing (FOSS) nerves.Upward pipe-soil interaction (PSI) was investigated through a series of scaled tests, in which the FOSS and image analysis techniques were used to capture the failure patterns. The published prediction models were evaluated and modified according to observations in the present study as well as a database of 41 pipe loading tests assembled from the literature. Axial strain measurements of FOSS nerves horizontally installed above the pipeline were correlated with the failure behavior of the overlying soil. The test results indicate that the previous analytical models could be further improved regarding their estimations in the failure geometry and mobilization distance at the peak uplift resistance. For typical slip plane failure forms,inclined shear bands star from the pipe shoulder,instead of the springline,and have not yet reached the ground surface at the peak resistance.The vertical inclination of curved shear bands decreases with increasing uplift displacements at the post-peak periods. At large displacements, the upward movement is confined to the deeper ground, and the slip plane failure progressively changes to the flow-around. The feasibility of FOSS in pipe uplift resistance prediction was validated through the comparison with image analyses.In addition,the shear band locations can be identified using fiber optic strain measurements. Finally, the advantages and limits of the FOSS system are discussed in terms of different levels in upward PSI assessment, including failure identification, location, and quantification.

1. Introduction

Buried pipelines operated at high pressure and temperature are prone to thermal buckling. The upward bending (so-called upheaval buckling)of pipelines due to axial expansion is most likely to appear and lead to structural failures, owing to the limited soil resistance imposed in this direction (Thusyanthan et al., 2010; Liu et al., 2013). Once local wrinkling or fracture occurs, gas or oil leakage will bring serious economic and environmental consequences. Furthermore, large differential soil movements induced by landslides,normal faults displacements and ground settlements can also pose upward pipe-soil interaction (PSI) issues (O’Rourke,2010; Chian et al., 2014; Wang et al., 2015; Ni et al.,2018).

Rational design against upheaval buckling requires an adequate depth of soil cover that can provide expected restraint on the vertical uplift of pipes. The uplift resistance is closely associated with the failure behavior of backfill soil(White et al.,2001;Cheuk et al.,2008; Thusyanthan et al., 2017; Gong et al., 2018). Many studies have investigated the force-displacement response during pipe uplift(e.g.Trautmann et al.,1985;White et al.,2008;Zhuang et al.,2021). The results show that the mobilization of soil resistance is significantly influenced by soil density and burial depth. Solutions based on the limit equilibrium method(LEM)were given to predict the peak uplift force.The vertical slip plane model has been widely used to depict the failure mechanism(e.g.Matyas and Davis,1983;Schaminee et al.,1990). Two components determine the uplift capacity, i.e. the weight of the soil block being lifted and the shear resistance on vertical slip surfaces. In the centrifuge tests conducted by White et al. (2001), it was observed that the peak resistance is correlated with the shear mechanism along inclined planes bounding the failure wedge. Given the new geometry configuration, the solution of the inclined plane model was developed by assuming the stress distribution along shear planes.

To assess the authenticity of the LEM solution, improved techniques for the soil displacement field collection are necessary when capturing the failure geometry. Image analysis is an effective approach to obtain soil deformation in geotechnical testing(White et al., 2003; Li et al., 2019, 2022; Wang et al., 2021). It has been widely used in upward PSI investigations to capture the displacement field of soil (Cheuk et al., 2008; Thusyanthan et al., 2010;Huang et al., 2015; Zhang and Askarinejad, 2019; Zhang et al.,2022). The technique facilitates identification of the failure geometry. With its aid, different forms of failure wedges, including the slip plane and the flow-around behaviors, have been identified by Cheuk et al. (2008) and Thusyanthan et al. (2010). According to these observations,assumptions of conventional prediction models were reassessed. The normality, i.e. the vertical inclination of the shear surfaces is equal to dilation and friction angles,was proven to be unrealistic. Accordingly, the limit theorems of plasticity are not suitable since they have assumed an upward block which is wider than the actual value.

To overcome the limits of normality, White et al. (2008) used Bolton’s (1986) stress-dilatancy correlations to obtain the vertical inclination of the slip plane based on relative density,ID,and stress level.This solution is based on the observation from a series of tests conducted by Cheuk et al. (2008), which are consistent with the ensuing tests (e.g. Thusyanthan et al., 2010; Zhuang et al., 2021).The analytical solution was given by assuming the Mohr’s circles in situ and at peak resistance. However, infilling in the post-peak periods is not incorporated in analyses. Likewise, most existing prediction models did not consider the uplift resistance at large displacements.In fact,the localized infilling beneath the pipe invert has significantly affected the post-peak uplift capacity.For instance,due to the thermal stress, the localization infilling at the pipe bottom triggers upward bending.The uplift segments cannot back toward the original configuration even after cooling.Hence,Cheuk et al.(2008)suggested that the peak uplift resistance should be reevaluated based on the elapsed thermal cycles pipeline experienced. In addition, nearly all LEM-based solutions in the literature are derived from the slip planes mechanism. They are only applicable to medium to dense sands and shallow embedments(Cheuk et al.,2008;Thusyanthan et al.,2010).In the case of loose sand and deep embedment,the soil heave is limited in deep ground(Cheuk et al.,2008;Zhuang et al.,2021).Thus,the slip planes model should be modified to adapt to the new failure geometry.

Apart from physical modeling tests and theoretical investigations,numerous studies have been conducted using various numerical methods(Yimsiri et al.,2004;Jung et al.,2013,2016;Roy et al., 2018a, b; Zhang et al., 2022). To describe realistic uplift mechanisms, constitutive models considering strain softening,density-dependent,and stress-dependent soil behaviors have been established (Robert and Thusyanthan, 2018; Roy et al., 2018a, b).However, these approaches are not routinely used in practice,mainly owing to the difficulty in selecting appropriate parameters to define dilatancy and plastic flow. In addition, most of them are incapable of describing flow-around behaviors because highquality meshes cannot be maintained at large uplift displacements.

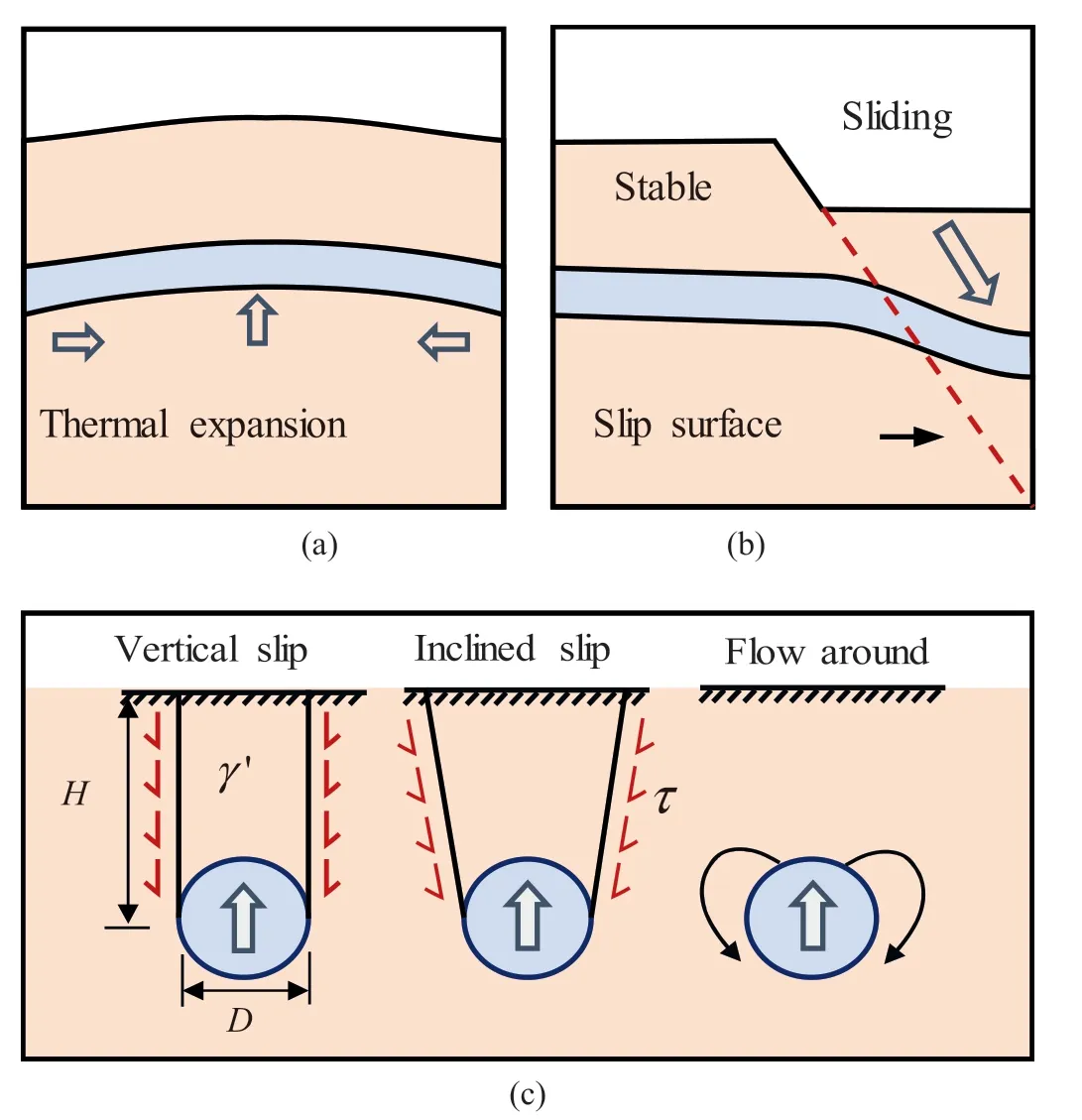
Fig. 1. (a) Upheaval buckling induced by thermal stress; (b) Vertical pipe-soil interaction due to landslide movements;and(c)Pipe uplift geometry and simplified failure mechanisms.

The post-peak softening of the soil resistance attracts considerable attention,especially for medium and dense sand conditions(e.g. Cheuk et al., 2008; Thusyanthan et al., 2010; Zhuang et al.,2021). However, prediction models for uplift resistance incorporating softening are rarely reported in the literature.In addition,the precise geometry of the failure wedge is hard to obtain since it is influenced by many factors, such as the relative density, burial depth,moisture content,grain size of the soil,and roughness of the pipe wall. More importantly, the backfill condition changes after pipeline installation, making failure mechanism determination more difficult. For instance, for offshore pipelines in sands, the backfill soil deposits at the loose or medium dense state during installation could be subsequently densified due to environmental loading (Clukey et al.,1989; Cathie et al., 2005; Thusyanthan and Robert, 2021). Given these facts, a distributed monitoring system for the soil cover layer is the most reliable tool to capture the realistic failure geometry.

One of the main objectives of this study is to provide a solution for uplift capacity assessment. This method relies on a fiber optic strain sensing (FOSS) system for real-time monitoring of the deformation and failure process. In this system, the fiber optic cables act as human nerves for feeling strain distributions along the cable lengths, enabling sensitive-condition monitoring functions for geomaterials and geo-infrastructures such as tunnels and pipelines(Wang et al.,2021;Zhu et al.,2022).A series of laboratory tests were conducted, in which specially designed FOSS nerves were horizontally installed above the model pipe.The performance of the FOSS technique in uplift failure identification was evaluated in comparison with image analyses. The correlation between the axial strain measurements and the uplift failure mechanism is investigated. In addition, empirical relationships between the mobilization distance and peak resistance were proposed to improve the existing bilinear or trilinear models. Design practice(e.g.DNV,2007;ALA,2005)and commonly used prediction models against uplift capacity are evaluated based on observations in the present study and a database assembled from the published literature. The advantages and drawbacks of FOSS in uplift resistance prediction are discussed concerning the different levels in uplift capacity prediction, with the focus on challenging issues in practical applications.

2. Problem definition

The upward PSI induced by relative pipe-soil motion can be broadly classified into two categories: active and passive PSI in terms of inducements of relative pipe-soil displacements.Upheaval buckling due to the thermal stress is a typical form of active PSI(Fig.1a). The passive interaction refers to that caused by large differential ground movements,such as the landslide and normal fault displacements (Ni et al., 2018; Akhtar and Li, 2020), as shown in Fig.1b. It has been identified that the uplift resistance and the geometry of the failure mechanism vary with the soil density and embedment ratio(H/D,where D is the diameter of the pipe buried in the sand with an effective unit weight of γ′, and the soil cover depth, H, is defined with respect to the springline of the pipe)(Trautmann et al.,1985; Thusyanthan et al., 2010). Fig.1c presents two distinct forms of soil reaction widely used in the industry:soil block uplift and flow-around mechanisms.

Vertical and inclined slip surface models are commonly used to describe the uplift model for medium to dense sand (Schaminee et al., 1990; White et al., 2008; Roy et al., 2018a, b). Previous studies have found that the inclination of the failure plane depends on soil dilatancy. According to observations from model tests conducted by Cheuk et al. (2008) and Huang et al. (2015), the inclination of idealized slip planes to the vertical is approximately equal to the peak dilation angle.Localized infilling initiates at large displacements, accompanied by the transition from mainly soil block heave to flow-around. For pipes deeply buried in loose deposits, upward movements in shallow ground surfaces are rarely observed.Therefore,local flow-around behaviors have been proven to be more realistic in these cases (Zhuang et al., 2021).

Various analytical idealizations were proposed to predict the peak uplift resistance based on the previously mentioned models.Several representative models were summarized and evaluated according to the observations from the present study and recent literature. The vertical slip model was the most commonly used mechanism and has been accepted by design practice (e.g. ASCEGuidelines,1984; DNV, 2007). The peak uplift resistance based on this prediction model can be expressed as

where P is the uplift resistance per unit length, K is the earth pressure coefficient,and φ is the internal friction angle of soil.The variant of Eq. (1) is reported by O’Rourke et al. (2015) and Thusyanthan et al.(2017).In view of inclined shear bands observed in centrifuge tests,White et al.(2001)proposed a prediction model to incorporate the effect of soil dilatancy. An assumption of stress distributions on simplified shear planes was raised, in which the normal stress increases beyond the at-rest value while the normal stress remains unchanged. Based on this assumption, the normalized peak uplift resistance can be expressed as

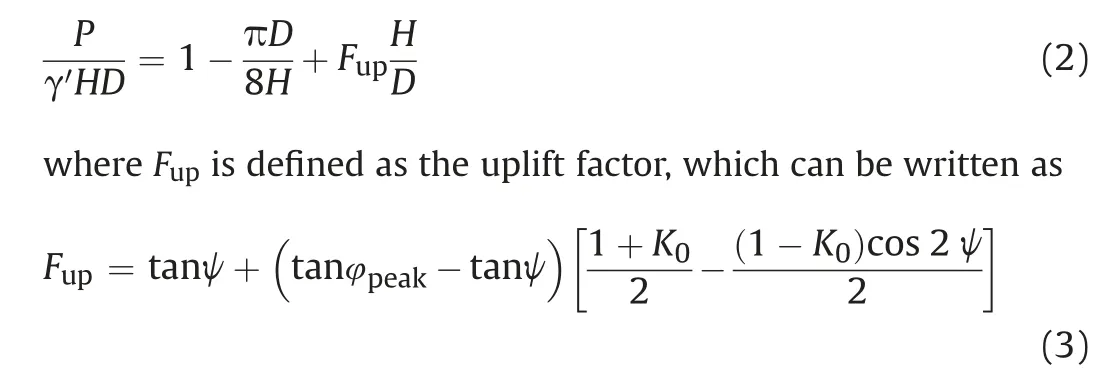
where ψ is the dilation angle, K0is the at-rest earth pressure coefficient, and φpeakis the peak internal friction angle of the soil.

More recently, Roy et al. (2018b) proposed a prediction model for the uplift resistance (Ps) after softening based on the inclined slip model. Taking into consideration the surface ground heave at large uplift displacements, Roy et al. (2018b) recommended the following equation for Ps:

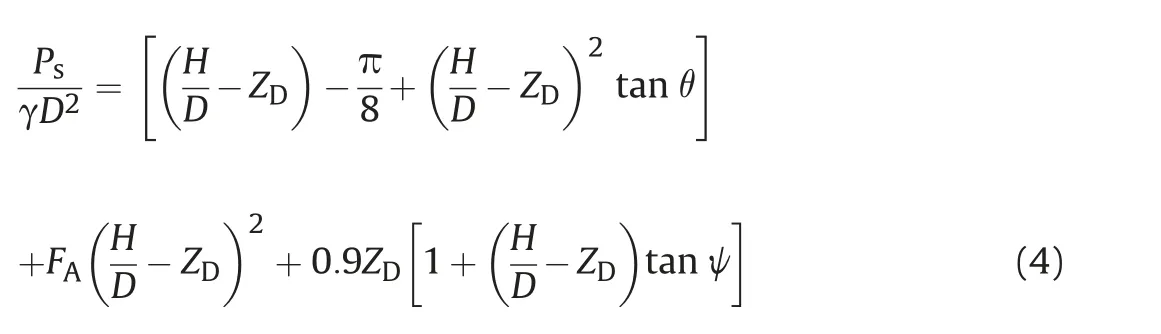
where ZDis the uplift displacement of the pipe normalized against the pipe diameter,θ is the inclination of slip planes to the vertical,and FAis an uplift factor different with Fupin Eq.(3),which can be written as

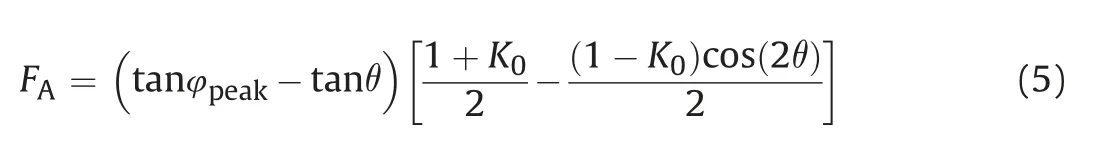
The prediction models summarized above are directed toward pipelines buried in sands. This matches closely the mechanical backfilling condition of most pipeline practices. Compared with sand backfill, the resistance assessment on the clay is relatively scarce in the literature.However,we sometimes have to resolve the problem that pipelines are buried in clayey soil.For instance,Cheuk et al. (2007) reported the uplift reaction of soft clay in the Gulf of Mexico. Liu et al. (2015) investigated the displacement-force relationship during upward movements of pipelines buried in Bohai soft clay. In these cases, the uplift resistance depends on the drainage condition and the bond condition at the pipe invert.Under the unbonded condition,the failure geometry of soil cover is similar to the vertical slip model stated previously.This model cannot hold in other cases since the adhesion from the soil underneath the pipe would play an important role in the resistance mobilization.

3. Experimental design

3.1. Equipment

The test setup is presented in Fig. 2. The test container has inside dimensions of 500 mm × 500 mm × 250 mm(length×height×width).It is constructed of 20 mm-thick acrylic sheets to avoid excessive deformations. The transparent walls facilitate the observations of soil displacement fields via particle image velocimetry(PIV)technique and digital speckle correlation method (DSCM) during pipe loading. To reduce side friction,polyester films were affixed to the inner walls of the container.Preliminary direct shear test results show that the polyester film has an interface friction angle of 16°-18°, about 0.5 times that of sand alone. The pipe model (diameter 50 mm) is a solid cylinder made of acrylic and fits flush between two sides of the chamber container to achieve plane-strain conditions. Polytetrafluoroethylene caps were installed at the pipe ends to reduce friction.A polished steel rod with a diameter of 6 mm connects the pipe model to the loading frame through a clamp fixed to the middle section of the pipe. A load cell fixed on the loading frame was used to capture the soil reaction transmitted through the rod.Upward movements were imposed through the actuator controlled by a computer.

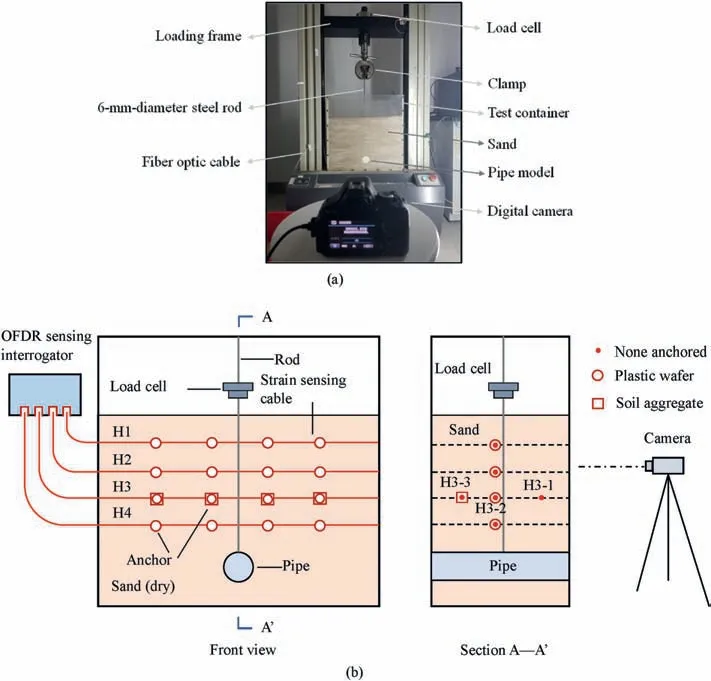
Fig. 2. (a) Annotated photograph of the model test setup and (b) Schematic diagram of the model test configuration.

3.2. Materials and model preparation

Fujian standard sand was used in the tests. Its physical and mechanical properties have been well documented in the literature(Yang and Wei, 2012; Wei and Yang, 2014). The particle size distribution of the sand samples is shown in Fig. 3. All the tests were performed in dry sand.When constructing the physical model,the expected dry densities corresponding to different relative densities(91% and 22%) were reached by tamping samples every 25 mm.

Fig. 3. Grain size distribution of the soil in this study.

The model container was filled up until the elevation corresponded to the central line of the pipe. The pipe model was then buried and screwed to the rod after removing the redundant particles at the expected position.Model construction continued until the positions of the FOSS nerves were reached.The artificial nerves for monitoring soil deformation were made of specially designed fiber optic cables. Their physical and mechanical properties are summarized in Table 1. As shown in Fig. 2, four layers of FOSS nerves (denoted as their elevation: H1, H2, H3, and H4) were carefully laid on the soil surface and connected to an optical frequency domain reflectometry (OFDR) sensing interrogator SILIXA OSI 2.0. The installation of the specially designed FONS nerves is presented in Fig. 4. To cover the area of interest and facilitate temperature compensation, the measurement distance of the sensing cable was set to about 4 m. The OFDR interrogator with high sensing precision for strain (10-6) and temperature (0.1°C)was used to collect the soil strains with a sampling interval of 10 mm. After filling up the container to the expected height, the upper end of the rod was connected to a load cell through the fixture. A digital camera was placed against the front wall of the model container to facilitate image analyses based on PIV and DSCM.The tests were performed at the room temperature of 22°C.

3.3. Testing procedure

A series of loading tests with various soil densities(22%and 91%)and embedment ratios (4.5, 4.8, 5.4, 5.5 and 8.5) was performed.The three dense sand tests were numbered D1-D3 while the twoloose sand tests were numbered L1-L2, as listed in Table 2. The conditions were selected to conform to the typical offshore and onshore pipeline practice and appropriately modified considering the stress level in the scaled model tests. They also permit comparison with the results reported in the literature (e.g. Trautmann et al., 1985; Cheuk et al., 2008; Zhuang et al., 2021). The pullout speed was 2 mm/min, corresponding to approximately one sand grain per 15 s. The photograph was captured at an interval of 30 s(corresponding to a pipe displacement of 0.01D). The pipe model was pulled upwards up to a maximum displacement of 1.2D. This normalized displacement can guarantee that the steady-state part of soil resistance is reached. Referencing maximum displacements chosen by Trautmann et al. (1985) (0.3-1D), Cheuk et al. (2008)(1D), and Zhuang et al., (2021) (0.2D), the force-displacement curve has experienced post-peak and entered the residual stage before 1.2D.

Table 1 Physical and mechanical properties of the fiber optic cable for strain sensing in the tests.

Fig. 4. Annotated photograph illustrating the layout of fiber optic cables (top view of the model when the soil was constructed to the H3 layer. Unit: mm).

4. Results and analysis

4.1. Force-displacement response

To eliminate the influence of frictional force imposed on pipe ends against the inner walls of the container, a pipe loading test without sand particles was conducted. The measured forcedisplacement curve was subtracted from others obtained in normal tests. Even so, there are still errors since the influence of finer particles trapped between the container walls and pipe ends on force measurements could not be quantified.

The force-displacement response during loading is shown in Fig.5,in which the uplift force has been normalized against γ′HDL(L is the length of pipe model). Uplift displacements have been plotted as a dimensionless quality ZD=ZP/D(ZPis the actual uplift displacement of pipe). Two distinct response forms dependent on relative density can be observed. Dense sand tests experienced a sharp increase in uplift resistance at relatively small displacements.The curves peaked at ZDof 0.02-0.04, and then a steep drop reflecting the strain-softening behavior of sand was observed.With increasing uplift displacement, the force fluctuated due to the accumulation and release of stress induced by the localization infilling around the pipe. The points of interest that remain for further analyses are labeled A-E in Fig. 5a for H/D = 4.8.

The force seems to be independent of the burial depth in loose tests because the curves for H/D = 5.5 and 8.5 present slight differences (Fig. 5b). Similar phenomena have also been observed in contractive soil in pipe loading tests conducted by Schaminee et al.(1990). The uplift resistance was mobilized at relatively low displacements. However, no obvious post-peak decrease was observed.Instead,the force has reached essentially constant values at large displacements (0.3D). In addition, the force-displacement curves fluctuated at a lower displacement than the dense cases,mainly due to the earlier mobilization of the flow-around behavior.

The upward responses revealed in this study are consistent with previous studies (e.g. Trautmann et al., 1985; White et al., 2001;Cheuk et al., 2008) except for the nearly identical plots under different burial depths in the loose tests (Fig. 5b). The unexpected findings could be partly attributed to the very loose condition in this study.

4.2. Mathematical representation of force-displacement relationship

The pre-peak hardening in mobilization of the uplift resistance is of concern for uplift capacity prediction. By normalizing the force-displacement curves with respect to the points at which the uplift force peaks,the data are plotted on transformed axes in Fig.6.Their responses are shown to be identical, even for different relative densities and embedments. Hence, an average mathematical relationship was achieved by ExpAssoc fitting on the database covering all variables considered in this study:

where FNis the normalized uplift force,FN=(F/γ′HDL)/Nv;Nvis the peak dimensionless uplift force,Nv=Fp/(γ′HDL),in which Fpis the peak uplift force;ZNis the normalized uplift displacement,ZN=ZD/(Zf/D); Zfis the uplift displacement to the peak uplift force, Zf/D is the dimensionless displacement corresponding to Fp.Fig.6 plots Eq.(6) and the diluted data for all conditions. According to the relationship, the force-displacement response for the pre-peak mobilization can be obtained, provided that Nvand Zf/D are known.

A simplified bilinear representation of the FN-ZNcurve is commonly used in PSI analysis(Trautmann et al.,1985;Jung et al.,2013). The secant slope at 0.7Nv(labeled it Kv70in Fig. 6, which corresponds to the secant slope at 0.7Nv) is recommended for pipeline design practice. The peak resistance is mobilized at ZN= 0.037 under the simple idealization based on Kv70. Then, the displacement to peak uplift resistance (i.e. mobilization to peak resistance),Zf/D,requires to be estimated for design of the pipelines in practice. Trautmann et al. (1985) suggested that 0.01H can be a closer approximation to Zf/D. The empirical equation seems not always amenable when the soil density and embedment are extrapolated outside the conditions established in their tests.

The published results over the last decades permit improved quantification.Fig.7 summarizes the mobilization displacement in a database of 41 pipe uplift tests assembled from the literature(Trautmann et al., 1985; Dickin, 1994; White et al., 2001; Palmer et al., 2003; Dickin and Laman, 2007; Cheuk et al., 2008;Thusyanthan et al., 2010) and five tests obtained in the current study. For the convenience of comparison with DNV (2007), the plot has been normalized in Zf/H.However,as shown in the figure,it is difficult to derive a specific equation to describe the relationship between the embedment ratio and the mobilization distanceat the peak resistance. The mobilization mechanism seems to be independent of the soil condition.More importantly,monotonicity cannot hold for H/D < 1.5, especially for partially buried cases (H/D < 0.5).

Table 2 Summary of test conditions.

By normalizing the data against the pipe diameter, D, the mobilization distance at the peak resistance was proven to be a function of H/D, as shown in Fig. 8. Two types of responses depending on the relative density have been observed. However,the apparent deviation in loose tests reported by Trautmann et al.

(1985) from the trend line at high embedment is unexpected. Zf/D reached essentially constant values. The problem has also been addressed by Thusyanthan et al. (2010). Considering the explanation by Trautmann et al.(1985),the abnormal results appear to be caused by the inflexible measurement system. By excluding these data,two good trends for mobilization versus the embedment ratio can be determined in Fig. 8. The following relationships are established to predict the mobilization distance at the peak resistance in loose sand:

It is noted that the database backing in Fig.8 and Eqs.(7)and(8)involves dry,moist,and saturated sand tests,respectively.From the distribution of data points, the mobilization distance has little relevance to soil saturation.Hence,the influence of moisture on the soil reaction is not incorporated into Eqs. (7) and (8).

Fig. 6. Mathematical representation of force-displacement response for the pre-peak phase (Kv50, Kv70, and Kv80 correspond to the secant slope at 0.5Nv, 0.7Nv, and 0.8Nv,respectively).

The specification of DNV (2007) has partially followed the empirical relationship proposed by Trautmann et al.(1985)with an assumption that uplift resistance has been fully mobilized at 0.005-0.01H.This implies that Zfis independent of the dimension of pipes and may result in unconservative estimates of soil resistance when using bilinear or trilinear models. Given the relationship presented by Eqs. (7) and (8), the secant slope, (Kv70) can be computed by dividing the displacement into the maximum force.For the loose sand, we have

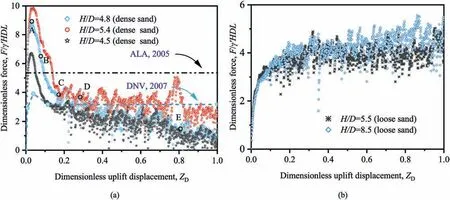
Fig. 5. Force-displacement response for pipe loading tests: (a) Dense sand and (b) Loose sand. ZD = ZP/D (ZP is the actual uplift displacement of pipe).

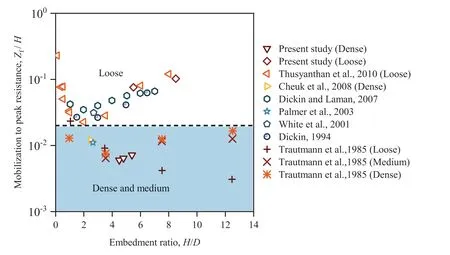
Fig. 7. Summary of mobilization results.

Combining the previously summarized prediction models for Nv,the bilinear representation of resistance mobilization in pre-peak stages can be determined by Eqs. (9) and (10).

4.3. Uplift failure mechanism in dense sand

4.3.1. Displacement field

The mobilization of the uplift force depends on the failure modes of the backfill. Using the DSCM and PIV analyses, the displacement field of the soil was obtained to reveal the failure mechanism. Fig. 9 depicts the region of interest of image analyses for all the tests. The evolution of accumulated displacement with increasing uplift movement is shown in Fig.10 for dense test D1.By examining the failure features corresponding to critical points A-E marked in Fig. 5a, the generic mechanisms for pipelines buried in medium to dense sand were presented.

The load cell captured the peak uplift resistance at ZD= 0.03(Zf= 0.0063H), which is within the range reported in published results (Trautmann et al., 1985; Cheuk et al., 2008; Thusyanthan et al., 2010). An inverted trapezoidal soil prism bounded by a pair of shear bands was formed at the initial stage. The uplift force peaked when the upward movement reached the ground surface,and then it experienced a sharp drop. The post-peak reduction in Segment AB(Fig.5a)can be attributed to the softening at slip planes due to excessive shear deformation.At Point B,localization infilling at the pipe waist was initiated, and the vertical inclination of slip planes was reduced to half of that observed at Zf. With increasing upward movement, the inclination of shear bands continued to change, and the flow-around behavior became dominant in Segment BC.Accordingly,the uplift force decreased monotonically due to the reduction in the weight of the trapezoidal soil wedge and the release of soil stress.

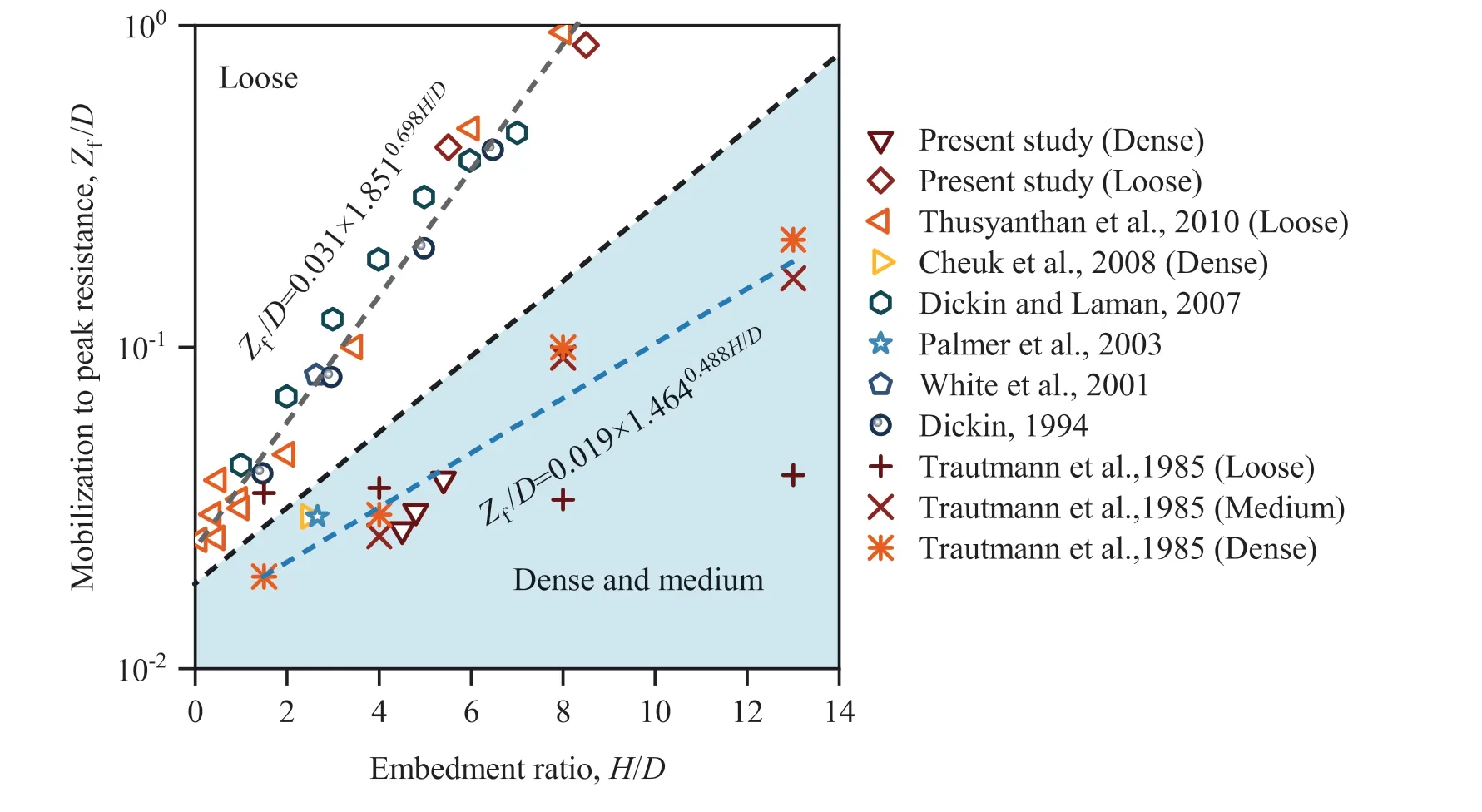
Fig. 8. Mobilization distance to peak uplift resistance vs H/D trend line.

Fig.9. A planar region of interest(ROI)for PIV and DSCM analyses(32×32 pixel size patches).

Segments AB and BC in the FN-ZDcurve are called the softening response followed by residual stages. At large deformations (i.e.ZD> 0.3), considerable oscillations were observed in the FN-ZDcurve since the flow-around behavior was dominant. As shown in Fig. 10, inclined shear planes gradually curve outward near the ground surface in Segment CD (ZD= 0.16-0.3), where the soil density roughly remains at its initial level, and the stress level is lower than that of deeper layers. The surface heave was no longer observed after Point D, implying that the failure wedge cannot be lifted as a whole.The flow-around mechanism fully controlled the reaction. Segments after Point D represent residual stages, also referred to as steady states of the force-displacement response.The displacement field at Point E (ZD= 0.5) reflecting the typical soil response in the residual phase is shown in Fig.10.

4.3.2. Soil lifting and shear band formation

The weight of the lifted block and the shear resistance on the slip surfaces are the two components in prediction models for uplift resistance (White et al., 2008). Given the geometry of the failure mechanism shown in Fig.10,both components can be determined provided that the vertical inclination is known. Fig.11 shows the incremental shear strain contours and displacement vectors within 30 s (ΔZD= 0.02) at Points A-D marked in Fig. 5a.

At the peak resistance (Point A), two symmetric shear zones staring from the pipe waist with a vertical inclination of 32°are generated in the backfill. The magnitude of shear strain is not identical inside the shear zones but varies with the depth. In addition,the concentrated shear zone appears to be confined below the H2 level, implying that the slip mechanism has not yet been fully mobilized at Point A. Instead of idealized planes, two symmetric distributed dilating shear zones bound the failure wedge. A similar observation was announced by Cheuk et al.(2008)and Thusyanthan et al.(2010).A pair of lines should be simplified from the shear bands to obtain a representative value of θ.The peak dilation angle(ψp)has been proven to be a closer approximation to the vertical inclination(θ) of the idealized surfaces at Point A (White et al., 2001, 2008).Because ψpis a strong function of confining pressure, Roy et al.(2018b) suggested that the mean effective stress at the pipe waist[(1+2K0)γH/3]could be used for determining ψp.

Fig.10. Accumulated displacement field at the dimensionless uplift displacement (unit:mm) of(a) 0.02;(b) 0.04;(c)0.08;(d)0.16;(e)0.3;and(f) 0.5.The points A-D marked in Fig. 5a correspond to the dimensionless uplift movements of 0.03, 0.08, 0.16, and 0.3, respectively.

As shown in Fig. 11b and c, the post-peak degradation of θ is captured.The shear zones have reached the ground surface at Point B,implying initiation of the slip mechanism,leading to an obvious surface heave. Meanwhile, the shear bands with an average inclination of 25°curve outward in the shallow backfill(Fig.11b and c)shows the shear strain and the vectorial displacement field at Point C,at which the flow-around mechanism tends to dominate the soil behavior. The influence of localization infilling can be seen from differences in the shear strain at the slip planes among Points A,B,and C.Compared with the sliding mechanism shown in Fig.11a and b, the upward movement of failure wedge is quite small, even if their inclinations are practically identical. The contribution of soil heave to uplift resistance continued to decrease with increasing uplift displacement at large deformations and tended to zero at Point D (Fig.11c).

4.4. Performance of FOSS for failure mechanism identification

Even if the mobilization mechanism of uplift resistance has been elaborated previously, accurately predicting the force remains challenging due to complex site conditions and intricacies of the PSI. A distributed system for ground deformation monitoring is necessary for evaluating the uplifting capacity of buried pipelines.One of the main objectives of this paper is to present the correlation between the failure feature and the strain measurements of the FOSS nerves. The influence of environmental temperature fluctuation on the strain measurements should be quantified because of the cross-sensitivity of Rayleigh backscattering to temperature.Raw data from the reference optical fiber shows that strain noise resulting from the temperature variation fluctuated within the range of ±12 ( × 10-6) during tests. Compared with the strain measurements reflecting the soil deformation, the interference could be neglected.

4.4.1. Strain measurements in slip plane failure

The slip failure planes and localization infilling mechanism were identified through image analyses based on external digitals(Figs.10 and 11). In contrast, the FOSS technique collects soil deformations through the structural response of infinitely flexible cables. A kinematic representation of the strain-sensing cables subjected to shear deformation mobilized in slip models is shown in Fig.12. Cables may exhibit large shear deformations within the shear zones and the areas directly above the pipe.Hence,the width of the failure wedge is expected to be determined through the strain distribution along a cable.

Strain measurements at the H2 level are shown in Fig. 13. As expected,the concentrated densification area above the central line of the pipe experiences larger deformation because of the thrust resulting from pipe movements. However, considerable compressive strains have been recorded at the normalized distance (the horizontal distance from the pipe central line normalized against the pipe diameter) of ±3 until ZDreaches 0.1 (Fig.13a). The variation in strain with ZDat these positions is shown in Fig.13c. The compressive strain near the shear bands was also reported by Sang et al.(2019).Considering the kinematically constrained problems in the upward PSI, it could be attributed to the compressive deformation resulting from the lateral movement of sand particles adjacent to shear bands and the bending curvature of cables. As captured by image analyses, the particles move away from the shear bands because of sand dilation.

According to the response of FOSS nerves to transverse ground deformations reported in the literature (Zhang et al., 2018; Sang et al., 2019), the inflection points (marked in Fig.13) at distancestrain curves indicate a close approximation of the location of shear bands.The shear band locations identified by FOSS(Fig.13a)and PIV analyses (Figs.10 and 11) are in close agreement. Fig.13b shows the development of strain measurements inside the initial shear bands at the peak resistance(Point A in Fig.5a).Rapid growth corresponding to pre-peak hardening was observed at ZD<0.1.As the vertical inclination decreases at Point B (Fig. 11b), shear deformations gradually weaken and disappear at the initial position of shear bands. Accordingly, the strain growth slows down in Segment BC (ZD= 0.10-0.16) and even declines after Point C(ZD=0.16),owing to the lateral compaction from new shear bands.At large displacements, especially for ZD> 0.5, the strain measurement increases monotonically due to the release of axial tension of cable segments directly above the pipe. The strain distribution at the distance of -2 seems to differ from other positions since the shear deformation there is weaker than inside the right shear band. This speculation can be confirmed through a comparison with PIV analysis. As shown in Fig. 11b, large shear strains of the left shear band were concentrated in the deeper ground and had yet not reached the ground surface.

Fig.11. Incremental shear strain contours and displacement vectors during pipe loading:(a),(b),(c),and(d)correspond to the points A,B,C,and D marked at Fig.5a.The data has been normalized against the maximum shear strain at each stage. 0 represents non-distortion while 1 represents the maximum shear strain.

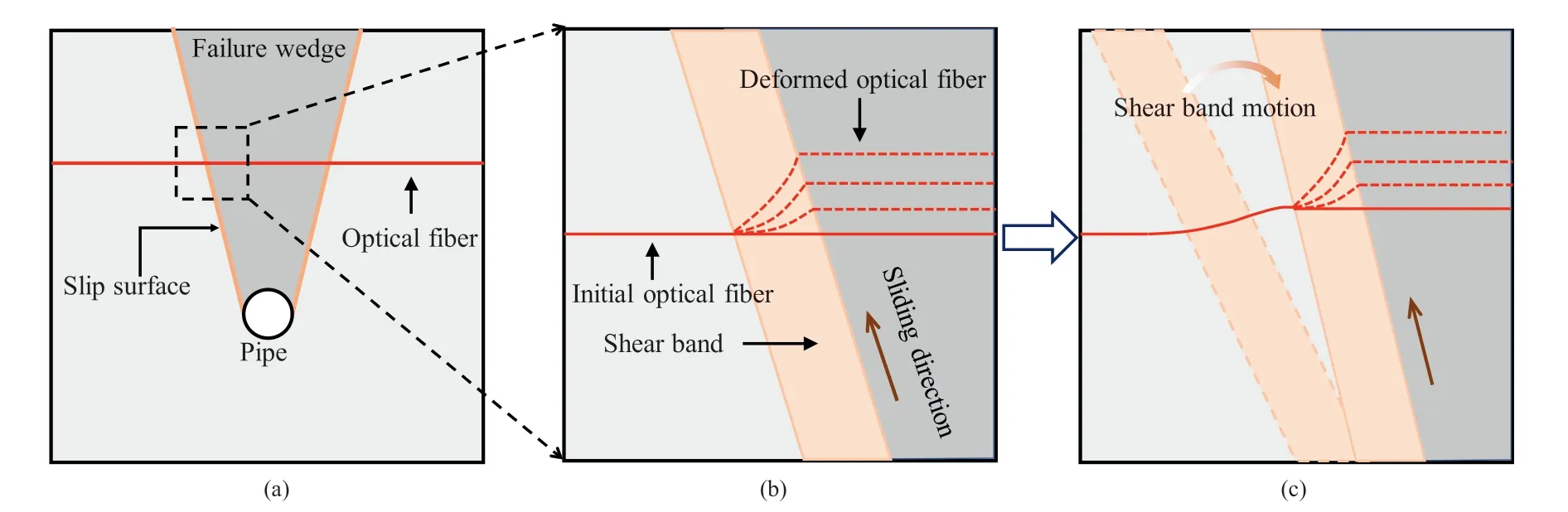
Fig.12. Response of buried strain sensing cables to ground shear deformation:(a)Cable crossing failure wedge;(b)Shear deformation imposing on cable and(c)Inclination change in shear band.

Fig.13. Strain measurements of cables at H2 level:(a) Spatial distribution; (b)Development at the normalized distance of -2, 2, 2.4; (c) Development at the normalized distance of -3.4, -3.2, -3, 3.6, 3.8; and (d) Development at the normalized distance of -0.2, 0, 0.8. Normalized distance means the distance normalized against pipe diameter D.

The strain-uplift displacement response inside the failure wedge has been divided into four segments Fig. 11d), which are consistent with the stages of uplift force mobilization shown in Fig. 4a. More specifically, the slowed growth in Segment BC indicates the initiation of localization infilling, whereas the steady decline from Point D implied that the flow-around behavior had been the dominant mechanism. At residual stages, the alternate stress accumulation and release in the failure wedge directly above the pipe were captured via FOSS and behaved as the oscillation of the curves in Fig.13d.

4.4.2. Strain measurements in flow-around failure

Detecting the flow-around model evolving from the slip plane model using the FOSS nerves has been proven feasible,as shown in Fig. 13. However, this may differ from loose sand cases because there is no accumulated deformation before flow behavior under these conditions. A distinct form of strain distribution in Test L1 is shown in Fig. 14. The results from Test L2 present a close trend.Large deformations inside the soil cover directly above the pipe were monitored, at which the sand was densified due to pipe movements. The strain increases quickly with the uplift displacement until ZDreaches 0.1. For this case, PSI was restricted to the deeper ground and had yet not propagated to the ground surface.Thus,image analyses captured little uplift movement above the H3 level, even though hundreds of microstrains were recorded via FOSS.The flow-around mechanism featuring particles infilling from the crown to the cavity was identified through compressive deformation at the H4 level Fig.14b).

Fig.14c depicts the strain development directly above the pipe.A compacted block above the pipe was observed at small uplift displacements (ZD< 0.5). The rapid growth of strain due to densification was restricted by localization infilling. Subsequently,sand particles flow continuously to the gap beneath the pipe.A pair of symmetrical slopes with an inclination of 33°forms in the cavity.As a result of the period flow, strain measurements fluctuated significantly at large uplift displacements(ZD<0.3),which shows a good agreement with the force-displacement curves in Fig. 5.

5. Implication for uplift capacity prediction

5.1. Peak resistance prediction models

Plasticity solutions have been experimentally proven inappropriate for peak uplift resistance prediction because the normality is violated according to the geometry observed in model tests(White et al.,2001;Cheuk et al.,2008).Simple analytical idealization based on LEM remains the most commonly used procedure in the industry (DNV, 2007; White et al., 2008; Roy et al., 2018b). Representative applications for these models are summarized in Eqs.

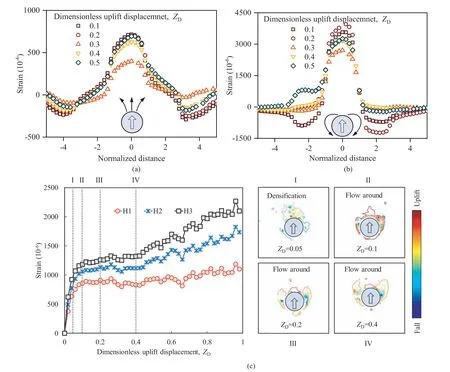
Fig.14. Strain measurements of cables at(a)H2; (b)H4 and (c)Strain development above central line of pipe and instantaneous vertical displacement field at typical points(Test L1).

Fig.15. Geometry change of the sand during uplift loading (Test D1): (a)-(f) correspond to the dimensionless uplift displacement (Unit: mm) of 0, 0.02, 0.1, 0.24, 0.3, and 0.5,respectively.

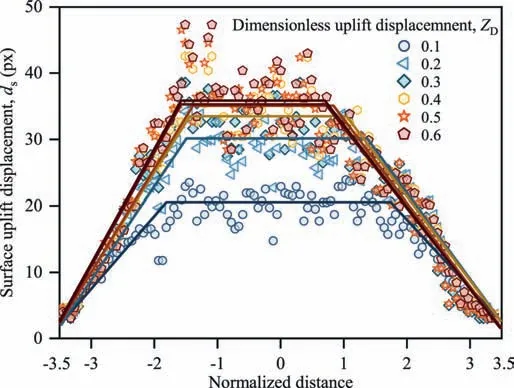
Fig.16. Vertical displacement of ground surface.

(1)-(5), which are evaluated regarding their assumptions. The vertical slip plane model could not be supported by the observations in the present study and published results (e.g. White et al.,2001; Cheuk et al., 2008; Zhuang et al., 2021), although these studies almost covered the range of H/D and D in practice. The design may be overly conservative because of the deducted weight of soil blocks and the length of shear planes.

The prediction model proposed by White et al. (2001) reflects well on the geometry of the mechanism observed in model tests(Cheuk et al.,2008;Zhuang et al.,2021).This implies that the peak resistance is mobilized when the slip mechanism fully initiates.However, the concentrated shear zones have not yet reached the ground surface at the peak resistance, according to the image analysis shown in Fig. 11. Hence, the peak resistance would be overestimated because of the additional shear resistance. In addition,shear planes are assumed to form at the pipe springline in the existing vertical slip models.Nevertheless,the initiation points are located above the pipe springline and appear to vary with confine pressure,relative density,and pipe-soil interface conditions(Cheuk et al., 2008; Zhuang et al., 2021). Of course, the assumed shear surface would lead to an overestimate of uplift resistance.

5.2. Prediction models for resistance after post-peak softening

It is also essential to evaluate the uplift capacity at large displacements for the whole life design of pipelines. Therefore, great attention should be given to the infilling and surface ground heave behavior during operation. The surface ground heave and gravitydriven slope failures beneath the pipe during pipe uplift are shown in Fig.15.Sand particles began to flow into the gap when ZDreached 0.08-0.1 in three dense tests (Point A). A pair of slopes at an inclination of 33°formed when the dimensionless uplift displacement increased to 0.24. At Point D (ZD= 0.3), the surface heave stopped, and the upward movement of sand was restrained to the deep ground below the H3 level.

Considerable surface heave implies that additional samples have been lifted.The extra weights should be calculated to quantify their contribution to the uplift force. As shown in Fig. 16, the vertical movement of the ground surface (termed surface uplift displacement, ds) is idealized as a form of trapezoidal heave, which facilitates the estimation of overburden for LEM. The angle of the heaving slope remains essentially constant during pipe uplift in the present study. In addition, the surface ground heave was concentrated in the pre-peak and post-peak stages(ZD<0.3).The growth is barely detectable at large displacements, and the surface becomes raised and lowered. Fig.17 shows the development of the heaving displacement of the ground surface and the strain measurements at the H1 level for test D1.

Relatively few studies were available for the post-peak degradation of soil resistance. Recently, Roy et al. (2018b) proposed a prediction model to evaluate the uplift capacity at large displacements based on the results obtained from finite element analysis,as shown in Eqs.(4)and(5).In the equations,0.9ZDwas suggested to describe the maximum height of the idealized heave throughout the uplift loading. However, the present study shows that the proportion of maximum heave displacement to the uplift displacement of the pipe is not constant and varies with ZD. The positive correlation between the normalized surface uplift displacement, dN, and the dimensionless uplift displacement ZDis shown in Fig.18, in which the curves were divided into five segments according to the principle declared in Fig.5a.A steady status is reached at Point D, indicating that the slope is equal to 0 for ZD> 0.3.

The vertical inclination with a constant value of 8°is used to determine the weight of the failure block. Eq. (5) seems to follow the stress distribution on the shear planes assumed by White et al.(2001). A fixed value could not be held in the post-peak and large deformation periods, which has been experimentally proven by Cheuk et al. (2008), Thusyanthan et al. (2010), and Zhuang et al.(2021). In Fig.18, the geometry of the lifted wedge should be reevaluated in the segments following Point D because the soil heave has been limited in the deeper ground. It is difficult to calculate the weight of the lifted block and the shear resistance at large deformations.Moreover,as the stress level inside the soil has changed significantly due to flow-around behavior, it is not appropriate to use the value of K0and other stress-dependent parameters determined from the initial state.

6. Discussion

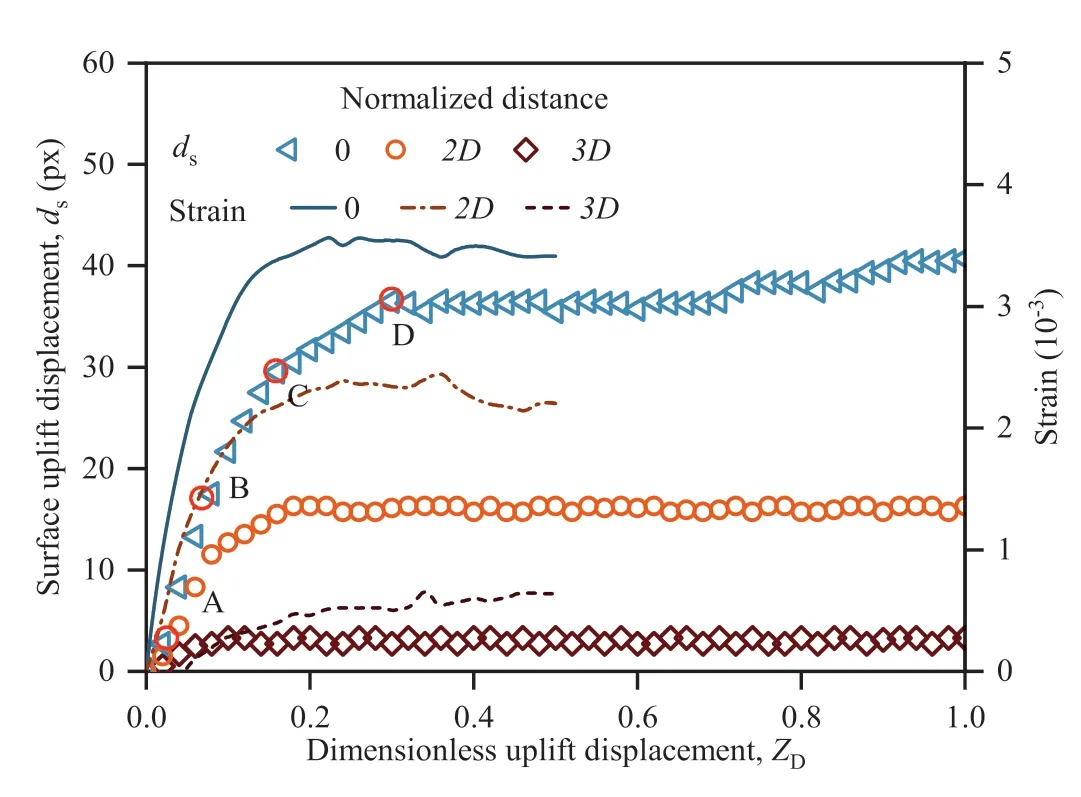
Fig.17. Surface ground heave and fiber optic strain measurements at H1 level for pipe loading tests.

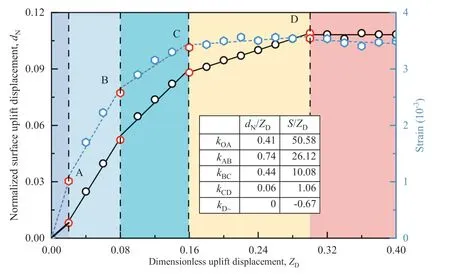
Fig.18. Normalized vertical displacement of ground surface and internal strain at H1 level, versus the dimensionless uplift displacement. Points A-D correspond to points marked at Fig. 5(a) dN is the surface uplift displacement normalized with the pipe diameter D.

Apart from the density and the burial depth, the surface roughness of pipe and sand particle characteristics,such as particle size and psephicity, can also impact the failure mechanism. The micro-mechanism problems in pipe uplift capacity assessment have been addressed in the previous studies (Cheuk et al., 2008;Reddy et al., 2022). Considering uncertainties and complexities in uplift mechanism, it is not recommended to use analytical idealizations for failure geometry estimation,especially at the post-peak degradation stages. A measured shape of failure wedge based on FOSS can provide a more useful solution for the LEM.

The feasibility of the FOSS technique to fulfill the different levels of upheaval buckling monitoring, i.e. identification, location, and quantification of failure, is addressed below. Firstly, the basic detection of the abnormal state induced by relative pipe-soil movement is easily achieved by decoding the spectral shift. Secondly,capturing the failure geometry(position of distributed shear bands) is also shown to be feasible in comparison with image analysis results(Fig.13a).FOSS based on the OFDR technique has an improved precision (10-6) and spatial resolution (submillimeter scale). In the present study, the sampling interval was artificially reduced to 10 mm for the convenience of data processing. In addition, the anchorages aiming to enhance the deformation compatibility in small-scale tests have negatively influenced the resolution. These anchor measures are unnecessary for full-scale tests and field monitoring (Klar et al., 2014; Huang et al., 2016).Given these reasons, the FOSS technique is sufficient for locating the shear band and determining the failure geometry in practical applications.

The change in strain measurement is localized both in time and space, which can be used to identify the stage of resistance mobilization,such as the transition from primarily slip to primarily flowaround behavior,as shown in Figs.13,14,17 and 18.However,it may be technically difficult to quantify the actual uplift displacement using strain measurements, considering the poor deformation compatibility between cables and the surrounding soil in smallscale tests (Zeni et al., 2015; Wang et al., 2021). The difference between the measured and actual strains arises from the coupling of the cable-soil interface and the shear lag effect inside cables.The cable-soil coupling cannot be guaranteed at large deformation.They will have relative sliding if the interfacial shear stress exceeds the strength. The range of a given fiber optic sensor buried in a specific soil condition can be determined through laboratory tests(Li et al., 2022). Due to the shear lag effect, the axial fiber strain would be presented over a larger zone when the soil deformation transfers through the substrate of cables wrapping the core(Berrocal et al., 2021; Tan et al., 2021; Mahjoubi et al., 2022). The commercial silica fibers are always packaged with a series of layers,including claddings, sheaths and jackets, to enhance the robustness. Hence, the shear lag effect should be considered for accurate strain measurements.

The FOSS nerves for pipeline uplift capacity assessment can serve as an important part of conditions of monitoring systems for buried pipelines. Besides uplift failure estimation, it can also be made multi-functional and provide early warning on ground deformation, pipeline leakage, and third-party intrusion. Considering massive quantities data obtained in practical applications,data-driven artificial intelligence techniques are necessary to help engineers to identify the failure initiation and avoid false alarms due to ambient noise (Bai et al.,2021a, b).

7. Conclusions

The uplift failure mechanism of pipelines buried in sands has been experimentally studied using FOSS and image analysis techniques. A methodology for capturing the failure mechanism using the strain measurement based on FOSS was given. The published prediction models for uplift resistance were evaluated in terms of a database of 46 tests assembled in the present study and the literature. A more reliable mathematical representation describing the pre-peak mobilization of uplift resistance was provided for the conventional bilinear or trilinear models.The main results obtained in this paper can be summarized as follows:

(1) The mobilization distance at the peak uplift resistance and the embedment ratio has strong positive correlation. This relationship depends on the relative density of sand and is almost irrespective of soil saturation.

(2) In slip plane failure process, a pair of inclined shear bands staring from the shoulder of the pipe instead of springline forms when the peak uplift resistance is mobilized. The slip failure plane mechanism was not fully mobilized at this stage. The vertical inclination of curved shear bands decreases with increasing uplift displacements during postpeak softening. At large displacements, the upward movement is confined to deeper ground,and the slip plane failure progressively changes to the flow-around.

(3) In flow-around failure forms,the failure geometry features a concentrated densification area above the pipe. Reaction from the compacted soil prism comprises the entirety of net force during pipe loading. Corresponding to this failure mechanism, there is no clear degradation on forcedisplacement curves.

(4) The feasibility of FOSS in failure geometry quantification is validated in comparison with image analyses.The inflection point of a fiber optic cable identified by raw data of axial strain measurements represents the shear band location.

The empirical formula for pre-peak mobilization of soil resistance should be universal for pipeline practice since the database has covered a large range of burial depths,pipe diameters,and soil conditions. The uplift mechanism and the data interpretation methodology for strain profile were verified at only two specific burial depths and densities,which is typical for slip plane and flowaround failure. This behavior, such as the post-peak softening and the fiber-soil coupling, may differ from other cases outside this range. This paper provides an innovative insight into evaluating uplift capacity of buried pipelines. Further studies addressing the uncertainty in soil condition and compatibility between the sensing cable and surrounding soil are required for promoting engineering applications of the FOSS technique.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors gratefully acknowledge the financial support provided by the National Natural Science Foundation of China (Grant No.42077235),the Science and Technology Plan Project of Xuzhou,China (Grant No. KC21310), and the Open Fund of the State Key Laboratory for Geomechanics and Deep Underground Engineering(Grant No. SKLGDUEK 1902). The assistance provided by Zheng-Yuan Liu and Chao Wei in the experimental works is also gratefully acknowledged.