北京大學(xué)附屬中學(xué)(100190) 單治超

“更相減損之術(shù)”是中國古代數(shù)學(xué)專著《九章算術(shù)》中提到的用來求兩個正整數(shù)的最大公約數(shù)的算法,是中國古代數(shù)學(xué)的杰出成就.

“更相減損之術(shù)”的正確性可以用現(xiàn)代數(shù)學(xué)的語言表述如下:

定理1 任給兩個正整數(shù)a,b,構(gòu)造一個數(shù)列{an},使得a1=a,a2=b,且對任意正整數(shù)n,an+2=|an+1-an|,那么{an}中一定存在為0 的項,且第一個為0 的項的前一項就是a,b的最大公約數(shù).

2019 年北京市朝陽區(qū)高考一模試題壓軸題就是以此為背景命制的.

證明 假設(shè){an}中所有項非0. 那么對任意正整數(shù)n,一定有an+2＜max{an+1,an},同理

an+3＜max{an+2,an+1}≤max{an+1,an}.所以max{an+3,an+2}＜max{an+1,an}.

設(shè)bn= max{a2n-1,a2n}, 則{bn}是單調(diào)遞減且取正整數(shù)值的數(shù)列. 因此對任意n ∈N*,bn+1≤bn-1, 所以bn≤b1-(n-1).n ＞b1+1 時,bn ＜0,與bn是正整數(shù)矛盾! 所以{an}中存在值為0 的項.

設(shè)m= min{n ∈N+|an= 0}. 由于am-1能整除am,am-1, 所以am-1能整除am-2, 依此下去,am-1能整除a1,a2, 因此am-1能整除a1,a2的最大公約數(shù). 反過來,a1,a2的最大公約數(shù)能整除a1,a2,因此能整除a3,依此下去,也能整除am-1. 因此am-1就是a1,a2的最大公約數(shù).

推論 對于定理1 中的數(shù)列{an},{an}中第一個為0 的項之后,將是0 與a1,a2的最大公約數(shù)交錯出現(xiàn).

下面我們試圖把問題一般化: 任給兩個正整數(shù)a,b,構(gòu)造數(shù)列{an}, 使得a1=a,a2=b, 且對任意正整數(shù)n,an+2=|pan+1-qan|(p,q ∈N+). 易見,p=q=1 時,我們就得到定理1 中的數(shù)列. 一般情形下,數(shù)列{an}會有什么性質(zhì)呢?

定理2 如果p= 1,q= 2,那么以下三種情況有且僅有一個發(fā)生: (1){an}是常數(shù)列;(2){an}中存在唯一項為0,且此項之后是一個非零的常數(shù);(3){an}中不存在最大項.

證明 如果a=b,第(1)種情況發(fā)生.

如果a/=b,且{an}中存在為0 的項. 設(shè)m= min{n ∈N+|an=0}. 易見am+1/=0,且任意n≥m+1,an=am+1.第(2)種情況發(fā)生.

如果a/=b, 且{an}中不存在為0 的項. 假設(shè){an}存在最大值M. 設(shè)m= min{n ∈N+|an=M}. 如果m ＞1,如果am-2am-1＞0,那么am+1=am-2am-1,am+2=|am+1- 2am| =am+ 2am-1＞ am, 矛盾!如果am- 2am-1= 0, 那么am+1= 0, 矛盾! 如果am- 2am-1＜0, 那么am+1=-am+ 2am-1,am+2=|am+1-2am|=3am-2am-1＞am,矛盾!

如果m=1,由a/=b得a2＜a1,所以a3=2a1-a2＞a1. 矛盾!

定理3 如果|q-p|≥2,那么{an}中不存在最大項.

證明 先考慮q≤p-2 的情形:

如果{an}中存在為0 的項,設(shè)m=min{n ∈N+|an=0}, 易見am+1＞0, 從而am+2=pam+1＞am+1, 進而am+3=pam+2-qam+1＞pam+2-qam+2≥am+2,依此下去,對任意n≥m+1,an+1＞an,{an}中不存在最大項.

如果{an}中不存在為0 的項, 那么存在正整數(shù)m,am+1≥am,am+2=pam+1-qam≥pam+1-qam+1＞am+1,依此下去,對任意n≥m+1,an+1＞an,{an}中不存在最大項.

再考慮q≥p+2 的情形:

假設(shè){an}存在最大值M. 顯然M ＞0.

設(shè)m= min{n ∈N+|an=M}, 那么am+2=qam-pam+1≥qam-pam ＞am. 矛盾!

定理4 如果q=p-1,那么以下兩種情況有且僅有一個發(fā)生: (1){an}從某一項起是常數(shù);(2){an}中不存在最大項.

證明 如果第(1)種情況不發(fā)生,當{an}中存在為0 的項時, 證明同定理3 證明中q≤p-2 的第一段; 當{an}中不存在為0 的項時, 把定理3 證明中q≤p-2 的第二段中“存在正整數(shù)m,am+1≥am”加強為“存在正整數(shù)m,am+1＞am”,后續(xù)證明類似.

注 如果a=b,那么{an}是常數(shù)列. 但是a/=b時,第(1)種情況也可能發(fā)生,例如取p= 3,q= 2,a= 2,b= 1,此時數(shù)列是2,1,1,1,...

定理5 (定理2 的一般化)如果q=p+1,那么以下兩種情況有且僅有一個發(fā)生: (1){an}從某一項起為常數(shù);(2){an}中不存在最大項.

證明 假設(shè){an}存在最大值M. 設(shè)m= min{n ∈N+|an=M}. 如果am+1=am, 那么對任意n≥m,an=am, 第(1) 種情況發(fā)生; 如果am+1＜ am, 那么am+2=|pam+1-(p+1)am|=am+p(am-am+1)＞am,矛盾!

定理6 (定理1 的一般化)如果p=q≥4,{an}中不一定存在為0 的項,例如a=1,b=2 時,{an}中就不存在為0的項.

證明 設(shè)a= 1,b= 2. 我們證明an+2-an+1≥2(an+1-an)且an+2≥2an+1,從而立得結(jié)論.

n=1 時顯然兩個不等式成立.

設(shè)n=k(k ∈N+)時兩個不等式成立,那么n=k+1

定理7 (定理1 的一般化)如果p=q=2 或3,{an}中一定存在為0 的項.

證明 如果p=q= 2,利用數(shù)學(xué)歸納法可以證明: 對任意j ∈N,a2j+1,a2j+2都能被2j整除.

假設(shè){an}中不存在為0 的項,對任意i ∈N+,設(shè)ai=c,ai+1=d,分類討論如下表:

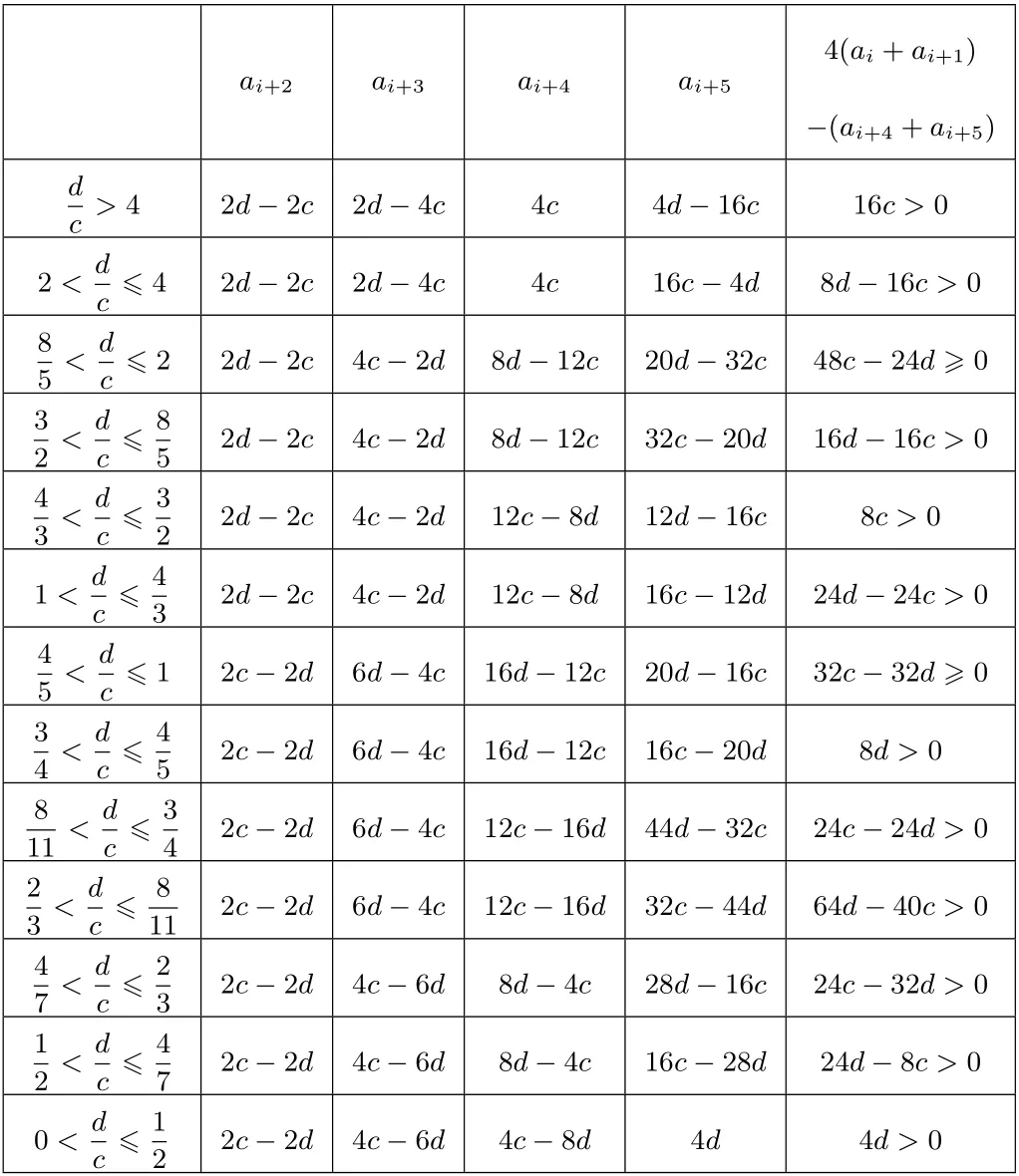
ai+2 ai+3 ai+4 ai+5 4(ai+ai+1)-(ai+4+ai+5)d 2d-2c 2d-4c 4c 4d-16c 16c ＞0 c ＞4 2 ＜d 2d-2c 2d-4c 4c 16c-4d 8d-16c ＞0 c ≤4 8 2d-2c 4c-2d 8d-12c 20d-32c 48c-24d ≥0 5 ＜d c ≤2 3 2d-2c 4c-2d 8d-12c 32c-20d 16d-16c ＞0 2 ＜d c ≤8 5 4 2d-2c 4c-2d 12c-8d 12d-16c 8c ＞0 3 ＜d c ≤3 2 1 ＜d 2d-2c 4c-2d 12c-8d 16c-12d 24d-24c ＞0 c ≤4 3 4 2c-2d 6d-4c 16d-12c 20d-16c 32c-32d ≥0 5 ＜d c ≤1 4 ＜d 3 2c-2d 6d-4c 16d-12c 16c-20d 8d ＞0 c ≤4 5 8 2c-2d 6d-4c 12c-16d 44d-32c 24c-24d ＞0 11 ＜d c ≤3 4 2 2c-2d 6d-4c 12c-16d 32c-44d 64d-40c ＞0 3 ＜d c ≤ 8 11 4 2c-2d 4c-6d 8d-4c 28d-16c 24c-32d ＞0 7 ＜d c ≤2 3 1 2c-2d 4c-6d 8d-4c 16c-28d 24d-8c ＞0 2 ＜d c ≤4 7 0 ＜d c ≤1 2 2c-2d 4c-6d 4c-8d 4d 4d ＞0

從上表可知,當