劉利利 ,張 劍 ,李雅芝 ,楊俊元

(1.山西大學 復雜系統(tǒng)研究所,山西太原 030006;2.黔南民族師范學院 數學與統(tǒng)計學院,貴州都勻 558000)

§1 引言

傳染病長期以來威脅著人類健康,給社會造成沉重的經濟負擔.結核病是由結核分枝桿菌感染引起的一種呼吸道傳染病,是全球十大死因之一,也是單一感染源的主要死因.世界衛(wèi)生組織發(fā)布的2020 年度《全球結核病報告》顯示,2019年我國約有83.3萬人新發(fā)現(xiàn)結核病,其中3.3萬人死亡[1].我國結核病防控形勢依舊嚴峻.

借助傳染病動力學的理論和方法對結核病進行定性和定量研究,揭示其發(fā)展和傳播機制,從而為人們制定防控策略提供理論依據[2-4],這是傳染病理論研究的一個重要內容.近年來,已有學者將最優(yōu)控制理論用于分析結核病的傳播問題.最優(yōu)控制理論是數學的成熟分支之一,廣泛應用于工程和其他科學分支.該理論研究結核病傳播問題的工作比較少,文獻[5]首次利用優(yōu)化控制分析結核病的傳播,建立了一類具有兩菌株的結核病模型,以潛伏和感染者的人數最少和治療成本最低作為目標,設計最優(yōu)治療的控制策略.自此以后,有學者開始關注結核病優(yōu)化控制模型的研究,如: 文獻[6]考慮了具有外源感染和快慢進程的結核病模型,以對潛伏感染者進行治療為優(yōu)化策略,從而降低基本再生數.文獻[7]考慮了具有重復感染和外源感染的結核病控制模型,設計了兩種優(yōu)化控制策略.上述工作均是基于龐特里亞金極大值原理分析最優(yōu)控制存在的必要條件,所研究的模型是均勻混合的常微分結核病模型.

年齡是傳染病傳播過程中不可忽視的因素,很多學者已經研究了年齡結構的傳染病模型的閾值動力學行為[8-11].由于年齡結構的傳染病模型是偏微分方程和常微分方程的耦合系統(tǒng),狀態(tài)空間是 無窮維空間,不具有緊性,傳統(tǒng)的龐特里亞金極大值原理不再適用于該問題,因此研究其最優(yōu)控制問題的難度較大,很難找到收斂到優(yōu)化集和優(yōu)化狀態(tài)的序列.近年來,已有學者對年齡結構傳染病模型進行優(yōu)化控制研究.郭中凱等在文獻[12]中研究了年齡結構SIR傳染病模型的最優(yōu)接種和治療問題,Yang等在文獻[13]中研究了具有多傳播途徑的年齡結構霍亂模型的穩(wěn)定性和最優(yōu)控制問題.Cao等在文獻[9]中研究了潛伏者具有年齡結構和康復者具有復發(fā)的結核病模型,建立模型

其中S(t),E(t,a),I(t),R(t)分別表示易感者,潛伏者,感染者和康復者在時刻t的數量,初始條件S0,I0,R0∈R+,且E0(a)∈L1((0,∞),R+).易感者的輸入率為Λ,傳染率為β,自然死亡率為μ,感染者因病死亡率為δ,α(a) 表示依賴年齡的潛伏者到感染者的轉化率,γ表示潛伏者到康復者的轉化率,感染者的治愈率為θ,康復者的復發(fā)率為k.文獻[9]主要研究了模型解的適定性,無病平衡態(tài)和正平衡態(tài)的局部穩(wěn)定性和無病平衡態(tài)的全局穩(wěn)定性.

本文將進一步考慮模型(1)的最優(yōu)控制問題,從感染者和康復者出發(fā),研究結核病的藥物治療和康復者復發(fā)的最優(yōu)控制策略.

§2 結核病優(yōu)化控制模型

基于上面的分析,考慮感染者的藥物治療和康復者復發(fā),本文建立如下潛伏者具有年齡結構的結核病優(yōu)化控制模型

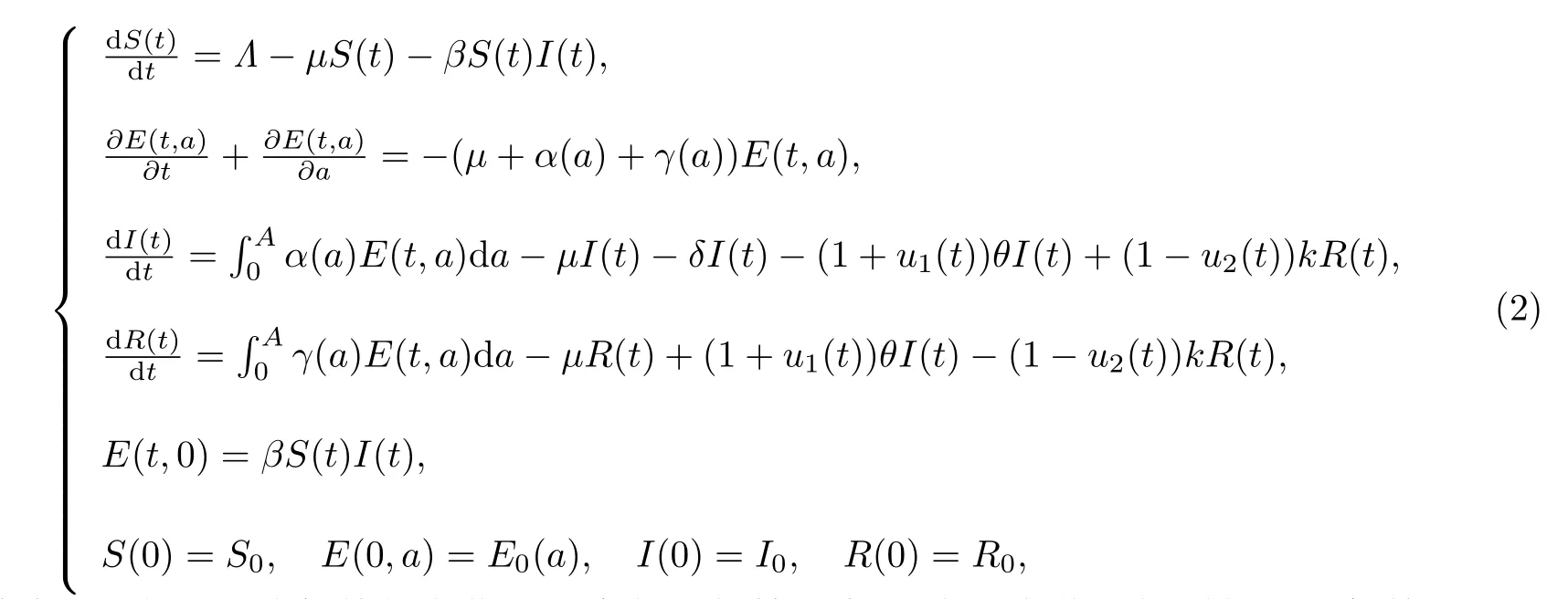
其中γ(a)表示依賴年齡的潛伏者到康復者的轉化率,A表示潛伏者控制的終止年齡,u1(t),u2(t)是Lebesgue可積函數,代表優(yōu)化控制變量.其他參數的生物意義與模型(1)相同.應用文獻[9]中模型適定性分析過程,可以得到模型(2)的適定性.即

引理2.1當t ＞0時,系統(tǒng)(2)的所有解都是非負且有界的.

§3 控制策略

本節(jié)將利用Gateaux導數和Ekeland變分原理分析結核病模型的最優(yōu)控制問題.

控制變量記為U(t)=(u1(t),u2(t)),定義控制集為

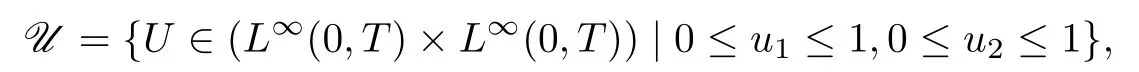
其中T代表控制的終止時刻.定義目標函數

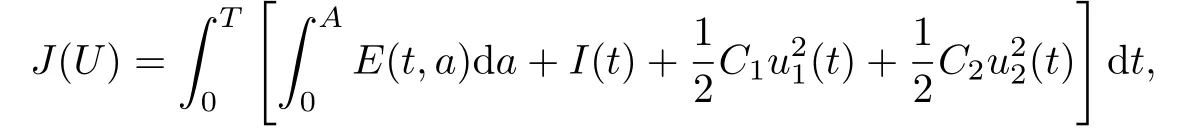
其中C1與C2是權重系數,表示控制所投入的成本,這里假設采取措施消耗的費用為非線性二次函數.控制目標是找到最優(yōu)控制U*使得J(U*)最小,即潛伏者和染病者數目最少且控制投入成本最低.

3.1 最優(yōu)控制的存在性

通過如下定理證明最優(yōu)控制的存在性.

定理3.1存在最優(yōu)控制使得J(U*)=minU∈U J(U).

證顯然控制集U非空且是閉凸的.令X=(S(t),E(t,a),I(t),R(t))T.假設

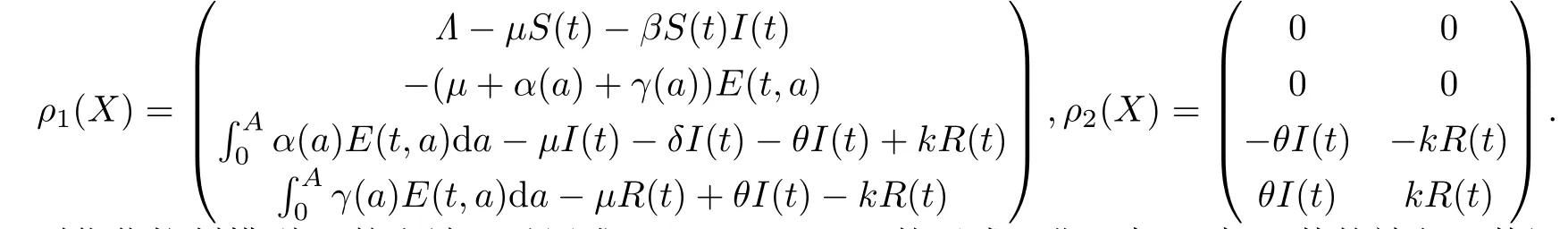
則優(yōu)化控制模型(2)的右端可以寫成ρ1(X)+ρ2(X)U的形式.進一步,目標函數的被積函數記為. 顯然,L(X,U)在控制集U上關于U(t)是凸的.根據文獻[14]中定理4.1可以得到最優(yōu)控制U*的存在性.

3.2 伴隨系統(tǒng)

Gateaux導數是求解系統(tǒng)(2)伴隨系統(tǒng)的一個重要方法.令l(t)=(l1(t),l2(t))是控制集U在U處的切錐,l1(t),l2(t)∈(0,1).對于充分小的常數ξ ＞0,定義輔助控制變量Uξ=由于狀態(tài)變量關于控制變量是連續(xù)依賴的,則有(S,E,I,R)=(S,E,I,R)(u1,u2)和.因此,系統(tǒng)(2)可以改寫成如下形式

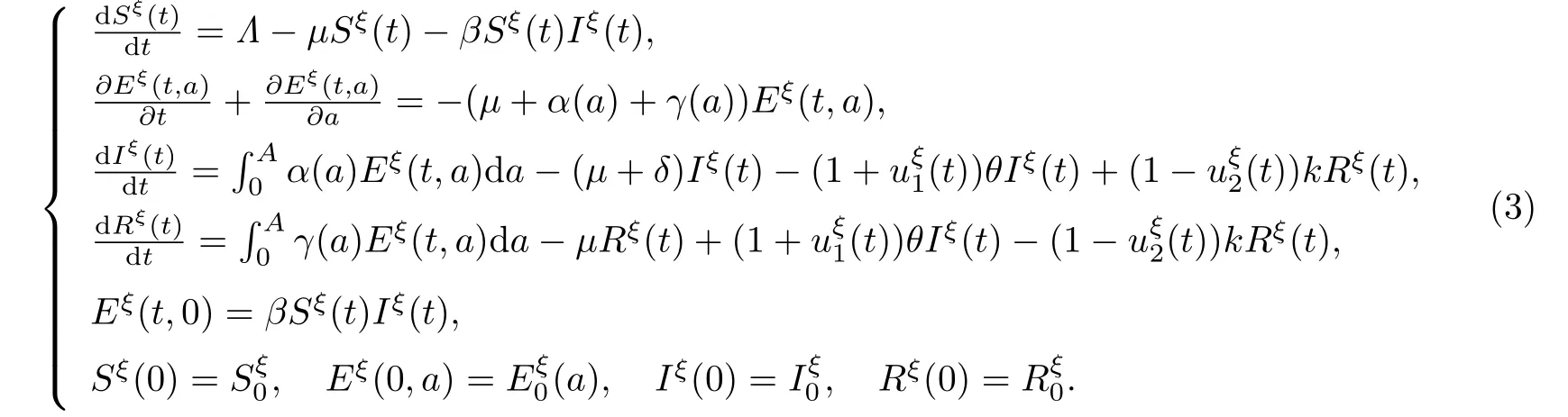
當ξ →0+時,可以得到狀態(tài)變量的弱導數是

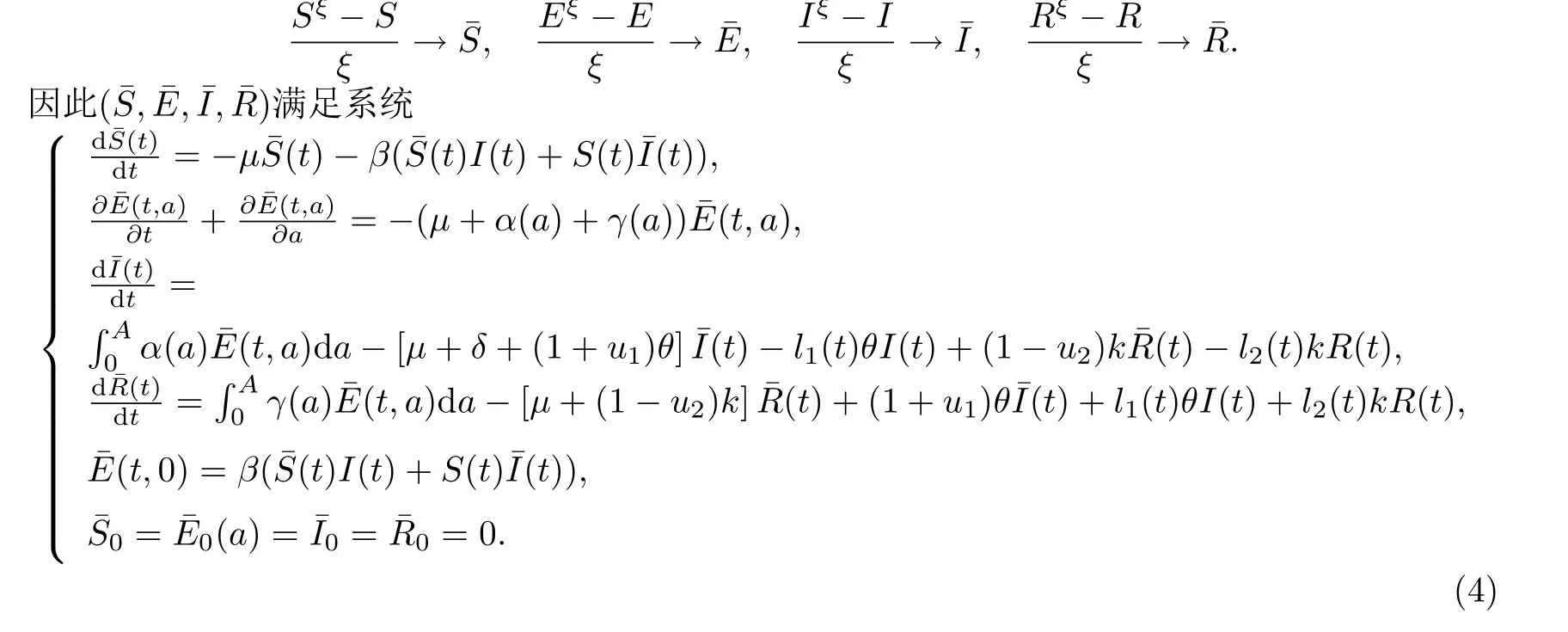
為求系統(tǒng)(2)的伴隨系統(tǒng),引入與系統(tǒng)(2)相對應的伴隨變量λS(t),λE(t,a),λI(t) 和λR(t).利用條件,λS(T)=0和分部積分法,對系統(tǒng)(4)的第一個方程進行運算得到

目標函數J(U)關于控制變量U的Gateaux導數為

結合等式(5)-(9),可以得到系統(tǒng)(2)的伴隨系統(tǒng)

進一步,系統(tǒng)(10)存在一個弱解,記為

且此弱解Lipschitz連續(xù).

3.3 最優(yōu)控制的形式

現(xiàn)在給出最優(yōu)控制的具體形式.

定理3.2若存在U* ∈(L∞(0,T))2使得J(U) 取得最小值,那么

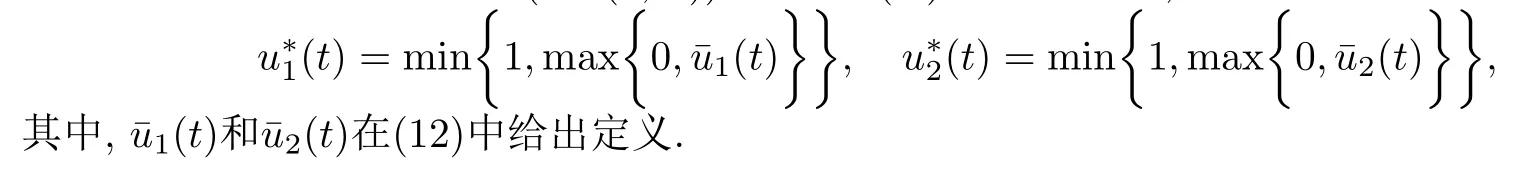
證將系統(tǒng)(10)代入方程(9)中,可以得到

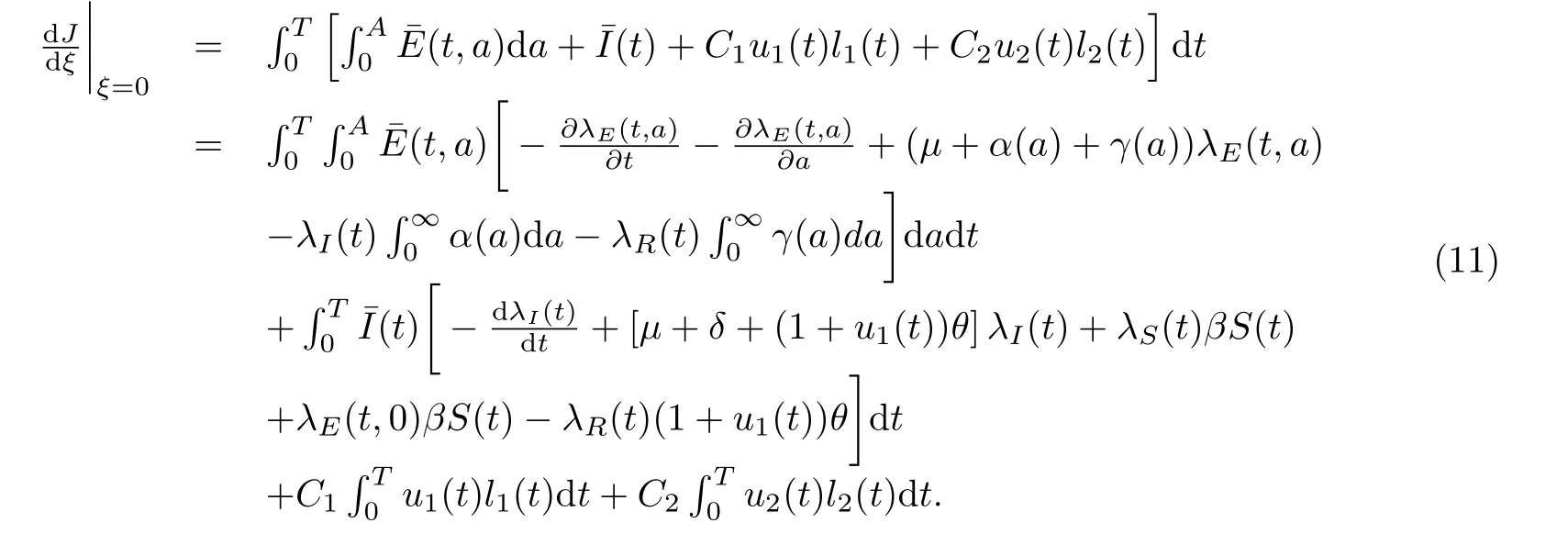
將方程(5)-(8)帶入方程(11),則對于所有U ∈U,有

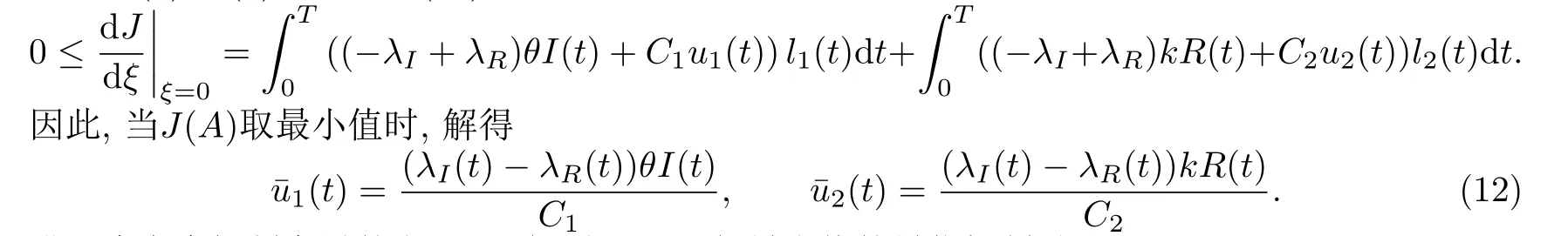
進一步考慮控制變量的上下界,得到J(A)取得最小值的最優(yōu)控制是

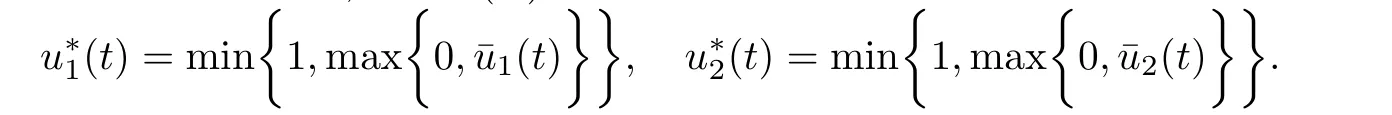
3.4 最優(yōu)控制的存在唯一性

年齡結構的傳染病模型是一階偏微分方程,由于其狀態(tài)空間不具有緊性,故很難找到收斂到優(yōu)化集和優(yōu)化狀態(tài)的序列.為了克服該困難,本文采用Ekeland變分原理[15]尋找近似函數的最小值.定義下面的輔助目標函數

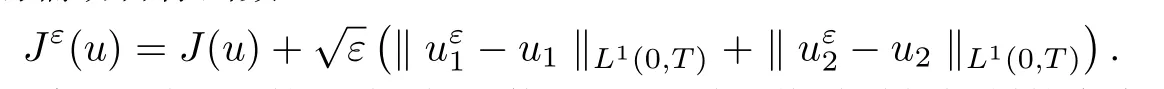
采用[16]的理論方法和文獻[13]的思路,得到使Jε(u)取最小值時最優(yōu)控制的存在唯一性,即有下面的定理

定理3.3若Jε(u) 存在最優(yōu)控制使其取得最小值,那么

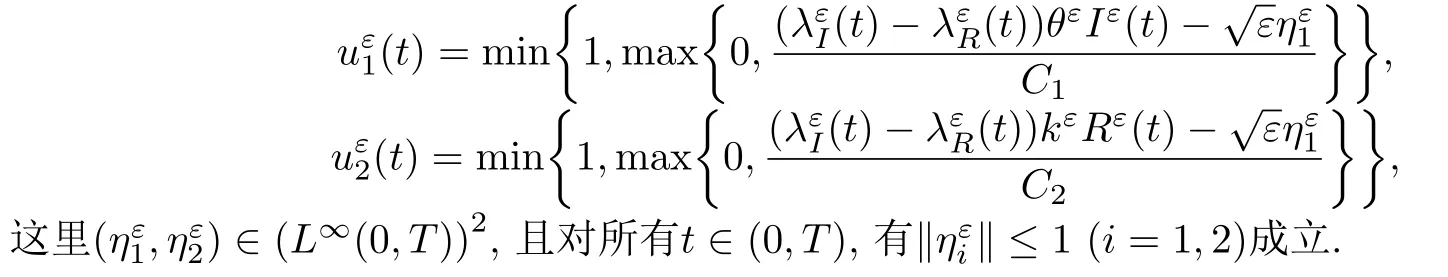
由Ekeland變分原理及L∞空間上的Lipschitz估計,得到最優(yōu)控制的存在唯一性.

定理3.4若T/C1和T/C2足夠小,那么存在唯一的最優(yōu)控制使J(U) 取到最小值.

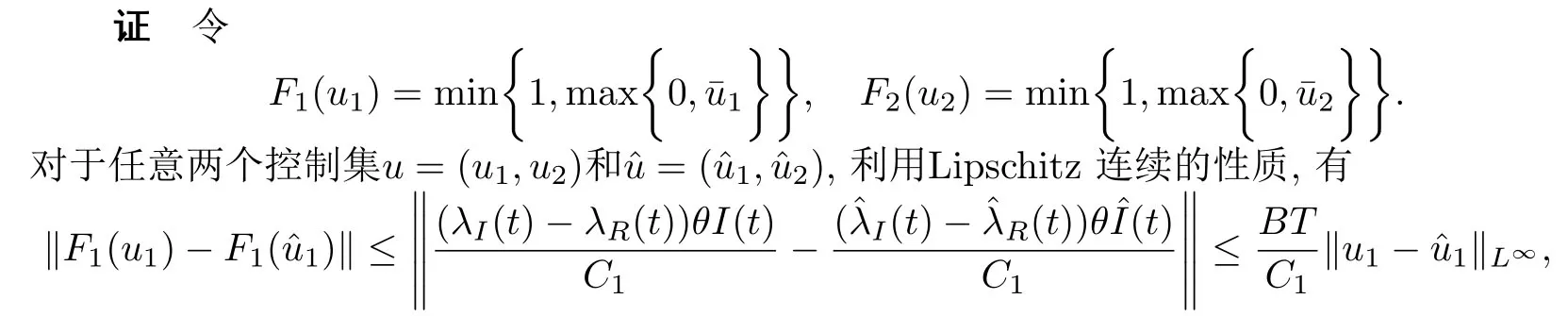
其中B是常數,取決于狀態(tài)方程與伴隨方程的解以及Lispschitz常數.類似可得

如果T/C1足夠小,那么

從而當ε →0+時,.由Ekeland變分原理,則有當ε →0+時,J(U*)≤infU∈U J(U).

§4 數值實驗

在本節(jié)中,主要對最優(yōu)控制進行數值模擬以論證優(yōu)化控制策略的合理性.為此使用差分法結合伴隨系統(tǒng)和狀態(tài)系統(tǒng)進行數值模擬.為了進行最佳狀態(tài)下的數值模擬,采取較小的時間和年齡步長,即Δt=Δa=0.05,并假設最大年齡為60,對患者進行365天的優(yōu)化控制.模型的初始值為S(0)=9800,I(0)=10,T(0)=100,E(0,a)=320 cos2(0.46a),權重系數C1=C2=10.最后,根據文獻[9],定義了部分參數,如表1所示

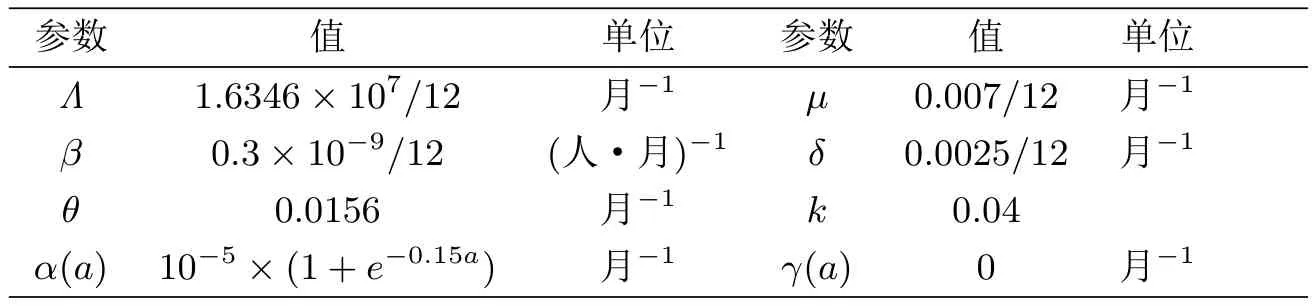
表1 數值模擬中的參數

圖1表示最優(yōu)控制率(u1與u2)隨時間變化的曲線圖.由圖1可以觀察到在結核病的優(yōu)化控制中,復發(fā)率的優(yōu)化控制在短時間(實施控制的第100天左右)由控制的下界達到控制的上界,而治愈率的優(yōu)化控制以較慢的速度(實施控制的第135 天左右)才達到控制的上界.

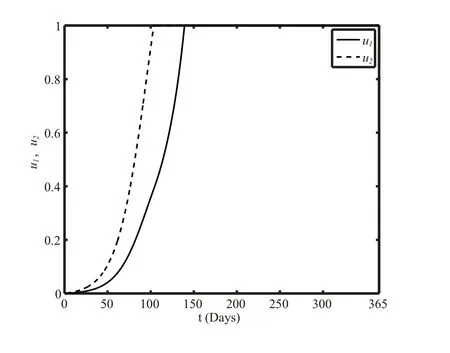
圖1 最優(yōu)控制率隨時間的變化

圖2表示最優(yōu)控制策略對結核病感染人數的影響.為此,設計了四種不同的最優(yōu)控制情形.在情形1(沒有任何控制措施,即u1=u2=0),第60天左右結核病感染人數達到最大值,感染人數持續(xù)在高感染水平并且是緩慢下降;在情形2(只有最優(yōu)治愈控制措施,即u10,u2=0),第50天左右結核病感染人數達到最大值,染病人數開始持續(xù)下降到第100天,染病人數下降的趨勢則變得很慢;在情形3(只有最優(yōu)復發(fā)控制措施,即u1=0,u20),第45天左右結核病感染人數達到最大值,染病人數開始迅速下降到第200天左右染病人數開始在低感染狀態(tài)緩慢下降;在情形4(最優(yōu)綜合控制措施,即u10,u20),第40天左右結核病感染人數達到最大值,染病人數迅速下降,并且很快(第190天左右)達到無感染的穩(wěn)定狀態(tài).類似分析可以得到不同最優(yōu)控制策略對結核病復發(fā)人數的影響.對比情形2和情形3,可以知道只有最優(yōu)復發(fā)控制(u2)比只有最優(yōu)治療控制(u1)的控制效果好,這說明了在實際防控結核病傳播的時候,控制復發(fā)率更為重要.對比情形3和情形4,可以知道最優(yōu)綜合控制策略的效果最好.

圖2 不同最優(yōu)控制策略對感染人數和康復人數的影響

為了研究控制成本對結核病感染人數的影響.分析了3種不同控制成本的情形,如圖3所示.情形1表示低成本(C1=C2=1)時,感染者與康復者的變化.在10天左右,結核病感染人數達到最大值并迅速下降,并在120天左右處于低感染狀態(tài)并緩慢下降.情況2表示成本適中(C1=C2=10)的情況下,染病人數在50天左右達到峰值,并迅速下降至200天左右趨于穩(wěn)定狀態(tài).在情況3中,可以看出,在高成本(C1=C2=100)的情況下,感染者迅速上升,在80天左右達到最大人數,在300天左右才達到相對穩(wěn)定的低感染狀態(tài).對比三種情況可以看出,不同的成本對最優(yōu)控制存在影響,由于經濟狀況的限制,在投入相同的情況下,成本越低,控制所達到的效果越好.

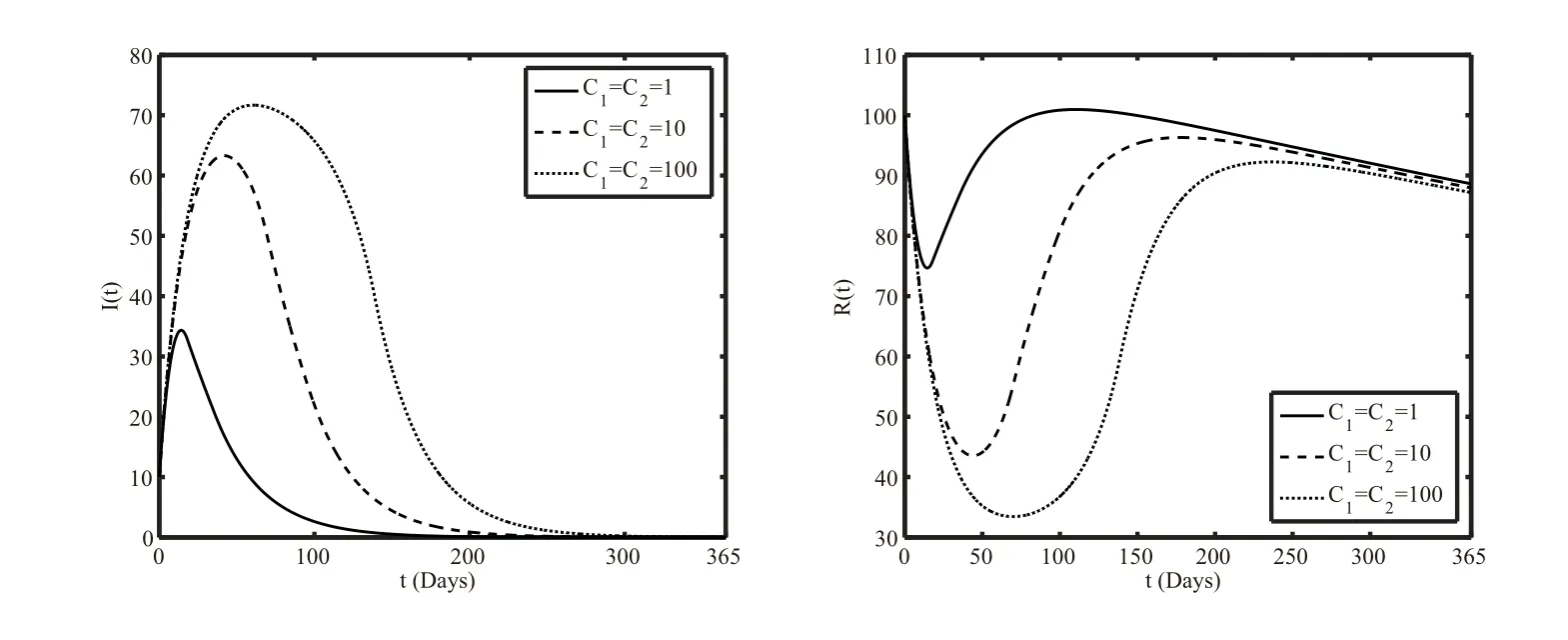
圖3 不同成本下I(t)(左)與R(t)(右)的變化.(1) 低成本: C1=C2=1;(2) 中成本: C1=C2=10;(3)高成本: C1=C2=100

§5 結論

本文研究了潛伏者具有年齡結構的結核病模型考慮治療和復發(fā)的最優(yōu)控制模型.通過建立目標泛函,利用Gateaux導數及Ekeland變分原理分別確定了最優(yōu)控制的具體表達式和存在唯一性;最后結合數值模擬對比分析不同優(yōu)化控制和控制成本對結核病感染人數和康復人數的影響;結果發(fā)現(xiàn): 幾種最優(yōu)控制的效果,最優(yōu)綜合控制最好,最優(yōu)復發(fā)控制次之,并且控制成本越低,效果越好.