周海林

(南京理工大學(xué) 泰州科技學(xué)院,江蘇泰州 225300)

§1 引言

約束矩陣方程的最小二乘問(wèn)題是指矩陣方程的最小二乘解需要滿(mǎn)足某一約束條件.不同的約束條件或不同的矩陣方程,就得到不同的約束矩陣方程的最小二乘問(wèn)題.

約束矩陣方程的求解具有重要的理論意義和很高的應(yīng)用價(jià)值.來(lái)源于系統(tǒng)與控制理論中提出的矩陣方程AXB+CXD=F,在特征結(jié)構(gòu)配置[1],觀測(cè)器設(shè)計(jì)[2]和帶有輸入約束的系統(tǒng)控制[3]等方面起著重要的作用,也受到矩陣論和數(shù)值分析學(xué)者的關(guān)注,取得了一些成果[4-11].這些文獻(xiàn)主要應(yīng)用廣義逆,奇異值分解和廣義奇異值分解,得到了矩陣方程的解的充要條件及解析表達(dá)式.

迭代法是求解約束矩陣方程的另外一種方法,盡管它不能給出通解表達(dá)式,但在不考慮舍入誤差的情況下,能通過(guò)有限步迭代得到滿(mǎn)足給定約束條件的解.應(yīng)用共軛梯度法,文[12-14]構(gòu)造迭代算法分別求解了矩陣方程AXB+CXD=F的一般解,對(duì)稱(chēng)解和在任意線(xiàn)性子空間約束下的解.文[15-17]研究了Hermitian解和極小范數(shù)最小二乘Hermitian解.更多求解矩陣方程AXB+CXD=F的迭代算法可參考文獻(xiàn)[18-28].

記Rm×n表示m×n實(shí)矩陣集合,AT表示A的轉(zhuǎn)置矩陣.對(duì)任意的矩陣A,B∈Rm×n,定義矩陣內(nèi)積〈A,B〉=tr(BTA),則由它誘導(dǎo)的范數(shù)為Frobenius范數(shù),即

本文主要考慮下面兩個(gè)問(wèn)題.

問(wèn)題I給定矩陣A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任意線(xiàn)性子空間R ?Rs×t,求X*∈R,使得

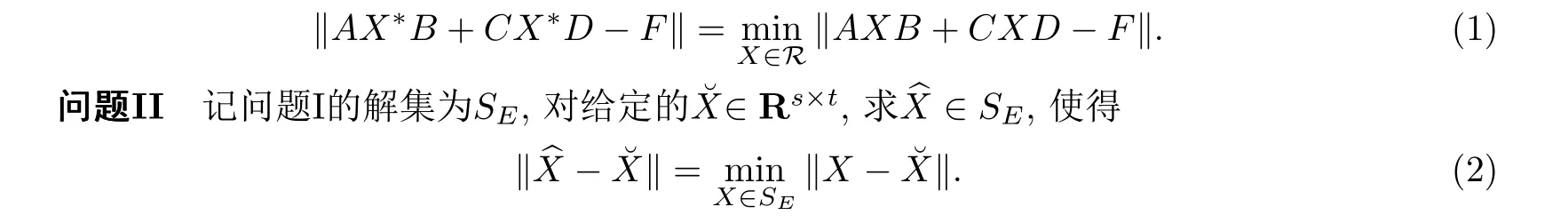
相應(yīng)地,問(wèn)題I和問(wèn)題II的解稱(chēng)為矩陣方程AXB+CXD=F滿(mǎn)足線(xiàn)性子空間R約束條件下的最小二乘解和最佳逼近解.本文應(yīng)用共軛梯度法,結(jié)合線(xiàn)性投影算子,將負(fù)梯度到所求線(xiàn)性子空間上的投影矩陣作為迭代過(guò)程中下一步的更新矩陣,給出迭代算法,求解了矩陣方程AXB+CXD=F在任意線(xiàn)性子空間上的最小二乘解及其最佳逼近.

本文以下內(nèi)容安排如下:§2構(gòu)造迭代算法求解了問(wèn)題I ;§3應(yīng)用問(wèn)題I的算法進(jìn)一步求解了問(wèn)題II;§4給出兩個(gè)數(shù)值例子證實(shí)了算法的有效性;§5對(duì)全文進(jìn)行了小結(jié).

§2 迭代求解問(wèn)題I

定義2.1對(duì)矩陣M,N ∈Rm×n,若〈M,N〉=0,則稱(chēng)矩陣M,N相互正交.

對(duì)任意的線(xiàn)性子空間R ?Rs×t,其正交補(bǔ)空間R⊥是存在唯一的,且有Rs×t=R ⊕R⊥.在Rs×t上定義線(xiàn)性投影算子FR:Rs×t -→R.

顯然,對(duì)任意的X∈Rs×t和任意的S∈R,有〈X,S〉=〈FR(X)+FR⊥(X),S〉=〈FR(X),S〉成立.

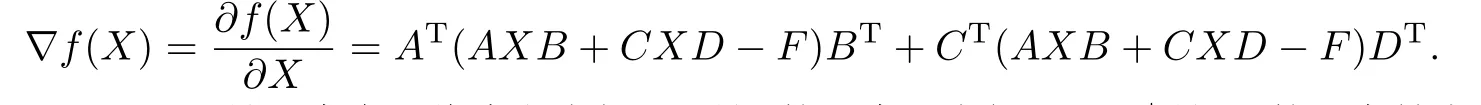
引理2.1設(shè)S是一個(gè)有限維內(nèi)積空間,M是S的一個(gè)子空間,且M⊥是M的正交補(bǔ)空間.則對(duì)于任意給定的向量s ∈S,必存在著唯一的向量m0∈M,使得

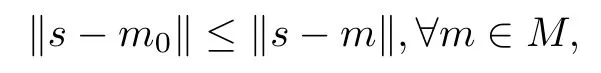
其中‖·‖是內(nèi)積空間S所定義的范數(shù),并且m0∈M是唯一的極小化向量的充要條件是(sm0)⊥M,即(s-m0)∈M⊥.

引理2.2設(shè)線(xiàn)性子空間R ?Rs×t,FR是從Rs×t到R的線(xiàn)性投影算子,記R*=F -(AX*B+CX*D),則X*是矩陣方程AXB+CXD=F在線(xiàn)性子空間R上的最小二乘解的充要條件是FR(?f(X*))=0.

證定義集合

顯然,L為線(xiàn)性子空間.假設(shè)矩陣X*∈R,記F*=AX*B+CX*D,則F* ∈L.由引理2.1知,X*是矩陣方程AXB+CXD=F的最小二乘解,當(dāng)且僅當(dāng)

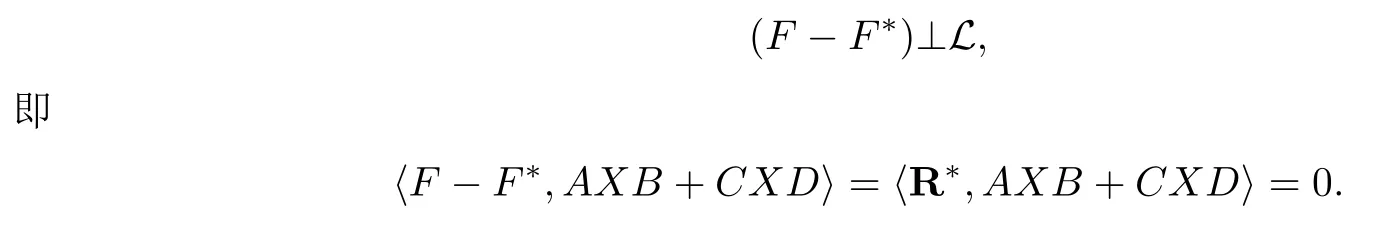
另外對(duì)任意的X ∈R有

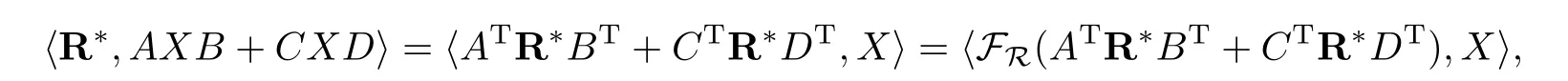
從而FR(ATR*BT+CTR*DT)=0,即有FR(?f(X*))=0,故引理得證.

應(yīng)用共軛梯度法,結(jié)合線(xiàn)性投影算子,本文構(gòu)造如下迭代算法.

算法I

輸入矩陣A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任取初始矩陣X0∈R.

(1) 計(jì)算

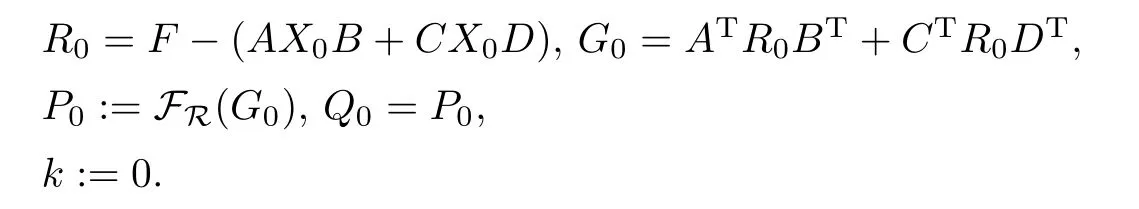
(2) 如果Pk=0,停止;否則進(jìn)行下一步.

(3) 計(jì)算

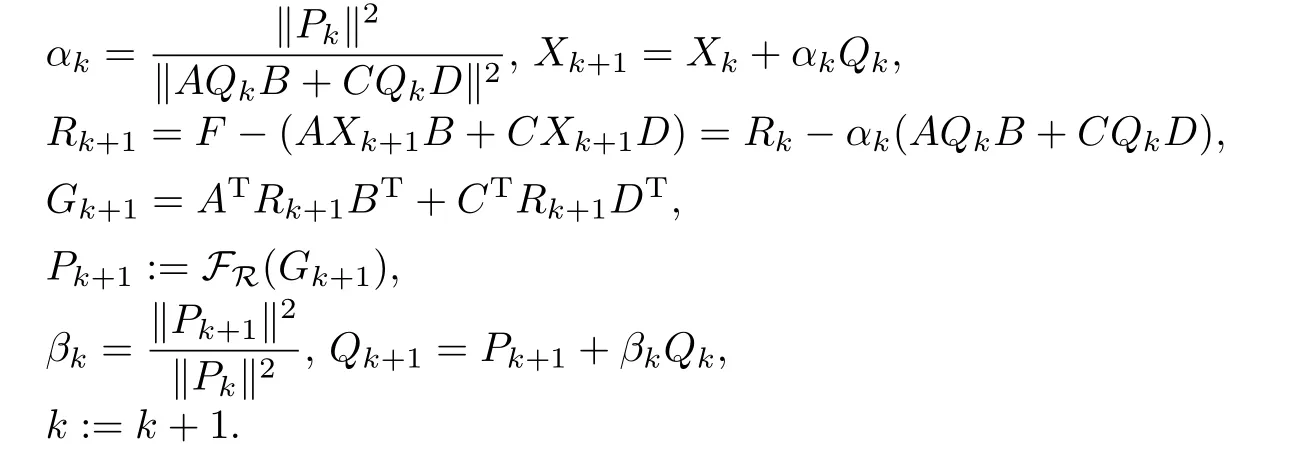
(4) 轉(zhuǎn)回到(2).

顯然,Pi=FR(ATRiBT+CTRiDT)=FR(-?f(X)|X=Xi)∈R,Qi ∈R,Xi ∈R,i=0,1,2,3,···.

此外在步驟(3)中

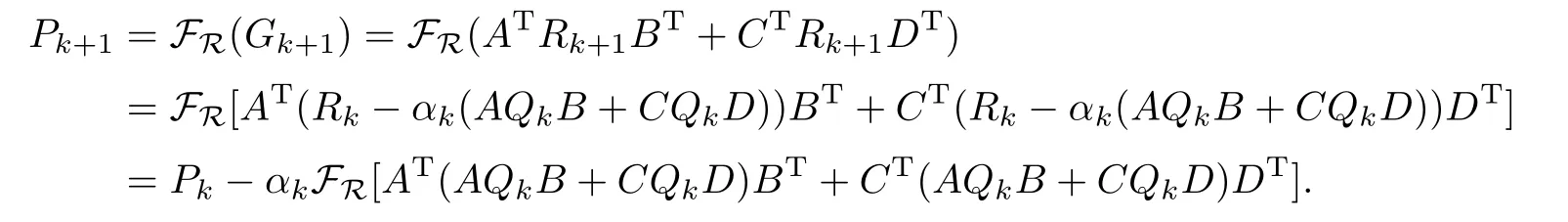
引理2.3若算法I在第k步迭代尚未停止,則迭代過(guò)程中產(chǎn)生的Pi,Pj,Qi,Qj,(i,j=0,1,21),有

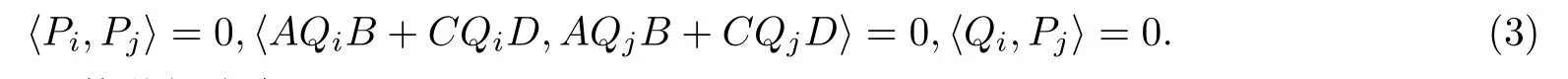
證用數(shù)學(xué)歸納法證明.

由于對(duì)任意矩陣M,N∈Rm×n,有〈M,N〉=〈N,M〉,故只需證明0≤i ＜j ≤k時(shí)結(jié)論成立即可.

首先注意到

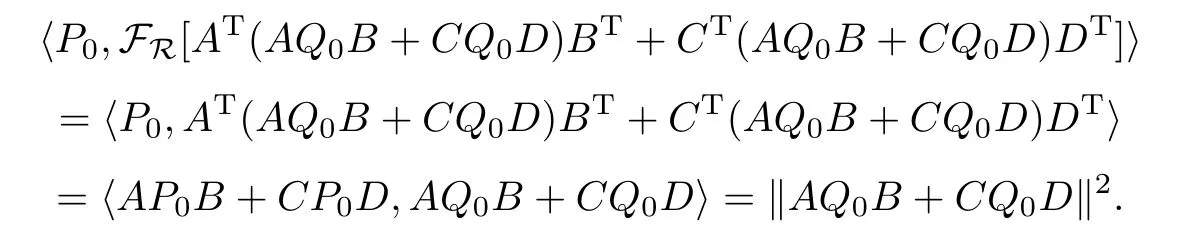
對(duì)t=1,由算法I有

設(shè)(3)式對(duì)t=s(1≤s ≤k-1)成立,即

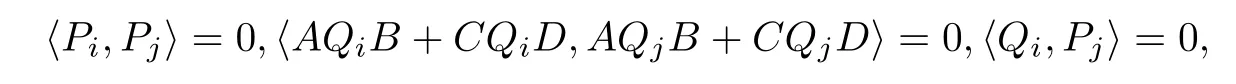
i,j=0,1,21,則當(dāng)t=s+1時(shí),由算法I,與(4)式相類(lèi)似的證明有

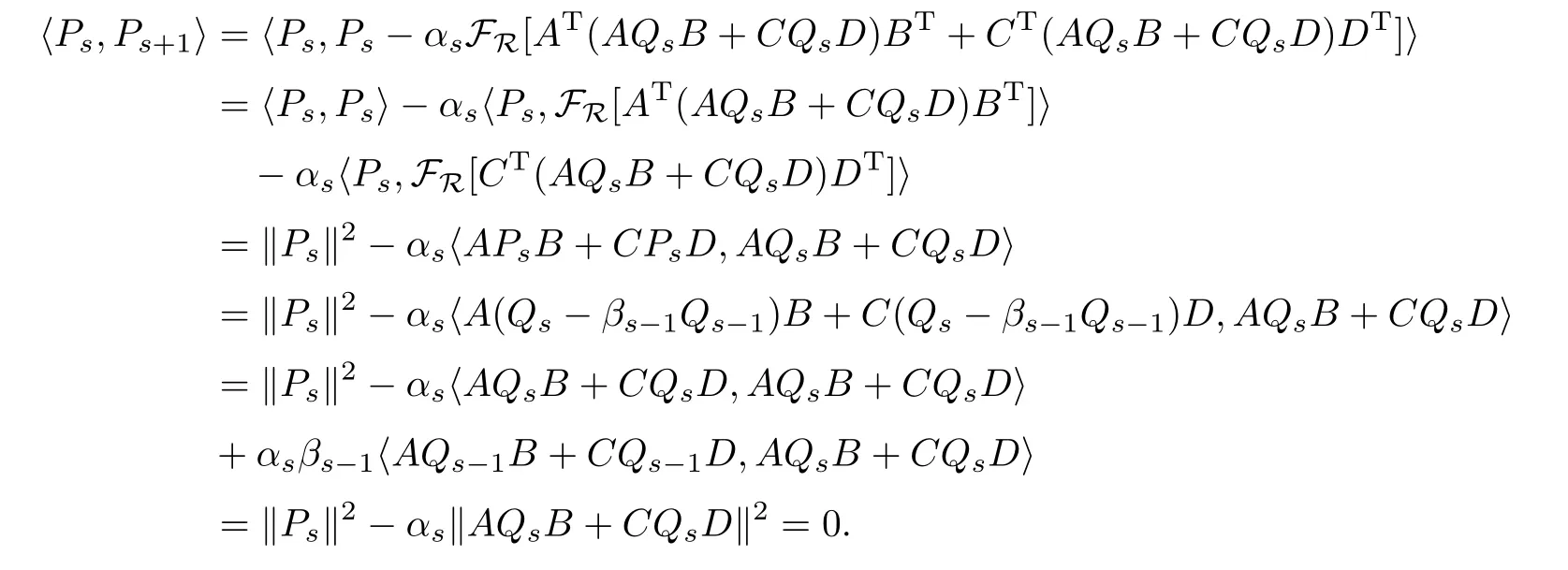
由算法I,與(5)式相類(lèi)似的證明可得到

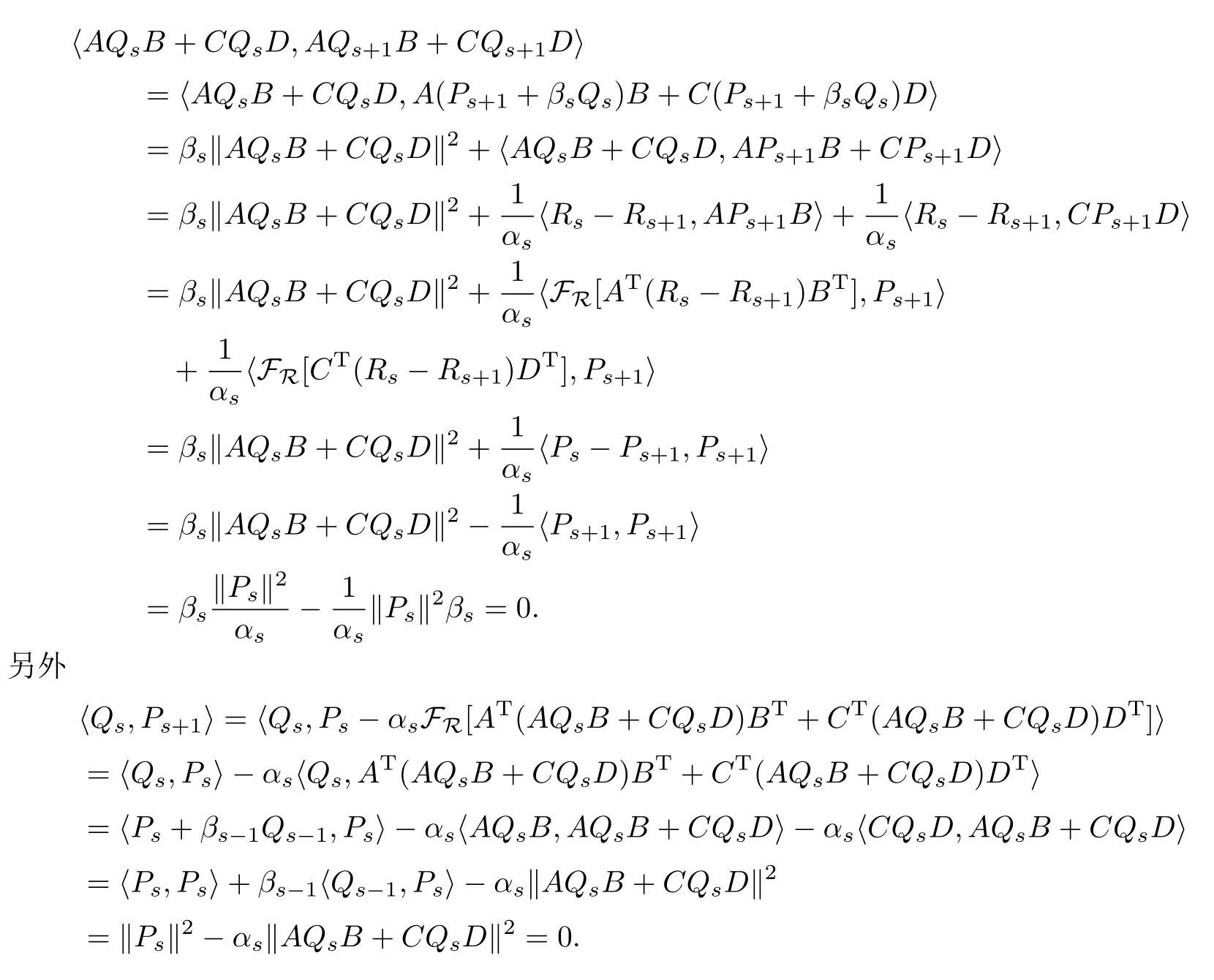
對(duì)i=1,2,3,···,s-1,注意到

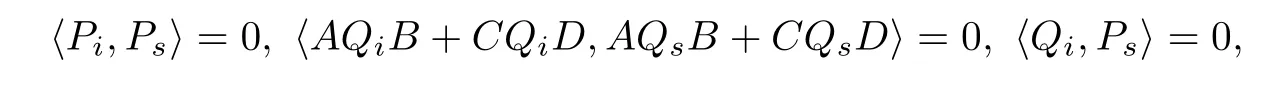
由算法I得到

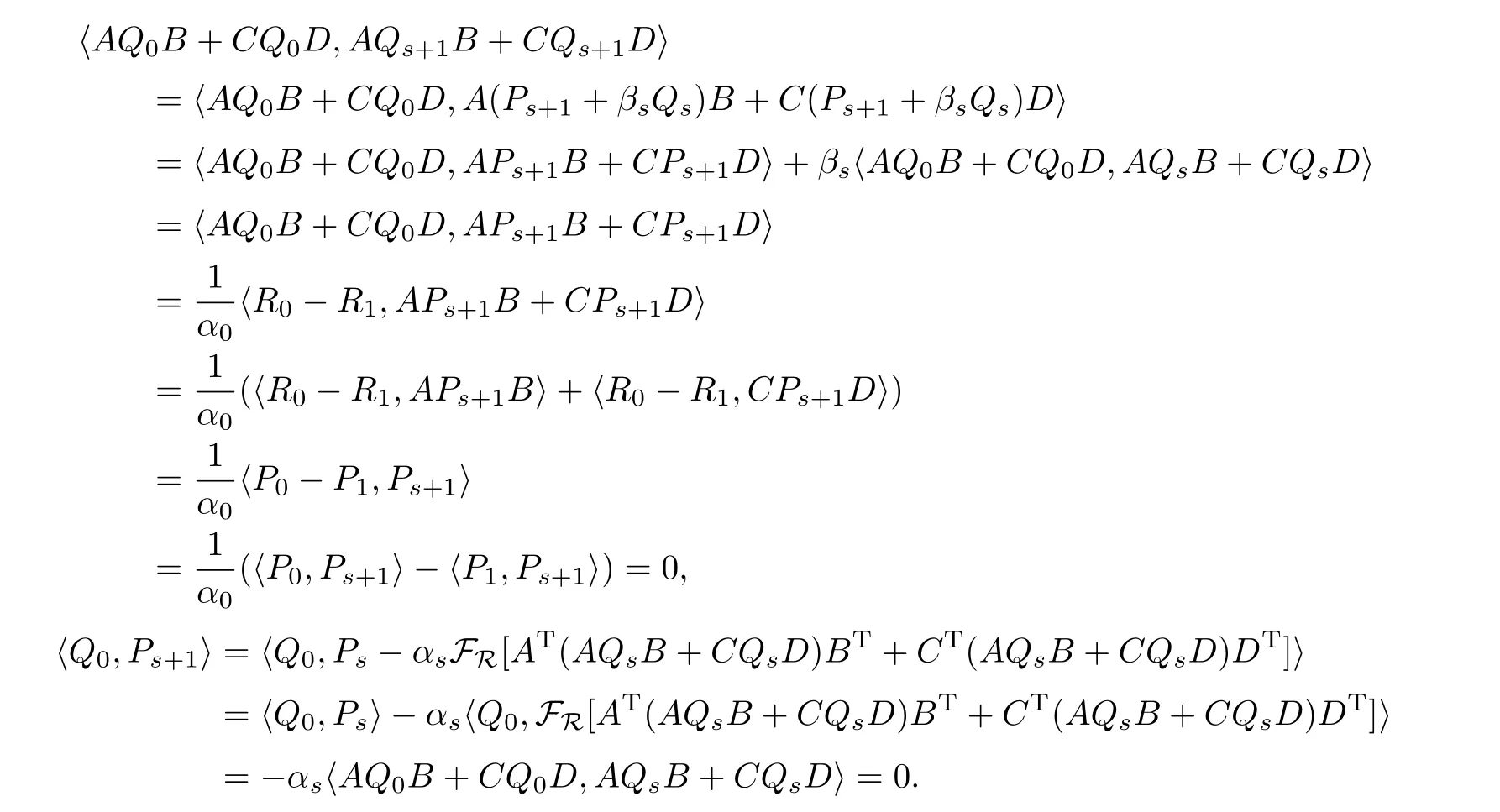
因此對(duì)t=s+1(3)式成立.

由數(shù)學(xué)歸納法知,引理2.3得到了證明.

注引理2.3中,若算法I在第k步迭代尚未停止,則意味著當(dāng)i=0,1,2,···,k時(shí),有Pi0,從而αi0且AQiB+CQiD0.下面予以說(shuō)明.

若AQiB+CQiD=0,則

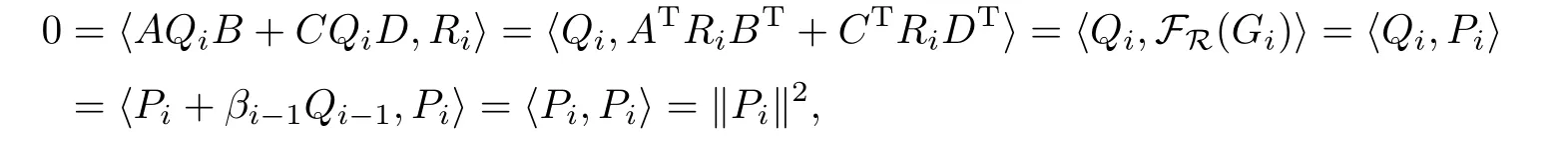
從而有Pi=0,故AQiB+CQiD0.

引理2.3表明,由算法I產(chǎn)生的矩陣序列P0,P1,P2···在矩陣空間R上是相互正交的,從而必定存在一個(gè)正整數(shù)r ≤st,使得Pr=0,從而得到下面的定理.

定理2.1在不考慮舍入誤差的情況下,對(duì)任意給定的初始矩陣X0∈R,算法I可在有限步內(nèi)計(jì)算出問(wèn)題I的解.

引 理2.4若是問(wèn)題I的解,則問(wèn)題I的任意解均可表示為,其中X∈R且滿(mǎn)足AXB+CXD=0.

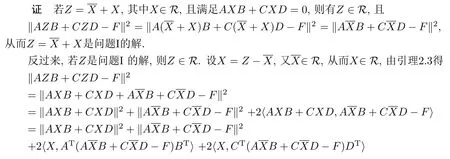
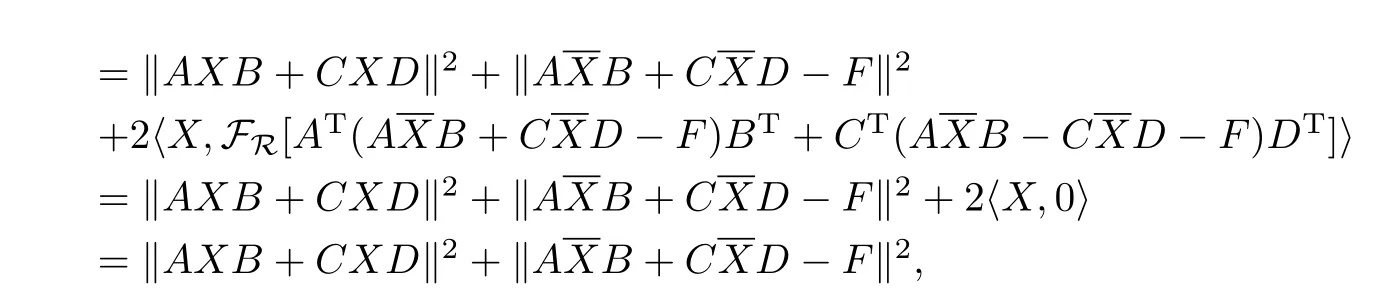
從而‖AXB+CXD‖2=0,即AXB+CXD=0.

定理2.2若取初始迭代矩陣X0∈FR(ATHBT+CTHDT),其中H是Rm×n中的任意矩陣,或者特別地,令X0=0s×t,則由算法I,通過(guò)有限步迭代可以得到問(wèn)題I唯一的極小范數(shù)解.

證定義集合

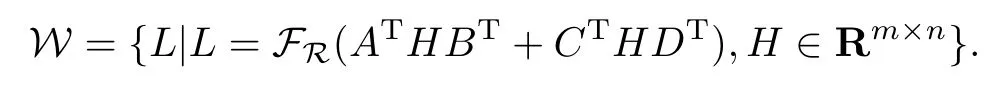
顯然W為線(xiàn)性子空間.若令初始迭代矩陣X0∈W,則由算法I得到的迭代更新矩陣Xk∈W.(k=1,2,···) 由算法I和定理2.1知,經(jīng)有限步迭代可得到問(wèn)題I的解X*,且X*∈W.即存在H*∈Rm×n,使得X*=FR(ATH*BT+CTH*DT).

由引理2.4知,問(wèn)題I的任意解可以表示為X*+X,其中X∈R,且滿(mǎn)足AXB+CXD=0.又

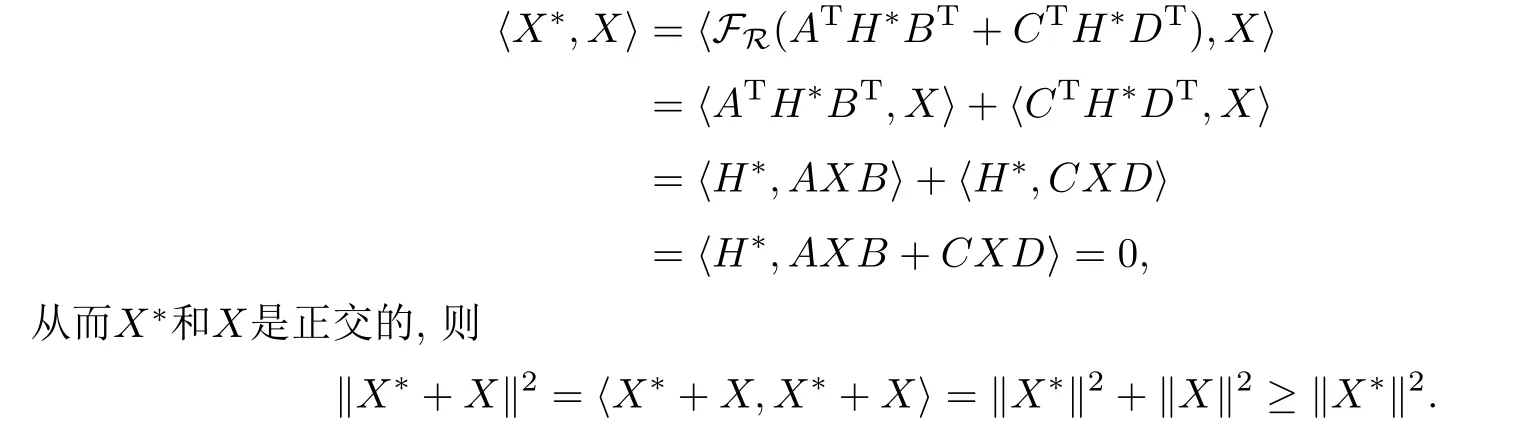
故X*為問(wèn)題I的極小范數(shù)解.不難驗(yàn)證問(wèn)題I的解集SE為非空閉凸集,其極小范數(shù)解存在且是唯一的.所以X*也是問(wèn)題I的唯一極小范數(shù)解.

§3 問(wèn)題II的解

因?yàn)閱?wèn)題I的解集SE是非空閉凸集,故問(wèn)題II的解存在且唯一.對(duì)問(wèn)題II中給定的∈Rs×t,由于X∈R,因此

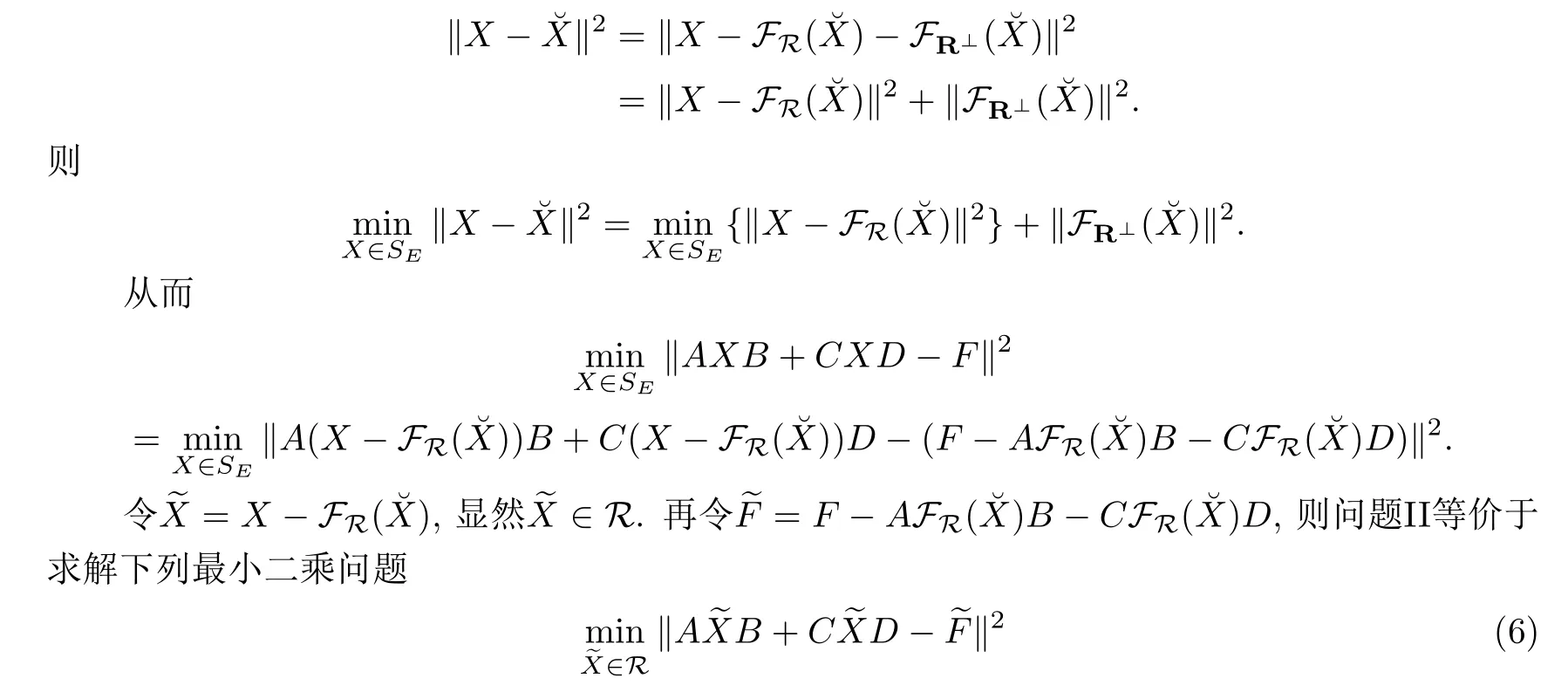
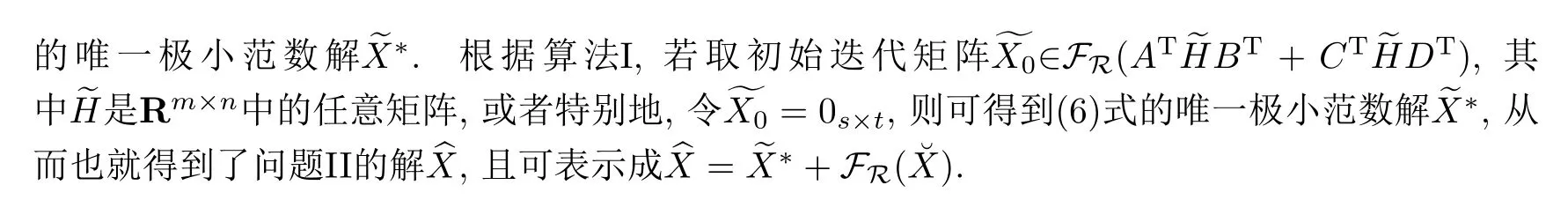
§4 數(shù)值例子

以下例子通過(guò)編寫(xiě)M文件(見(jiàn)附錄solution.m)在Matlab R2017a(運(yùn)行環(huán)境: 64位Win7操作系統(tǒng),Intel(R) Core(TM) i3-2350M CPU @ 2.30GHz處理器,4.00GB內(nèi)存) 上運(yùn)行,所得結(jié)果證實(shí)了該算法的有效性.

例1在本例中將R取為n階實(shí)對(duì)稱(chēng)矩陣集合,顯然,R為線(xiàn)性子空間.

在Rn×n上定義如下線(xiàn)性投影算子

由于計(jì)算誤差的影響,在具體的迭代過(guò)程中,Pi(i=0,1,2,···)一般不會(huì)等于零,迭代次數(shù)也不一定完全符合理論所需次數(shù).因此任取充分小的ε,譬如ε=1.0e-010(Matlab程序運(yùn)行結(jié)果中顯示,意思是1.0×10-10),當(dāng)‖Pk‖＜ε=1.0e-010時(shí),停止迭代,視Xk為問(wèn)題I和問(wèn)題II的解.

為了保持重復(fù)試驗(yàn)中結(jié)果的一致性,在Matlab中輸入隨機(jī)矩陣之前,需要將隨機(jī)發(fā)生器置于相同的初始狀態(tài).

(I) 不妨在Matlab中將隨機(jī)發(fā)生器置于狀態(tài)rand(’twister’,0),讓X0=rand(5)(注: rand(5)在Matlab中指的是各元素來(lái)自[0,1]區(qū)間且服從均勻分布的5階隨機(jī)矩陣).

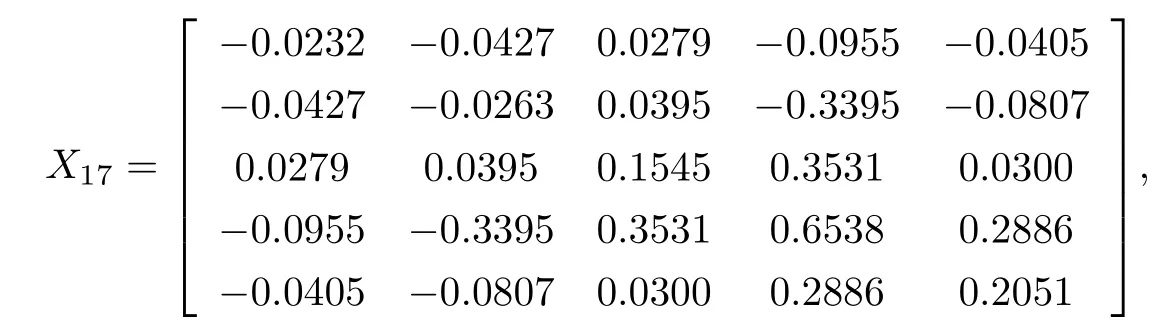
且‖P17‖=2.7559e-11＜ε,‖X17‖=1.0889,‖R17‖=14.9474,耗時(shí)t=0.0050秒.

若取初始迭代矩陣X0為5階零矩陣,經(jīng)過(guò)13(＜st=25)步迭代,得到問(wèn)題I的唯一極小范數(shù)解

且‖P13‖=4.9355e-11＜ε,‖X13‖=0.3178,‖R13‖=14.9474,耗時(shí)t=0.0099秒.

在例1中,記迭代次數(shù)為k,定義r(k) :=log10‖Pk‖.下面圖1是r(k)與迭代次數(shù)k的變化曲線(xiàn)圖,它間接顯示了梯度投影矩陣范數(shù)‖Pk‖與迭代次數(shù)k的變化情況.

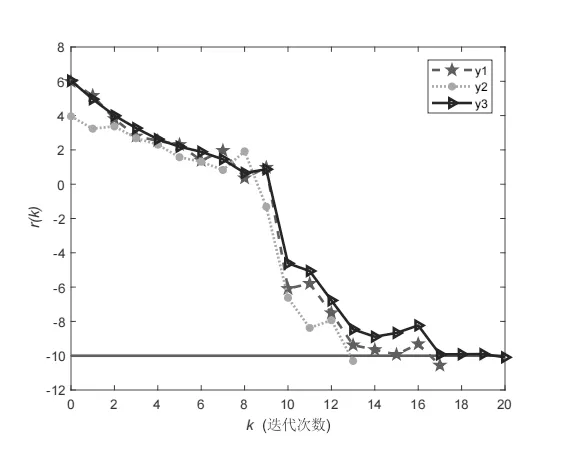
圖1 例1中r(k)曲線(xiàn)圖

圖1中,曲線(xiàn)y1和y2分別描述了求解問(wèn)題I 時(shí),初始迭代矩陣X0分別為rand(5)和05×5時(shí)函數(shù)r(k)的變化情況,曲線(xiàn)y3描述了求解問(wèn)題II 時(shí)函數(shù)r(k)的變化情況.圖1也顯示算法I在求解例1中的問(wèn)題I和II時(shí)是可行的,有效的.

例2記R表示所有n階主對(duì)角線(xiàn)元素為零的矩陣構(gòu)成的集合.顯然R為線(xiàn)性子空間.

對(duì)任意的矩陣X=(xij)∈Rn×n,令

顯然X=X1+X2,且這樣的X1和X2唯一,又,故在Rn×n上定義線(xiàn)性投影算子

為了討論方便,不妨讓本例中的矩陣A,B,C,D,F,分別為例1中的矩陣,n=5.

(I) 在Matlab中將隨機(jī)發(fā)生器置于狀態(tài)rand(’twister’,0),不妨讓X0=rand(5),取初始迭代矩陣X0=X0-diag(diag(X0)),應(yīng)用算法I,經(jīng)過(guò)16(＜st=25) 步迭代,得到矩陣方程AXB+CXD=F在子空間R上的一個(gè)最小二乘解

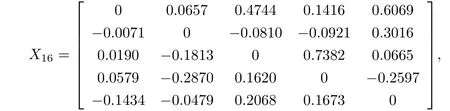
且‖P16‖=4.6810e-11＜ε,‖X16‖=1.2567,‖R16‖=14.9474,耗時(shí)t=0.0011秒.

若取初始迭代矩陣X0為5階零矩陣,經(jīng)過(guò)12(＜st=25) 步迭代,得到問(wèn)題I的一個(gè)極小范數(shù)解

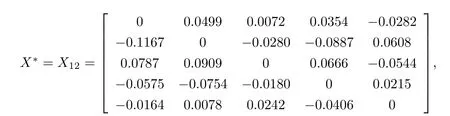
且‖P12‖=1.8840e-12＜ε,‖X12‖=0.2545,‖R12‖=14.9474,耗時(shí)t=0.0039秒.

顯然,X16∈R,X12∈R,‖X12‖＜‖X16‖,‖R16‖=‖R12‖.

在例2中,同樣地,定義r(k) :=log10‖Pk‖.下面圖2是r(k)與迭代次數(shù)k的變化曲線(xiàn)圖,它間接顯示了梯度投影矩陣范數(shù)‖Pk‖與迭代次數(shù)k的變化情況.

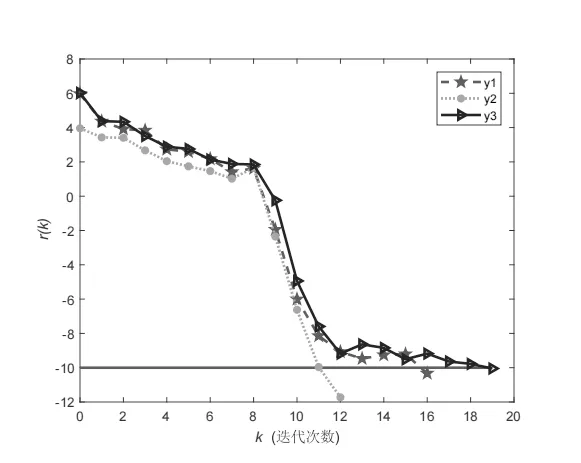
圖2 例2中r(k)曲線(xiàn)圖

圖2中曲線(xiàn)y1和y2分別描述了求解問(wèn)題I時(shí),初始迭代矩陣X0分別為rand(5)和05×5時(shí)函數(shù)r(k)的變化情況,曲線(xiàn)y3描述了求解問(wèn)題II時(shí)函數(shù)r(k)的變化情況.圖2也顯示算法I在求解例2中的問(wèn)題I和II時(shí)是可行的,有效的.

§5 結(jié)論

應(yīng)用共軛梯度方法和線(xiàn)性投影算子,討論了矩陣方程AXB+CXD=F在任意線(xiàn)性子空間R約束下的最小二乘解問(wèn)題.與最優(yōu)化中將負(fù)梯度在邊界上的投影作為迭代點(diǎn)前進(jìn)方向的梯度投影法不同的是,本文將矩陣函數(shù)的負(fù)梯度投影到所求線(xiàn)性子空間(矩陣空間)上的矩陣作為迭代過(guò)程中下一步的更新矩陣,以此來(lái)保證更新矩陣自動(dòng)滿(mǎn)足線(xiàn)性子空間的約束.可以證明,在有限的誤差范圍內(nèi),所給算法經(jīng)過(guò)有限步迭代可得到矩陣方程AXB+CXD=F的最小二乘解,極小范數(shù)解及相應(yīng)的最佳逼近.最后分別以實(shí)對(duì)稱(chēng)矩陣和主對(duì)角線(xiàn)元素為零的矩陣為對(duì)象進(jìn)行數(shù)值實(shí)驗(yàn),進(jìn)一步證實(shí)了算法的有效性.一般地,在Rs×t上定義線(xiàn)性投影算子F,就得到相應(yīng)的線(xiàn)性子空間R.因此,對(duì)于某線(xiàn)性子空間,只要定義相應(yīng)的線(xiàn)性投影算子,文中的迭代算法就可以用來(lái)求解矩陣方程AXB+CXD=F在該線(xiàn)性子空間約束下的最小二乘問(wèn)題.

致謝審稿人提出的意見(jiàn)和建議極大地促進(jìn)了對(duì)原稿件的提升和完善,作者在此表示衷心的感謝.