A GROUND STATE SOLUTION TO THE CHERN-SIMONS-SCHR?DINGER SYSTEM*
Jin DENG (鄧金) Benniao LI (李本鳥)
School of Mathematics and Statistics,Jiangxi Normal University,Nanchang 330022,China
E-mail: jindeng 2016@126.com;benniao li@jxnu.edu.cn
Abstract In this paper,we consider the Chern-Simons-Schrdinger system where u ∈H1(R2),p ∈(2,4),Aα: R2 →R are the components of the gauge potential(α=0,1,2),N: R2 →R is a neutral scalar field,V (x) is a potential function,the parameters κ,q >0 represent the Chern-Simons coupling constant and the Maxwell coupling constant,respectively,and e >0 is the coupling constant.In this paper,the truncation function is used to deal with a neutral scalar field and a gauge field in the Chern-Simons-Schrdinger problem.The ground state solution of the problem (P) is obtained by using the variational method.
Key words Chern-Simons-Schrdinger systems;ground state solution;variational method
1 Introduction
In this paper,we are interested in the following system:

The Lagrange density,which corresponds to system (1.1)–(1.5),is given by
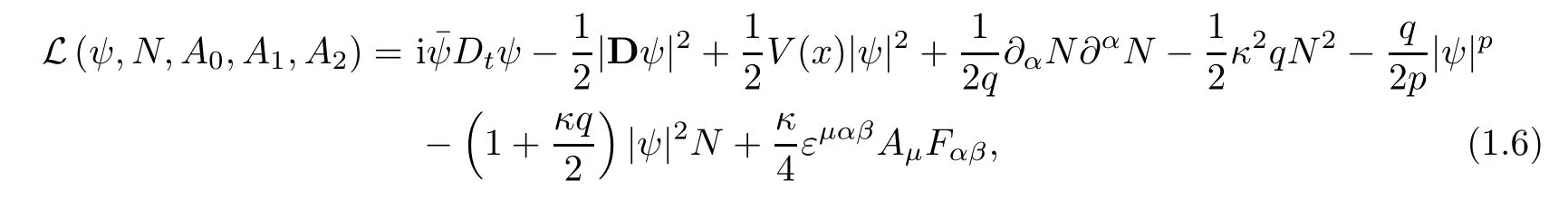
whereψ(x,t): R2× R →C is a charged scalar field,Dt=?t-ieA0,D=?-ieA,(A0,A)=(A0,A1,A2) is the gauge field,i is the imaginary unit,the parametersκ,q >0 represent the Chern-Simons coupling constant and the Maxwell coupling constant,respectively,ande >0 is the coupling constant.Moreover,Fαβ:=?αAβ-?βAα,andεμαβis the Levi-Civita tensor.εμαβAμFαβis called the Chern-Simons term.
This system arises from the study of (2+1)-dimensional Abelian Higgs models in [9],in which a charged nonrelativistic matter field interacts with a massive gauge field containing only a Chern-Simons term in the gauge action.Since the early 1980s,Chern-Simons theories have been applied widely in various areas of quantum physics,including the fractional quantum Hall effect,highTcconductivity,and the quantization of Heisenberg ferromagnets [16].For more physical details regarding the system,readers can refer to [1,13–15,18].
In recent years,there have appeared a lot of works on the Chern-Simons-Schrdinger system.For the case without a neutral scalar field,Byeon,Huh,and Seok [3] studied
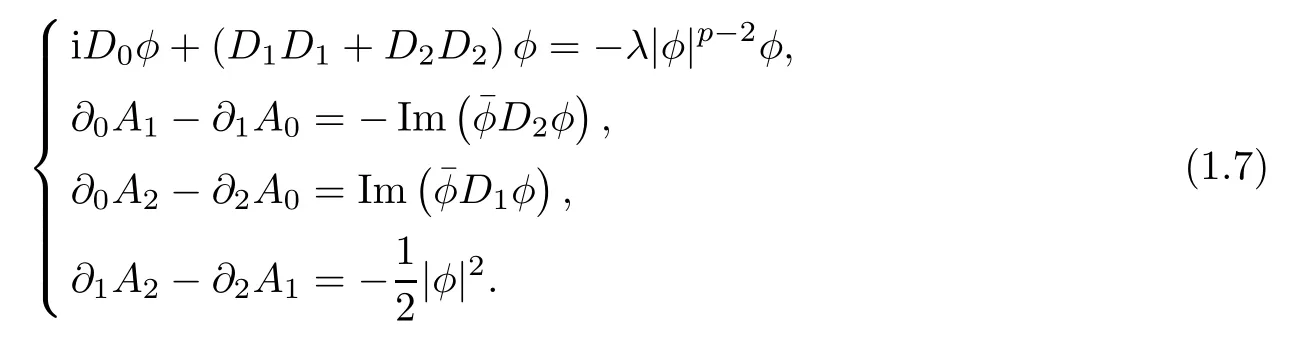
By the variational method,they considered the existence of radial solutions for the Chern-Simons-Schrdinger system,and sought the standing wave solution,forp >2,of the form

Later,in [2],Byeon,Huh,and Seok studied a standing wave solution of the form (1.8),with a vortex for the nonlinear Chern-Simons-Schrdinger system under the conditions ofp=4 andthe existence and the nonexistence of standing wave solution were proven forλbeing positive.
For more general cases with the nonlinear term in (1.7),Tan and Wan [22] were concerned with the Chern-Simons-Schrdinger system
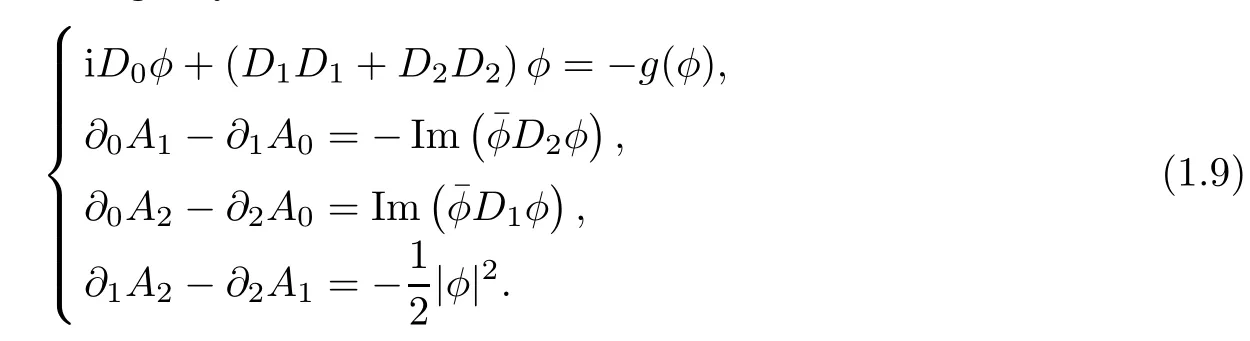
They showed the existence,non-existence,and multiplicity of a standing wave solution to this problem with asymptotically linear nonlinearities which do not satisfy the Ambrosetti-Rabinowitz condition.More existence and nonexistence results about radial solutions can be found in [2–4,10,12,19,20,22].
For non-radial results,the Chern-Simons-Schrdinger system
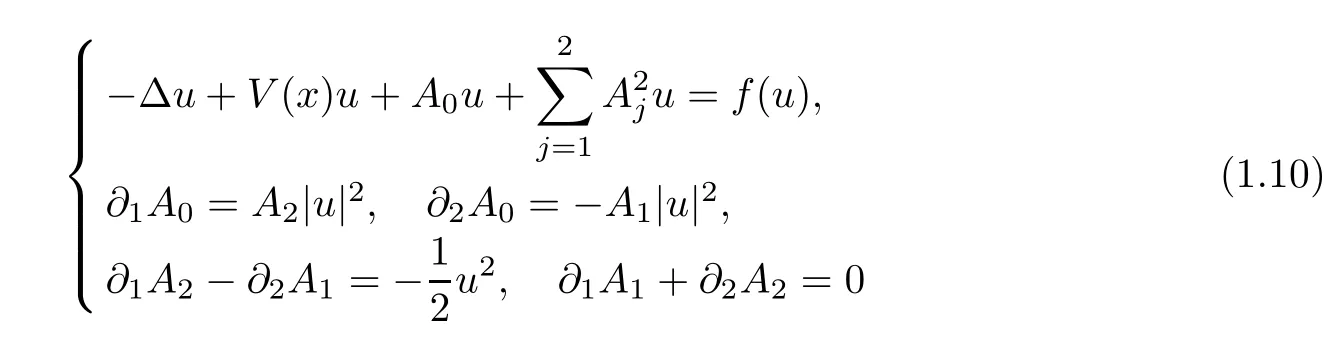
has been studied in [23] for the case thatV(x) is non-radial.The authors of this work proved the existence of nontrivial solutions to system (1.10) by using the concentration compactness principle and an argument of global compactness.Further non-radial results can be found in[5,17,21,23] and references therein.
On the other hand,for the case of a the system coupled a neutral scalar field,Han,Huh and Seok [11] studied the Schrdinger equation coupled with a neutral scalar field,
They showed the existence of standing wave solutions to system (1.11) and verified the Chern-Simons limit for these solutions in.Moreover,the Schrdinger-Chern-Simons-Higgs system involving the gauge field and neutral scalar field,
was investigated by d’Avenia and Pomponio in [6],whereu,N: R2→R are radially symmetric andthey proved the existence of a radial solution for system (1.12)with small coupling constantseby a truncated functional and the variational method.The existence of a standing wave solution of the Chern-Simons-Schrdinger equations coupled with a neutral scalar field is also found in [6–8,11].
However,there are a few results about solutions of the Chern-Simons-Schrdinger system(1.1)–(1.5) for the case thatV(x) is not constant or is non-radial.Here,we are concerned with a static solution of system (1.1)–(1.5) whenV(x) is not radial.
Assume that A=(A1,A2) is a coulomb gauge,that is,
(V2)V∈C1(R2,R) andtt2α-2[(2α-2)V(tx) -?V(tx) · (tx)] is nondecreasing in(0,+∞) for anyx∈R2.
In this paper,we will establish the existence of the ground state solution for the Chern-Simons-Schrdinger system (1.1)–(1.5) coupling a neutral scalar field and a gauge field under condition (1.13).Our main theorem is as follows:
Theorem 1.1Suppose thatp∈(2,4) and that the functionVsatisfies (V1) and (V2).Then there existse*>0 such that,if 0<e <e*,system (1.1)–(1.5) has a ground state solution.
Theorem 1.1 is proved mainly by the variational method.Actually,the system (1.1)–(1.5)with condition (1.13) can be reduced into a single equation.However,the problem is not only non-compact,but has also been involved in a gauge field and a neutral scalar field,which makes the problem more complicated,since the gauge field and the neutral scalar field have to be solved as two non-local terms.SinceV(x) is non-radial,it is very difficult to prove the compactness result in order to obtain the existence of nontrivial solutions inH1(R2) by the variational method.Moreover,two nonlocal terms appearing in the functional make it much tougher to verify the Mountain Pass structure and the boundedness of the Palais-Smale sequence.The concentration compactness principle is applied in order to deal with the difficulty resulting from the lack of compactness.In addition,in order to solve the competition among the neutral scalar field and the gauge field,we will use the trick of a truncation function in order to prove the boundedness.
It is hard to show that the Mountain Pass solution is the ground state solution for system(1.1)–(1.5) by using a normal Nehari manifold.Thus,in this paper,the existence of a ground state solution is achieved by constructing a special manifold: the Nehari-Pohozaev manifold.In order to deal with the uniqueness on the Nehari-Pohozaev manifold,we need the assumption of (V2).
Remark 1.2There are many functionsV(x) satisfying (V1) and (V2).For example,satisfies (V1) and (V2) fora >3b >0 andβ1=β2>1.The rest of this paper is organized as follows: in Section 2,we introduce some fundamental lemmas that will be used throughout the rest of the paper.In Section 3,we will show the Mountain Pass theorem and the boundedness of the Palais-Smale sequence,and that the minimum value on the Nehari-Pohozaev manifold is attainable and equals the Mountain Pass value.In Section 4,we will give some lemmas for the proof of the compactness and prove the existence of the ground state solution for system (1.1)–(1.5) for the case that the potential is a constant.Finally,we will complete the proof of Theorem 1.1 in Section 5.
2 Preliminaries
In this section,we will outline the variational framework and some fundamental lemmas that will be used throughout the rest of the paper.
The functional associated to problem (1.1)–(1.5) with the condition (1.13) is given by
whereF12=?1A2-?2A1.SinceA1andA2satisfy (1.3),the functional in (2.1) can be reduced as follows:
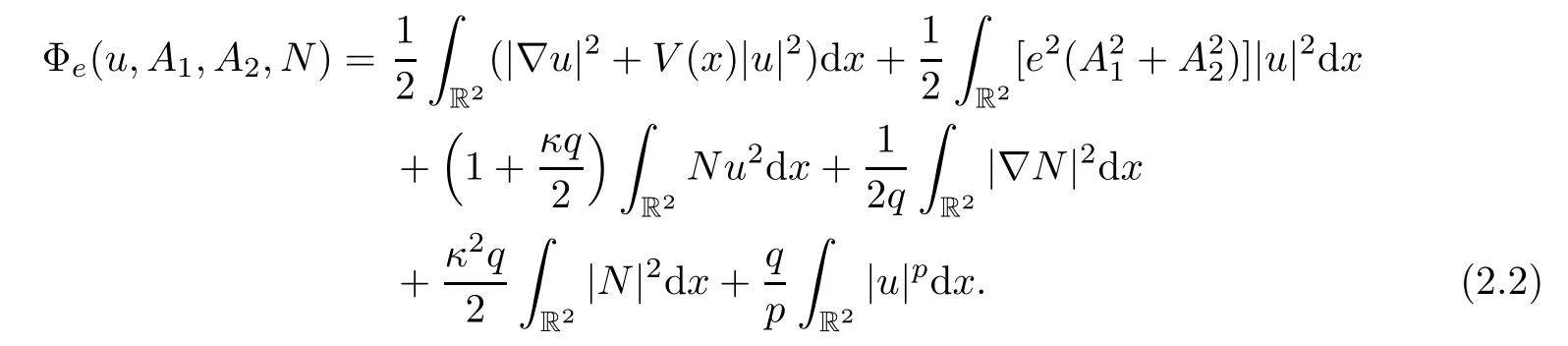
By the Coulomb gauge condition?1A1+?2A2=0 and equation (1.3),we obtain that
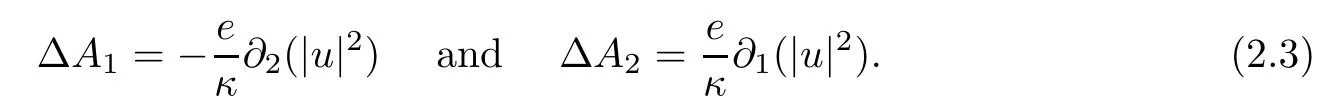
Hence,for eachu,A1,A2can be expressed as
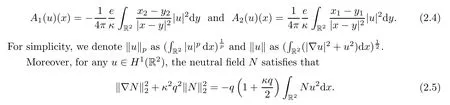
Therefore,by (2.2) and (2.5),the functional (2.2) can be reduced as follows:

On the other hand,in [11],the neutral fieldNis determined uniquely byu;that is,for any givenu∈H1(R2),the uniqueNuis given by
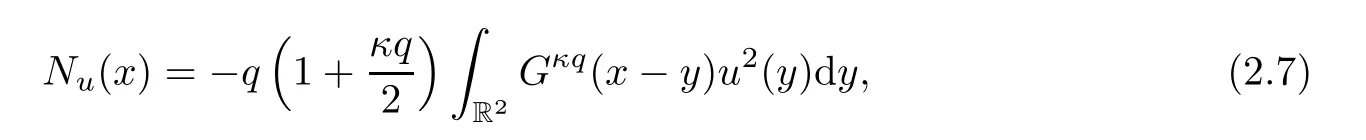
where the integral kernelGμ(x) is the Yukawa potential defined by
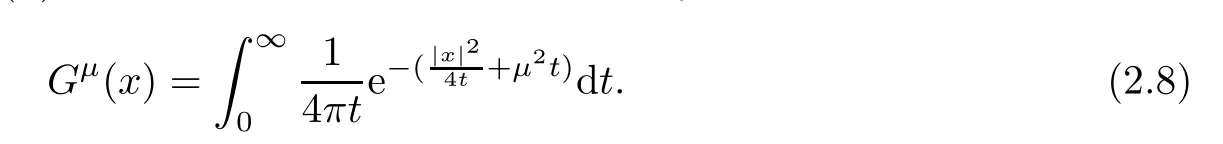
Thus,Nuhas the following properties in [11]:
Lemma 2.1For everyu∈H1(R2),there exists a uniqueNu∈H1(R2) which solves(1.2).Moreover,
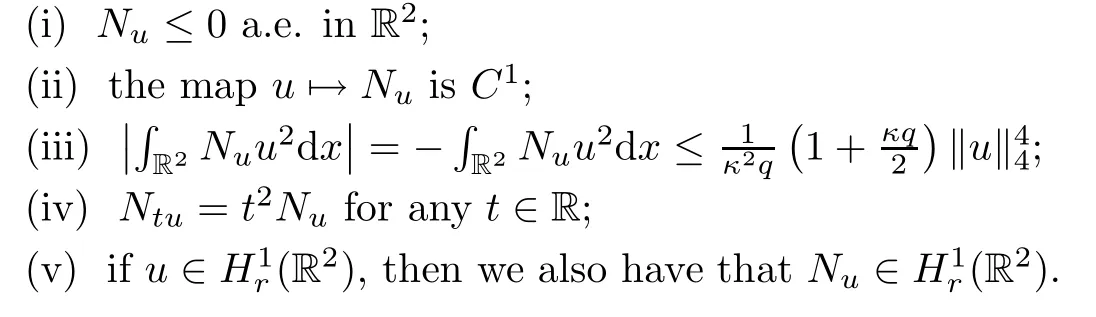
As a result,the functional Φe(u,N) can be written as
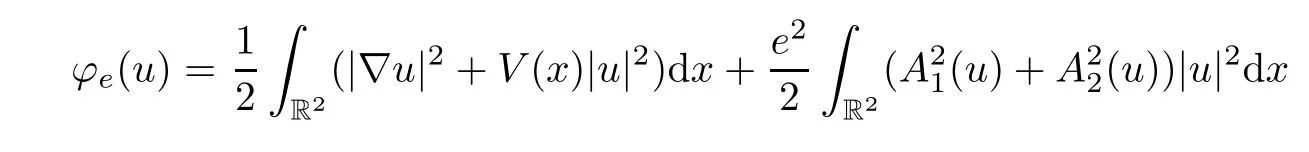
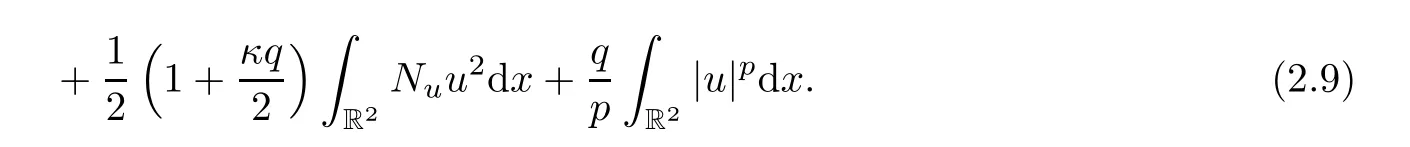
Thus,the existence of solutions to system (1.1)–(1.5) is equivalent to finding a critical point ofφe(u).
To deal with the termsA1(u) andA2(u) in the functionalφe(u),we need the following inequalities (which were proven in [23]).
Lemma 2.2Let 1<s <2 andWe then have three claims.
(i) There is a constantCdepending only onsandqsuch that
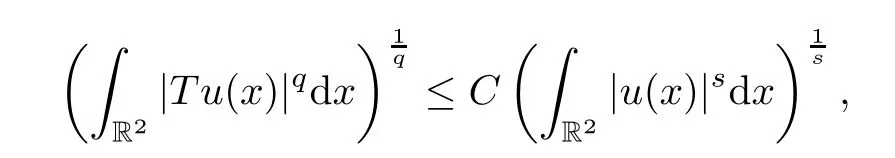
where the integral operatorTis given by
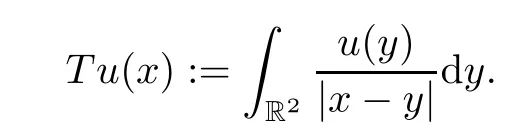
(ii) Ifu∈H1(R2),then we have,forj=1,2,that
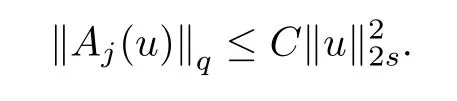
(iii) Forq′=,j=1,2,
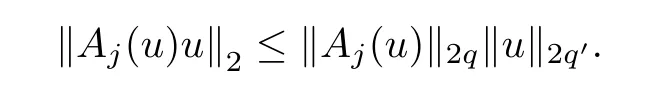
ProofClaim (i) comes directly from Hardy-Littlewood-Sobolev inequality,while (ii) follows from (i),and (iii) is a consequence of Hlder’s inequality. □
3 The Modified Functional and Mountain Pass Structure
In this section,we will introduce a modified functional which fulfills the conditions of the Mountain Pass theorem given in Lemma 3.2.On the other hand,since there is the competition between the gauge field and the neutral field in the functionalφe,the boundedness of the Palais-Smale sequence is not easy to verify.To overcome this difficulty,we use the trick of a truncation function.The truncation functionχ∈C∞(R+,R) is chosen as
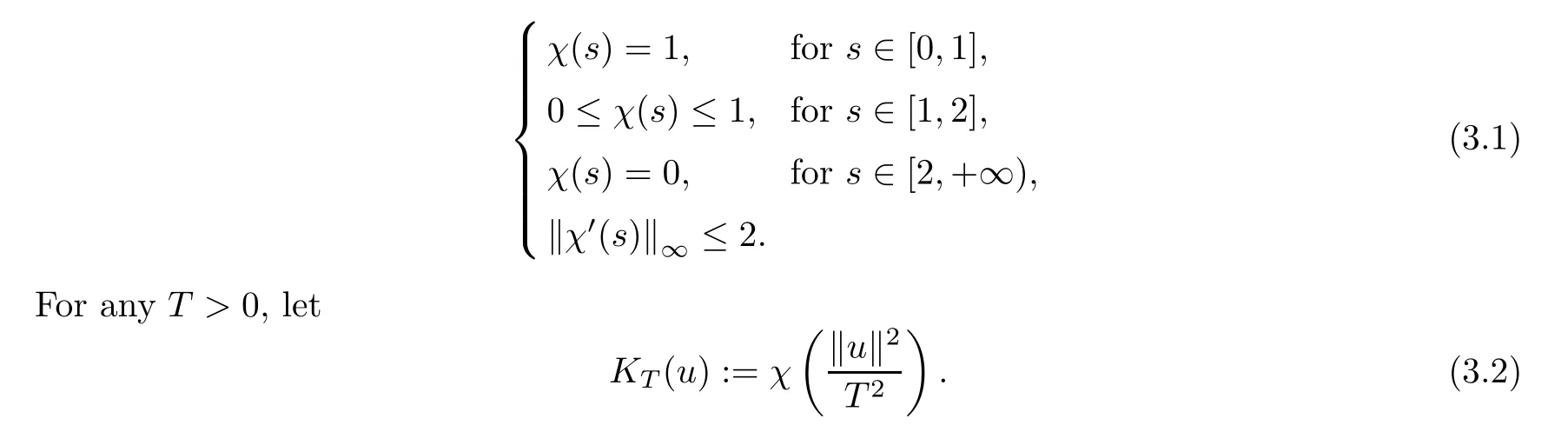
Now,we define the following truncated functionalφe,T:
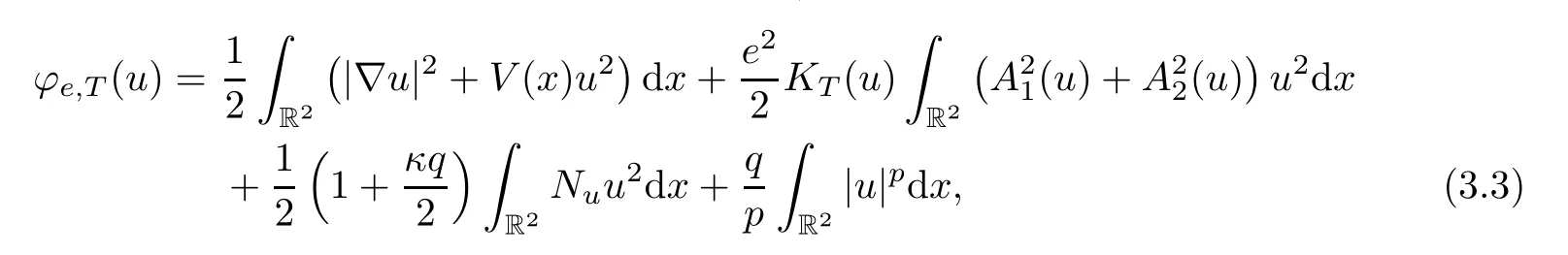
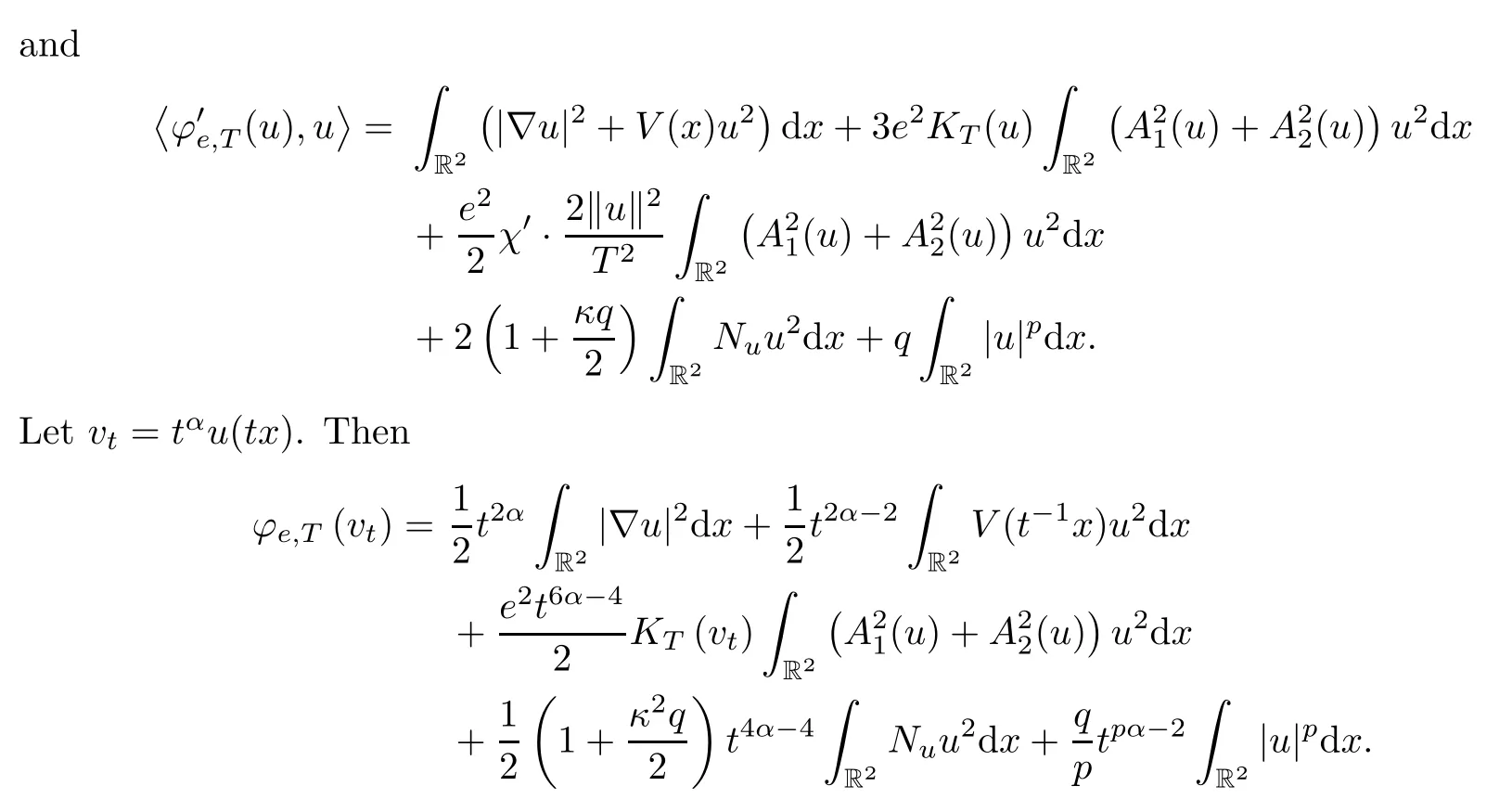
Taking the derivative with respect totand lettingt=1,
And how should I know that thou speakest truth? answered Tsar Dolmat. Hadst thou come to me first I would have given thee the Fire Bird with honor. How will it be with thee now when I send into all Tsardoms, declaring how thou hast acted shamefully29 in my borders? However, Tsarevitch Ivan, I will excuse thee this if thou wilt30 serve me a certain service. If thou wilt ride across three times nine countries to the thirtieth Tsardom of Tsar Afron, and wilt win for me from him the Horse with the Golden Mane, which his father promised me and which is mine by right, then will I give to thee with all joy the Fire Bird. But if thou dost not serve me this service, then will I declare throughout all Tsardoms that thou art a thief, unworthy to share thy father s honors.

which is from the Pohozave identity in the next lemma achieved in a way similar that of [23].In fact,we have the following:
Lemma 3.1Letube a critical point ofφinH1(R2).Then we have the following Pohozaev identity:
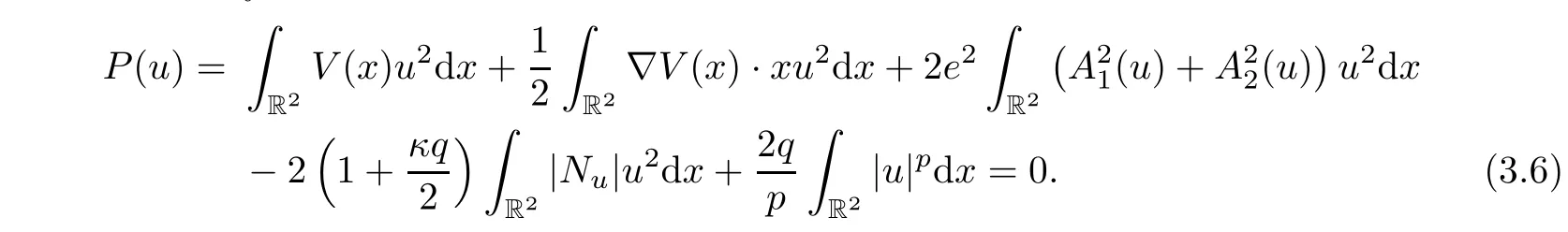
On the other hand,we define the set
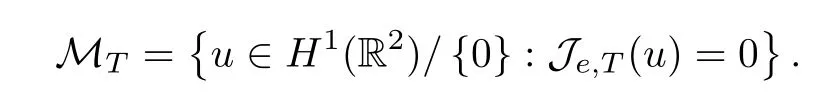
Next,we show that MTis a manifold,as follows:
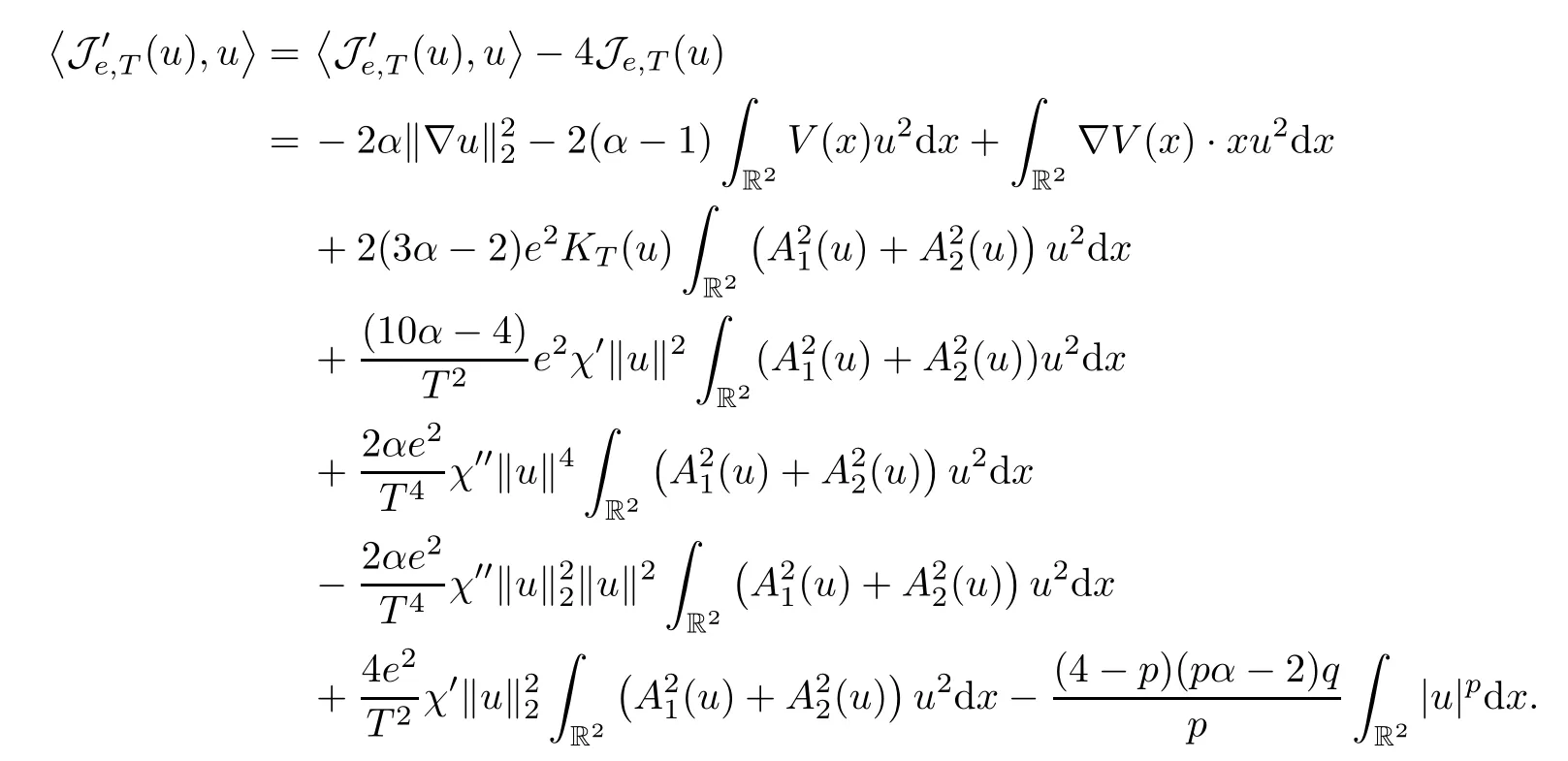
If ‖u‖ is large enough,we can getKT(u) ≡0,χ′≡0 andχ′′≡0,so we have that
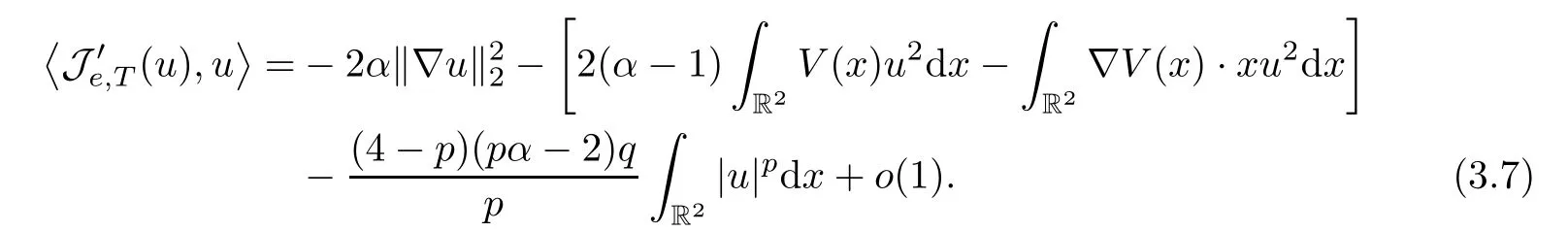
If ‖u‖ is bounded,we choose 0<e <e*small enough so that we can also get equation (3.7).By (V2),we have (2α-2)V(x) -?V(x) ·x≥0 (see Lemma 3.5 below),soThus,the set MTis a manifold called the Nehari-Pohozaev manifold.
Lemma 3.2The functionalφe,Tsatisfies the following properties:
(i) there existr >0 andθ >0 such that ‖u‖<r,soφe,T(u) ≥θ;
(ii) there existρ >r >0 such that ‖u‖>ρ,soφe,T(u)<0,whereρ,randθare independent ofeandT.
Proof(i) If ‖u‖ is small enough,by Lemma 2.1,we have that
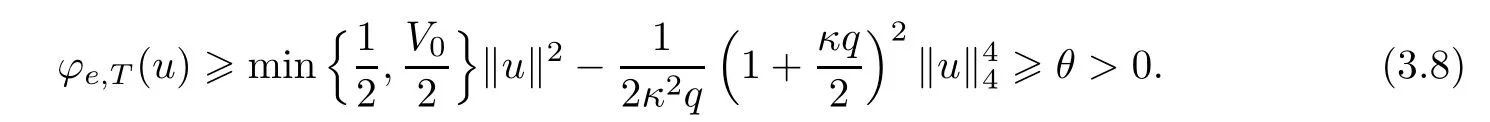
(ii) If ?u∈H1(R2) {0},and we letvt=tαu(tx),then
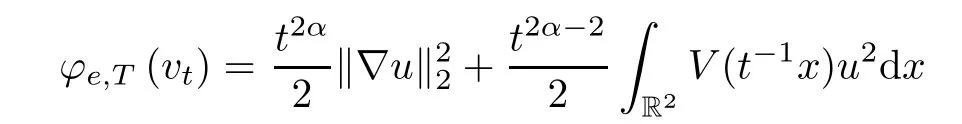
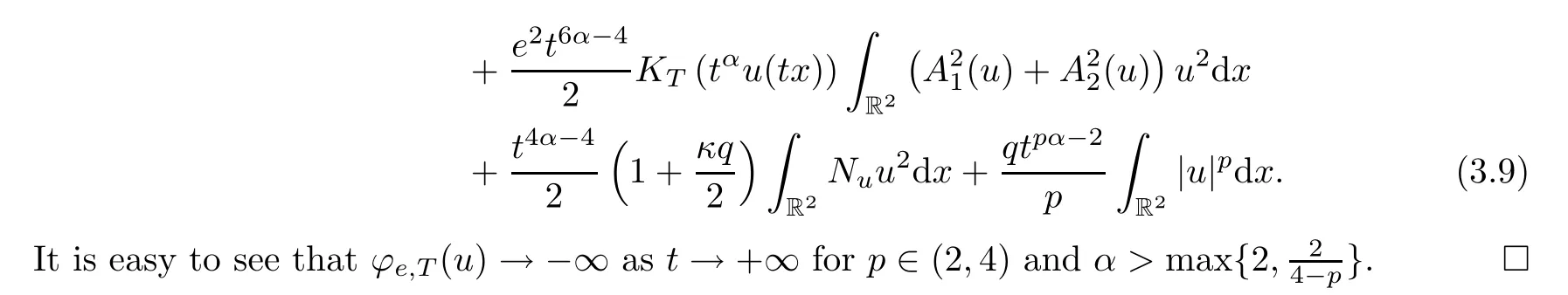
For anye,T >0,letce,Tbe the Mountain Pass level for the functionalφe,T(u),namely,
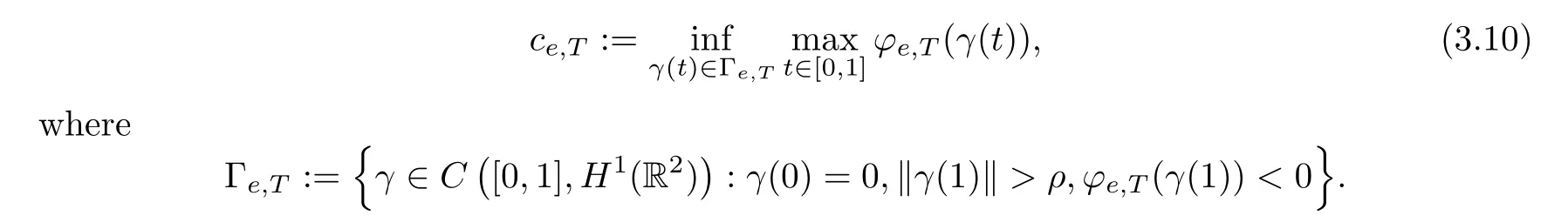
Using Lemma 3.2,there exists a Palais-Smale sequence {un} inH1(R2) forφe,Tat levelce,T,namely,φe,T(un) →ce,Tand(un) →0 asn→∞.
In fact,the Palais-Smale sequence {un} is bounded.
Lemma 3.3There exists ˉT >0 independently oneandsuch that,if 0<e <e*,then
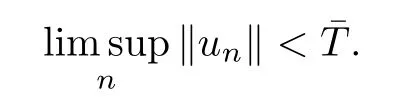
ProofWe argue by contradiction.For anyT >0,there existse >0,such that

Since {un} is a Palais-Smale sequence,we have that

By Lemmas 2.1 and 2.2,
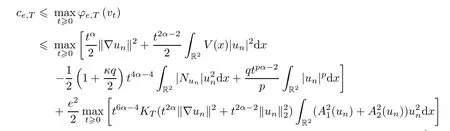
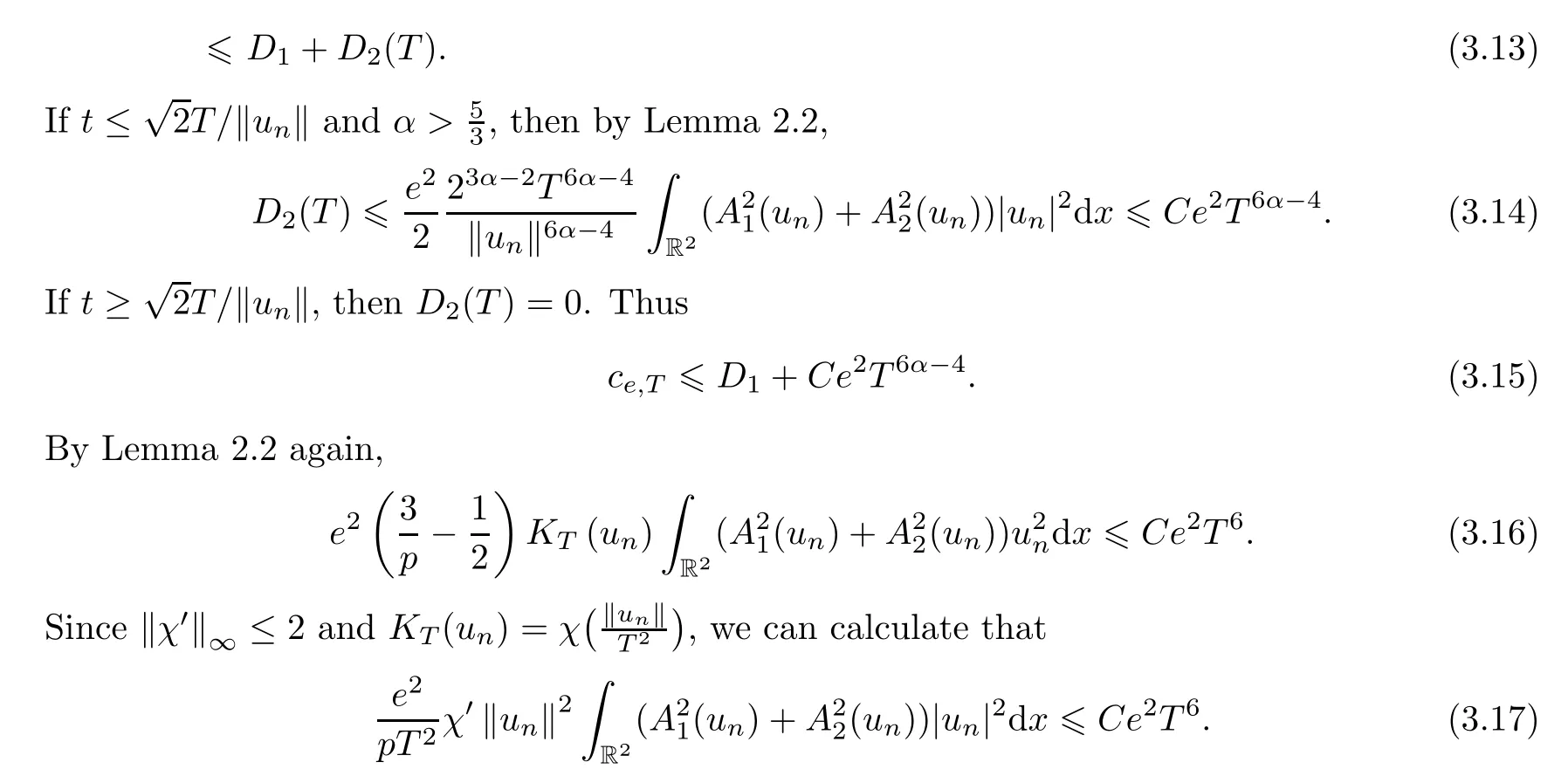
Hence,by (3.12),(3.15),(3.16) and (3.17),we have that
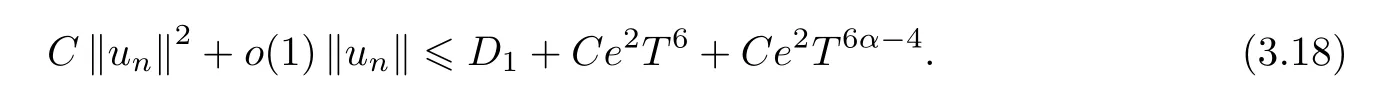
Combining this with (3.11),we can get that
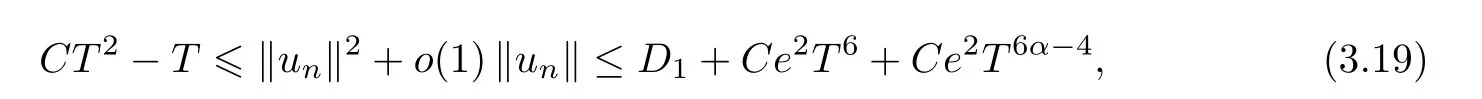
which leads to a contradiction whene=e(T) is sufficiently small for largeTandα >.Therefore,there exist>0 ande*such that,if 0<e <e*,then lim supn‖un‖<,which implies that the Palais-Smale sequence is bounded;that is,‖un‖ ≤.By the definition ofKT(u),we haveand

Before proving the existence of the ground state solution,we will give some results on MT.
Lemma 3.4Assume that (V1) and (V2) hold,that 0<e <e*,α >1 and ?u∈H1(R2) {0},there existstu>0 such that(tux) ∈MT.
ProofLetvt=tαu(tx) andge,T(t)=φe,T(vt).Then
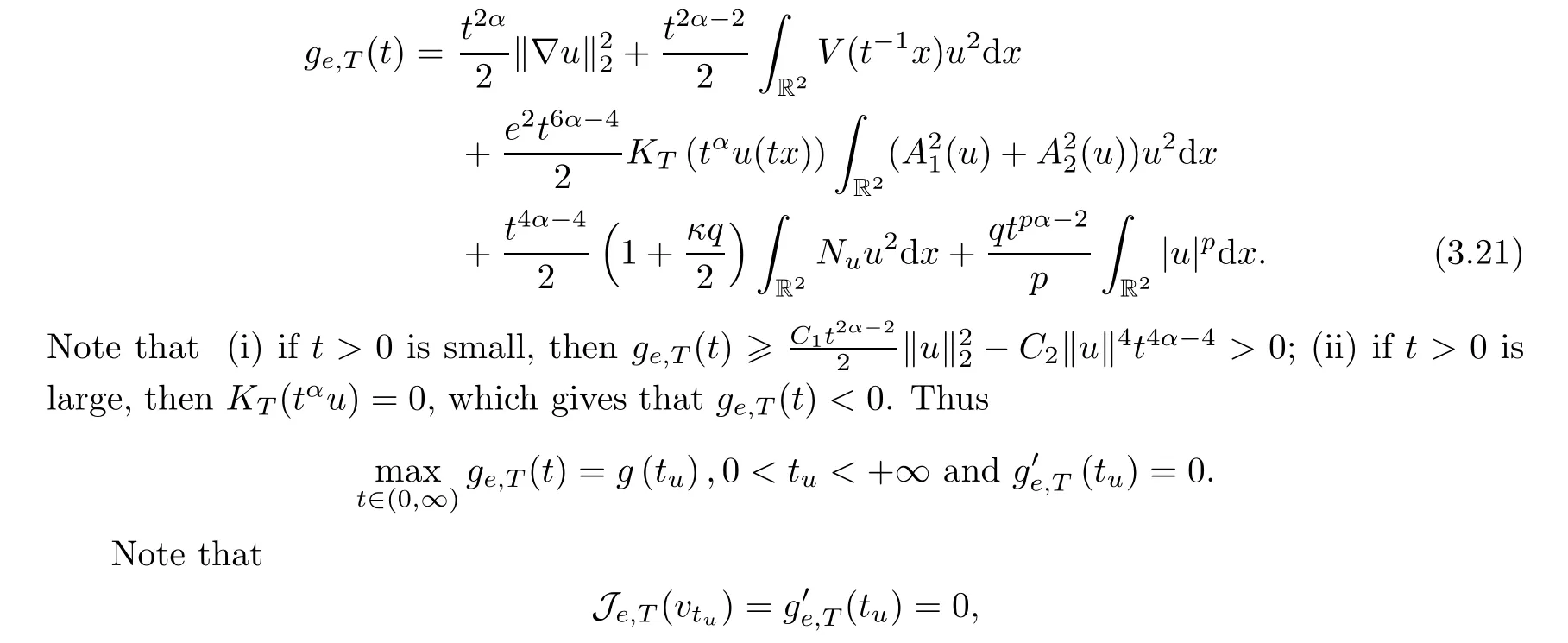
sovtu∈MT. □
In what follows,we will state thattuis unique.To prove the uniqueness,we need several lemmas.
Lemma 3.5Assume that (V1) and (V2) hold,and that 0<e <e*andα >1.Then
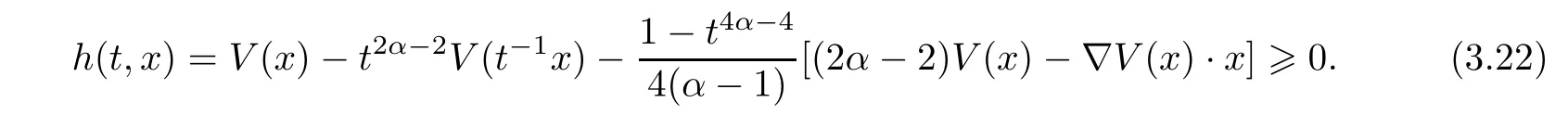
Moreover,forx∈R2,

whereC1andC2are positive constants.
ProofFor anyx∈R2,by (V1) and (V2),we have that
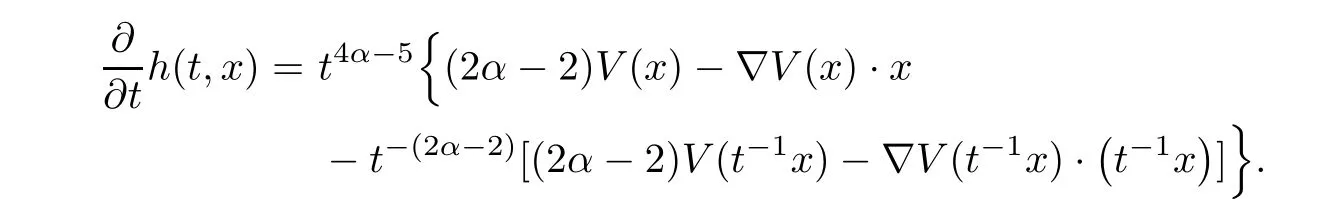
By (V2),we have thatfor 0<t <1,which implies thath(t,x) ≥h(1,x)=0 for allt≥0 andx∈R2.Thus,(3.22) holds.By (3.22),one has that
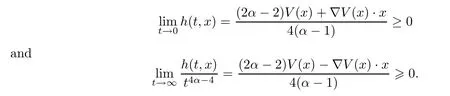
Moreover,we also have that (2α-2)V(x)-?V(x)·x≤(4α-4)V(x).By (V1),we have that.By (3.22),we have that

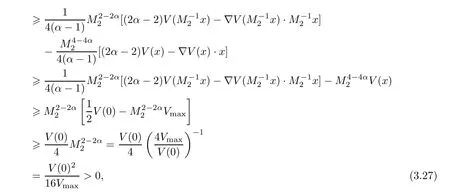
which implies that (2α-2)V(x)-?V(x)·x≥:=C2>0.Thus,we have completed the proofs of (3.23) and (3.24). □
Lemma 3.6Assume that (V1) and (V2) hold,and that 0<e <e*,Then,
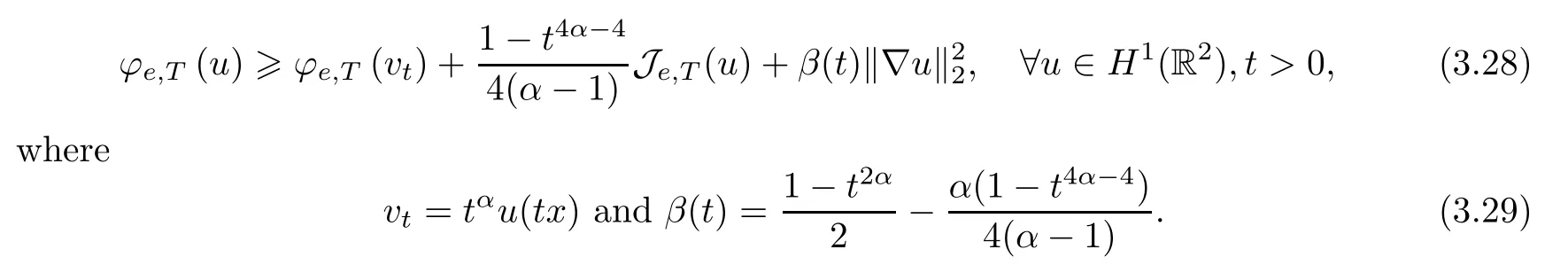
ProofBy some computations,we have that


It is easy to verify thatt=1 is the minimum point ofβ′(t) forα >2,which implies thatβ(t) ≥β(1)=0.Moreover,let
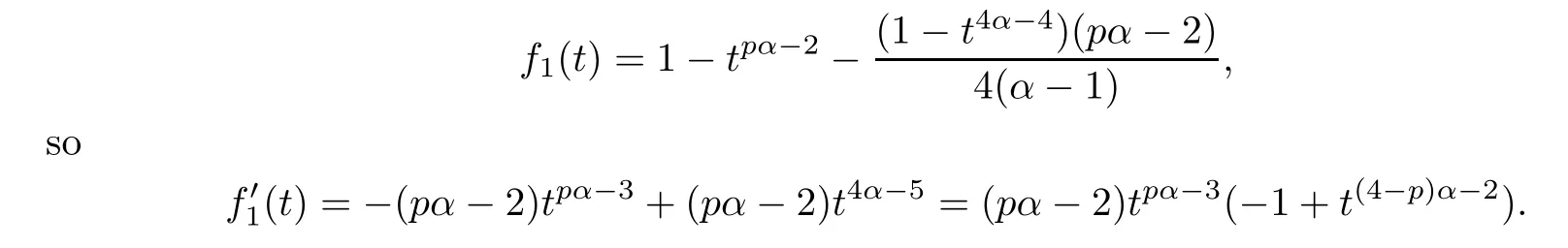
Similarly,it is easy to verify thatt=1 is the minimum point off1(t) forα >,sof1(t) ≥f1(1)=0.
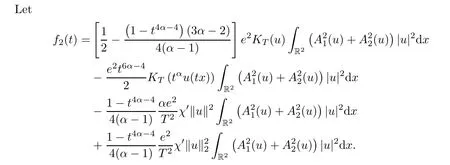
If ‖u‖ is large enough,thenKT(tαu(tx))=0 andχ′=0,which means thatf2(t)=0.If ‖u‖is bounded,by choosingesmall enough,we get thatf2(t)=o(e2).By Lemma 3.5 again,we have that
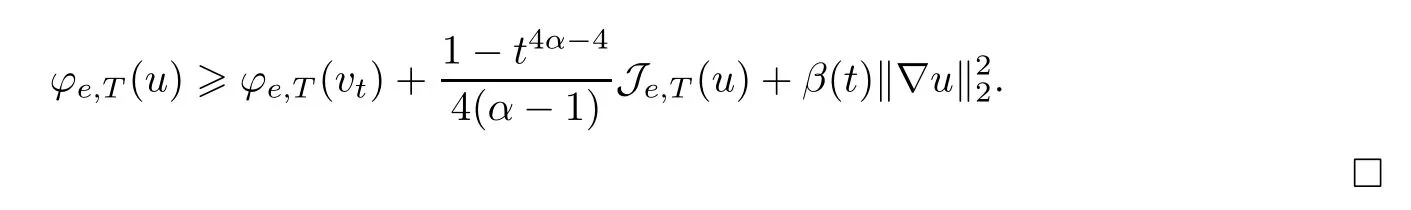
Finally,we prove the uniqueness oftuby Lemma 3.6.
Lemma 3.7Under the conditions (V1) and (V2),for anyu∈H1(R2) {0},there exists onlytu>0 such thattαuu(tux) ∈MT.

which is a contradiction.Thus,tu>0 is unique for anyu∈H1(R2) {0}. □
Set that
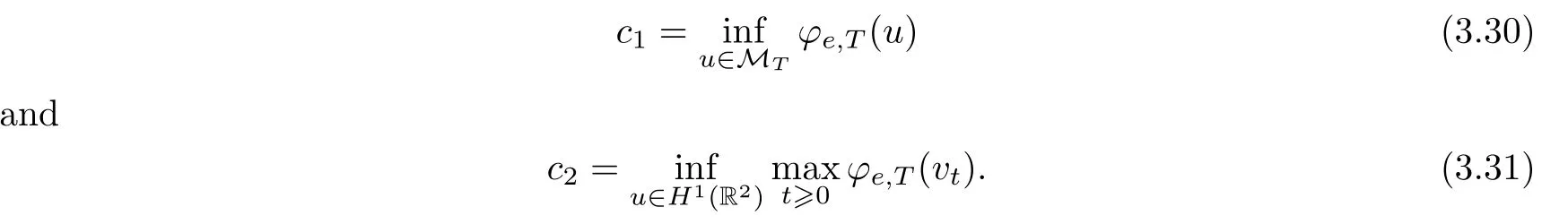
Lemma 3.8Under the conditions (V1) and (V2),and that 0<e <e*,there existsC0>0 such thatc1≥C0,wherec1is given by (3.30).
ProofSince Je,T=0 for allu∈MT,we have that
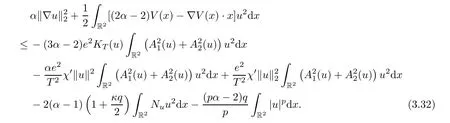
By Lemma 2.1 and (3.24),we can deduce that

By Sobolev’s imbedding theorem,we have that

The last equality is from the definition ofKT(u) and the choice of a sufficiently smalle.Since Je.T=0 foru∈MT,0<e <e*,we have that
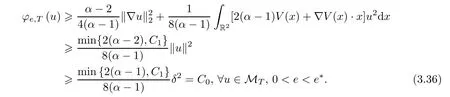
Hencec1≥C0. □
Theorem 3.9Under the conditions (V1),(V2) and 0<e <e*,we have thatc1=c2=ce,T,wherece,Tis the Mountain Pass value of the functionalφe,T(u).
ProofWe assume thatvt∈MTis the maximum value ofφe,T(vtu,1) foru∈H1(R2){0},so that is,ce,T≤c2.
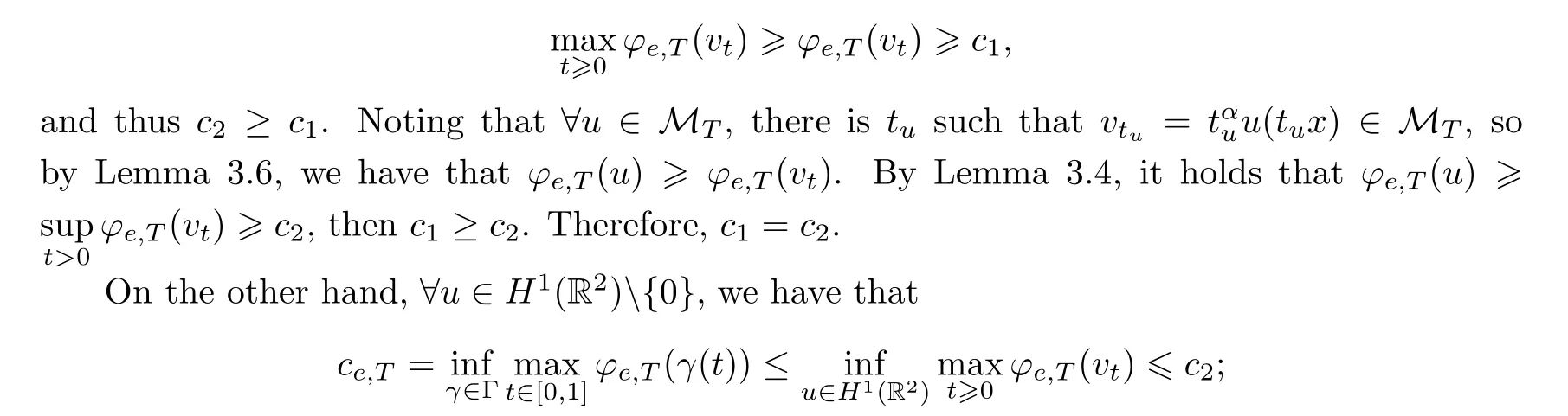
Thus,it remains to show thatce,T≥c1.We set thatX1={u∈H1(R2): Je,T(u) ≥0}andX2={u∈H1(R2): Je,T(u)<0}.
(i) Ifδ >0 is small andBδ(0) ?X1,by Lemmas 2.1,3.5 and (3.4),we have that
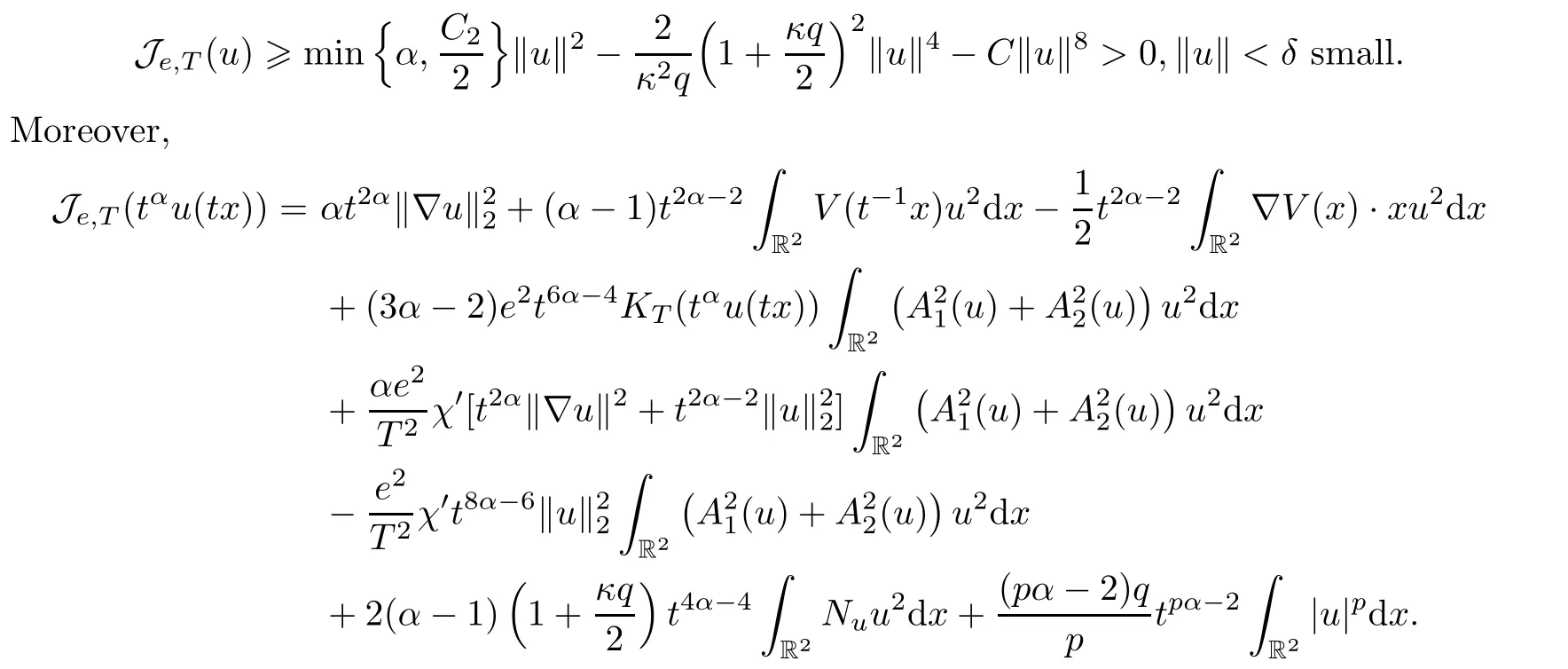
Therefore,iftis large enough such that,thenKT(tαu(tx))=0 andχ′=0,from which we can deduce that Je,T(tαu(tx))<0 for 0<e <e*.Hence,Je,T(u(x)) ≥0 for smallu∈X1,and Je,T(u(x))<0 for someu∈X2.Hence,there exist a pathγandssuch thatφe,T(γ(s))<0 andγ(s)/∈Bδ(0) ?X1,soγ∈Γ has to cross the manifold MTfromX1toX2;that is,,and hencec1≤ce,T.Therefore,we have thatc1=c2=ce,T.□
Theorem 3.10Under the conditions (V1),(V2) and 0<e <e*,ifv∈MTandφe,T(v)=c,thenvis critical of the functionalφe,T(v).
ProofAssumev∈MT,φe,T(v)=candThen there existδ >0 andλ >0 such that ‖u-v‖ ≤3δ,LetandS=Bδ(v).By using Lemma 2.3 in [24],there existsηsuch that
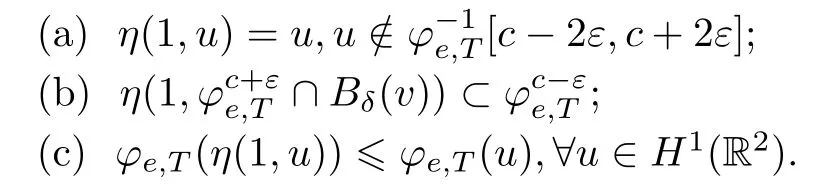
Sincev∈MT,φe,T(tαv(tx)) reaches its maximum value att=1,when |tαv(tx) -v|<δandtαv(tx) ∈Bδ(v)=S,we have thatφe,T(tαv(tx))<φe,T(v)=c <c+ε;that is,tαv(tx) ∈S∩.By (c),we have thatφe,T(η(1,tαv(tx)) ≤φe,T(tαv(tx))<0 fortlarge.By (a),φe,T(η(1,0))=φe,T(0)=0,soη(1,tαv(tx)) ∈Γ={γ∈C([0,1],H1(R2)) :γ(0)=0,φe,T(γ(1))<0}.By using (b),we get thatc≤φe,T(η(1,tαv(tx))<c-ε,which is a contradiction.Hence,□
4 Compactness Result
We will prove the compactness of the Palais-Smale sequence via a comparison between the Mountain Pass value of the system and the least energy of the limit functional corresponding to system (1.1)–(1.5).In this section,we will show some lemmas which are prepared in order to prove the compactness result.
Proposition 4.1(see [23]) Suppose thatunconverges weakly touinH1(R2),asn→∞.Then
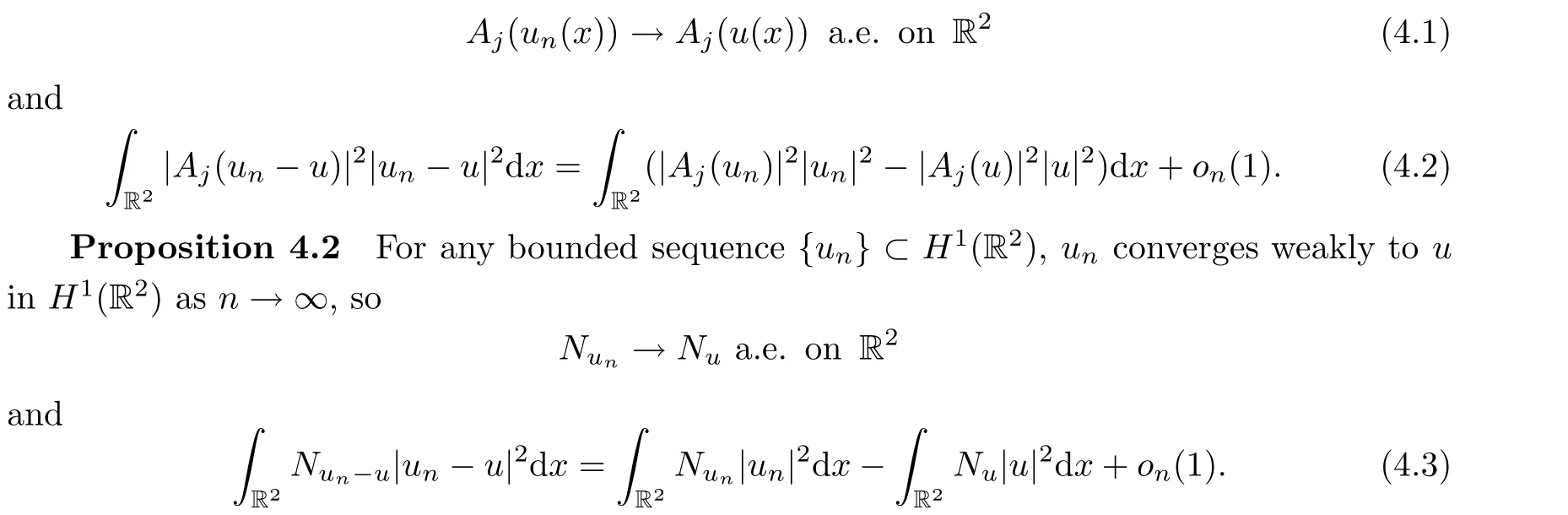
ProofFor anyφ∈H1(R2),and sinceunconverges weaklyuinH1(R2),we have that

The results have been proven completely. □
We consider the following Chern-Simons-Schrdinger system:
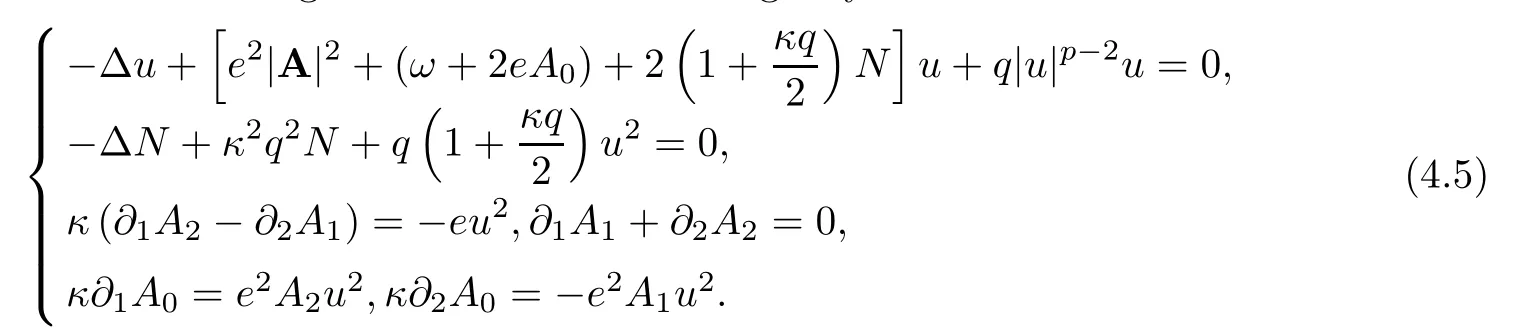
The functional corresponding to system (4.5) is defined by

Theorem 4.3Under the conditions (V1) and (V2),suppose thatω >0 and 0<e <e*,then problem (4.5) has a ground state solution ?u∈H1(R2){0} such that
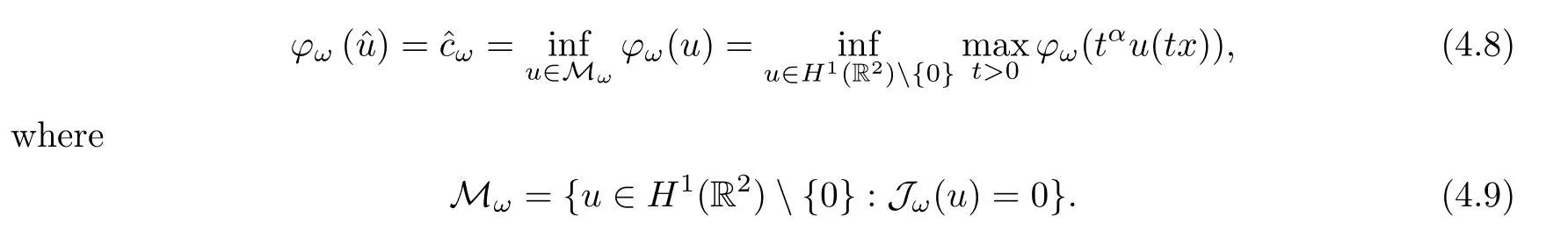
ProofWe will use the same method of a modified functional as before to prove this theorem.Note that all conclusions onφe,T,Je,T,Me,Tandce,Tin the above lemmas are also true forφω,T,Jω,T,Mω,Tandω,T.We will prove that ?cωis achieved.
Let {un} ?Mωandφω(un) →ω.First,we will prove the boundedness of the sequence{un}.By direct computation,
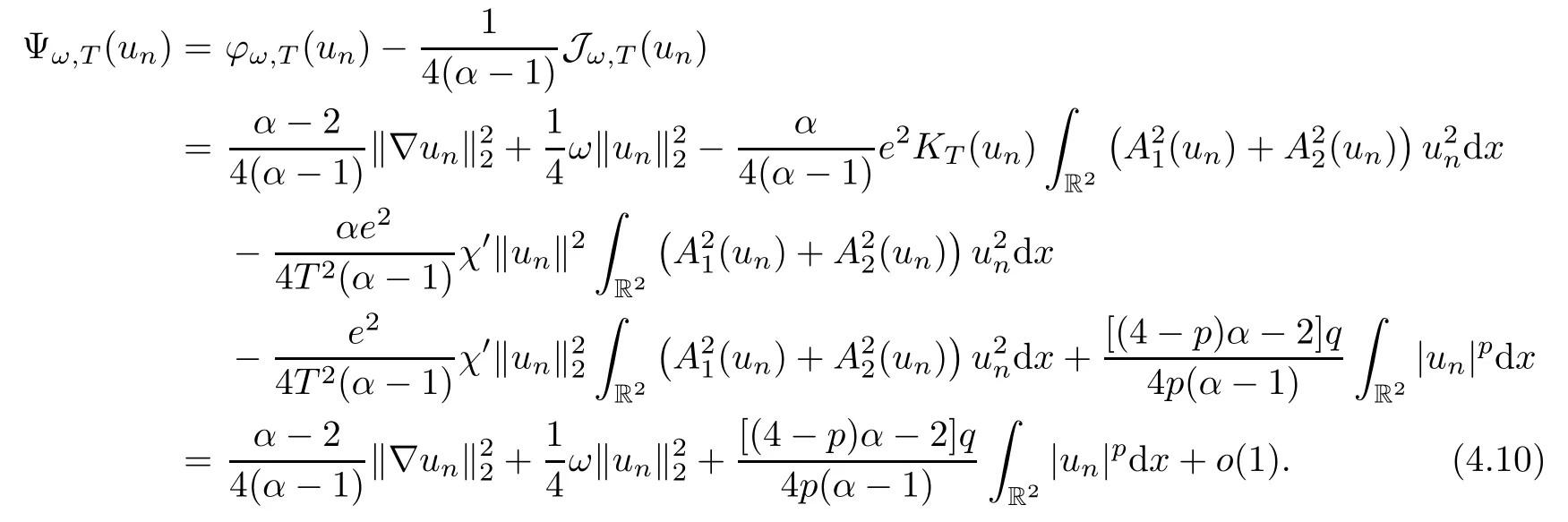
If ‖un‖ is large enough,by the definition ofKT,KTandχ′vanish.If ‖un‖ is bounded,by choosingesufficiently small,the terms witheare sufficiently small as well.Thus,the last equality in (4.10) holds.Since Jω,T=0,and by (4.10) and,we have that
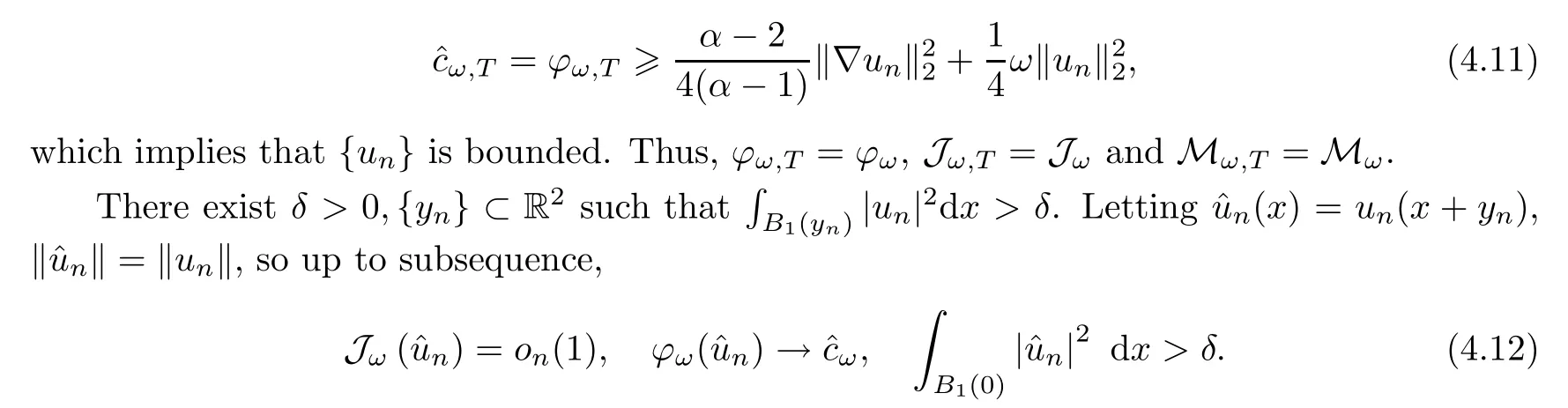
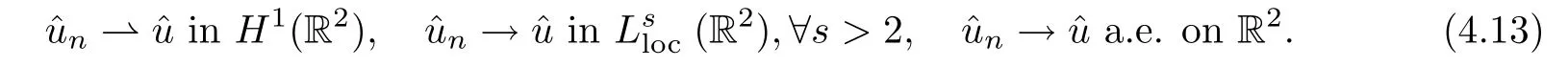
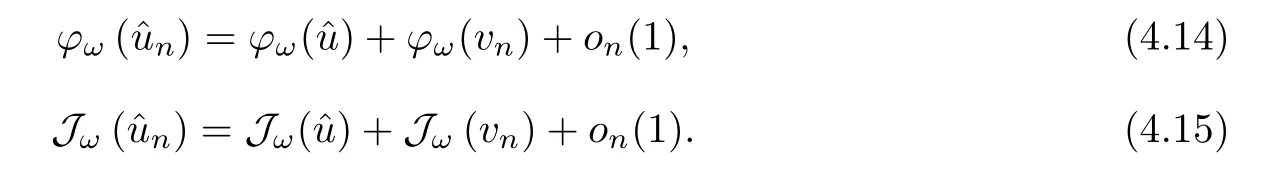
Using (4.12),(4.14) and (4.15),it holds that
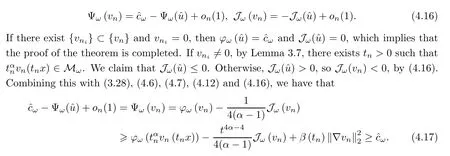
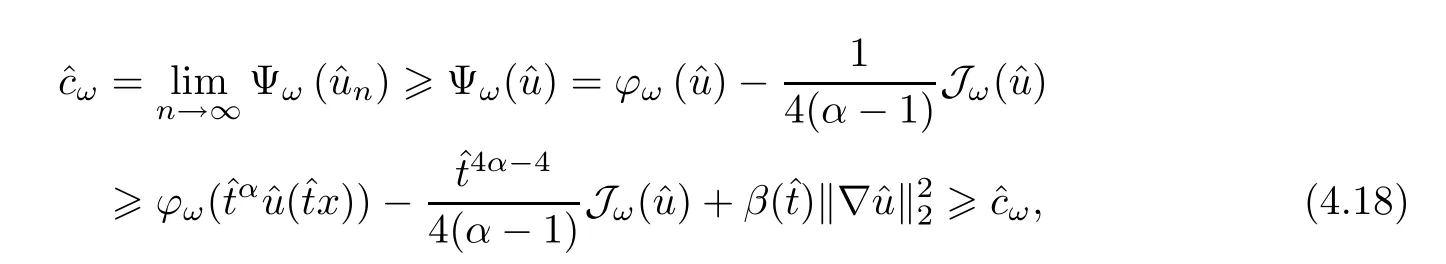
which means thatφω(?u)=?cωand Jω(?u)=0.This completes the proof. □
5 Proof of Main Result
In this section,we will give the proof of our main theorem.Define
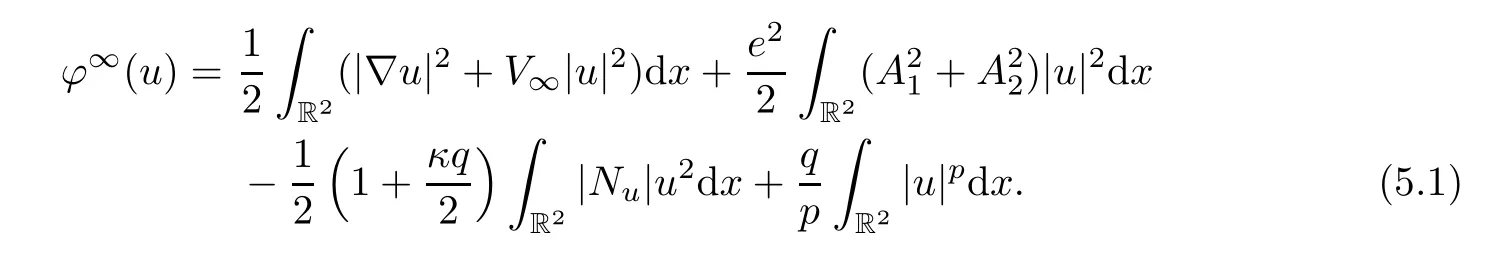
Now we prove that ifV(x) ≤V∞andV(x)V∞,thenc <c∞.
Lemma 5.1Assume that (V1) holds.Thenc <c∞.
ProofAccording to Theorem 4.3,we have that there existsu∞∈M∞such that

It follows from (V1) that
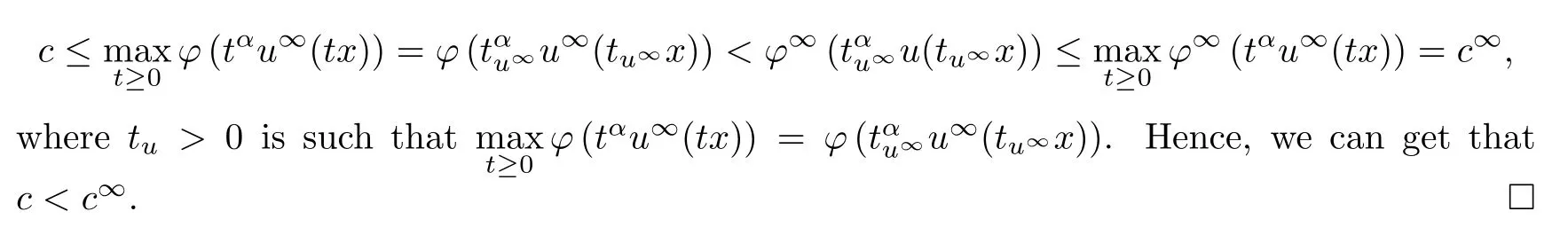
Lemma 5.2Assume that (V1) and (V2) hold,and that 0<e <e*.Then there existsu∈H1(R2){0} such that

ProofBy Lemmas 3.2 and 3.3,there exists a bounded sequence {un} ?H1(R2) satisfying‖un‖ ≤.Hence
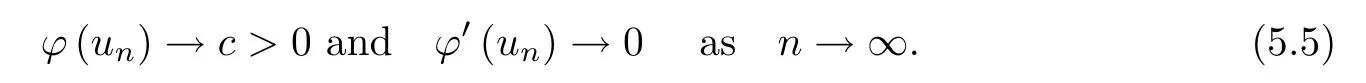
By the boundedness of {un},there exists a subsequence of {un},still denoted by {un},andu∈H1(R2) such thatun?uinH1(R2) andφ′(u)=0.By the global compactness lemma,there existl∈N+∪{0} andw1,···,wl∈H1(R2){0} with (φ∞)′(wk)=0,1 ≤k≤lsuch that

Sinceφ′(u)=0,by (3.24) and Lemma 3.1,we have,for 0<e <e*small,that
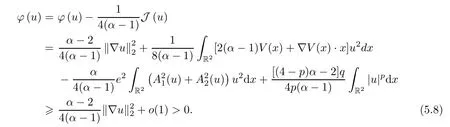
Hence,we have thatc >c∞with (5.7) and (5.8) forl≠0,which contradicts Lemma 5.1.Thus,l=0 andun→uinH1(R2),by (5.6) and (5.7).The result is proven. □
Proof of Theorem 1.1Proceeding as in Lemma 5.2,there exists {un} ?H1(R2){0},up to subsequence,for 0<e <e*,such that

From (V2),(5.8) and (5.9),
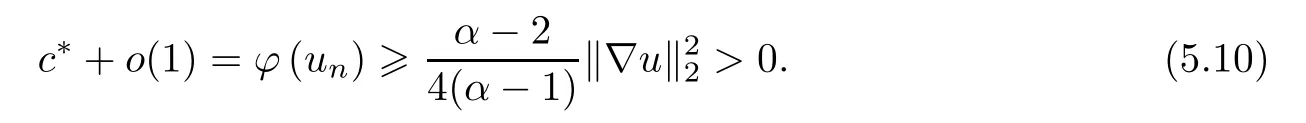
We can prove that {un} is bounded as in Theorem 4.3.It follows from Lemma 5.2 that there exists∈H1(R2){0} satisfying that

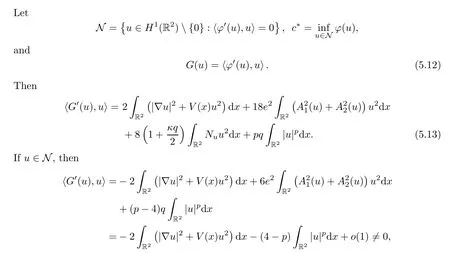
which implies that N is a manifold.On the other hand,we note that N? by (5.11) and the fact thatc*≤cforu∈N.By Lemma 3.1,P(u)=0,and thus J (u)=α〈φ′(u),u〉-P(u)=0,which means that M=N.Moreover,we can get thatc*>0 with Theorem 3.9,Lemma 5.2 and (5.10).Let {un} ?N be such that Thus,it holds thatc*≤c <c∞,by Lemma 5.1.By arguing as in proof of Lemma 5.2,there existsu*∈H1(R2){0} such that
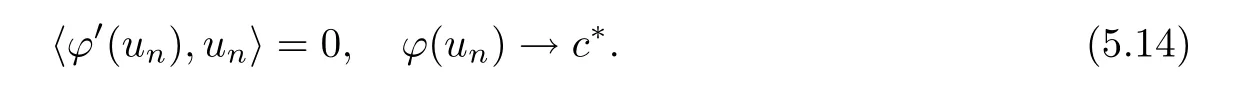
Hence,u*∈H1(R2){0} is a ground state solution of system (1.1)–(1.5). □
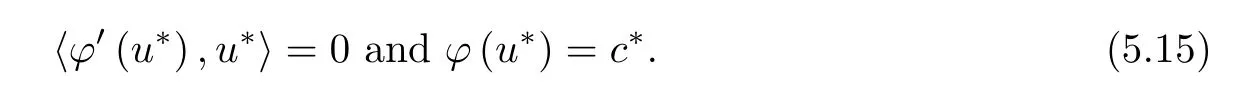
AcknowledgementsThe authors would like to thank Professor Jianfu Yang for many helpful discussions and comments.
 Acta Mathematica Scientia(English Series)2022年5期
Acta Mathematica Scientia(English Series)2022年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ERRATUM TO: SEEMINGLY INJECTIVE VON NEUMANN ALGEBRAS(Acta Mathematica Scientia,2021,41B(6): 2055–2085.)*
- EXPONENTIAL STABILITY OF A MULTI-PARTICLE SYSTEM WITH LOCAL INTERACTION AND DISTRIBUTED DELAY*
- THE ASYMPTOTIC BEHAVIOR AND SYMMETRY OF POSITIVE SOLUTIONS TO p-LAPLACIAN EQUATIONS IN A HALF-SPACE*
- GLOBAL WELL-POSEDNESS FOR THE FULL COMPRESSIBLE NAVIER-STOKES EQUATIONS*
- POINTWISE SPACE-TIME BEHAVIOR OF A COMPRESSIBLE NAVIER-STOKES-KORTEWEG SYSTEM IN DIMENSION THREE*
- PROBING A STOCHASTIC EPIDEMIC HEPATITIS C VIRUS MODEL WITH A CHRONICALLY INFECTED TREATED POPULATION*
