張瀛月, 杜潤梅

(長春工業(yè)大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 長春 130012)

0 引 言

考慮如下發(fā)展型p-Laplace方程的初邊值問題:

其中Ω是N中一個有界閉集, ?Ω是光滑的,n是?Ω上的單位外法向量,c∈L∞(QT),p>2,u0∈L2(Ω)是一個非負(fù)有界函數(shù),h是熱傳導(dǎo)系數(shù), 也是控制函數(shù).定義成本泛函為

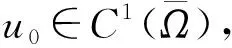
1 預(yù)備知識

定義V=W1,p(Ω),V′表示V的對偶空間.〈u,v〉(u∈V′,v∈V)表示V′-V的對偶積.

定義1如果?φ∈C(0,T;L2(Ω))∩LP(0,T;V)∩L2(0,T;V′), 如下積分等式成立：

則非負(fù)函數(shù)u∈C(0,T;L2(Ω))∩LP(0,T;V)稱為問題(1)-(3)的弱解, 其中τ∈(0,T).

引理1[1]對任意u,v∈LP(0,T;W1,P(Ω)), 下列不等式成立：

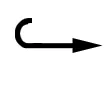
則fn在C0([0,T],X-w)中相對緊.

2 主要結(jié)果

定理1對任意非負(fù)函數(shù)u0∈L2(Ω),h∈UM, 問題(1)-(3)存在唯一弱解u, 滿足

‖u‖L∞(0,T;L2(Ω))+‖u‖LP(QT;n)≤C1‖u0‖L2(Ω),

其中C1是一個與u0和M無關(guān)的常數(shù).進(jìn)一步, 有ut∈L2(0,T;V′), 并且‖ut‖L2(0,T;V′)≤C2, 其中C2是一個僅依賴于u0和M的常數(shù).

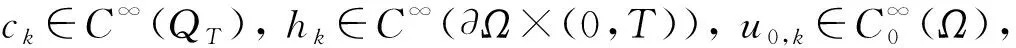
‖ck‖L∞(QT)≤‖c‖L∞(QT), ‖hk‖L∞(?Ω×(0,T))≤‖h‖L∞(?Ω×(0,T)), ‖u0,k‖L2(Ω)≤2‖u0‖L2(Ω).

考慮問題：

由分部積分公式, 得

則有

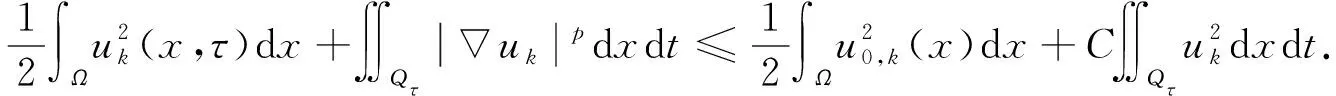
(7)

由Gr?nwall不等式, 有

(8)

由式(7)和式(8), 可得

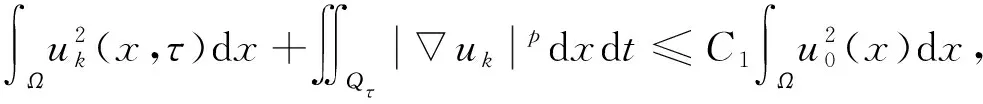
(9)

其中C1是一個與u0和M無關(guān)的常數(shù).對于?φ∈L2(0,T;V), 有

由分部積分可得

其中C2為一個與u0和M有關(guān)的常數(shù).因此,

‖(uk)t‖L2(0,T;V′)≤C2.

(10)

由嵌入定理可知,

且‖ut‖L2(0,T;V′)≤C2.

由于uk是問題(4)-(6)的弱解, 因此對于?φ∈C(0,T;L2(Ω))∩LP(0,T;V)∩L2(0,T;V′), 有

在式(11)中令k→∞, 并利用uk的收斂性, 得

因此,u是問題(1)-(3)的弱解.

下面證明對任意h∈UM, 問題(1)-(3)存在唯一解u.假設(shè)u1,u2為問題(1)-(3)的兩個解, 做差得

對所有的τ∈(0,T), 令φ=u1-u2, 有

對所有的τ∈(0,T), 由引理1有

則

即

定理2若Zd∈L2(QT),u0∈L2(Ω), 且滿足兼容性條件

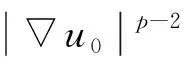
則存在一個最優(yōu)控制h*∈UM, 使得成本泛函J(h)最小.

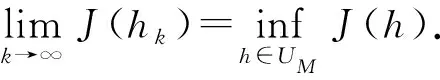
‖uk‖L∞(0,T;L2(Ω))+‖uk‖LP(QT;n)+‖(uk)t‖L2(0,T;V′)≤C,

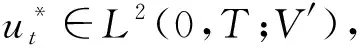
在式(13)中令k→∞, 并利用uk的收斂性, 得

因此,u*是問題(1)-(3)當(dāng)h=h*時的弱解.由J(h)的弱下半連續(xù)性, 有

因此,h*是J(h)在UM上的最優(yōu)控制.