Ship Weather Routing Based on Hybrid Genetic Algorithm Under Complicated Sea Conditions
ZHOU Peng, ZHOU Zheng, WANG Yan, and WANG Hongbo
Ship Weather Routing Based on Hybrid Genetic Algorithm Under Complicated Sea Conditions
ZHOU Peng, ZHOU Zheng, WANG Yan, and WANG Hongbo*
State Key Laboratory on Integrated Optoelectronics, College of Electronic Science and Engineering,Jilin University, Jilin130012, China
Considering the effects of increased economic globalization and global warming, developing methods for reducing shipping costs and greenhouse gas emissions in ocean transportation has become crucial. Owing to its key role in modern navigation technology, ship weather routing is the research focus of several scholars in this field. This study presents a hybrid genetic algorithm for the design of an optimal ship route for safe transoceanic navigation under complicated sea conditions. On the basis of the basic genetic algorithm, simulated annealing algorithm is introduced to enhance its local search ability and avoid premature convergence, with the ship’s voyage time and fuel consumption as optimization goals. Then, a mathematical model of ship weather routing is developed based on the grid system. A measure of fitness calibration is proposed, which can change the selection pressure of the algorithm as the population evolves. In addition, a hybrid crossover operator is proposed to enhance the ability to find the optimal solution and accelerate the convergence speed of the algorithm. Finally, a multi-population technique is applied to improve the robustness of the algorithm using different evolutionary strategies.
genetic algorithm; simulated annealing algorithm; weather routing; ship speed loss
1 Introduction
Economic globalization has become an inevitable current trend. In this process, ocean transportation is the core of the cross-border transportation network that supports supply chains and international trade (Veneti, 2017; Wang, 2018). According to the annual maritime industry summary report released by the United Nations Con- ference on Trade and Development in 2016, the estimated total volume of global maritime trade in 2015 exceeded 10 billion tons, accounting for more than 80% of the world’s total merchandise trade (United Nations Publications Staff, 2016). Thus, maritime transport is an essential link in the global economy and is thus of vital importance.
In this process, opportunities and risks coexist. With the increasing demands for the development and utilization of marine environments, maritime traffic has become increasingly dense; moreover, the complexity of the maritime transportation environment has brought huge challenges to the maritime industry worldwide (Roberts, 2014; Zis, 2020). As a result, increasing attention has been paid to the role of ship weather routing in improving the efficiency of shipping, economy, and safety of maritime transport. The development of ship weather routing technology not only remarkably improves the navigation econ- omy but also improves the seaworthiness of ships in transocean navigation. As an important aspect of navigation technology, ship weather routing has always occupied a crucial position for ensuring safety and efficiency (Tsou and Cheng, 2013; Vettor and Guedes Soares, 2016). Furthermore, an excellent ship route reduces operating costs and improves the economic benefits for shipping companies.
Ship weather routing refers to the process of obtaining the optimal shipping route according to weather forecast data and specific ship parameters that are determined in advance (Padhy, 2008; Lin, 2013). The optimization goal of ship weather routing is not a single item. According to the actual needs, the optimization goals can include minimizing the voyage distance, voyage time, total fuel consumption, and voyage risk. The traditional route optimization goal is to minimize the route length and thus reduce the sailing time. However, with the vigorous developments made in the maritime industry and navigation technology, the traditional optimization goal has become less applicable to the modern maritime industry. Instead, advances in science and technology have enabled relevant meteorological data to be more easily obtained during navi- gation with greater accuracy. Accordingly, the shipping industry has put forward higher requirements for energy efficiency and safety during navigation, such as minimizing ship fuel consumption and gas emissions (Perera and Soares, 2017). According to the greenhouse gas research report released by the International Maritime Organization (IMO) in 2014, the average annual carbon dioxide emission equivalent of the global shipping industry from 2007 to 2012 was 10.15 million tons, accounting for 3.1% of the total global carbon emissions (IMO, 2014). The shipping industry has clearly become one of the main sources of carbon emissions. According to IMO estimates, if effective emission reduction measures are not taken, the global shipping industry’s total greenhouse gas emissions by 2050 could increase 50% to 250% based on the 2012 emission level. On the background of a global agreement on emissions reduction, it is particularly important for the shipping industry to reduce these emissions. The most important factor is to ensure safety in the ship’s navigation because the risk of casualties and environmental risks caused by maritime accidents in maritime transportation is often very high. This is particularly true in the transfer of hazardous substances such as chemicals or petroleum, which have an irreversible adverse impact on the marine ecology. Therefore, in this study, the main consideration is to maximize the safety of ships during navigation. Ship route optimization, another important optimization objective, must be constrained by meteorological information and sea conditions. Marine hydrological and meteorological conditions are important guarantee for ensuring safe navigation and economical shipping. In the marine environment, ships encounter resistance caused by wind, waves, and currents, which results in slamming and swing, often leading to ship speed loss, ship structural damage, and serious maritime accidents. Shao(2012) determined that the efficiency of ocean-going ship route planning is determined mainly by the following three aspects:
1) the accuracy of predicting the hydrodynamic behavior of ships under different weather conditions;
2) the accuracy of the meteorological information;
3) the performance and practicability of the algorithm used for ship route optimization.
In this study, on the basis of accurate meteorological information, sea conditions, and ship parameters, the minimum fuel consumption and voyage time of the ship are set as the ship route optimization objectives for ensuring navigation safety. This study focuses on mathematical model of weather routing and optimization algorithm. Because weather routing has very important practical significance, this problem has attracted the attention of many researchers who have proposed numerous optimization algorithms. James (1957) applied the isochrone method to ship the weather routing problem, which was the earliest algorithm used for ship optimal route design. However, this method essentially calculated the ship route trajectory by manual operation, correction of the trajectory resulted in considerable difficulty and inconvenience. Hagiwara and Spaans (1987) improved the isochrone method using a computer to perform route optimization calculations to determine the optimal ship route with the greatest benefits according to the sailing requirements. However, the isochrone method has the so-called ‘isochrones loop’ disadvantage. To solve this problem, Roh (2013) proposed an improved isochrone algorithm. Lin(2013) proposed a three-dimensional isochrones method (3DMI) that considered water depth factors as well as weather factors. This approach can effectively optimize the ship’s route by adjusting the weight factor in the objective function. Dynamic programming based on Bellman’s optimal principle is another method thatuses computer programming for weather routing (Bellman,1956). Shao(2012) proposed a three-dimensional dy- namic programming (3DDP) method and set the reduction of fuel consumed during the ship’s voyage as the optimization goal. In their study, floating point state technology was adopted to reduce the number of iterations in the optimization process, thereby improving computational efficiency. The simulation results showed a fuel savings of 3.1%. The calculus of variations method was originally proposed by Haltiner(1962). Bijlsma (2001) improved this method to find the route of minimum fuel consumption. However, this approach is limited to theoretical analysis, and the calculation is time-consuming; thus, it is not suitable for practical application (Tsou and Cheng, 2013). Pathfinding algorithms such as the Dijkstra algorithm and the A* algorithm have also been applied in weather routing problem. Padhy(2008) designed a method for solving this problem based on the Dijkstra algorithm to obtain a reliable, optimum route in a given random sea state. Mannarini(2016) applied the Dijkstra algorithm to weather routing and designed a ship routing decision support system that took meteorological and marine data as environmental factors and used the improved Dijkstra algorithm to select the best ship route. Sen and Padhy (2015) pointed out that the disadvantage of the Dijkstra algorithm is that its route optimization is not smooth. Park and Kim (2015) combined the A* algorithm with a speed scheduling phase problem to obtain the optimal route with minimum fuel consumption. Bentin(2016) applied the A* algorithm to ship weather routing problems and also considered wind-assisted propulsionFlettner rotors. The simulation showed that the optimized route could reduce fuel consumption to save costs.
In recent years, many intelligent heuristic algorithms have been applied to ship route planning. Compared with traditional methods, intelligent heuristic algorithms have the outstanding feature of solving problems faster and can quickly search the solution space to obtain a satisfactory solution. Popular intelligent heuristic algorithms in current usage include simulated annealing algorithm, ant colony algorithm, and genetic algorithm. Kosmas and Vlachos (2012) proposed a method for optimizing ship weather routes based on the simulated annealing algorithm. The cost function was set as the weighted sum of the voyage time and voyage comfort, and the safety during the voyage was also considered. Tsou and Cheng (2013) applied the ant colony algorithm to the optimal route design problem and introduced the genetic algorithm operation to optimize the ship route from the starting port to the destination port. Maki(2011) regarded the weather routing problem as a multimodal function problem and applied a real-coded genetic algorithm to search for the global optimal route. This method takes parametric roll risk as one of its objective functions and is numerically verified with other objective functions having different weighting ratios between fuel efficiency and ship safety. The results showed that the relationship between economy and safety is a compromise and that the safest ship route is not necessarily the most economical. Kang(2012) proposed a meta-heuristic method based on the genetic algorithm and applied it to solving the ship weather routing problem. This model served as the basis for developing a maritime traffic planning support system for providing decision support for the ship’s navigation. Pan(2021) developed an approach based on the modified genetic algorithm to optimize the ship weather route. To address an incomplete ship speed fuel consumption table, SPSS software was used to obtain the fitting formula of ship fuel consumption to calculate the fuel consumption value of the ship route. In many research fields, the hybrid genetic algorithm has been applied. However, no scholars have combined the simulated annealing algorithm and the genetic algorithm to optimize the ship route in the field of weather routing. The present research uses these two algorithms as research methods to propose a hybrid genetic algorithm for solving the problem of ship weather routing under com- plicated sea conditions. Essentially, the objective is to determine the route with the shortest voyage time or fuel consumption from the starting port to the destination port for ocean-going ships with routes that are comprehensively affected by multiple dynamic weather elements. The pro- posed algorithm is then evaluated by performing a series of numerical simulation experiments in the North Atlantic Ocean.
This paper is organized as follows. In Section 2, the ma- thematical model of ship weather routing is constructed. In Section 3, the ship speed loss and fuel consumption calculation are introduced. In Section 4, the calculation method of risk during navigation is introduced, and the application of a hybrid genetic algorithm for ship weather routing is described in Section 5. In Section 6, a series of simulation experiments is designed to verify the validity of the proposed algorithm.
2 Mathematical Model of Ship Weather Routing
2.1 Environment Modeling
The environmental model of ship navigation has a significant impact on the performance of the algorithm. Considering the practicability, effectiveness, and difficulty of implementation, a grid system was used to model the ship’s navigation environment owing to its strong suitability for the weather route planning of ships and high compatibility with the weather forecast information. The actual environment of the ship’s navigation is a three-dimensional grid system composed of countless two-dimensional grid systems. Each two-dimensional grid system corresponds to the actual environment model of ship navigation at different moments of time, as shown in Fig.1. At the timeof the ship’s voyage, the sailing area is divided into a×grid system, denoted as(,,). The pink cylinders represent static obstacle areas during the ship’s navigation, such as islands or forbidden zones in the environment modelin Fig.2. The navigation areas are divided at equal intervals along the directions of longitude and latitude lines, respectively.represents the number of divisions along the latitude line, andrepresents the number of divisions along the longitude line. The resolution of the selected environmental model needs to be matched with that of the marine weather forecast data. The higher resolution of the grid makes the accuracy of the constructed environment model higher, which is closer to the actual situation. However, the amount of data processed also increases greatly. A ship route will be divided into more waypoints, and the calculation complexity of the route will increase sharply. Considering the above factors, the spatial resolution adopted in this paper was 1?×1?. The navigation area used to verify the optimization algorithm was selected as the North Atlantic Ocean between latitude lines 0? and 60?N, longitude lines 90? and 1?W.The corresponding values are=90 and=61, and the entire environment model had 5490 grid nodes. Each node can be encoded with a natural number from 0 to 5489. The node number for a given latitude and longitude coordinate can be calculated using the following formula:

Similarly, given a node number, the corresponding latitude and longitude coordinates can be calculated using the following formulas:
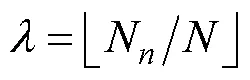
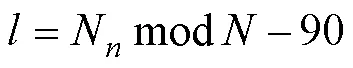
whereNis the node number,is the latitude, andis the longitude.
As a part of the ship’s decision supporting system, the results of the weather routing need to be embedded in an electronic chart display and information system (ECDIS) for usage. The Mercator projection map is used in this research algorithm; accordingly, if the optimized ship route is to be applied in the ECDIS, the conversion between the geographic coordinate system and the Cartesian coordinate system in the projection map must be completed (IOGP, 2019).
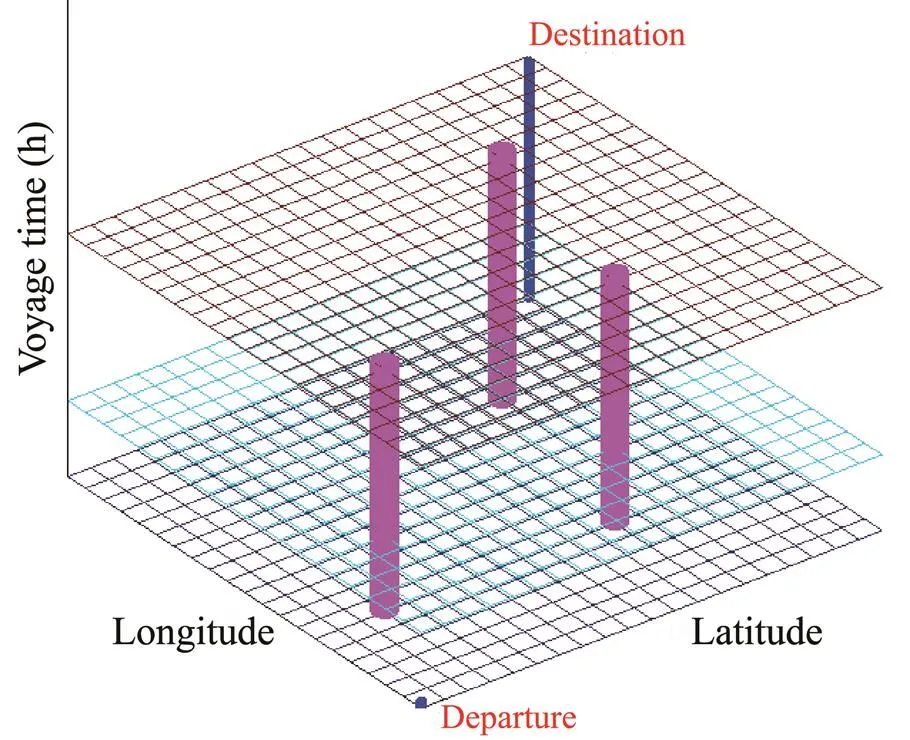
Fig.1 Schematic of the navigation area.
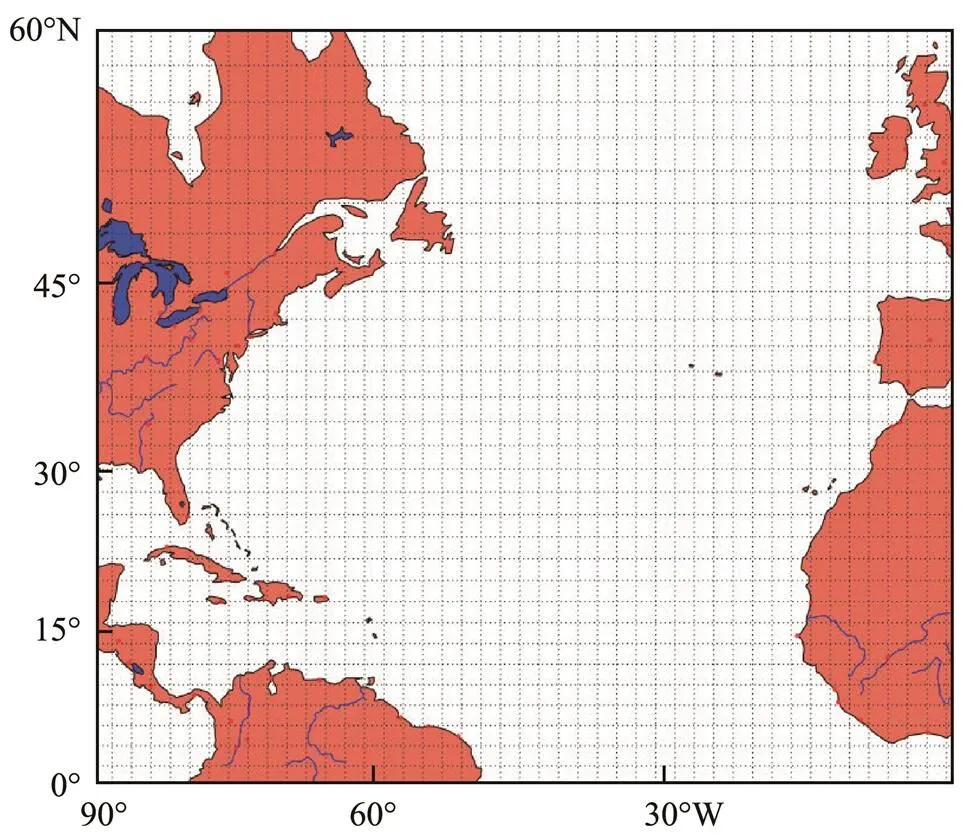
Fig.2 Environment model of the navigation area.
We set the geographic coordinates of the Earth as (,). The formulas for converting the geographic coordinates (,) into Cartesian coordinates (h,Y) of Mercator projection are
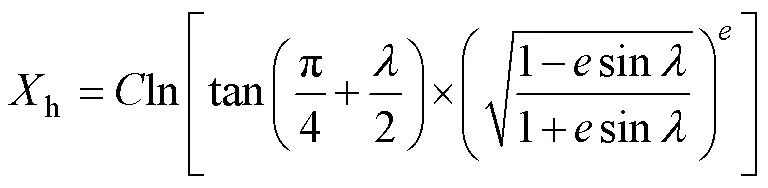
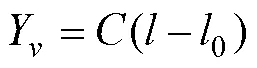

where0represents the base latitude of Mercator projection,0represents the prime meridian,is the first eccentricity of the Earth ellipsoid, and,are the long and short radius of the Earth ellipsoid, respectively.
Using the Mercator inverse solution formula, the Mercator projection is inversely transformed, and the Cartesian coordinate (h,Y) is transformed into geographic coordinates (,). The transformation formula is as


2.2 Determinating Subspace for Searching the Optimal Ship Route
After the environmental model of route planning was established, the search space of the optimal solution was determined. After the starting point S and end point D of the route are set, the optimal ship route can be obtained by searching the solution space using the optimization algorithm. However, not all of the very large established sailing area needs to be used to find the optimal ship route. Therefore, it is necessary to reduce the original grid system to consider only a small area of navigation. First, a reference route was established from the starting point to the end point, and a strip-shaped navigation area was then established on the basis of this reference route to determine the search subspace of the optimal ship route. The route solution space for finding the optimal solution can be greatly reduced through this operation; the calculation amount of the algorithm is reduced; and the speed and efficiency in searching for the optimal route are improved. Because an evolutionary algorithm was used in this study, there was no need to search in the entire solution space; rather, searching only in its subspace quickly resulted in a feasible solution that fully meets the navigation needs of shipping companies.
Fig.3 shows a schematic diagram of the constructed route solution subspace, including the strip-shaped navigation area from starting point S to end point D. First, we established a great circle route from the starting point to the end point as a reference route, and we determinedequidistant nodes on the reference route. Theseequidistant nodes divide the reference route into?1 equal parts, and then make orthogonal lines perpendicular to the reference route through the nodes on the Mercator projection graph. The length of the orthogonal linePdetermines the range of the search subspace, each orthogonal linePcan be defined as the following.
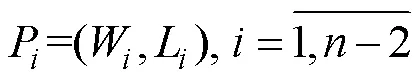
whereWrepresents theth waypoint on the reference route, andLrepresents the actual distance of the orthogonal line on the Mercator projection graph. On both sides of the reference route, the endpoint of each orthogonal line is successively connected from the starting point to the end point, and the navigation area enclosed by the connecting line determines the search space of the route solution.
Fig.3 Subspace for searching optimal ship route.
2.3 Objective Function
In practice, many criteria can be used for building a ship weather routing model, and the optimization results of the algorithm continue to move toward the optimal solution under the constraint of optimization criteria. In this study, two criteria were used for optimizing the ship routes: voyage time and fuel consumption. These two criteria were thus used as optimization objectives for ship weather routing.
2.3.1 Minimization of ship voyage time
Within the defined navigation area, if the route constraints are met, a ship route appears from the starting port to the destination port that makes the navigation of the ship the least time-consuming. From the perspective of minimum voyage time, the route is indeed the optimal solution of the entire solution space but is not necessarily usable. Because we convert in this study the route planning problem from a continuous optimization problem to a discretization optimization problem, the total navigation time from the departure port to the destination port is
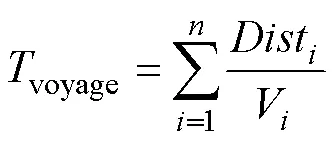
whereDistis the length of the-th route segment,Vis the actual ship’s speed along the-th segment, andvoyageis the total voyage time from the departure port to the destination port. The optimization goal of minimizing the ship’s voyage time is to minimize the value ofvoyage. The calculation of ship speed will be explained in detail in Section 3.
2.3.2 Minimization of fuel consumption
The total fuel consumption of ships in a voyage is a keyindicator for measuring the economic benefits and energy-saving performance of the ships. Shipping companies hope to minimize the fuel consumption of navigation to save operating costs while saving energy and reducing emissions, which is beneficial for the ecological environment. Therefore, fuel consumption is also a key criterion for selecting the optimal ship route. The total fuel consumption of ships from the departure port to the destination port is expressed as
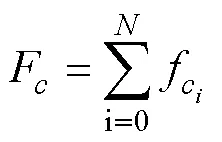
Ensuring safety during navigation is the basis of ship weather routing; thus, the safety of ship navigation is also an important factor to be considered in searching for the optimal ship route. For this reason, a penalty function was imposed on the objective function of route planning in this study. The penalty function considers two variables: the value of the objective function and the risk of the ship’s navigation. Estimation of the ship’s navigation risk will be explained in detail in Section 4. The introduction of penalty function makes unsafe route solutions relatively easy to be eliminated in the population evolution process and also ensures that the final optimal route solution is safe and feasible. Therefore, the objective function of ship wea- ther routing is expressed as
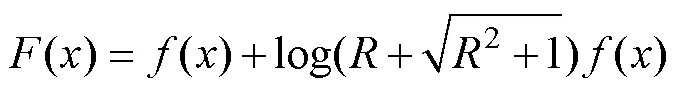
where() is the objective function,() is the ship’s voyage timevoyageor fuel consumptionF, andis the risk of the ship’s navigation.
3 Ship Speed Loss and Fuel Consumption
Compared with that in still water, when a ship sails on the ocean, it will inevitably be affected by the marine environment. These effects could be adverse or beneficial in the ship’s navigation. James (1957) found that the most important factor hindering the navigation of ships is the effect of surface waves, which is reflected in two main aspects: natural speed loss and voluntary speed reduction. The ship speed loss is an important basis for the ship’s weather routing. The calculation of the speed loss will directly affect the quality of the final solution; thus, to calculate the voyage time of each segment, it is necessary to estimate the actual speed of the ship in the wind and wave environment. For calculation of the actual ship speed in themarine environment, calculation of ship speed loss in different weather conditions is essential. In this study, Eq. (13) (Liu, 1992) was adopted to calculate the ship speed loss. The model reduces the prediction error of the ship speed loss to a certain extent and has a relatively wide application range:
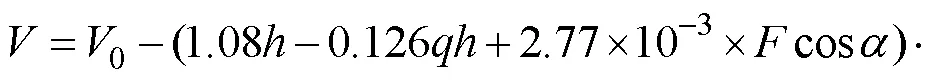

whereis the actual ship speed in a wind and wave environment (kn),0is the corresponding ship speed in still water (kn),is the significant wave height (m),is the relative angle between ship’s course and wave direction (rad),is the wind speed of the ship’s environment (m s?1),is the relative angle between the wind direction and ship’s course (rad), andis the actual displacement of the ship (tons).
An appropriate calculation method for the ship’s fuel consumption is of great significance for improving the economic benefits of ship navigation and for reducing the energy consumption, which is critical to the quality of the optimal solution. For the calculation of fuel consumption, the mathematical interpolation method was adopted in this study. The Lagrange interpolation method was introduced to construct the fuel consumption model for ship weather routing. First, according to the historical navigation data of the ship, a rough corresponding relationship between the ship speed and fuel consumption of the S-175 container ship was obtained, as shown in Table 1. Obviously, these data are far from sufficient and are not accurate enough for obtaining the actual fuel consumption of the ship. Thus, we combined the Lagrangian interpolation method with the ship speed and fuel consumption table to construct an effective and practical model for evaluating the fuel consumption per unit time of the ship at a certain speed. The Lagrange interpolation formula serves as the basis function at the node to provide a linear combination of this function, and the combination coefficient is the node function value. Lagrangian interpolation is a classic polynomial inter-polation method. The Lagrangian polynomial used for inter- polation of ship fuel consumption is as follows.
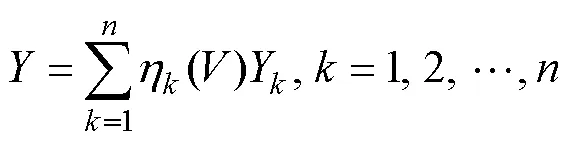
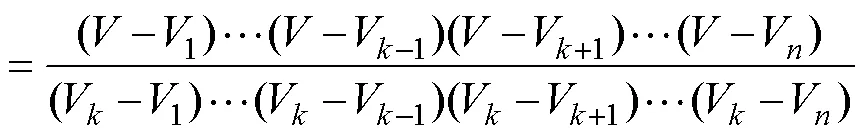
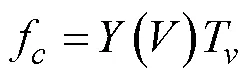
wherefis the amount of fuel consumed by the ship on a certain route segment,() is the fuel consumption value per hour of the container ship,andTis the time spent on the route segment.
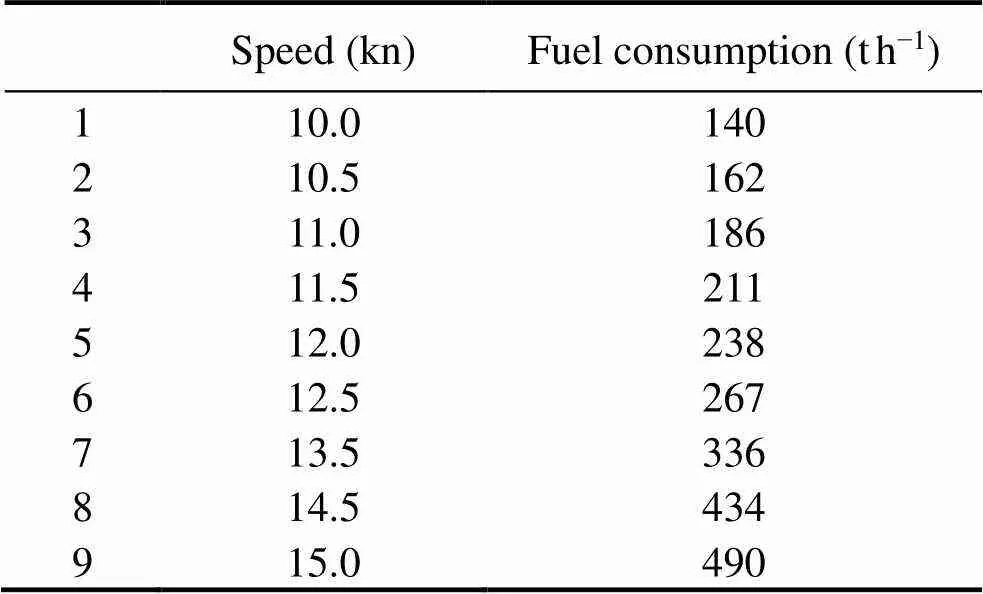
Table 1 Relationship between speed and fuel consumption of the container ship

Fig.4 Fuel consumption interpolation results.
4 Estimation of Navigation Risk
A ship sailing under severe weather conditions is likely to encounter various dangerous conditions that can cause the ship to capsize or experience violent rolling motion, resulting in human casualties as well as serious cargo and equipment losses. When planning the optimal ship route, whether the optimization goal is the minimum fuel consumption or the minimum sailing time, the safety of the ship during the voyage must be ensured before other goals can be considered. Therefore, weather routing requires an effective estimation method for the safety of the ship during navigation.
Many different factors should be considered when assessing the navigation risk of the selected ship route, such as the meteorological and environmental conditions of the navigation area, specific ship parameters, and crew operation. In the optimization algorithm used in this study, the navigation risk assessment method of the ship route considers the characteristics of the navigation area, specific ship parameters, and weather forecast information. The me- thod of risk estimation proposed in this study takes into account the guidance of the IMO (Szlapczynska, 2015), which offers advice on avoiding dangerous situations under severe weather and sea conditions. This document lists se- veral dangerous situations that ships might encounter in harsh marine environments, such as successive high-wave attacks. On this basis, to calculate navigation risk, the wea- ther warning area was defined for the route risk in this study. The sea area where the wave height exceeds 4.6m or the wind speed exceeds 21ms?1during navigation is de-fined as the weather warning area, which should be avoided by ships during navigation.
When ships enter such dangerous areas, the probability of navigation accidents will greatly increase. Therefore, in the final optimization results, the optimal route will not pass through the dangerous areas specified by the IMO, and the risk value of the optimal route should be minimized. In this study, the frequency of the ship route passing through the dangerous zone specified by IMO’s guidance (IMO, 2007) was used as the criterion for estimating the risk of the ship route. When a ship route passes through the dangerous area more frequently, the navigation risk will be higher, and the accident probability will increase. The chromosomes represented by such routes will be quickly eliminated during the evolution of the population. In the optimization algorithm, a route risk counterwas defined to count the number of times the ship route entered dangerous seas of the weather warning area; the value of the counter was recorded when the ship reached the destination. In addition, a risk coefficientwas introduced to help eliminate individuals with low seaworthiness and to improve the execution efficiency of the algorithm. The calculation formula that quantitatively expresses the risk value of ships at sea is

whereis the number of segments of a ship route;represents a ship route, corresponding to a chromosome inthe genetic algorithm population;() is a set of ship routes to be optimized, corresponding to a complete population of the ship route; Ωis the static navigable sea area, obtained by removing static obstacle areas such as land, islands, and forbidden zones in navigation area; and0is the time difference between the ship’s departure time and the latest weather data update time prior to the departure time, which is less than the estimated time of arrival of the ship (ETA). The coefficient value ofwas set as 10.
5 Ship Weather Routing Based on Hybrid Genetic Algorithm
First proposed by Holland (1992) in 1975, the basic genetic algorithm was inspired by Darwin’s natural selection mechanism and is an essential global parallel stochastic search method. This algorithm is a type of heuristic evolutionary algorithm with three basic operations–selection, crossover, and mutation operations–which largely determine the performance of the algorithm and provide a basic framework for various genetic algorithms. In this study, a hybrid genetic algorithm was proposed to optimize the ship routes. A simulated annealing algorithm based on the standard genetic algorithm was introduced to strength- en the local search capability of the optimization algorithm and to ensure its convergence. In this study, because the ship’s navigation area is a continuous search space, the real coding was used in the hybrid genetic algorithm to find the optimal ship route in the search space, which is more efficient and compatible for the ship weather routing problem than the binary coding. For the problem of route planning, each ship route can be encoded as a chromosome in the hybrid genetic algorithm, and the corresponding fitness is assigned to each chromosome in the population. The process of the hybrid genetic algorithm in this study is shown in Fig.5.
5.1 Tunable Ship Route Variables
If all factors in the navigation process are considered, the optimal route design problem will become extremely complicated or even unsolvable; thus, simplification of the optimization problem is necessary. In this study, the ship route is composed of multiple route segments, each connected by a rhumb line, which is a line on the chart that intersects all meridians at the same angle. On a plane surface, this would be the shortest distance between two points. Each segment of the route contains the information of latitude and longitude coordinates, heading angle, and ship speed of the waypoint, as shown in Fig.6, where S, D are departure and destination, respectively;Nrepresents the waypoint of the-th segment; (,l) are the latitude and longitude coordinates of the-th waypoint, respectively;is the heading angle of the-th segment of the route, which is 0? in the north direction, increasing in the clockwise direction; andVis the still water speed of the ship on the-th segment of the route.

Fig.5 Hybrid genetic algorithm flow chart.
Fig.6 Route segments and ship route variables.
To convert the considered problem into a finite-dimensional optimization problem, it is necessary to introduce a set of independent adjustable variables, which can be used to determine the ship’s complete route. These adjustable variables include the number of route segments, the latitude and longitude coordinates of the waypoints, the heading angle, and the still water speed of the ship on each seg- ment of the route. Assuming that the ship route consists ofsegments, the vectorcan be defined to represent a ship route as
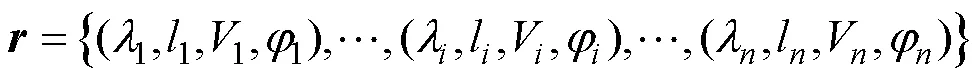
To be compatible with the genetic algorithm to handle route planning problems, let encode the route vectorinto the chromosome formas
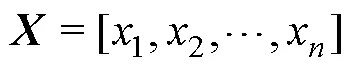
where the first and second halves of the components of the vectorcontain the position information of the waypoint of the route and the speed information of the ship on each route segment, respectively.
In the genetic algorithm, a chromosome represents an individual in the population. For the weather routing problem, the data structure of the population can be expressed as a matrix, shown as
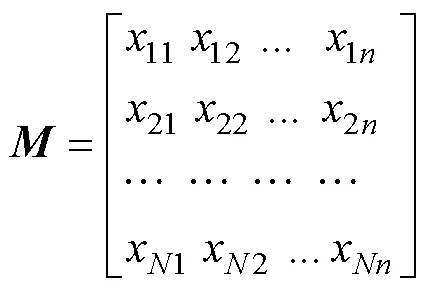
whereis the number of individuals in the population.
5.2 Fitness Calibration
Fitness is the criterion used for evaluating the quality of each individual in the population and is the only criterion for selection operations. Driven by this, the genetic algorithm can continue to evolve toward the optimal solution. To solve the problem of the weakening of the algorithm selection function in later periods, this study calibrated the individual fitness as
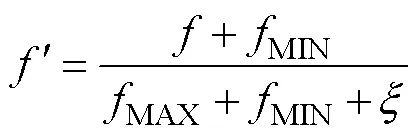
whereis the original fitness value,is the individual fitness after calibration,MINis the lower limit of the population fitness value,MAXis the upper limit of the population fitness value, andis a random number between 0 and 1. The introduction ofincreases the randomness of the genetic algorithm and adjusts the selection pressure of the optimization algorithm so that even the worst individual in the population can reproduce. This maintains the diversity of the population in the wide-area search range and keeps the convergence in the local search range.
5.3 Selection Operation
In the search process of the genetic algorithm, the selection operation embodies Darwin’s natural selection me- chanism. On the basis of the individual fitness value, the selection operator randomly selects relatively good individuals from the parent population according to the given selection strategy and copies these individuals to the offspring population with a certain probability and number. As a result, the good genes of the present generation can be passed on to the next generation. The genetic algorithm provides many selection methods, each of which has advantages and disadvantages. In this study, the selection operator adopted the stochastic universal selection strategy, which is similar to roulette selection. However, the roulette selection method requires multiple roulette rotations, stochastic universal selection needs only one roulette rotation to complete the overall selection operation. The rotating pointers are used to locate and select the individuals in the population and are uniformly distributed on the roulette wheel. The number of rotating pointers is equal to the population size. Assuming that the fitness of the-th individual in the population isfand the population size is, the first pointer1is randomly generated in the range of [0, sum(f)/], and the remaining pointers are generated at equal intervals at a distance of sum(f)/. By turning the roulette wheel once, the selected individual is determined according to the interval at which the pointer falls, as shown in Fig.7. Compared with roulette selection, this method enables inferior individuals in the population to have a chance to be selected. Even individuals with low fitness and poor performance still have the opportunity to reproduce offspring. Thus, to a certain extent, fair competition between individuals of the population is guaranteed.
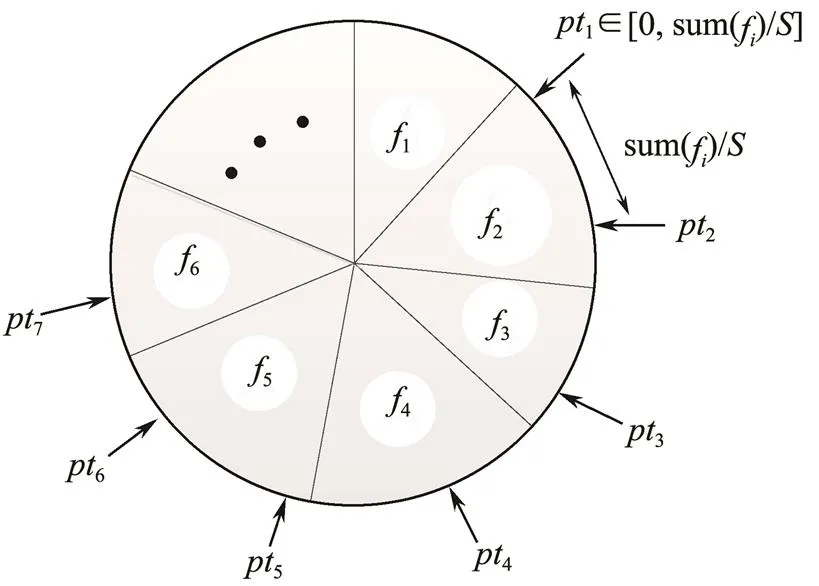
Fig.7 Stochastic universal selection.
5.4 Crossover Operation
In genetics, two homologous chromosomes form a new chromosome through recombination, thereby producing a new individual or species. The crossover operation of the genetic algorithm simulates this phenomenon. In the evolution of the population, the crossover operator is used to first generate new individuals and then to search effectively in the solution space of the weather routing, which determines the global search ability of the algorithm. Because the real-coded method was used in this study, the optimization algorithm adopted the Laplace crossover operator (Deep and Thakur, 2007) and discrete directed cross- over operator to perform the recombination operation. Theseoperators were applied to different subpopulations to achieve different evolutionary effects.
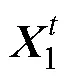
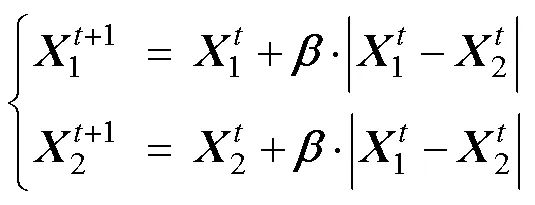
whereis a parameter vector with the same dimension as the chromosome, and each componentof the vector is a random number that follows the Laplace distribution. The calculation formula of component is as
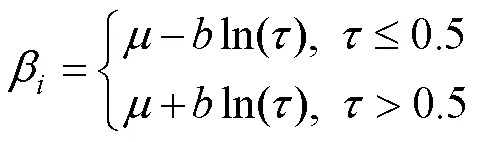
where?R is the position parameter of the Laplace distribution,is the scale parameter, andis a uniformly distributed random number in [0, 1].
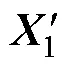
5.5 Gaussian Mutation
The crossover operator is the main component used for generating new population individuals in the genetic algorithm and determines its global search ability. The crossover operator is considered to be the main genetic operator, and the mutation operator is an auxiliary operator for the crossover operation, which is combined with the crossover operation to search the solution space together. The algorithm in this study adopted the Gaussian mutation method. After the population of ship routes undergo the recombination operation, the Gaussian mutation operation is performed to obtain the population after the mutation operation. Assuming that the route individual before the Gaussian mutation operation is=[1,2, ···,x, ···,x] and the route individual after the mutation operation is=[1,2, ···,, ···,x]; then, the individual componentxis the mutation point. Considering the bound- ary constraints of the route, the new individual componentcan be determined by the following formula:
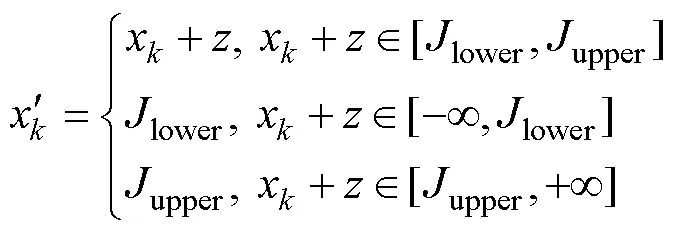
whereupperandlowerrepresent the upper and lower limits of an individual component, respectively, andis a Gaussian random number with a mean value of 0 and a variance of 1.
5.6 Simulated Annealing Operation
In this study, the genetic algorithm and simulated annealing algorithm (SAA) were combined to design a hybrid genetic algorithm for optimizing the ship weather routes.Both algorithms have unique advantages and disadvantages. On the basis of the genetic algorithm, the introduction of simulated annealing algorithm can help the genetic algorithm overcome the limitation of its weak local search ability, thereby greatly improving the reliability and efficiency of the algorithm and weakening the strict requirements on the selection of algorithm control parameters.Regarding the annealing method of the SAA, the temperaturechanges from high to low according to the attenuation function. Annealing in the optimization algorithm in this study was performed according to the following formula:

whereis the attenuation factor, which is a positive number less than 1. Generally, the value is between 0.8 and 0.99 to enable sufficient transfer attempts for each temperature. In addition,0is the initial temperature.
To combine the SAA with the genetic algorithm to achi- eve the purpose of global optimization, the random disturbance imposed on the solution of the problem needs to be considered. The disturbance model needs to be designed according to a specific problem. The key is to construct an appropriate neighborhood function so that each route chromosome can generate a new chromosome within its individual neighborhood in the SAA and then receive or discard the newly generated route chromosome in a certain manner. Ingber (1989) proposed a very fast simulated annealing algorithm (VFSA), which used a temperature-dependentpseudo Cauchy distribution to achieve a good effect. Accordingly, we applied the disturbance method to the ship route planning problem and made corresponding adjustments to ensure compatibility with the calculation method of the route chromosome in the genetic algorithm. Assuming that a chromosome of the population in the genetic algorithm is=[1,2, ···,x, ···,x], the calculation method of the new chromosome after random disturbance is
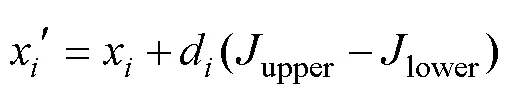
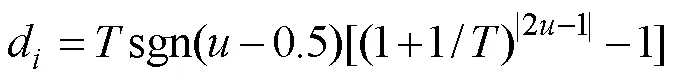
wherexis theth component of the chromosome vector;upperandlowerare the ranges ofx, which represent the upper and lower boundary constraints of the navigation area, respectively; sgn is the sign function; and?[0, 1] is a uniformly distributed random number.
According to the SAA’s Metropolis criterion, the deteriorating solution can be accepted in the optimization process. That is, in the process of route optimization, a non-optimal ship route will be accepted with a certain probability, which enables more possibilities in the solution space.is a chromosome representing a route individual after being disturbed; its probability of acceptance is calculated as
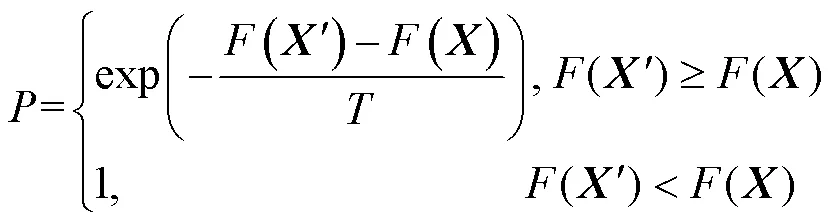
In this equation,() is the objective function of the route individual, which is set as the voyage time and fuel consumption in the algorithm. In this case, the possibility of accepting the non-optimal route solution in the population continued to decrease with a decrease in temperature.
5.7 Multi-Population Technique
In this study, the multi-population technique was used to divide the complete population into several parts and to apply different algorithm control parameters and evolution strategies in different sub-populations so that each sub-pop- ulation can optimize ship routes in parallel. The optimal ship route is the comprehensive result of the co-evolution of multiple sub-populations.
Because the sub-populations are independent of each other, in order to achieve co-evolution, each sub-popula- tion communicates with each other through the migration operator. According to the migration rate, the migration operator is used to periodically migrate the individuals withhigher fitness in each sub-population to another sub-popu- lation to realize the exchange of genetic information between sub-populations. This research adopted the adjacent migration mode to enable the migration of individuals be- tween adjacent sub-populations with no migration occurring between non-adjacent sub-populations. The migrationdirection is arbitrary. For example, individuals can migrate only between sub-population 1 and sub-population 2, as shown in Fig.8.
Fig.8 Adjacent migration mode.
6 Experimental Results
In this research, an S-175-type container ship with a displacement of24742m3was chosen for the simulation experiment for route optimization. The interim_dailywea- ther data were obtained from the public database of the European Centre for Medium Range Weather Forecasts. The weather data included the following parameters: 10 meterwind component, 10 meterwind component, mean wave direction, mean wave period, and significant height of combined wind waves and swell. The resolution of weather data was 1?×1?, and the time interval for updating was 6h. The sea area of the North Atlantic Ocean selected for the simulation experiment had a longitude range of [90?W, 1?W] and a latitude range of [0?, 60?N]. Figs.9 and 10 show the weather conditions of wave and wind in the navigation environment model at certain times on November 4, 2018.
In all simulation experiments, the genetic algorithm and the SAA had the same parameter settings. For the genetic algorithm, the maximum number of iterations was set to 150, the number of sub-populations was 6, the size of each subpopulation was 20, the mutation probability was set to 0.2, and the migration probability was 0.2. As SAA parameters, the initial temperature was 150℃, the low temperature threshold was 10℃, the number of inner loop iterations was 20, and the temperature attenuation factor was 0.85. The algorithm proposed in this study run in the MATLAB environment with the following computer configuration: Intel Core i5-7400 CPU, 3.00 GHz, 16 GB RAM. This algorithm aimed to optimize the ship route as a single goal. Three different simulation experiments were designed to verify the performance and effectiveness of the algorithm; the simulation results are analyzed and explained in this section. The first and second simulation ex- periments were performed to optimize the ship’s route with the minimum voyage time and the minimum fuel consum- ption, respectively, while considering the weather conditions and marine environment constraints. The third simulation experiment verified the influence of the simulated annealing mechanism on the local search ability of the algorithm.
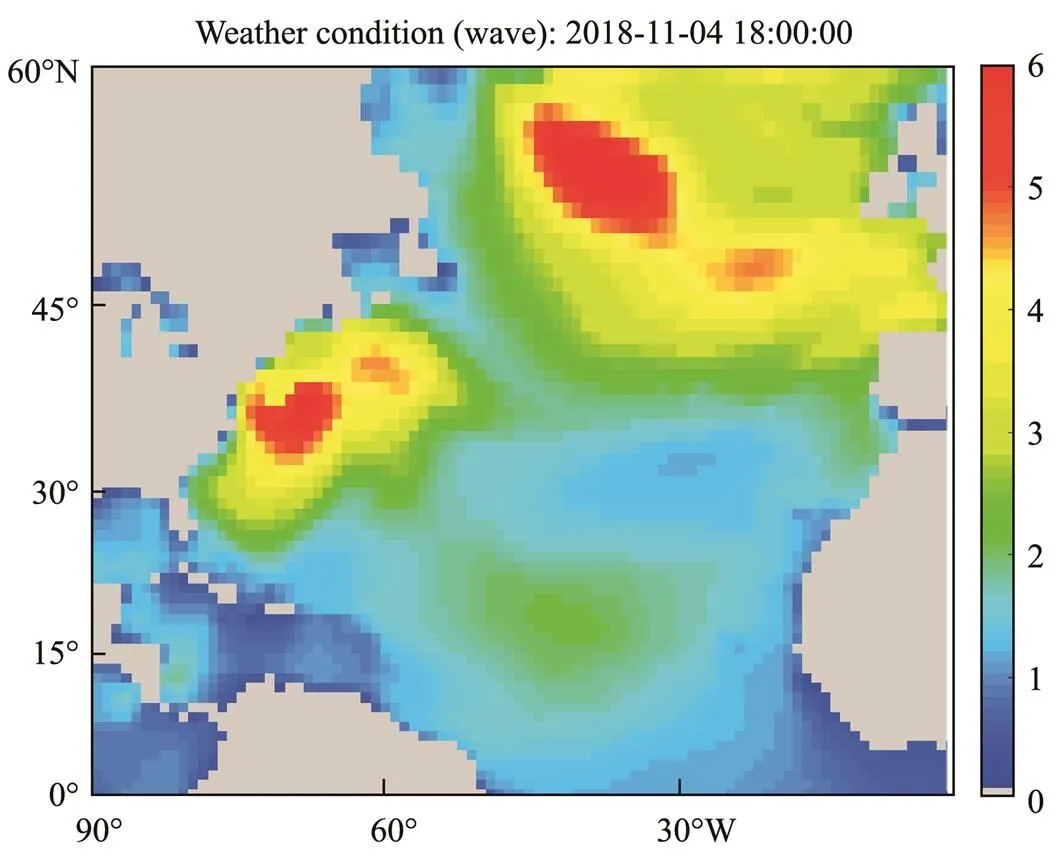
Fig.9 Wave information.
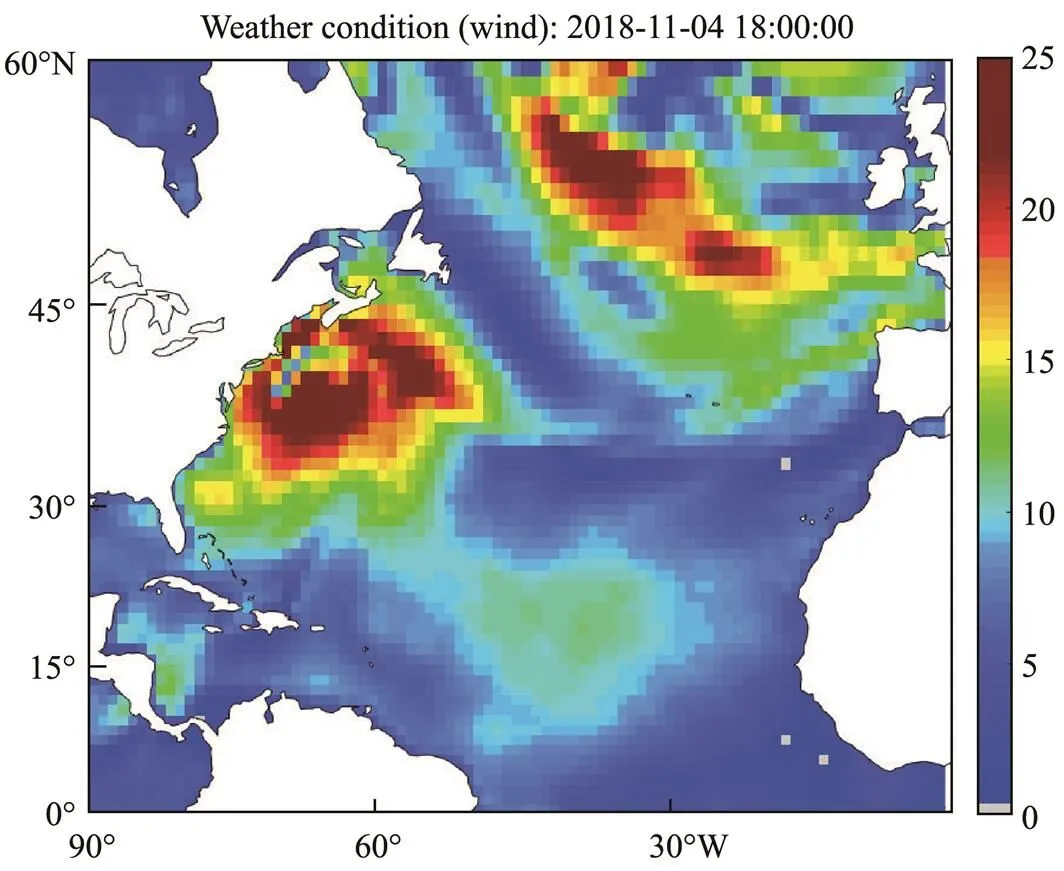
Fig.10 Wind information.
6.1 Optimization Objective: Minimize Voyage Time
In this simulation experiment of ship route optimization, the optimization objective was set as the minimum voyage time. The geographic coordinates of the departure and destination ports were (65?W, 12?N) and (10?W, 39?N), respectively, and the departure time was selected as 00:00:00 on November 1, 2018. The optimal route optimized by the hybrid genetic algorithm is shown in Fig.11. The still water speed of each segment of the optimal route was applied to the great circle and rhumb routes for calculation and comparison. As shown in Table 2, the voyage time of the optimal route was several hours less than that of the rhumb routeand slightly longer than that of the great circle route. However, the risk value of the great circle route was 0.07. According to the definition of navigation risk, some of the ship route segments passed through the weather warning areas during the navigation. If a ship sails along this route, the navigation safety can not be guaranteed. The risk value of the optimal route was 0, indicating that the optimal route has bypassed the weather warning areas and has avoided all islands in the navigation area, thereby ensuring navigation safety.

Table 2 Comparison of optimization results
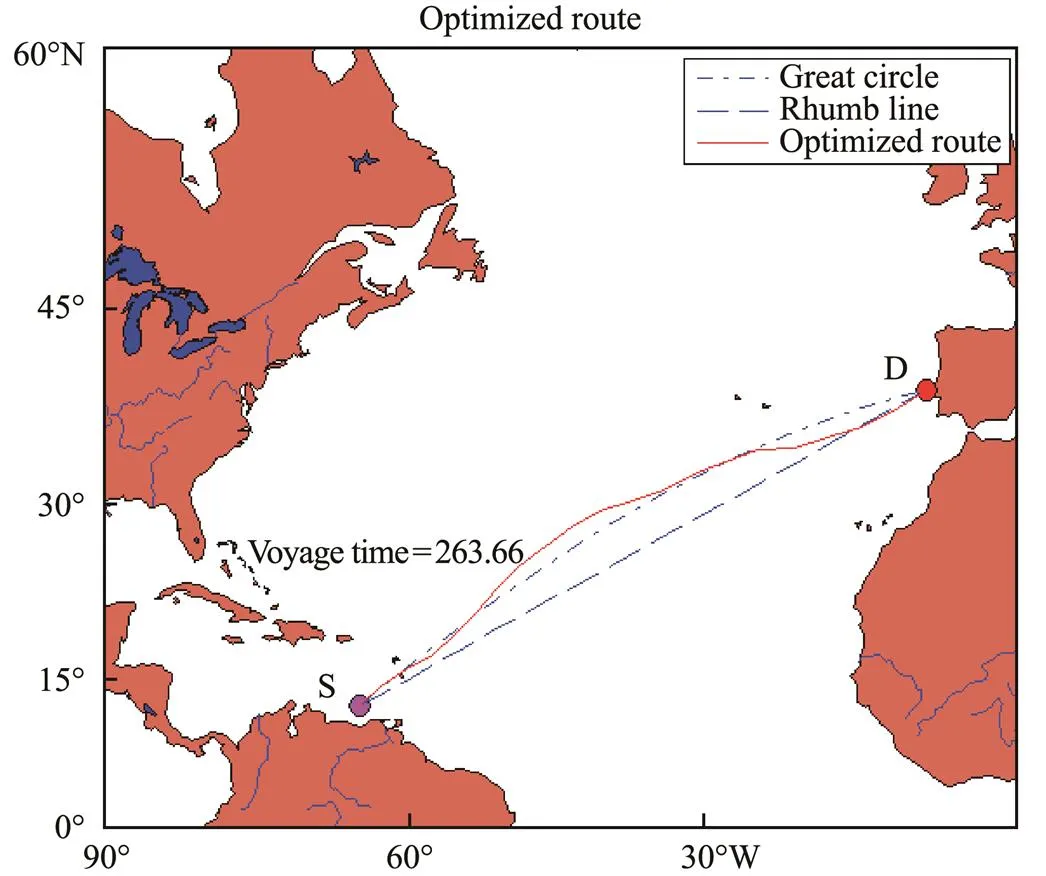
Fig.11 Optimization result of the route with minimum voy- age time.
Fig.12 shows the performance curve of the hybrid genetic algorithm. As the algorithm continued to iterate, the optimal individual objective of each generation population decreased continuously until converging to the optimal solution. Figs.13 and 14 show comparisons of speed and course changes in the optimal, great circle, and rhumb route. In Fig.13, the average speed of the ship on the optimal route is shown to be higher than the average speed of other routes, which indicates that the voyage time of the optimal route is shorter. Fig.14 shows that the ship’s course changed frequently when sailing along the optimal route. In addition, Fig.15 shows the significant wave heights of the sea areas through which the optimal route passed. In the figure, the red curve represents the warning wave height of the ship sailing at the corresponding position; in this algorithm, the warning wave height was set as 4.6m.These curves indicate that the algorithm converged in about the 110th generation of the population and that the simulated annealing operation attempted to lead the algorithm to jump out of the local optimal solution in the early stage and when the algorithm was about to converge. This caused the convergence curve to fluctuate in a small range. The objective function value of the optimal route ultimately con- verged to 263.66. In addition, the significant wave height of the optimal route was less than the warning wave height. Therefore, the ship was able to avoid the hazards caused by huge waves to achieve safe navigation. In summary, we conclude that this algorithm can be used to find a ship route with the least voyage time while ensuring safety.
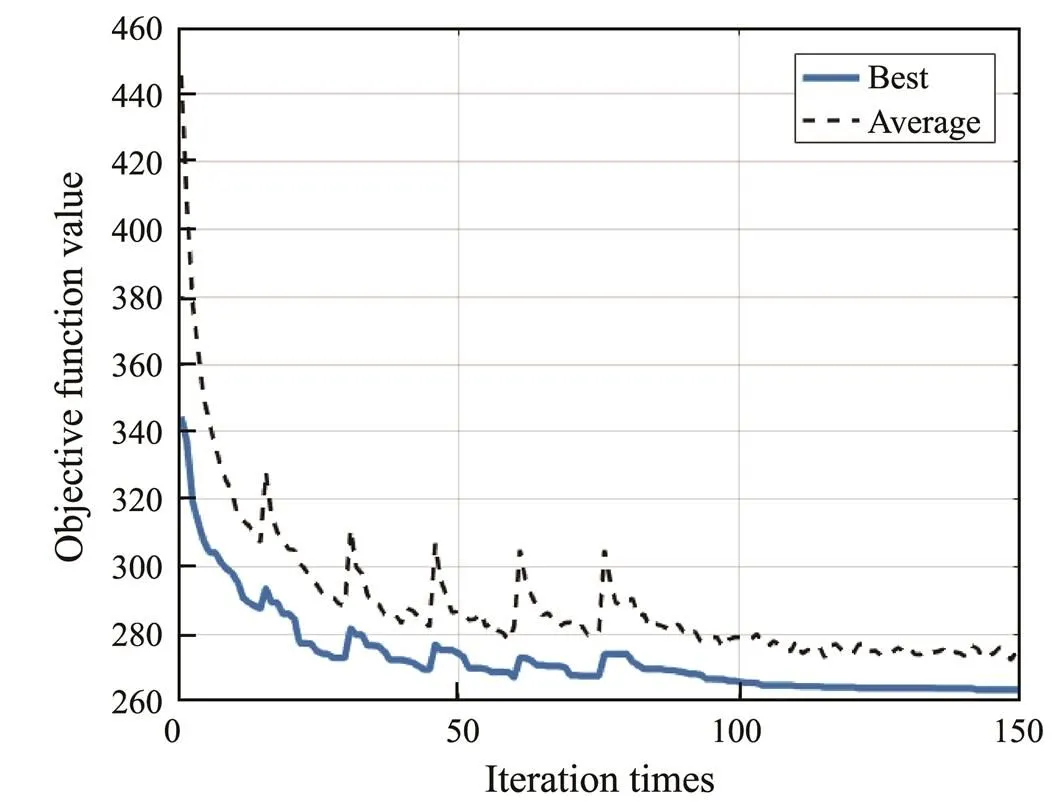
Fig.12 Algorithm convergence curve.
Fig.13 Comparison of speed changes.
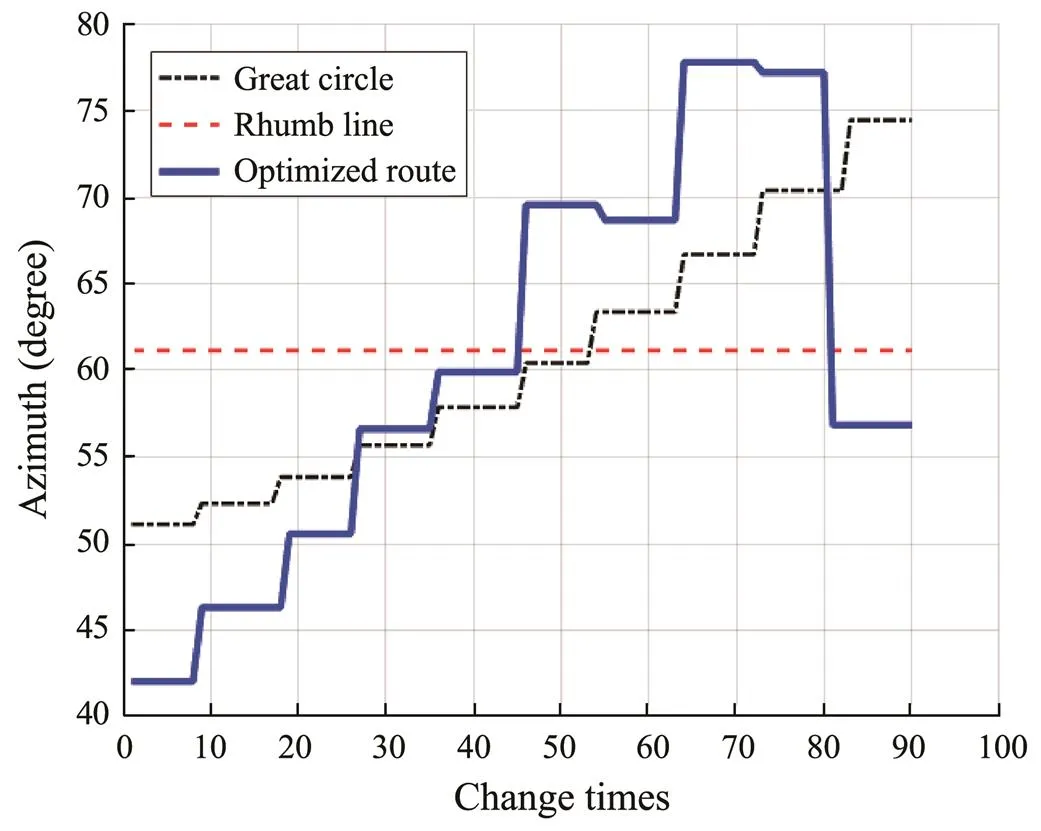
Fig.14 Comparison of course changes.
Fig.15Significant wave height of optimal route passage.
6.2 Optimization Objective: Minimize Fuel Consumption
In this simulation experiment of ship route optimization, the optimization objective of the route was set as the minimum fuel consumption. The geographic coordinates ofthe departure and destination ports were (65?W, 12?N) and (10?W, 39?N), respectively, and the departure time was selected as 00:00:00 on November 1, 2018. The optimal route optimized by the algorithm is shown in Fig.16. The still water speed of each segment of the optimal route was applied to the great circle route and the rhumb route for calculation and comparison. The results are shown in Table 3. From the results in Table 3, it can be seen that although the optimized route had the longest route distance, it had the smallest fuel consumption and shortest voyage time, which were slightly less than the great circle route. However, the risk value of the great circle route was not zero, indicating that some ship’s route segments passed through the weather warning areas during navigation. Suppose the ship sails along this route, the safety of navigation cannot be guaranteed. The risk value of the optimal route was 0, indicating that the optimal route has bypassed the weather warning areas and, at the same time, avoided all the islands in the navigation area, ensuring the safety of the ship’s navi- gation.
Fig.17 shows the performance curve of the hybrid genetic algorithm. Figs.18 and 19 show the comparison of speed changes and course changes of optimal route, great circle route, and rhumb route. Fig.20 shows the significant wave heights of the sea areas through which the optimal route passed, and the red curve represents the warning wave height of the ship sailing at the corresponding position; the warning wave height is set as 4.6m in this algorithm. It can be seen from these curves that the algorithm converged in about the 130th generation of the population, and the simulated annealing operation attempted to lead the algorithm to jump out of the local optimal solution in the early stage and when the algorithm is about to converge, causing the convergence curve to fluctuate in a small range. Finally, the objective function value of the optimal route converged to 631.95. In addition, the significant wave height of the optimal route was less than the warning wave height. Thereby, the ship was able to avoid the hazards caused by huge waves. As shown in Figs.13 and 18, the ship’s speed obtained by this simulation experiment was lower than the ship’s speed of the minimum voyage time experiment, indicating that the algorithm reduces the fuel consumption by reducing the ship’s speed. Although it in- creased the voyage time, fuel consumption was much low- er than the minimum voyage time experiment, achieving the goal of minimizing fuel consumption. In summary, we conclude that this algorithm can be used to find a ship route with the minimum fuel consumption while ensuring safety.
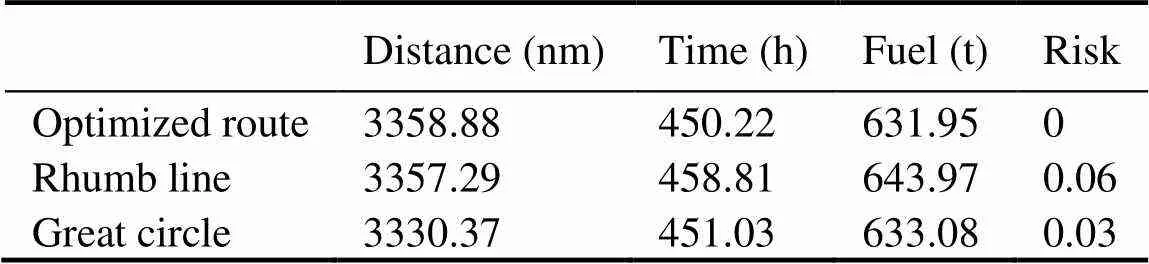
Table 3 Comparison of optimization results

Fig.16 Optimization result of the route with minimum fuel consumption.
Fig.17 Algorithm convergence curve.

Fig.18 Comparison of speed changes.
Fig.19 Comparison of course changes.
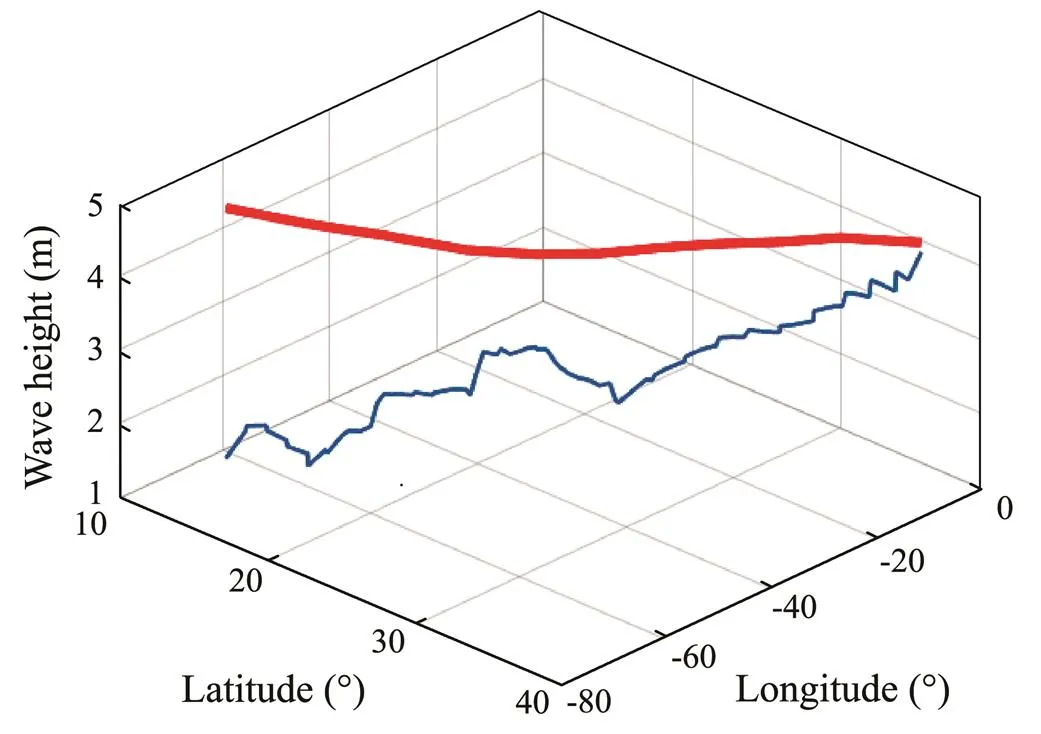
Fig.20 Significant wave height of optimal route passage.
6.3 Verification of the Simulated Annealing Mechanism Effect
This simulation experiment was performed mainly to verify the decisive effect of the simulated annealing mechanism on the local search ability of the algorithm used in this study, with the optimization goal set as the minimum voyage time.The geographic coordinates of the departure and destination ports were (67?W, 11?N) and (10?W, 39?N), respectively, and the departure time was selected as 00:00:00 on November 1, 2018. First, the optimization algorithm used to remove the mutation operator and retain the annealing mechanism was applied to optimize the ship route from the starting port to the destination port. The optimization results are shown in Fig.21(a). Then, the optimization algorithm was used to remove the mutation operator, and the simulated annealing operator was used to optimize the ship route from the starting port to the destination port. The optimization results are shown in Fig.21(b). The optimization results obtained in these two cases are shown in Table 4.
Fig.22 shows the performance curves of the optimization algorithm used in these two cases. The optimization algorithm converged prematurely in the absence of the mu- tation operation and the simulated annealing mechanism before converging to a local optimal solution of 300.58 in about the 70th generation.In addition, the final route obtained was not smooth. However, in the case of no mutation operation but retaining the simulated annealing mecha- nism, the optimization algorithm did not fall into the local optimal solution and ultimately reached the global optimal route, which converged to the global optimal solution of 274.95 in about the 120th generation. In addition, this optimized route was smoother than that optimized by the non-annealing and non-mutation algorithm, and its optimization effect was better. Therefore, when the hybrid genetic algorithm does not have the local search function of the mutation operator, relying on only the annealing me- chanism can help the optimization algorithm to jump out of the local optimal solution and avoid premature con- vergence. Its powerful local search capability can ensure the convergence and reliability of the algorithm.
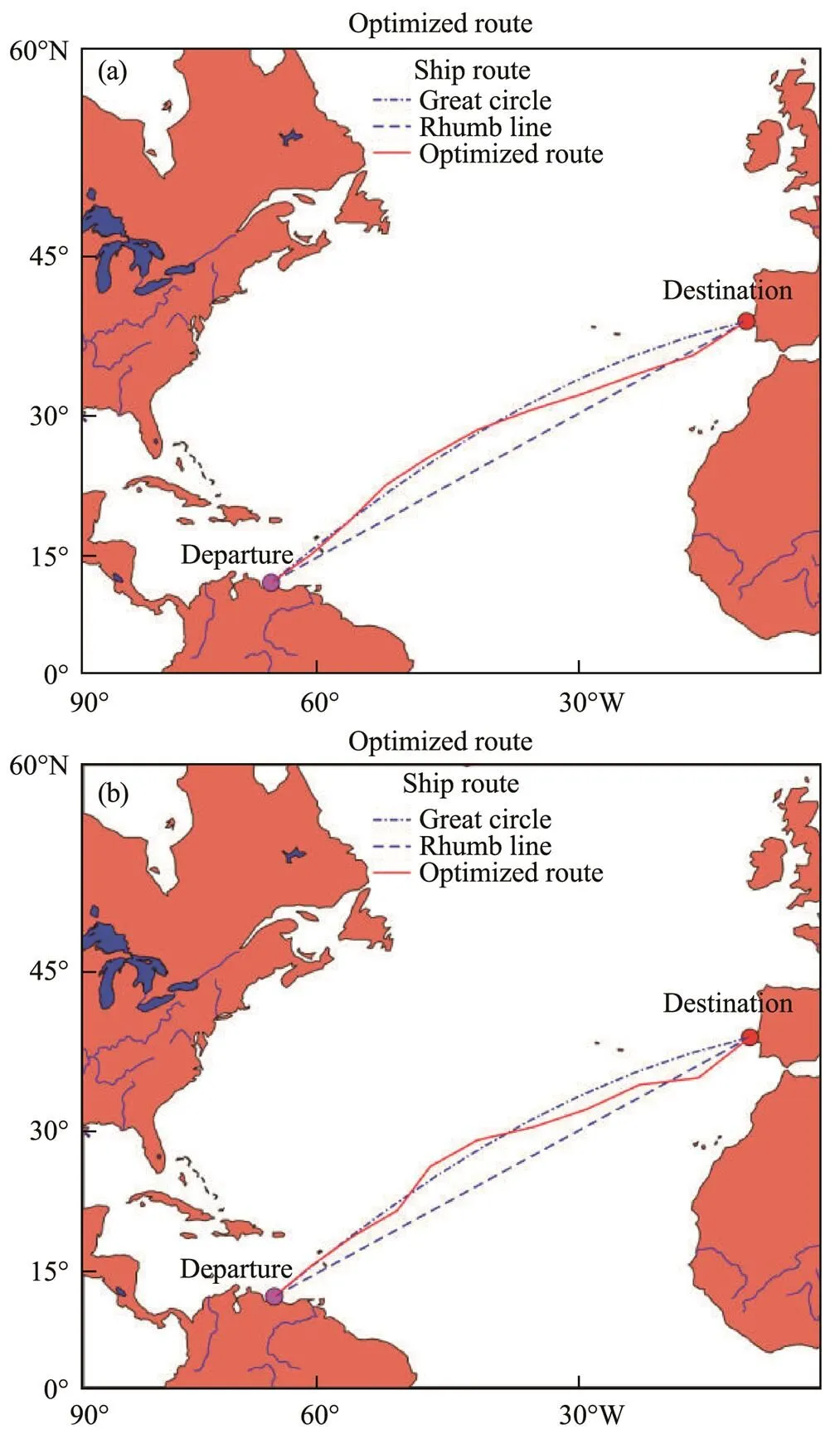
Fig.21 Ship route optimization results.(a),optimization result of case 1;(b),optimization result of case 2.
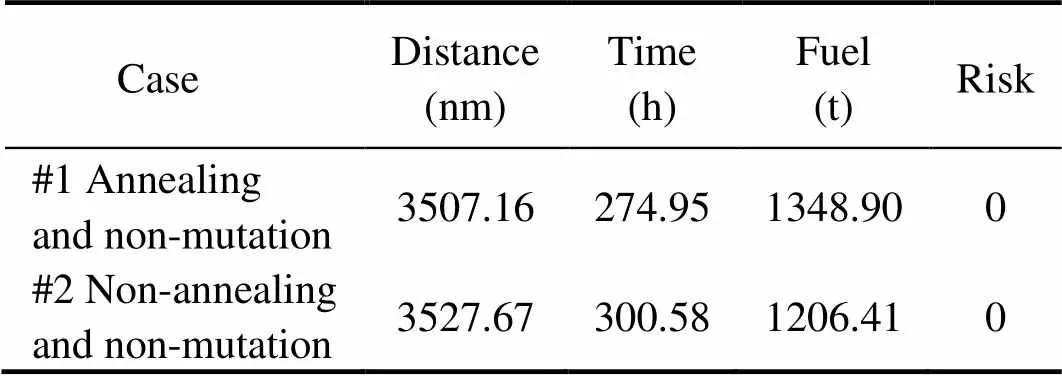
Table 4 Comparison of optimization results
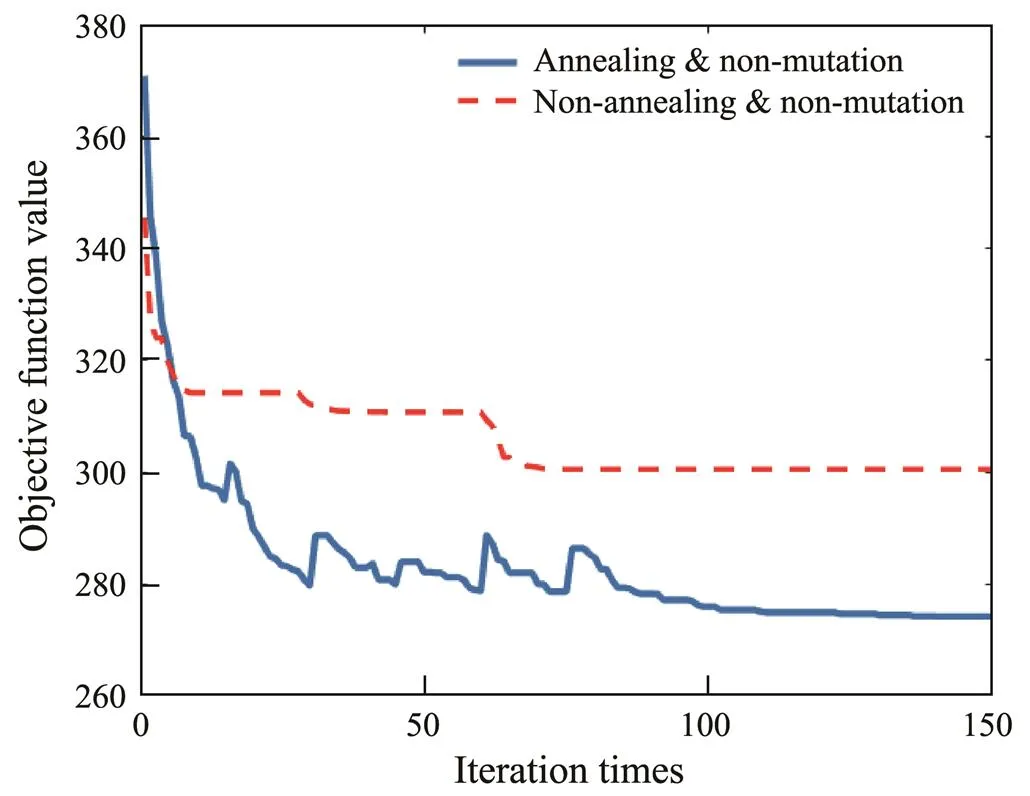
Fig.22 Algorithm convergence curve in the two cases.
7 Conclusions
Ship weather routing has great economic,social, and ecological benefits. Efficient routinghas great practical value by ensuring the safety of ships, saving operating costs, and reducing greenhouse gas emissions.With the developments made in the shipping industry, intelligent decision-making tools can be used to provide assistance in ship navigation by realizing automation and serving as a reference for decision-making in route planning. In this study, a hybrid genetic algorithm is proposed to provide decision-making for ship weather routing. The ship’s voyage time and fuel consumption are used as the optimization criteria for the ship routes. The experimental results show that the algorithm can be used to optimize the ship route by minimizing the voyage time or fuel consumption, andthe optimized route successfully can avoid dangerous locations in the navigation area, ensuring safety during navigation. The effectiveness of the algorithm proposed in this study has been proved by numerical simulations. Future research will focus on optimizing ship routes while considering multiple optimization objectives as a multi-objec- tive route optimization problem. Moreover, we hope to use the algorithm proposed in this study for practical application, which will continuously improve the model.
Acknowledgement
This study has been funded by the Russian Foundation for Basic Research (RFBR) (No. 20-07-00531).
Bellman, R., 1956. On the theory of dynamic-programming–A warehousing problem., 2 (3): 272-275.
Bentin, M., Zastrau, D., Schlaak, M., Freye, D., Elsner, R., and Kotzur, S., 2016. A new routing optimization tool-influence of wind and waves on fuel consumption of ships with and with- out wind assisted ship propulsion systems., 14: 153-162.
Bijlsma, S. J., 2001. A computational method for the solution of optimal control problems in ship routing., 48 (3): 145-154.
Deep, K., and Thakur, M., 2007. A new crossover operator for real coded genetic algorithms., 188 (1): 895-911.
Hagiwara, H., and Spaans, J. A., 1987. Practical weather routing of sail-assisted motor vessels., 40 (1): 96-119.
Haltiner, G. J., Hamilton, H. D., and Arnason, G., 1962. Minimal-time ship routing., 1 (1): 1-7.
Holland, J. H., 1992. Adaptation of codings and representations. In:MIT Press, Cambridge, Massachusetts, 141-158.
IMO, 2007. Revised guidance to the master for avoiding dangerous situations in adverse weather and sea conditions. Technical Report. International Maritime Organization (IMO), London, 1-8.
IMO, 2014. Scenarios for future emissions from international shipping. Third IMO Greenhouse Study. International Maritime Organization (IMO), London, 89-111.
Ingber, L., 1989. Very fast simulated re-annealing., 12 (8): 967-973.
IOGP, 2019..Intetnational Association of Oil & Gas Producers, 1-162.
James, R. W., 1957. Application of wave forecasts to marine nav- igation., 43 (1): 195-205.
Kang, M. H., Choi, H. R., Kim, H. S., and Park, B. J., 2012. Development of a maritime transportation planning support system for car carriers based on genetic algorithm., 36 (3): 585-604.
Kosmas, O. T., and Vlachos, D. S., 2012. Simulated annealing for optimal ship routing., 39 (3): 576-581.
Lin, Y. H., Fang, M. C., and Yeung, R. W., 2013. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements., 43: 184-194.
Liu, F., 1992. Study on the ship’s loss-speed in wind and waves., 1992 (4): 347-351.
Maki, A., Akimoto, Y., Nagata, Y., Kobayashi, S., Kobayashi, E., Shiotani, S.,, 2011. A new weather-routing system that accounts for ship stability based on a real-coded genetic algorithm., 16 (3): 311-322.
Mannarini, G., Pinardi, N., Coppini, G., Oddo, P., and Iafrati, A., 2016. VISIR-I: Small vessels least-time nautical routes using wave forecasts., 9 (4): 1597-1625.
Padhy, C. P., Sen, D., and Bhaskaran, P. K., 2008. Application of wave model for weather routing of ships in the North Indian Ocean., 44 (3): 373-385.
Pan, C., Zhang, Z. S., Sun, W. K., Shi, J., and Wang, H. B., 2021. Development of ship weather routing system with higher accuracy using SPSS and an improved genetic algorithm., 26 (4): 1324-1339.
Park, J., and Kim, N., 2015. Two-phase approach to optimal wea- ther routing using geometric programming., 20 (4): 679-688.
Perera, L. P., and Soares, C. G., 2017. Weather routing and safe ship handling in the future of shipping., 130: 684-695.
Roberts, S. E., Nielsen, D., Kotlowski, A., and Jaremin, B., 2014. Fatal accidents and injuries among merchant seafarers world- wide., 64 (4): 259-266.
Roh, M. I., 2013. Determination of an economical shipping route considering the effects of sea state for lower fuel consumption., 5 (2): 246-262.
Sen, D., and Padhy, C. P., 2015. An approach for development of a ship routing algorithm for application in the North Indian Ocean region., 50: 173-191.
Shao, W., Zhou, P. L., and Thong, S. K., 2012. Development of anovel forward dynamic programming method for weather routing., 17 (2): 239-251.
Szlapczynska, J., 2015. Multi-objective weather routing with cus- tomised criteria and constraints., 68 (2): 338-354.
Tsou, M. C., and Cheng, H. C., 2013. An ant colony algorithm for efficient ship routing., 20 (3): 28-38.
United Nations Publications Staff, 2016. Review of maritime transport 2016.. Geneva, 1-105.
Veneti, A., Makrygiorgos, A., Konstantopoulos, C., Pantziou, G., and Vetsikas, I. A., 2017. Minimizing the fuel consumption andthe risk in maritime transportation: A bi-objective weather routing approach., 88: 220-236.
Vettor, R., and Soares, C. G., 2016. Development of a ship wea- ther routing system., 123: 1-14.
Wang, H. B., Li, X. G., Li, P. F., Veremey, E. I., and Sotnikova, M. V., 2018. Application of real-coded genetic algorithm in ship weather routing., 71 (4): 989-1010.
Zis, T. P. V., Psaraftis, H. N., and Ding, L., 2020. Ship weather routing: A taxonomy and survey., 213: 107697.1-107697.18.
(April 2, 2021; revised May 24, 2021; accepted August 31, 2021)
? Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2023
Corresponding author. E-mail: wang_hongbo@jlu.edu.cn
(Edited by Xie Jun)
 Journal of Ocean University of China2023年1期
Journal of Ocean University of China2023年1期
- Journal of Ocean University of China的其它文章
- Quality Changes and Safety Evaluation of Ready-to-Eat Roasted Antarctic Krill (Euphausia superba) During Storage at Room Temperature (25℃)
- The Influence of Sea Sprays on Drag Coefficient at High Wind Speed
- Highly Efficient Heavy-Metal-Ion Removal from Shellfish Processing Liquid with Low Protein and Polysaccharide Loss by Hybrid Mesoporous Silica Diol-APDC-SBA15
- L-Band Analysis of the Effects of Oil Slicks on Sea Wave Characteristics
- A Method for Reducing Ocean Wave-Induced Magnetic Noises in Shallow-Water MT Data Using a Complex Adaptive Filter
- Wave Force on the Crown Wall of Rubble Mound Breakwaters at Intermediate Depths
