Odd Chromatic Number of a 1-Planar Graph is at Most 21*
GUO Chunqiang,WU Baoyindureng
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)
Abstract: A proper vertex coloring φ of a graph G is said to be odd if for each non-isolated vertex x ∈V(G) there exists a color c such that|φ-1(c)∩NG(x)|is odd.A graph is 1-planar if it can be drawn in the plane so that each edge is crossed by at most one other edge.We prove every 1-planar graph admits an odd 21-coloring.This improves a recently obtained bound,23,due to Cranston,Lafferty and Song.
Key words: proper coloring;odd coloring;1-planar graph
0 Introduction
LetG=(V(G),E(G))be a finite simple,undirected graph.As usual,|V(G)|and|E(G)|are called the order and the size ofG,respectively.Ifuv∈E(G),then we say thatuis a neighbor ofv.For every vertexv∈V(G),the open neighborhood ofvis setNG(v)={u∈V(G):uv∈E(G)}and the closed neighborhood ofvis the setNG[v]=NG(v)∪{v}.The degree of a vertexv∈V(G)isdG(v)=|NG(v)|.A vertexvis calledk-vertex(respectively,k+-vertex ork--vertex)ifdG(v)=k(respectively,dG(v) ≥kordG(v) ≤k).ByF(G) we denote the face set of a plane graphG,and for any facef∈F(G),we usedG(f)(respectively,k+-face ork--face)to denote the degree offinG(respectively,dG(f)≥kordG(f)≤k).For every planar graphG,for every elementx∈V(G)∪F(G),we usech(x)to denote the initial charge ofxandch*(x)to denote the new charge ofxafter applying some discharging rules.
The minimum degree and maximum degree of a graphGare denoted by δ(G)and Δ(G)(simply by δ and Δ).A vertexv∈V(G)is said to be odd ifdG(v)is odd.For any setS?V(G),G-Sdenotes the graph obtained by deletingSfromG.We refer to[1]for undefined notations and terminology.
A proper coloring φ of graphGis said to be odd if for each non-isolated vertexx∈V(G) there exists a colorcsuch that|φ-1(c)∩NG(x)|is odd.A graphGis oddk-colorable if it has an oddk-coloring.The odd chromatic number of a graphG,denoted χo(G),is the minimumksuch thatGhas an oddk-coloring.This notion was introduced by Petru?evski and ?krekovski[2],and they showed that χo(G)≤9 for any planar graphGand posed the following conjecture.
Conjecture 1For any planar graphG,χo(G)≤5.
Caro,Petru?evski and ?krekovski[3]present an alternative proof for the result that χo(G)≤9 for any planar graphG.The bound is further improved to 8 by Petr and Portier[4].Cranston[5]investigated the odd colorings of spares graphs in terms of the maximum average degree.Cho,Choi,Kwon,et al.[6]proved that every planar graphGwith girth at least 5 is odd 6-colorable.
Recall that a graph is said to be 1-planar graph if it can be drawn in the plane so that each edge is crossed by at most one other edge.Cranston,Lafferty and Song[7]proved that every 1-planar graph admits an odd 23-coloring.The main aim of the paper is to reduce the bound to 21.
Theorem 1Every 1-planar graph admits an odd 21-coloring.
For an odd coloring φ ofGand for eachv∈V(G),|{c: |φ-1(c)∩NG(v)|is odd}|≥1.For convenience,let us denote by φo(v)a color in{c: |φ-1(c)∩NG(v)|is odd}.Further,φo(NG(v))={φo(x):x∈NG(v)}.
1 Several Key Lemmas
For positive integerc≥3,a vertexv∈V(G)is said to be big ifd(v)≥「c/2,otherwise,small.
IfGis a minimum 1-planar graph which does not admit an oddc-coloring.The following hold:
Lemma 1δ(G)≥2.
ProofSuppose,to contrary,that δ(G) ≤1.Letvbe the vertex withdG(v)=δ(G) ≤1,andG′=G-v.ThusG′is 1-planar.By the minimality ofG,let φ be an oddc-coloring ofG′.We can extend φ to an oddc-coloring ofGby coloringvfromca contradiction.
Lemma 2For each odd vertexv,thend(v)≥「c/2.
ProofSuppose not,there exists an odd vertexvwithdG(v)≤「c/2-1.
LetG′=G-v,by the minimality ofG,we can obtain thatG′admits an oddc-coloring φ.Since2×(「c/2-1),at least one color is available forv,a contradiction.
Lemma 3No two small vertices are adjacent.
ProofSupposeuandvare adjacent small vertices,i.e.dG(u)≤「c/2-1 anddG(v)≤「c/2-1.LetG′=G-{u,v}.By the minimality ofG,G′has an oddc-coloring φ.By Lemma 2,both(u)|and(v)|are odd.We can extend φ toG.
First,assignua color,which does not belong to φ((u))∪φo((u))and φo(v)(at mostc-2),and then assign a color tov,which does not belong to φ(NG(v))∪φo(NG(v))(at mostc-1 colors in all).
Assume thatGis a minimum 1-planar graph which does not admit an odd coloring withc,and subject to this,the number of crossings is as small as possible.The following hold:
Lemma 4Every edge ofGincident to a small vertex has a crossing.
ProofSuppose thatuv∈E(G) has no crossing,wherevis a small vertex.LetG′=G-v+{uz:z∈NG(v)NG[u]}.Clearly,G′is a 1-planar.By the minimality ofG,G′has a proper oddc-coloring φ.By forbidding at mostc-1 colors atv(namely,at most φ(NG(v))∪φo(NG(v))),at least one color remains forv.
Lemma 5Every 3-face is incident with at most one virtual 4-vertex inH,whereHis the plane graph obtained fromGby replacing each crossing with a virtual 4-vertex.
ProofClearly,Hhas no 2-face and loop.SinceGis 1-planar,no two virtual 4-vertices are adjacent.It implies that every 3-face is incident with at most one virtual 4-vertices inH.
By Lemma 5,no 3-face inHincident to a small vertex.So,every 3-face inHincident to either a virtual 4-vertex and two big vertices or three big vertices.
Lemma 6Every 2-vertex inHincident to a 4+-face and a 5+-face.
ProofSuppose not,there exists a 2-vertexu∈V(G) incident to two 4-facesf1=uyvxandf2=uxwy,see Fig 1.It follows thatvw∈E(G),otherwise,this contradicts the minimality ofG.This implies thatGhas a multiple edge betweenvandw,a contradiction.

Fig 1 vw ∈E(G)
Lemma 7No two 4-faces inHincident with a 2-vertex are adjacent.
ProofLetf1=uyvxandf2=uyzwbe two adjacent 4-faces inH.By the minimality ofG,neithervnorzis adjacent tou.So,vz∈E(G),see Fig 2.However,this contradicts Lemma 6.Therefore,the Lemma 7 holds.
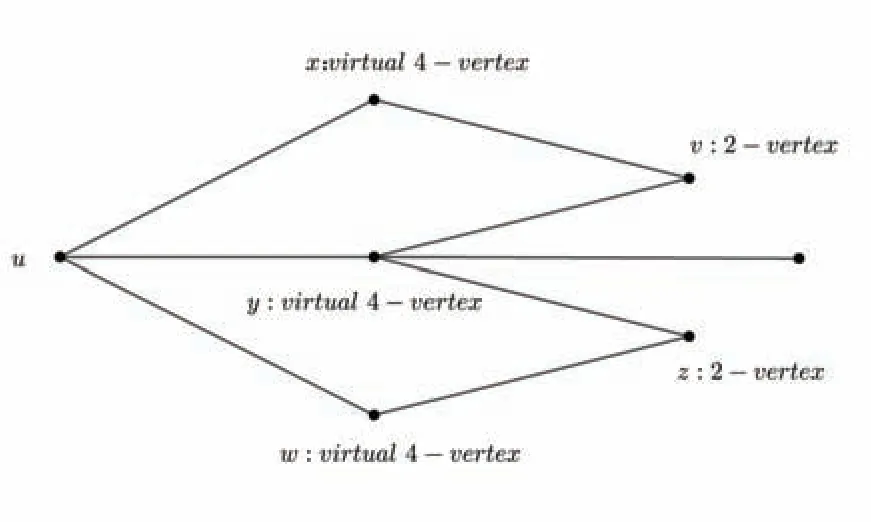
Fig 2 vz ∈E(G)
Lemma 8Every 6-face is incident to at most two special 2-vertices,where a 2-vertexvis said to be special if it is incident with a 4-facef=uyvx,in whichx,yare virtual 4-vertices.
ProofSupposef=uxvywzis a 6-face incident with three special 2-vertices inH,whereu,vandware special 2-vertices,see Fig 3(a).This implies thatx,yandzare virtual 4-vertices.Now we can conclude thatvc∈E(G),aw∈E(G),bv∈E(G) andwc∈E(G).One can see that the new embedding ofGas shown in Fig 3 (b) has fewer crossings than the embedding ofGas we assumed,a contradiction.

Fig 3 f=uxvywz is a 6-face in G(left)and its new embedding of G with fewer crossings(right)

Fig 4 The discharging rules R1~R3
2 Proof of Theorem 1
Theorem 1Every 1-planar graph admits an odd 21-coloring.
ProofLetGbe a counterexample to Theorem 1 with the minimum number of vertices and as few edge crossings as possible.So,Gis a graph with χo(G)≥22.LetHbe the plane graph formedGby replacing each crossing with a virtual 4-vertex.Note the graphHhas no 2-face.Recall that a vertexv∈V(G)is said to be a big vertex ifdG(v)≥11,otherwise,vbe a small vertex.A 3-facef=uvxinHis called to be true 3-face ifu,vandxare big vertices ofG,andf=uvxinHis called to be false 3-face if two ofu,vandxare big vertices and another is virtual 4-vertex.A 4-facef=uyvxis said to be a special 4-face inHifdH(v)=2 andx,yare virtual 4-vertices.Moreover,vis called special 2-vertex.
By Lemmas 1~8,we can get the following claims.
Claim 1δ(G)≥2.
Claim 2Every odd vertex inGhas degree at least 11.
Claim 3No two small vertices are adjacent inG.
Claim 4Every edge incident to a small vertex inGhas a crossing.
Claim 5Every 3-face inHis either true 3-face or false 3-face.
Claim 6Every 2-vertex inHis incident to a 4+-face and a 5+-face.
Claim 7No two 4-faces inHincident with a 2-vertex are adjacent.
Claim 8Every 6-face is incident to at most two special 2-vertices.
A 4-facef=uyvxis said to be a special 4-face of type-I inHifuis a big vertex,dH(v)=2 andx,yare virtual 4-vertices.Moreover,vis called special 2-vertex of type-I.f=uyvxis said to special 4-face of type-II inHifuis a small vertex,dH(v)=2 andx,yare virtual 4-vertices.Moreover,vis called special 2-vertex of type-II.
A 5-face is said to be a special 5-face if it is incident to a special 2-vertex of type-II or a 2-vertex which is incident to a 6-face,see Fig 5(R4).
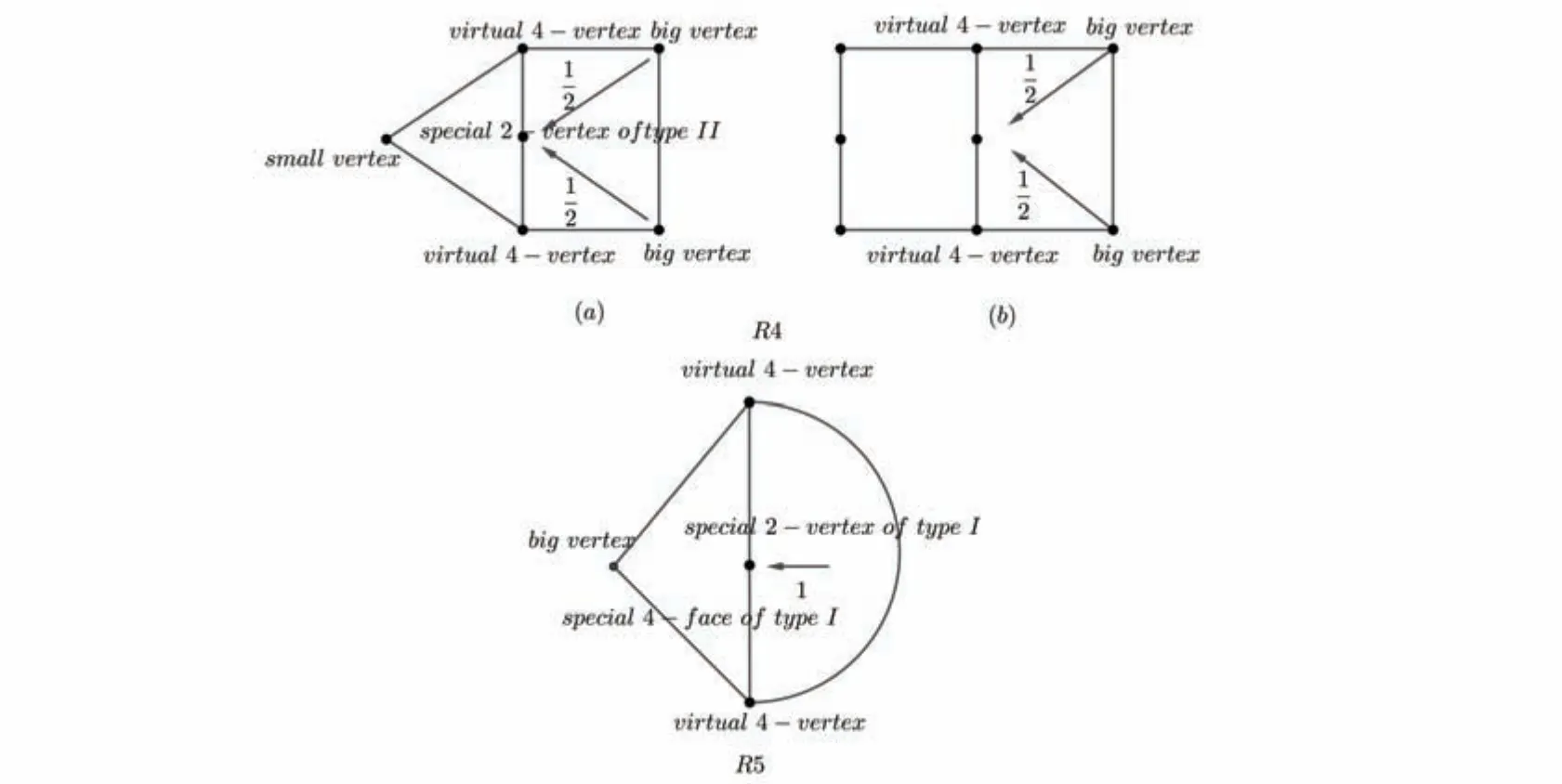
Fig 5 The discharging rules R4~R5
We useHto denote its planar embedding andF(H),the set of faces.We assign initial charge for anyx∈V(G)∪F(G)by puttingch(x)=dH(x)-4.Rewriting Euler’s formula
We use the following discharging rules(see Fig 4 and Fig 5)so that the charges are transferred among the elements inH.
R1.Every big vertex sends 1/3 to its incident true 3-face.
R2.Every big vertex sends 1/2 to its incident false 3-face.
R3.Every big vertex incident with special 4-face of type-I sends 1 to the 2-vertex on the same face.
R4.Every big vertex incident with special 5-facefsends 1/2 to the 2-vertex on the same face.
R5.Every 5+-face inHsends 1 to each of its incident special 2-vertices of type-I(if there exists).
R6.After applying R1~R5,every 5+-face inHredistributes its charge equally to each of its incident 2-vertices (if there exists).
Letch*denote the new charge,after applying R1~R6.By showingch*(x)≥0 for everyx∈V(H)∪F(H)by a series of Claims,we reach a contradiction,and hence prove Theorem 1.
First,ch*(f)=ch(f)=0 andch*(v)=ch(v)>0 for 4-facefand vertexvof degree between 4 and 10 since there are no discharging rules that applies to them.Therefore,we just need to prove that thech*≥0 of the remaining vertices and faces.
Claim 9ch*(f)≥0 for every 3-facefinH.
ProofIffis a true 3-face,thench*(f)=3-4+3×(1/3)=0 by R1.Iffis a false 3-face,thench*(f)=3-4+2×(1/2)=0 by R2.
Claim 10ch*(f)≥0 for every 5-facefinH.
ProofSincefis a 5-face,fis incident to at most one 2-vertex.
Iffis not incident with a 2-vertex,thench*(f)=ch(f)=5-4 >0 since there is no discharge rule applicable tof.
Assume thatfis incident with a 2-vertex.If the 2-vertex is a special 2-vertex of type-I,thench*(f)=5-4-1=0 by R5.If the 2-vertex is a non-special 2-vertex of type-I,thench*(f)=5-4-1=0 by R6.
Claim 11ch*(f)≥0 for every 6-facefinH.
ProofSincefis a 6-face,fis incident to at most two 2-vertices of type-I.By R3,ch*(f)=6-4-2×1=0.
Claim 12ch*(f)≥0 for every 7+-facefinH.
ProofClaim 3 and Claim 4,everyd-face has at mostd/2 2-vertices ifdis even,and otherwise,at most (d-3)/2 2-vertices.By R5 and R6,ch*(f)=d-4-(d/2)≥0 ifdis even andch*(f)=d-4-(d-3)/2 >0 ifdis odd.
Claim 13If a special 2-vertexvof type-II is incident with a 6+-facef,thenfcan send at least 2 tov.
ProofLetf1=uxvybe a special 4-face of type-II incident tov,whereuis a small vertex,andfbe the 6+-face are shown in Fig 6(a).Letu1andu2be vertices incident withfandxu1∈E(H),yu2∈E(H).This implies thatuu1∈E(G)anduu2∈E(G).By Claim 3,u1andu2are two big vertices.Letabe the number of special 2-vertices of type-II that are incident withf,andb,the number of the remaining 2-vertices which are incident withf.By Claim 3,there are at leasta-1+b+1 virtual 4-vertices.Sinced(f)≥(a-1+b+1)+(a+b)+(5-1)=2a+2b+4,by R5,vcan receive[d(f)-4-a]/b≥(2a+2b+4-a-4)/b≥2.

Fig 6 Cases 1 and 2 of Claim 14
Claim 14ch*(v)≥0 for every 2-vertexvinH.
ProofLetf1andf2be the two faces incident tov,respectively.By Claim 6,d(f1)≥4 andd(f2)≥5.We consider two cases.
Case 1dH(f1)=4.
Letf1=uxvy.Ifvis a special 2-vertex of type-I anduis a small vertex,thench*(v)=2-4+1+1=0 by R3 and R5.
Assume thatvis a special 2-vertex of type-II.Iff2is a special 5-face,then by R4 and R6,ch*(v)=2-4+1+2×(1/2)=0,see Fig 5 R4(a).
Iff2is a 6+-face,see Fig 6(a).By Claim 13,ch*(v)≥2-4+2=0 by R6.
Case 2dH(fi)≥5 fori∈{1,2}.
IfdH(f1)=dH(f2)=5,thench*(v)=2-4+1+1=0 by R6,see Fig 6(b).
If min{dH(f1),dH(f2)}=5 and max{dH(f1),dH(f2)}=6,thench*(v)=2-4+1+2×(1/2)=0 by R4 and R6,see Fig 5 R4(b).
IfdH(f1)=dH(f2)=6,then letxandybe neighbors ofvinH,u1u2andw1w2be edges ofGthat pass through the crossingsxandy,respectively,such thatuiandwiare vertices onfi,wherei=1,2.By Claim 3,there exists at least two big vertices amongu1,u2,w1andw2.If there existsi∈{1,2},such thatuiandwiare big vertices,thenfiis incident to one 2-vertex.By R6,ch*(v)≥2-4+2=0.If there existsz∈{u1,w1}andw∈{u2,w2}such thatzandware big vertices,thenfican send at least 1 tovfori∈{1,2}.By R6,ch*(v)≥2-4+1+1=0.
IfdH(fi) ≥7 fori∈{1,2},then everyd-face has at mostd/2 2-vertices ifdis even,and otherwise,at most (d-3)/2 2-vertices.This implies that there exists at most(d/2)-1 2-vertices of type-I ifdis even,and otherwise,at most[(d-3)/2]-1 2-vertices of type-I,thusch*(v)≥2-4+1+1=0 by R6.
Claim 15If there exists three consecutive faces that are incident with a big vertexv,thenvtotally sends to three faces at most 2.
ProofLetf1,f2andf3are three consecutive faces that are incident tov.
If one off1,f2andf3is a special 4-face of type-I,thenvtotally sends to three faces at most 1+(1/2)+(1/2)=2 by Claim 7,R1,R2 and R4.
If there exists two special 4-faces of type-I.By Claim 7,assume thatf1andf3are two special 4-faces,moreover,f2is definitely not 3-face or special 5-face.Thenvtotally sends to three faces at most 1+0+1=2 by R1 and R4.
Claim 16ch*(v)≥0 for every big vertexvinH.
ProofLetf1,f2,···,fdbe all faces incident withvin the clockwise order.Letaibe the amount of the charge which transferred fromvtofiiffiis a 3-face,or to the 2-vertex of type-I incident tofi,or to the 2-vertex incident to special 5-facefi.By Claim 15,bi=ai-1+ai+ai+1≤2,wherei-1,i+1 are taken modulod.
By R1~R6,ch*(v)≥d(v)-4-(2d/3)≥0 ifdH(v)≥12.
It remains to consider a vertexvwithdH(v)=11.
Ifvis incident with at most three special 4-faces of type-I,thench*(v)=11-4-3×1-8×(1/2)=0 by R5.
Ifvis incident with at least four special 4-faces of type-I.By Claim 7,there is ani∈{1,2,···,11}such thatfiandfi+2must be special 4-faces of type-I,wherei+2 is taken modulod.Assume thati=1,thenf1andf3are two special 4-faces of type-I.This implies thatf4andf11are not special 4-faces of type-I.By Claim 7,Claim 15 and R1~R5,b1≤(1/2)+1+0=3/2 andb3≤0+1+(1/2)=3/2.So,we can get the following inequality
Thus,ch*(v)≥11-4-7=0.
The proof of the Theorem 1 is completed.
3 Future Directions
A vertex coloring(may be improper)φ of graphGis said to be weak odd if for each non-isolated vertexx∈V(G)there exists a colorcsuch that |φ-1(c)∩N(x)| is odd.A graphGis weakly oddc-colorable if it has a weak oddk-coloring.The weak odd chromatic number of a graphG,denoted χwo(G),is the minimumksuch thatGhas a weak oddk-coloring.
For a weak odd coloring φ ofGand for eachv∈V(G),|{c: |φ-1(c)∩NG(v)|is odd}|≥1.For convenience,let us denote by φo(v)a color in{c: |φ-1(c)∩NG(v)|is odd}.Further,φo(NG(v))={φo(x):x∈NG(v)}.
It is obvious for χwo(G)≤χo(G).The following observations will help us to better understand this new concept.
Observation 1IfTis a non-trivial tree of ordern,then χwo(Tn)≤2.
ProofIfdT(v)is odd for every vertexv∈V(T),then χwo(T)=1.Next,assume thatTis not odd.We proceed on the induction onn.
Consider the longest pathP=v1v2···vlinT.LetS=N[v2]{v3}.Clearly,T-Sis a tree.By the induction hypothesis,there exists an odd 2-coloring φ ofT-S.Without loss of generality,φ(v3)=1.We consider two possible cases.
Case 1φo(v3)=1.
Extend φ toV(T)by setting φ(x)=2 for eachx∈S.It can be seen that φ is an odd coloring ofT,because φo(v2)=1 and φo(x)=2 for eachx∈S{v2}.
Case 2φo(v3)=2.
Extend φ toV(T)by setting φ(v2)=1 and φ(x)=2 for eachx∈S{v2}.It can be seen that φ is an odd coloring ofT,because φo(v2)=2 and φo(x)=1 for eachx∈S{v2}.
Observation 2For every integern≥2,
ProofIfnis even,then φ is an odd coloring ofKn,where φ(x)=1 for eachx∈V(Kn).It implies that χwo(Kn)=1.
Now assume thatnis odd,and letV(Kn)={v1,···,vn}.Let φ(vi)=ifori∈{1,2}and φ(vi)=3 for eachi≥3.It can be verified that φ is an odd coloring ofKn.It follows that χwo(Kn)≤3.On the other hand,it is not hard to see that there does not exist an odd coloring ofKnusing one color or two colors,implying χwo(Kn)≥3.
It seems that the following result is true.
Conjecture 2IfGis a planar,then χwo(G)≤4.

