江西省信豐中學(xué) (341600) 賴學(xué)鋒

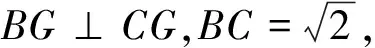
分析：本題是2018年湖北省預(yù)賽第5題,考查三角形的重心,正余弦定理,向量,基本不等式,圓等知識點,綜合性強,是一道較難題．

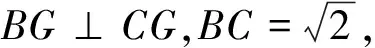
圖1

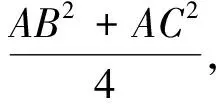
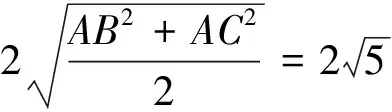
評析：本法利用三角形重心的結(jié)論,借助勾股定理和基本不等式,巧妙地求出最大值,比較簡潔．

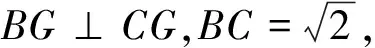
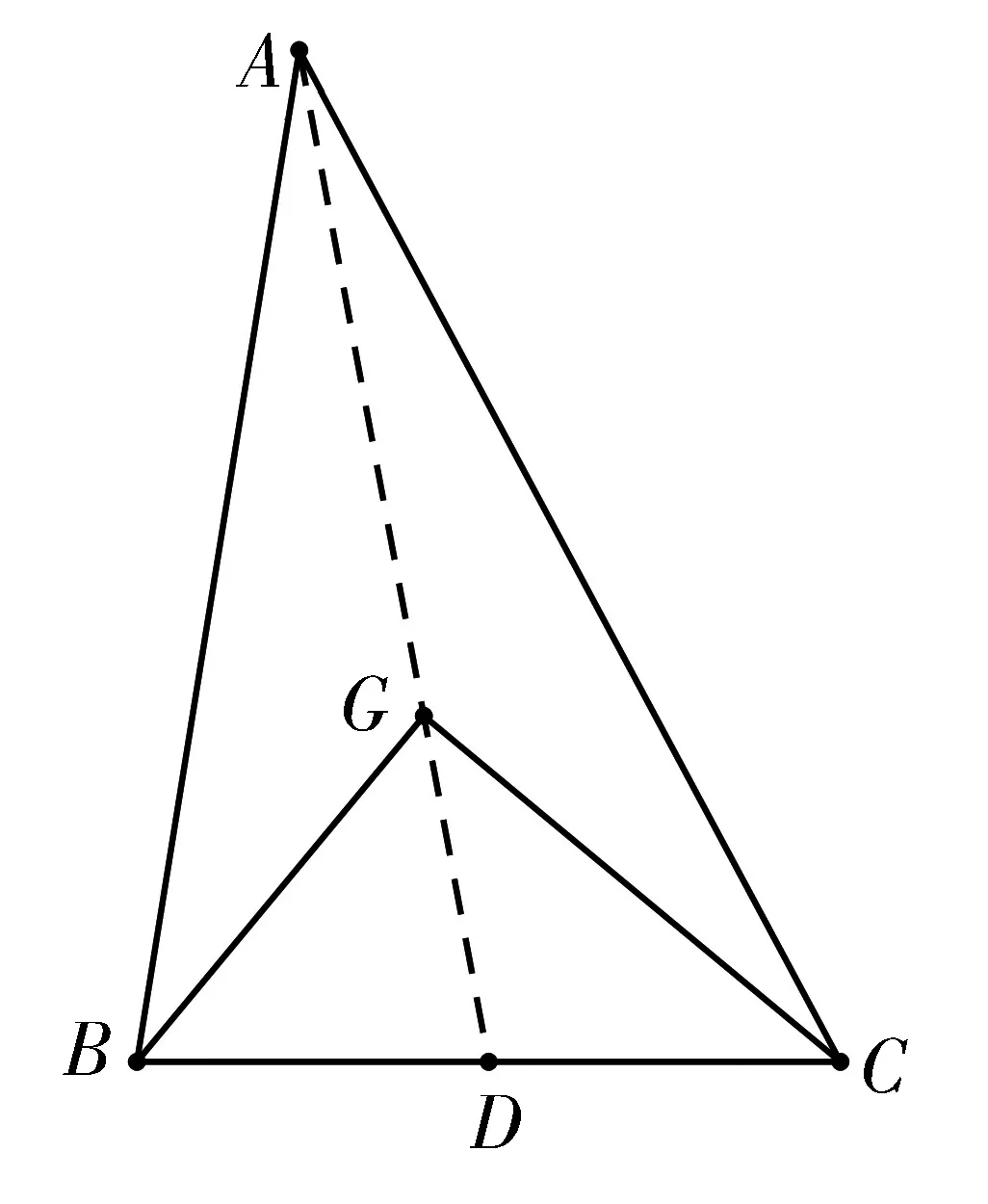
圖2

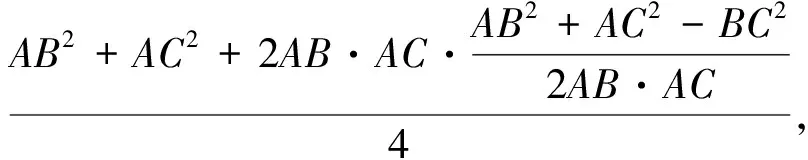
評析：本法利用三角形重心的結(jié)論,結(jié)合向量,余弦定理和基本不等式,順利求出最大值．

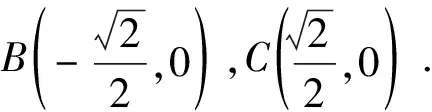
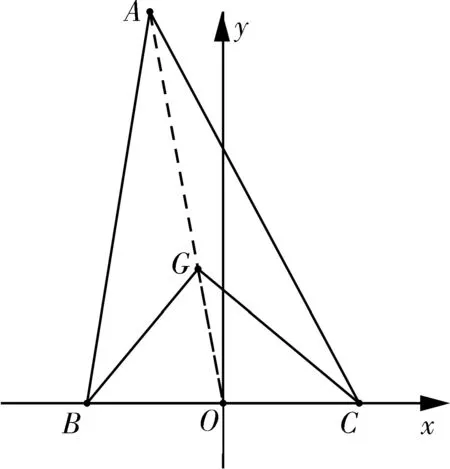
圖3

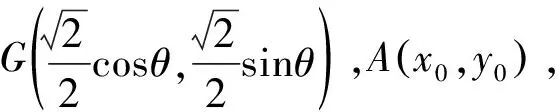
評析：本法為坐標(biāo)法,利用坐標(biāo)系建立圓的標(biāo)準(zhǔn)方程,再由圓的參數(shù)方程結(jié)合基本不等式進而求解,思路自然巧妙．

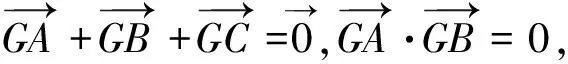
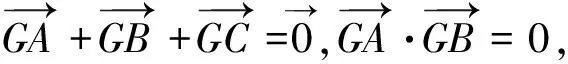
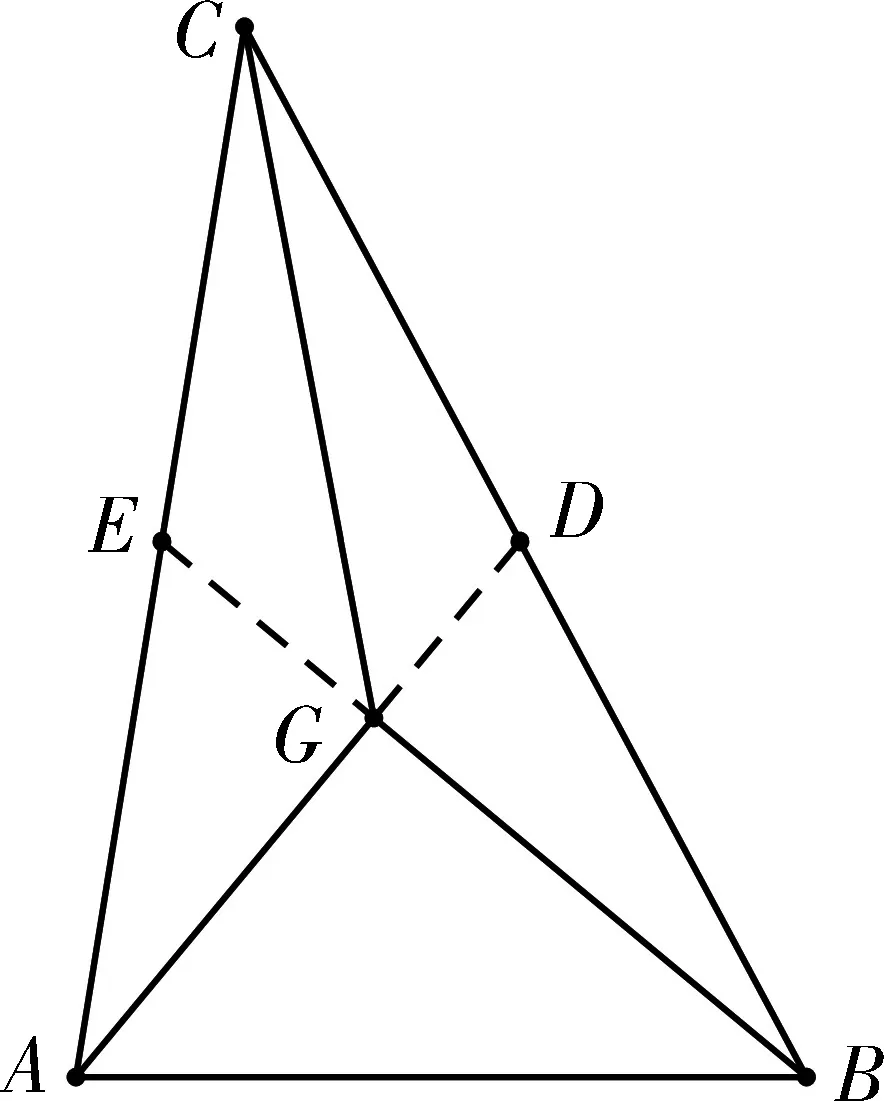
圖4

分別延長AG,BG交BC,AC于點D,E,則D,E分別為BC,AC的中點．

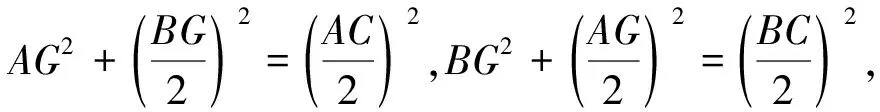
評析：顯然,變式1只是把題目的結(jié)論作了更改,方法與解法1如出一轍,只是所求目標(biāo)不同．

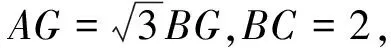
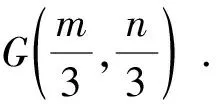
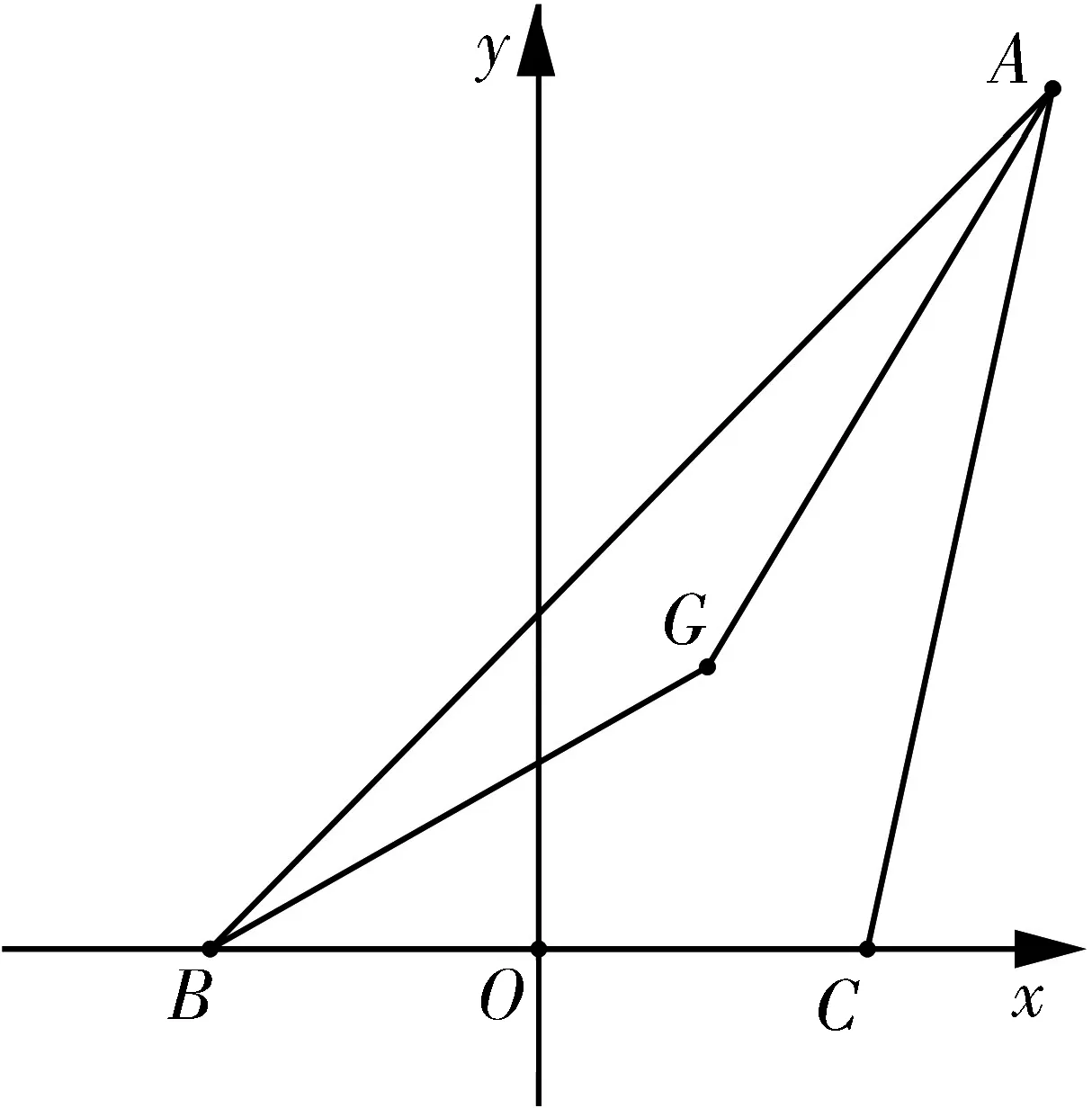
圖5

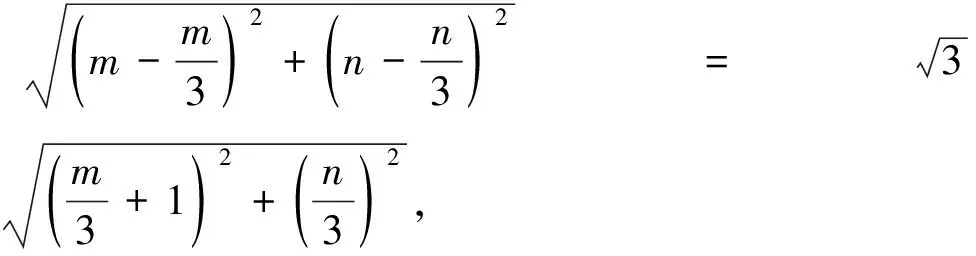
評析：變式2把題目的條件和結(jié)論都作了更改,方法上采用的是解法3的坐標(biāo)法,運用坐標(biāo)法輕易的得到點A的軌跡為圓,借助幾何直觀較簡便地求出了面積的最大值．