Efficient semi-quantum secret sharing protocol using single particles
Ding Xing(邢丁), Yifei Wang(王藝霏), Zhao Dou(竇釗),?, Jian Li(李劍),Xiubo Chen(陳秀波), and Lixiang Li(李麗香)
1Information Security Center,State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China
2Information Security Center,School of Cyberspace Security,Beijing University of Posts and Telecommunications,Beijing 100876,China
Keywords: semi-quantum secret sharing,efficiency,single particles,specific secret,particle reordering
1.Introduction
Secret sharing (SS)[1]is a widely used and efficient privacy protection protocol.It allows a dealer to share a secret among many agents,but only if they cooperate can the agents recover the dealer’s secret or they obtain nothing alone.[2–4]However, classical secret sharing (CSS) is unable to address the problem of eavesdropping if it is not combined with other technologies such as encryption,and the introduction of quantum algorithms brings a huge potential threat to classical encryption algorithms.[5,6]Fortunately, quantum cryptography can solve these security problems.By determining whether an eavesdropper has attempted to gain information about the secret, quantum secret sharing (QSS) can provide for secure secret transmission.
In 1999,Hilleryet al.[7]proposed the first QSS protocol based on the three-particle entangled GHZ states, attracting extensive attention.Since then,many researchers have studied the field of quantum secret sharing, and kinds of QSS protocols have been put forward.[8–15]However, those QSS protocols require all participants (both the dealer and the agents)to possess full quantum capabilities (e.g., quantum measurement,quantum states preparation,and so on)while in general quantum resources are valuable and quantum operations are not easy to implement.
In 2007,Boyeret al.[16]first presented the notion of semiquantum by presenting a protocol where one participant(Bob)is classical.In the definition of semi-quantum, two kinds of participants,quantum participant and classical participant are proposed.The quantum participant has full quantum capabilities and can perform all quantum operations while a classical participant can only perform the following operations when he accesses a segment of quantum channel: (a) generating qubits in the fixed computational basis(Zbasis){|0〉,|1〉};(b)measuring qubits in the fixedZbasis{|0〉,|1〉};(c)reflecting qubits without disturbance;(d)reordering qubits(via different delay lines).Since semi-quantum cryptography protocol only requires one participant to have the full quantum capability,it simplifies the execution difficulty of the protocols and has been widely applied to various quantum cryptography fields,such as semi-quantum key distribution,[17–19]semi-quantum secure direct communication,[20–22]semi-quantum private comparison[23–25]and semi-quantum secret sharing.[26–32]
In 2010,Liet al.[26]proposed the first semi-quantum secret sharing (SQSS) protocol using the maximally entangled GHZ states.Two years later, Wanget al.[27]considered an SQSS protocol using the two-particle entangled states.In 2013, Liet al.[28]utilized easier two-particle product states to implement an SQSS protocol.After that, Xieet al.[29]designed a new SQSS protocol with GHZ-like states,which can share a specific bit string compared with the previous protocols.In 2018,Liet al.[30]proposed an SQSS protocol where classical participants can realize secret sharing without making any measurements and quantum Alice does not need quantum registers, which improves the relative efficiency.In the same year,Yeet al.[31]proposed two circular SQSS protocols using single particles where the second one releases the classical parties from the measurement capability.A more practical and flexible SQSS protocol based on the Bell states was proposed by Tianet al.[32]in 2021, which can share specific secrets with classical parties.However, inefficiency is still a major problem of SQSS protocols.
In this paper,an SQSS protocol based on single particles is presented.An encoding method is used to make quantum Alice has the right to decide the shared secret message.After this, we use particle reordering to maximally utilize particles while ensuring security, so that there is no particle discarded or wasted in our protocol, improving the efficiency to nearly 100%.The resources used in the proposed protocol are simple single particles and are prepared only by the quantum party,reducing the difficulty of the resource preparation.Besides,the particles in our protocol are transmitted in a circular way,which makes the role of the agents equal, so this protocol is easy to be extended to multi-party secret sharing.And then,we analyze the security of the protocol to prove that our protocol is secure and can resist common attacks,such as interceptresend attack and measure-resend attack.
The remaining parts of the paper are organized as follows.In Section 2, a novel SQSS protocol is described in detail.Next, the security analysis is in Section 3 while the comparison of the SQSS protocol with previous protocols is analyzed in Section 4.In Section 5,a conclusion is given.
2.The proposed SQSS protocol
In this section,we first present an encoding method.Secondly,we propose a three-party SQSS protocol based on single particles.Then,such SQSS protocol is generalized to the multiparty case.After that,we use an example to show the process of the protocol in detail.
2.1.Encoding method
To encode any integer as a bit string with equal numbers of 0 and 1, we try to present an encoding method, which can be applied in the protocol proposed thereafter.
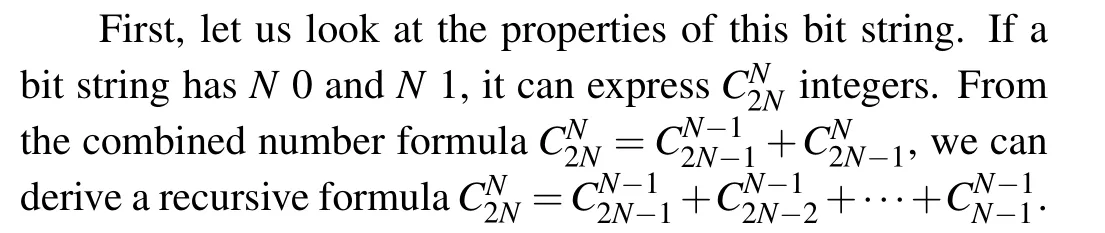
Inspired by this, based on the location where the first 1 appears, a 2N-bit string can be divided intoN+1 groups.If the first 1 appears in thei-th position, the remainingN ?1 1 can only appear in the later 2N ?iposition,so this group hascombinations.Then every group can be further divided into sub-groups based on the location where the next 1 appears and so on.Once theN-th 1 is located,all 1 are well positioned and the remaining positions will be filled with 0.According to this idea, we can propose an encoding method which is suitable for any numberN.
An integerxwithin the range ofcan be expressed asx=C?b1?b2?···?bN,where
1≤i ≤N,ai ∈N+.Theaiis a parameter to build parameterbiand indicates encoding positions.ThePiis an intermediate value
If eachbi /= 0, the positions from the first 1 to theNth 1 will be 2N ?a1,2N ?a2,...,2N ?aN, or they will be 2N ?a1,2N ?a2,...,2N ?ak?1,N+k,N+k+1,...,2N,(k=min{i|bi=0}).
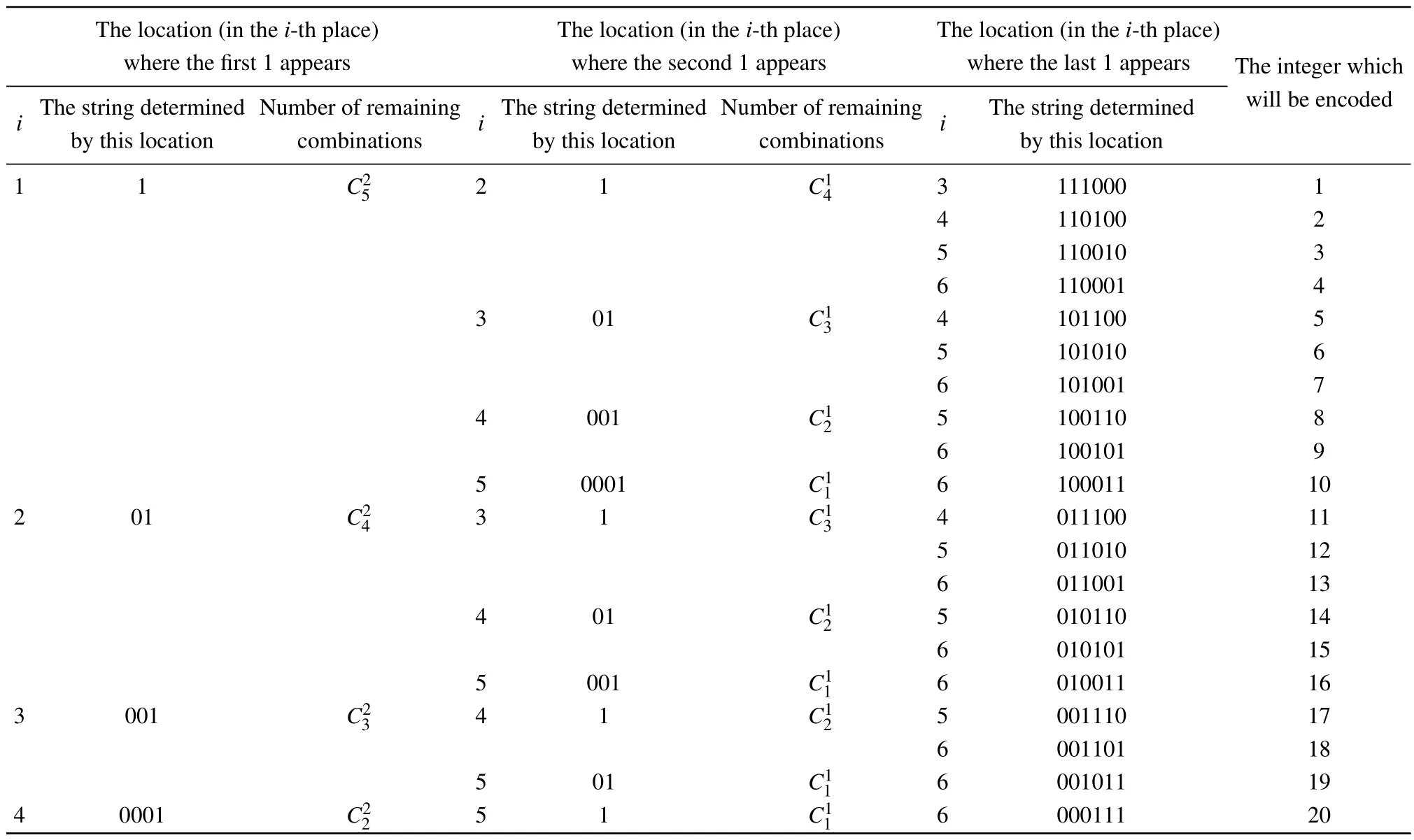
Table 1.Encoding method and encoded results for N=3.
2.2.Three-party SQSS protocol
Suppose Alice has quantum capabilities while the others two participants Bob and Charlie are classical.Alice wants to share a secret with Bob and Charlie securely.The proposed three-party SQSS protocol is composed of the following steps.
Step 1Alice decides the content of the shared secret at will and encodes the secret into a bit string with equal numbers of 0 and 1 by using the encoding method in Subsection 2.1.Suppose the length of this bit string is 2a.
Step 2Alice first randomly selects one basis fromZbasis{|0〉,|1〉}andXbasis{|+〉,|?〉}.Using the particles|0〉and|+〉to stand for the classical bit and particles|1〉and|?〉to stand for the classical bit 1, based on the encoded string,Alice prepares all 2asingle particles from the selected one basis.After that, Alice reorders these particles.Note that the rearrangement order of particles is only known to Alice.
Step 3Alice preparesmdecoy photons,each of which is randomly in one of the four states{|0〉,|1〉,|+〉,|?〉},inserts decoy photons to the reordered particles in random positions,and sends them to Bob.
Step 4After confirming that Bob has received the particles, Alice publishes the insertion positions of a fraction of decoy photons.Before she publishes the states of these decoy photons,Bob must measure those photons inZbasis.For those photons in|0〉or|1〉,Bob checks the error rate,and for those in|+〉 or|?〉, Bob checks whether the measurements are evenly distributed.He aborts the protocol if the error or deviation rate exceeds a preset threshold.After the check,he disturbs the order of the remaining particles.Only Bob himself knows the rearrangement order of them.Finally,Bob sends all particles to Charlie.
Step 5After Charlie announces the receipt of all particles from Bob, Alice publishes the insertion positions of another fraction of decoy photons.Then Bob publishes the transposition order of those photons,so Charlie can accurately measure those decoy photons inZbasis.She checks the measurements just like Bob based on the states published by Alice.After that,she does not need to do anything else but reorder the remaining particles secretly and send them back to Alice.
Step 6After receiving particles from Charlie,Alice publishes the original positions of the rest of decoy photons.Bob and Charlie publish in turn their transposition order of these photons so Alice could get the final positions of the decoy photons in the existing particle sequence.Alice performs measurements in the corresponding basis of the decoy photons at these positions.By comparing the measurement results to the originally prepared photon states,Alice can calculate an error rate.If the error rate exceeds a preset threshold,they will abort this communication and restart the protocol.Otherwise, they continue to the next step.
Step 7Alice measures all the remaining particles with the basis selected in step 2 and publishes the measurement results, that is, the encoded string that has been reordered by Alice,Bob,and Charlie.After that,Alice announces her rearrangement order.Only Bob and Charlie have cooperated,can they recover the original encoded string by sharing their own rearrangement order.Finally, they can get Alice’s secret by decoding the encoded string.
2.3.Multi-party SQSS protocol
The three-party SQSS protocol is easily generalized to multi-party SQSS protocol.
Steps 1–5 are roughly the same as our three-party SQSS protocol,but at the end of step 5,Charlie sends the particles to the next classical participant,David,instead of Alice.
Step 6After David announces the receipt of all particles,Alice publishes the insertion positions of a fraction of decoy photons and previous classical participants publish their transposition order of those decoy photons.Subsequently, David measures decoy photons and checks the measurements just like the Bob in step 4 based on the states published by Alice.After the check, he disturbs the order of remaining particles and sends the particles to the next classical participant.The remaining participants also operate as above, except that the last participant Zach sends the particles back to Alice.
Step 7After receiving particles from Zach, Alice could get the final positions of the decoy photons with the help of all classical participants.The same as in step 6 in Subsection 2.2,Alice can make the corresponding measurements and calculate an error rate to detect eavesdropping.
Step 8Alice publishes her rearrangement order and the measurement results of all the remaining particles measured in the basis selected in step 2.Classical participants can recover the encoded string only by cooperating.Finally, they can decode the encoded string to get Alice’s secret.
The proposed multi-party SQSS protocol is implemented as above.
2.4.Example
Now,an example of our proposed SQSS protocol will be given in this part.


3.Security analysi s
In general, in the QSS protocol, internal attackers are more powerful than external eavesdroppers because they know more information about the secret.Therefore, we will focus on the security of the proposed SQSS protocol for dishonest internal participants below.
3.1.Intercept-resend attack
If Bob is a dishonest internal attacker, to obtain Alice’s shared secret, Bob can try to launch an intercept-resend attack as follows: he uses Alice’s particles as usual to perform the step 4.Then, he prepares a string of fake single particles and sends it to Charlie.After Charlie finishes his operation,Bob intercepts the particles that Charlie sends to Alice.By measuring this string of particles,Bob tries to obtain Charlie’s rearrangement order of the particles.
However, Bob cannot determine the transposition order for particles in the same state|0〉 or|1〉.For example, if the sequence{|0〉,|1〉,|1〉,|0〉}is reordered to{|0〉,|1〉,|0〉,|1〉},the|1〉 on the second position may be unchanged or may be reordered to the fourth position.Consequently, Bob can not get exactly how Charlie disturbs the particles.Even if Bob can get Charlie’s rearrangement order,since he does not know the positions and states of decoy photons when he sends the fake particle sequence,his attack will introduce errors when Alice and Charlie detect eavesdropping.
Therefore, Bob can obtain almost no information by launching intercept-resend attack without being detected.As a result,the intercept-resend attack fails.
3.2.Measure-resend attack
Without loss of generality, supposing Bob is a dishonest internal attacker, to obtain Alice’s shared secret, he can take two strategies below to perform measure-resend attack.
(i)Bob intercepts the string of particles transmitted from Alice and measures all particles using the same basis (ZorXbasis).Based on the measurements, Bob generates a new quantum sequence with the same measurement results and resends it to Charlie.If Bob’s attack is not detected, Bob has a 1/2 chance of choosing the right basis Alice selects and obtaining access to the secrets Alice wants to share.However, his attack will introduce errors and be detected before he obtains any useful information.Suppose Charlie checksμdecoy photons inZbasis and Alice measuresηdecoy photons.If Bob chooses to measure all particles inZbasis, the probability that Bob will not be detected is (1/2)η/2, and if Bob chooses to measure all particles inXbasis,the probability that Bob will not be detected is (1/2)(η/2)+μ.Therefore,the average probability that the attack will not be detected is 1?(1/2)(η/2)+1×,and whenηis large enough,Bob’s attack cannot be successfully implemented.
(ii) Bob intercepts the particles sent to Alice and measures all particles using the same basis (ZorXbasis).As the rearrangement order of the particles is only known by the operator himself,Bob cannot accurately obtain Alice’s shared secret without the help of Charlie, and this operation will be detected by eavesdropping detection.
Stated thus, the proposed protocol is secure against measure-resend attack.
3.3.Entanglement-measure attack
Suppose a malicious internal attacker Bob attempts to steal the secret shared by Alice through the entangle-measure attack.As this protocol only uses decoy photons to detect eavesdropping, we only consider the effect on decoy photons for entangle-measure attacks.The entangle-measure attack from Bob can be described as follows: the unitary operationsUFattacking particles as they go from Bob to Charlie and the unitary operationsURattacking particles as they go back from Charlie to Alice, whereUFandURshare a common probe space with the state|ε〉.
Theorem 1For the entangle-measure attack(UF,UR)performed by Bob inducing no error in eavesdropping detection,the final state of Bob’s probe should be independent of Alice’s measurement result.As a result, Bob gets no information on Alice’s shared secret.
ProofAfter Bob has performedUF, the following relations should be established:
where|ε00〉,|ε01〉,|ε10〉and|ε11〉represent the un-normalized states of Bob’s probe.
For particles of any order, Bob needs the final state of the first register to be the same as the original state to pass the eavesdropping detection,soURmust satisfy the following conditions:
From the equations above,it should hold that
After inserting Eq.(11)into Eqs.(7)–(10),we have
According to Eq.(12),if Bob is not detectable in the security check,he can not distinguish his final probe states.As a result,Bob gets no information on Alice’s shared secret QED.
3.4.Trojan horse attack
Here,Bob plans to use Trojan horse attack.After finishing his normal operation, he attaches the invisible photons or the spy photons to his particles and transmits all of them to Charlie for Trojan horse attack.[33]By analyzing spy photons in this string of particles sent to Alice by Charlie,Bob tries to obtain Charlie’s order of the particles.Nevertheless,by applying a photon number splitter(PNS)and a wavelength filter device(WF),the malicious operations can be easily resisted.[34]Hence, the presented protocol is secure against Trojan horse attack.
3.5.Collusion attack
In collusion attack, some participants can collude together to get the shadow of the share of other participants.
In our protocol, to facilitate the description, we denote the classical participants of the(n+1)-party protocol asP1,P2,...,Pn.Suppose participantsPj?1andPj+1try to perform the protocol dishonestly to get thePj’s rearrangement order.Since particle reordering is an independent operation and the rearrangement order is known only toPjhimself,two dishonest participants can attack no more than the previous dishonest Bob did alone,they can not get this order by colluding together to perform attacks.
Moreover,even(n?1)dishonest participants collude together, they do not know the positions and states of decoy photons beforePjreceives particles,which means they are unable to escapePj’s eavesdropping detection by publishing fake transposition order of decoy photons.As a consequence,their collusion attack will introduce errors and the protocol will be aborted,so Alice’s secrets will not be leaked.
Therefore,our protocol is secure against collusion attack.
4.Comparison
We analyze and compare the performance of the proposed protocol with existing SQSS protocols.Our protocol makes progress in the following three aspects: simplifying the quantum resources,improving the protocol efficiency,and transmitting specific secrets.In Table 2, we make a more detailed comparison with the typical SQSS protocols in Refs.[26,28,31,32].

As shown in Table 2,our protocol is based on single particles rather than entangled states or product states,reducing the difficulty of resource preparation.Moreover, we can see that the qubit efficiency of the proposed protocol is higher than all of the compared protocols, because it can approach 100% asNincreases (the decoy photons are ignored).Lastly, in most previous protocols,the shared secret is not specific,whereas in our protocol Alice can decide which secret message to share.
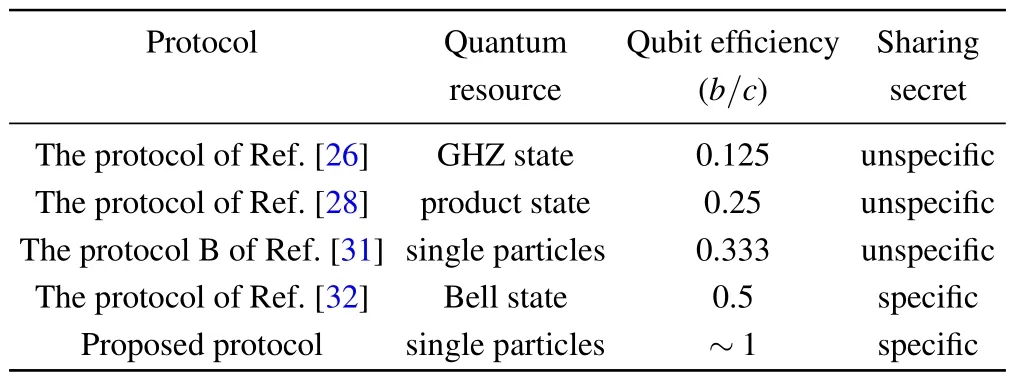
Table 2.Comparisons of the SQSS protocols.
Through the above comparison,the proposed protocol is more efficient and practical than existing ones.
5.Conclusion
We have presented a more efficient and practical SQSS protocol.The efficiency of protocol could approach 100%as the length of message increases.Our protocol is based on single particles,reducing the difficulty of resource preparation.In addition,the shared secret message can be determined by Alice herself which cannot be realized by some previous protocols.Finally,we analyze the security of the proposed protocol and fully prove that our protocol can resist common attacks.High efficiency is a big advantage of our protocol,and we will explore how to improve the efficiency of protocols in other semi-quantum cryptography fields in future work.
Acknowledgments
Project supported by the National Key Research and Development Program of China(Grant No.2020YFB1805405),the 111 Project(Grant No.B21049),the National Natural Science Foundation of China (Grant No.62272051), the Foundation of Guizhou Provincial Key Laboratory of Public Big Data(Grant No.2019BDKFJJ014),and the Fundamental Research Funds for the Central Universities of China (Grant Nos.2019XD-A02 and 2020RC38).
- Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing

