強 靜, 邵 虎, 張雙圣

(1.中國礦業(yè)大學 數(shù)學學院, 江蘇 徐州 221116; 2.徐州工程學院 環(huán)境工程學院, 江蘇 徐州 221018)

0 引 言

國內大多數(shù)《高等數(shù)學》(《微積分》)教材[1-3]在曲率一節(jié)中,首先引入弧微分,然后才給出曲率的定義,最后運用弧微分公式推導曲率公式.開篇引入弧微分,略顯突兀,而且在證明弧微分公式時直接使用了“弧長和弦長的比值極限為1”這個假設,證明過程不嚴謹,學生對此常常感到疑惑.

目前,一些研究《高等數(shù)學》的學者試圖運用微分理論證明弧微分公式,提出了一些有趣的方法[4-5],但這些方法有不足之處.比如,文獻[4]構造了一個不等式,運用夾逼準則證明弧微分公式,雖然弦長確實小于弧長,但是弧長未必小于文獻[4]中所給兩條線段的和,證明過程出現(xiàn)了疏漏;文獻[5]運用單調有界數(shù)列必有極限定理,僅證明了光滑曲線弧在一種分割方式下內接折線長度的極限存在,就認為光滑曲線弧是可求長的,據(jù)此又證明了弧微分公式,這種證明過程顯然也有漏洞.另外,《數(shù)學分析》[6]中運用積分理論,證明了光滑曲線弧(曲線方程為參數(shù)方程)是可求長的,從而得到了弧微分公式,但該證明方法比較繁瑣,其中涉及到一致連續(xù)的性質的使用,對于非數(shù)學專業(yè)學生來說難度較大,不易理解.

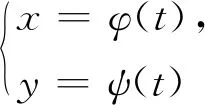
為了解決上述問題,本文首先引出曲率的定義,并給出一種新的曲率的定義形式;在高等數(shù)學知識體系內給出一種嚴謹證明弧微分公式的方法;針對上述四種不同形式的曲線方程,推導并總結了四種不同方程下的曲率公式及適用條件;給出二個典型例題說明四種曲率公式的情景應用;最后,給出了一個運用曲率公式求解實際工程問題的案例.以期為研究平面曲線的曲率問題提供借鑒,也為《高等數(shù)學》教材改革中曲率部分的編寫提供參考.

1 曲率的定義

在生產實踐和工程技術中,研究曲線的彎曲程度是經常遇到的一類問題,比如火車軌道緩和曲線設計問題,火車通過彎曲軌道時向心力大小的影響問題以及大橋在荷載作用下產生彎曲變形問題等.因此如何定量描述曲線的彎曲程度具有重要的現(xiàn)實和理論意義.曲率就是描述曲線的彎曲程度的量.

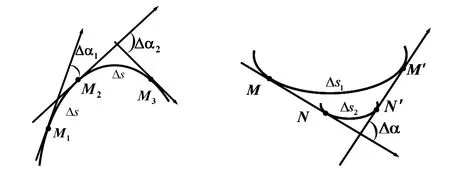
圖1 弧長相同條件下的曲線 圖2 轉角相同條件下的曲線

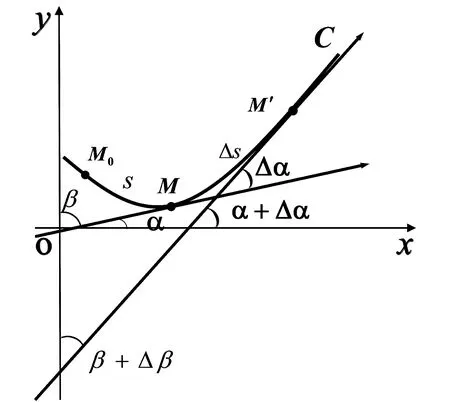
圖3 一般情況下的曲線C

2 弧微分公式推導

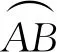
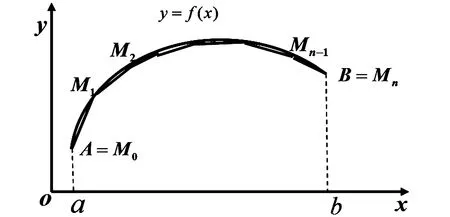
圖4 曲線y=f(x)上弧及其內接折線

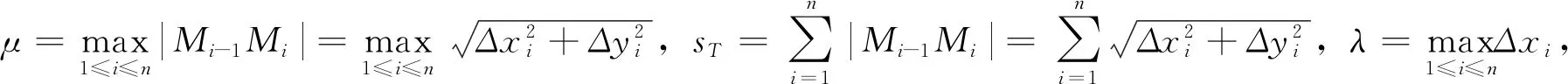
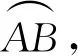
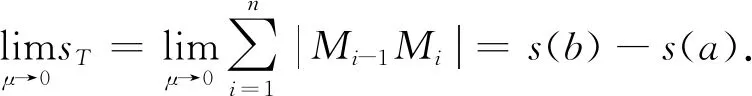
定理1假設曲線y=f(x)在區(qū)間[a,b]上可導且導函數(shù)f′(x)連續(xù),則曲線是可求長的,且

證由微分中值定理得

Δyi=f(xi)-f(xi-1)=f′(ξi)Δxi,ξi∈[xi-1,xi].

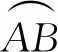
又因為

當μ→0時,對于?i(1≤i≤n),均有

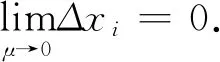
根據(jù)極限運算的換元法則得

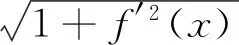
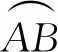
3 曲率公式推導

曲線方程(i):y=f(x),且f(x)具有二階導數(shù).

在圖3中,因為tanα=y′,所以

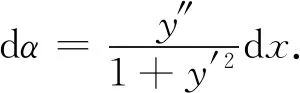
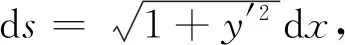
(1)

曲率公式(1)的適用條件是y=f(x)二階可導.

曲線方程(ii):x=h(y),且h(y)具有二階導數(shù).

在圖3中,因為tanβ=x′,所以

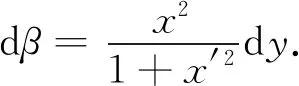
(2)

曲率公式(2)的適用條件是x=h(y)二階可導.

由于φ′2(t)+ψ′2(t)≠0,不妨設φ′(t)≠0,根據(jù)參數(shù)方程求導公式可得

代入公式(1)得到曲率公式如下:

(3)

如果φ′(t)=0,則ψ′(t)≠0,根據(jù)參數(shù)方程求導公式可得

代入公式(2)可得曲率公式:

與公式(3)相同.

曲率公式(3)的適用條件是x=φ(t)及y=ψ(t)均二階可導,且φ′2(t)+ψ′2(t)≠0.

曲線方程(iv):由極坐標方程ρ=ρ(θ)給出,ρ(θ)二階可導,且ρ2(θ)+ρ′2(θ)≠0.

x′(θ)=ρ′(θ)cosθ-ρ(θ)sinθ,x″(θ)=ρ″(θ)cosθ-2ρ′(θ)sinθ-ρ(θ)cosθ,

y′(θ)=ρ′(θ)sinθ+ρ(θ)cosθ,y″(θ)=ρ″(θ)sinθ+2ρ′(θ)cosθ-ρ(θ)sinθ.

將上述4式代入到曲率公式(3)可得極坐標系下曲率公式,如下:

(4)

曲率公式(4)的適用條件是ρ=ρ(θ)二階可導,且ρ2(θ)+ρ′2(θ)≠0.

4 例 題

為了進一步說明各曲率公式的適用條件,給出兩個典型例題.其中,例1用來說明曲率公式(1)-(3)適用條件,例2用來說明曲率公式(4)的適用條件.

例1求橢圓4x2+y2=4在點(1,0)及點(0,2)處的曲率.

解① 點(1,0)處的曲率

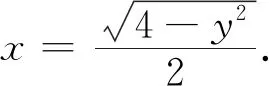
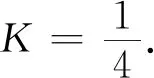
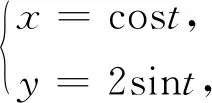
x′(t)=-sint,x″(t)=-cost,y′(t)=2cost,y″(t)=-2sint.

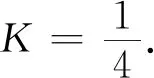
② 點(0,2)處的曲率

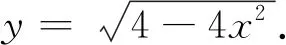
根據(jù)公式(1)可知點(0,2)處的曲率K=2.

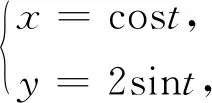
滿足曲率公式(3)適用條件,根據(jù)公式(3)可得點(0,2)處曲率K=2.

例2試求阿基米德螺線ρ=aθ(a>0)上任一點處曲率,并討論哪一點處曲率最大.

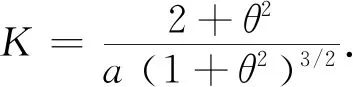
5 實際應用

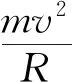
這雖然是一個經典實際問題,在文獻[6,14]中都有闡述,但是文獻[6]中沒有詳細解答過程,文獻[14]中緩和曲線推導過程比較復雜.本文給出一種更合理的方法設計緩和曲線.

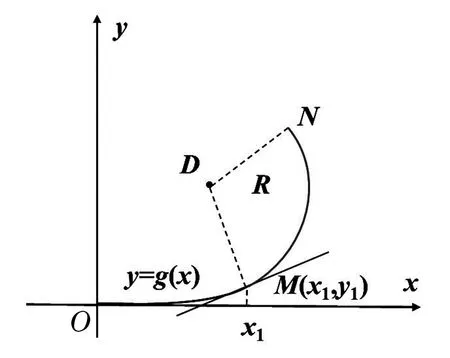
圖5 鐵軌緩和曲線示意圖

g(0)=0,g′(0)=0,g″(0)=0,

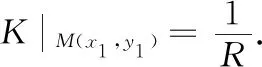
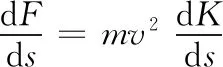
(5)

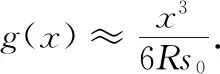
6 結 論

在高等數(shù)學知識體系內,利用曲線直角坐標方程得到了弧長與有向弧段的值之間的關系,證明了弧微分公式.證明過程中不需要使用一致連續(xù)的性質,相對簡潔,且避免了弧微分公式推導過程中“弧長和弦長的比值極限為1”這個假設,使弧微分公式及曲率公式的推導過程更加嚴謹.

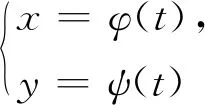
致謝作者非常感謝相關文獻對本文的啟發(fā)以及審稿專家提出的寶貴意見.