Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
Haiyun Tan(譚海云), Tianyuan Huang(黃天源), Peiyu Ji(季佩宇),Mingjie Zhou(周銘杰), Lanjian Zhuge(諸葛蘭劍), and Xuemei Wu(吳雪梅),?
1School of Physical Science and Technology&Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China
2Key Laboratory of Advanced Optical Manufacturing Technologies of Jiangsu Province&Key Laboratory of Modern Optical Technologies of Education Ministry of China,Soochow University,Suzhou 215006,China
3School of Optoelectronic Science and Engineering,Soochow University,Suzhou 215006,China
4Analysis and Testing Center,Soochow University,Suzhou 215123,China
Keywords: particle-in-cell,direct implicit simulation,finite-grid-instability
1.Introduction
Low-temperature bounded plasmas, such as capacitively coupled plasmas (CCPs) or magnetron plasmas, have generated significant research interest due to their applications in film preparation, hi-tech industries, materials surface treatment, and other areas.[1-3]Charged particles in plasmas play significant roles in plasma-based material processing.Therefore,researching the particle dynamics and microscopic physical processes in plasma is crucial for optimizing the plasma technological processes.
Particle-in-cell(PIC)methods are useful simulation tools for the kinetics study of plasma.At present, explicit PIC algorithms is perhaps the most widely used method.[4-8]Such the method calculates the electromagnetic(EM)field based on the known information of the particles,at the currently calculation step.Explicit PIC algorithms require very small spatial step ?xand time-step ?tto obtain the desired numerical stability.In practice,one needs ?x<λDeandωpe?t<0.2,[9]where theλDeandωperepresent the electron Debye length and the electron plasma frequency,respectively.In addition,hundreds of macro-particles per cell are needed to reduce the statistical error originating from the sampling of the distribution function by macro-particles.[10]As a result, a very large number of meshes, calculation-steps and macro-particles are needed in traditional explicit PIC methods, and it is time-consuming to use explicit PIC methods for the kinetics study of plasma.
Despite the aforementioned challenges, explicit PIC methods remain attractive, especially since there is a desire to address high-frequency plasma oscillations in many situations.Several methods have been proposed to improve the calculation speed of the explicit PIC.Firstly, parallel computation using multiple processors or GPUs can be used to accelerate the task.[11-13]Speed gains can also be achieved through mathematical and physical methods.For example, a large time-step ?ti??tefor heavy ions can be used since ions are much heavier than electrons and their macroscopic properties can be analyzed on a longer timescale.[14]Here,the subscripts‘i’ and ‘e’ represent ion and electron, respectively.Another method is the scaling principle,which involves the scaling of mass of ions, vacuum permittivity and geometric size of the system.[15-17]Such the method is widely used in the research of Hall thrusters.Besides,different spatial steps can be used in different plasma regions.For instance, small spatial step and time-step should be employed near the plasma sheath to track fast electrons and resolve the sheath,whereas larger steps can be used in the bulk region.[18]
On the other hand,if the high-frequency electron plasma oscillation is not the main physical process that determines plasma character, then implicit methods can be used to accelerate the computing by using large spatial and temporal steps with coarse resolution in Debye length and electron oscillation.The traditional implicit methods, such as direct implicit methods[19]or implicit-moment methods,[20]are developed to relax the numerical stability constraint of explicit PIC on time-step.Further research has shown that a large spatial step is also allowed in these implicit PICs because the highfrequency electron oscillation causing finite-grid-instability is damped.[21]In recent years, some implicit methods with energy conservation have been developed,[22-24]which can relax the requirements of numerical stability on time-step and spatial step significantly.
Implicit methods are attractive as they allow PIC simulations to be run with large time-step and spatial step.However,their performance is limited in researching bounded plasma due to several reasons.Firstly, it is time-consuming to solve the implicit field equations for the traditional implicit PIC since the equations contain time-dependent coefficients.[25]On the other hand, the particle pusher in the implicit PICs with energy conservation is sophisticated to maintain total energy conservation.[26]Moreover, the spatial step must be smaller than one-fifth of sheath thickness to resolve plasma sheath,[21]which means that very large spatial step is not allowed, and a small time-step is also required to meet the Courant-Friedrichs-Lewy(CFL)condition.[9]In general, the implicit PIC methods relax the constraints on time-step and spatial step by a factor of~10.[26]
Therefore,the ideal PIC method for researching bounded plasma should simulate plasma behavior accurately,using the spatial step large enough to resolve plasma sheath and the time-step large enough to track fast electron group.In addition, it should have efficient field solvers and particle pushers, and be compatible with existing PIC frameworks to utilize various speed-up techniques.This work proposes a PIC method with damping of high-frequency electron oscillation,which obtains the future fields by solving traditional explicit field equations with constant matrix coefficient and uses the same particle pusher as that used in the direct implicit PIC method.Section 2 briefly reviews the theoretical background of the explicit and direct implicit PIC methods, while Section 3 describes the algorithm of the proposed damped PIC.In Section 4, several numerical experiments are implemented to evaluate the performance of the new method.The last part is a summary and a description of the future work.
2.Theoretical background
In this section,we will review two traditional PIC methods, namely explicit PIC (EXPIC) and direct implicit PIC(DIMPIC).We begin with a charged particle having velocityvn-1/2,locating at positionxn,at time stepn.The central difference equations of motion for the charged particle are then used to compute the position and velocity at next time step,as follows:[3]
here ?tis the time-step,an(xn)andΩn=(q/m)Bn(xn)represent the electric field acceleration and the cyclotron frequency of the particle atxn,respectively,whereBnrepresents the magnetic field andq/mrepresents charge mass ratio of the particle.For convenience,we only consider electrostatic case.
2.1.Explicit PIC
It is both convenient and intuitive to track the motion of the particle by using EXPIC.In this method,the positionxnis first used to obtain the charge densityρnat a given mesh using some interpolation methods.Next,the electric fieldEnat the current time step is obtained by solving the explicit Poisson equation with source term ofρn,which in turn is used to update the velocity and position.Finally,the solution is completed,and the calculation proceeds to the next time step.The algorithm of EXPIC is as follows:
(i)xn →ρn(interpolation of charge density from the particles);
(ii)solving the explicit Poisson equation to obtainEnat the mesh,that is,
whereφrepresents potential andε0is the permittivity of vacuum;
(iii)an(xn) = (q/m)En(xn) (interpolation of the field from mesh);
(iv)vn+1/2=vn-1/2+an(xn)?t+(?t/2)[(vn+1/2+vn-1/2)×Ωn];
(v)xn+1=xn+vn+1/2?t;
(vi)Ωn+1=(q/m)Bn+1(xn+1)(interpolation of the field from mesh).
The dispersion relationship for the electrostatic Langmuir wave with frequency ofωpepredicted by the EXPIC is expressed as follows:[27]
whereωrepresents the frequency predicted by numerical calculation.As shown in Eq.(3), the EXPIC is numerically unstable whenωpe?t>2.In addition, the EXPIC is a method that cannot damp wave oscillation.Thus,using a large spatial step here with coarse resolution in Debye length will result in finite-grid-instability since the numerical oscillations enhance gradually.[3]
2.2.Direct implicit PIC
The DIMPIC is developed to relax the numerical stability constraint on time-step.In such method, equation (1) is modified as follows:[28]

If one wishes to calculatean(xn) accurately by usingan+1(xn+1),it is necessary to usexn+1to obtainρn+1,which in turn can be used to calculateEn+1.However,this process is often nearly impossible, and one must rely on some approximate methods.To obtainan+1(xn+1),DIMPIC uses a method proposed by Langdonet al.,[29]in which the approximate fieldEn+1is first obtained by solving the implicit Poisson equation.Then,the approximatean+1(xn+1)is obtained by some interpolation algorithms.

Final-pusher:

wherez ≡e-iω?tandωrepresents the frequency predicted by numerical simulations.By numerically solving Eq.(7),one can obtain the relationship between the amplitude|z|andωpe?t,which shows that the amplitude is damped and the numerical stability is independent of the time-step ?t.Besides,the damping of the wave is also helpful to suppress the grid heating caused by a large spatial step with poor resolution in Debye length.
It can be seen that DIMPICs allow the use of large spatial and temporal steps while maintaining numerical stability,which is not possible in EXPICs.However,the latter method has a simpler particle pusher.Additionally, DIMPIC has a more complex algorithm, and has a lower efficiency in solving the implicit Poisson equations as compared to solving the explicit Poisson equations.It becomes more challenging to solve such implicit equations in the high dimensional magnetized plasma systems becauseχis now anisotropic.In addition, the parallelism strategies for DIMPIC and EXPIC are different.For explicit PICs,significant CPU time gains can be obtained by only paralleling particle process since most of the CPU time is related to the particles.[9]For the direct implicit PICs, however, it is very important to parallel solve both the field solving process and particle process,because the time of field solving here takes a significant fraction of the total simulation time.[20]Meanwhile,parallel solving the implicit Poisson equation is troublesome due to the time-dependent matrix coefficientsχ.
3.Descriptions of damped explicit PIC method
The descriptions of the new method are started with the central difference equations of motion used in DIMPIC, and one can still suppose
As mentioned before, the traditional DIMPIC solves the implicit Poisson equation first to obtain an approximate fieldEn+1.Then,the approximatean+1(xn+1)is obtained by both this estimatedEn+1and the quantity ?xn+1provided by the prepusher, using some interpolation algorithms.Here, however,we adopt a different strategy.Firstly,we give an approximate ?an+1(xn+1), and then pre-push the particle to obtain the approximate fieldEn+1by solving an explicit Poisson equation.Finally,we re-obtain an approximatean+1(xn+1)to finish the push process.
To obtainan+1(xn+1), we suppose that an estimated ?an+1(xn+1) is already known.It is reasonable to set the estimated ?an+1(xn+1)as follows:

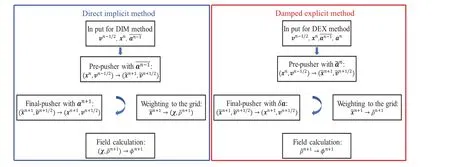
Fig.1.Differences between the flowchart of the DEXPIC and that of the DIMPIC.

It can be seen from the above loop that the unknown future electric field is now obtained by solving an explicit Poisson equation with source term obtained by the position from explicitly propulsion of the particle.In addition,the new method can damp high-frequency plasma oscillation strongly,as described below.For these reasons, the new PIC method is namely as damped explicit PIC (DEXPIC).For the new method, solving the Poisson equation parallel is expected to be easier due to the time-independent matrix coefficients.Figure 1 shows the differences between the flowchart of DEXPIC and that of the DIMPIC in the case where magnetic field is ignored.
In the following studies, we will examine the numerical accuracy and stability of the DEXPIC method.Furthermore,we will demonstrate that the method maintains the desirable damping of high-frequency electronic oscillation,while accurately describes low-frequency phenomena.
4.Numerical experiments
In this section, several numerical experiments will be performed to check the performance of the DEXPIC, including the motion of charged particles in EM fields, magnetized plasma sheath, and free diffusion of magnetized plasma into vacuum.
4.1.Particle pusher test
The motion of a charged particle in EM fields is first tested to check the accuracy of the particle pusher.We consider a test particle with massm=1 and chargeq=-1 that moves in an electric field varying withxand a constant static magnetic field:
At the beginning,the particle enters the computational domain with position(0,0,0)and velocity(0,0,0).The test runs until the total simulation timeT=12.
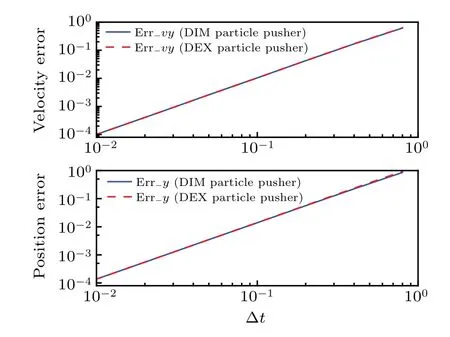
Fig.2.Accuracy analysis of the DEX particle pusher.The errors increase with the time-step,and show second-order accuracy.
To analyze the accuracy of the particle pusher with varying time-steps, we use three methods to calculate the trajectory of the particle.The first method,denoted as#1,solves the equations of motion through ODE solvers with a small timestep of ?t=1.25×10-4, which provides the equivalent analytical solutions.The other two methods are the DIM particle pusher and the DEX particle pusher,where different timesteps are used.The following relationship is introduced to analyze the accuracy of the particle pusher with respect to the time-step:[31]
Herexnandvnrepresent the position and velocity at timestepn.The subscript‘test’indicates that the data are obtained by the DIM particle pusher or DEX particle pusher,while‘ref’represents the reference value provided by the method#1.The


Equation (14) shows that the DEXPIC is numerical unstable whenωpe?t> 1 because one has|z|> 1 now.It is worth noting that the dispersion relationship described by Eq.(14)is approximate because the value ofan+1(xn+1) is estimated at ?xn+1rather thanxn+1.In the actual tests, we have found that the stability constraint on time-step is more restrictive,as shown in the Subsection 4.2.
4.2.Magnetized plasma sheath
We have implemented the DEX particle pusher in a custom short electrostatic PIC code with one-dimensional (1D)in space and three-dimensional (3D) in velocity.In this subsection, we will use the DEXPIC to simulate magnetized plasma sheath for the following purposes.Firstly,the numerical stability constraint on time-step of the DEXPIC will be derived from the experimental data.Secondly, we will observe how well the DEXPIC does at damping high-frequency electron oscillations,and what consequences such damping might have.To analyze the performance of the new method,we will compare the results obtained by DEXPIC with those obtained by the standard EXPIC and the DIMPIC.
In all tests, we assume the ions are immobile, and only consider the dynamics of electrons.At the beginning, a 1D uniform plasma plate with electron number density of 1×1016m-3and Maxwell velocity distribution for electrons with temperature of 1 eV is distributed between two parallel electrodes placed along thexdirection.Meanwhile,a constant transverse static magnetic fieldBzis present,and the potential of the electrodes is set zero.Additionally, every particle that reaches the electrodes will be absorbed and removed from the simulation.Moreover, no secondary electron emission, electron reflection,and particle-particle collisions are considered.The simulation time is normalized to 1/ωpe.
In first test #1, we use the following parameters to find the required constraint for numerical stability: system lengthL= 120λDe, 30 uniformly spaced grid points, 256 macroparticles per grid,Bz=10 Gs (1 Gs=10-4T), and tunable time-steps.The simulations run for time of 10000.Figure 3 shows the time history of the center potential predicted by the DEXPIC.One can observe obviously numerical instability whenωpe?t=0.895.In fact,whenωpe?t ≤0.894,we do not observe numerical instability in simulations run for long time(up to millions plasma oscillation period).It is worth noting that the CFL condition is ensured in all tests.

Fig.3.Time history of the center potential predicted by the DEXPIC with different time-steps.One can observe the numerical instability when ωpe?t=0.895.
As shown in Fig.3,the desired numerical stability at large time-step cannot be ensured by the DEXPIC.However, this method can still damp high-frequency oscillation significantly and suppresses the numerical instability originating from the coarse spatial resolution in the Debye length.As a result,the DEXPIC is stable when a large spatial step is used,as shown in the following studies.
Now we consider the second test #2 using the following parameters: system lengthL=30λDe, 30 uniformly spaced grid points, 256 macro-particles per cell, time-stepωpe?t=0.2, andBz=10 Gs.The simulations run for time of 1000.Figure 4 shows the time history of the center potential obtained by three methods, in which the illustration shows the history fromt=900 tot=1000.For the EXPIC,the time history shows a stable numerical oscillation,which actually captures the electron plasma oscillation.[34]If a large spatial step(?x ?λDe) is used, then such numerical oscillation will be amplified and result in significant fine-grid-instability.[3]However,the EXPIC cannot damp such high-frequency oscillation very well,as shown in the blue line.As a result,it must use a very small spatial step,even when the electron plasma oscillation is no longer important.
On the other hand,the DIMPIC is a well-known method with damping of high-frequency wave.[28]Therefore,the time history obtained by the DIMPIC shows that the numerical oscillation weakens gradually over time, as shown by the red line.Interestingly, for the DEXPIC,the time history shows a similar result to that of the DIMPIC,proving that this method can also damp the high-frequency plasma oscillation,thereby suppress possible numerical instability.Now, it has been demonstrated that DEXPIC is a damped PIC method by comparing the time history of the center potential obtained by the three methods.
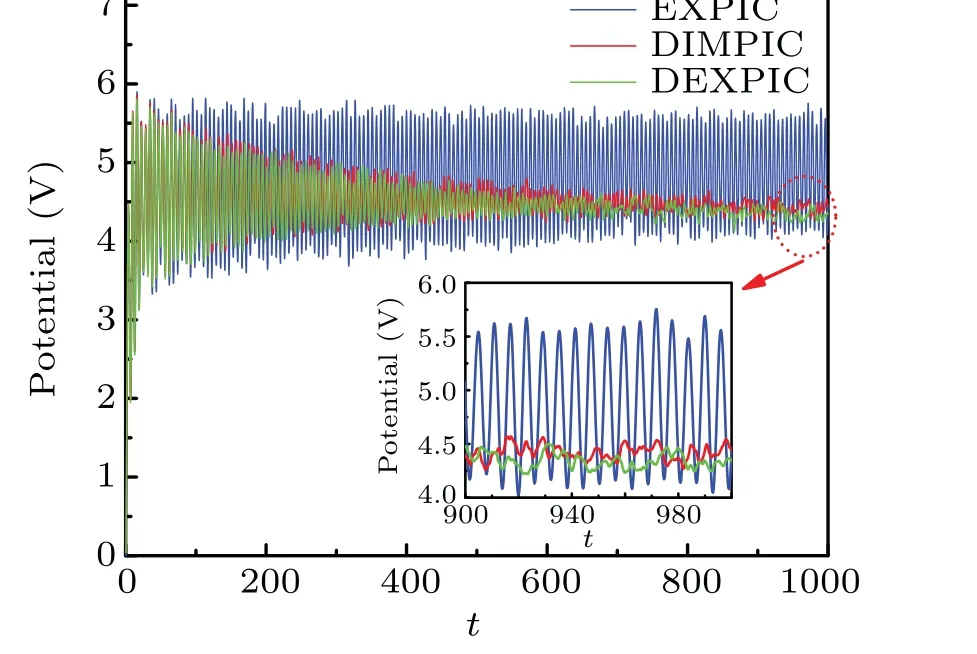
Fig.4.The time history of the center potential obtained by three methods.The electron plasma oscillation is damped by both DIMPIC and DEXPIC.

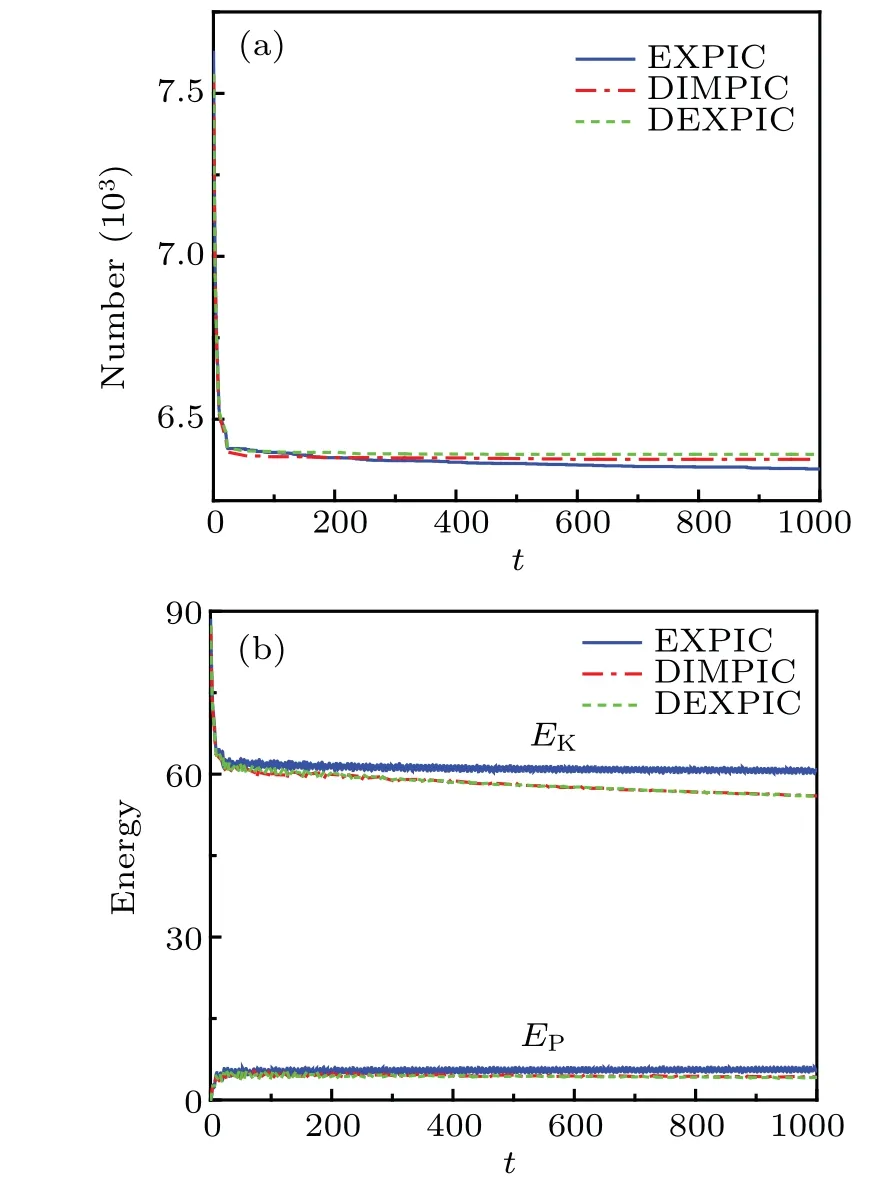
Fig.5.Damping of the DEXPIC on the energy of the particles.(a)The time history of electron number.(b)The time history of electron kinetic energy and electric field energy.
The reduction of the energy is related to the numerical cooling.The cooling rate depends onωtr?t, whereωtrrepresents the frequency of motion of the particles following the force fields.[30]As a result,the energy decreases while the particle number remains constant.The errors caused by such numerical cooling may lead to incorrect results.However, the cooling mentioned above is tolerable whenωtr?tis small.In other words,such numerical cooling is expected to be ignored when plasma is dominated by low-frequency force fields,such as radio frequency(RF)fields.For example,if we apply a voltage source with amplitude ofV=V0sin(ωt)to one electrode,whereV0=200(Te/e) andω=0.02ωpe, then the cooling is tolerable,as shown in Fig.6.
The damping of high-frequency plasma oscillation favor suppression of finite-grid-instability resulting from the coarse spatial resolution in the electron Debye length.To prove this conclusion, we consider the third test #3: system lengthL= 150λDe, 30 uniformly spaced grid points (?x= 5λDe),256 macro-particles per cell,time-stepωpe?t=0.8,andBz=30 Gs.The simulations run for time of 1000.The time history of the center potential and the total energy of the system obtained by three methods are plotted in Fig.7.
In this test, the spatial step is large enough so it causes significant fine-grid-instability, which results in the instability of EXPIC.Both the amplitude of the potential and the total energy of the system obtained by the EXPIC increase with time,as indicated by the blue line in Fig.7.In contrast,both DIMPIC and DEXPIC remain stable as they damp the numerical oscillation,as shown in the red and green lines in Fig.7(a).Meanwhile, it seems that the damping provided by DEXPIC is stronger than that provided by DIMPIC,as shown in the red dot-dashed line and the green dashed line in Fig.7.In addition, the damping of both DIMPIC and DEXPIC in this case is stronger due to the larger time-step.Of course, when the plasma is dominated by low-frequency fields, the numerical cooling will be tolerable,as mentioned in test#2.
4.3.Free diffusion of magnetized plasma into vacuum
In Subsection 4.2,we have evaluated the performance of the DEXPIC using the magnetized plasma sheath,in which the plasma is dominated by the high-frequency electron plasma oscillation.The results show that the DEXPIC can damp the numerical oscillation strongly and suppress fine-gridinstability.Here, we consider another experiment in which the physical process depends on low-frequency bipolar electric fields,specifically free diffusion of plasma into vacuum.[35]In all tests,we consider a 1D uniform plasma plate with thickness ofDplaced at the center of the computational domain, with number density of 1×1016m-3,Maxwell velocity distribution for both electrons and ions,Te=Ti=1 eV andmi/me=900.The constant transverse static magnetic field is equal to 30 Gs.The particle boundary and potential boundary are the same as that in Subsection 4.2.
In the first test#1,the simulations run with the following parameters:system lengthL=1000λDeandD=100λDe.The EXPIC uses 2000 uniformly spaced grid points,ωpe?t=0.1 and 256 macro-particles per cell, and its simulation results are treated as standard data.Both the DIMPIC and DEXPIC use 200 uniformly spaced grid points,ωpe?t=0.8 and 2560 macro-particles per cell.All simulations run untilt=1000,and the system length is long enough so that the total particle number remain constant in the simulations.
Figure 8 shows the evolution of the bipolar electric field over time obtained by three methods,where the field has been normalized toTe/λDe.It can be seen that the results offered by three methods agree well.Initially, the electrons in the outer layer of the plasma escape from the bulk region at fast speeds, leaving a shell full of positive charge density, which is surrounded by negative charge density.[23]As a result, one can observe an ambipolar electric field near this shell.On the other hand, the shell will be filled with negative charge density and be surrounded by positive charge density when the simulations run for longer term, because the drift velocity of the electron group is slower than that of ion group due to the effect of the transverse magnetic field.[1]Therefore,the direction of the bipolar field has reversed.It should be noted that the results obtained by both the DIMPIC and DEXPIC provide a correct description of the evolution of the bipolar fields over time,even they have poor spatial resolution.
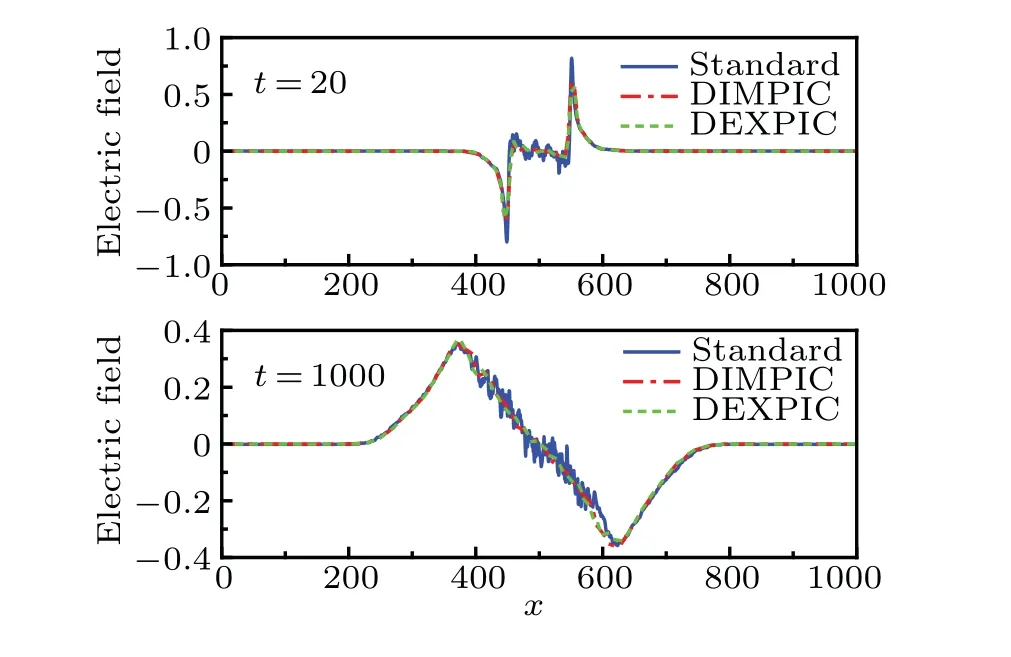
Fig.8.The evolution of the bipolar electric field over time,in which the results obtained by three methods agree well.
The velocity distributions of electrons and ions att=1000 are plotted in Fig.9, along with the initial distributions att=0 represented by the black line, where the velocity has been normalized to the initial average velocityv, and the velocity space is[0,4],discretized by 100 cells.The ambipolar fields tend to pull back the escaped charged particles towards the bulk region, while accelerate the charged particles in the outer layer of the plasma.[1]As a result, the velocity distributions of both electrons and ions are modulated.The figure demonstrates that the average velocity of electrons increases,while that of ions decreases,with the results obtained by three methods showing good agreement.
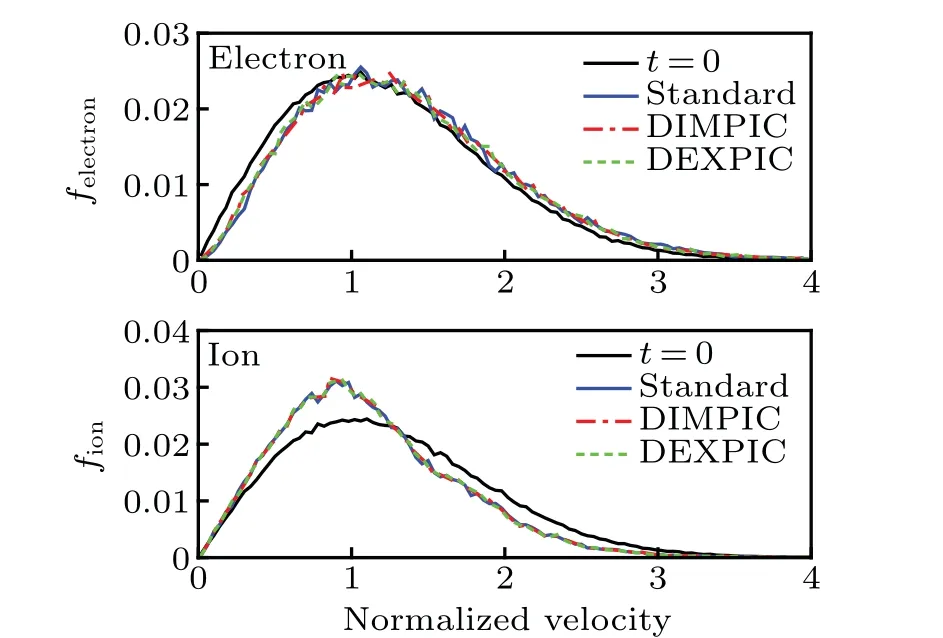
Fig.9.The velocity distributions of electron and ion at t =1000.The average velocity of electrons increases while that of ions decreases due to the effect of ambipolar field.The results obtained by the three methods agree well.
Figure 10 shows the time history of the total energy of the system obtained by three methods,in which the green dot-line represents the results obtained by the EXPIC using the same parameters as that used in DIMPIC and DEXPIC.It can be seen that the standard result shows good energy conservation.On the other hand, the result obtained by the EXPIC using poor resolution in Debye length and high frequency electron plasma oscillation shows that the total energy raises over time,which indicates numerical instability in the simulations run for long time.As a comparison,the total energy obtained by both DIMPIC and DEXPIC decreases rapidly firstly and stabilizes gradually over time.The decreased energy originates from the numerical cooling mentioned before.As time increases, the plasma gradually becomes dominated by low-frequency bipolar electric field so that the cooling is tolerate.Again, the figure indicates that the DEXPIC provides stronger damping compared to that of DIMPIC.The stronger damping may be beneficial when larger space step or fewer macro-particles per cell is used,as it can suppress the heating caused by numerical noise more effectively.
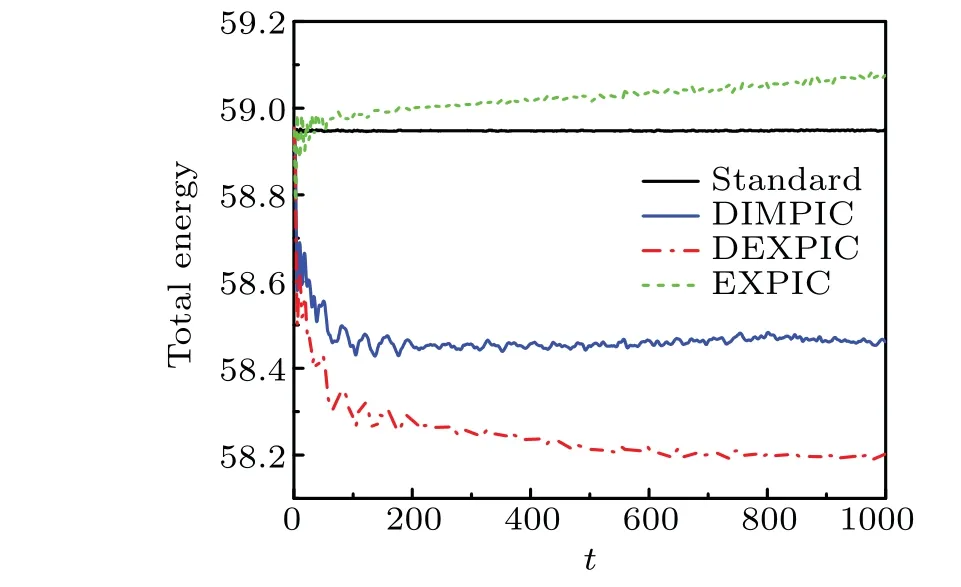
Fig.10.The time history of the total energy of the system obtained by three methods.The total energy predicted by the EXPIC increases over time.
Now, we consider the second test #2 to check the accuracy of the DEXPIC using the spatial step and time-step with different resolutions in Debye length and high-frequency electron plasma oscillation.The simulations run with the following parameters: system lengthL=1000λDe,D=100λDe,and the total simulation time is equal to 1000.The EXPIC uses the same spatial step and time-step as that in test#2.Both the DIMPIC and DEXPIC use 200,250,320,400,500,625,and 1000 uniformly spaced grid points respectively, and the total particle number is the same as that of the EXPIC so that the initial velocity distribution function is constant.The time-steps used in the DIMPIC and DEXPIC are varied with spatial step to ensurevthe?t/?xis constant so that CFL condition is constant, wherevtherepresents the thermal velocity of electrons.However,when ?x=5λDe,the time-step is set asωpe?t=0.8 rather thanωpe?t=1.0 since the stability constraint on the time-step of the DEXPIC requiresωpe?t ≤0.894.
To calculate the accuracy,we determine the errorε(fe)in the velocity distribution functionfeof the electrons using the following relation:
wherefrefrepresents the reference distribution function taken from the standard EXPIC.The integral element ?vis 0.04.Equation(15)is actually another version of Eq.(11).The differences between the distribution function obtained by three methods are shown in Fig.11.It can be seen from the figure that the accuracy of both DIMPIC and DEXPIC is acceptable as the resolution in Debye length and high frequency electron plasma oscillation gets worse,in which the maximum error of the DEXPIC is only around 0.15%.It should be noted here that both the DIMPIC and DEXPIC use the same total particle number as that used by the standard EXPIC,which means that the number of the macro-particles per cell increases as the number of grids decreases.The increased number of the macro-particles per cell helps reduce numerical errors.[10]
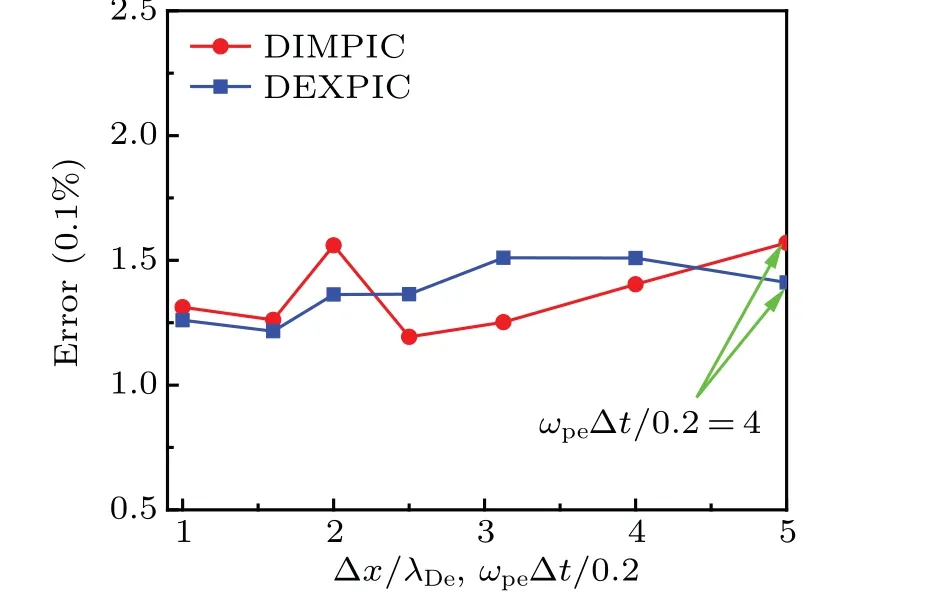
Fig.11.Differences between the results obtained by standard EXPIC,DIMPIC, and DEXPIC.The accuracy of the DIMPIC and DEXPIC is acceptable when the resolution in Debye length and high frequency electron plasma oscillation gets worse.
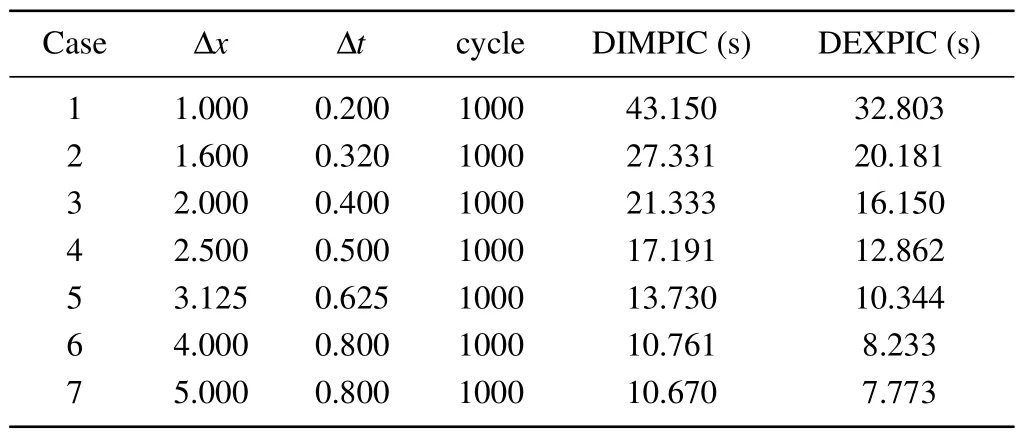
Table 1.The evolution of the computation time spent by DIMPIC and DEXPIC,as a function of spatial step and time-step.The CPU time spent by the standard EXPIC is equal to 53.632 s.
Both figures 9 and 11 show that the DEXPIC can describe the modulation of the bipolar electric fields to the velocity distribution function of charged particles accurately, as the DIMPIC does.More importantly, the DEXPIC takes less computation time compared to that of the DIMPIC,as shown in Table 1,which shows the evolution of the computation time spent by the two methods as a function of spatial step and timestep.Here,the CPU time spent by the standard EXPIC is equal to 53.632 s.For both DIMPIC and DEXPIC,when they push the particles, we do not calculate the magnetic field felt by the particles based on their positions, because the magnetic field here is uniform.For the DIMPIC, however, we calculate the magnetic field felt by each particle according to their positions before solve the implicit Poisson equation and consider the contribution of the charge and magnetic field carried by each particle to the total polarizabilityχ, to simulate the plasma with non-uniform magnetic fields, even the magnetic field here is actually uniform.It can be seen that the DEXPIC runs faster than DIMPIC in all cases.Compared with DEXPIC, the additional computational time required by DIMPIC is almost used to calculate the polarizability of electrons and ions.
5.More discussions and the future of work
In conclusion, we proposed a damped explicit PIC method in this work to improve the computational speed of traditional direct implicit methods in the research of bounded plasma.The new method obtains the future electric field by solving explicit Poisson equation with source term obtained by the position from explicitly propulsion of the particles,and provides stronger damping of high-frequency numerical oscillation compared to that provided by the direct implicit method.However, the new method cannot ensure numerical stability when very large time-steps are used.Nonetheless, it can still suppress numerical instability originating from the poor resolution in Debye length and high frequency electron plasma oscillation significantly.In tests,the performance of the damped method using a large spatial step ?x=5λDeand a large timestepωpe?t=0.8 is well while that of the traditional explicit method using the same parameters is poor.
The damped explicit method may be useful in certain specific plasma studies, such as magnetron discharges, where a small time-stepωce?t=0.2 is required to capture the dynamics of the system accurately,[36]whereωcerepresents electron cyclotron frequency.In this case,the advantages of traditional direct implicit methods are limited since a very large timestepωce?t ?0.2 is not allowed.Therefore, the new damped method is expected to be a better choice because its field solver is more efficient,and it provides stronger damping of numerical heating when larger spatial steps are used.
Other estimated future acceleration ?an+1(xn+1) can be used in the damped method.For example, one can set the estimated ?an+1(xn+1)as zero oran(xn),as mentioned in Section 3,and the differences between the results obtained by the damped method using different estimated ?an+1(xn+1) can be observed in terms of damping,as shown in Fig.12,which displays the time history of the total energy of the system described in the test #3 in the numerical experiment of plasma sheath.It can be seen that the damping provided by the damped method using ?an+1(xn+1)=0 is similar to that provided by the direct implicit method,while the damped method using ?an+1(xn+1)=an(xn) provides the strongest damping.In addition, if a smaller estimated ?an+1(xn+1) is used, then a larger time-step can be used because now the constraint is relaxed toωpe?t ≤1.549.

Fig.12.The time history of the total energy of the system, where the simulation parameters are the same as those of the test#3 in the experiment of plasma sheath.The damped method using different estimated future accelerations produces different levels of damping.
Finally, the damped explicit PIC method is expected be coupled with Monte Carlo collision (MCC) method to form a damped explicit PIC/MCC method for simulate plasma discharge.In addition, the damped method with tunable damping is also attractive.The construction of rotational symmetry electrostatic damped explicit PIC/MCC method with tunable damping is a topic for future studies.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant No.2022YFE03050001),also partly by the National Natural Science Foundation of China (Grant No.12175160), and the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions(PAPD).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures
- Improving dynamic characteristics for IGBTs by using interleaved trench gate

