Controllable high Curie temperature through 5d transition metal atom doping in CrI3
Xuebing Peng(彭雪兵), Mingsu Si(司明蘇), and Daqiang Gao(高大強(qiáng)),?
1School of Physical Science and Technology,Lanzhou University,Lanzhou 730000,China
2School of Materials and Energy,Lanzhou University,Lanzhou 730000,China
Keywords: ferromagnetism,magnetic anisotropy energy,Curie temperature,half-metal
1.Introduction
Although two-dimensional (2D) materials have been explored for more than a decade,magnetic order rarely survives in atomically thin films due to thermal fluctuations.[1,2]The realization of 2D magnets is a big challenge.An early strategy was to introduce local defect states with magnetic elements into non-magnetic materials.[3–6]The magnetism introduced by this method is short-range.A new method to achieve lowdimensional ferromagnets is to use intrinsic magnetic order.In 2017, monolayer CrI3and few-layer Cr2Ge2Te6were simultaneously reported.[7,8]Immediately afterwards, in 2018,Denget al.successfully prepared monolayer Fe3GeTe2with intrinsic ferromagnetism.[9]These works opened the door for the study of 2D magnetic materials and provided a novel material platform for the future development of low-dimensional spintronics.
CrI3as a layered magnetic material was first systematically studied by Dillon and Olson[10]and realized in the monolayer limit by Huanget al.[7]A spin-orientation-controlled band structure offers the opportunity for the study of second harmonics in solid state physics.[13,14]Due to its special crystal structure,CrI3has a topologically protected spin magnetic moment[15]as well as Kitaev interaction induced by shared edge I?.[16]With a strong layer-dependent effect,the magnetic ground state can be changed from ferromagnetic(FM)to antiferromagnetic(AFM)as the monolayer becomes a bilayer.[17]The excellent magnetism of CrI3makes it potentially promising for applications in the field of spintronics.Most research is based on the intrinsic magnetism of CrI3.However,the Curie temperature(Tc)of CrI3is only 45 K,[18]which severely limits practical applications.Thus, increasing theTcof CrI3is a focus of research.
The magnetism of monolayer CrI3has been modulated by strain,[19,20]carrier doping,[21]defect introduction,[22,23]applied electric field[24]and surface adsorption.[25–27]For example,Guoet al.adsorbed Li atoms on the surface to semimetallize CrI3and increaseTc.[28]Yanget al.used Sc atoms to dope CrI3and increasedTcfrom 47 K to 131 K.[29]The gain or loss of electrons causes an increase in the magnetic moment of Cr, which eventually increasesTc.In fact, the above methods are not particularly effective ways to increaseTcbecause Li and Sc atoms have almost no magnetic moment in a honeycomb lattice.Recently, Birgeneau’s group successfully prepared Fe5GeTe2,which has a higherTc(over 400 K)than Fe3GeTe2.The underlying physics originates from the increasing coordination number of the Fe ion.[30]Based on the above ideas,we chose 5d transition metal(TM)atoms to dope CrI3,because 5d TM atoms with a larger spin–orbit coupling(SOC) may increase the magnetic anisotropy energy (MAE)to stabilize long-range FM order.
In this work, we investigate the crystal stability, MAE,Tc,FM stability and electronic properties of TM@CrI3based on first-principles calculations.Formation energy and phonon spectra calculations show that TM@CrI3is thermodynamically stable, and the absence of imaginary modes in phonon spectra indicates that TM@CrI3monolayers (TM=Hf, Ta,W, Re and Os) are also dynamically stable.Due to the increase in magnetic moment induced by the doping of TM atoms,TM@CrI3has a higherTcthrough Monte–Carlo(MC)simulation.Among these,Tcof W@CrI3reaches 254 K.By further increasing the doping concentration of W atoms, aTcabove room temperature can be achieved.Intriguingly,a large MAE for W@CrI3can stabilize long-range FM order.Moreover,FM stability of TM@CrI3is enhanced.Most TM@CrI3change from a semiconductor to a half-metal.These results provide knowledge relevant to potential applications of CrI3monolayers in spintronics.
2.Computational details
We use the framework of density functional theory as implemented in the Viennaab initiosimulation package to perform first-principles calculations.[31,32]The Monkhorst–Pack scheme of 5×5×1k-point sampling in the entire Brillouin zone (BZ) was used to perform momentum space integration for a 2×2×1 TM@CrI3supercell.[33]MAE was calculated with a 12×12×1k-point mesh.The plane-wave cutoff energy was set to 500 eV.The generalized gradient approximation with the Perdew–Burke–Ernzerhof realization was used for the exchange correlation functional.[34]The Hellmann–Feynman forces acting on each atom were entirely relaxed during structural optimization until they were less than 10?3eV·?A?1;the electronic convergence requirement was set to 10?7eV.Since the system is a 2D nanosheet,a vacuum region of 20 ?A along the direction perpendicular to the surface of the nanosheet was introduced to avoid interference between the periodic images.A 30×30×1 supercell was used to simulateTcbased on the MC method.[35]
3.Results and discussion
Monolayer CrI3possesses the space group ofp-31m(No.162).Cr3+ions are sandwiched by octahedra formed by shared-edge I?ions and form a hexagonal honeycomb structure, as shown in Fig.1(a).The optimized lattice constant isa=b=7.00 ?A.The Cr3+–I?and Cr3+–Cr3+bond distances are 2.7 ?A and 4.0 ?A, respectively.The magnetic moment of each Cr3+ion is 3.06μB.The band structure of CrI3is displayed in Fig.1(b).The valence band maximum and the conduction band minimum appear for the spin-up channel,giving a band gap of 1.21 eV.All these results are in good agreement with previously reported results.[29,36]Here, we dope CrI3with one 5d TM atom, introducing it into the interstitial hollow position of a 2×2×1 supercell,as shown in Fig.1(c).
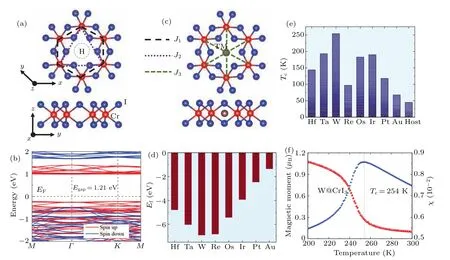
Fig.1.(a)Top(top panel)and side(bottom panel)views of the crystal structure of CrI3,where H represents the hollow position.(b)Calculated band structure of CrI3.The Fermi energy is set to 0 eV.(c)Crystal structure of a transition metal(TM)atom introduced into the hollow position.(d)Formation energies of TM@CrI3.(e)Calculated Curie temperature(Tc)of TM@CrI3 and host CrI3.(f)Magnetic moment and specific heat of W@CrI3 versus temperature from Monte–Carlo simulation.
To reveal the thermodynamic stability of atomic doping, we calculate the formation energy, which is defined asFf=Edop?ECrI3?μTMwhereEdopis the total energy of TM@CrI3,ECrI3is the total energy of CrI3andμTMis the chemical potential of the TM atom.As shown in Fig.1(d),the formation energies of all TM@CrI3are negative, indicating that all are thermodynamically stable.We also calculate the phonon dispersion over a 2×2×1 supercell using the PHONOPY package,[37]which is based on density functional perturbation theory.[38]The absence of imaginary modes in the entire BZ is displayed in Figs.S1(a)–S1(e),indicating that monolayer TM@CrI3(TM=Hf, Ta, W, Re and Os) are dynamically stable.However, doping with Ir, Pt and Au atoms is not dynamically stable as the imaginary frequencies appear near theΓpoint(Figs.S1(f)–S1(h)).
To estimateTcof TM@CrI3,we calculate exchange couplings between magnetic atoms via the Heisenberg exchange interaction,H=∑i,δ JNSi·Sδ, whereJNrepresents the exchange couplings between magnetic atoms,iis the magnetic atomic site andδrepresents the nearest neighbor distance.Siis the spin quantum number.Here, we mainly consider the nearest and next-nearest exchange couplings between Cr3+and Cr3+ions as well as the nearest exchange coupling between Cr3+ions and the TM atom, denoted asJ1,J2andJ3,respectively.J3is only considered for W and the Ta atoms with the larger magnetic moments.One FM and three AFM configurations(N′eel,zigzag and stripy)are used in the calculations of exchange coupling, as shown in Fig.3(a).The three magnetic coupling constants can be extracted from the following equations:
whereSA,SBandSCare the spin operators of magnetic ions on A, B and C sites.The exchange coupling constants are given in Table S1.
Based on the 2D Ising model, we employ Metropolis Monte–Carlo(MC)simulation to studyTc.Figure 1(e)shows theTcof TM@CrI3.Tcof the host CrI3is also calculated to be 45 K, which is in line with the result reported in previous work.[7]In TM@CrI3,Tcis significantly increased.Tcof Au@CrI3is about 64 K,which is slightly higher than that of the host CrI3.Tcof W@CrI3reaches 254 K, nearly six times higher than that of the host CrI3,and is much increased in comparison with 3d TM@CrI3.[29]Meanwhile,in Fig.1(f)variation of the average magnetic moment and specific heat of W@CrI3with temperature is shown.We further exploredTcfor W@CrI3for different doping concentrations: 5.9%and 8.6% represent 2×2×1 CrI3doped with two and three W atoms, respectively(Fig.S4).It is pleasing to note thatTcof CrI3is significantly improved with increasing W doping concentration.As shown in Fig.2(a),at a doping concentration of 5.9%,Tcincreases from 254 K to 306 K,which is above room temperature.With continuing increase in the doping concentration,Tcof W@CrI3is increased to 348 K(Fig.2(b)).
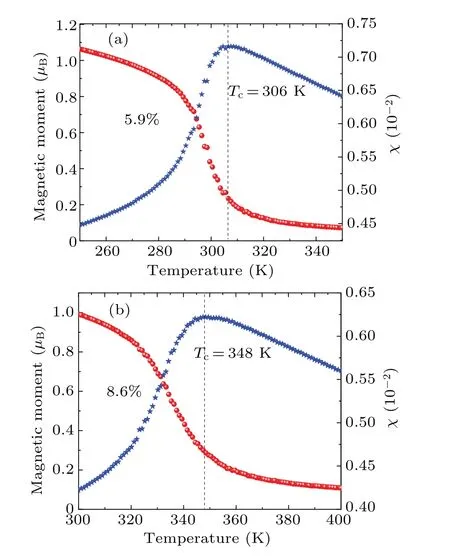
Fig.2.Magnetic moment and specific heat versus temperature for doping concentrations of(a)5.9%and(b)8.6%for W@CrI3.
To account for variation ofTc,we calculated the exchange energy, which is defined asEAFM–EFM.Here, zigzag-AFM is chosen as a reference due to its lower energy.Among the TM@CrI3, the W atom has the highest exchange energy, the Ta atom the next and the Au atom the least,but their exchange energy is greater than that of CrI3,as shown in Fig.3(b).The pattern of variation of exchange energy is consistent withTc.Similarly, the magnetic moments of TM atoms also show the same pattern of variation.For example, the W atom with the largest magnetic moment has the highestTc(Fig.3(c)).The Au atom has almost no magnetic moment,and the increase inTcis not significant.This result indicates thatTcis related to the magnetic moments of TM atoms.The magnetic moments of TM atoms increase the exchange coupling and coordination number between the magnetic atoms.Further, according to a mean-field treatment, results for the magnetic transition temperature follow, whereZNNandJNNare the coordination number and exchange coupling of magnetic atoms,respectively.[9,39]The larger the magnetic atomic coordination number, the exchange coupling and the magnetic moment,the higher the evaluatedTc.Therefore,the magnetic moments induced by doping with TM atoms can increaseTc.
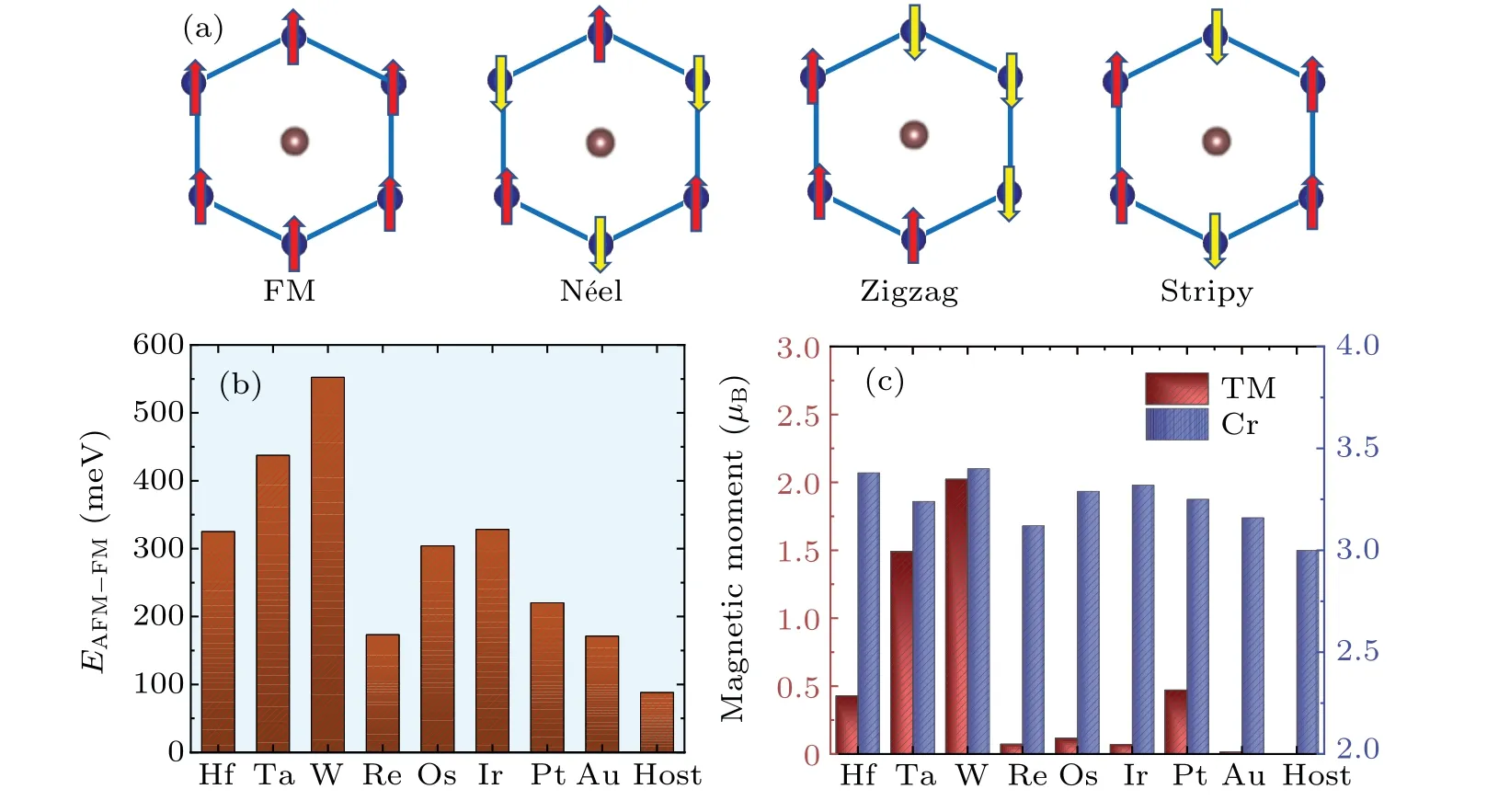
Fig.3.(a)Four magnetic configurations:ferromagnetic(FM),N′eel antiferromagnetic(AFM),zigzag AFM and stripy AFM.(b)The calculated exchange energy of TM@CrI3 and the host CrI3.(c)The magnetic moments of TM atoms and Cr3+ ions(TM,transition metal).
Next,we discuss the underlying physics of the W atomic magnetic moment in W@CrI3.The spin-density distribution shows that the total magnetic moment stems from the Cr atoms and the W atom(Fig.4(a)).The W atom tends to lose the partial electrons of the outermost electron shell(5d46s2)through strong electronegative action around I?ions, and picks up a magnetic moment of about 2μB.We calculated the Bader charge of W@CrI3,where the W atom loses 0.6eand every I?ion gains 0.11e(Table S2).In the projected density of states,d-resolved orbitals of the W atom have a large spin polarization and hybridization(Fig.4(b)).Both the dxzand dyzorbitals are occupied by a fractional electron, and contribute 0.15μBand 0.14μB,respectively.In contrast,the dz2orbital with more spin-up electrons has a magnetic moment of 1.04μB.This is because the dz2orbital rarely overlaps with the p orbitals of the surrounding I?ions.The dx2?y2and dxyorbitals protected by C3symmetry are degenerate below the Fermi level, and their magnetic moments are 0.35μB.Furthermore, the magnitude of magnetic moments can be understood from the asymmetry of spin polarization below the Fermi level in the density of states(DOS)of TM atoms,as shown in Figs.4(c)–4(f).For example,the spin polarized asymmetry of the Hf atom is weaker than that of the Ta atom, so the magnetic moment of the Ta atom is larger.Similarly, the W atom has a larger spin polarized asymmetry than the Ta atom,leading to a larger value for the W atom.The Os atom has the weakest asymmetry.The W atom therefore has the largest magnetic moment.For low-dimensional materials, a large MAE driven by SOC would resist the thermal fluctuation to stabilize the longrange FM order.Due to the large SOC of 5d TM atoms,the induced MAE would be large, and is defined asEMAE=E(100)?E(001).Positive or negative values of MAE represent that the magnetic easy axis is along the out-of-plane or inplane direction, respectively.In Table 1, the magnetic easy axis of TM@CrI3(TM=Hf, Ta, W, Re and Ir) is along the out-of-plane direction: Re@CrI3has the largest MAE,which mainly originates from the Re atom.The magnetic easy axis for doping with Os,Pt and Au atoms is along the in-plane direction.Except for Os,the absolute values of MAE after doping are enhanced with respect to CrI3, whose MAE is about 0.804 meV.[20]Therefore,doping with TM atoms can enhance the MAE of CrI3.
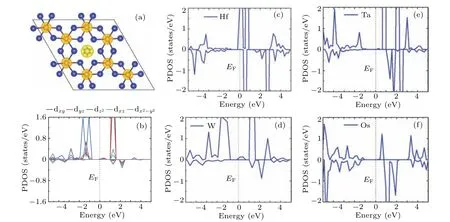
Fig.4.(a) The spin density distribution of W@CrI3 and (b) projected density of states (PDOS) of the W atom.Density of states (DOS) of(c) Hf, (d) W, (e) Ta and (f) Os atoms in TM@CrI3.The positive and negative values of DOS represent spin-up and spin-down channels,respectively.The Fermi energy is set to 0 eV.
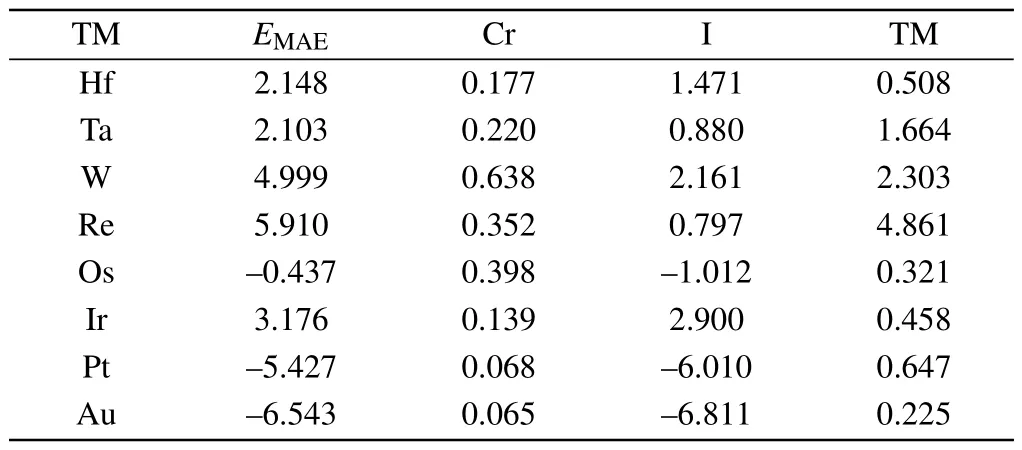
Table 1.The MAE(EMAE)in TM@CrI3.The contribution from Cr,I and TM atoms is also listed.The unit is meV.
We now discuss the FM stability of TM@CrI3.The FM coupling of monolayer CrI3can be understood by the Goodenough–Kanamori–Anderson model as a competition between two exchange interactions: a direct exchange interaction between Cr3+ions by electron hopping and a superexchange between the Cr3+ions mediated by intermediate nonmagnetic I?ions.As schematically shown in Fig.5(a), stable AFM coupling depends sensitively on the distancedbetween Cr3+ions.Stable FM coupling is dominated by superexchange interactions and is controlled by theθof Cr3+–I?–Cr3+ions.Except for the Ta atom,dof Cr3+–Cr3+after doping is increased with respect to the host CrI3(Fig.5(b)),indicating that AFM coupling of direct exchange is weakened.Theθfor all TM@CrI3is decreased,and is close to 90°,giving rise to stronger FM stability.
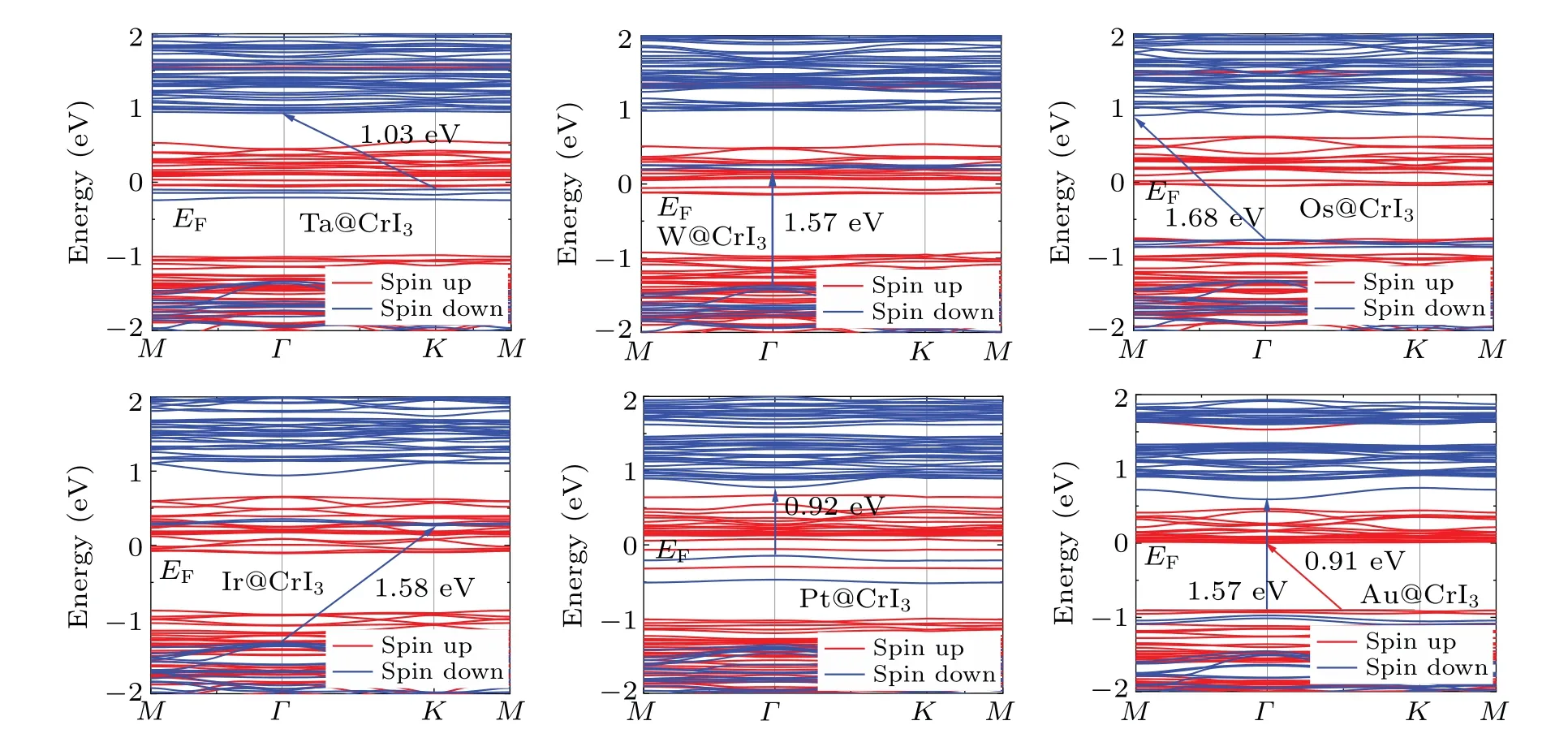
Fig.6.The band structure of TM@CrI3 (TM=Ta,W,Os,Ir,Pt,Au).The Fermi energy level EF is set to 0 eV.
Electronic structure is a key concern in the study of physical properties.We display the band structure of TM@CrI3(TM=Ta, W, Os, Ir, Pt, Au) in Fig.6.Because of the gain or loss of valence electrons (Table S3), the impurity energy levels are induced in the band structure.Therefore,the energy bands of TM@CrI3(TM=Ta,W,Os,Ir,Pt)cross the Fermi energy level to change from semiconductors to half-metals.Hf@CrI3and Re@CrI3are also half-metals (Fig.S6).Such materials have promising applications in advanced magnetic recording,magnetic storage,high-efficiency magnetic sensors,spin-emitting diodes and many other fields.[40]In particular,for TM@CrI3(TM=W, Os, Ir), the band gaps of the spindown channel are greater than 1.5 eV, which prevents thermal activation effects from exciting the forbidden carriers to reduce the polarization rate.[41]Au@CrI3is a semiconductor because the Au atom has almost no gain or loss of electrons.
4.Conclusions
In summary, we have performed a systematic study of TM@CrI3through the combination of a first-principles method and MC simulation.All TM@CrI3are thermodynamically stable due to their negative formation energy, and the absence of imaginary modes in the phonon spectra indicates that TM@CrI3monolayers(TM=Hf,Ta,W,Re and Os)are also dynamically stable.Tcof TM@CrI3is increased, with a highest value of 254 K for W@CrI3.As the doping concentration of W atoms is increased to 8.6%,Tcis increased to above room temperature(348 K).Interestingly,W@CrI3has a large MAE of 4.999 meV to stabilize long-range FM order.Furthermore, the FM stability of TM@CrI3is enhanced.Except for doping with Au atoms,TM@CrI3become half-metallic.It is hoped that these results will provide theoretical guidance for experimentally tuning MAE,Tcand electronic structure.
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals
- Majorana noise model and its influence on the power spectrum

