Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
Huiping Li(李慧平), Shuaiwei Pan(潘帥唯), Zhe Wang(王喆),Bin Xiang(向斌), and Wenguang Zhu(朱文光),?
1International Center for Quantum Design of Functional Materials(ICQD),Hefei National Research Center for Physical Sciences at the Microscale,University of Science and Technology of China,Hefei 230026,China
2Department of Physics,University of Science and Technology of China,Hefei 230026,China
3Department of Physics,Southern University of Science and Technology,Shenzhen 518055,China
4Department of Materials Science&Engineering,University of Science and Technology of China,Hefei 230026,China
Keywords: exchange bias, two-dimensional ferromagnetic/antiferromagnetic bilayers, asymmetric magnetic interaction
1.Introduction
Exchange bias(EB),also known as exchange anisotropy,is characterized by a shift of the magnetic hysteresis loop along the applied magnetic field axis.[1,2]Since first reported in Co/CoO core–shell nanoparticles,[3,4]EB has been extensively investigated in a wide range of ferromagnetic/antiferromagnetic(FM/AFM)heterostructures and other magnetic interfacial systems because of its significant application value in spintronics.[5–7]Intuitively, FM magnetization presents a preferred orientation as a consequence of the asymmetric magnetic interactions implied in EB systems.The widely accepted model for FM/AFM interfaces proposes that the interactions between the FM spins and the AFM uncompensated spins drive the unidirectional anisotropy for the FM moments.[1]Numerous factors contribute to the origin of uncompensated spins, including defects or domain structures,[8–12]interfacial roughness,[13,14]interfacial random anisotropy,[15]and spin frustrations.[16–18]In compensated interfaces,the asymmetry can arise from various factors inherent to specific systems.One is the asymmetrical spatial arrangement of the FM spins relative to the different spin sublattices of the AFM layer,as exhibited in the Fe/FeF2(110)system.[19,20]Other specific factors, such as the Dzyaloshinskii–Moriya(DM)interaction or ferroelectric ionic displacements,are also considered as driven forces for inducing EB phenomena.[21–23]
The complexity of interfacial structures in conventional three-dimensional systems has hindered a definitive understanding of EB.However, the recent development of twodimensional (2D) van der Waals (vdW) materials and their heterostructures offers an ideal platform to uncover and explore the underlying mechanisms of EB.[24]In particular, vdW magnetic heterostructures provide both pristine intralayer spin configurations and atomically sharp, clean interfaces.[25–28]Recent experiments have revealed the EB phenomena in various 2D material systems, such as MnPX3(X=S,Se)/Fe3GeTe2,[29,30]FePSe3/Fe3GeTe2,[31]Fe3GeTe2nanoflakes,[32–35]and CrI3/MnBi2Te4.[36]The EB effect in these vdW systems is attributed to the spatially inhomogeneous interlayer couplings between the FM and AFM spins at the interfaces,where uncompensated spins in the interfacial AFM layer play a crucial role.However, the unambiguous spin structures in these systems remain unclear, leaving behind uncertainties in the microscopic mechanism of EB.
In this study,by stacking FM monolayers onto fully compensated AFM monolayers,we theoretically investigate asymmetric magnetic interactions and the emergent EB effect in 2D FM/AFM bilayers,as exemplified in the VS2/MnPSe3and CrBr3/MnPSe3heterostructures.We identify that the EB effect is primarily driven by the imbalanced magnetic interactions between the FM layer and the two spin sublattices of the AFM layer within the asymmetric stacking registries.Strikingly,the EB effect can be switched on and off,and its polarity can be changed through interlayer sliding in CrBr3/MnPSe3.Further electronic structure analyses elucidate the magnetic exchange interactions and their tunability by an externally applied electric field.
2.Computational methods
2.1.First-principles calculations
The first-principles density functional theory (DFT) calculations were performed by using the Viennaab initiosimulation package[37,38]within the projector augmented-wave method.[39]The Perdew–Burke–Ernzerhof[40]parameterized generalized gradient approximation (GGA) method was used to describe electron exchange and correlation interactions.A cutoff energy of 500 eV was set for plane-wave basis sets,and aΓ-centered 12×12×1 Monkhorst–Pack[41]mesh was adopted fork-point sampling for all heterostructures.A vacuum region of more than 15 ?A in the out-of-plane direction was set to avoid interactions between periodic images.Heterostructures were constructed by adapting the FM monolayers to the lattice of the MnPSe3monolayer.VdW corrections were included using the zero-damping DFT-D3 method of Grimme[42]in bilayer structures.Considering the localized characteristics of 3d orbitals of transition metal elements, we used the GGA+Umethod proposed by Dudarevet al.,[43]withU=3.0 eV, 3.0 eV, and 5.0 eV for V, Cr, and Mn atoms, respectively.This method has been effectively applied in previous studies.[44–46]Optimized atomic structures were achieved until the Hellmann–Feynman forces on all the atoms were less than 0.01 eV/?A.The climbing image nudged elastic band method[47]was implemented to calculate the barriers of the transition between different stackings of the CrBr3/MnPSe3heterostructures.
2.2.Characterization of magnetic properties
The exchange interaction coefficients were extracted by the Heisenberg model
whereJijrepresents the exchange coupling between the spin siteiand spin sitej;SiandSjdenote the spin vectors.In numerical calculations,|S| was fixed at 1/2, 3/2, and 5/2 for V,Cr, and Mn, respectively.The most common method for determining the parameters is the total energy mapping method,which fits the Hamiltonian by constructing different magnetic configurations to solve linear equations.However,the Heisenberg model itself can break down if the chosen magnetic configurations deviate significantly from the ground state.[48]To circumvent this issue,we instead utilized the Green’s function method proposed by Liechtensteinet al.,[49]as implemented in the TB2J code.[48]Compared to freestanding monolayers,intralayer interactions exhibit only minor changes (see Table S1 in supporting information),suggesting robust magnetic orders within each stacking block layer.In addition to estimating the spin-flop critical field of the AFM MnPSe3layer,the four-state mapping analysis[50]was adopted to extract the single-ion anisotropy (A) due to the infeasibility of the TB2J code,[48]which yielded a value of +0.034 meV.According to the classical spin-flop picture,[51]the spin-flop critical field was estimated to be approximately 3.7 T, as determined by
2.3.Monte Carlo simulations
Hysteresis loops were simulated using the Monte Carlo method with a single-site update Metropolis algorithm on 25×25 and 30×30 spin lattices for the VS2/MnPSe3and CrBr3/MnPSe3heterostructures, respectively.The spin Hamiltonian for these systems is expressed as
where the single-ion anisotropy (A) was set to +0.18 meV and?0.019 meV for V and Cr, respectively, and?represents the external magnetic field for the loops.Considering that the magnetic ground states exhibit a collinear in-plane spin arrangement, we applied the sweeping magnetic field in thex-axis direction.Additionally,because the saturation field for both the VS2and CrBr3monolayers is much smaller than 1 T,[53–55]we constrained the spin orientations of the two N′eel sublattices of Mn and used a magnetic field below 3 T to simulate the hysteresis loops.The magnetic field intervals were set to 0.2 T and 0.1 T for VS2and CrBr3, respectively.At each magnetic field step,initial 104Monte Carlo steps(MCSs)were used for the equilibration process,followed by 3×104MCSs for collecting magnetization information.Finally,the magnetization was normalized.
3.Results and discussion
The key feature of the EB effect lies in the unidirectional exchange anisotropy of FM moments induced by the pinning effect from the AFM layer,which means that the spin-up and spin-down states in the FM layer are no longer equivalent.The preferred direction of FM magnetization corresponds to a lower energy state, whereas the opposite direction corresponds to a higher energy state.In general, the difference can be understood as an inequality in the magnetic proximity interactions between these two states,as only the direction of FM moments has changed.To establish such an asymmetry,it is essential to prevent the exchange interactions between the FM spins and the AFM spins from canceling each other out,which can be achieved by constructing asymmetric magnetic exchange interactions in the FM/AFM heterostructures.The stacking of 2D magnetic monolayers provides an effective method to manipulate the magnetic exchange interactions via artificially designed atomic stacking registries,[56,57]which can be used to induce asymmetric interlayer magnetic proximity couplings and the consequent exchange anisotropy phenomenon.Following this, we constructed two FM/AFM heterostructures,VS2/MnPSe3and CrBr3/MnPSe3,to investigate the EB effect therein.
The MnPSe3monolayer has been selected as the AFM building block for the heterostructures due to experimentally demonstrated N′eel AFM order below 40 K.[58]As depicted in Fig.1(a), the MnPSe3monolayer consists of two magnetic Mn ions and a P2Se6ligand, with each Mn ion octahedrally coordinated with six Se atoms.It belongs to the?3m(D3d) point group, and the Mn ions form a hexagonal honeycomb lattice, where the in-plane aligned Ising-type spins exhibit largeXYanisotropy.[58]To facilitate the analysis of magnetic interactions, we prioritized materials for the FM blocks that are commensurate with the MnPSe3lattice,such as the VS2and CrBr3monolayers.The lattice constants for these two FM monolayers are 3.18 ?A and 6.45 ?A,respectively, allowing a 2×2 supercell of VS2and a 1×1 unit cell of CrBr3to match well with the MnPSe3monolayer(with lattice constants of 6.39 ?A), with a lattice mismatch of less than 1%.The H-phase VS2monolayer, with the?6m2(D3h) point-group symmetry, is a semiconductor in contrast to its metallic T-phase and has been theoretically predicted to be a strongly correlated ferromagnet with in-plane magnetic anisotropy.[59,60]The CrBr3monolayer,sharing the same crystal symmetry with MnPSe3,is a Heisenberg-type ferromagnet with a Curie temperature of 30 K but with an out-of-plane easy axis of magnetization.[53,61]Considering the noticeable differences between these two FM monolayers, it can be anticipated that the VS2/MnPSe3and CrBr3/MnPSe3heterostructures constructed by adding an AFM MnPSe3monolayer will yield diverse properties.
As shown in Fig.1(a),the MnPSe3lattice is taken as the reference basal plane, with the spin configuration fixed.An H-phase VS2monolayer is stacked onto the MnPSe3monolayer to form the FM/AFM heterostructure, and the stacking sequences are expressed using the fractional coordinates relative to the in-plane basis vectors.The stacking energy profile shown in Fig.1(b)illustrates four local minima at the stacking coordinates of[1/6,1/3], [1/6, 5/6], [2/3, 1/3], and[2/3, 5/6].However,these four stacking configurations are actually identical due to the 2×2 supercell of VS2.Consequently,only one stable stacking configuration exists for the VS2/MnPSe3heterostructure, with the atomic structure shown in Fig.1(c).In this configuration, one Mn atom (marked by Mn1) is located beneath a V atom, whereas the other Mn atom (marked by Mn2) is situated under the hollow site of the remaining three V atoms.Various spin configurations are comprehensively investigated in the stable stacking structure, indicating that the collinear spin arrangements,where the spins of V atoms align in parallel with Mn1,exhibit the lowest energy(Fig.S1 in supporting information).Notably,different spin arrangements do not change the most stable stacking because the effect of different spin arrangements on the energy is on the order of a few meV, whereas the energy difference between different stacking registries is on the order of tens of meV(see Figs.1(b)and S3).
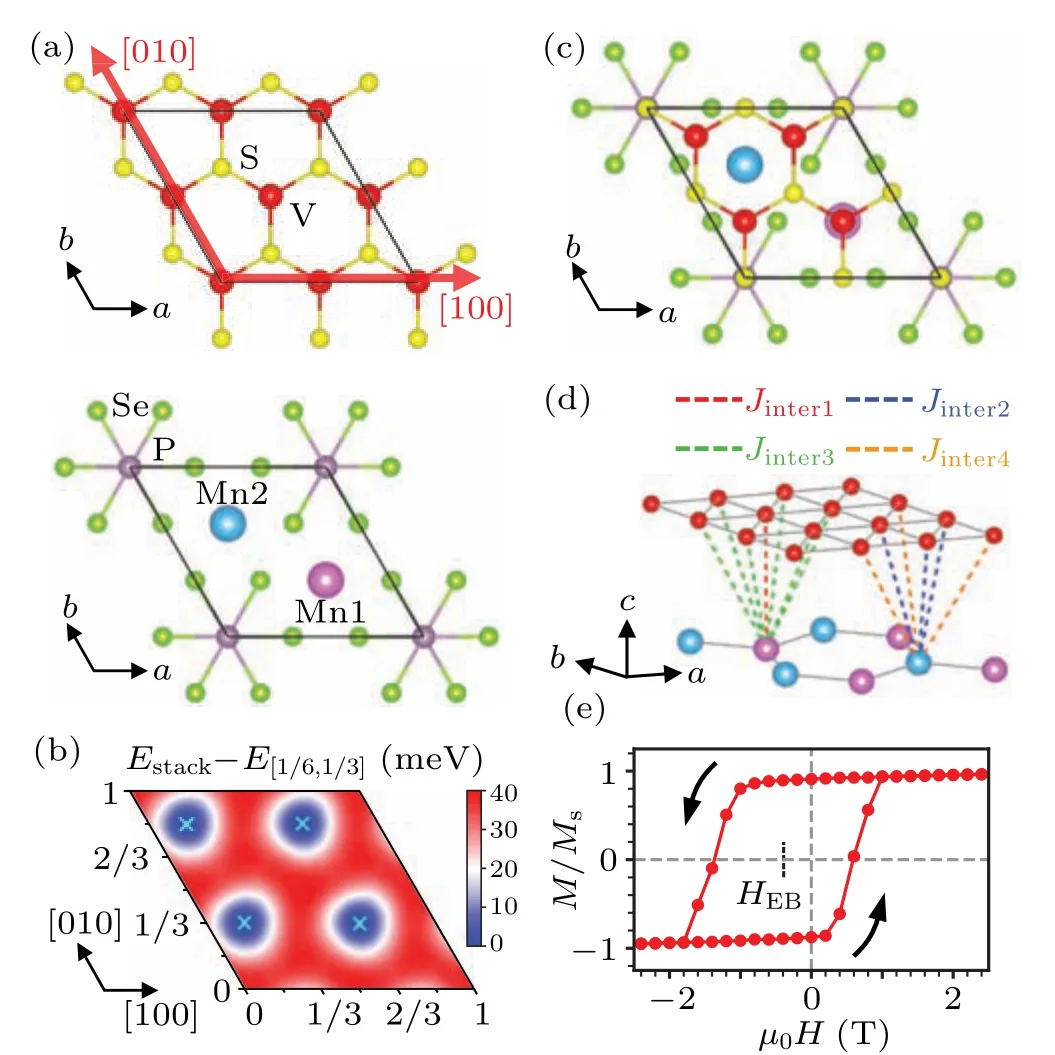
Fig.1.Stacking structure and EB of VS2/MnPSe3.(a) The stacking strategy for constructing VS2/MnPSe3 heterostructures.The red thick arrows represent the[100]and[010]lateral shift directions.(b)Stacking energy as a function of the full space of lateral shifts.The heat map was drawn by interpolating over neighboring data points on a 12×12 grid.The cyan markers indicate the energy minima.(c) The atomic structure of the stable stacking sequence of VS2/MnPSe3.(d)Schematic of the interlayer magnetic exchange pathways.(e)Simulated magnetic hysteresis loop, where the black arrows represent the sweep directions of the magnetic field. HEB is the EB field.
In the VS2/MnPSe3heterostructure,it is noteworthy that reversing the spins of VS2while maintaining the AFM spins of MnPSe3fixed results in an energy difference.Specifically,the V–Mn1 antiparallel magnetic structure(where spins of V align antiparallel to the spin orientation of Mn1) has an energy of~1.5 meV higher than the V–Mn1 parallel magnetic structure(where spins of V atoms align parallel to the spin orientation of Mn1).This indicates that there is a preferred direction for the FM VS2layer,which is a critical feature manifested by the EB effect.Because spin arrangements remain consistent with the pristine monolayers(Fig.S1),the energy difference mainly stems from interlayer magnetic interactions.Figure 1(d) displays the magnetic interactions between V and Mn, labeledJinter1,Jinter2,Jinter3,andJinter4,according to their atomic separation distances and environments.It is evident that the opposite spins of Mn1 and Mn2 are differently influenced by the FM layer.For Mn1, there is oneJinter1and sixJinter3exchange pathways,whereas for Mn2,there are threeJinter2and threeJinter4pathways.We adopted the Heisenberg model to extract the magnetic exchange interaction coefficients(see Table S1)and found that these asymmetrical interlayer magnetic interactions cannot be compensated, resulting in the energy difference when the FM spins flip.Concomitantly,the asymmetric magnetic interactions yielded a pinning effect on the spins of the FM layer.This is quite similar to the inexpiable magnetic interactions in the Fe/FeF2(110) heterostructure[20]and the uncompensated interactions induced by DM in the IrMn3/Co(111) system.[23]Thus, an EB phenomenon is expected to arise in the VS2/MnPSe3heterostructure.
According to the exchange pathways shown in Fig.1(d)and Table S1, the interlayer couplings contribute to the total energy due to the spin flip of the FM layer,which is estimated by ΔE=(2Jinter1?6Jinter2+12Jinter3?6Jinter4)|SV·SMn|=0.4 meV/unit cell, whereSVandSMnare spin vectors of V and Mn, respectively.This value is much smaller than the difference in the total energies obtained from the DFT calculations,which can be attributed to other interactions not involved in the Heisenberg model.Nevertheless,this energy difference adequately demonstrates the asymmetric characteristics of interlayer magnetic interactions.Furthermore,we used the Monte Carlo method to simulate the hysteresis loop.Considering that the estimated spin-flop critical magnetic field of MnPSe3monolayer was much larger than the saturation magnetic field of VS2, we fixed the spins of Mn and only considered the variations of the FM spins in the simulation.The resulting hysteresis loop,as shown in Fig.1(e),obviously exhibited a center deviating from the origin of the magnetic field axis(HEB≈?0.39 T),indicating the presence of an EB effect in the VS2/MnPSe3heterostructure.
With the spin arrangement of Mn atoms determined, the preferred orientation of FM spins in VS2is parallel to the spin direction of Mn1 in the VS2/MnPSe3heterostructure.This implies that the polarity of the EB field is also determined by the V–Mn1 spins.If the two spin sublattices of MnPSe3were interchanged,the EB would change its sign,corresponding to a reversal of the EB polarity.This can be achieved by applying a large opposite magnetic field to magnetize and subsequently restore the AFM order in the MnPSe3layer.In addition, we note that the energy difference caused by the flip of the FM spins varies with the stacking configurations(Fig.S3).In certain cases,for example the[1/3,1/6]stacking sequence,the energy difference is positive,potentially corresponding to a positive EB.However, in commensurate VS2/MnPSe3heterostructures,it is challenging to achieve different EB polarities by stacking manipulation,as there is only one stable stacking configuration.
For the CrBr3/MnPSe3heterostructure, due to the same symmetry of both the FM CrBr3and AFM MnPSe3monolayers,several(meta-)stable stacking configurations exist.As shown in Fig.2(a),we used the same stacking strategy to construct CrBr3/MnPSe3heterostructure as with the VS2/MnPSe3case.The stacking energy profile shown in Fig.2(b)presents several local minima, corresponding to four stacking sequences with coordinates of [0, 0], [1/3, 0], [1/3, 2/3], and[2/3, 1/3].These configurations are denoted by AA, AB',AB,and AC,respectively,analogous to the notations adopted for bilayer CrI3.[56]But herein, one layer is substituted with MnPSe3, represented by A in the presented notations.By sliding the CrBr3monolayer along the two paths depicted in Fig.2(b), these four stackings can transition to each other.The energy barrier for shifting from AA stacking to AB'is 48 meV/unit cell, whereas the transitions between the others are~30 meV/unit cell (see Figs.2(c) and S4).These barriers are comparable to the sliding barrier between the FM and AFM stackings in bilayer CrI3(~26 meV/unit cell),[56]indicating that these stackings are stable,and interlayer sliding is feasible.
Consistent with the VS2/MnPSe3case, the interlayer magnetic exchange interaction of the CrBr3/MnPSe3heterostructures is depicted in Fig.2(f).For the two spin sublattices of Mn with opposite orientations, it is apparent that the local atomic environments in the AA and AB'stackings are identical, resulting in counterbalanced magnetic interactions.Conversely, the local registries in the AB and AC stackings are different,leading to imbalanced interactions between the Mn sublattices and Cr spins, as shown in Fig.2(f).For the AB stacking, there is oneJinter1and threeJinter2exchange pathways in Mn1, but threeJinter3and threeJinter4in Mn2.The situation is reversed for the AC stacking.Therefore, upon the reversal of the FM spins, the energies of the AA and AB'stackings remain unchanged, whereas those of AB and AC are altered.Notably, the magnetic anisotropy of the CrBr3monolayer is distinct from that of MnPSe3.Nevertheless, when these two monolayers are stacked together,the magnetic ground state shows collinear spin arrangements due to the magnetic proximity effect (Fig.S2).Accordingly,we used collinear magnetic configurations to calculate the energy differences caused by the reversal of FM spins, which show identical total energies for the AA and AB'stackings but nonzero values for the AB and AC stackings, as marked in Fig.2(d).This implies that the AA and AB'stackings do not exhibit the EB effect, whereas the AB and AC stackings do show this phenomenon.Notably,because of the equivalent atomic structures, the energy differences for AB and AC are opposite, corresponding to the opposite polarities of EB.The Monte Carlo simulations presented in Fig.2(g)show EB fields of?0.32 T for AB and+0.32 T for AC,which are in agreement with the analysis described previously.Specifically, the hysteresis loop centers for the AA and AB'stackings are situated at the origin,indicating the absence of EB,whereas the AB and AC stackings display EB with opposite polarities.
Distinct from the VS2/MnPSe3heterostructure, the(meta-)stable stacking configurations undergo alterations with interlayer sliding in the CrBr3/MnPSe3heterostructures, and the positive and negative energy differences caused by the reversal of Cr spins can be reversed,as shown in Fig.2(d).Correspondingly,the polarities of EB are altered during the interlayer sliding process.For example,along the zigzag transition path illustrated in Fig.2(b), EB can be turned on and off by transiting from AA or AB'to AB or AC stacking,and the polarities can be switched between the AB and AC stackings.
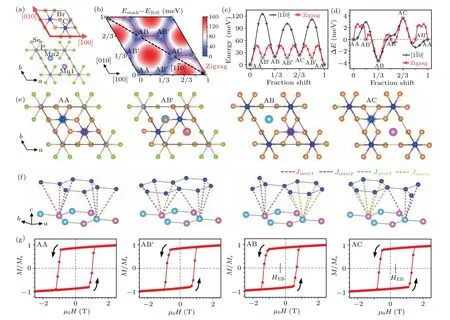
Fig.2.Stacking structures and EB of CrBr3/MnPSe3.(a)The stacking strategy for constructing CrBr3/MnPSe3 heterostructures.The red thick arrows represent the [100] and [010] lateral shift directions.(b) Stacking energy as a function of the full space of lateral shifts, drawn by interpolating over neighboring data points on a 6×6 grid.The cyan cross markers represent the energy minima.The red and black dashed arrows represent interlayer sliding along the[1ˉ10]direction and a zigzag path, respectively.(c)Stacking energies for the[1ˉ10]direction(black)and the zigzag path(red)shown in (b).(d) Energy differences caused by the reversal of FM spins along the [1ˉ10] direction (black) and the zigzag path (red).(e) Top views of the(meta-)stable stacking configurations of the CrBr3/MnPSe3 heterostructure.(f)Schematics of the interlayer magnetic exchange pathways between the d orbitals of magnetic atoms.(g)Simulated hysteresis loops for the AA,AB',AB,and AC stacking registries of CrBr3/MnPSe3,respectively.
We compared our proposed bilayers with the previously reported vdW EB systems,[24]as summarized in Table S2.The most prominent feature of the VS2/MnPSe3and CrBr3/MnPSe3bilayers is that their EB effects originate from the imbalanced magnetic interactions between the FM layer and the two sublattices of the AFM layer.This allowed us to push the limits of the EB systems to extremely thin bilayer thicknesses and offered the potential for tuning the EB field through interlayer sliding,thanks to their vdW nature.
To better understand the magnetic interactions presented in the VS2/MnPSe3and CrBr3/MnPSe3heterostructures exhibiting EB, we examined the electronic structures of these systems, as shown in Fig.3.All three constituent monolayers are semiconductors,and upon vertical contact between the FM and AFM layers, they form a type-II band alignment while maintaining global energy gaps, as shown in Figs.3(a)and 3(b).Based on the arrangements of the d orbitals of the magnetic atoms in energy bands, we provide a simplified schematic model of the interlayer magnetic exchange couplings, as shown in Fig.3(c), which can be divided into the FM and AFM types.FM coupling mainly occurs through hopping between the occupied and unoccupied orbitals of another atom, whereas AFM coupling primarily takes place between the occupied d orbitals.The projected bands show minimal overlaps between the d orbitals of FM V/Cr atoms and AFM Mn atoms,indicating weak direct exchange interactions.Additionally, a disparity exists between the majority-spin and minority-spin bands,leading to weaker exchange interactions between the different spins.The global band gap is determined by the majority-spin bands,indicating that FM coupling is primary for interlayer magnetic interactions in these heterostructures.This is in line with the exchange coefficients calculated in the Heisenberg model(Table S1).The p orbitals of the nonmagnetic atoms serve as a bridge for magnetic exchange interactions,as evidenced by the mixed bands of S and Se or Br and Se.The stacking process alters the symmetry of the surfaces,leading to electron redistribution, as evidenced by the differential charge density revealing the largest charge differences in the interlayer area (Fig.S5).Considering that the external electric field is effective to manipulate the charge distribution,it can be used to tune the strength of magnetic exchange interactions.[62]As shown in Figs.3(d)and 3(e),by applying an out-of-plane electric field,the energy differences caused by the reversal of FM spins exhibit a monotonic relationship with respect to the field.In CrBr3/MnPSe3heterostructures,the energy difference remains unchanged for the AA and AB'stackings lacking EB, but it varies oppositely for the AB and AC stackings because of their opposite EB polarities (Fig.3(e)).These findings suggest that the strength of the EB field can be modulated by the electric field.For heterostructures with EB,a positive electric field would enhance the EB field,which can be understood by the enhancement of FM couplings by lowering the energy gap between the d orbitals of magnetic atoms(Fig.S6).[63]
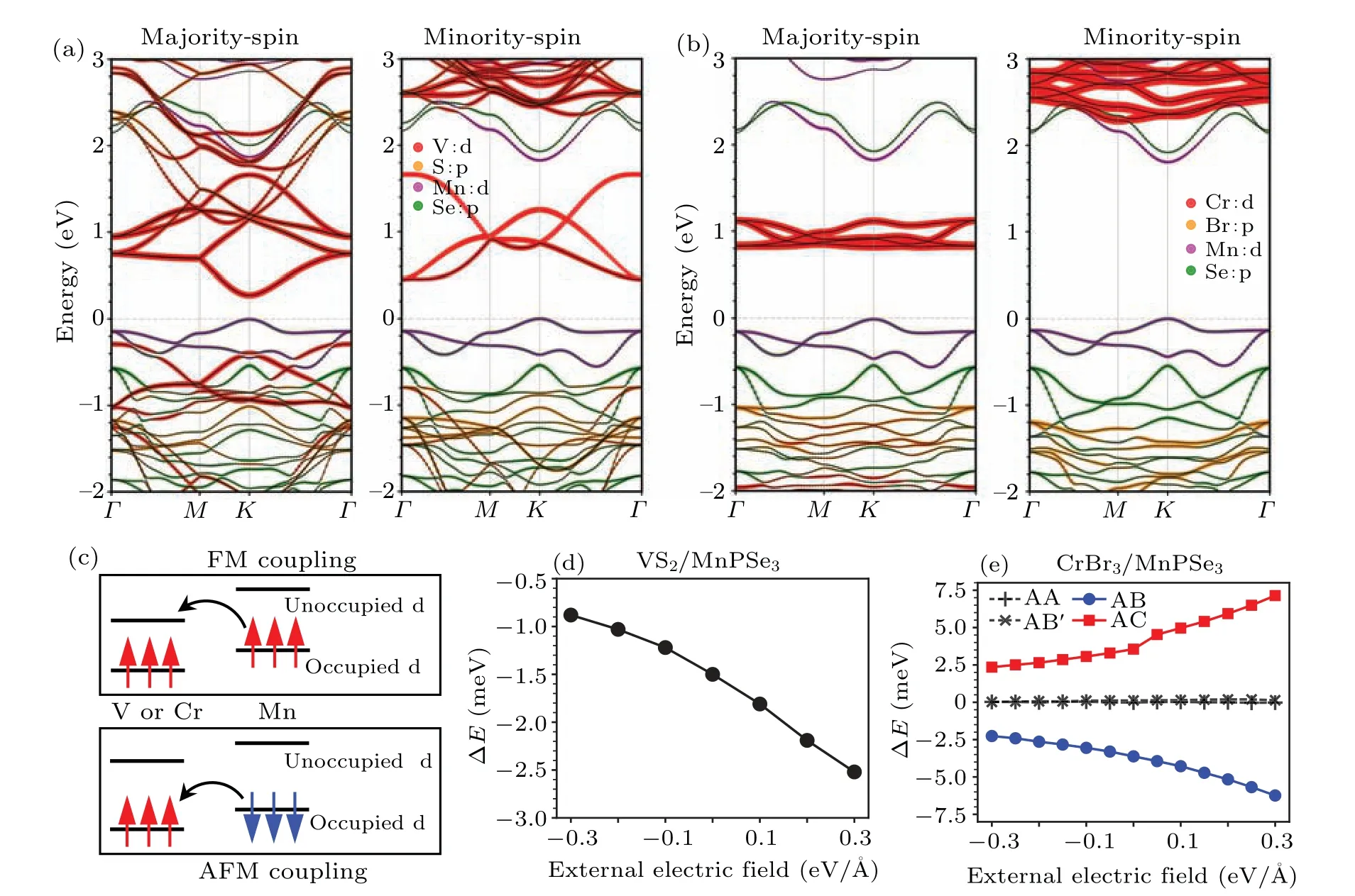
Fig.3.Band structures and electric field responses for the VS2/MnPSe3 and CrBr3/MnPSe3 heterostructures.(a)Spin-resolved band structures of the VS2/MnPSe3 heterostructure.(b) Spin-resolved band structures of the AB-stacking CrBr3/MnPSe3 heterostructure.(c) Schematic diagram of the interlayer exchange couplings for the d orbital electrons of magnetic atoms, including FM and AFM couplings.(d) Energy difference caused by the reversal of FM spins as a function of the external electric field for the VS2/MnPSe3 heterostructure.(e) Energy differences caused by the reversal of FM spins as a function of the external electric field for the CrBr3/MnPSe3 heterostructures.
So far, we have proven the presence of EB in 2D FM/AFM bilayer systems, which necessitates that the interlayer magnetic exchange interactions between the FM and AFM layers cannot be canceled out, as exemplified by the VS2/MnPSe3and CrBr3/MnPSe3heterostructures.Following a similar strategy, we further propose that other systems,such as the 1T-VS2/MnPSe3and CrCl3/MnPS3heterostructures, can also exhibit the EB effect, as manifested by the energy alterations caused by the spin flips of the FM layers(Fig.S7).
4.Conclusion and perspectives
In summary, we demonstrated the existence of the EB effect in the proposed 2D FM/AFM bilayers by introducing asymmetric interlayer magnetic interactions through stacking engineering.Explicitly, we stacked 2D FM and AFM monolayers following the rule that ensures the interlayer magnetic interactions between the FM spins, and the two spin sublattices of the AFM layer cannot be canceled out,thus leading to the arising of the EB effect.As the stacking registry changes,the EB exhibits on/off switching and polarity reversal capabilities,with the strength tuned by an external electric field.Our results provide new insights into the microscopic understanding of the interfacial exchange interactions with the EB effect in 2D compensated magnetic heterostructures.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant No.2019YFA0210004),the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No.XDB30000000), and the Fundamental Research Funds for the Central Universities (Grant No.WK3510000013).Computational support was provided by the National Supercomputing Center in Tianjin.
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals
- Majorana noise model and its influence on the power spectrum

