Universal basis underlying temperature,pressure and size induced dynamical evolution in metallic glass-forming liquids
H P Zhang(張華平), B B Fan(范蓓蓓), J Q Wu(吳佳琦), and M Z Li(李茂枝),3,?
1Department of Physics,Beijing Key Laboratory of Opto-electronic Functional Materials&Micro-nano Devices,Renmin University of China,Beijing 100872,China
2Songshan Lake Materials Laboratory,Dongguan 523808,China
3Key Laboratory of Quantum State Construction and Manipulation(Ministry of Education),Renmin University of China,Beijing 100872,China
Keywords: metallic glass-forming liquids,structure relaxation,dynamical heterogeneity,Debye–Waller factor
1.Introduction
Upon rapid cooling, if liquids, such as polymers, biomaterials, and metallic melts, avoid crystallization, they will cross a glass transition temperature and solidify into glasses accompanying a drastic increase of the shear viscosity in approximately 17 orders of magnitude.[1,2]In the liquid–glass transition, temperature (T) governs the underlying relaxation dynamics,known as primary(α)relaxation,which constitutes a central topic and long-standing issue in glassy physics and materials science.[3–10]Apart fromT,the pressure(P)or density (ρ) may also play a significant role in the relaxation dynamics in glass-forming liquids.Experimental and numerical simulation studies have revealed thatPcan effectively change the structure and dynamics of glass-forming liquids,thus influencing the liquid–glass transition and resulting in different glassy states.[11–14]It has also been observed that the relaxation time at differentTandPcollapses onto a single curve.[15,16]In addition, the relative importance ofTandρin determining the relaxation time is found to be described by a scaling variable ofργs/Tin various glass-forming liquids,whereγsis a material-specific constant.[17–22]These findings indicate that pressure may play a role similar to temperature in relaxation dynamics in glass-forming liquids,but the intrinsic physics remains controversial.
On the other hand,a scaling relation between temperature and shear stress has also been established for viscous flow in glass-forming materials,indicating that mechanical stress also has important impact on both the glass transition temperature and liquid viscosity.[23–25]In addition, experiments and simulations have revealed that for finite-sized liquid droplets,the glass transition temperature and structural relaxation time decrease drastically with reduction of the droplet size, exhibiting a strong size dependence.[26–28]Therefore, size, as another important parameter, can be utilized to manipulate the dynamics and properties of glasses and liquids at the nanometer scale.[29,30]
The dynamical evolution and glass transition in glassforming liquids have been extensively investigated by studying their relations with various parameters,including temperature,pressure,stress,density and size.However,little attention has been paid yet to a fundamental issue:Whether there exists any common basis underlying the dynamical evolution induced by these different parameters in glass-forming liquids? Answer to this question may provide fundamental understanding of the mechanism of dynamic arrest and glass transition.It may also offer insights into the mechanism of jamming transition associated with density,temperature and mechanical stress in colloidal and granular materials.[31,32]
In this work,we systematically investigated the influence of temperature and pressure on the relaxation dynamics and dynamical heterogeneity in Ni50Zr50metallic glass-forming liquids via classical molecular dynamics (MD) simulations.The finite-size droplets of Ni50Zr50liquids were also simulated to investigate the size effect on the relaxation dynamics and dynamical heterogeneity.It is revealed that all the temperature-,pressure-,and size-dependent relaxation dynamics and dynamical heterogeneity can be universally determined by the Debye–Waller (DW) factor in metallic glass-forming liquids.It allows one to see unambiguously that the glass transitions induced by different state parameters are manifestations of the same phenomenon.
2.Model and method
In this work, we studied the dynamics in both the bulk liquids and nanodroplets of a Ni50Zr50model alloy using MD simulations implemented with the LAMMPS code.[33]Here a realistic embedded-atom method (EAM) potential was employed to accurately describe the interatomic interactions in Ni50Zr50alloy.[34]Briefly,the bulk metallic system contained 40000 atoms in a cubic box with periodic boundary conditions applied in three directions.For the liquid droplets, samples with different numbers of atoms ranging from 128 to 16000 were simulated with overall translation and rotation being prohibited.Samples were first equilibrated at 2000 K for 2.0 ns,followed by hyper-quenching to 100 K with cooling rate of 1.0×1012K/s in NPT(constant particle number,pressure,and temperature)ensemble.At each temperature of interest,after the samples were annealed for 2.0 ns in NPT ensemble,the ensemble was switched to NVT (constant particle number, volume,and temperature)ensemble and the samples were further annealed for sampling.
To characterize the atomic dynamics in bulk liquids and liquid droplets,both self-intermediate scattering function(SISF)ofFs(q,t)=N?1∑〈exp[iq·(rj,t ?rj,0)]〉and mean square displacement (MSD) of Δr2(t) =N?1∑〈(rj,t ?rj,0)2〉were calculated for samples at various temperatures under different pressures (see supplementary Fig.S1), whereNis the number of atoms,rj,tthe coordinate vector of atomjat timet,qthe wave vector fixed at|q|=qmax(~2.7 ?A?1)which corresponds to the first peak position of the structure factor,and〈〉the ensemble average.Based on SISF and MSD,the relaxation timeτand DW factor〈u2〉can be obtained.In general,τis defined as the time scale when SISF decays to e?1,[9,15,16]and〈u2〉is defined as the MSD at a few picosecond(~0.33 ps)[35–40]when it starts to reach the quasi-plateau region(see supplementary Fig.S1).
The basis of defining〈u2〉 of liquid lies in the notion that liquid can be treated as a solid within a very short time scale.[35]However,choosing a proper time for measuring〈u2〉should be careful, especially at high temperatures.[35]Although the MSD at low temperatures (such as 900 K) does show a clear plateau region, denoting the vibration within cage.Whereas at high temperatures,the MSD does not show such a clear plateau region(such as 1600 K).To deal with such situations,previous studies[36–40]usually defined the cage time according to the minimum derivative of MSD in double-log plot.Further analysis indicated that in Ni50Zr50system the cage time increases as temperature decreases(see supplementary Fig.S2).And the cage time at a high temperature of 1600 K is around 0.33 ps.For simplicity, we chose it as a constant time for measuring the〈u2〉in all cases.Note that a constant time for measuring〈u2〉was also applied in a previous study on polymer glass.[37]We have verified that even if we chose the variable cage time for measuring〈u2〉, the data points ofτand〈u2〉under different temperatures and pressures still collapse on a master curve (see supplementary Fig.S3).This indicates that the connection between relaxation time and DW factor is intrinsic.
3.Results and discussion
3.1.Relationship between τ and 〈u2〉 in bulk liquids and droplets
First, we studied the relation between structural relaxation timeτand DW factor〈u2〉in Ni50Zr50liquid at different temperatures under zero pressure.Figures 1(a)and 1(b)show the temperature dependence of〈u2〉 andτatP=0 GPa, respectively.It can be seen that while〈u2〉decreases a little with decreasing temperature,τdrastically increases several orders of magnitude.We also investigated the pressure dependence of〈u2〉andτat various fixed temperatures,as shown in Figs.1(c)and 1(d),respectively.Similarly,at a given temperature,while〈u2〉 decreases,τincreases as pressure increases.It can be seen that pressure suppresses the rattling amplitude of atoms within cages formed by the nearest neighbors and slows down the structural relaxation in metallic glass-forming liquids.The smaller the〈u2〉,the longer the relaxation timeτ.If one plotsτas a function of〈u2〉,all data collapse onto a master curve ofτ[P,T]≡τ〈u2〉 without introducing any additional parameters, as shown in Fig.1(e).This indicates that the long-time relaxation dynamics in glass-forming liquids are intrinsically correlated to the short-time vibrational dynamics,regardless of whether the relaxation dynamics in glass-forming liquids are induced by temperature or pressure.This finding suggests that liquids with the same vibrational〈u2〉 share the same relaxation timeτ, thus implying that the structural relaxation time in liquids is fundamentally determined by the DW factor.
Notably,previous studies have revealed that the combined effects ofTandρon relaxation dynamics follow a scaling relationship ofτ[T,ρ]=τ[ργs/T]in various glass-forming liquids,whereγsis a material-specific constant.[17–22]As shown in Figs.2(a) and 2(b), the relaxation timeτin Ni50Zr50system also follows the scaling law ofτ[T,ρ]=τ[ργs/T],whereγs=1.25 (±0.10).This observed scale invariance is consistent with a previous study in a ternary Zr50Cu44Al6system,[20]indicating that the influences ofTandρon liquid dynamics share common basis in metallic glass-forming liquids.Here,we revealed that this common basis can be described with〈u2〉,i.e.,.Considering the scaling relationship ofτ[T,ρ]=τ[ργs/T], it is derived that〈u2〉 also obeys the scaling relationship of〈u2〉[T,ρ]=〈u2〉[ργs/T].As shown in Figs.2(c) and 2(d), we have verified the validity of the thermodynamic scaling of〈u2〉.This result indicates that the correlation betweenτand〈u2〉is intrinsic.

Fig.1.(a)and(b)The vibrational〈u2〉and relaxation time τ changing with temperature along the zero pressure isobar(P=0 GPa)in Ni50Zr50 bulk liquid.(c)and(d)The〈u2〉and τ changing with pressure along different isotherms(1000 K,1100 K and 1300 K).(e)The relaxation time τ versus〈u2〉,they naturally collapse on a well-defined master curve.

Fig.2.(a)and(b)The relaxation time τ changing with density ρ and with the variable ργs/T,where γs=1.25(±0.10),along the zero pressure isobar(P=0 GPa)and along different isotherms(T =1000 K,T =1100 K and T =1300 K).(c)and(d)The vibrational〈u2〉changing with density ρ and with the variable ργs/T,respectively.
To verify the universality of the relation between the DW factor and structural relaxation time, we further investigated the size-induced dynamical evolution in finite-sized droplets of Ni50Zr50glass-forming liquid.Figures 3(a)and 3(b)show the variations of DW factor〈u2〉and structural relaxation timeτwith droplet size, respectively.It can be observed that〈u2〉decreases as the droplet size increases.However,τincreases with increasing the droplet size.Therefore, dynamics become faster as the liquid droplet becomes smaller, consistent with previous studies.[27]We also compared the variation ofτwith〈u2〉 for liquid droplets with various sizes.As shown in Fig.3(c),all data for different sizes and temperatures collapse onto a master curve ofτ[N,T]≡τ〈u2〉 without introducing any parameters.This indicates that the long-time relaxation dynamics in finite-sized liquid droplets are also intrinsically correlated to the short-time vibrational dynamics,independent of the droplet size.
To verify whether the dynamics induced by temperature,pressure and size share the same fundamental basis,we combined all the data from bulk liquids and liquid droplets into a single plot.Surprisingly,all of these data points collapse onto a single curve, as shown in Fig.4.This remarkable observation provides strong evidence that the relation between structural relaxation time and DW factor is intrinsic and universal,independent of temperature, pressure and size.These parameters actually change the DW factor,which fundamentally determines the relaxation dynamics in glass-forming liquids.
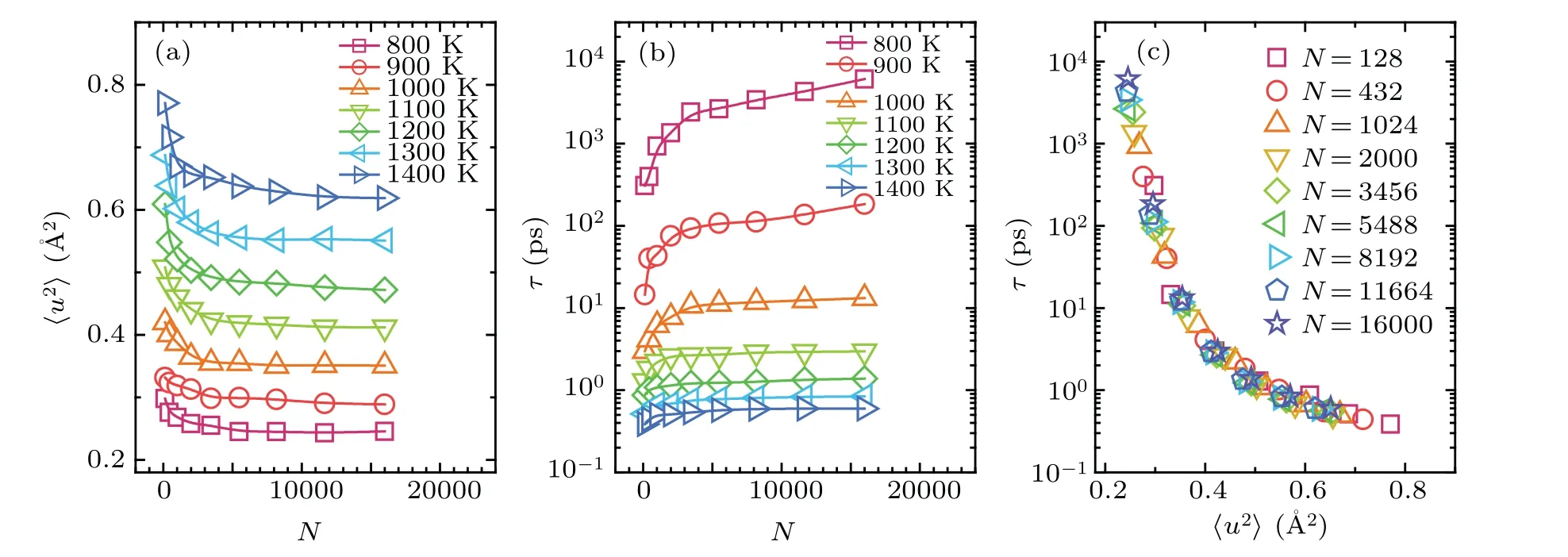
Fig.3.(a) and (b) The vibrational 〈u2〉 and relaxation time τ changing with the size (total number of particles) of Ni50Zr50 nanodroplets along different isotherms from 800 K to 1400 K.(c)The relaxation time τ of nanodroplets with different sizes,as functions of〈u2〉.They also collapse on a master curve.
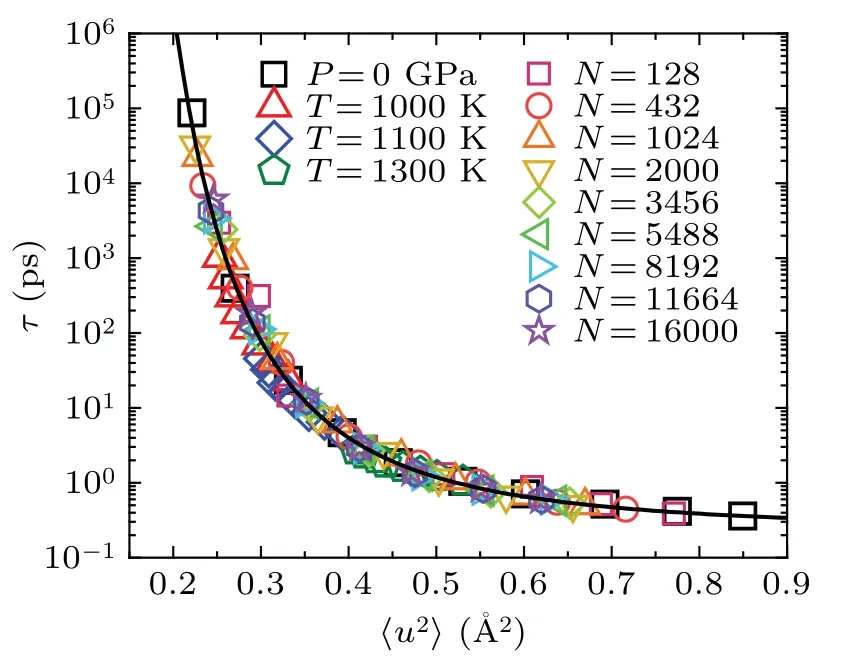
Fig.4.The relaxation time τ versus〈u2〉for both the Ni50Zr50 bulk liquids and nanodroplets,they all collapse on a master curve which can be well fitted by Eq.(2)with u20 =0.607 ?A2 and γ =2.5(dark solid line)(see supplementary Section II for more details about the fitting).
In previous studies, some different phenomenological equations have been proposed to quantify the relationship between structural relaxation time and DW factor in glass-forming liquids.For example, by treating the viscous flow events as activated jumps between neighbor harmonic wells, Hall and Wolynes relatedτto〈u2〉 byτ∝expa2/〈u2〉 , whereais the displacement to overcome the barrier.[36]This approach was recently extended by Leporini and coworkers,[37–40]assuming a Gaussian distribution ofa2(withaverage andvariance) as a way of modeling the structure heterogeneity of glasses and leading to
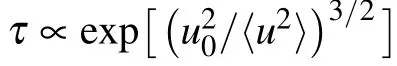
Alternatively, by relating the free volume to the DW factor, i.e.,vf∝〈u2〉3/2in a simulated coarse-grained polymeric glass-former,Starret al.found another scaling forτand〈u2〉as.[41]It was argued by Douglas and coworkers that the exponent of 3/2 here is due to the perfectly isotropic growth of free volume with temperature,[42–44]and the exponent can be larger than 3/2 for anisotropic cases.Therefore,this formula was generalized to be

3.2.Relationship between τ and〈u2〉in local atomic structures
We conducted further analysis to check whether such a correlation also holds for local atomic structures in liquids.For bulk liquid ofP=0 GPa at different temperatures (from 800 K to 1300 K),〈u2〉of each atom can be calculated based on its mean-square displacement.Atoms were sorted by their〈u2〉from low to high, and divided into 10 groups, each containing 10% of the total atoms.Within each group, the averaged〈u2〉 were calculated, as shown in Fig.5(a).SISF of atoms in each group can be also calculated, as shown in Fig.5(b), allowing us to extract the corresponding relaxation time for each group.Consequently, the correlation between relaxation time and DW factor within each group can be obtained.We then plottedτand〈u2〉at different temperatures for all the 10 groups together,as shown in Fig.5(c).Remarkably,the data from all groups collapse onto a master curve,similar to the overall case.

Fig.5.The dynamics of slow and fast atoms in bulk liquids at P=0 GPa.(a)Sorting and grouping the atom by its〈u2〉at 1000 K.(b)SISF for these 10 groups of atoms at 1000 K.(c)τ for these 10 groups of atoms as functions of their atomic〈u2〉at different temperatures(from 800 K to 1300 K).The black line is taken from Fig.4.
It has been proved that atoms near the surface of liquid droplet exhibit much faster relaxation dynamics than those in the interior.[27]In our study,for liquid droplets ofN=16000 at different temperatures,we partitioned them into some concentric shells with a thickness of 3 ?A from surface to the center.Similarly, the averaged〈u2〉and relaxation time of the atoms within each shell can be calculated.As shown in Figs.6(a)and 6(b), the group of atoms near the surface display larger〈u2〉and smallerτ,indicative of fast relaxation dynamics,consistent with previous studies.[27]Figure 6(c)shows that all the data from the liquid droplets at different temperatures collapse onto a master curve.Moreover, we combined all data from the above two cases, encompassing both the bulk liquids and liquid droplets,and found that they all collapse onto a master curve, which can be well described by Eq.(2), as shown in Fig.7.This result demonstrates that the long-time relaxation dynamics and DW factor in local regions are also valid.

Fig.6.The dynamics of local atoms from inner to outer layers in the nanodroplet (N =16000) at different temperatures (from 800 K to 1200 K).(a)and(b)The〈u2〉and τ of atoms at different shells in the nanodroplet,while the thickness of each shell is 3 ?A and core atoms(with r <18 ?A)are treated as one shell.It is noted that atoms near the surface of nanodroplet have faster dynamics than inner atoms.(c)τ versus〈u2〉for different local shells.The black line is taken from Fig.4.
Thus, our finding indicates that there is an intrinsic relationship between long-time relaxation dynamics and shorttime vibration dynamics in glass-forming liquids.As shown in Figs.4 and 6,regardless of how the dynamics in glass-forming liquids are changed or whether it is global or local, the longtime relaxation dynamics is universally correlated to the shorttime rattling motion within the cage of the nearest neighbors.It indicates that DW factor intrinsically controls the long-time relaxation dynamics in glass-forming liquids.
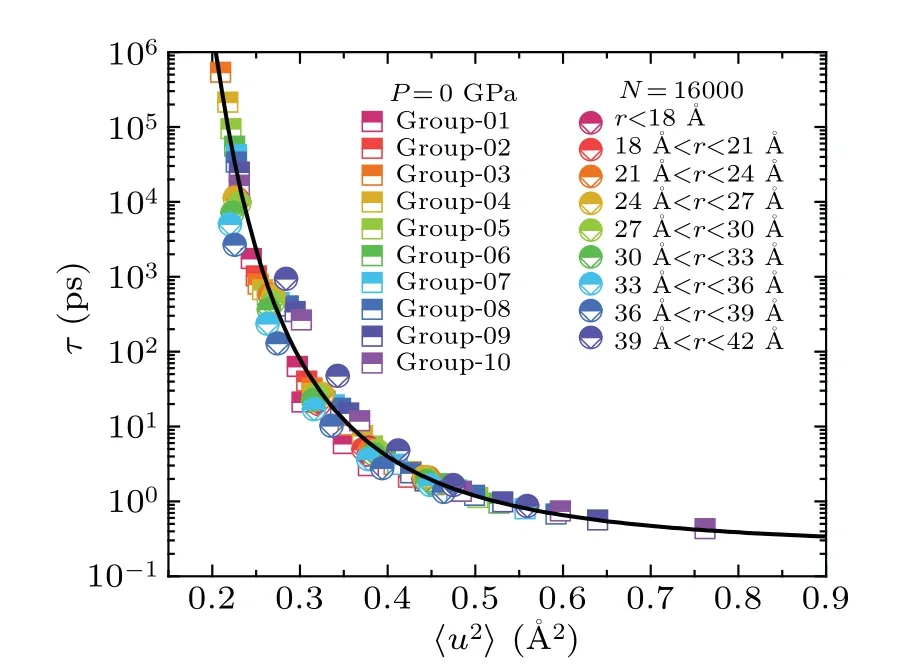
Fig.7.Universal correlations between τ and 〈u2〉 for different local atom groups in both the Ni50Zr50 bulk liquids and nanodroplets.The dark solid line is fitted with Eq.(2),the same as the one shown in Fig.4.
3.3.Relationship between〈u2〉and dynamical heterogeneity
Next, we examined the relationship between DW factor and dynamical heterogeneity in glass-forming liquids.It has been widely recognized that upon cooling, the dynamics in glass-forming liquids are drastically slowed down, and become increasingly heterogeneous.[16,45–48]The dynamical heterogeneity in supercooled glass-forming liquids can be quantitatively characterized using the non-Gaussian parameter,[16]where Δris the displacement of an atom in time scalet.The peak amplitude ofα2,maxand the peak position ofτα2,maxcan be used to estimate the most heterogeneous dynamics in a glass-forming liquid atT.As the temperature decreases,bothα2,maxandτα2,maxincrease significantly,indicating that dynamics in liquids become more heterogeneous with decreasing temperature (see supplementary Fig.S5(a)).Figures 5(a) and 5(b) show that for bulk metallic glass-forming liquids at different temperatures and pressures and metallic liquid droplets with various sizes, all data ofα2,max~〈u2〉andτα2,max~〈u2〉collapse together, following a universal behavior, respectively.This observation indicates that dynamical heterogeneity in glass-forming liquids is intrinsically correlated to the DW factor.[49,50]
3.4.Insight into the kinetic fragility
The kinetic fragilitymis defined as
which is constructed by Angell[1]to describe how fastτchanges with temperature near glass transition temperatureTg.Previous studies have revealed that the fragilitymof a glass-forming system generally increases with increasing pressure,[12–14]and decreases with decreasing particle size.[28]For comparison,we conducted analysis on kinetic fragility in Ni50Zr50system.For simplicity,three typical cases were studied, including the bulk liquids under two different pressures(P=0 GPa andP=9 GPa), as well as the nanodroplet containing 2000 atoms (N=2000).As shown in Fig.9(a), the relaxation timeτcan be well fitted with the VFT equation of.Following previous studies,[20,28]we definedτgas 104ps,and calculatedTgaccordingly.It is observed thatTgunderP=9 GPa is higher than that underP=0 GPa for bulk liquids, and thatTgof nanodroplet is the lowest among them.Importantly,as shown in Fig.9(b),the kinetic fragilitymis different in the three different cases.We observed that the fragilitymunderP=9 GPa is higher than the one underP=0 GPa for bulk liquids,and that fragilitymof nanoparticle is the lowest among them.That is, similar toTg, the kinetics fragilitymin Ni50Zr50system increases with increasing pressure,and it also decreases with decreasing particle size.This result is consistent with the previous studies.
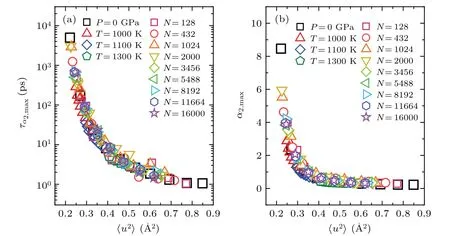
Fig.8.The τα2,max (a)and α2,max (b)as functions of〈u2〉.They also collapse on master curves,respectively.
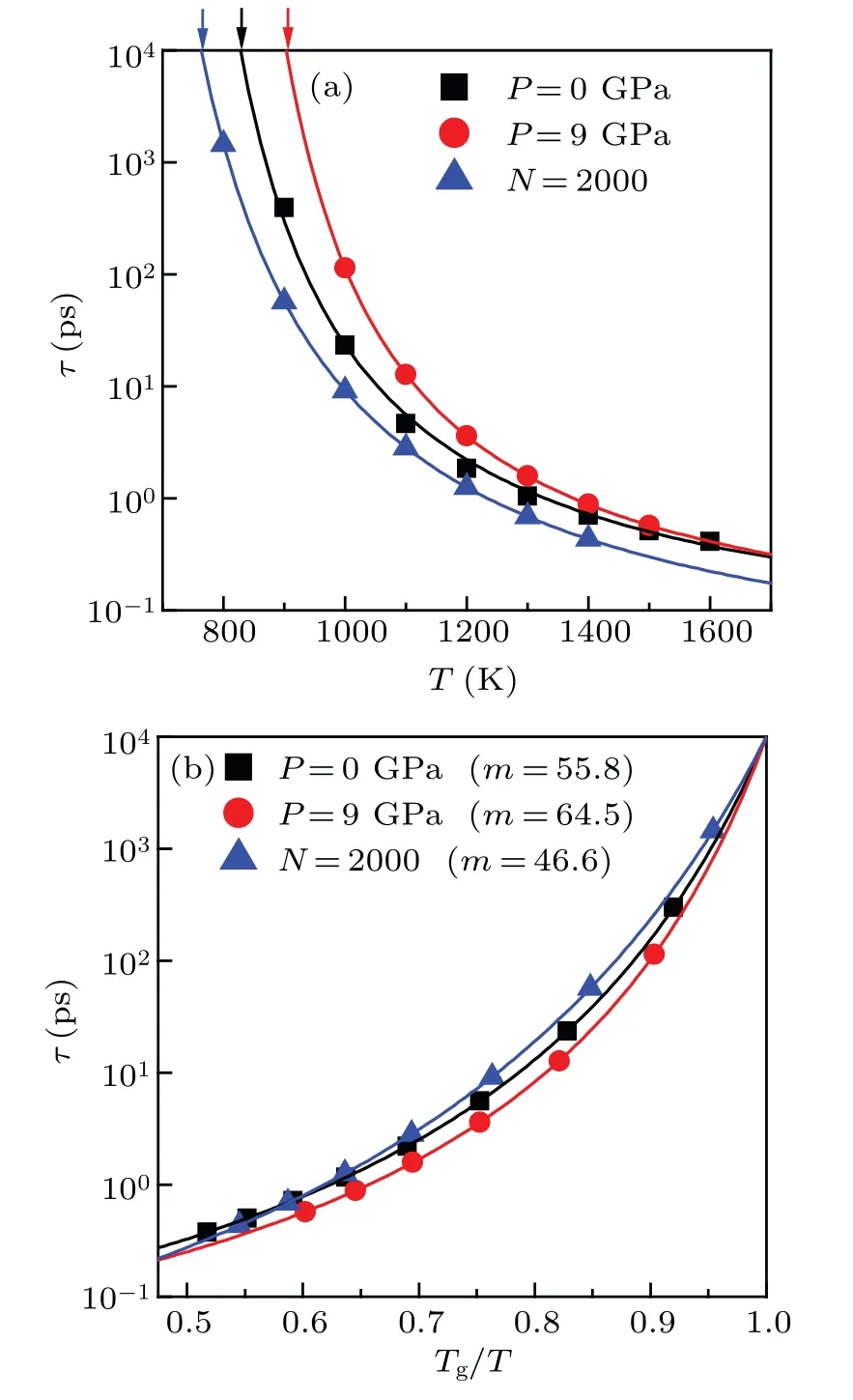
Fig.9.(a)and(b)The relaxation time τ changing with temperature and with Tg/T for three selected cases,including the bulk liquids under two different pressures(P=0 GPa and P=9 GPa)and a nanodroplet that contains 2000 atoms(N=2000).The solid line represents VFT fitting,and the arrow denotes Tg at which τ equals τg(defined as 104 ps).[20,28]
Significantly, the observation of intrinsic connection betweenτand〈u2〉provides insightful understanding of the kinetic fragility.Considering the relationship ofτ[T,P,N]≡, the kinetics fragility can be presented as
The first term can be simplified into
which is an intrinsic part and independent of pressure and size.Whereas the second term can be simplified into
which is proportional to bothTgand the gradient of〈u2〉.Finally,the overall fragility can be simplified into
When the pressure or size changes, onlyTgand the gradient of〈u2〉 may change accordingly.Generally, a larger gradient of〈u2〉 means a much faster decay of〈u2〉 with temperature, leaving〈u2〉 reachingu2gat a higherTgduring cooling process.It indicates thatTgand the gradient of〈u2〉are connected with each other,and share consistent trends with pressure and size.As a consequence, one can easily obtain the trend of fragility with pressure and size according to the trend ofTg.For example, if one knows thatTgincreases as pressure increases, one can infer that the gradient of〈u2〉also increases.Based on the above equation,one can quickly deduce that the fragility should increase accordingly.Theoretically,with a proper choice of the pressures and size, the Ni50Zr50bulk liquid and nanodroplet could have the sameTgand the same fragility curve.It suggests that the fragility curve could be considered as a subset of the master curve representing the relationship betweenτand〈u2〉.
It is an interesting question whether the parameterγis connected with the scaling exponentγs.According to the above discussion,γis intrinsically related to the kinetic fragility.Whereas for the density scaling exponentγs, previous studies have revealed thatγsis closely related to the interatomic interactions.[17–22]Some studies argued that the interatomic interactions are also highly connected with the kinetics fragilitym.[51–53]Therefore,both of these two parameters are connected with fragility.However,it does not mean that these two parameters are directly connected with each other.The exponentγmeasures how fastτchanges with〈u2〉,independent of the temperature,density and size.Whereasγsmeasures the relative importance of density as opposed to temperature on dynamics.Therefore,γandγsdescribe different physical processes, and they are not directly correlated with each other.The value ofγcannot be inferred from the value ofγs, and vice versa.
3.5.Relationship between〈u2〉and shear modulus and relaxation time
Based on the above analysis, it is evident that both the structural relaxation time and the dynamical heterogeneity are determined by the DW factor in the glass-forming liquids.Whereas in glasses, it has been proven that the DW factor is universally related to the shear modulusG, that is,, whereVais the average atomic volume,kBis Boltzmann constant andC ≈0.5 is a universal constant for all glasses.[54]For the same metallic glass,V1/3ais comparable to the atomic diameter,which changes little with temperature or pressure or droplet size.Therefore,at a given temperature,the decrease of DW factor induced by pressure or size is directly related to the increase of shear modulus in glasses.In the supercooled liquid,there still exists the instantaneous shear modulus referring to time scales that are much shorter than the relaxation time.As can be seen in Figs.1(c)and 3(a),the DW factor decreases with the increase of pressure or droplet size at a given temperature.Consequently,this infers that the instantaneous shear modulus increases with the increase of pressure or droplet size.From the potential energy landscape (PEL)perspective,[56]αprocesses correspond to the transitions between meta-basins in PEL,and the slope of the meta-basin in PEL is determined by the shear modulus.[57,58]Thus, the increase of pressure and droplet size can increase the slope of the meta-basins,thereby restraining theαprocess.[58]This is consistent with our observations that the relaxation time gets longer with the increase of pressure(Fig.1(d))and droplet size(Fig.3(b)).
Notably,the intrinsic correlations betweenτandG∞and〈u2〉can be well understood in terms of the Shoving model.[5]Theoretically, the Shoving model assumes that the activation energy of relaxation in liquid is mainly the shear elastic energy which is located in the surroundings of the flow event.[5]Based on this assumption,it establishes a correlation between relaxation time and shear modulus and DW factor as
where the parameterdis the average interatomic distance.Importantly, the Shoving model supposes an intrinsic connection between shear modulus and DW factor asG∞∝kBT/(d〈u2〉), which has been proved to be valid in various metallic glasses.[54]It provides a convenient way to evaluate the trend ofG∞from the trend of〈u2〉with pressure and size at a fixed temperature.Based on our result of〈u2〉,we inferred that at fixed temperature the shear modulusG∞increases with increasing pressure,and decreases with decreasing size.More importantly,the Shoving model also supposes an intrinsic connection between relaxation time and DW factor.Here, we observed an intrinsic connection between relaxation time and DW factor,independent of temperature,pressure and size.To this point, our results are well consistent with the Shoving model.
However, it should be noted that data points ofτand〈u2〉 for Ni50Zr50system do not follow the equation ofτ∝exp,as predicted by the Shoving model.Instead,they follow the equation ofτ∝exp, as developed by Douglas and coworkers.[42–44]The discrepancy indicates that the Shoving model might miss the important parameterγthat controls the explicit relationship betweenτand〈u2〉, though it has seized the intrinsic connection between them.According to Douglas and coworkers,[42–44]the parameterγis due to the anisotropic nature of local vibration and relaxation.Therefore, it is possible to improve the Shoving model by considering the anisotropic nature.Further studies are necessary to clarify this issue.
3.6.Relationship between 〈u2〉 and boson peak and fivefold local symmetry
Recently, a universal equation has been also derived for the boson peak intensityIBPand Debye–Waller factor〈u2〉in disorder materials at different temperatures under different pressures,[59]given as, whereA ≈0.215 is a universal constant, andmis the average atomic mass.This indicates that the DW factor fundamentally determines the boson peak intensity in disordered materials.[59]All these findings suggest that the Debye–Waller factor is the universal basis underlying the dynamics in wide time scales from high-frequency boson peak to long-time structure relaxation in disordered materials.On the other hand,a quantitative relationship was also established between the structure parameter of five-fold local symmetry in atomic clusters and dynamics in both short- and long-time relaxation dynamics in metallic glass-forming liquids, suggesting that there exists a common structural basis underlying the dynamics in different time scales in glass-forming liquids.[60]Whether this structural parameter is suitable for describing the dynamics induced by different state parameters needs further investigations.
4.Conclusion
In conclusion, via comprehensive computer simulations of Ni50Zr50bulk liquids and nanodroplets,we studied dynamics evolution in the multivariate phase space,especially along the isotherm with the change of pressure or droplet size.An universal correlation betweenτand〈u2〉 is observed, independent of the way we tune the dynamics, and they all stay on a master curve with changing relaxation timeτover 5 orders of time scales.Moreover,this universal correlation even holds locally.We also found that the dynamical heterogeneity is closely related to the short-time vibrational DW factor.It infers that the long-timeαrelaxation is mainly controlled by the short-time vibrational DW factor in liquids.These findings would help understanding the long-standing challenges of dynamic arrest mechanism and the physical nature of dynamical heterogeneity.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.52031016).Computational resources have been provided by the Physical Laboratory of High Performance Computing at Renmin University of China.
- Chinese Physics B的其它文章
- Photophysics of metal-organic frameworks: A brief overview
- Anelasticity to plasticity transition in a model two-dimensional amorphous solid
- Ab initio nonadiabatic molecular dynamics study on spin–orbit coupling induced spin dynamics in ferromagnetic metals
- Ultrafast dynamics in photo-excited Mott insulator Sr3Ir2O7 at high pressure
- Valley filtering and valley-polarized collective modes in bulk graphene monolayers
- Sharing quantum nonlocality in the noisy scenario

