Ab initio nonadiabatic molecular dynamics study on spin–orbit coupling induced spin dynamics in ferromagnetic metals
Wansong Zhu(朱萬(wàn)松), Zhenfa Zheng(鄭鎮(zhèn)法), Qijing Zheng(鄭奇靖),?, and Jin Zhao(趙瑾),2,?
1Department of Physics and ICQD/Hefei National Research Center for Physical Sciences at the Microscale,University of Science and Technology of China,Hefei 230026,China
2Department of Physics and Astronomy,University of Pittsburgh,Pittsburgh,Pennsylvania 15260,USA
Keywords: nonadiabatic molecular dynamics,spin dynamics,spin–orbit coupling,ferromagnetic metal
1.Introduction
The manipulation of material magnetism on the femtosecond timescale holds great significance in the field of spintronics.[1–3]This is primarily due to the crucial role played by the magnetic medium’s information storage speed in determining the operational velocity of spintronic devices.[4,5]The development of femtosecond laser technology and other related advancements have established optical excitation as a commonly employed approach to studying magnetic materials.[6–8]As early as 1996, researchers discovered the phenomenon of optically induced demagnetization in ferromagnetic metals.One notable example is the work conducted by Beaurepaireet al., who investigated the ultrafast spin dynamics of Ni.They observed a rapid decrease in the magnetization intensity of a 20 nm-thick Ni film within a picosecond under the influence of a 60 fs laser pulse.[6]The demagnetization of Ni has been subsequently confirmed by many experiments.[9–13]Similar demagnetization phenomena have also been observed in Co and Fe materials.[7,8]Under the excitation of a 50 fs laser pulse,a 10 nm-thick Co film reaches its maximum demagnetization ratio at around 400 fs.[7]Similarly,a 7 nm-thick Fe film exhibits varying degrees of demagnetization when subjected to a 60 fs laser pulse by altering the laser flux.[8]
To comprehend the principles of photoexcitation induced demagnetization in ferromagnetic metals and further predict and design relevant optional materials,people have employed various theoretical methods to investigate the mechanisms and dynamics of photoexcitation induced demagnetization.[6,9–25]Beaurepaireet al.proposed a three-temperature model[6]to account for the interactions among the electronic, spin, and lattice systems when studying ultrafast demagnetization.Subsequently, Koopmaset al.introduced a microscopic model based on Elliott–Yafet-type spin–phonon scattering,where the spin-flip probability is determined by the spin-mixing states induced by spin–orbit coupling.[12]Oppeneeret al.simulated Elliott–Yafet-type spin–phonon scattering using firstprinciples calculations of the full electron–phonon matrix elements and phonon dispersions.[14]Theoretical investigations have also explored the effects of photoexcitation, electron–electron scattering, high temperatures as well as the magnon formation and dynamics in photoexcitation induced ultrafast demagnetization.[15–17,20,24,25]
Among these different mechanisms, spin–orbit coupling(SOC)is believed to be an important factor in the ultrafast demagnetization.In previous studies, the influence of SOC on charge transfer or the relaxation of hot carriers has been investigated using first-principles nonadiabatic molecular dynamics(NAMD)simulations.[26,27]Recently,Zhenget al.have developed an SOC-includedab initioNAMD approach and applied it to study the ultrafast demagnetization in Ni.[28]The spindiabatic representation using spin-polarized Kohn–Sham(KS)basis sets and spin-adiabatic representation using spinor basis sets are applied.The simulations investigate the relaxation process of electrons from spin-majority or spin-minority initial states to the final states close to Fermi level (EF) which are nearly all spin-minority states.The spin-diabatic representation suggests a picture that due to the magnitude of electron–phonon coupling (EPC) being one order of magnitude larger than SOC,the excited spin-minority electrons relax to the same spin final states predominantly through EPC.On the other hand,the excited spin-majority electrons,because of lacking the same-spin final states, can only undergo spin-flip relaxation through SOC to reach the spin-minority final states.The reduction in spin-majority electrons and the increase in spin-minority electrons lead to a decrease in the system’s magnetic moment.The spin-adiabatic representation provides an Elliott–Yafet spin–phonon scattering picture.[11,14]To reach a comprehensive understanding of how the SOC plays a role in the ultrafast demagnetization in ferromagnetic materials,it will be interesting to further study the SOC induced spin dynamics in Co and Fe.
In this work, we employ theab initioNAMD method including SOC to investigate the SOC-induced spin dynamics in Co and Fe materials using both spin-diabatic and spinadiabatic representations.Similar to Ni, in both Co and Fe,EPC is one order of magnitude larger than SOC.Therefore,the excited electrons prefer to relax to the same-spin unoccupied states.The SOC induced spin flip will occur only when there are no same-spin unoccupied states available.Then, it is revealed that the SOC induced spin dynamics in Co is very similar to that in Ni,because the final states near theEFare dominated by the spin-minority states,it is revealed that the excited spin-minority electrons relax to the same-spin states and the spin-flip occurs in the excited spin-majority electrons,leading to the reduction in spin-majority electrons and the increase in spin-minority electrons and resulting in the ultrafast demagnetization.Our results indicate a demagnetization timescale of approximately 100 fs, with a maximum demagnetization ratio of 20% under conditions of exciting 4% of the electrons.However, for bcc Fe, the spin-majority states are dominated close to theEF.In this case, we observe an increase in the total magnetic moments induced by SOC instead of demagnetization.Only if we shift theEFto higher energy by 0.6 eV,it is dominated by the spin-minority states and the SOC induced demagnetization processes can be observed.This work offers a new aspect for comprehending the SOC induced spin dynamics mechanism in magnetic metal systems.
2.Method
The Hefei-NAMD program is used to study the SOC induced spin dynamics.The program is based on a framework that combines the fewest-switches surface hopping(FSSH)[29]and time-dependent density functional theory(TDDFT).[30–32]Spin-diabatic and spin-adiabatic representations are implemented in Hefei-NAMD.[28,33]In the spin-diabatic representation, the spin-polarized KS orbitals are used and SOC is treated as perturbation to determine the probability of spin flip.In this representation, the non-radiative relaxation between different spins is determined by EPC,while the probability of spin flipping is governed by SOC.In the spin-adiabatic representation, the basis sets are two-component spinor.In this case,the spin evolves with lattice relaxation,and the EPC and SOC are mixed together in the nonadiabatic(NAC)matrix elements,which determine the probability of spin flip and energy relaxation.
In the spin-diabatic representation, the SOC Hamiltonian is built up using the wavefunciton calculated by Viennaab initiosimulation package (VASP).[34,35]Details can be found in the supporting information.In the spin-adiabatic representation, the spinor basis sets are also calculated using VASP.The DFT calculations use the projector augmented wave(PAW)method to account for the electron–nuclei interactions,[36]and the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE) exchange–correlation functional is used.[37]For the two systems, hcp Co and bcc Fe,structural optimizations are performed on the unit cells at 0 K to obtain the electronic structure information.The residual forces on the system atoms are relaxed to below 0.01 eV/?A,and the total electronic energy convergence criterion is set to 10?6eV.A Gaussian broadening with a width of 0.1 eV is used for partial occupancy of each orbital.And the cutoff energy is 520 eV.Thek-point grids are generated automatically,centered at theΓpoint.For the Fe unit cell, a 15×15×15kpoint grid is used, while for the Co unit cell, an 11× 11×11k-point grid is used.Under the aforementioned conditions,the calculations achieve convergence.
Forab initioNAMD simulation, theab initiomolecular dynamics(AIMD)simulation is needed to get the nuclear trajectory.To be able to sample the phonon excitation at differentq-points,we need to use supercell in the AIMD simulation,so that the phonons at non-Γ qpoints in the primitive cell can be folded to theΓpoint in the supercell.In this regard,we use a 6×6×2 supercell for Co with a 2×2×4k-point grid,resulting in a total of 144 Co atoms.For Fe,we use a 4×4×4 supercell with a 3×3×3k-point grid,leading to a total of 128 Fe atoms.The 0 K structures are obtained by performing structural optimizations on the supercells using the same accuracy criterion.Then the velocity rescaling method is used to raise the system temperature to 300 K, ensuring that temperature fluctuations are below 5% in the equilibrium state.Once the equilibrated systems are obtained,a microcanonical ensemble with a time step of 1 fs is utilized to generate a 5000-step (5 ps) AIMD trajectory.Subsequently, the final 2000 steps (2 ps) of the AIMD trajectory are selected for self-consistent field (SCF)calculations to get the basis sets for NAMD calculation.The results from NAMD are obtained by averaging over 100 randomly chosen initial structures at different time points within this 2 ps trajectory.For each randomly selected time point,2×104NAMD trajectories are simulated using it as the initial structure,with each trajectory consisting of 1000 steps(1 ps).
3.Results and discussion
3.1.SOC induced spin dynamics in Co
Firstly, we investigated the SOC induced spin dynamics in Co.Before discussing theab initioNAMD results,it is necessary to understand its electronic structure.Here we define the spin-up and spin-down states as spin-majority and minority states,respectively.Figure 1 shows the band structure and density of states(DOS)of Co using the primitive cell, where the red color denotes the spin-up and the blue color denotes spin-down.From Fig.1(b),it can be observed that within the energy range of?5 eV to 2 eV,the DOS of d orbital electrons is much higher than that of sp orbital electron, corresponding to the d bands with weak dispersion in Fig.1(a).The energy splitting of the spin-up and spin-down orbitals induces the magnetic moment of Co.From Fig.1(b), it can also be inferred that the states near theEFare predominantly occupied by spin-down electrons.These characteristic features of the Co electronic structure will play an important role in spin dynamics,which will be further discussed below.
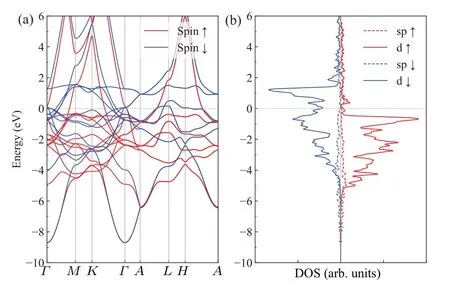
Fig.1.Band structure(a)and DOS(b)of Co calculated using primitive cell.The projected DOS of sp and d orbitals are shown in(b).The EF is set to be the energy reference.
Next,we investigated the dynamics of photo-excited electrons with different spins in hcp Co.First we excite one spin-up electron to around 2.6 eV above theEF, as schematically shown in Fig.2(a).Figures 2(b) and 2(c) show the time-dependent energy and spin relaxation of the excited electron using both the spin-diabatic and spin-adiabatic representations.One can see that the two different representations give similar results, where the spin-up electron flips its spin and relaxes to the spin-down electron close to theEF.Such spin flip process is fitted with a Gaussian function and yields a time scale of 317 fs.Then we study the relaxation process of a spindown electron.As shown in Figs.2(d)–2(f),when a spin-down electron is excited to 1.5 eV aboveEF,it will relax toEFwith a timescale of 39 fs without spin flip.One can see that the spin flip occurs for the spin-majority (spin-up) electron while the spin is preserved for the spin-minority (spin-down) electron.Thus one can expect a demagnetization after photoexcitation in Co.
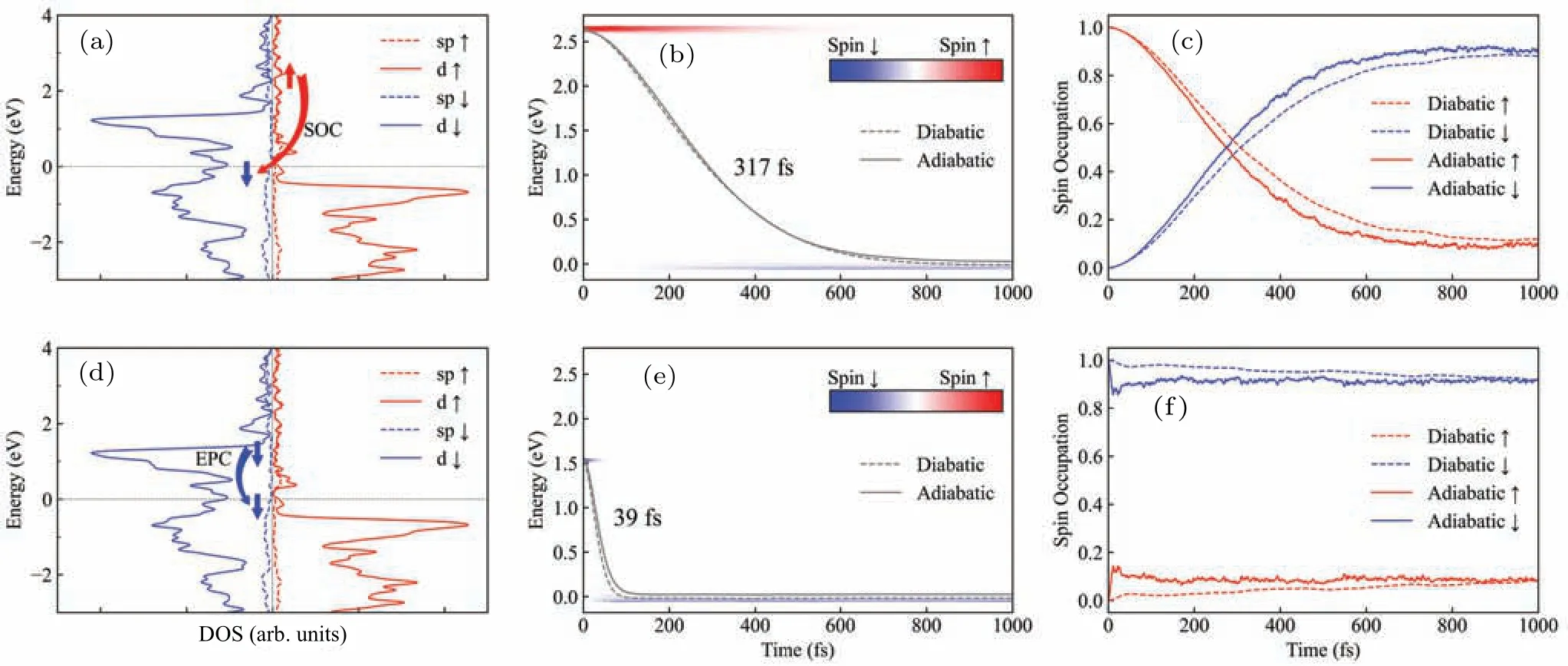
Fig.2.Spin dynamics of spin-majority(a)–(c)and spin-minority(d)–(f)in NAMD simulations for Co.(a),(d)The electron relaxation process schematically shown with DOS plotting.(b), (e) Energy relaxation of excited electron, where the color map shows the spin occupancy.(c),(f) Spin relaxation of excited electron.In panels (b)–(c) and (e)–(f), solid and dashed lines are results from spin-adiabatic and spin-diabatic representations,respectively.
In the spin-diabatic representation,the electron relaxation among the same-spin states is determined by the EPC elements while the spin flip probability is controlled by the SOC.The EPC and SOC elements can be clearly distinguished as shown in Fig.3.From Fig.3(a)it can be seen that the EPC between the nearest energy states is always the largest.Therefore the spin-down electron always prefers to relax to the nearest lower energy state.This is because the EPC term in NAMD simulation can be written as
which is inversely proportional to the energy difference between the two states.However, from Fig.3(b) it can be seen that the SOC elements do not follow the same trend.Instead,it depends on the orbital composition.Comparing the d–d,d–sp,and sp–sp SOC,one can find that d–d SOC is the largest while sp–sp SOC is the smallest.For the spin-up electron,the initial state is the sp state and it relaxes to spin-down d state close to theEF, passing the spin-up d states around 0.4 eV aboveEF.Thus the determining factor for spin splitting is the sp–d and d–d SOC elements.It can be seen that the SOC elements are around one order of magnitude smaller than EPC ones.That is the reason that the spin-down electron relaxes around 10 times faster than the spin-up electron.
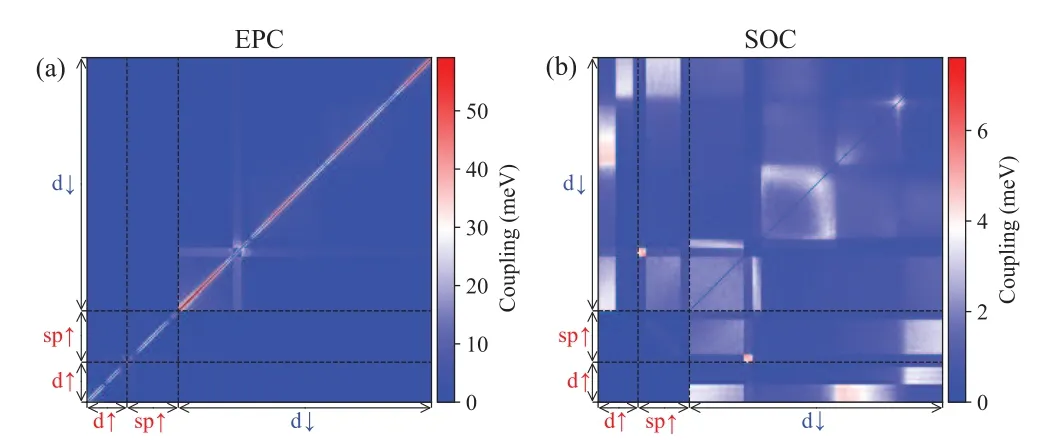
Fig.3.EPC(a)and SOC(b)between electronic states involved in the simulations for hcp Co.“d↑” and “d↓” comprise spin-up d orbitals around 0.4 eV and spin-down d orbitals below 1.5 eV corresponding to EF.“sp↑”comprises the spin-up sp states around 2.5 eV above EF.
The results in Fig.2 are based on single-electron excitation.To further understand the demagnetization phenomenon,we also performed simulation of multi-electron excitation under both representations.In the multi-electron simulations,an equal number of electrons were excited to states above theEFin the range of 1.20–2.65 eV.Figure 4(a)shows snapshots of DOS contributed by the two spin components at different time with 4% electrons excited using the spin-diabatic representation.It can be observed that, initially, the numbers of electrons in both spin states are equal, but as the relaxation process progresses,the population of spin-up electrons gradually decreases,and ultimately,only spin-down electrons remain in the final states.Figure 4(b) shows the variation of the relative magnetic momentMt/M0as a function of the percentage of excited electrons(ranging from 1%to 4%)under both representations, whereM0andMtrepresent the initial and timedependent magnetic moments at timet, respectively.The results indicate a rapid decrease in the relative magnetic moment within 100 fs, and the final demagnetization proportion increases with a higher percentage of excited electrons.With 4%electron excitation,Mt/M0can reach around 80%.In the multi-electron simulations, some of the spin-up electrons can only be excited to spin-up d orbitals around 0.4 eV aboveEF.Compared to the higher-energy initial states in the sp orbitals,they can relax more quickly to the spin-down d orbitals,leading to a faster demagnetization process compared to that in single-electron simulations.The spin-diabatic representation predicts a slightly higher demagnetization rate compared to the spin-adiabatic representation.It is due to the mixing of spin-up and spin-down components in the spinor basis sets.
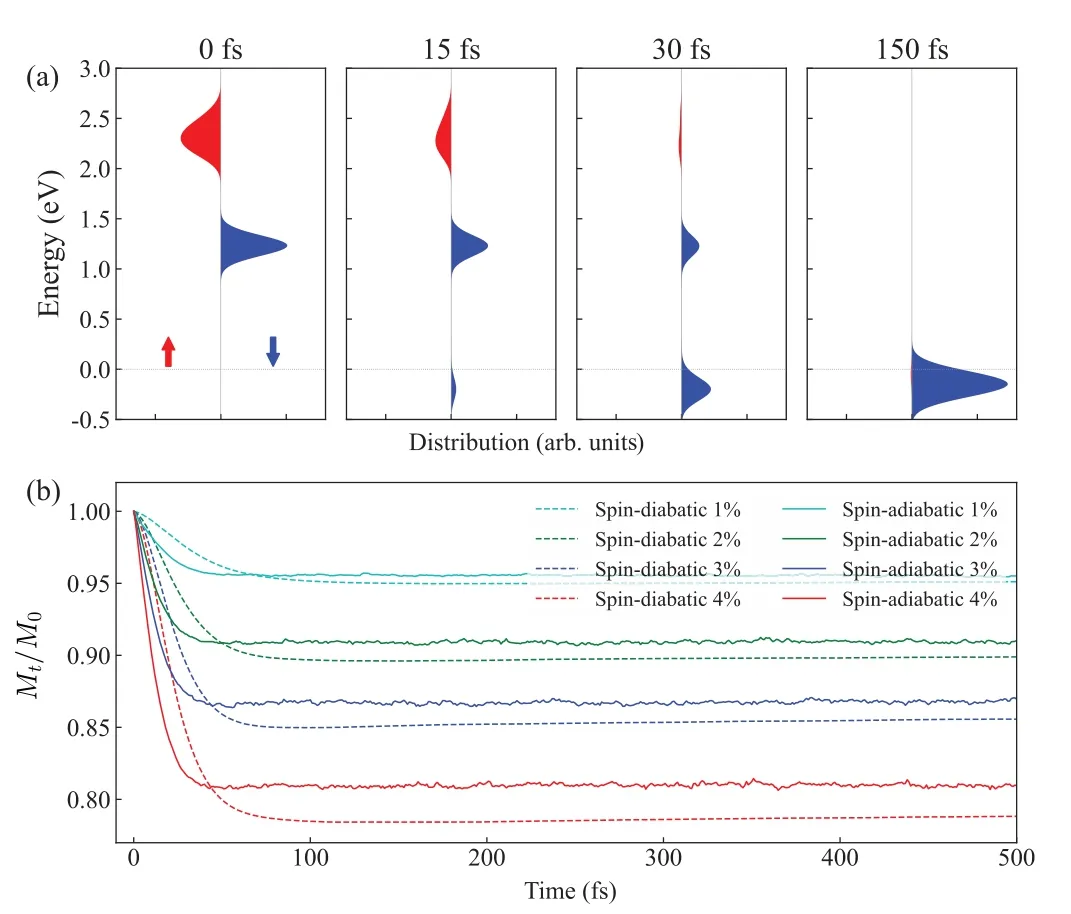
Fig.4.(a)Distribution of electrons at different times in multi-electrons NAMD simulation for Co.(b)Evolution of relative magnetic moments at different electron excitation rates,where solid and dashed lines are results from spin-adiabatic and spin-diabatic representations,respectively.
3.2.SOC induced spin dynamics in Fe
Next, we will discuss the SOC induced dynamics in Fe.Figure 5 shows the band structure and DOS of Fe with bcc structure.Similar to Co, the magnetization of Fe is also contributed by the d bands ranging from?5 eV to 3 eV.Here we also define the spin-up and spin-down electrons as spinmajority and minority states, respectively.The energy splitting of spin-up and spin-down d bands in Fe is around 2.5 eV,which is larger than that in Co.By comparing Fig.5(b)with Fig.1(b), it can be found that the states near theEFof Fe are primarily occupied by spin-up electrons, which is different with Co and Ni.Such a difference will lead to distinct spin dynamics behavior.
The dynamics of single excited electron in bcc Fe is shown in Fig.6.Here the final state for electron is set to be around theEF, which is contributed by the spin-up d orbital.As shown in Figs.6(a)–6(c),if a spin-up electron is excited to an sp orbital at 2.3 eV, it will relax to theEF, driven by the EPC.By contrast, if we excite one spin-down electron to a d orbital at 1.5 eV,it will flip its spin and relax to the spin-up d orbital close to theEF.This process is driven by the d–d SOC.Since the d–d SOC is larger than the sp–d SOC,which is dominated in Ni[28]and Co.Here we observe a relatively faster spin flip in Fe.The time scale is fitted to be 110 fs, which is comparable to the EPC driven electron relaxation between the same spins.The EPC and SOC elements are plotted in Fig.10.Despite EPC still being larger than SOC, the large EPC interactions are mainly distributed between adjacent electronic states.As a result,the relaxation of electrons induced by EPC occurs level by level,moving downwards.On the other hand,SOC is more widely distributed, and an electronic state can have strong SOC interactions with multiple other electronic states.Consequently,the relaxation induced by SOC can proceed through multiple channels,leading to a similar time scale for the relaxation processes induced by EPC and SOC.
In bcc Fe system,we can observe that despite both spindiabatic and spin-adiabatic representations providing qualitatively consistent results, they still exhibit some differences.Particularly,in Fig.6(c),when the spin-up electron relaxes to lower energy,the spin-adiabatic representation shows a partial spin flip within 20 fs,followed by a recovery.It suggests that in Fe the SOC is stronger, leading to larger mixing between the spin-up and spin-down components compared to that in Co and Ni.In this case,the spin-adiabatic representation provides more accurate results and the spin-diabatic representation is only appropriate for situations where the SOC is relatively weak.
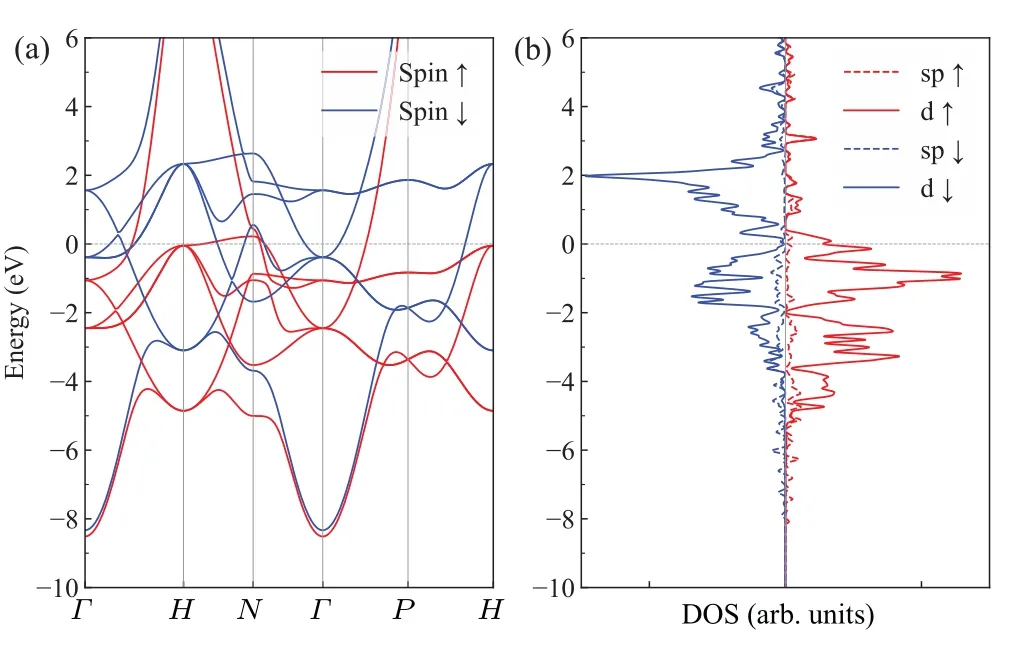
Fig.5.Band structure(a)and DOS(b)for Fe with bcc structure.The Fermi level is set as energy reference.
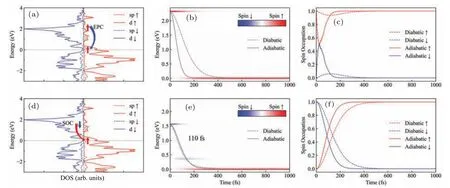
Fig.6.Spin dynamics of spin-majority (spin-up) (a)–(c) and spin-minority (spin-down) (d)–(f) in NAMD simulations for Fe.(a), (d) The relaxation process schematically shown with DOS plotting.(b),(e)Energy relaxation of excited electron,where the color map shows the spin occupancy.(c),(f)Spin relaxation of excited electron.In panels(b)–(c)and(e)–(f),solid and dashed lines are results from spin-adiabatic and spin-diabatic representations,respectively.
The main distinct character of Fe compared to Ni,Co lies in the fact that itsEFis contributed by the spin-majority(spinup) electronic states.As a result, we observe that the spinmajority electrons do not flip their spins, but instead, they cause the spin-minority (spin-down) electrons to flip.This phenomenon does not lead to demagnetization; on the contrary, it results in an increase in the magnetic moment.It is confirmed through the multi-electron dynamics simulations.In Fig.7, we present the time dependent relative magnetic moment after exciting 1%–4% of electrons (Mt/M0).It is found that after approximately 150 fs, the magnetic moment increases by about 15%.
It can be seen that within the theoretical framework of only considering the influence of SOC on spin dynamics, the increase or decrease of the magnetic moment is determined by the spin polarization of the final states close to theEF.If the electronic states nearEFare predominantly spin-majority states, a magnetization enhancement will occur; if they are spin-minority states,a demagnetization will happen.Thus,we can control the spin dynamics by changing the position of theEF.Here, if we move theEFof Fe upwards by 0.6 eV in energy,theEFwill be dominated by spin-minority states.In this case,in the single-electron simulation,it can be observed that spin-majority electrons undergo flipping, while spin-minority electrons maintain their spin direction (Fig.8).In the multielectron simulation,after exciting 4%of the electrons,Mt/M0reaches 0.85 at around 100 fs,leading to 15%demagnetization(Fig.9).
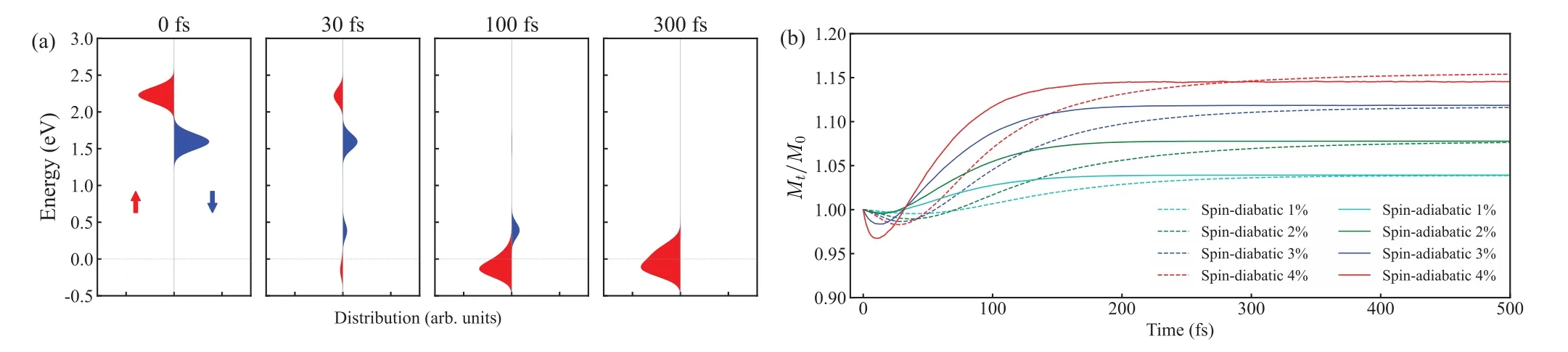
Fig.7.(a)Distribution of electrons at different times in multi-electrons NAMD simulation for Fe.(b)Evolution of relative magnetic moments at different electron excitation rates,where solid and dashed lines are results from spin-adiabatic and spin-diabatic representations,respectively.
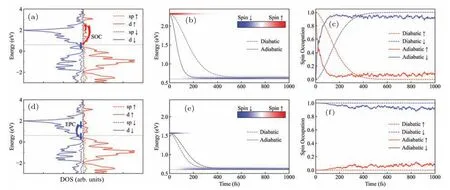
Fig.8.Spin dynamics of spin-majority(spin-up)(a)–(c)and spin-minority(spin-down)(d)–(f)in NAMD simulations for Fe with EF moving upwards by 0.6 eV in energy.(a), (d) The relaxation process schematically shown with DOS plotting.(b), (e) Energy relaxation of excited electron, where the color map shows the spin occupancy.(c), (f) Spin relaxation of excited electron.In panels(b)–(c) and(e)–(f), solid and dashed lines are results from spin-adiabatic and spin-diabatic representations,respectively.
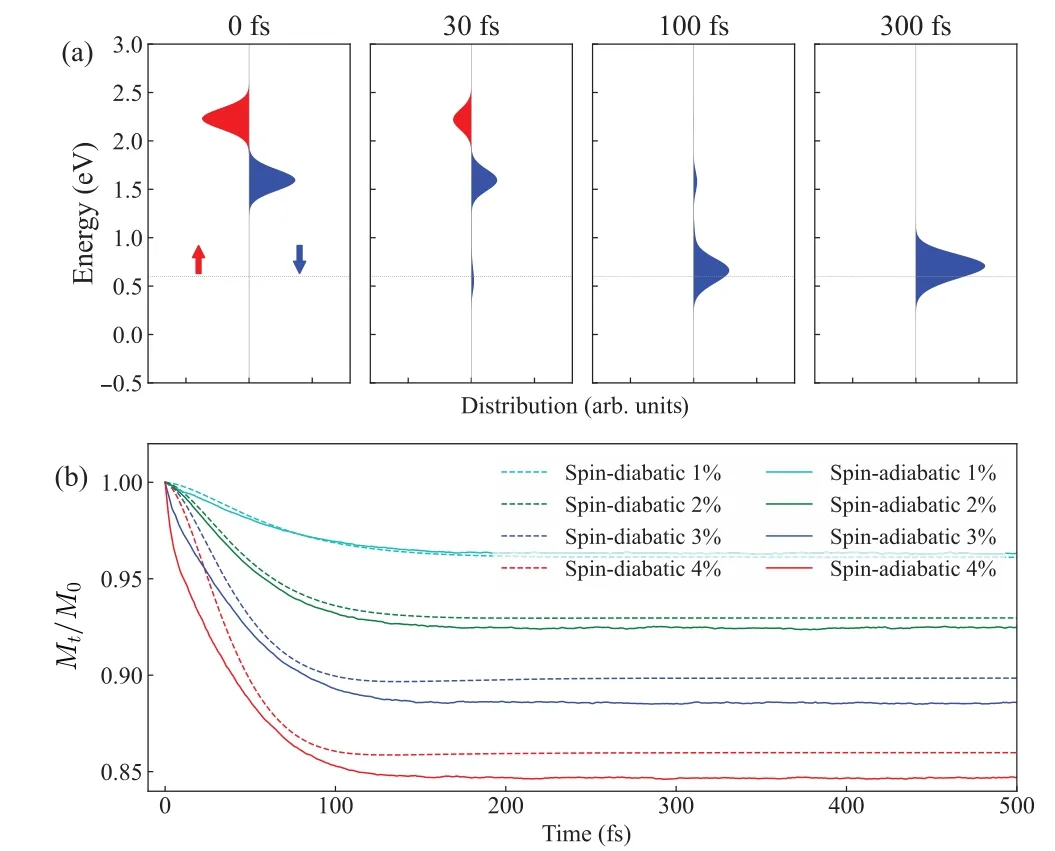
Fig.9.(a) Distribution of electrons at different times in multi-electrons NAMD simulation for Fe with EF moving upwards by 0.6 eV in energy.(b)Evolution of relative magnetic moments at different electron excitation rates,where solid and dashed lines are results from spin-adiabatic and spindiabatic representations,respectively.
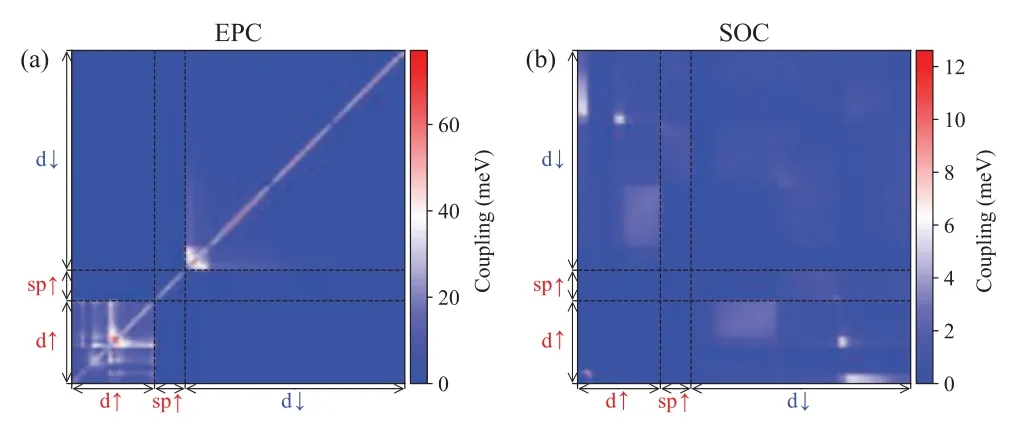
Fig.10.EPC(a)and SOC(b)between electronic states involved in the simulations for bcc Fe.“d↑”and“d↓”comprises spin-up d orbitals below 0.6 eV and spin-down d orbitals below 1.6 eV corresponding to EF.“sp↑”comprises the spin-up sp states around 2.2 eV above EF.
4.Discussion
In this work, we investigate the SOC induced spin dynamics in Co and Fe.Together with the SOC induced demagnetization process in Ni, which was studied by Zhenget al.,we can achieve a comprehensive understanding of how SOC and EPC affect the electron relaxation and spin flip.For all the three systems,the EPC determines the electron relaxation between the same-spin electronic states while the probability of electron flipping between different spin orbitals depends on the SOC.If we only consider the electron flip and relaxation,the spin polarization of the final states close theEFdetermines the tendency of spin flipping: whether it is up-todown or down-to-up flip.In Ni and Co,theEFis dominated by spin-down states,therefore the up-to-down spin flip process is dominated and spin demagnetization happens.By contrast,in Fe,theEFis dominated by spin-up states,thus the down-to-up spin flip plays a leading role, and a magnetization enhancement is observed.Spin flips in Fe occur faster compared to Co and Ni because spin flips in Fe are induced by d–d SOC,whereas in Co and Ni,they are caused by sp–d SOC.
It is noticed that the magnetization enhancement in Fe does not agree with the experimental observation.[8]There can be different reasons for this disagreement.One possible reason is that theEFmay be lifted to higher energy after the photoexcitation.As shown in our results, if theEFis moved 0.6 eV higher,the demagnetization will occur.Another possible reason is that during the demagnetization process in Fe,not only electrons are involved but also holes may play a role.It is noticed that Longet al.used similar approach to study the spin dynamics in Fe,where they have considered the photoexcited holes and have achieved the demagnetization results.[38]However, it is not clear why they only included the hole states in the energy range of[?1.0,0.0]eV.In addition,they used theMpoint electronic structure to do the simulation, which does not reproduce the dominating spin-up d bands at theEF.We propose a future research to estimate the distribution of hot electrons and hot holes starting from the absorption spectrum.Subsequently,the relaxation of electron–hole pairs can be performed to gain a deeper understanding of the demagnetization process in magnetic metals.
During the hot electron relaxation,the energy of the electron will transfer to the lattice.The temperature increase of the system can be approximately calculated using the formula ΔT= ∑i Ei/(n·cm), whereEirepresents the energy transferred from the excited electron to the lattice,nis the amount of substance contained in the supercell, andcmis the molar heat capacity of the lattice.For the simulations in Figs.2(a)–2(c),the Co supercell contains 144 atoms.Initially,an electron is excited to 2.6 eV,and after relaxation,all the energy is transferred to the lattice.Due to the small electronic heat capacity at high temperature, Co’s heat capacity can be approximated as the lattice heat capacity, which is 24.81 J/(mol·K).Therefore, the temperature increase can be estimated to be 70 K.Through similar calculations, it can be determined that when the excitation electron proportions are 2%, 3%, and 4%, the corresponding temperature increases are 1203 K,1787 K,and 2494 K,respectively.One should note that such a simple calculation overestimates the temperature since it supposes the energy transfer from the hot electron is limited in the supercell.In reality,the thermal diffusion to the whole crystal occurs.
It should be recognized that the effects of photoexcitation,electron–electron scattering,as well as the magnon formation and dynamics are not included in the simulation.These effects can also influence the spin dynamics in magnetic metals.
5.Summary
In summary, we employed SOC includedab initioNAMD simulation to investigate the excited electron induced spin dynamics in Co and Fe using both spin-diabatic and spinadiabatic representations.The EPC and SOC determine the electron relaxation among the same-spin states and the spinflip between spin-up and spin-down states, respectively.The excited electrons are expected to relax to the final states close to theEF.In Co system,theEFis dominated by the spin-down electronic states.Thus the spin-up electrons flip their spin during the relaxation due to SOC while the spin-down electrons preserve their spin polarization during the relaxation led by EPC.Such different relaxation behavior induces demagnetization occurring in 100 fs.The SOC induced spin dynamics in Co is highly similar to Ni.By contrast, in Fe system,EFis contributed by spin-up electronic states.Therefore the spin-up electrons keep their spin while the down-to-up spin flip occurs for spin-down electrons.In this case, the magnetization enhancement is achieved in Fe, which is not in agreement with the experimental observation.We have discussed possible reasons to induce such disagreement.
Acknowledgements
J.Z.acknowledges the support of Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No.XDB0450101), the National Natural Science Foundation of China (Grant Nos.12125408 and 11974322), and the Informatization Plan of Chinese Academy of Sciences (Grant No.CAS-WX2021SF-0105).Q.Z.acknowledges the support of the National Natural Science Foundation of China (Grant No.12174363).Calculations were performed at Hefei Advanced Computing Center,ORISE supercomputing center and Supercomputing Center at USTC.
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

