Electromagnetic Ion Beam Instability in the Solar Corona
Wen Liu , Jin-Song Zhao, De-Jin Wu, Huan-Yu Jia, and Si-Ming Liu
1 School of Mechanics and Aeronautics, Southwest Jiaotong University, Chengdu 610000, China; liuwen@my.swjtu.edu.cn
2 School of Physical Science and Technology, Southwest Jiaotong University, Chengdu 610000, China
3 Key Laboratory of Planetary Sciences, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210023, China
Abstract Remote-sensing measurements indicate that heavy ions in the corona undergo an anisotropic and mass-charge dependent energization.A popular explanation to this phenomenon is the damping of the Alfvén/ion cyclotron waves.In this paper, we propose that the ion beam instability can be an important source of the Alfvén/ion cyclotron waves, and we study the excitation of the ion beam instability in the corona at the heliocentric distance~3R⊙and the corresponding energy transfer process therein based on plasma kinetic theory.The results indicate that the existence of the motionless heavy ions inhibits the ion beam instability.However,the anisotropic beams of heavy ions promote the excitation of the ion beam instability.Besides, the existence of α beams can provide a second energy source for exciting beam instability.However,when both the proton beam and the α beam reach the instability excitation threshold, the proton beam driven instability excites preferentially.Moreover, the excitation threshold of the Alfvén/ion cyclotron instability driven by ion beam is of the local Alfvén speed or even less in the corona.
Key words: plasmas – instabilities – waves – Sun: corona
1.Introduction
The solar corona is characterized by its unusually high temperatures (Cranmer & Winebarger 2019).Besides, the effective temperature of minor ions in the solar corona is proportional to their atomic mass number and they are strongly anisotropic, with Ti⊥>Ti//, where ⊥and //are respect to the background magnetic fields (Kohl et al.1997, 1998).One of the most popular physical explanations for highly anisotropic minor ions in the solar corona is the cyclotron interactions between ions and Alfvén/ion cyclotron waves (Cranmer et al.1999; Isenberg et al.2001; Liewer et al.2001; Marsch &Tu 2001; Hollweg & Isenberg 2002).
There are several theories about the origin of the Alfvén/ion cyclotron waves.First,these waves are generated by the smallscale magnetic activity in the chromospheric network and directly launched into corona(Axford&McKenzie 1992,1995;Tu&Marsch 1997).Second,these waves may be produced by a turbulent cascade from much lower frequencies (Li et al.1999; Hollweg & Isenberg 2002; Li et al.2004).Third, the microinstabilities that locally excited by the electrons and electric currents in the corona may be their source (Forslund 1970; Toichi 1971; Markovskii 2001; Markovskii &Hollweg 2002).Besides, Alfvén/ion cyclotron waves can also be locally generated by plasma instabilities related to ion temperature anisotropy(Gary 1993;Klein&Howes 2015;Sun et al.2019)and ion beams(Montgomery et al.1976;Daughton& Gary 1998; Liu et al.2021).In this paper, we mainly focus on this mechanism.However, in this mechanism, it is much easier to excite Alfvén/ion cyclotron waves through ion beam instability processes in a low-β environment like the solar corona(Hellinger et al.2006;Sun et al.2019;Liu et al.2021).Therefore, ion beam instability may play an important role in the energization processes of coronal ions.
In situ observations of the solar wind show that there are usually differential flows between different ion components,where these differential flows are also named as ion beams in the proton core frame.(Feldman et al.1973, 1974; Marsch et al.1982;Goldstein et al.2000;Tu et al.2004;Alterman et al.2018; ?urovcová et al.2019; Verniero et al.2020; Mostafavi et al.2022).Recently, based on in situ observations of Parker Solar Probe (PSP) in the near-Sun solar wind, Verniero et al.(2020) have shown that the number density of proton beam component can be unexpectedly large relative to proton core component, and most of the coexistent ion-scale waves are excited by proton beams.Besides, significantly enhanced ionscale waves are observed in the near-Sun solar wind (Bowen et al.2020, 2020; Liu et al.2023) and they are more likely excited by ion beams (Verniero et al.2020; Klein et al.2021;Liu et al.2021).Moreover, Bowen et al.(2022) have found obvious cyclotron resonant heating in the near-Sun solar wind.These observations seem to show that the energy transfer processes related to ion beams may play a much important role in ion energization of the near-Sun solar wind and corona.
In this paper, considering the potential importance of ion beams in the corona environment, we study the excitation of electromagnetic ion beam instability and related energy transfer processes in the corona.Unlike previous studies, we not only consider the major particles (protons, electrons, and α particles), but we also consider the influence of several minor ions (oxygen ions, magnesium ions, and iron ions).
This paper is organized as follows.Section 2 introduces the theoretical model and plasma parameters.Section 3 exhibits our main results and related analysis.The discussion and summary are shown in Sections 4 and 5, respectively.
2.Theoretical Model and Plasma Parameters
2.1.Theoretical Model
In this paper, we ignore weak collision in the solar corona and treat it as collisionless plasma.To study the wave dynamics in the solar corona, we use the model consisting of Vlasov’s equation and Maxwell’s equation to obtain the wave equation in Fourier space
where?=iσ/(?0ω)+I,?0is the permittivity of free space,?is the dielectric tensor,σ is the conductivity tensor,ω is the wave frequency, and E is the wave electric field.The plasma wave eigenmodes correspond to solutions of Equation (1).Xie &Xiao (2016) and Xie (2019) develop a numerical solver (BO/PDRK) for Equation (1) and this solver is useful to perform a comprehensive study for ion and electron kinetic instabilities(Sun et al.2019, 2020; Liu et al.2021).In this paper, we use BO/PDRK to give the wave dispersion relation in the coronal ion beam plasma.
In plasma instability study,it is very important to understand the kinetic processes when instability is generated.In this paper,we use the energy transfer rate to quantify the exchanged energy between particles and waves.The energy transfer rate is calculated by using the plasma current J and the wave electric field E.The equations of the energy transfer rate are shown as follows:
and
where WEB=?0|E|2/2+|B|2/2μ0is the electromagnetic energy.The detailed derivation processes are shown in the appendix of Liu et al.(2021).The advantage of Equation(3)is that Pt=-γ.Hence, we can directly measure the contribution of each resonance effect on the wave growth or damping.Here γ represents the imaginary part of ω in which γ>0 (or <0)corresponds the wave growth (or damping).
2.2.Parameter Specification
In order to study ion beam instability in the solar corona at heliocentric distance ~3R⊙, we use radial distributions of magnetic field strength and plasma parameters stated in Bale et al.(2016).The magnetic field strength is
where the solar wind velocity is
The electron number density is given by (also see Sittler &Guhathakurta 1999)
with N0=3.26×105cm-3.The proton temperature is
where T0=226.4 eV.Therefore, the basic parameters used in this paper are as follows: B0=2.0766×104nT,Ne=4.5547×105cm-3, Tp=151.3129 eV and VA=634.8629 km s-1, here the Alfvén speed
In this paper, excepting four kinds of usual particles (proton core“pc,”proton beam“pb,”alpha particles“α”and electrons“e”), we also consider three typical heavy ions in the corona,i.e., oxygen ions “O,” magnesium ions “Mg” and iron ions“Fe.” The velocity distributions of all these seven types particles follow drifting Maxwellian distribution, i.e.,expwhere ms, Ns, Tsand Vsdenote the mass, number density,temperature,and drifting speed for each particle component“s”;kBis Boltzmann constant; the subscript //and ⊥ present directions parallel and perpendicular to the background magnetic field, respectively.
Based on recent observations of PSP, the number density ratio of proton beam in the near-Sun solar wind is found to be usually higher than 0.1 Ne(Verniero et al.2020; Klein et al.2021).Therefore, the number density of proton beam in this paper are set as Npb=0.25Ne.In addition,according to Level 3 data obtained by Solar Probe ANalyzers for Ions(SPAN-I;Livi et al.2022) on board PSP, the number density ratio of α particles are set as Nα=0.05Ne.Moreover, based on observations of Solar and Heliospheric Observatory (SoHO) (Kohl et al.1997,1998),we chose three heavy ions(O5+,Mg9+,and Fe11+).The number density of these heavy ions is as follows:NO?0.001Ne, NMg?0.0001Ne, and NFe?0.0001Ne(Reames 1994; Wu & Yang 2007).We note that the abundances of these heavy ions here are relatively higher than those in Asplund et al.(2009).This may be caused by the difference in the abundance of elements between the photosphere and the corona.Lastly, to ensure the charge neutrality condition,the number density of proton core is Npc=0.643Ne.
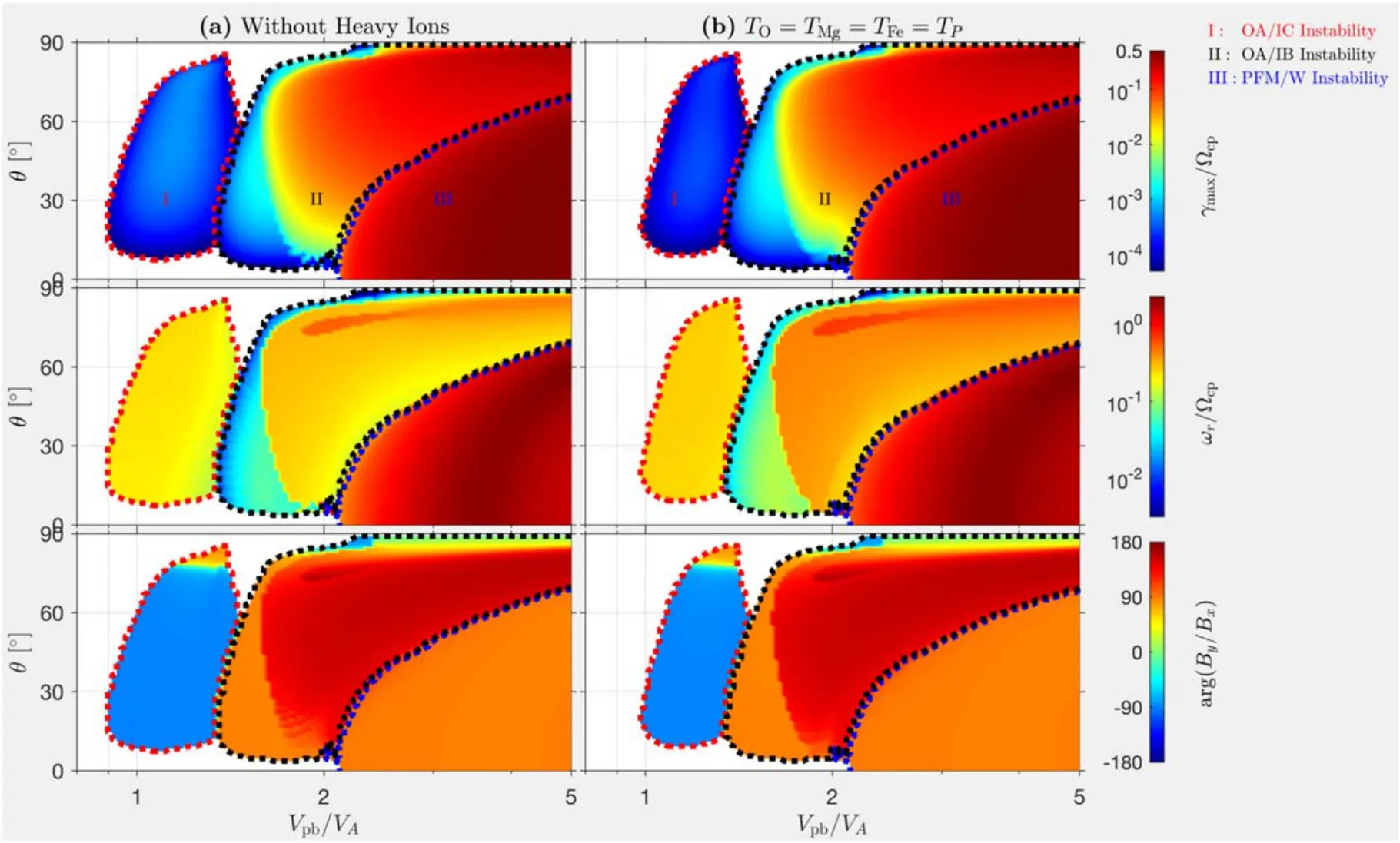
Figure 1.Vpb–θ distributions of the ion beam instabilities at r=3R⊙.(a)The plasma consists of proton core,proton beam,α particles and electrons;(b)three types heavy ions(oxygen ions,magnesium ions and iron ions)are added on the basis of case(a).All ions in two cases have same temperature.(Top panels)The maximum growth rate,γm ax; (middle panels)the real frequency ωr at γm ax ;(bottom panels)the argument of By/Bx at γmax.The regions controlled by OA/IC,OA/IB and PFM/W instabilities are denoted by I, II and III, respectively.OA/IC=oblique Alfvén/ion cyclotron; OA/IB=oblique Alfvén/ion beam; PFM/W=parallel fastmagentosonic/whistler.
We study ion beam instability in proton core frame which means Vpc=0.In order to be consistent with the observations,we not only consider the proton beam, but also consider other factors.For example, observed alpha particles and heavy ions are usually drifting faster than proton core component(Marsch et al.1982; von Steiger et al.1995; von Steiger &Zurbuchen 2006; Alterman et al.2018; ?urovcová et al.2019).Besides,the temperature of ions in the corona is usually proportional to their atomic mass number and they are strongly anisotropic, with Ti⊥>Ti//(Kohl et al.1997, 1998; Li et al.1998).Therefore, the differential speed with proton core and temperature anisotropy of heavy ions are taken into account.Here, we use drifting electrons to ensure zero current conditions, i.e., ΣisNisVis-NeVe=0, where “is” denotes each ion particle component.In addition,the temperature of protons and electrons are same.
3.Ion Beam Instability Analysis
3.1.Influence of Temperature Isotropic Minor Ions
In this part, we only consider the influence of the temperature isotropic heavy ions on the ion beam instability.Based on magnetic field and plasma parameters listed in Sub Section 2.2, the Vpb–θ distributions of the proton beam instability at r=3R⊙is exhibited in Figure 1, where θ represents the angle between the wave propagating direction and the background magnetic field.The plasma in Figure 1 consists of only proton core, proton beam, α particles and electrons in case(a)and all particles have the same temperature as protons; case (b) considers three additional heavy ions(oxygen ions, magnesium ions, and iron ions) and all particles have the same temperature as protons.Obviously,in both cases of Figure 1,only three types ion beam instabilities are excited.They are the oblique Alfvén/ion cyclotron instability (OA/IC,region I surrounded by red dots),the oblique Alfvén/ion beam instability(OA/IB,region II surrounded by black dots)and the parallel fast-magentosonic/whistler instability (PFM/W,region III surrounded by blue dots).Comparing case (a) and case (b) in Figure 1, we can see that the most obvious change occurs in region I, which is mainly manifested in the increase of excitation threshold (Vpbthre? 0.9V Ain case (a) andVpbthre? 1V Ain case (b)) and the decrease of excitation range.This indicates that the oblique Alfvén/ion cyclotron instability is most easily influenced by heavy ions.In a word,in a plasma where all particles have same temperature, the addition of temperature isotropic heavy ions will inhibit the excitation of the oblique Alfvén/ion cyclotron instability (reducing the parameter range of the instability excitation).
However, in actual observations of the solar corona, the temperature of ions is different and proportional to their atomic mass number (Kohl et al.1997, 1998).Besides, the remote observations from SoHO indicate that the heavy ions always flow faster than protons(Kohl et al.1997,1998).Therefore,we also take these two influence factors into account,respectively.The related results are shown in Figure 2.Considering that observed velocity of proton beam are usually concentrated in the region less than twice of the local Alfvén speed, the velocity of proton beam are limited in 0.1–2 VA.Compared with the results shown in Figure 1(b), the excitation of the oblique Alfvén/ion cyclotron instability, which is exhibited in Figure 2(a), will be further inhibited when ions have the temperature proportional to their atomic mass number.
In Figure 2(b), the temperature settings for all ions are the same as that in Figure 1(b).However, the α particles, oxygen ions, magnesium ions and iron ions flow faster than the core protons, and their relative drifting speed is the local Alfvén speed.Different from Figure 1(b), the excitation range of the oblique Alfvén/ion cyclotron instability has a significant change.There are two obvious excitation regions of the oblique Alfvén/ion cyclotron instability.This indicates that the addition of other four types ion beams will promote the excitation of the oblique Alfvén/ion cyclotron instability.In this case,there are five types ion beams(proton beam,α beam,oxygen beam,magnesium beam and iron beam)and all of them can become the energy source of excited instabilities.To figure out which ion beams are the main energy source of the oblique Alfvén/ion cyclotron instability, it is necessary to analyze its excitation mechanism, which is helpful to understand the energy transfer process therein.

Figure 3.Vpb–θ distributions of (a) total, (b) parallel, (c) perpendicular energy transfer rate in instabilities shown in Figure 2(b).These energy transfer rates are normalized by max(|Ps|),which corresponds to main energy flowing from the instability source particles into unstable waves.The top to bottom panels present energy transfer rates associated with proton beam, proton core, α particles, electrons, oxygen ions, magnesium ions and iron ions, respectively.The meaning of the dotted lines is same as that in Figure 2(b).The green labels“1”and“2”represent two regions of the oblique Alfvén/ion cyclotron instability.The regions marked by“+”represent normalized energy transfer rate is equal to -1, where the yellow “+” and cyan “+” represent the proton beam and α beam, respectively.
Hence, based on Equation (3), the energy transfer rate of all ions in the instabilities shown in Figure 2(b) is exhibited in Figure 3.In Figure 3, the energy transfer rates are normalized by max(|Ps|),which corresponds to main energy flowing from the instability source particles into unstable waves.Therefore,the color region representing -1, which is marked by “+” in Figure 3 (the yellow “+” and cyan “+” represent the proton beam and α beam,respectively),is the main source of the free energy required for instability excitation.The oblique Alfvén/ion cyclotron instability has two regions, one in the region of low proton beam speed (region 1, 0 ≤Vpb/VA≤0.5) and the other in the region of relatively high proton beam speed(region 2, 0.9 ≤Vpb≤1.5VA).The oblique Alfvén/ion cyclotron instability in region 1 is totally marked by cyan “+” and this indicates that the energy source of this unstable region is α beam.Similarly, the oblique Alfvén/ion beam instability region (surrounded by black dotted lines) is totally marked by yellow “+” and this means that its energy source is from proton beam.The oblique Alfvén/ion cyclotron instability in region 2 is relatively complicated.At relatively lager propagating angle (~50°–80°), the oblique Alfvén/ion cyclotron instability is totally excited by proton beam.The rest areas in region 2 are influenced by both proton beam and α beam,where the region marked by cyan“+”is dominated by α beam and the rest region is mainly controlled by proton beam.Generally, the oblique Alfvén/ion cyclotron instability in region 2 mainly dominated by proton beam.Obviously, when the proton beam is slowed down due to excitation instability,the existence of the α beam can provide the second energy source for the excitation of the instability in the solar corona.
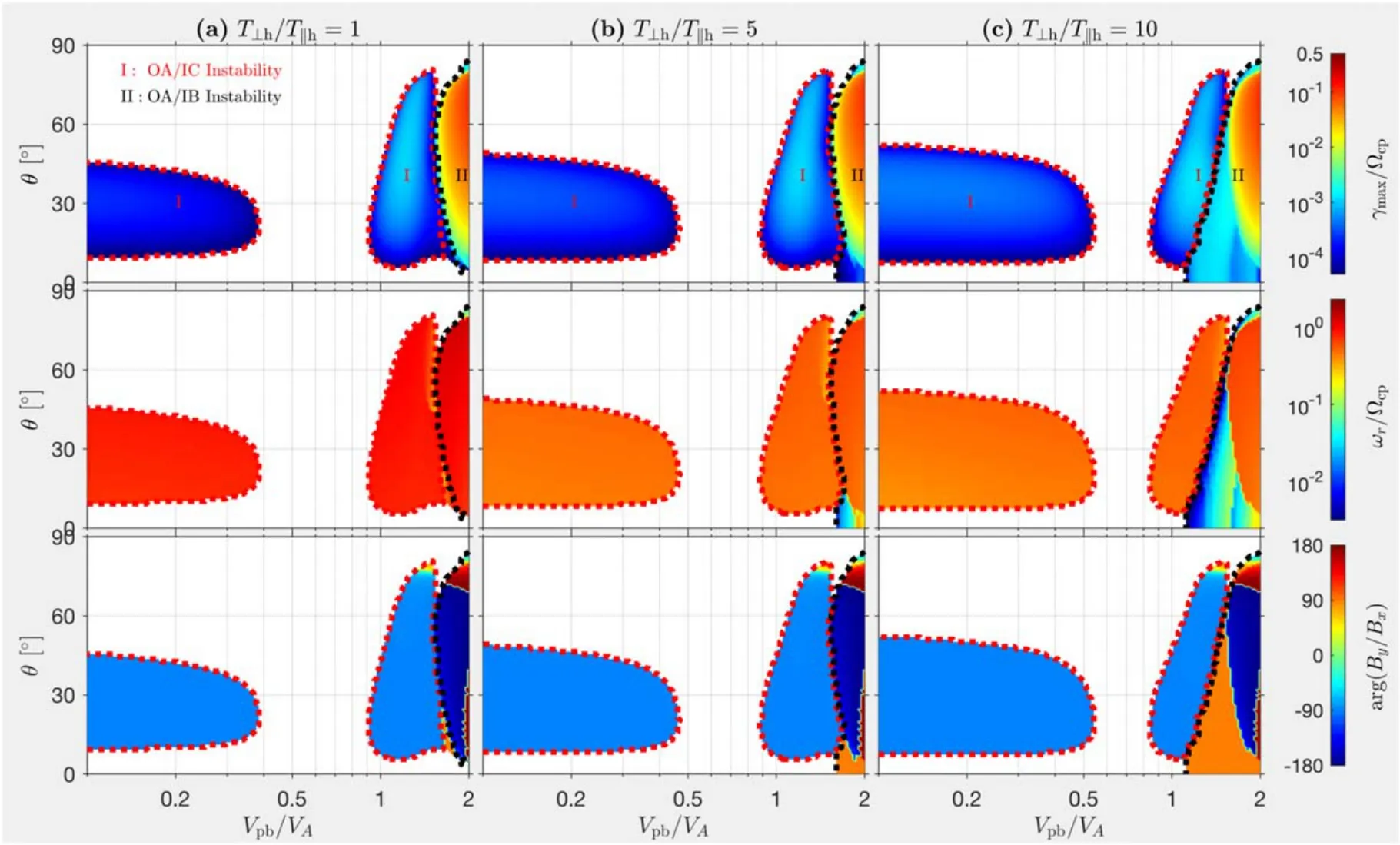
Figure 4.Vpb–θ distributions of the ion beam instabilities at r=3R⊙.The plasma consists of proton core,proton beam,α particles,electrons,oxygen ions,magnesium ions and iron ions.The temperatures of all ions are proportional to their atomic mass number,Tis=MisTp/Mp.The α beam,oxygen beam,magnesium beam and iron beam have a speed of the local Alfvén speed,Vαb=VOb=VMgb=VFeb=VA.The temperature of three types heavy ions(oxygen ions,magnesium ions and iron ions)is anisotropic, with Th⊥/Th//=(a) 1, (b) 5, (c) 10.Other labels are the same as those in Figure 2.
3.2.Influence of Temperature Anisotropic Minor Ions
In the solar corona, the remote sensing observations reveal that the effective temperatures of ions are strongly anisotropic,with Ti⊥>Ti//, where ⊥and //are respect to the background magnetic fields(Kohl et al.1998;Li et al.1998).Therefore,in this section,we perform instability analysis at parameters closer to the actual coronal plasma environment.The temperature of ions are proportional to their atomic mass number.In addition,α particles, oxygen ions, magnesium ions and iron ions flow faster than core protons with a relative speed of the local Alfvén speed.Moreover, the temperature of three types heavy ions (oxygen ions, magnesium ions, and iron ions) is anisotropic, with Th⊥/Th//=1, 5, 10.The instability results of three cases are shown in Figure 4.The instability results shown in Figure 4 are similar to Figure 2(b).Besides, the excitation parameter range of both oblique Alfvén/ion cyclotron instability and oblique Alfvén/ion beam instability becomes larger with the increase the temperature anisotropy of heavy ions.
In this case, ion beams and temperature anisotropy of ions both can provide free energy to excite instabilities.Hence, the same analysis as shown in Figure 3 is necessary.Due to the fact that three cases in Figure 4 are similar, we only use analysis case (c).The energy transfer rate results of Figure 4(c) are presented in Figure 5.The energy transfer rate shown in Figure 5 is similar to that in Figure 3.Both oblique Alfvén/ion cyclotron instability(in region 2)and oblique Alfvén/ion beam instability are mainly excited by proton beam.However, the energy source of the oblique Alfvén/ion cyclotron instability close to Vpb=0.9VAin region 2 is from anisotropic oxygen beam and α beam and the oxygen ions dominate.Besides, the excitation of the oblique Alfvén/ion cyclotron instability in region 1 is also driven by both anisotropic oxygen beam and α beam, and the contribution of oxygen ions is concentrated in regions with relatively larger proton beam velocity, while the contribution of α particles is the opposite.These results indicate that the anisotropic beams of heavy ions can also promote the excitation of the Alfvén/ion cyclotron waves in the actual coronal plasma environment.Hence, the instability driven by ion beams can be a very important source of the Alfvén/ion cyclotron waves in the corona.

Figure 5.Vpb–θ distributions of (a) total, (b) parallel, (c) perpendicular energy transfer rate in instabilities shown in Figure 4(c).The labels are same as those in Figure 3.The new label (the magenta “+”) represents the regions dominated by oxygen ions.
4.Discussion
Since remote observations revealed the unusually high temperature of the coronal ions (Kohl et al.1997, 1998;Cranmer & Winebarger 2019), finding out the main physical mechanism for heating coronal ions has been a fundamental problem in solar and space physics.Especially,the coronal ions are highly anisotropic, with Ti⊥>Ti//(Kohl et al.1997, 1998;Li et al.1998).This suggests that the heating process of coronal ions is anisotropic,in particular,that the heating is concentrated in the perpendicular direction with respect to the background magnetic fields.The cyclotron damping of Alfvén/ion cyclotron waves is usually used to explain this observed phenomenon(Cranmer et al.1999;Isenberg et al.2001;Liewer et al.2001;Marsch&Tu 2001;Hollweg&Isenberg 2002).In this paper,we find that proton beam and α beam can both drive oblique Alfvén/ion cyclotron instability to generate Alfvén/ion cyclotron waves.Especially, in the low beta plasma environment like the solar corona, the excitation threshold of ion beam instability is easily met.In addition, Jets associated with magnetic reconnection are injected into the coronal background environment,which can be the source of ion beam(Feldman et al.1996).Recently, Phan et al.(2022) found that the leaked high-energy protons during the magnetic reconnection process may be the source of the proton beam in the near-Sun solar wind.Through checking the velocity distribution function(VDF)of protons in Phan et al.(2022),we found that the proton beam generated by magnetic reconnection process usually has relatively high number density ratio.Verniero et al.(2020), Klein et al.(2021) also found that the number density of the proton beam in the near-Sun solar wind usually have higher number density ratio than that beyond 0.3 au.This may indicate that the number density ratio of ion beam can be higher when getting close to the Sun.Theoretically, the region of excitation parameters of ion beam instability increases with the increase of ion beam number density (Liu et al.2021).Therefore, based on these observed phenomena, we think that instabilities driven by ion beams can play an important role in energizing corona ions.
To better understand the energy transfer rate in the background plasma of corona, we find the Alfvén wave mode without any instabilities and give the energy transfer rate related to this wave mode.The results are shown in Figure 6,where λpk is the wavevector k normalized by the proton inertial length λp.Here, the plasma consists of all ions mentioned before.In addition, there is only one type ion beam (proton beam, Vpb=0.8VA) and all particles have the same temperature.In Figures 6(a)–(b), the Alfvén wave mode are divided into three regions by the cyclotron frequencies of iron and oxygen ions and the corresponding damping rates in these two places become larger suddenly.From Figure 6(d),We can see three peaks, from left to right, representing the energy absorption peaks of iron,oxygen and magnesium ions.Besides,the energy absorption of heavy ions are concentrated on the perpendicular direction.Therefore,heavy ions in corona can be heated perpendicularly through this process with the existence of excited Alfvén waves.This also suggests that the ion beam instability that excites Alfvén waves may play an important role in the process of coronal ion energization.
Through studying the ion beam instability in the coronal environment, this work mainly reveals that the ion beam instability is easily excited and is an important source of the Alfvén/ion cyclotron waves.This also indicates that the instability driven by ion beams may play an important role in energizing corona ions.However, the heavy ions are not preferentially heated in perpendicular during ion beam instability excitation.Actually, when ion beam instability is excited, the free energy of ion beams mainly follows into core protons and the unstable wave mode(the Alfvén/ion cyclotron wave).Finally, the energy of these excited Alfvén/ion cyclotron waves can preferentially heat heavy ions in perpendicular by wave-particle interaction process.Simulations can be used to study this entire process and we will present it in our future work.
5.Summary
Based on the plasma kinetic theory, this work mainly study the excitation of ion beam instability in corona at heliocentric distance ~3 R⊙and the corresponding energy transfer process therein.Our results indicate that the addition of the heavy ions will inhibit the excitation of ion beam instability, which is manifested in both its excitation threshold and parameter range.On the other hand, anisotropic beams of heavy ions can promote the excitation of the ion beam instability.Moreover,the existence of α beams can provide the second energy source for exciting beam instability in the corona.When both the proton beam and the α beam reach the instability excitation threshold, the proton beam driven instability excites preferentially.In addition, through the ion beam instability, the energy of ion beams mainly follows into core protons and unstable waves.Besides, the excitation threshold of the Alfvén/ion cyclotron instability driven by ion beam is of the local Alfvén speed or even less.This indicates that ion beams can easily excite Alfvén/ion cyclotron waves through ion beam instability process in the corona.Due to the fact that the Alfvén/ion cyclotron waves can energize corona ions through waveparticle interactions, the ion beam driven instability may play an important role in corona ion energization.
Acknowledgments
This work was funded by the National Natural Science Foundation of China (NSFC) under No.12347166.
ORCID iDs
Wen Liu https://orcid.org/0000-0002-8376-7842
 Research in Astronomy and Astrophysics2024年2期
Research in Astronomy and Astrophysics2024年2期
- Research in Astronomy and Astrophysics的其它文章
- A Fermi-LAT Study of Globular Cluster Dynamical Evolution in the Milky Way: Millisecond Pulsars as the Probe
- Application of Regularization Methods in the Sky Map Reconstruction of the Tianlai Cylinder Pathfinder Array
- Effect of Cosmic Plasma on the Observation of Supernovae Ia
- Variable Stars in the 50BiN Open Cluster Survey.III.NGC 884
- Free Energy of Anisotropic Strangeon Stars
- Data-driven Simulations of Magnetic Field Evolution in Active Region 11429:Magneto-frictional Method Using PENCIL CODE
