The Precursor of GRB211211A: A Tide-induced Giant Quake?
Enping Zhou, Yong Gao, Yurui Zhou, Xiaoyu Lai, Lijing Shao , Weiyang Wang, Shaolin Xiong, Renxin Xu,Shuxu Yi, Garvin Yim , Han Yue, and Zhen Zhang
1 School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China; ezhou@hust.edu.cn
2 Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, China
3 School of Physics, Peking University, Beijing 100871, China
4 Research Center for Astronomy, Hubei University of Education, Wuhan 430205, China
5 University of Chinese Academy of Sciences, Beijing 100049, China
6 Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
7 School of Earth and Space Sciences, Peking University, Beijing 100871, China
Abstract The equilibrium configuration of a solid strange star in the final inspiral phase with another compact object is generally discussed, and the starquake-related issue is revisited, for a special purpose to understand the precursor emission of binary compact star merger events(e.g.,that of GRB211211A).As the binary system inspirals inward due to gravitational wave radiation,the ellipticity of the solid strangeon star increases due to the growing tidal field of its compact companion.Elastic energy is hence accumulated during the inspiral stage which might trigger a starquake before the merger when the energy exceeds a critical value.The energy released during such starquakes is calculated and compared to the precursor observation of GRB211211A.The result shows that the energy might be insufficient for binary strangeon-star case unless the entire solid strangeon star shatters,and hence favors a black hole-strangeon star scenario for GRB211211A.The timescale of the precursor as well as the frequency of the observed quasi-periodic-oscillation have also been discussed in the starquake model.
Key words: stars: neutron – (stars:) gamma-ray burst: general – black hole physics
1.Introduction
It is well known that the puzzling nature of pulsar’s interior is essentially relevant to the fundamental strong interaction at lowenergy scale, the challenging non-perturbative quantum chromodynamics (or strong QCD Epelbaum et al.2009), but this unknown state could be the first big problem to be solved in the era of multi-messenger astronomy(Baiotti 2019).Besides the conventional neutron star (NS) model, pulsars are proposed alternatively to be solid strange stars(Xu 2003)(or strangeon stars),and we are then developing a strangeon star model in order to understand extreme and mysterious events in astrophysics.Certainly, quakes can naturally occur on solid strangeon stars, and a giant quake model has already been proposed for the super-flares of isolated soft γ-ray repeaters(Xu et al.2006).Furthermore, tide-induced quakes in binary have also been discussed,appearing as so-called a sudden change in the tidal deformability at a certain breaking frequency of gravitational wave(GW)(Lai et al.2019).Can tideinduced quakes be manifest in the electromagnetic (EM) wave?This is our focus here,and luckily,the precursor of GRB211211A could be a typical example.In the future, more such events,especially combined with the LVK-O4 observing run (e.g.,Coupechoux et al.2023), would surely be expected.
Without doubt, the observation of GW170817(The LIGO Scientific Collaboration & The Virgo Collaboration 2017)together with its EM counterparts GRB170817A and AT2017gfo(The LIGO Scientific Collaboration et al.2017) has announced the birth of the multi-messenger astronomy era.This event has largely enriched our knowledge on the nature of short gamma-ray bursts(sGRB)(Narayan et al.1992;LIGO Scientific Collaboration et al.2017), the state of matter at supranuclear densities(Bauswein et al.2017; Margalit & Metzger 2017;Rezzolla et al.2018;Ruiz et al.2018;Kiuchi et al.2019;Shibata et al.2019) as well as the origin of heavy elements in the Universe(Eichler et al.1989; Abbott et al.2017).The EM counterparts have been detected in almost every band from radio to gamma-ray,however,these observations all happen during the post-merger phase.As an implementation, EM signals prior to the merger (i.e., the precursor observation Troja et al.2010), if detected, could significantly improve our understanding of the properties of the merging objects, as well as improve the detection and localization of the following GW signal.
Interestingly, 2021 December 11th, a very peculiar gammaray burst (GRB) has been detected by Fermi/GBM(Mangan et al.2021), Swift/BAT(D’Ai et al.2021) and Insight-HXMT/HE (GRB211211A)(Zhang et al.2021).An excess in optical/near-infrared has been identified, the multi-band properties of which are quite similar to those of AT2017gfo(Rastinejad et al.2022; Xiao et al.2022).Together with the non-detection of a supernova at the GRB location,this GRB is suggested to be associated with merger event involving an NS,though the duration of the main emission is relatively longer(~8 s)compared with typical sGRBs.More intriguingly,a fast rising and exponentially decaying precursor has been observed approximately 1 s prior to the main emission.The precursor lasts for ~0.2 s and a quasi-periodic-oscillation (QPO) with frequency ~22 Hz has been identified in it (Troja et al.2022;Xiao et al.2022).
Following this interesting observation, various models have been suggested to explain the precursor of GRB211211A.Previous force-free simulations of NS magnetosphere have shown that the interaction of the magnetic fields of two inspiralling-in NSs could produce Poynting flux strong enough to be observed as precursor emissions (Carrasco & Shibata 2020).If a magnetar is involved in the merger event, a catastrophic flare of the magnetar during the inspiral phase could also be the source of the precursor (Xiao et al.2022;Zhang et al.2022).In addition, a resonant shattering of the solid crust of the merging NSs is also invoked to explain the observation,with certain demands on the NS spin and magnetic field (Suvorov et al.2022).
In this paper,we come up with a starquake model to explain the precursor of GRB211211A based on a solid strangeon star scenario, in which the energy budget could be satisfied regardless of the spin and magnetic field strength of the merging NSs.In this model, the equilibrium configuration of the solid compact star changes as the binary gets closer in the inspiral stage and tidal field of the companion becomes stronger.Stress will be accumulated as the elastic structure resists the change in the configuration.Eventually, the elastic strain might exceed a critical value before merger and the solid structure of the star cracks (i.e., a starquake happens).Thus, a precursor will be triggered by energy released during the starquake and the reconfiguration of the star.
The paper will be organized as the follows:in Section 2,we will introduce the configuration of a solid strange star in the tidal field of its companion;a quantitative comparison with the observation will be made in Section 3; future observational prospects of this scenario will be discussed in Section 4.
2.The Model
2.1.Equilibrium Configuration of a Solid Strange Star in Close Binary
The equilibrium configuration of a solid strange star in the tidal field of its companion is determined by the bulk energy of the star Etotal, which consists of several parts,
in which Ekis the kinetic energy of the star when rotation is considered, Egstands for the additional gravitational binding energy of the star,Eelais the elastic energy accumulated and Etis the energy possessed by the star due to the tidal field of its companion.
It is believed that an NS spins slowly before merger due to magnetic dipole radiation during the long inspiral stage.Moreover, it has been shown that the tidal interaction is insufficient to synchronize the NS spin before merger(Bildsten&Cutler 1992).Hence,it is reasonable to assume that both Ekand the change in Ekare negligible before merger.
Egand Etare related to gravity,and it is necessary to define a zero energy configuration as a reference.In the following, we will assume the spherically symmetric configuration to possess energy E0.In binary systems, however, the shape of the star will no longer be spherical and it is useful to define the shape of the star by the parameter of reduced ellipticity
in which I is the moment of inertia of the star with respect to the axis of the deformation and I0is that of the spherical star with the same baryonic mass.It is worth noting that,in the case of a rotating star,the star is flattened with respect to the rotation axis and ?will be positive.For tide-induced deformation, the star will be prolonged along the direction where the companion is.Hence, ?will be negative.For the consideration of this calculation, rotation effect is negligible as mentioned before and the principal axis is chosen to be the direction of the companion.For incompressible star and small ellipticity, ?is related to the geometrical eccentricity of the star (e) as?=-e2/3.With this definition, one can obtain
in which M and R are the mass and radius of the star,Mcis the mass of its companion,D is the separation of the binary system,Atand Agare coefficients related to gravitational binding energy which depend on the density distribution of the star.In the case of an incompressible star (which is a good approximation for strange stars), the following relation holds
and
in which κ is a dimensionless constant of order of unity.Ideally κ=3/5, but may vary due to the fact that the tide-induced deformation may not be perfectly along the direction of the companion or density structure of the star.For simplicity, we will use the notation A=GM2/R in the expressions below and A ~1×1054erg for typical NS value M=1.4 M⊙and R=10 km.
The elastic energy Eelais related to difference between the reference ellipticity ?0when the star solidified (for example,when the star suffers the previous starquake) and the current value ?.According to Hooke’s Law, one can obtain
Collecting all the ingredients we have
and the ellipticity of equilibrium configuration could be obtained by minimizing the total energy which requires?Etotal/??=0.Thus, we could obtain the reduced ellipticity
For a purely fluid star (or for a solid star when starquake happens,to reconfigure itself),the equilibrium ellipticity is then
It is worth noting that the solid star tends to resist from being deformed due to the accumulation of elastic energy.Hence, if the star was at its fluid equilibrium configuration before the previous solidification, then at any time during the later evolution, we should have ?>?eq,fl(note that ?is negative).Additionally, the tidal interaction becomes stronger as the binary gets closer during the inspiral stage,the ellipticity of the star would increase with time,so we could obtain the following inequality which holds during the entire inspiral stage
Previous calculation and observations indicate that the shear modulus of a strange star μ lies in the range between 1030and 1034erg cm-3(Xu 2003; Zhou et al.2004).Within this range,the value of B would be much smaller than A.Combining the inequality Equation(10),one could obtain that the second term in Equation (8) is negligible compared with the first term.Therefore, we will omit the second term in Equation (8) in the calculations below and assume the equilibrium configuration of a solid strange star satisfies
2.2.The Starquake Model
Equation (11) indicates how the ellipticity of the solid strange star increases as the separation of the binary shrinks during the inspiral stage, due to the dissipation of angular momentum and energy through GW radiation.Elastic energy gradually increases as the shape of the solid star changes.Depending on the microscopical model of the solid strange star,the maximum stress of the solid structure might be reached before the merger happens and hence a starquake takes place.During the starquake, the ellipticity of star tends to migrate from its solid equilibrium configuration (?eq,so)to its fluid case(?eq,fl).Therefore, not only the elastic energy but also the change in Eg+Etwill be released during the starquake as they are related to the ellipticity.This starquake scenario is quite similar to the starquake model of pulsar glitches(Baym &Pines 1971; Zhou et al.2004, 2014; Lai et al.2018).In the latter case, the accumulation of the elastic energy (i.e., the change in the ellipticity) is due to the change of pulsar spin,which results from the magnetic dipole radiation of pulsars.
We will first calculate the change in Eg+Etbefore and after the starquake.The change of the reduced ellipticity is the difference between ?eq,fland ?eq,so:
According to the feasible range of μ,B is at least two orders of magnitude smaller than A and hence we have δ?<0.1?eq,fl.Therefore, we could estimate the change in Eg+Etby an expansion with respect to ?:
However, ?eq,flis obtained by requiring ?(Eg+Et)/??=0.Consequently, the non-vanishing parts of Eg+Etare terms of δ?2and higher order ones and hence are negligible.Similar conclusion is found for the case of starquake scenario of pulsar glitches(Zhou et al.2014).As a result, the major contribution of energy release during such starquake is the release of the accumulated elastic energy before the starquake:
in which D0is the separation of the binary system when the solid strange star experienced its previous solidification.As the precursor happened very close to the merger (i.e., when the orbital separation shrinks rapidly), it is reasonable to make the following assumption D0?D.In addition, we remind that A ?B, then the elastic energy is approximately
It is easy to verify that the total change in Eg+Etis indeed~10%of Eelaat most and we will focus on Equation(15)when comparing with the observation in the next section.
3.Results
3.1.Energy Budget
The origin of GRB211211A is still under debate.Scenarios including binary neutron star (BNS) merger(Kunert et al.2023), black hole–neutron star (BH–NS) merger(Zhu et al.2022) as well as neutron star–white dwarf merger(Yang et al.2022) have been proposed.In this section, we will focus on BNS and BH–NS merger scenarios and test their feasibility and parameter space in producing the observed precursor within the starquake scenario.
The major difference between BNS and BH–NS merger scenarios is their mass ratio Mc/M and the orbital separation D when the starquake happens.For the BNS scenario, the most mass-asymmetric BNS system observed and the mass of which is precisely measured has mass ratio q=0.78 (Ferdman et al.2020).GW190425 was measured to have an even smaller mass ratio of 0.7, whereas it is still uncertain that whether its heavier component is an NS or a BH(The LIGO Scientific Collaboration et al.2020).Even though there are equation of state (EoS)models for solid strange stars which could reach maximum mass as high as above 3 M⊙(Lai&Xu 2009),this could merely push the possible range of q to about 0.5 (or, Mc/M ~2.0 when we consider the lighter star suffers the starquake).
For the BH–NS merger case, the range of the binary mass ratio could be much wider.GW observations indicate that MBH/MNScould be as small as 2.0, if heavier components of those mass gap events are indeed BHs.The upper limit for MBH/MNSfor the event GRB211211A should be constrained by the observation of associated kilonova.If the mass of the BH is too much larger than NS, the ejected mass from the NS would be insufficient for powering a kilonova even with an extreme BH spin.According to previous studies,we put 10.0 as a maximum possible value for MBH/MNS(Kyutoku et al.2015;Kawaguchi et al.2016).In the analysis below,we will assume Mc/M to be in the range of [2.0, 10.0] for the BH–NS merger scenario.
The orbital separation D when the starquake happens could be implied by the time when the precursor happens.For GRB211211A, the time between the precursor and the main burst is approximately one second, which means the starquake happens less than one second before merger happens as there might be time delay between the actual merger and the time when jet is launched (for instance, for the BNS merger GW170817, the time delay between the merger and sGRB is approximately 1.7 s).For BNS system this indicates an orbital separation D<~100 km according to Figure 1.For the BH–NS system the possible range of D is larger (i.e., could be as large as ~300 km), due not only to a wider range of the mass range, but also to BH spin which could affect the dynamics of the final inspiral phase.Particularly, extreme spin is necessary for significant mass ejection to take place for BH–NS system with large mass ratio.
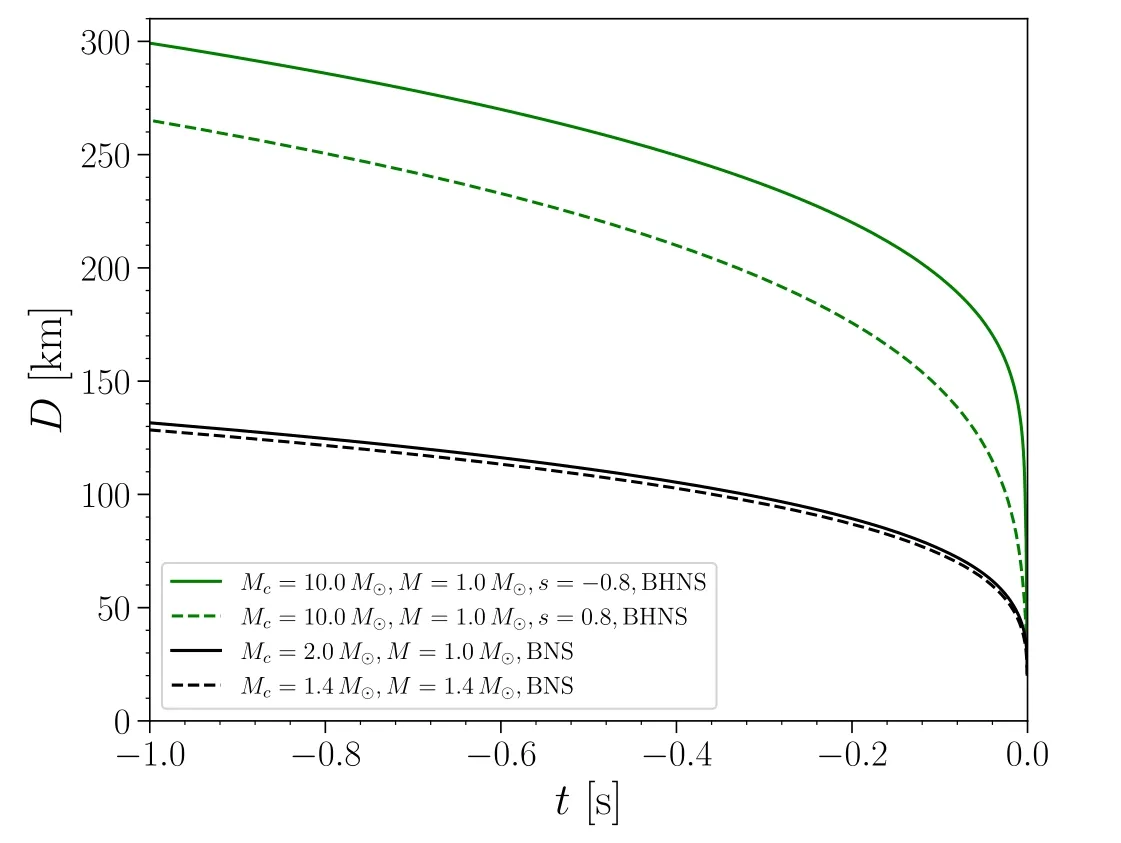
Figure 1.The evolution of the orbital separation D prior to the merger (the merger time is calibrated to t=0 in this figure) for BNS and BH–NS cases,obtained by effective-one-body (EOB) calculations(Damour & Nagar 2014;Nagar et al.2016, 2018, 2020a, 2020b; Riemenschneider et al.2021).The green solid and dashed curves on the top represent the BH–NS merger scenario with Mc/M=10 and BH spin of -0.8 (i.e., anti-aligned with the orbital angular momentum) and 0.8, respectively.The black solid and dashed curves on the bottom stand for the BNS merger cases with Mc/M=1.0 and 2.0,respectively.
For the BNS case, inserting the value of 50 km for D and unity for κ,one can obtain the total elastic energy contained in the entire star as the following
For the observation of GRB211211A, the energy released in the precursor in the form of electromagnetic emission is~7.7×1048erg which means the total energy released should be larger than this value.Therefore, the energy budget is very tense for explaining the precursor in the BNS case, unless the solid structure of the entire star shatters and the starquake has to happen at a closer range with the jet launching being delayed after the merger.Alternatively, one can count on a very massasymmetric merger with Mc/M as large as 2.0.Nevertheless,even in this case, the total elastic energy is not enough if D is larger than 100 km when the starquake happens.
The detailed result is shown in Figure 2.Even if we allow for a global starquake during which the elastic energy of the entire star is released and all converted into precursor EM emissions,the orbital separation at the moment of this starquake has to be smaller than ~60 km for an equal mass BNS merger.This upper limit on D could be relaxed to ~75 km if we consider extreme mass ratio cases.Nevertheless, as mentioned above,such global starquake is less likely to happen and a partial starquake which releases 10%of the elastic energy contained in the star is not possible unless the starquake happens at a binary separation less than 50 km and with large mass ratio.
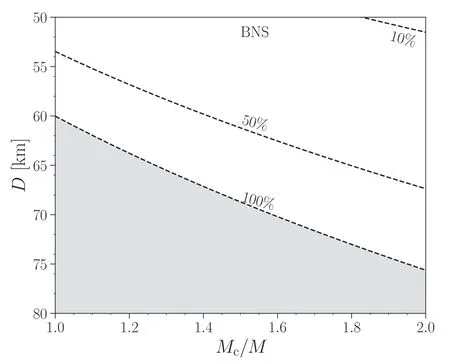
Figure 2.Constraints on the binary parameters according to the precursor observation of GRB211211A in the BNS case.Three dashed lines labeled by 100%, 50% and 10% represent the combination of the mass ratio Mc/M and orbital separation D when the starquake happens with which the corresponding percentage of the total elastic energy has to be released in order to explain the energy of the precursor observation.The gray shaded region is excluded since more than 100%of the total energy budget is required(and hence insufficient).If we consider that partial failure of the solid structure(i.e.,less than 10%of the elastic energy is released)is more realistic,the possible parameter space is very narrow unless the starquake happens extremely close to the merger (D smaller than 50 km).
Compared with the BNS case,the BH–NS merger scenario is more favored considering the energy budget due to a larger possible Mc/M.Ten percents of the total elastic energy converting into EM emission would be enough for the observed precursor luminosity.According to previous researches, it is shown that elastic energy is not uniformly accumulated throughout the solid star when deformation is induced.Partial failure in the solid structure is also demonstrated to be more reasonable to explain the observation of pulsar glitches(Lai et al.2018).In our case,the deformation is induced by the tidal field of the companion of a solid strange star.Consequently,the stress is expected to be the largest near the surface of the star,especially near the polar and equatorial region.Thus a small fraction of the solid star shatters and releases the elastic energy in this region is a more natural scenario.Indeed,there would be larger uncertainties in inferring the orbital separation by the time before merger for the BH–NS case.Therefore, we treat D as a free parameter and explore the possible combination for D and Mc/M for different amount of elastic energy required.
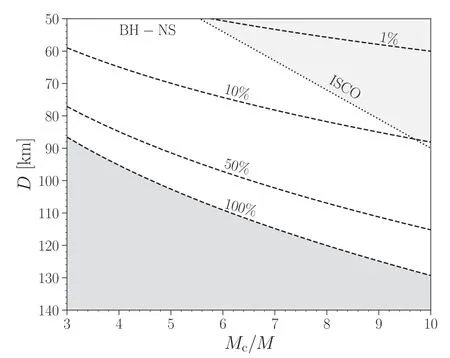
Figure 3.Constraints on the binary parameters according to the precursor observation of GRB211211A in the BH-NS case.Three dashed lines are plotted in the same way as in Figure 2.The darker bottom left gray shaded region is excluded according to the energy budget whereas the lighter gray shaded region on the top right is inside the ISCO of the BH companion(assuming that the mass of the NS is 1 M⊙and the BH is a Schwarzschild BH)and hence is excluded.Nevertheless,the ISCO of a spinning BH can be much smaller than that of a Schwarzschild BH and parameters in this region could as well be possible,as extreme spin is essential for sufficient mass ejection in the case of large mass ratio BH–NS mergers.
The results for the allowed parameter space of the BH–NS case are shown in Figure 3.As the larger allowed mass ratio benefits the accumulation of elastic energy, the separation of the binary could be as large as ~100 km when the starquake happens if we allow for a 100% release and conversion of the elastic energy.There is still plenty of possible parameter space even if we consider a partial (10%) elastic energy release for orbital separation D ~60 km.For even smaller fraction (such as 1% case), the binary separation at which the starquake happens lies inside the innermost stable circular orbit(ISCO)of a Schwarzschild BH with the same mass of the BH companion.However, as mentioned above, large spin is needed for large mass ratio (Mc/M ~5) BH–NS merger to produce a kilonova and the ISCO radius of a Kerr BH could be much smaller than that of the Schwarzschild case.Consequently,it is still possible for a tiny starquake to happen at such small separation and account for the precursor observation of GRB211211A.
3.2.Sequential Starquakes During the Insipiral
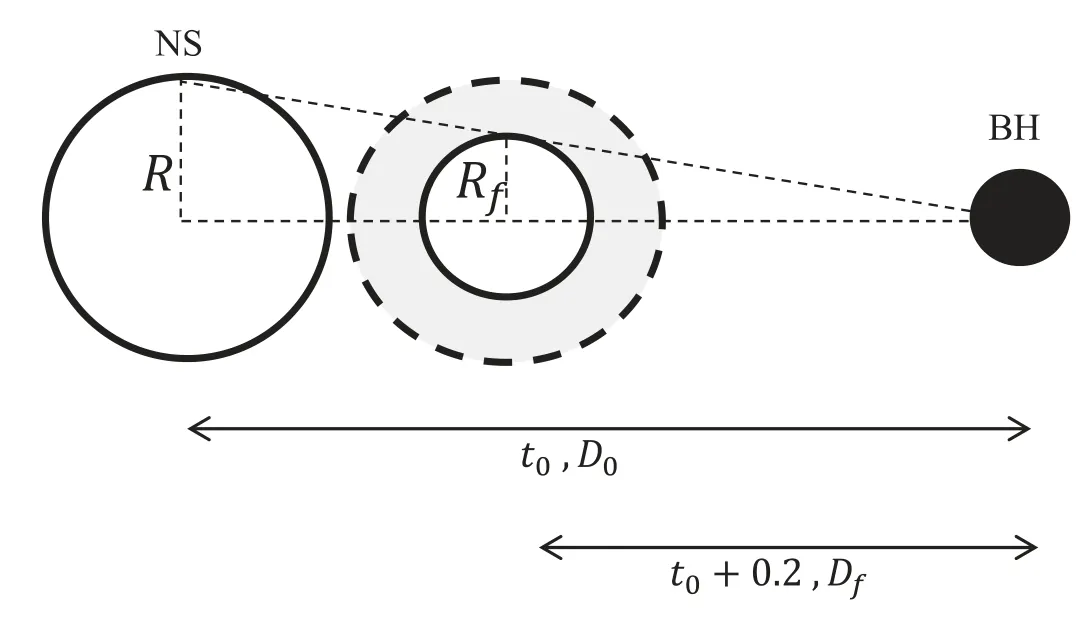
Figure 4.An illustration of the sequential starquake model as discussed in Section 3.2.The first starquake happens at t0 with binary orbital separation D0.After that, sequential starquakes take place with increasing depth inside the solid strange star, as the binary gets closer.At a later time (for instance,t0+0.2 s), only the matter inside a sphere with radius Rf could maintain its solid structure, with Rf approximately satisfies the following relation:Rf/Df=R/D0.The gray shaded region illustrates the part of star of for which the elastic energy could be released during this sequential starquake.
The above discussion is based on the assumption that the deformation induced is homogeneous in the entire star and only one starquake happens prior to the merger, which could either be a global quake or a local one.Nevertheless, the later in the inspiral stage, the faster the binary orbit shrinks (see Figure 1)and hence the elastic energy is accumulated much more rapidly.Moreover, the ellipticity induced by the tidal field increases as(R/D)3which suggests the deformation of the star is larger in its outer part for a realistic star(i.e.,which could not be incompressible)at a fixed separation.With these considerations, it is more likely that several sequential starquakes take place during the last of the inspiral phase, if the first starquake is a partial one.However,in this case elastic energy is partially released and we focus on the BH–NS scenario in this section,due to its larger parameter space.
Our sequential starquake model is demonstrated in Figure 4.The first starquake takes place at a separation of D0for the binary at time t0.As the deformation is largest in the outer part,only the surface part of the star suffers the quake(for instance,the region from R-δR to R, in which δR is the depth of this starquake).At a later time tf,the binary would be separated at a smaller distance of Df, and a shell of the star at a radius of Rfwould experience the same deformation as those at the surface of the star at the separation of D0, in which Rfis simply determined by the geometrical relation Rf/Df=R/D0.Thus,the matter at Rfmeets its limit for a failure in its elastic structure.In this case, several individual starquakes take place during the time t0to tf,from the surface of the star to the depth of R-Rf.
The observations of the precursor of GRB211211A indicate that the energy is released in several individual bursts with decaying peak amplitude in a time span of ~0.2 s,which is also the origin of the 22 Hz QPO.Such a feature could be well explained by a sequential starquake model: those later starquakes happen deeper inside the star and consequently the energy release tends to be diffused more slowly and hence the peak flux observed would be lower.
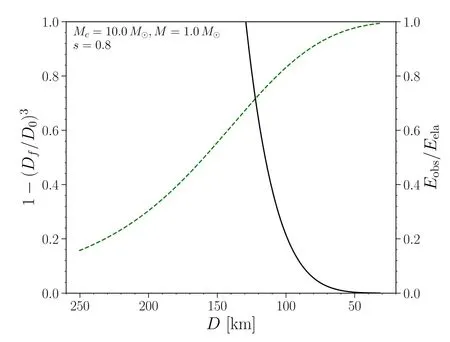
Figure 5.Constraint on the binary separation when the last quake takes place in the sequential quakes scenario.The mass ratio and BH spin is Mc/M=10 and s=0.8 for this model.With the green dashed curve we plotted the fraction of the volume of the star which suffers starquakes in the duration of 0.2 s(1 - (D f D0 )3), which is equal to the fraction of elastic energy released,assuming a uniform shear modulus.The black curve shows the ratio between the observed precursor energy and the total elastic energy (Eobs/Eela).The intersection point then sets up an upper limit for the parameter Df.
In such a model, the fraction of elastic energy released during the sequential starquakes over a certain duration depends on the binary separation of the first/last quake.As a result, in the sequential starquakes scenario, there will be additional constraint on the parameter space.The fraction of the elastic energy released in 0.2 s could be obtained as
in which Eelaalso depends on Dfas in Equation (16).Therefore, given the mass ratio and BH spin, D0could be determined by the EOB model and hence Ereleasecould be obtained.The fact that the energy released has to be greater than the observed value then sets a constraint on Df.
The result is shown in Figures 5 and 6, in which we have chosen the case of Mc/M=10 and 3, respectively.As mentioned above, for larger mass ratio case, large BH spin is also essential(Kyutoku et al.2015;Kawaguchi et al.2016)and we have chosen s=0.8 for the dimensionless spin for the Mc/M=10 case.For smaller mass ratio, we have explored three different BH spin(s=0,0.4 and 0.8)parameters to verify its impact on our results.Our result shows that a constraint is not very sensitive on the BH spin and upper limit for Dfis approximately 120 km for Mc/M=10 and 75 km for Mc/M=3, which are all much larger than the ISCO radius.It is worth noting that, if one assumes a certain energy conversion efficiency(η)from the released elastic energy to the
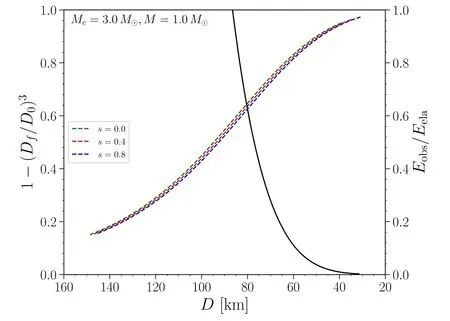
Figure 6.The same as Figure 5 but for a mass ratio of Mc/M=3.In this case we have also explored different values of BH spin to check its influence on our analysis,the green dashed curve,red dashed curve and blue dashed curve stand for the cases of s=0, 0.4 and 0.8, respectively.
EM emission, a tighter constraint could be made by requiring
which could be read from the result figures once a value of η is assumed.
In this model,the rising timescale of the precursor could also be understood.The change in the ellipticity of the star after the first quake happens approximately in a free falling timescale as
The timescale is larger for smaller mass ratio case as Mc/D0becomes smaller according to the analysis above.In the Mc/M=3.0 case, the above formula yields a rising timescale of ~0.8 ms, which is consistent with the observations.
In addition, the QPO frequency in the observation of the precursor of GRB211211A could also be naturally understood as the number of quakes during the entire process within 0.2 s.However,the number of quakes and the energy released in each quake in the entire sequential process depend on the thickness of the shells which suffer the failure of the solid structure during each quake.The thickness of the shattered shells could be very sensitive to properties which are difficult to predict such as crystal defects in the solid structure which might be caused during previous quakes.Hence, the observational properties (i.e.,the QPO frequencies)could be totally different even for sources with similar binary parameters.
3.3.Quake-induced Oscillation?
The enormous energy released during a tide-induced giant quake may set the entire star into vibration, producing oscillations at frequencies determined by the structure and elastic properties of the solid strange star.Typically,non-radial oscillations of solid stars include spheroidal and toroidal modes.Toroidal(torsional)modes are a type of oscillation that maintains the star’s shape.They are purely shear oscillations.QPOs following giant flares in soft gamma-ray repeaters and anomalous X-ray pulsars indicate the shear motion of the star after a giant quake(Duncan 1998; Watts & Strohmayer 2007).The spheroidal oscillations refer to waves that change the shape of the star, involving both radial and tangential displacements.These can be easily excited in a tidally induced starquake.Both types of oscillations have been observed in large earthquakes(Benioff et al.1961; Park et al.2005).Furthermore, these modes couple more easily with external magnetic fields than modes coming from the deep interior of the star.For these reasons, we expect that the tide-induced torsional modes may couple with Alfvén waves along the magnetospheric field lines,resulting in the QPO in the precursor of GRB211211A.
We denote (ξr, ξθ, ξφ) as the displacement amplitudes in spherical coordinate.To estimate the frequencies of toroidal and spheroidal modes, we model the solid strange star as a homogeneous, isotropic elastic sphere with uniform density and shear modulus.
The toroidal oscillations are divergence free with no radial components.For a particular eigenmode denoted by l and m,the separation of variable for the displacements takes the form(McDermott et al.1988)
where Ylm(θ,φ)are spherical harmonics.Inserting Equation(20)into the shear wave equation, we obtain the following equation for the radial eigenfunction W(r) (McDermott et al.1988)
where ρ and μ are the star’s density and shear modulus respectively.The torsional modes are referred by the notationntl, where n is the overtone number of radial nodes in the eigenfunction W(r).In this paper, we focus on the nodeless vibrations with n=0.By applying the boundary condition of vanishing surface horizontal traction, we can solve the eigenvalue problem analytically(Lamb 1881), obtaining the eigenfrequency
Here v=(μ/ρ)1/2is the shear speed,Clis a constant depending on l.The fundamental mode of torsional oscillation is0t2because0t0has zero displacement and0t1describes a constant azimuthal twist of the entire star, which does not exist for free oscillation.
We denote the spheroidal mode as0sl.The separation of variable for the displacement can be written as
Combined with perturbation in the gravitational potential, we can obtain the systematic differential equations governing the oscillation.We refer the readers to McDermott et al.(1988),Crossley(1975),Alterman et al.(1959)for those equations.To simplify the calculations and represent the eigenfreqeuency in a simple relation to the shear speed,we use the long wavelength approximation.The eigenfrequency of nodeless modes is
The oscillation of order l=1 does not exists, and the fundamental mode of the global nodeless spheroidal oscillation is0s2.
Both the strong and the electromagnetic interactions are involved in characterizing the shear modulus, μ, of solid strange matter.One may have μ ~1034erg cm-3if the strong force dominates the shear mode Xu (2003).In the catastrophic process of the tide-induced giant quake, the star may be fractured as a whole and release enormous energy.The modulus could be decreased after the fracture.
From Equations (22) and (24), we obtain the fundamental frequencies for the torsional and spheroidal modes
Here we take M=1.4 M⊙and R=10 km.There is one thing to be clarified, here we are discussing about the quake-induced oscillation modes, which are modes propagating in a solid star after the starquake.Therefore, the shear modulus involved in the calculation has to be smaller than that before the starquake which is applied in the calculations in Section 3.One can notice that the mode frequency is on the same order of the QPO frequency observed in GRB211211A if the shear modulus of the solid strange star decreases to the order of 1030–1031erg cm-3.In the mean time, the required shear modulus after the starquake is much smaller (i.e., 3 orders of magnitude smaller)than those applied before the starquake,and hence has only negligible influence on the calculation of the energy budget.As a conclusion, the model is capable of explaining the energy budget and QPO frequencies at the same time.In Figure 7, we show the fundamental frequencies with l=2, 3, 4 as functions of the shear modulus.
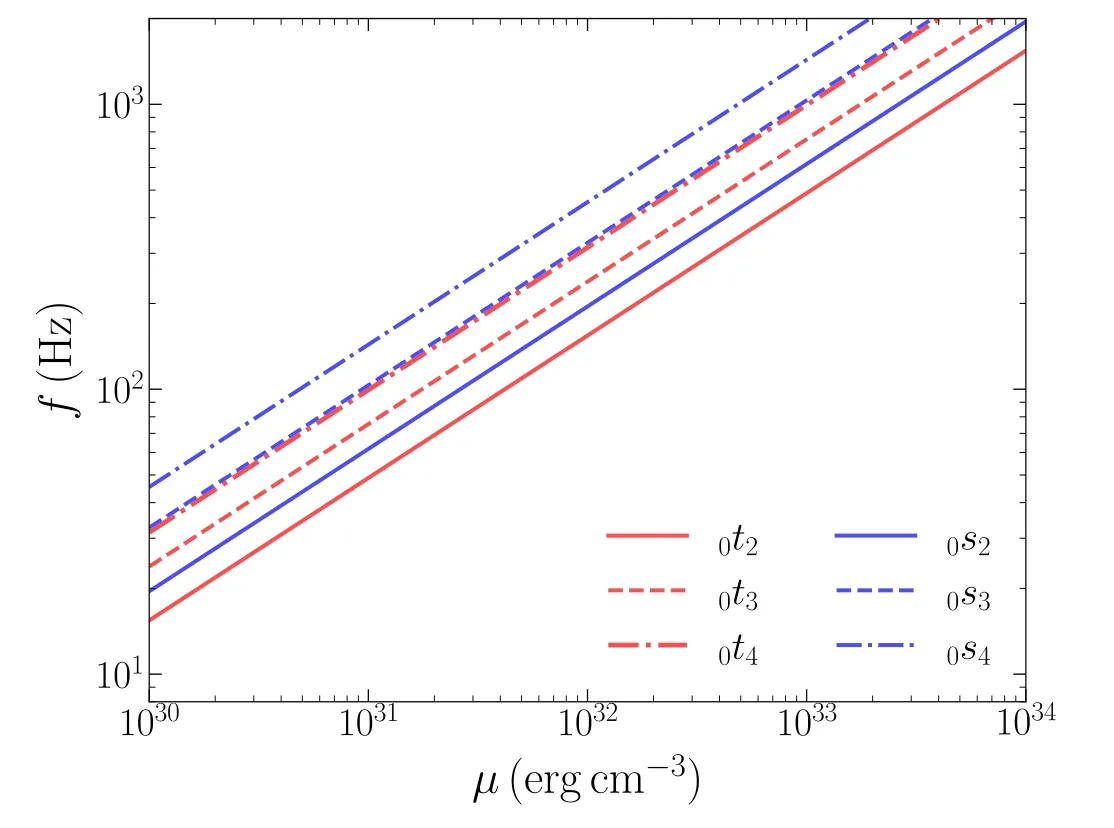
Figure 7.The relation between eigenfrequencies of the fundamental modes of the torsional and the spheroidal oscillations.We show the cases with l=2,3, 4.
In reality,the frequency of a mode will be shifted due to the effects of gravitational redshift and the Doppler effect.The gravitational redshift factor caused by the NS can be expressed as
where M and R represent the mass and radius of the NS,respectively.For example, assuming an NS with a mass of 1.4 M⊙and a radius of 10 km, the gravitational redshift factor is 0.306.
To estimate the redshift factor caused by the binary system,we neglect the spin of the companion and crudely treat the NS as a test particle.We assume that the observer is located in the orbital plane and at an orbital phase of φ=0 when the NS is closest to the observer.We select several special points to discuss the frequency shift.At φ=0, π, the redshift factor is given by:
where Mcrepresents the total mass of the binary system,and D represents the separation of the binary system.This equation takes into account both the gravitational redshift and the transverse Doppler effect caused by the motion of the NS in the binary system.
At φ=±π/2, the redshift factor for the binary system is given by
For a binary system with Mc=10 M⊙,D=100 km,M=1.4 M⊙,and R=10 km, the redshift factor zbinary(φ=0)=zbinary(φ=π/2)=0.34, zbinary(φ=π/2)=0.95, and zbinary(φ=-π/2)= -0.27.The redshift zbinaryis largest at φ=π/2.The frequency is blueshifted at φ=-π/2 since the Doppler effect dominates over the gravitational redshift.
The relation between the observed frequency fobsand the mode frequency in the local frame of the NS, f, can be approximated by:
The largest redshift corresponds to fobs(φ=π/2)=0.393f.
4.Conclusions and Discussions
In this paper, we introduced the scenario of a tidal induced starquake for a solid strange star8In fact, since we do not assume any details about the EoS model or mass–radius relation of the compact star, any model that could provide the required shear modulus would be able to explain the observations within our scenario.However, it is unlikely that NSs which is believed to have a superfluid core could accumulate to the required elastic energy budget before a starquake takes place.prior to the merger with a compact companion.As the binary inspirals closer,the tidal field will gradually deform the solid strange star, resulting in the accumulation of the elastic energy.A giant starquake might be triggered when the binary is close enough and the stress exceeds a critical value.This scenario is quite similar to the starquake model of pulsar glitches, in which the elastic energy is accumulated as the star deforms due to the spinning down process.
In particular, we demonstrated that such giant quake before merger could release sufficient energy to explain the precursor observation of GRB211211A.In the sequential quakes model,which we consider only part of the star suffers the starquake,the released energy is still enough at a separation larger than the ISCO radius.Moreover, the torsional mode frequencies are estimated by regarding the entire solid strange star as a homogeneous, isotropic elastic spheroid with uniform density and shear modulus.The result depends on the final shear modulus when starquake happens (i.e., after the failure of the solid structure takes place) and could be consistent with the observation with a reasonable range of the final shear modulus,without contradicting the energy budget calculations.
Although we have obtained sufficient energy budget to account for the total energy release and oscillation frequencies consistent with the QPO frequency of the observation, the mechanism for converting those energy into EM radiation(particularly in the hard X-ray and gamma-ray band) and the way to connect asteroseismology frequency with QPO is more complicated and is often not discussed in details in previous studies of GRB211211A(e.g.,Suvorov et al.2022)and QPOs of soft gamma-ray repeaters(Duncan 1998).Nevertheless,there are simulations indicating that accelerated charged particles in the magnetosphere of an orbiting NS might be capable of producing emissions in the X-ray and even gamma-ray bands(Carrasco &Shibata 2020; Carrasco et al.2021).Meanwhile, stellar oscillation is shown to be related to pulsar activities by affecting the magnetosphere(Lin et al.2015).Future investigations will be needed to connect these ingredients together and to better understand the entire scenario.
Our result favors a BH–NS scenario compared with the BNS case,due to much larger parameter space for the consideration of the energy budget.The BH–NS scenario is also more consistent with the event rates.sGRBs with confirmed precursor observation are quite rare, only as BH–NS binary systems are much fewer compared with BNS systems.We will estimate the event rates in the future and try to verify this argument.
We are expecting to test the model presented in this paper in the future, especially by combining the observations of gravitational and electro-magnetic signals.The LVK-O4 observing run(e.g., Coupechoux et al.2023) would start, and China’s megafacilities, especially the Gravitational wave high-energy Electromagnetic Counterpart All-sky Monitor(GECAM)(Li et al.2020),the Hard X-ray Modulation Telescope (HXMT)(Li et al.2018),as well as the planned Einstein Probe (EP)(Yuan et al.2022),would work.The model we proposed might then be soon falsified, but, conversely, would show its particular reasoning style in the coming years.
Acknowledgments
We thank the Computational Relativistic Astrophysics division in Albert Einstein Institute (Potsdam) for helpful discussions on the kilonova scenario of BH–NS mergers.This work was supported by the National SKA Program of China(2020SKA01201000,2020SKA0120300).E.Z.is supported by the National Natural Science Foundation of China (NSFC)grant No.12203017.Y.G.and L.S.are supported by the NSFC(11975027, 11991053) and the Max Planck Partner Group Program funded by the Max Planck Society.S.X.and Z.Z.are supported by the National Key R&D Program of China(2021YFA0718500), the NSFC (grant No.12273042).X.L.acknowledges the support by the Young Top-notch Talent Cultivation Program of Hubei Province.H.Y.is supported by NSFC grant No.42174059 and G.Y.is supported by NSFC grant No.12247180.S.Y.acknowledges the support from the Chinese Academy of Sciences (grant No.E329A3M1).
ORCID iDs
Lijing Shao https://orcid.org/0000-0002-1334-8853
Garvin Yim https://orcid.org/0000-0001-8548-9535
 Research in Astronomy and Astrophysics2024年2期
Research in Astronomy and Astrophysics2024年2期
- Research in Astronomy and Astrophysics的其它文章
- A Fermi-LAT Study of Globular Cluster Dynamical Evolution in the Milky Way: Millisecond Pulsars as the Probe
- Application of Regularization Methods in the Sky Map Reconstruction of the Tianlai Cylinder Pathfinder Array
- Effect of Cosmic Plasma on the Observation of Supernovae Ia
- Variable Stars in the 50BiN Open Cluster Survey.III.NGC 884
- Free Energy of Anisotropic Strangeon Stars
- Data-driven Simulations of Magnetic Field Evolution in Active Region 11429:Magneto-frictional Method Using PENCIL CODE
