不忘初“型”,方得始終
——例談運(yùn)用雙勾函數(shù)模型解題
2024-04-15 06:41:16江西省鄱陽(yáng)縣第一中學(xué)333100周方旦
中學(xué)數(shù)學(xué)研究(江西) 2024年4期
江西省鄱陽(yáng)縣第一中學(xué) (333100) 周方旦 高 明
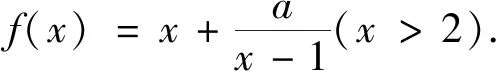
(1)當(dāng)a=2時(shí),求函數(shù)f(x)的最小值;
(2)當(dāng)0 評(píng)注:求解中有同學(xué)會(huì)把該題型與分離變量的問題搞混淆,本題中原函數(shù)的分子為一次函數(shù)而分母為二次函數(shù),注意到這個(gè)特征再將其轉(zhuǎn)化為雙勾函數(shù),從而問題得到解決. 例4 已知x>0,y>0,且4x+2y-xy=0,求2x+y的最小值. 變式已知x>0,y>0,x+3y+xy=9,求x+3y的最小值.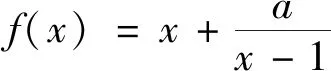
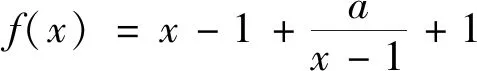

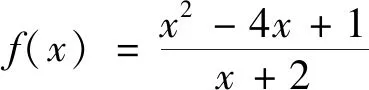
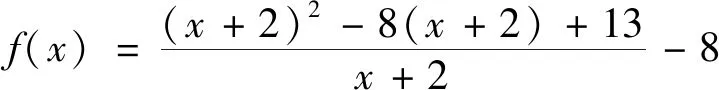
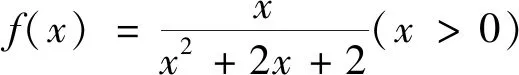
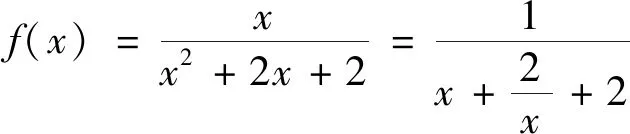
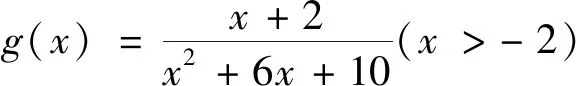
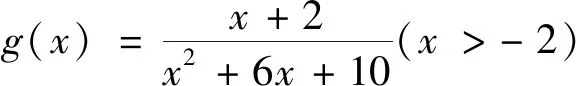
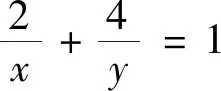
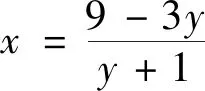
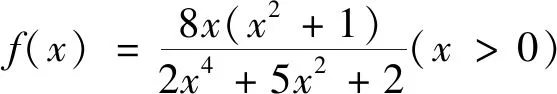

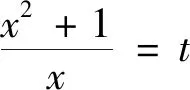
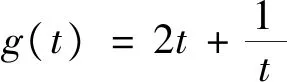
猜你喜歡
江西畜牧獸醫(yī)雜志(2022年1期)2022-04-27 09:29:28
新世紀(jì)智能(數(shù)學(xué)備考)(2021年9期)2021-11-24 01:14:32
江西畜牧獸醫(yī)雜志(2021年3期)2021-08-12 09:58:20
江西畜牧獸醫(yī)雜志(2020年4期)2020-09-12 06:36:26
生態(tài)經(jīng)濟(jì)評(píng)論(2019年1期)2019-12-09 08:38:42
21世紀(jì)商業(yè)評(píng)論(2019年3期)2019-03-26 08:14:00
新世紀(jì)智能(數(shù)學(xué)備考)(2018年9期)2018-11-08 11:07:34
中學(xué)生數(shù)理化·高一版(2018年10期)2018-11-08 11:06:56
理科考試研究·高中(2017年10期)2018-03-07 17:40:07
發(fā)明與創(chuàng)新(2016年6期)2016-08-21 13:49:38

