陽衛(wèi)鋒

(湖南工程學(xué)院數(shù)理系,湖南湘潭 411104)

牛頓變換Julia集的對(duì)稱性

陽衛(wèi)鋒

(湖南工程學(xué)院數(shù)理系,湖南湘潭 411104)

主要討論多項(xiàng)式的牛頓變換Julia集的對(duì)稱性問題.利用復(fù)動(dòng)力系統(tǒng)理論,證明了多項(xiàng)式P(z)的Julia集的對(duì)稱群是其牛頓變換NP(z)的Julia集的對(duì)稱群的子群.獲得了Julia集為一水平直線的充分必要條件.

牛頓變換;Julia集;對(duì)稱群;共形歐氏變換

1 引言

Julia集的性質(zhì)是復(fù)動(dòng)力系統(tǒng)研究的主要部分,而Julia集的幾何對(duì)稱性問題是其中一個(gè)重要課題.文[7]研究了多項(xiàng)式函數(shù)的Julia集的對(duì)稱性,文[8]研究了臨界有限的有理函數(shù)的Julia集的對(duì)稱性,文[9]分析了有理函數(shù)的Julia集具有平移不變性的情形.

定義1.1設(shè)R是一個(gè)有理函數(shù),R的Julia集的對(duì)稱群Σ(R)為保持J(R)不變的共形歐氏變換σ構(gòu)成的群,即Σ(R)={σ∈ε:σ(J)=J},其中ε={σ:σ(z)=az+b,|a|=1}.

當(dāng)R是一多項(xiàng)式函數(shù)

其首項(xiàng)系數(shù)An=1,An?1=0.

文[7]證明了下列兩個(gè)定理

定理A設(shè)多項(xiàng)式P(z)的次數(shù)deg(P)≥2.則對(duì)稱群Σ(P)是由以P(z)的形心為中心的旋轉(zhuǎn)變換構(gòu)成的.如果P(z)是標(biāo)準(zhǔn)型的,而且Σ(P)是有限的,則Σ(P)的階為使得P(z)可表示成P(z)=zrQ(zm)的最大整數(shù)m,其中Q(z)為一多項(xiàng)式.

定理B設(shè)多項(xiàng)式P(z)的次數(shù)deg(P)≥2.如果對(duì)稱群Σ(P)是無限的,那么J(P)是一個(gè)圓周,并且P(z)共軛于zn,其中n=deg(P).

由定理A知多項(xiàng)式的Julia集的對(duì)稱群只由旋轉(zhuǎn)變換構(gòu)成,而有理函數(shù)的Julia集的對(duì)稱群中可以存在平移變換.文[9]得到下列重要定理

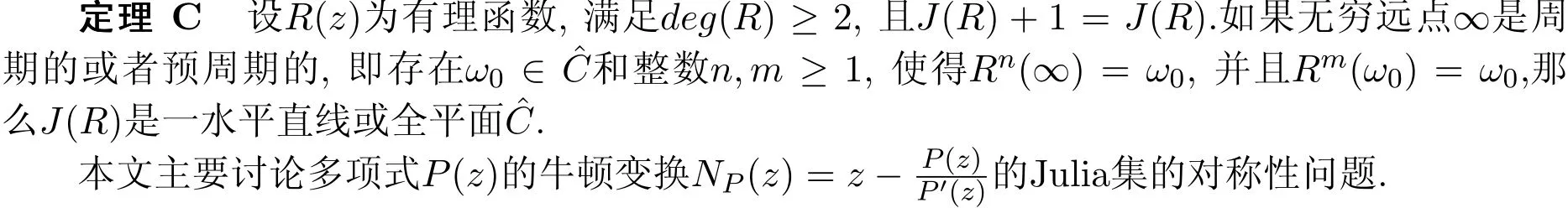
2 牛頓變換Julia集的對(duì)稱性

由于多項(xiàng)式P(z)與其標(biāo)準(zhǔn)型多項(xiàng)式是共形共軛,所以具有相同的動(dòng)力學(xué)性質(zhì),然而各自的牛頓變換之間不一定是共形共軛的,從而可能具有不同的動(dòng)力學(xué)性質(zhì).

易知n次多項(xiàng)式P(z)有至多n個(gè)標(biāo)準(zhǔn)型多項(xiàng)式與之對(duì)應(yīng),我們將P(z)的標(biāo)準(zhǔn)型多項(xiàng)式均記為PN(z).

即S?NP?S?1(z)=NPN(z),因此NP(z)與NPN(z)是共形共軛的.

以上表明牛頓變換對(duì)多項(xiàng)式不是保共軛.但是下面的定理表明,在一定程度上,牛頓變換對(duì)Julia集是保對(duì)稱的.

顯然有σ?NP?σ?1(z)=NP(z),故σJ(NP)=J(NP),從而可知σ∈Σ(NP).因此可得Σ(P)?Σ(NP).

定理3設(shè)多項(xiàng)式P(z)的次數(shù)deg(P)≥2,NP(z)是對(duì)應(yīng)的牛頓變換,則J(NP)的對(duì)稱群Σ(NP)包含平移變換σ(z)=z+1當(dāng)且僅當(dāng)J(NP)是一水平直線.

證明當(dāng)J(NP)是一水平直線時(shí),顯然對(duì)稱群Σ(NP)包含平移變換σ(z)=z+1.

另一方面,若Σ(NP)包含平移變換σ(z)=z+1,則NP(z)滿足定理C的條件.故J(NP)是一水平直線或全平面.然而多項(xiàng)式P(z)次數(shù)至少為2,至少有一個(gè)零點(diǎn),從而NP(z)有一個(gè)吸性不動(dòng)點(diǎn),因而F(NP)/=?,J(NP)/=?C.所以J(NP)是一水平直線.

那么,什么情況下牛頓變換的Julia集是一條直線?下面的定理回答了這個(gè)問題

定理4當(dāng)且僅當(dāng)多項(xiàng)式P(z)=c(z?a)n(z?b)n(n≥1,a/=b)時(shí),J(NP)是一條直線.

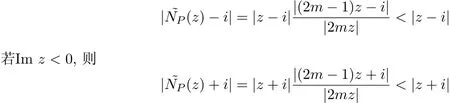
[1]Beardon A F.Iteration of Rational Functions[M].Berlin:Springer-Verlag,1991.

[2]Milnor J.Dynamics in One Complex Variable[M].3rd ed.Princeton:Princeton University Press,2006.

[3]Carleson L,Gamelin T.Complex Dynamics[M].Berlin:Springer-Verlag,1993.

[4]周維民,任福堯.有理函數(shù)系隨機(jī)迭代系統(tǒng)的Julia集[J].科學(xué)通報(bào),1991,36(21):1604-1604.

[5]龔志民,任福堯.關(guān)于隨機(jī)動(dòng)力系統(tǒng)的Fatou-Julia猜測(cè)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),1996,12(2):23-27.

[6]陽衛(wèi)鋒,李穎,龔志民.有限個(gè)有理函數(shù)的隨機(jī)復(fù)動(dòng)力系統(tǒng)的Julia集[J].數(shù)學(xué)進(jìn)展,2004,33(4):447-452.

[7]Beardon A F.Symmetries of Julia sets[J].Bull.London Math.Soc.,1990,22:575-582.

[8]Levin G.Symmetries on a Julia set[J].Adv.in Sov.Math.,1991,3:131-141.

[9]Boyd D.Translation invariant Julia sets[J].Proc.Amer.Math.Soc.,2000,128:803-812.

Symmetries of the Julia sets for Newton’s method

YANG Wei-feng
(Department of Mathematics Physics,Hunan Institute of Engineering,Xiangtan411104,China)

The symmetries of Julia sets of Newton’s method is investigated.Using the theory of complex Dynamical system,it is shown that the group of symmetries of Julia sets of polynomial is a subgroup of that of the corresponding Newton’s method.A necessary and sufficient condition for Julia sets of Newton’s method to be a horizontal line is arrived.

Newton’s method,Julia set,group of symmetries,conformal Euclidean isometry

O174.5

A

1008-5513(2009)03-0530-04

2008-09-28.

湖南省教育廳項(xiàng)目(06C245).

陽衛(wèi)鋒(1977-),碩士,研究方向：復(fù)解析動(dòng)力系統(tǒng).

2000MSC:30D05