(徐州師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,江蘇 徐州 221116)

0 引言

隨機(jī)偏微分方程是偏微分方程或Banach空間中常微分方程的隨機(jī)擾動(dòng),對(duì)其可積性與解的研究越來(lái)越受到眾多數(shù)學(xué)家和物理學(xué)家的重視,而隨機(jī)波方程是隨機(jī)偏微分方程的一個(gè)重要研究課題.帶隨機(jī)擾動(dòng)的可積系統(tǒng)的研究始于1983年,M.Wadati利用反散射方法構(gòu)造非線(xiàn)性隨機(jī)KdV方程的精確解[1].XIE[2,3]首先在Wick型隨機(jī)波方程這一領(lǐng)域開(kāi)展工作,并取得了大量研究成果.本文在此基礎(chǔ)上利用白噪聲分析理論,截?cái)嗾归_(kāi)方法[4]研究了(2+1)維Wick型隨機(jī)ANNV孤子系統(tǒng):

(1)

其中?是Kondratiev分布空間(S)-1上的Wick型積,A(t),B(t),Γ(t)和D(t)均為(S)-1值白噪聲泛函,且A(t)?D(t)≠0,B(t)≠-Γ(t).

式(1)的變系數(shù)ANNV孤子系統(tǒng)為:

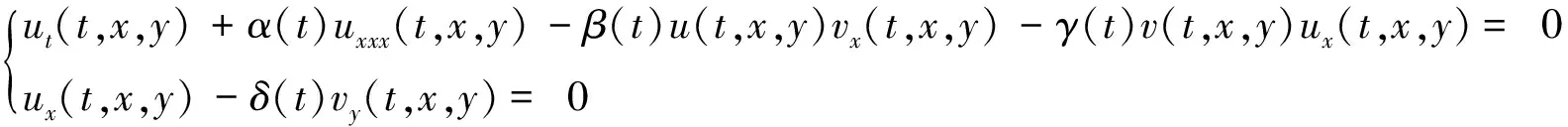
(2)

其中α(t),β(t),γ(t),δ(t)為t的函數(shù),且α(t)δ(t)≠0,β(t)≠-γ(t).

式(2)源于(2+1)維非對(duì)稱(chēng)Nizhnik-Novikov-Veselov(ANNV)孤子系統(tǒng):

(3)

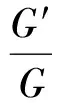
1 (2+1)維Wick型隨機(jī)ANNV系統(tǒng)的解

為了得到隨機(jī)孤子系統(tǒng)的解,由文獻(xiàn)[2]中定理2.1,當(dāng)d=2時(shí),對(duì)(1)進(jìn)行Hermite變換,得到下面:

(4)

這里z=(z1,z2,…)∈CN是向量參數(shù).簡(jiǎn)記

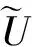
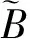
則(4)表示為:

(5)

其中α(t,z),β(t,z),γ(t,z),δ(t,z)是關(guān)于t,z的函數(shù).令

u(t,x,y,z)=u(ξ),v(t,x,y,z)=v(ξ)

(6)

其中ξ=k(t,z)x+l(t,z)y+s(t,z)+c0,在這里k(t,z),l(t,z),s(t,z)是關(guān)于t,z的待定函數(shù),且k(t,z)l(t,z)≠0,c0是任意常數(shù).

將(6)式代入(5)有

k(t,z)u′(ξ)-δ(t,z)l(t,z)v′(ξ)=0,

對(duì)其積分一次并令積分常數(shù)為零得

從而有常微分方程

(xkt(t,z)+ylt(t,z)+st(t,z))δ(t,z)l(t,z)u′(ξ)+

α(t,z)δ(t,z)l(t,z)k3(t,z)u?(ξ)-k2(t,z)(β(t,z)+γ(t,z))u(ξ)u′(ξ)=0

(7)

2(xkt(t,z)+ylt(t,z)+st(t,z))δ(t,z)l(t,z)u(ξ)+2α(t,z)δ(t,z)l(t,z)k3(t,z)·

u″(ξ)-k2(t,z)(β(t,z)+γ(t,z))u2(ξ)=0

(8)

設(shè)(8)有如下形式的解

(9)

其中ai(t,z)(i=0,1,…,n)是關(guān)于t,z的待定函數(shù),F(ξ)滿(mǎn)足:

(10)

利用齊次平衡法平衡(8)中最高階偏導(dǎo)項(xiàng)與非線(xiàn)性項(xiàng)得n=2,于是(9)式可寫(xiě)成:

u(ξ)=a0(t,z)+a1(t,z)F(ξ)+a2(t,z)F2(ξ)

(11)

注意到

u′(ξ)=a1(t,z)F′(ξ)+2a2(t,z)F(ξ)F′(ξ)

(12)

u″(ξ)=a1(t,z)F″(ξ)+2a2(t,z)F′2(ξ)+2a2(t,z)F(ξ)F″(ξ)

(13)

將(10)～(13)式代入方程(8),由于含有F(ξ)的各次項(xiàng)線(xiàn)性無(wú)關(guān),從而可得:

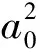
F(ξ):a1(t,z)k3(t,z)α(t,z)l(t,z)δ(t,z)-a0(t,z)a1(t,z)k2(t,z)(β(t,z)+γ(t,z))+

a1(t,z)l(t,z)δ(t,z)st(t,z)=0,

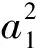
2a0(t,z)a2(t,z))(β(t,z)+γ(t,z))-2a2(t,z)l(t,z)δ(t,z)st(t,z)=0,

F3(ξ):(2a1(t,z)-10a2(t,z))k(t,z)α(t,z)l(t,z)δ(t,z)-a1(t,z)a2(t,z)(β(t,z)+

γ(t,z))=0,

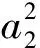
xF2(ξ):a2(t,z)kt(t,z)=0,yF2(ξ):a2(t,z)lt(t,z)=0.

從上述可以發(fā)現(xiàn)kt(t,z)=lt(t,z)=0,從而記k(z)=k(t,z),l(z)=l(t,z),通過(guò)Mathematic軟件,再利用(11)式得:

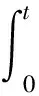
此情形(5)的截?cái)嗾归_(kāi)解為:

(14)

其中

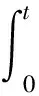
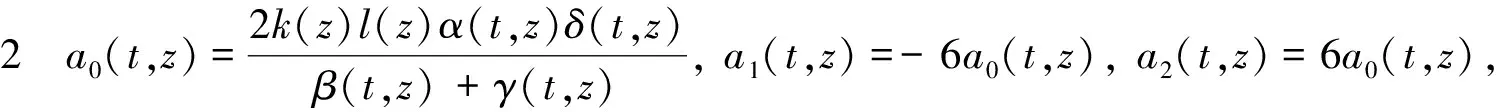
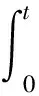
此時(shí)(5)的截?cái)嗾归_(kāi)解為:

(15)

其中

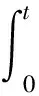
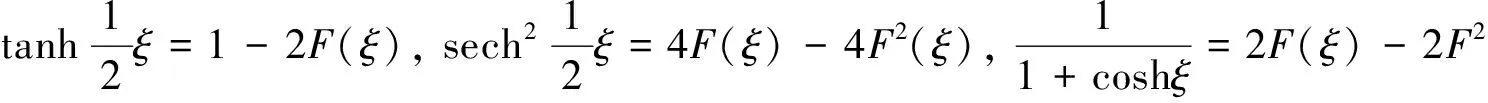
(16)

其中

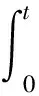
(17)

由(5)的解,存在有界開(kāi)集G?R+×R2及q>0,r>0,u(t,x,y,z),ut(t,x,y,z),ux(t,x,y,z),v(t,x,y,z),vx(t,x,y,z),vy(t,x,y,z)及uxxx(t,x,y,z)對(duì)(t,x,y,z)∈G×Kq(r)一致有界,對(duì)(t,x,y)∈G連續(xù),其中z∈Kq(r).由文獻(xiàn)[2]定理2.1知,存在U(t,x,y),V(t,x,y)∈(S)-1,使得u(t,x,y,z)=HU(t,x,y)(z),v(t,x,y,z)=HV(t,x,y)(z),且U(t,x,y),V(t,x,y)是(1)在空間(S)-1上的強(qiáng)解.

因此可得(1)的白噪聲泛函解,即有如下結(jié)果.

定理1 設(shè)U(t,x,y),V(t,x,y)分別是u(t,x,y,z),v(t,x,y,z)的Hermite逆變換,且滿(mǎn)足隨機(jī)偏微分(1),令N(t)=kA(t)?(B(t)+Γ(t))?(-1),則有U(t,x,y),V(t,x,y)白噪聲泛函的具體表示:

注: 如果在沒(méi)有隨機(jī)干擾的環(huán)境下將所有的Wick積變成普通積,那么可以得到(2+1)維變系數(shù)ANNV系統(tǒng)(2)的顯式精確解.

2 小結(jié)

1)Wick-型泛函一般很難計(jì)算,然而可以給出一些非Wick-型的白噪聲泛函作為隨機(jī)偏微分方程的特殊解,如文獻(xiàn)[8]中的例子.Wiener白噪聲空間與Possion白噪聲空間之間存在一個(gè)酉映射,通過(guò)這個(gè)單一映射可以由Gaussian SPDEs的解得到Possion SPDEs的解[9],從而可以給出(1)的Possion白噪聲泛函解.

2)求解隨機(jī)偏微分方程是一件較困難的事情,而截?cái)嗾归_(kāi)方法是一種非常簡(jiǎn)便有效的工具,可以用來(lái)求得一大類(lèi)Wick-型隨機(jī)可積系統(tǒng)的白噪聲泛函解,本文中得到了(2+1)維隨機(jī)非對(duì)稱(chēng)Nizhnik-Novikov-Veselov孤子系統(tǒng)的解,對(duì)于更高維的情形也可以做類(lèi)似討論,這里不再論述.

[1]Wadati M.Stochastic Korteweg-de Vries equation[J].J Phys Soc Jpn,1983,52: 2642-2648.

[2]Xie Y C.Exact solutions for stochastic KdV equations [J].Phys Lett A,2003,310(2):161-167.

[3]Xie Y C.Exact solutions for stochastic mKdV equations[J].Chaos Solitons &Fractals,2004,20(2):337-342.

[4]張解放,陳躍芳.截?cái)嗾归_(kāi)方法和廣義變系數(shù)KdV方程新的精確類(lèi)孤子解[J].物理學(xué)報(bào),2001,50(9):1648-1650.

[5]Boiti M,Leon J P,Manna M,et al.On the spectral transform of a KdV equation in two spatial dimensions[J].Inver Prob,1986(2):271-279.

[6]李幫慶,馬玉蘭.(G′/G)展開(kāi)法和(2+1)維非對(duì)稱(chēng)Nizhnik-Novikov-Veselov系統(tǒng)的新精確解[J].物理學(xué)報(bào),2009,58(7):4373-4378.

[7]周振春,馬松華,方建平,等.(2+1)維孤子系統(tǒng)的多孤子解和分形結(jié)構(gòu)[J].物理學(xué)報(bào),2010,59(11):7540-7545.

[8]Chen B.White noise functional solutions of Wick-type stochastic NLS equations[J].Mathematica Applicata,2010,23(2): 292-298.

[9]Benth F E,Gjerde J.A remark on the equivalence between Possion and Gaussian stochastic partial differential equations[J].Potential Analysis,1998,8(2):179-193.