王積建

(浙江工貿(mào)職業(yè)技術(shù)學(xué)院基礎(chǔ)部,浙江溫州 325003)

多元函數(shù)有無窮多個(gè)駐點(diǎn)時(shí)的極值問題

王積建

(浙江工貿(mào)職業(yè)技術(shù)學(xué)院基礎(chǔ)部,浙江溫州 325003)

討論了二元函數(shù)和三元函數(shù)在有無窮多個(gè)駐點(diǎn)時(shí)的極值的判定方法,并進(jìn)一步介紹了該判定方法在證明不等式方面的應(yīng)用.

多元函數(shù);駐點(diǎn);極值;偏導(dǎo)數(shù)

多元函數(shù)在一般情況下求極值時(shí),是先找其駐點(diǎn),即令所有一階偏導(dǎo)數(shù)為零,求解方程組得到駐點(diǎn),進(jìn)一步驗(yàn)證駐點(diǎn)是不是極值點(diǎn).我們的問題是,在一定條件下,函數(shù)有無窮多個(gè)駐點(diǎn),它們位于一條曲線上,極值問題怎樣處理.例如,函數(shù)f(x,y)=x2+y2-2xy,顯然對(duì)任何實(shí)數(shù)x,y,f(x,y)有極小值0.但根據(jù)二元函數(shù)求極值的方法有

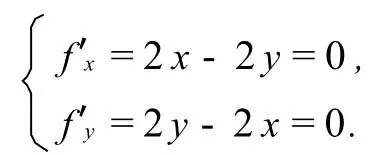
即直線y=x上的所有點(diǎn)都是f(x,y)的駐點(diǎn),在每一個(gè)駐點(diǎn)上-fxxfyy=0均成立,這說明用現(xiàn)有的方法不能判定此類情況.為了方便,我們把滿足多元函數(shù)所有偏導(dǎo)數(shù)為零的無窮多個(gè)點(diǎn)所在的曲線稱為該多元函數(shù)的駐線.如y=x為f(x,y)=x2+y2-2x y的駐線,y=±為f(x,y)=sin(x y)的駐線.

假設(shè)f(x,y)具有二階連續(xù)偏導(dǎo)數(shù),如果f(x,y)有駐線,即方程組

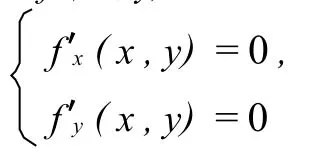
有曲線解,設(shè)為x=φ(t),y=ψ(t),進(jìn)一步設(shè)此駐線為光滑曲線,如果簡(jiǎn)記二階偏導(dǎo)數(shù)在(φ(t),ψ(t))的值為fij(i,j=1,2),則有

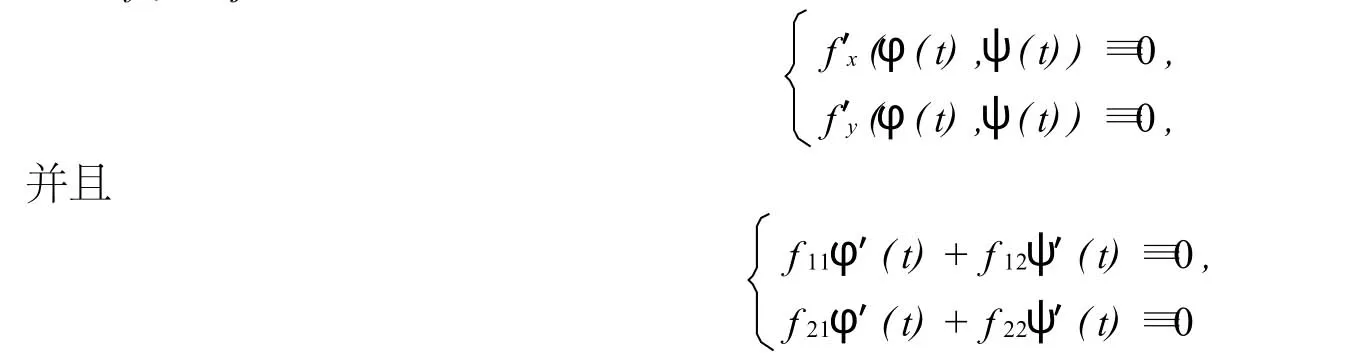
對(duì)所有的t成立.這是關(guān)于φ′(t),ψ′(t)的線性方程組,因而有非零解的充要條件為

在駐線上處處成立.

同樣地,設(shè)三元函數(shù)F(x,y,z)具有二階連續(xù)偏導(dǎo)數(shù),如果F(x,y,z)有駐線,設(shè)x=φ1(t), y=φ2(t),z=φ3(t)為F(x,y,z)的光滑駐線,如果簡(jiǎn)記二階偏導(dǎo)數(shù)在(φ1(t),φ2(t),φ3(t))的值為Fij(i,j=1,2,3),則有

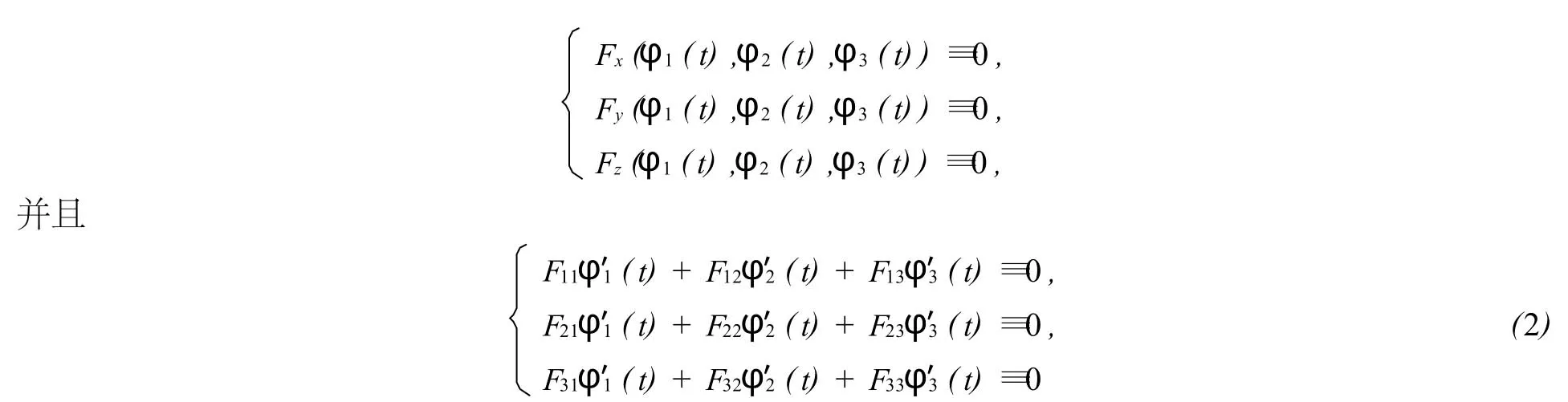
對(duì)所有的t成立.這是關(guān)于φ′1(t),φ′2(t),φ′3(t)的線性方程組,因而有非零解的充要條件為

在駐線上處處成立.總之我們有以下定理.

定理1 如果具有二階連續(xù)偏導(dǎo)數(shù)的函數(shù)f(x,y)有光滑駐線:x=φ(t),y=ψ(t),則⑴式成立,其中fij(i,j=1,2)為f(x,y)的二階偏導(dǎo)數(shù)在(φ(t),ψ(t))的值.如果具有二階連續(xù)偏導(dǎo)數(shù)的函數(shù)F(x,y,z)有光滑駐線:x=φ1(t),y=φ2(t),z=φ3(t),則(3)式成立,其中Fij(i,j=1,2,3)為F(x,y,z)的二階偏導(dǎo)數(shù)在(φ1(t),φ2(t),φ3(t))的值.

例1 考慮三元函數(shù)

一般情況下,二元函數(shù)f(x,y)在駐點(diǎn)處成立f2xy-fxxfyy＜0時(shí)有極值.而三元函數(shù)在駐點(diǎn)處有極值的充分條件為矩陣

在駐點(diǎn)處為正定的.顯然例1中的函數(shù)H和K均不滿足矩陣(4)為正定.下面的兩個(gè)定理來分別解決二元函數(shù)和三元函數(shù)有駐線時(shí)取極值的條件.

定理2 設(shè)具有二階連續(xù)偏導(dǎo)數(shù)的函數(shù)f(x,y)有光滑的駐線C:x=φ(t),y=ψ(t),如果對(duì)所有的t,

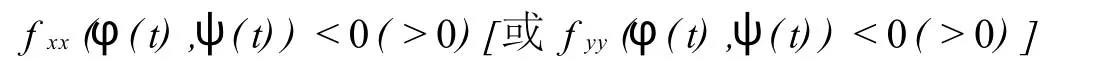
成立,則f(x,y)在C上取得極大(小)值.

證在平面內(nèi)過C上任一點(diǎn)(φ(t0),ψ(t0))及其附近一點(diǎn)(x0,y0)引一條直線

其中λ為任意常數(shù).在空間內(nèi)⑸式為一平行于z軸的平面,它與z=f(x,y)的交線的參數(shù)方程為

時(shí)取極大(小)值.

證過三維空間內(nèi)曲線C上任一點(diǎn)(φ1(t0),φ2(t0),φ3(t0))任意引一平面π:

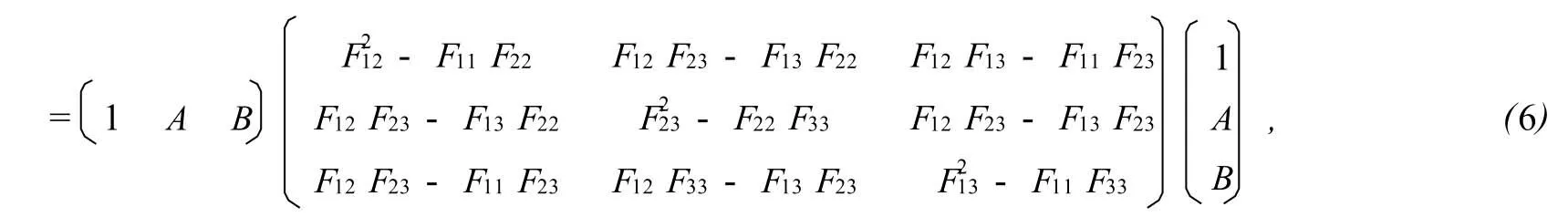
其中Fij(i,j=1,2,3)表示F的二階偏導(dǎo)數(shù)在(φ1(t0),φ2(t0))處的值.由于(2)對(duì)t=t0成立,以及φ′1(t0),φ′2(t0),φ′3(t0)不同時(shí)為零,不妨設(shè)φ′3(t0)≠0,則根據(jù)(2)有

由定理3容易得到例1中的函數(shù)H=x2+y2+z2-xy-yz-x x有極小值0;函數(shù)K在C1上無極值,在C2上有極大值;在C3上有極小值.

例2 證明下列不等式

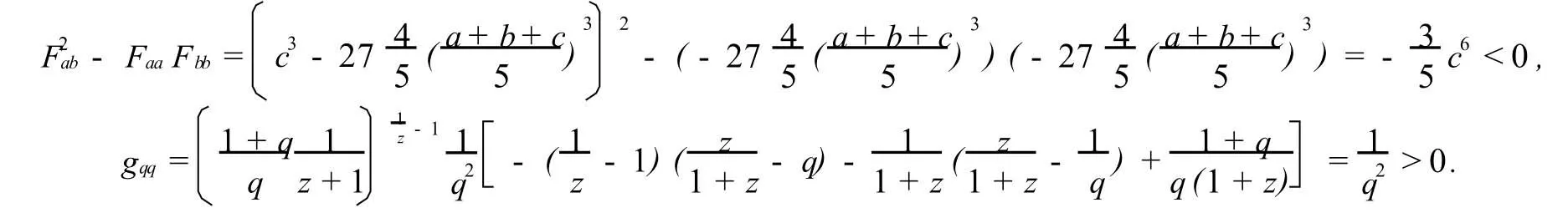
由定理2,3知f,F,g在其駐線上分別取極小值,極大值和極小值,從而不等式(7),(8),(9)成立.

[1] 陳治中.線性代數(shù)[M].北京：科學(xué)出版社,2001：182-183.

[2] 朱培勇,黃家琳.數(shù)學(xué)分析(下冊(cè))[M].成都：四川大學(xué)出版社,2002：91-93.

[3] 北京大學(xué)數(shù)學(xué)力學(xué)系.高等代數(shù)[M].北京：人民教育出版社,1978.

The Extremum Problems of Function of Several Variables When They Have Limitless Stationary Points

WA N G J i-jian
(Zhejiang Industrial&Trade Polytechnic,Wenzhou,Zhejiang 325003,China)

The article elaborates the judging methods of the extremum when bivariables and tri-variables have limitless stationary points.It gives further introduction about the application of such judging merhods to prove inequalities.

function of several variables;stationary point;extremum;partial derivatives

O172.1

C

1672-1454(2011)03-0189-05

2008-07-14